雷达天线是雷达系统的重要组成部件，其在服役过程中面临着复杂严酷的风载荷。天线特征尺寸的多样性、服役工况的复杂性，极大地制约了其风载荷预示的准确性和时效性。准确预示雷达天线阵面所承受的风载荷不仅是探究雷达天线阵面强度和刚度的重要基础，也是指导雷达天线阵面总体设计、结构设计，以及地面试验的关键依据。因此，开展雷达天线阵面的风载分析具有重要的理论研究意义和工程应用价值。
目前确定风载的主要手段有：数值仿真、理论分析、现场测量和风洞试验等[1-2]。近年来，随着计算机技术的飞速发展以及数值计算理论的不断成熟，结构风载研究越来越多地使用数值模拟的方法，其中计算流体动力学(Computational Fluid Dynamics，CFD)在结构风工程中被广泛使用。在雷达阵面风载荷CFD计算中，仅能针对特定尺寸结构、特定工况，通用性较差，且计算耗时较长。而基于响应面的代理模型是一种可兼顾计算精度和计算效率的数学模型，该方法能将结构几何特征尺寸、工况等作为输入变量因素，对不同工况下不同特征尺寸的结构进行风载分析，具有一定的通用性。
多项式响应面模型凭借形式简单、计算量小等优点被广泛使用[3]。Knill等[4]利用不完全多项式响应面模型来预测高速民用飞行器超音速阻力的欧拉解；Unal等[5]在解决翼身融合航天器的局部优化问题时使用了响应面代理模型；Fleming等[6]通过响应面方程拟合了多种运载火箭的最大有效运载能力；陈力波等[7]提出了一种基于改进响应面方法的公路简支梁桥易损性模型构建流程；在航空航天、土木工程等领域，响应面模型常被应用于有限元模型修正，避免了多次迭代，极大地提高了修正效率[8-11]；而在机械、车辆等领域，响应面模型常被用于对结构进行优化设计研究[12-16]。响应面方法需要通过试验设计采集一定数量的样本，然后构造合适的代理模型。而代理模型取代实际模型进行计算的精度，不仅取决于代理模型形式的选择，更依赖于试验样本集的数量。对雷达阵面结构进行CFD数值仿真过程较为繁复，在构建响应面模型时，对每一个样本进行“几何建模-网格划分-CFD计算”将会耗费大量人力，亟待发展一种集成的自动化仿真平台，实现几何建模、有限元建模、CFD分析全流程的自动化，使雷达阵面风载响应面模型的构建更有效率。
多项式响应面模型是一种使用较为广泛的数学模型，但尚未有学者将其运用于风载分析。传统的CFD分析需要对阵面进行精细的气动外形建模，流场网格划分，CFD数值计算求解，工作量较大，并且只能针对特定结构、特定工况，通用性较差。本文提出一种基于多项式响应面代理模型的高效风载分析方法，该方法可在保证精度的同时显著提高计算效率。在进行风载分析时，以雷达天线阵面的特征尺寸、阵面倾角、风速、风向角为变量因素，以雷达阵面的平均面压为输出响应，构造雷达阵面风压的不完全4阶多项式响应面模型，具有形式简单、计算量小、通用性强的显著优点，可极大提高风载分析效率。同时，在构建天线阵面的气动载荷模型时，发展一种集成的自动化仿真平台，实现对样本库计算的全流程自动化，可极大提高响应面模型的构建效率。
1 雷达天线阵面风载荷数值计算
大部分雷达天线的工作环境均处在大气边界层中，故本文仅研究雷达天线在大气边界层中的风场。典型车载雷达天线结构如图1所示。
图1 雷达天线示意图
Fig.1 Radar antenna panel
本文研究的空气在大气边界层中的流动属于湍流，为低速、不可压缩的粘性牛顿流体，其密度不随时间和空间变化[1]。粘性不可压流体流动的基本方程包括质量守恒方程(又称连续性方程)和动量守恒方程( Navier-Stokes方程)，在直角坐标系中的表示形式分别如式(1)和式(2)所示：
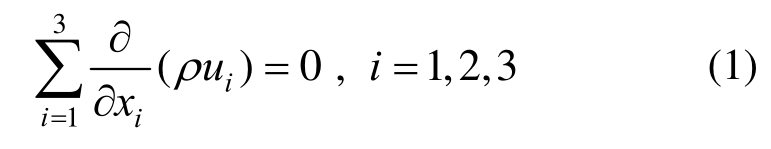
式中：ρ为空气密度；ui分别为在直角坐标x(x1)、y(x2)、z(x3)方向的流体速度分量。
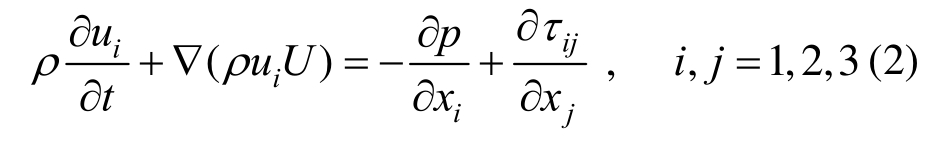
式中：U=(u1, u2, u3)；p为流体微元上的压力；τij为微元体表面上粘性应力τ的分量。
将湍流运动视作由平均流动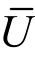
和脉动流动U′叠加而成，即：
将式(3)分别代入式(1)和式(2)，并对时间取平均，得到Reynolds时均方程[17]，表达式如下：
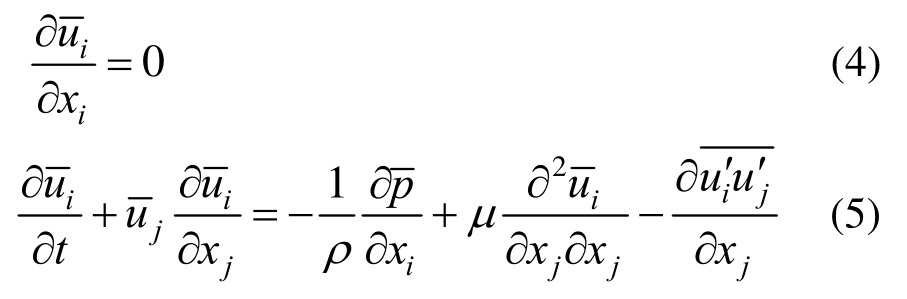
根据对湍流应力作出的假定或处理方式不同，较为常用的有Reynolds应力模型和涡粘模型。其中，两方程涡粘模型已在工程实际中被广泛采用。对于强旋流或有弯曲壁面的流动，采用标准k-ε模型会出现一定的失真；而雷达天线背风面存在一系列的漩涡，为此，需将标准k-ε模型进行改进。而RNG k-ε (renormalization group k-ε)模型对流线弯曲程度较大的流动有较好的模拟效果，故采用RNG k-ε模型对雷达阵面进行CFD数值计算。
现将车载天线结构简化为一平板，尺寸与实际雷达天线阵面模型相同，天线尺寸12 m×12 m×0.6 m，面板倾角30°，计算域大小为300 m×300 m×900 m，面板置于距速度入口边界1/3处，天线面板几何模型与计算域分别如图2(a)、图2(b)所示。
图2 天线几何结构与流场计算区域
Fig.2 Geometric model of antenna and computation domain
流体网格的类型和网格的数量对计算结果的准确性有较大的影响，非结构网格具有很好的灵活性和适应性，易于进行网格自适应[18]，故采用非结构网格对其周围流体进行网格划分。网格划分剖面如图3所示。
图3 计算域网格纵剖面示意图
Fig.3 Mesh of computation domain
CFD计算时，流域入口边界采用速度入口边界条件，出口边界采用完全发展出流边界条件，计算域四周采用对称边界条件，风速35 m/s，计算得到的天线阵面压力云图与壁面附近的速度矢量图分别如图4和图5所示。
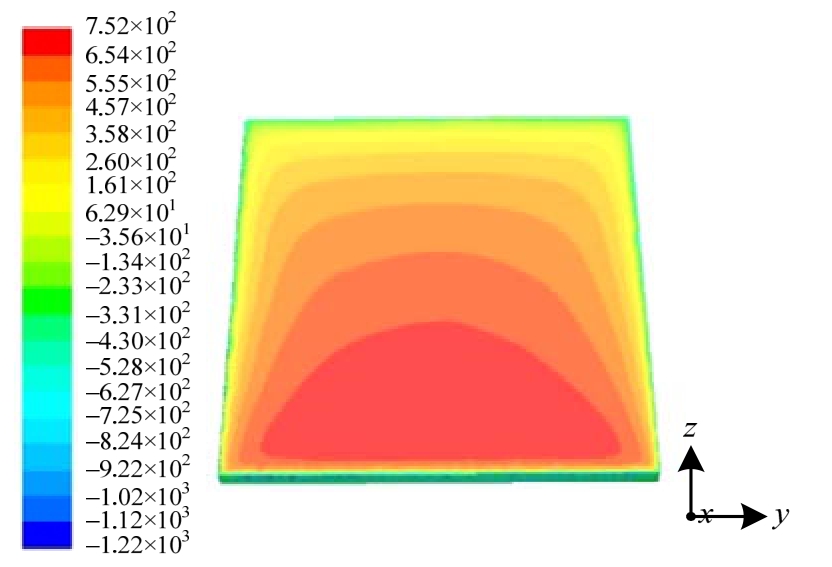
图4 天线迎风面风压云图
Fig.4 Pressure contour of the windward side
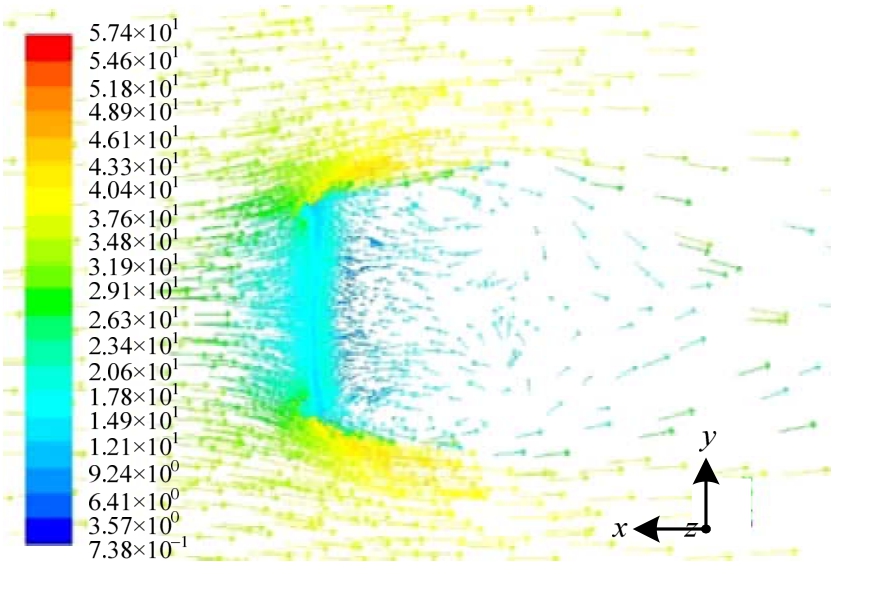
图5 流场水平剖面速度分布
Fig.5 Horizontal velocity distribution
由图4和图5分析可知：1) 阵面迎风面受到的风载在大部分区域为正压；2) 由于阵面倾角的存在，阵面风压自底部向上递减，在阵面边缘风压最低，并出现负压；3) 由于壁面的阻碍，气体流速在靠近壁面时迅速降低；4) 在天线的边缘出现了流动分离现象，气体在天线背风面形成较明显的回流区。
2 雷达天线风压响应面模型的构建
2.1 总体思路
雷达天线处在完全开放的流动风场中时，天线阵面会面临不同姿态、面临不同方向的风载，并在天线支座处产生风致俯仰力矩与风致扭转力矩。为了模拟该力矩效果，并综合考虑构建响应面模型时的计算量与模型的复杂程度，将矩形天线阵面划分为对称的4个区域，如图6所示。若关注天线阵面的局部区域的压力变化情况，或天线表面压力分布梯度较大时，可将天线阵面划分为更多个区域。对于每一个区域，平均面压的压力中心为该区域的几何中心，不同区域间的压力差能够对阵面轴线产生力矩的作用。
图6 天线划分示意图
Fig.6 Division of antenna
针对雷达阵面开展不同姿态下的风载荷分析时，若对各个工况进行分析，需要逐个建模、划分网格、CFD分析，计算量大且效率低。为了兼顾计算精度和成本，采用代理模型是一种有效的解决途径。其思路是：在设计域内通过试验设计方法选取一定数量的设计点，并采用CFD高精度分析获取设计点性能的样本数据库；然后利用样本数据构造代理模型，并验证其准确性。
为了得到具有一定通用性的多项式响应面模型，选取雷达天线阵面的5个典型设计参数：天线阵面的长度、宽度、倾角、来流风速、风向角。对于设计参数所构成的设计空间内的变量，首先需要使用试验设计(Design of Experiments，DOE)方法构造样本的设计矩阵以减小响应面模型多项式拟合时的噪声，改善设计空间表述[19]。优化拉丁超立方法是一种常用的试验设计方法，该方法是在拉丁超立方抽样的基础上做了一定的改进，使得样本空间中的各个样本分布尽可能地均匀，从而保证构建的近似模型在整个设计空间的近似精度[20]。本文采用优化拉丁超立方法构造样本的设计矩阵，并选取62个样本点进行计算。
在构建响应面模型的过程中，对设计矩阵内每一个样本点，需要进行几何建模、流场网格划分、CFD数值计算才能得到其对应的输出响应。如果对每一个样本均进行逐个分析，工作量巨大，为此本文借助iSIGHT软件，通过对CAD、CFD软件进行数据集成和过程集成，实现了整个流程的自动化。具体的响应面模型构建流程如图7所示。
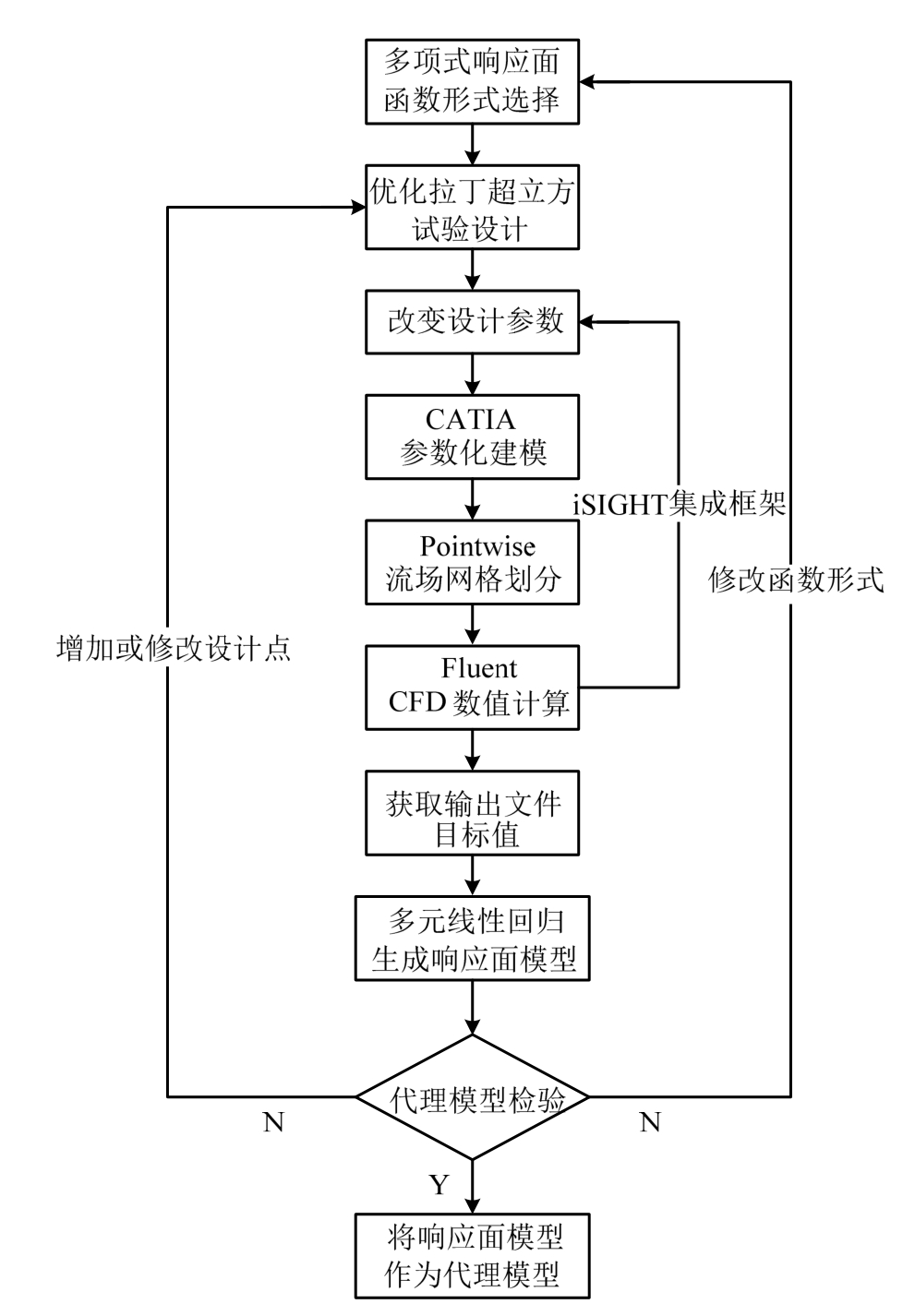
图7 响应面模型构建流程
Fig.7 Flowchart of RSM model construction
2.2 4阶不完全多项式风载响应面模型构建
多项式响应面代理模型凭借形式简单、计算量小，且能有效过滤数值噪声[3]等优点，在工程中被广泛使用，其一般表达式为：
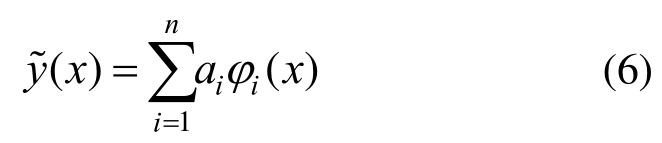
式中：n代表多项式基函数ϕi(x )的个数；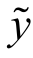
(x)为预测的响应；ai为待求解的系数。
低阶多项式函数常用于拟合线性问题，高阶多项式函数则主要用于拟合非线性程度较高的输入变量与输出响应间的关系。本文所研究问题的设计变量之间独立性较强，响应与输入变量之间的关系较为复杂，因此采用非线性拟合精确度更高的不完全4阶多项式作为响应面近似函数。典型的4阶多项式基函数项表达式为：
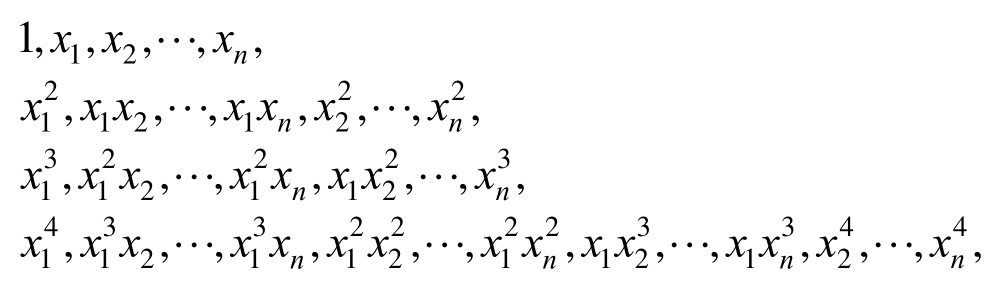
利用最小二乘法，可得未知系数矩阵为：
式中：
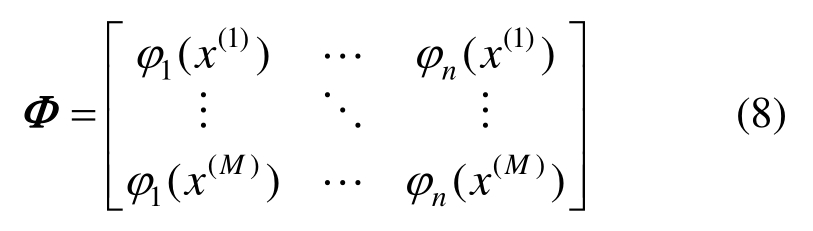
式中，M为采样点数目。
由于使用过多的基函数项可能导致过拟合，反而降低近似函数的预测精度，为了减少基函数的数目，采用不完全4阶多项式响应面模型，其函数形式为：
式中：xi为设计因素；n为因素个数；a0、ai、aij、aii、aiii、aiiii，为不完全4阶多项式待定系数；对于该模型至少需调用[(n+1)(n+2)/2]+2n次精确计算。
构建雷达天线阵面4阶不完全多项式响应面模型时，通过对商业软件的二次开发实现数据流和工作流的定制，实现对试验样本库进行数值求解的全流程自动化，集成过程如图8所示。其中，DOE模块是试验设计模块，采用优化拉丁超立方法进行抽样。设计参数的变化范围及含义见表1。
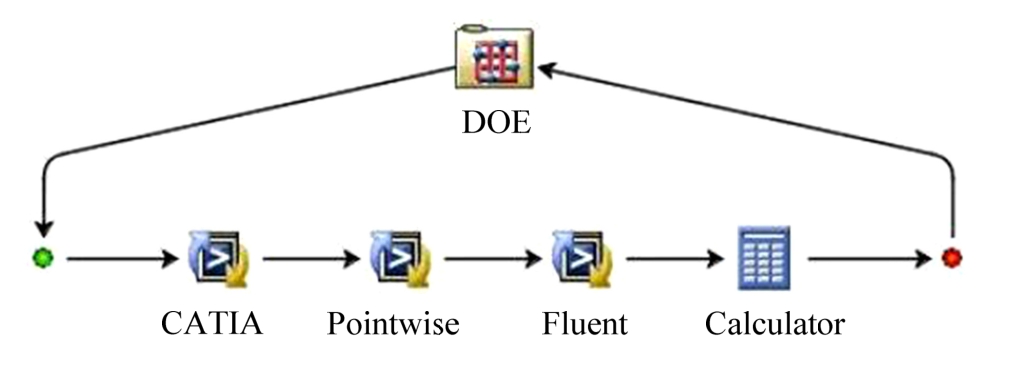
图8 集成过程
Fig.8 Integration process
表1 设计参数变化范围及含义
Table 1 Variation range and meanings of design parameters
参数名称 变量下限 变量上限 在模型中的意义X1/m 2 20 天线阵面长度X2/(m/s) 20 50 来流风速X3/m 2 20 天线阵面宽度X4/(°) 60 90 天线阵面倾角X5/(°) 0 180 来流风向角
CATIA模块为面板参数化建模模块。以面板的长宽特征尺寸，倾角与转角为参数进行参数化建模。通过导出参数设计表，修改其中的参数值，最终将参数化零件保存为几何模型文件。
Pointwise模块为流场网格划分模块。在建模完成后，需要对流场进行网格划分与边界条件的设置。由于几何模型在不断更新，对每一次更新后的几何模型均需要进行网格划分、边界条件的设定，工作量较大，故通过编写Pointwise脚本语言Glyph2[21]，实现自动流场网格划分与边界条件的施加。
Fluent模块为CFD计算模块。Fluent是通用流场求解器，将Pointwise的CAE输出文件进行CFD数值计算，得到雷达天线阵面的面压数据。为实现对样本库流场计算的自动化，本文基于TUI (Text User Interface)语言编写Fluent的Text Command[22]命令行，执行效率更高且设置过程无需辅助GUI(Graphical User Interface)，避免操作者对系统的操作干预GUI，使自动化过程中断。
根据上述流程及研究方法，5个设计变量通过试验设计方法确定62个试验设计点。通过iSIGHT进行所有样本的全流程自动化计算，并对得到的面压数据进行4阶不完全多项式拟合，得到4个区域平均面压P1、P2、P3、P4(单位Pa)的响应面模型如下：
2.3 响应面模型有效性检验
为了评价构造的多项式响应面函数，通过复相关系数和修正的对上述近似模复相关系数型试验点的拟合程度进行判定。
其中复相关系数定义为：
式中，R2的值位于0和1之间，该值越接近1，说明响应面模型的逼近程度越好。但是，多项式中变量数目较多时，该值也会相应较大，而多项式响应面模型的预测精度并不一定较好。因此，引入修正的复相关系数：
式中：M为样本点数目；n为多项式ϕi(x)的个数。
剩余平方和(SSE)和总平方和(SST)为：
式中，
分别代表响应值、预测响应值和实际响应值。
表2给出了4个区域平均面压的多项式响应面模型的复相关系数与修正的复相关系数。4个区域响应面模型的复相关系数与修正的复相关系数均接近于1，表明多项式响应面函数对试验点有较好的拟合程度，且有较好的预测精度。
表2 各区域响应面模型的复相关系数与修正的复相关系数
Table 2 R2 and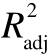 
of RSM models
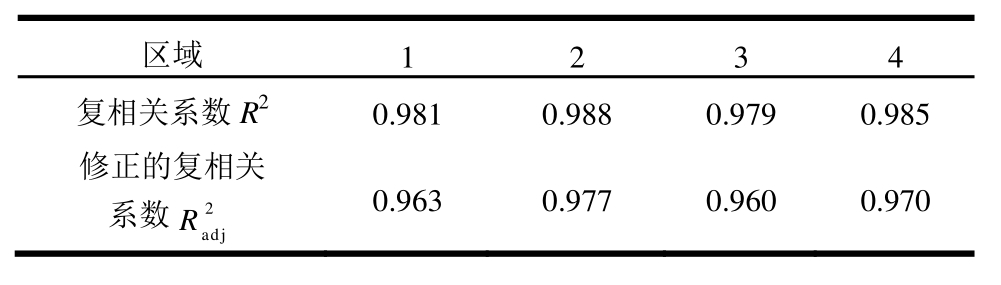
区域 1 2 3 4复相关系数R2 0.981 0.988 0.979 0.985修正的复相关系数2R 0.963 0.977 0.960 0.970 adj
为进一步预测构造的多项式响应面模型在实际应用中的准确度，采用留一法交叉验证，对构造的4个4阶不完全多项式响应面模型进行检验。
交叉验证是统计预测中一种评价统计分析结果是否可推广到独立的数据集上的技术，即估计一个预测模型在实际应用中的准确度。交叉验证可用于各种模型的选择，无需任何前提与假定。
留一法交叉验证是交叉验证方法中较为常见的一种[23]。其原理是：首先，选择一个样本数据作为验证数据，剩余样本作为训练样本集构造出一个新的模型，并采用最先取出的样本数据来检验该模型的精度，并重复以上步骤N次。模型的预测能力由预测均方根误差(root-mean-square error of prediction，RMSEP)以及观测值与模型预测结果之间的复相关系数R2来衡量。RMSEP可表示为：
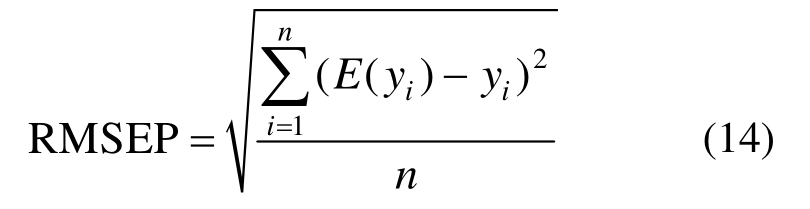
式中：E(yi)表示第i个实际观测值；yi为模型计算出的第i个预测值；n是观测样本总数。RMSEP值越低，复相关系数R2越接近于1，则模型精度越高。
表3 留一交叉法验证得到各个区域响应面模型的均方根与复相关系数
Table 3 RMSEP and R2 of RSM models using leave-one-out cross validation method
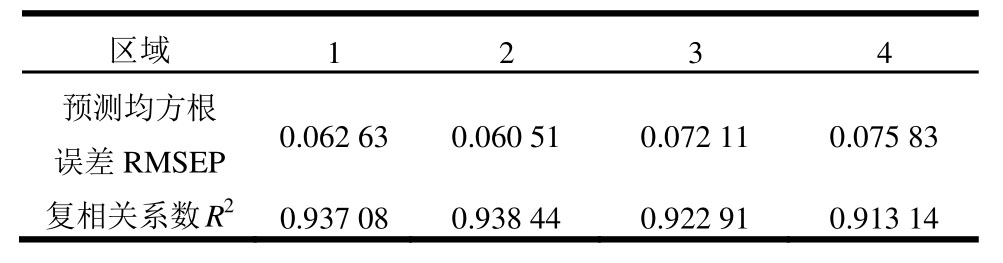
区域 1 2 3 4预测均方根0.062 630.060 51 0.072 11 0.075 83误差RMSEP复相关系数R20.937 080.938 44 0.922 91 0.913 14
基于留一交叉验证方法，选取35个误差分析样本，得到的均方根与复相关系数如表3所示。4个区域响应面模型的复相关系数均接近于1，RMSEP数值均较低，表明构建的多项式响应面模型在实际应用中有较好的预测准确度。
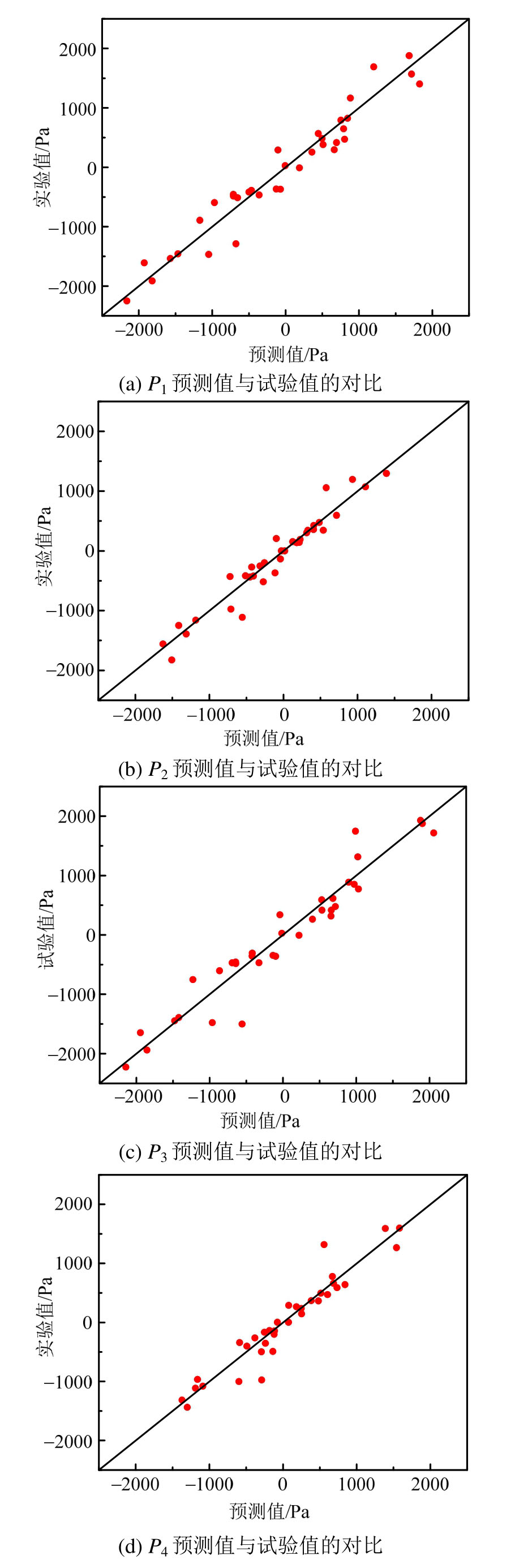
图9 各区域预测值与试验值的对比
Fig.9 Comparisons between the predicted pressure and test pressure
4个区域平均面压P1、P2、P3、P4 (单位Pa)的预测值与实际值的对比如图9(a)、图9(b)、图9 (c)、图9(d)所示。图中离散的点为留一法交叉验证选取的35个误差分析样本设计点，纵坐标与横坐标分别为该设计点对应的响应面模型预测值和数值仿真值。数据点与直线距离越近，代表该工况下响应面模型的近似程度越高。可见，构建的响应面近似模型精度较为理想。
综上分析，本文构造的雷达天线阵面风载响应面近似模型具有可靠的精度，极大地减少了天线阵面风载计算的工作量，具有较强的工程应用价值。
3 结论
风载分析对露天工作的雷达天线阵面结构至关重要，然而传统的CFD分析工作量较大，并且只能针对特定结构、特定工况，通用性较差。本文提出了一种基于多项式响应面代理模型的雷达阵面高效风载计算方法，选取了阵面的几何特征尺寸、倾角、风速、风向角为输入变量，阵面区域平均风压为输出响应，构建了天线阵面的气动载荷模型，其形式简单、计算量小、通用性好，具有较高的工程实用价值。在构建响应面模型时，采用优化拉丁超立方试验设计方法设计样本点，对每一个样本点进行精确计算，通过商业软件的二次开发实现CATIA参数化建模，Pointwise自动流场网格划分与边界条件施加，以及Fluent自动流场解算功能。其中涉及自编程序和商业软件的数据流和工作流的交互，发展成为一种集成的自动化仿真平台，无需手动对样本空间进行求解。结果表明，构造的不完全4阶多项式响应面模型精度较高，是雷达天线阵面风载计算的一个有效模型，能够为后续结构动力响应分析提供参考依据。
[1]杜强.雷达天线风载特性的数值计算方法及应用研究[D].成都: 电子科技大学, 2011.Du Qiang.Research and application on numerical method for characteristic computation of wind loads on radar antennas [D].Chengdu: University of Electronic Science and Technology of China, 2011.(in Chinese)
[2]王丽君, 佟丽莉.地面雷达天线罩风载下的数值模拟与风洞试验研究[J].工程力学, 2016, 33(增刊1):283―289.Wang Lijun, Tong Lili.Numerical simulation and wind tunnel test on ground radar radome under wind load [J].Engineering Mechanics, 2016, 33(Suppl 1): 283―289.(in Chinese)
[3]穆雪峰, 姚卫星, 余雄庆, 等.多学科设计优化中常用代理模型的研究[J].计算力学学报, 2005, 22(5): 608―612.Mu Xuefeng, Yao Weixing, Yu Xiongqing, et al.A survey of surrogate models used in MDO [J].Chinese Journal of Computational Mechanics, 2005, 22(5): 608―612.(in Chinese)
[4]Knill D L, Giunta A A, Baker C A, et al.Response surface models combining linear and euler aerodynamics for supersonic transport design [J].Journal of Aircraft,1999, 36(1): 75―86.
[5]Unal R, Lepsch R, McMillin M.Response surface model building and multidisciplinary optimization using D-optimal designs [C]// 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, 1998: 4759.
[6]Fleming E, Lafleur J, Saleh J.Response surface equations for expendable launch vehicle payload capability [C]// AIAA SPACE 2009 Conference &Exposition, 2009: 6656.
[7]陈力波, 黄才贵, 谷音.基于改进响应面法的公路简支梁桥地震易损性分析[J].工程力学, 2018, 35(4):208―218.Chen Libo, Huang Caigui, Gu Yin.Seismic vulnerability analysis of simply supported highway bridges based on an improved response surface method [J].Engineering Mechanics, 2018, 35(4): 208―218.(in Chinese)
[8]韩建平, 骆勇鹏, 郑沛娟, 等.基于响应面的刚构-连续组合梁桥有限元模型修正[J].工程力学, 2013,30(12): 85―90.Han Jianping, Luo Yongpeng, Zheng Peijuan, et al.Finite element model updating for a rigid frame-continuous girders bridge based on response surface method [J].Engineering Mechanics, 2013, 30(12): 85―90.(in Chinese)
[9]费庆国, 韩晓林, 苏鹤玲.响应面有限元模型修正的实现与应用[J].振动、测试与诊断, 2010, 30(2): 132―134.Fei Qingguo, Han Xiaolin, Su Heling.Response surface based finite element model updating and its application[J].Journal of Vibration, Measurement & Diagnosis,2010, 30(2): 132―134.(in Chinese)
[10]程霄翔, 费庆国, 何顶顶, 等.基于响应面的大型输电塔结构有限元模型动力修正[J].振动与冲击, 2011,30(5): 116―122.Cheng Xiaoxiang, Fei Qingguo, He Dingding, et al.Dynamic updating of a large transmission tower’s finite element model based on response surface methodology[J].Journal of Vibration and Shock, 2011, 30(5): 116―122.(in Chinese)
[11]鲍诺, 王春洁.基于响应面优化的结构有限元模型修正[J].北京航空航天大学学报, 2014, 40(7): 927―933.Bao Nuo, Wang Chunjie.Structural finite element model updating based on response surface optimization [J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 927―933.(in Chinese)
[12]董彦鹏, 吕振华.基于蜂窝材料结构相似有限元模型的夹层结构抗爆炸冲击特性优化设计分析[J].工程力学, 2013, 30(7): 248―254.Dong Yanpeng, Lü Zhenhua.Analysis and optimization of blast-resistant sandwich structure utilizing structural similar FE model of honeycomb material [J].Engineering Mechanics, 2013, 30(7): 248―254.(in Chinese)
[13]Nguyen P T L, Lee J Y, Yim H J, et al.Optimal design of vehicle structure for improving small-overlap rating [J].International Journal of Automotive Technology, 2015,16(6): 959―965.
[14]Mitra A C, Patil M V, Banerjee N.Optimization of vehicle suspension parameters for ride comfort based on RSM [J].Journal of The Institution of Engineers (India):Series C, 2015, 96(2): 165―173.
[15]Kim M S, Kang D O, Heo S J.Innovative design optimization strategy for the automotive industry [J].International Journal of Automotive Technology, 2014,15(2): 291―301.
[16]邓磊, 乔志德, 宋文萍, 等.基于响应面方法的风力机叶片多目标优化设计研究[J].空气动力学学报, 2012,30(3): 405―410.Deng Lei, Qiao Zhide, Song Wenping, et al.Multi-objective aerodynamic optimization design of wind turbine blade based on response surface methodology [J].Acta Aerodynamica Sinica, 2012,30(3): 405―410.(in Chinese)
[17]钱建魁, 毛筱菲, 王孝义, 等.基于CFD和响应面方法的最小阻力船型自动优化[J].船舶力学, 2012,16(增刊1): 36―43.Qian Jiankui, Mao Xiaofei, Wang Xiaoyi, et al.Ship hull automated optimization of minimum resistance via CFD and RSM technique [J].Journal of Ship Mechanics,2012, 16(Suppl 1): 36―43.(in Chinese)
[18]Murakami S, Mochida A, Sakamoto S.CFD analysis of wind-structure interaction for oscillating square cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72: 33―46.
[19]吴先宇, 罗世彬, 陈小前, 等.基于响应面模型的二维高超声速进气道优化[J].宇航学报, 2007, 28(5):1127―1132.Wu Xianyu, Luo Shibin, Chen Xiaoqian, et al.Optimization of the 2D hypersonic inlet based on response surface model [J].Journal of Astronautics,2007, 28(5): 1127―1132.(in Chinese)
[20]卢健钊, 殷国富, 王玲.基于iSIGHT的机床结构CAD/CAE集成优化方法研究[J].组合机床与自动化加工技术, 2013(2): 22―24.Lu Jianzhao, Yin Guofu, Wang Ling.Research on the CAD/CAE integrated optimization method of machine tool structures based on iSIGHT [J].Modular Machine Tool & Automatic Manufacturing Technique, 2013(2):22―24.(in Chinese)
[21]Pointwise, Inc.Pointwise |User Manual [EB].2016.
[22]Fluent, Inc.Fluent Documentation [EB].2014.
[23]李燕.基于交叉验证的基本解法求复杂区域边界值问题[D].太原: 太原理工大学, 2015.Li Yan.The method of fundamental solution with LOOCV for boundary value problems in complicated domains [D].Taiyuan: Taiyuan University of Technology, 2015.(in Chinese)