现实工程中的结构均为有阻尼结构,在动力作用下需要考虑能量耗散作用,因此在结构动力分析中需要对结构的耗散机制建立正确合理的模型[1]。有限质点法(finite particle method,FPM)将结构离散成质点,以质点的广义运动来描述结构在外力作用下的位移,各质点始终处于一种“运动的平衡状态”。在现有FPM研究及应用中,阻尼力一般按照动力松弛法中的定义,通过质量阻尼系数设置虚拟阻尼[2-12]。这种阻尼设置方法,是一种“空气阻尼”[13],一般仅作为额外的阻尼项使用,在实际中并不存在[1]。在应用于准静态问题时,可以通过合理设置临界阻尼而达到加速求解的目的[4]。
阻尼问题从20世纪40年代便开始得到了人们的关注[14-17]。线性阻尼体系是工程中应用的最广泛的阻尼形式。为了计算方便,一般将阻尼矩阵假设为对称且正定的实矩阵,实际上它可能是非对称的或者复阻尼的形式[18]。对于线性阻尼系统,当结构阻尼满足振型正交化条件(即经典阻尼)时,便能加速求解运动方程。Rayleigh[14]曾提出当阻尼较小时,可以选取部分振型用于表达结构整体的阻尼。Rayleigh方法只选取少量振型用于近似表达整体结构阻尼,存在一定的局限性。Caughey等[16]在此基础上提出了扩展的近似阻尼方法。而其他非经典阻尼问题,也有各自的处理方法[18-21]。针对这些处理方法,对于其近似效果的讨论也是探讨的热点。如Shahruz[20]采用直接选取未正交化阻尼矩阵对角项的方法,并通过讨论无穷范数对近似程度进行评估。Knowles[22]则在探讨线性阻尼的问题上引入了F范数用于评估等效方法的近似性。Udwadia[18]等则探讨了当结构刚度矩阵、阻尼矩阵均非对称或者非正定下的近似效果。最近,Huang等[23]提出了一种能在一定频率范围能够提供均匀耗散性能,并能在弹塑性条件下,降低阻尼耗散能力的阻尼方法。
然而,不论是经典阻尼还是非经典阻尼,它们的构造均基于传统的动力学方程。有限质点法是一种内禀式的无网格方法,本身没有所谓的“刚度”矩阵,需要建立一种适合自身的计算质点阻尼力的有效方法。因此从材料阻尼系数的角度构造结构的阻尼的方法较适合FPM。但是通过结构的尺度、构件尺寸、材料性质来直接构造阻尼矩阵是不现实的[24]。这种方法仅在研究固体材料阻尼、流体阻尼、或者摩擦阻尼等问题上才有较好的效果[25-28]。
本文从Rayleigh阻尼构造方法出发,提出两种阻尼构造方法:基于质点静态虚拟刚度的方法和基于质点质量和动态虚拟刚度的方法。本文首先介绍有限质点法的基本原理和原有阻尼形式,并提出两种新的阻尼构造方法。然后将通过一个单层网壳算例和框架振动实验验证所提出方法的正确性。
1 有限质点法基本原理
有限质点法将连续体结构离散成质点[2]。如图1所示的空间结构,其有限质点法模型为质点和单元的集合(如图2)。结构所有的质量均集中在质点上,单元的变形和内力用以表示质点间的位置和内力变化。质点的运动满足牛顿第二定律,如下式:
式中:mi表示质点i的质量; 表示质点i的加速度向量;
表示质点i的加速度向量;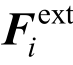 表示质点i所受外力向量;
表示质点i所受外力向量;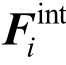 表示质点i的内力向量(由单元变形得到);
表示质点i的内力向量(由单元变形得到);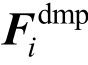 表示质点i的阻尼力向量。
表示质点i的阻尼力向量。

图1 连续质量分布的空间结构
Fig.1 Space structure with continuous mass distribution

图2 有限质点法结构离散模型
Fig.2 Discreate structure model of FPM
图3为时域下,单元在各时间点下的位置。质点在时域中的连续运动被离散成各时间步上的运动[29]。例如,ta≤t≤tb 便可视为一个“途径单元”[2]。根据式(1),计算质点在不同时间点的位置需要计算质点的内力。有限质点法中通过虚拟运动的步骤求解质点内力[2-3,29-30]。首先需通过逆向的刚体位移和刚体转动求得单元的纯变形算得单元自身的内力(图4(a)),之后通过虚拟的正向运动回到单元的真实位置,并将内力通过坐标变换得到统一坐标系下的内力(图4(b))。
2 有限质点法的阻尼构造方法
现有的有限质点法研究与应用中,阻尼按动力松弛法中的定义[31]设置一个虚拟阻尼:
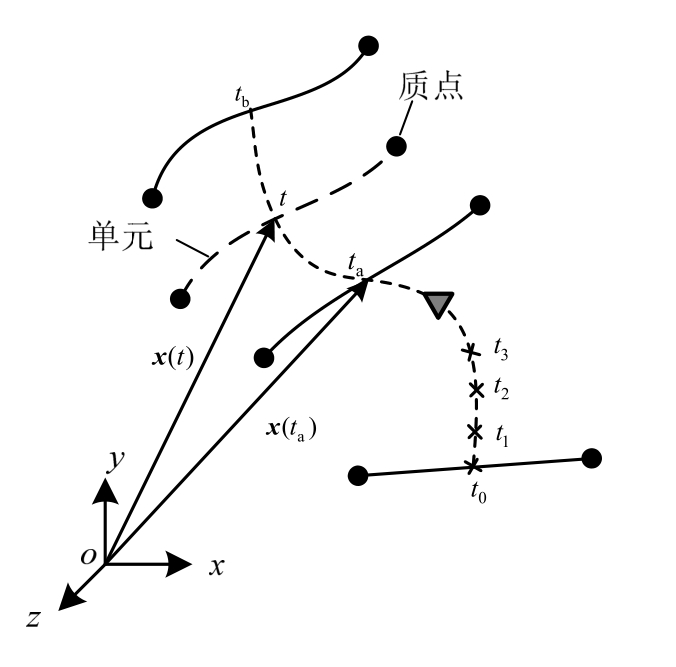
图3 途径单元
Fig.3 Path elements

图4 质点内力计算
Fig.4 Particle internal force calculations
式中:μ为质量阻尼系数;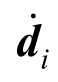 为质点i的速度向量。μ的取值并没有一个定论。从Rayleigh方案出发,通过式(3)计算μ的值相对合理:
为质点i的速度向量。μ的取值并没有一个定论。从Rayleigh方案出发,通过式(3)计算μ的值相对合理:
式中:ζm为质量阻尼比项,可取0.01~0.05;ω0为Rayleigh方法中分析的起始频率。由于实际的结构阻尼并不认为与结构质量直接相关[1],仅考虑质量阻尼系数,存在无法完全有效地估计结构的阻尼的情况。
鉴于此,本文提出两种方法:1) 基于静态刚度的方法(式(4));2) 基于质量和动态刚度的方法(式(5))。
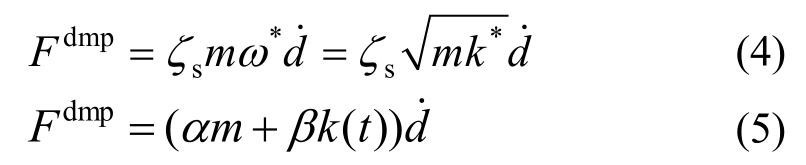
式中:ζs为静态阻尼系数,本文ζs取为2倍的结构阻尼比;m为质点的质量;k*为质点对应的静态虚拟刚度;ω*是质点在静态刚度下对应的虚拟自振频率;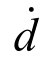 为质点速度;α为对应的质量阻尼系数(即μ,取值可以参考式(3),单位为s-1);β为对应的刚度阻尼系数,取法见式(6);k(t)为质点当前的动态刚度。
为质点速度;α为对应的质量阻尼系数(即μ,取值可以参考式(3),单位为s-1);β为对应的刚度阻尼系数,取法见式(6);k(t)为质点当前的动态刚度。

式中:ζk(t)为动态刚度阻尼比项,可取0.01~0.05;1ω为Rayleigh方法中分析频率范围的截止频率。
质点在结构刚度矩阵中对应的刚度需要考虑耦合作用。方法1:将质点间的关系考虑成由独立的3个线弹簧和3个角弹簧连接(如图5所示),并采用直接选取原矩阵对角元素的值的方法作为弹簧的刚度。这种刚度近似会带来一定的偏差,本文采取式(7)的方式对近似带来的偏差进行一定的修正:
式中:λ为修正系数;![]() 为质点在各方向弹簧的刚度系数;
为质点在各方向弹簧的刚度系数;![]() 为质点的静态虚拟刚度矩阵。当得到虚拟的质点静态刚度
为质点的静态虚拟刚度矩阵。当得到虚拟的质点静态刚度![]() 后,便可以得到质点对应的虚拟的质点自振频率ω*。
后,便可以得到质点对应的虚拟的质点自振频率ω*。
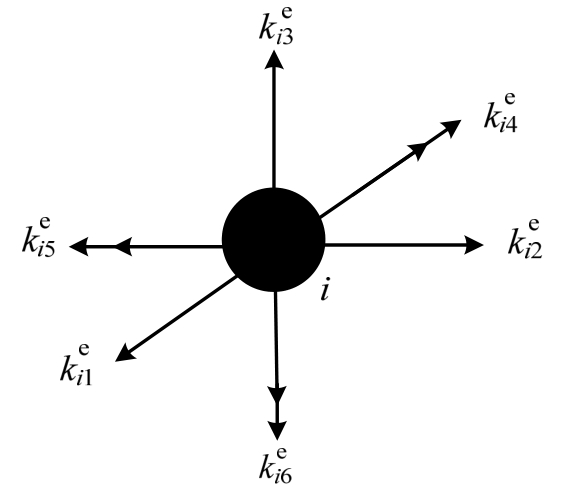
图5 质点静态刚度
Fig.5 Static stiffness of particle
合理的修正系数会得到更好的近似阻尼矩阵,本文通过令式(8)最小,计算修正系数λ:
式中:1C为方法一得到的结构阻尼矩阵;Dn为参照的阻尼矩阵,本文采用反正交化的振型阻尼作为Dn (式(9));![]() 表示F范数。
表示F范数。
式中:Cn为振型阻尼矩阵;Φ为结构的振型。
方法2:动态刚度的计算见式(10):
式中:ki(t)为质点的动态刚度矩阵;Δxi(t)为质点i在途径单元内的位移向量;“./”表示向量元素点除。方法2中,结构阻尼与瞬时的刚度相关,并同时考虑“空气(质量)阻尼”的贡献。
3 计算实例
本节计算实例采用单层的凯威特型空间网壳,跨度32 m,球半径32 m,矢高4.29 m,采用四点固定约束,如图6所示。材料参数如下:E=210 MPa;ν=0.3;ρ=7.85×103 kg/m3。输入的荷载形式为多点激励,直接作用于质点。ω0取2 rad/s,ω1取10 rad/s,ζm取1%,按式(3),μ(或α)取为0.04;方法1:修正系数λ,按式(7)取为1.5;方法2:ζk(t)取4%,按式(6),β取为0.008。将采用振型阻尼的动力学方法(阻尼比取2%)与3种阻尼方法下的有限质点法的计算结果进行对比。总计算时间步为4000,结点17和结点30的部分时程曲线如图7、图8所示,部分结点响应的统计值见表1。
3.1 单层网壳动力响应分析
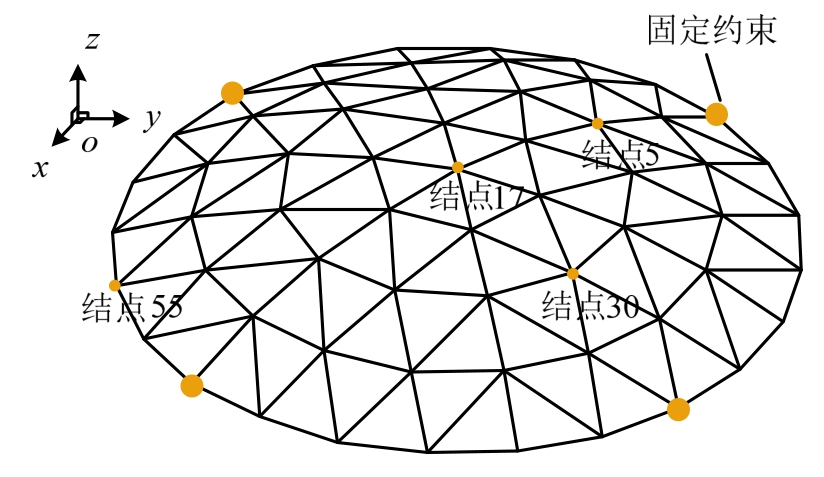
图6 凯威特型单层网壳模型
Fig.6 Kiewitt single-layer shell model

图7 结点17在z方向的位移响应时程对比
Fig.7 Time-history of displacement responses on z axis at node 17
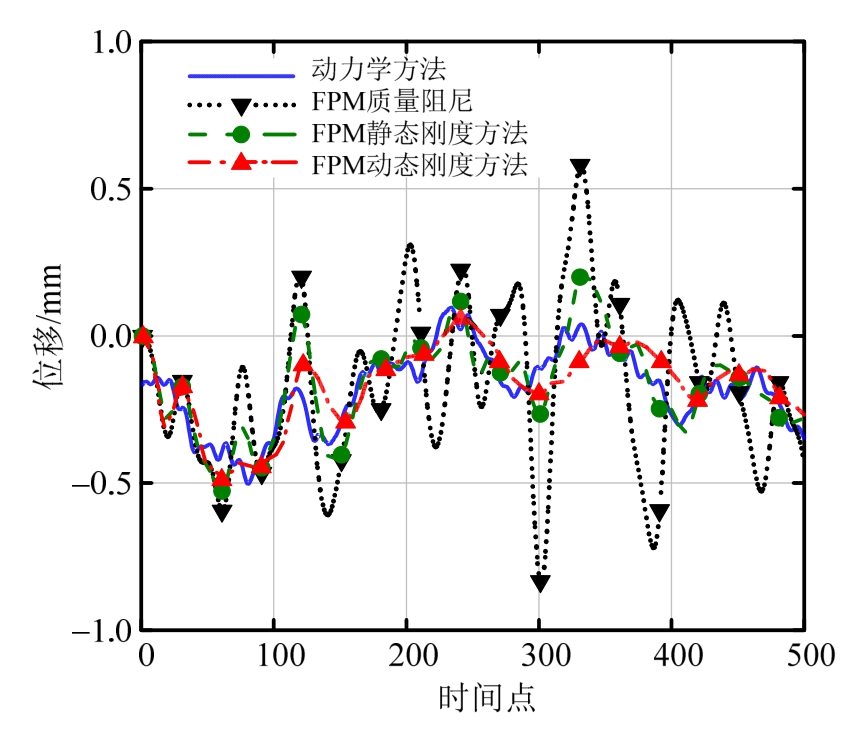
图8 结点30在z方向的位移响应时程对比
Fig.8 Time-history of displacement responses on z axis at node 30
表1 各阻尼方法下凯威特网壳z方向位移响应的统计值
Table 1 Statistics of displacement responses on z axis from all damping schemes in Kiewitt shell
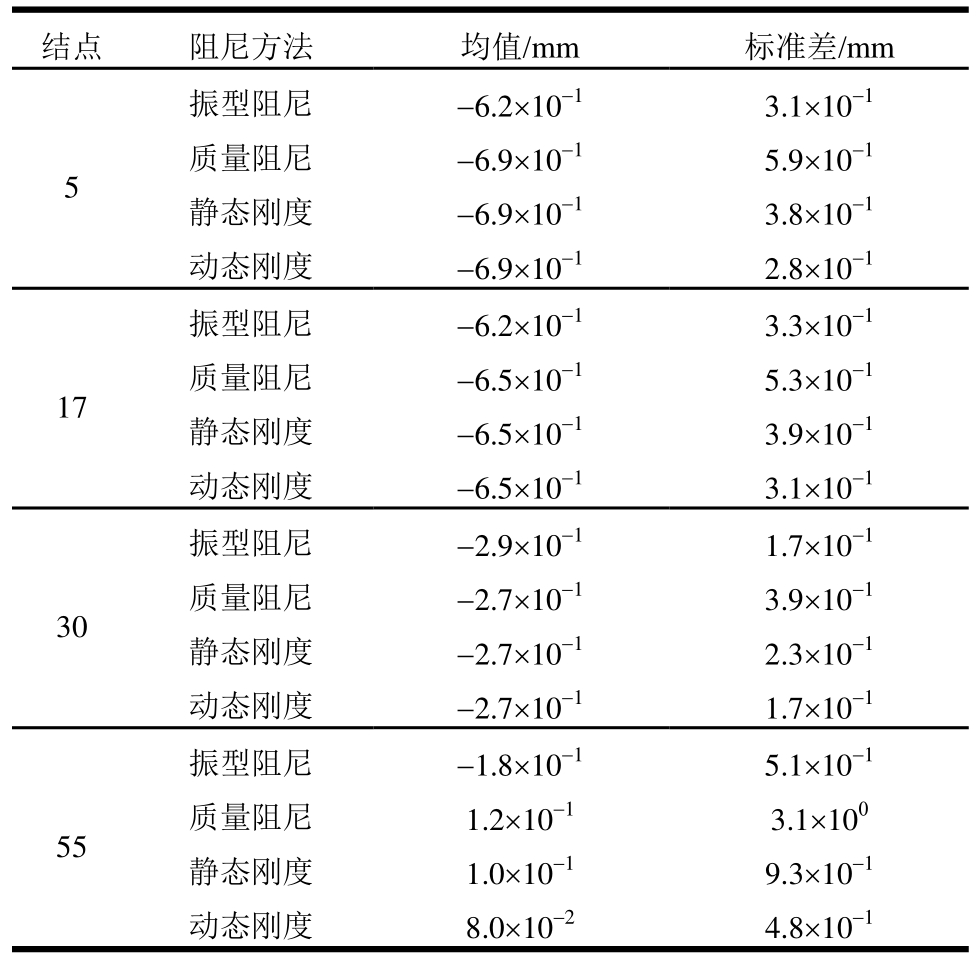
注:振型阻尼为传统结构动力学方法所使用。质量阻尼、静态刚度(阻尼)、动态刚度(阻尼)方法为有限质点法所使用。统计值来自整体4000步的计算结果。
结点阻尼方法 均值/mm 标准差/mm振型阻尼 -6.2×10-1 3.1×10-1 5质量阻尼 -6.9×10-1 5.9×10-1静态刚度 -6.9×10-1 3.8×10-1动态刚度 -6.9×10-1 2.8×10-1振型阻尼 -6.2×10-1 3.3×10-1 17质量阻尼 -6.5×10-1 5.3×10-1静态刚度 -6.5×10-1 3.9×10-1动态刚度 -6.5×10-1 3.1×10-1振型阻尼 -2.9×10-1 1.7×10-1 30质量阻尼 -2.7×10-1 3.9×10-1静态刚度 -2.7×10-1 2.3×10-1动态刚度 -2.7×10-1 1.7×10-1振型阻尼 -1.8×10-1 5.1×10-1 55质量阻尼 1.2×10-1 3.1×100静态刚度 1.0×10-1 9.3×10-1动态刚度 8.0×10-2 4.8×10-1
图7~图8及表1的结果表明:1) FPM原质量阻尼方法与采用振型阻尼的动力学方法差异最大;2) 静态刚度阻尼方法计算的位移响应比动力学结果稍大;3) 动态刚度阻尼方法结果最接近与动力学计算结果,但略小于采用振型阻尼的计算结果。
3.2 框架结构动力响应分析
本节采用有限质点法和动力学方法对框架结构的振动台实验进行模拟和分析,验证提出的阻尼构造方法的有效性。本实验在浙江大学建筑工程学院结构实验室进行,实验框架层数为5层,最大高度1.55 m,每层板的尺寸为0.3 m×0.3 m×0.04 m(0.02 m×2 m),立柱的横截面尺寸为0.05 m×0.005 m,立柱与板、振动台通过角钢连接件紧密连接(见图(9))。

图9 5层框架振动台实验模型
Fig.9 Vibration Stand test model of five-story frame
输入的基底加速度时程如图10所示,仅向立柱弱轴方向施振,且仅对比沿弱轴方向的位移响应。各层中央均设有一枚加速度传感器,加速度采样频率为128 Hz,总采样点数为6657个。
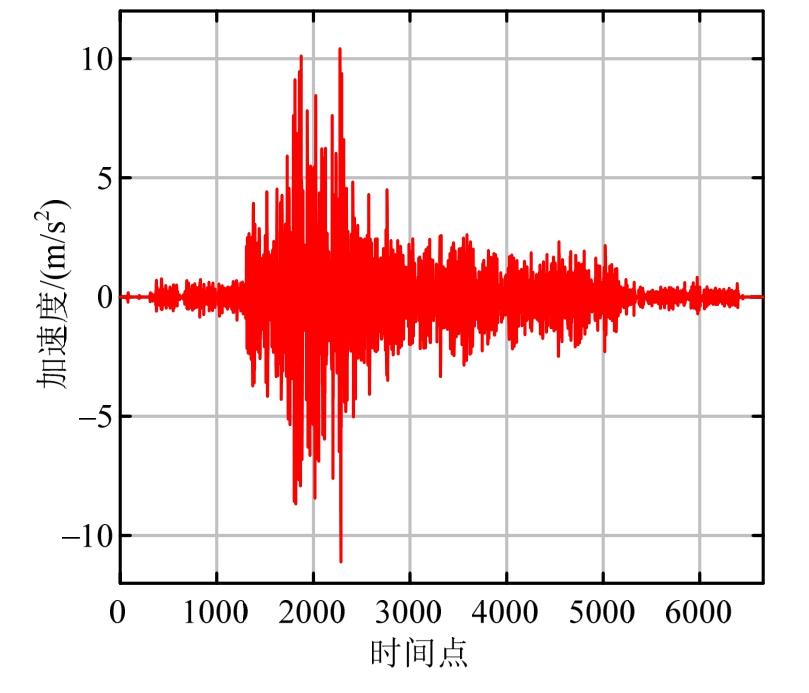
图10 框架基底振动台输入加速度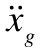
Fig.10 Input acceleration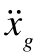 on vibration stand
on vibration stand
动力学方法采用完整模型和剪切刚架的简化模型(如图11)分别计算,计算采用阻尼比为2%。部分层结果见图12~图13,仅选取第2000步~2150步的响应进行对比。结果表明,动力学方法对结构低层响应的估计与实验值有比较明显的差异。其中,完整模型在第1层过低估计了响应,而简化模型则在第2层对响应估计偏高。可见动力学中常用的振型阻尼,在一些情况下存在不足。
使用图11的简化模型作为有限质点法的计算模型,按梁单元考虑立柱。ω0取20rad/s,ω1取25 rad/s,ζm取1%,按式(3),μ(或α)取为0.4;方法1:修正系数λ,按式(7)取为0.7;方法2:ζk(t)取5%,按式(6),β取为0.004。FPM各阻尼方法结果与实验数据的对比的结果见图14~图16。各层响应的统计值见表2。
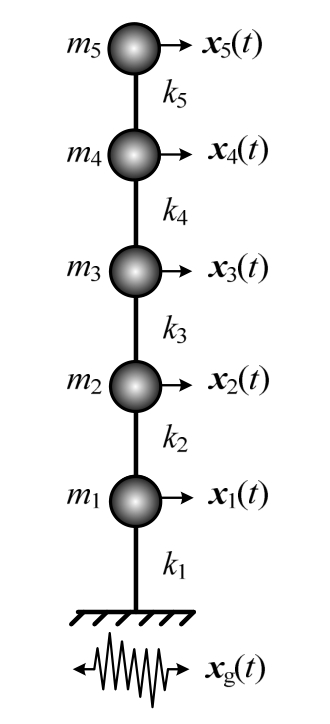
图11 简化计算模型
Fig.11 Simplified computing model

图12 第1层动力学两种模型与实测位移响应的对比
Fig.12 Comparisons of displacement responses from conventional dynamic analysis and test on the 1st floor

图13 第2层动力学两种模型与实测位移响应的对比
Fig.13 Comparisons of displacement responses from conventional dynamic analysis and test on the 2nd floor

图14 第1层FPM三种阻尼方法与实测位移响应的对比
Fig.14 Comparisons of displacement responses from three damping schemes of FPM and test on the 1st floor
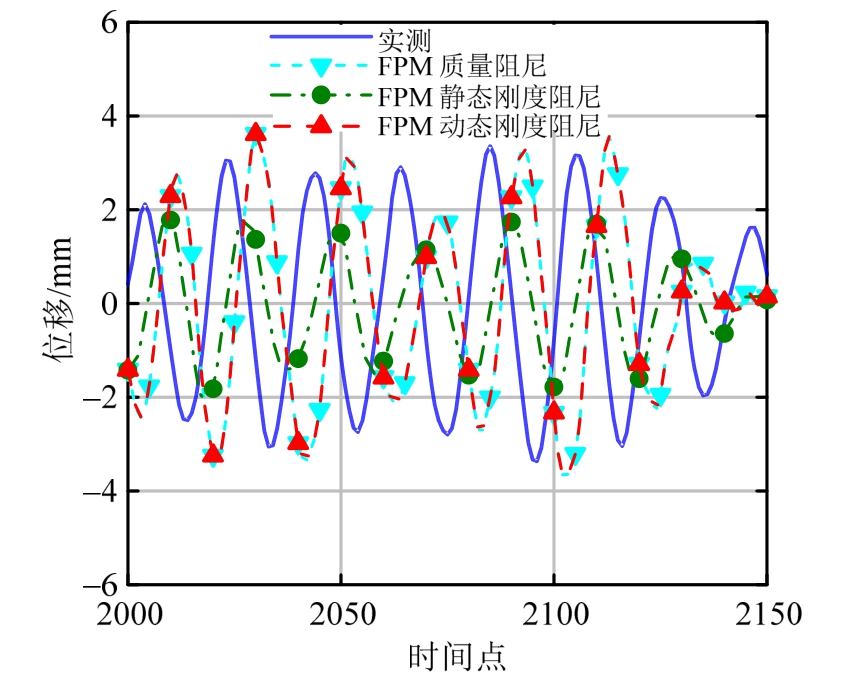
图15 第3层FPM三种阻尼方法与实测位移响应的对比
Fig.15 Comparisons of displacement responses from three damping schemes of FPM and test on the 3rd floor

图16 第5层FPM三种阻尼方法与实测位移响应的对比
Fig.16 Comparisons of displacement responses from three damping schemes of FPM and test on the 5th floor
图14~图16及表2结果表明:1) FPM质量阻尼方法和动态阻尼方法的结果类似,相比FPM静态刚度阻尼方法要更接近于试验结果;2) 静态刚度阻尼方法结果与实测结果相比偏小;3) 和单层网壳的结果不同,动态阻尼方法与质量阻尼方法结果十分接近,单纯考虑质量阻尼,就能有足够理想的结果;4) FPM各阻尼构造方法计算的响应在第1层均小于实测值,但是采用完整模型的动力学计算结果也有类似的情况。
表2 各阻尼方法下框架实例的施振方向位移响应统计值
Table 2 Statistics of displacement responses along forced vibration direction from all damping schemes in shake table test

注:实测统计值来自本文框架振动台实验。质量阻尼、静态刚度(阻尼)、动态刚度(阻尼)方法为有限质点法所使用。统计值来自整体6657步的计算结果。
层 阻尼 均值/mm 标准差/mm实测1质量阻尼静态刚度动态刚度实测2质量阻尼静态刚度动态刚度实测3质量阻尼静态刚度动态刚度实测4质量阻尼静态刚度动态刚度-4.2×10-9 3.3×10-1-1.7×10-2 9.9×10-2-4.0×10-3 4.6×10-2-1.8×10-2 9.8×10-2-2.2×10-6 3.3×10-1-1.8×10-2 3.4×10-1-3.3×10-2 1.7×10-1-1.8×10-2 3.3×10-1 1.5×10-5 6.2×10-1 1.8×10-2 6.6×10-1-4.0×10-2 3.7×10-1-1.9×10-2 6.6×10-1 4.3×10-5 9.2×10-1-1.9×10-2 1.1×100-2.9×10-2 6.0×10-1-2.0×10-2 1.1×100实测 6.4×10-5 1.1×100 5质量阻尼 -1.9×10-2 1.5×100静态刚度 -2.6×10-2 8.5×10-1动态刚度 -2.1×10-2 1.5×100
4 结论
有限质点法由于没有建立刚度的概念,导致它本身无法通过结构频率及结构阻尼比构造结构的阻尼。而现有的阻尼形式并不支持从材料的耗散系数出发构造结构的阻尼,这就导致有限质点法阻尼构造问题的困难。
本文提出了2种适用于有限质点法的阻尼形式,并完善了之前做法中质量阻尼系数设定的问题。通过和有限质点法既有的质量阻尼构造方法、实测计算结果以及传统动力学计算方法进行对比和分析,结果表明,相比之前的质量阻尼构造方法,本文提出的2种阻尼形式的计算结果与采用振型阻尼的动力学方法和实验的结果都更为接近。因此,这2种阻尼构造方法均能够更好地反应结构阻尼,并能弥补有限质点法仅采用质量阻尼时物理概念缺失的问题。
本文提出的2种阻尼构造方法是在不破坏有限质点法本身求解形式的基础上提出的,且结果具有较高的精度。后续研究将对提出的静态刚度阻尼方法的质点刚度近似、动态刚度阻尼方法的两参数问题等进行深入探讨。
[1]Hall J F.Problems encountered from the use (or misuse)of rayleigh damping [J].Earthquake Engineering &Structural Dynamics, 2006, 35(5): 525―545.
[2]喻莹.基于有限质点法的空间钢结构连续倒塌破坏研究[D].杭州: 浙江大学, 2010.Yu Ying.Progressive collapse of space steel structures based on the finite particle method [D].Hangzhou:Zhejiang University, 2010.(in Chinese)
[3]Yu Y, Paulino G H, Luo Y.Finite particle method for progressive failure simulation of truss structures [J].Journal of Structural Engineering, 2015, 137(10): 1168―1181.
[4]杨超.薄膜结构的有限质点法计算理论与应用研究[D].杭州: 浙江大学, 2015.Yang Chao.Research on computational theory and applications of finite particle method for membrane structure [D].Hangzhou: Zhejiang University, 2015.(in Chinese)
[5]Yu Y, Zhu X Y.Nonlinear dynamic collapse analysis of semi-rigid steel frames based on the finite particle method[J].Engineering Structures, 2016, 118(3): 83―93.
[6]朱明亮, 陆金钰, 郭正兴.新型环箍穹顶全张力结构局部断索抗连续倒塌性能分析[J].东南大学学报(自然科学版), 2016, 46(5): 1057―1062.Zhu Mingliang, Lu Jinjue, Guo Zhengxing.Analysis on progressive collapse resistance of novel torus-dome tensile structure due to cable rupture [J].Journal of Southeast University (Natural Science Edition), 2016,46(5): 1057―1062.(in Chinese)
[7]李阿龙, 袁行飞, 梁笑天.基于非线性力法及向量式有限元法的结构屈曲路径跟踪(英文)[J].空间结构,2017, 23(3): 89―96, 75.Li Along, Yuan Xingfei, Liang Xiaotian.Non-linear force method for buckling path analysis of space trusses with vector form intrinsic finite element [J].Spatial Structures, 2017, 23(3): 89―96, 75.(in Chinese)
[8]Hou X, Fang Z, Zhang X.Static contact analysis of spiral bevel gear based on modified VFIFE (vector form intrinsic finite element) method [J].Applied Mathematical Modelling, 2018, 60:192―207.
[9]王震, 赵阳, 杨学林.薄膜断裂和穿透的向量式有限元分析及应用 [J].计算力学学报, 2018, 35(3): 315―320.Wang Zhen, Zhao Yang, Yang Xuelin.Analysis and application of the vector form intrinsic finite element for fracture and penetration of thin-membrane [J].Chinese Journal of Computational Mechanics, 2018, 35(3): 315―320.(in Chinese)
[10]Duan Y, Tao J, Zhang H, et al.Real-time hybrid simulation based on vector form intrinsic finite element and field programmable gate array [J].Structural Control and Health Monitoring, 2019, 26(1): e2277.
[11]俞锋, 尹雄, 罗尧治, 等.考虑接触点摩擦的索滑移行为分析 [J].工程力学, 2017, 34(8): 42―50.Yu Feng, Yin Xiong, Luo Yaozhi, et al.Cable sliding analysis considering frictional effect [J].Engineering Mechanics, 2017, 34(8): 42―50.(in Chinese)
[12]张鹏飞, 罗尧治, 杨超.基于有限质点法的三维固体弹塑性问题求解 [J].工程力学, 2017, 34(4): 5―12.Zhang Pengfei , Luo Yaozhi , Yang Chao.Elastic-plastic analysis of 3D solids using the finite particle method [J].Engineering Mechanics, 2017, 34(4): 5―12.(in Chinese)
[13]Ryan Keri L, Polanco J.Problems with rayleigh damping in base-isolated buildings [J].Journal of Structural Engineering, 2008, 134(11): 1780―1784.
[14]Rayleigh J W S B.The theory of sound [J].Physics Today, 1957, 10(1): 32―34.
[15]Myklestad N O.The concept of complex damping [J].Journal of Applied Mechanics, 1952, 19(3): 284―288.
[16]Caughey T K, O’Kelly M E J.Classical normal modes in damped linear dynamic systems [J].Asce Journal of Applied Mechanics, 1965, 27(3): 269.
[17]Foss K A.Coordinates which uncouple the equations of motion of damped linear dynamic systems [R].Massachusetts Inst of Tech Cambridge Aeroelastic and Structures Research Lab, 1956.
[18]Udwadia F E.A note on nonproportional damping [J].Journal of Engineering Mechanics-ASCE, 2009, 135(11):1248―56.
[19]Chung K R, Lee C W.Dynamic reanalysis of weakly non-proportionally damped systems [J].Journal of Sound and Vibration, 1986, 111(1): 37―50.
[20]Shahruz S M.Approximate decoupling of the equations of motion of damped linear systems [J].Journal of Sound and Vibration, 1990, 136(1): 51―64.
[21]Roesset J M, Whitman R V, Dobry R.Modal analysis for structure with foundation interaction [J].Journal of the Structural Division, 1973, 99(3): 399―416.
[22]Knowles J K.On the approximation of damped linear dynamical systems [J].Structural Control and Health Monitoring, 2006, 13(1): 324―35.
[23]Huang Y, Sturt R, Willford M.A damping model for nonlinear dynamic analysis providing uniform damping over a frequency range [J].Computers & Structures,2019, 212: 101―109.
[24]Clough R W, Penzien J.Dynamics of structures [M].Computers & Structures, Inc, 1993.
[25]Jung W-Y, Aref A J.A combined honeycomb and solid viscoelastic material for structural damping applications[J].Mechanics of Materials, 2003, 35(8): 831―844.
[26]Galindo-Rosales F.Complex fluids in energy dissipating systems [J].Applied Sciences, 2016, 6(8): 206.
[27]de Vicente J, Klingenberg D J, Hidalgo-Alvarez R.Magnetorheological fluids: a review [J].Soft Matter,2011, 7(8): 3701―3710.
[28]Crewe A.Passive energy dissipation systems in structural engineering: by T.T.Song and G.F.Dargush, John Wiley& Sons, New York, ISBN 0-471-96821-8 [J].Structural Safety, 1998, 20(2): 197―198.
[29]Ting E C, Shih C, Wang Y K.Fundamentals of a vector form intrinsic finite element: Part 1.Basic procedure and a plane frame element [J].Journal of Mechanics, 2004,20(2): 113―122.
[30]Ting E C, Shih C, Wang Y K.Fundamentals of a vector form intrinsic finite element: Part II.Plane solid elements[J].Journal of Mechanics, 2004, 20(2): 123―132.
[31]Lewis W J, Jones M S, Rushton K R.Dynamic relaxation analysis of the non-linear static response of pretensioned cable roofs [J].Computers & Structures, 1984, 18(6):989―997.