中国古建筑历经数千年的发展演变,形成了以木结构为主的建筑体系。唐代殿堂型木结构建筑是我国古建筑遗存中弥足珍贵的文物,其数量稀少,结构形制特殊且极富时代特征,具有极其重要的历史文化与科学研究价值。由于建造年代久远,我国仅有的几座唐代木构建筑遗存残损均较为严重,为了保证其结构安全,亟需对其抵抗地震等灾害的能力进行科学评估,并对现状结构进行合理加固与保护,因此对此类结构受力性能与抗震机理的研究十分必要。
近年来,已有不少学者开展了古建筑木结构受力性能方面的研究。高大峰[1]进行了四梁四柱宋式古建筑木构架缩尺模型的振动台试验,结果表明该类型木构架主要以隔震方式抵御地震作用。隋䶮等[2]通过对宋式单朵斗拱、两朵斗拱组、四朵斗拱组缩尺模型的低周反复荷载试验研究了斗拱侧向刚度特性,得出铺作层通过水平滑移隔震耗能具有良好的抗震性能。Chen等[3]基于单层四梁四柱宋式亭榭类古建筑木结构足尺模型拟静力试验,研究了此类型木构架的滞回特性。陈春超[4]基于理论分析、有限元模拟和模型试验方法分别研究了清代单榀抬梁式和穿斗式木构架的受力性能。刘妍等[5]基于独乐寺山门一榀木框架的三维有限元模型,研究了典型辽代木构架在竖向荷载作用下的受力特征。Lee等[6]基于数值模拟与缩尺模型试验对韩国传统木构架进行了受力分析。Ayala等[7]对台湾地区传统木结构的叠斗进行节点实验,得到了叠斗节点的简化模型,并应用该模型进行了一榀木框架的有限元模拟,研究了叠斗式木构架的整体受力性能。
综上所述,已有研究所针对的古建筑木构架大多来源于宋清时期的建筑形制,在结构构造上与唐代殿堂型木构架具有较大差异。尤其是唐代木构建筑重要组成部分—铺作层在后期已十分弱化。目前国内外关于木结构的数值研究中,采用实体单元建立单榀木构架的精细化有限元模型尚不多见。因此为深入研究此类木构架的受力性能,本文基于文献史料、勘查报告[8―10]和现场调研,建立了某唐代殿堂型木结构一榀构架的精细化有限元实体单元模型,基于水平低周反复加载模拟,对其抗侧机理进行研究,深入分析了木构架的变形特点、破坏形态、滞回特性、抗侧刚度及耗能特征。
1 唐代殿堂型木构架基本构造
如图1所示的某典型唐代殿堂型木构架由多榀横向木框架通过数层纵向枋木、檩条连接构成,在结构上具有明显的水平分层,即由柱网层、铺作层和屋架层自下而上叠垒而成。柱网层木柱底端通过管脚榫平摆浮搁于础石上;顶端通过馒头榫与铺作层斗拱的栌斗相连,如图2所示。铺作层为由数层拱枋纵横搭扣而成的井干框格,其抗侧刚度远大于柱架层。因此木构架抗侧刚度在竖向具有突变性,柱脚节点和柱头-栌斗节点为结构的薄弱连接部位。
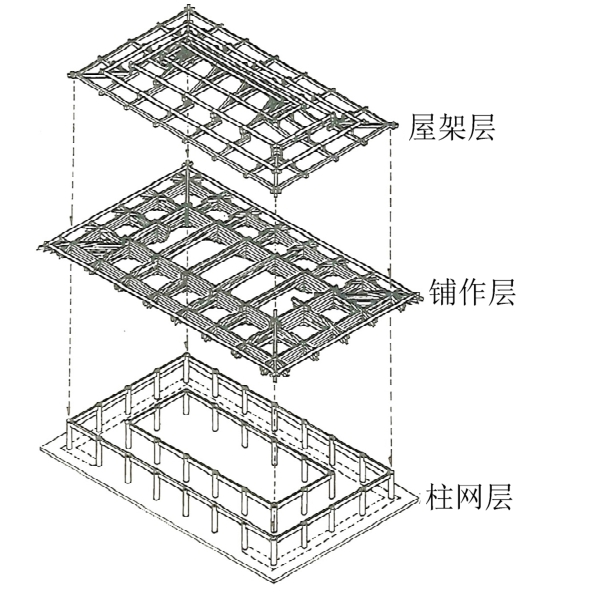
图1 唐代殿堂型木构架结构层[11]
Fig.1 Structural layers of the Palace-style wooden frame in Tang dynasty[11]
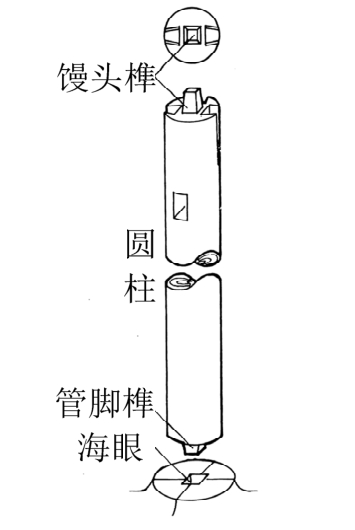
图2 柱脚管脚榫与柱头馒头榫[12]
Fig.2 Mortise and tenon joints of column foot and column head[12]
唐代殿堂型木构架的结构特殊性主要在于铺作层,其用材高约为柱高一半,具有较强整体性。如图3(d)所示的横向木构架由底部平置的柱网层(图3(a))、中间相联接的斗拱构成的铺作层(图3(b))、顶部叠置的屋架层(图3(c))构成。铺作层为井干构造的水平方格网架层,由图4(a)横向拱、栿(即梁)与图4(b)纵向柱头枋通过图4(c)所示的十字搭扣榫卯构成,相交处节点即为斗拱。铺作层外檐柱头斗拱在底层栌斗上部是一道泥道拱、四道纵向柱头枋分别与四道横向华拱、两斜昂木通过十字搭扣榫卯连接;内槽柱头斗拱在底层栌斗上部是六道横向拱木分别与纵向的一道泥道拱、五道柱头枋通过十字搭扣榫卯连接。横向叠置拱构件之间均有暗销或插销,包括顶部的横梁与垫木之间、檩条与替木之间,纵向叠置枋木构件之间通过散斗连接,而散斗与枋木之间均有暗销。外檐斗拱与内槽斗拱之间通过两道横向梁栿、一道横向枋木与内外柱头斗拱的拱木进行连接,内槽斗拱之间通过一道横向梁栿与拱木连接。详细构造见2.1图6所示。

图3 一榀木构架
Fig.3 A wooden frame

图4 铺作层构造
Fig.4 The construction of Dou-Gong brackets
2 精细化有限元模型
2.1 模型几何尺寸与有限单元
基于木构架横剖面,在单榀构架两侧跨中从屋架顶到柱脚依次截断檩条、柱头枋、阑额等横向构件,可得到一榀木构架。唐代已形成较为成熟的建筑尺度模数制度,即“材分制”[11]。其对建筑整体尺度有统一规定,结构各构件的尺寸都可以由材分制计算得到。本文模型构件尺寸见表1,以“分”为模数(1“分”等于21 mm)。基于ABAQUS有限元软件建立一榀木构架的三维精细化有限元足尺模型,如图5所示,共由244个木构件组成,构件全部通过榫卯或暗榫连接。有限单元为八节点六面体线性单元,其大小为2.5分(52.5 mm),构件接触处单元加密,大小为25 mm。模型单元总个数约为25万。模型组成与边界条件示意图,见图7。
表1 构件及尺寸信息 /分
Table 1 Dimensions of components

注:D为柱径,B、H分别为横截面的宽和高;L为构件长。

图5 精细化有限元足尺模型
Fig.5 Full scale refinement finite element model

图6 模型组成与边界条件示意图
Fig.6 Schematic diagram of boundary condition and model construction
2.2 材料特性
实际结构用木为油松,木材力学特性参数取为陕西油松,材料参数的设置参考文献[13―14]。采用正交各向异性理想弹塑性木材本构模型,所用木材材性参数见表2。
表2 木材材料参数
Table 2 Wooden property parameters
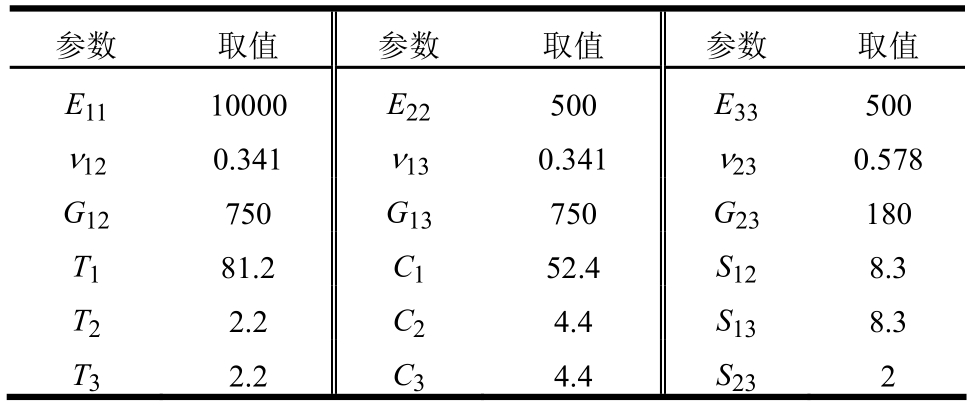
注:1 )E为弹性模量;G为剪切模量;ν为泊松比;T、C、S分别表示抗拉、抗压、抗剪强度;1、2、3分别代表顺纹方向、横纹径向和横纹弦向。弹性模量、剪切模量和强度的单位均为MPa。 2)油松密度取为432 kg/m3。3)础石弹性模量取230 000 MPa,密度取2500 kg/m3。4)木材与木材之间及木材与础石之间的摩擦系数均取0.4[13]。
2.3 荷载计算
根据官式建筑大式屋面分层做法,屋面层从上到下分别为合瓦、铺瓦泥、青灰背、月白灰背、滑秸泥背、护板灰、望板、椽(图7),脊檩上还有正脊荷载。通过估算合计各层材料重量得出模型屋盖荷载的大小[15―16],计算过程列于表3。屋盖面荷载为7 kN/m2,按各檩条负荷屋面宽度计算檩条所承受的线荷载q1~q7或按负荷面积折合为集中荷载,详见表4。集中荷载通过施加于檩条顶面耦合约束参考点作用于檩条顶面上(图7)。通过在草乳栿端部施加水平低周循环位移控制荷载,模拟地震作用下木结构的受力与变形性能。本计算中考虑了木材的自重。
表3 屋面每平米荷载计算
Table 3 Calculation of roof load
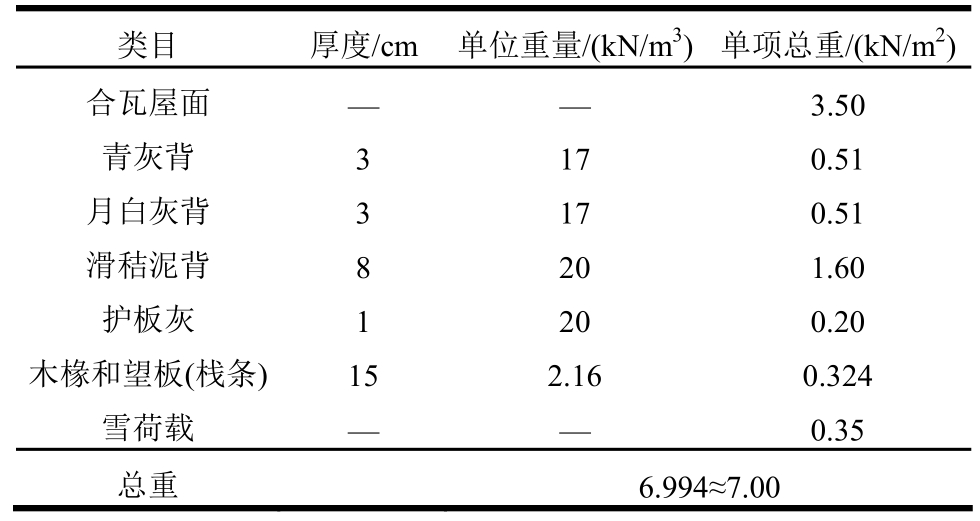
表4 框架顶部檩条的负荷计算
Table 4 Load calculation of purlin on the top of the frame

注:W = w /cos(α × π/180),q=Q×W ,F=q×L,脊槫线荷载计算中,屋脊荷载即每米正脊重量为276 kg,折算为2.76 kN/m,即q1 = 16.9 + 2.76 = 19.66kN/m , F1 = 19.66× 5.04 = 99.08 kN/m ,负荷长度为檩条长度,等于240 分 ×21 毫米/分 =5040毫米 。
2.4 边界条件
石底面固定,柱脚搁置在础石上面,采用管脚榫连接。檩条和柱头枋等纵向枋木的受力分析可简化为七跨连续简支梁受均布线荷载作用(图8),从剪力图和弯矩图可以看出,檩条和枋木的跨中(即一榀木构架檩条和枋木的两端)剪力为零而弯矩为最大值,故纵向的檩条、枋木两端均采用滑动铰约束,即约束纵向位移而竖向和水平向位移自由,两端能承受弯矩但不能承受剪力(图6)。
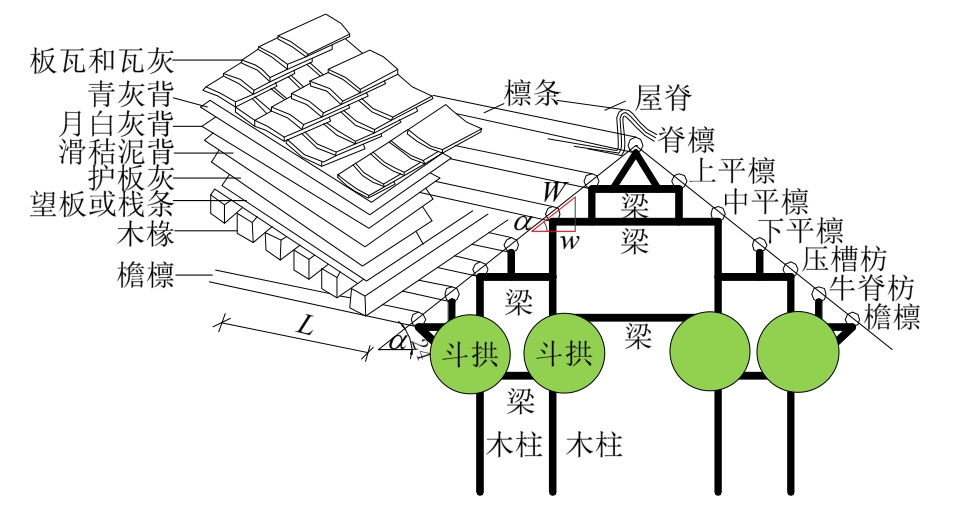
图7 屋面分层做法示意图
Fig.7 Constructional details of roof covering
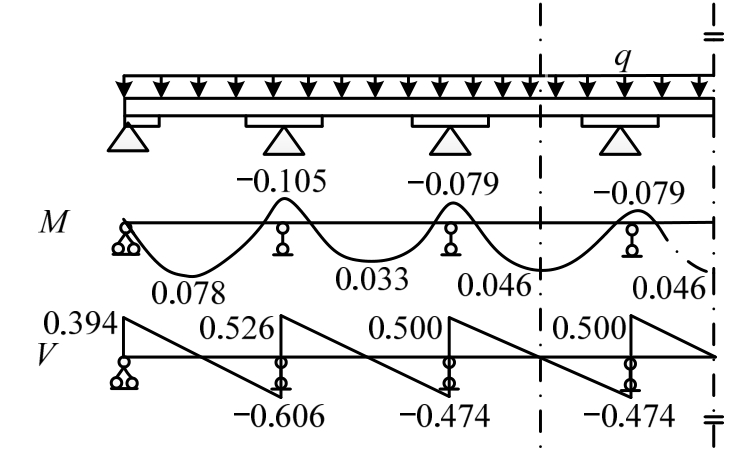
图8 檩条和枋木的受力图
Fig.8 Force diagrams of purlin and girder
2.5 接触面相互作用
木结构构件通过榫卯相互连接,因此相邻构件之间有多对接触面。在荷载作用下接触面间会产生相对滑动,由挤压变形和摩擦抵抗荷载作用。真实而准确模拟接触面间的相互作用对有限元模拟来说至关重要。模型应考虑构件间的接触挤压与分离、摩擦滑移作用。构件间的非线性接触状态由指定有限元分析的接触面和接触类型来实现。通过定义相互作用类型为面与面接触算法来指派面与面接触对,采用接触类型为法向硬接触和切向库伦摩擦接触。前者允许接触后分离,或者通过设置接触面间的摩擦系数来判断接触面滑移运动。当接触面间的剪力大于最大静摩擦力时,接触面间产生相对滑动。檩条与替木、替木与下部连接处的接触面均采用绑定约束接触处理。
3 变形特点与破坏形态
3.1 水平单调加载预分析及模拟合理性验证
作者在文献[17]中采用与本文相同的数值模拟方法,模拟了单根木柱在水平循环荷载作用下的受力性能,其数值模拟方法的有效性已得到拟静力模型试验的验证。为确定低周循环加载拟静力分析的各级加载位移,进行了水平单调加载预分析。荷载位移曲线与木材横纹受压应力-应变曲线变化过程相似(图9)。加载初期,随柱脚转动,柱与铺作层之间逐渐产生相对转动,榫卯节点逐渐挤紧,构件接触面逐渐发生挤压和剪切滑移,荷载随位移增大而迅速增大,木构架的初始抗侧刚度较大,荷载位移曲线初始段呈线弹性。在接近30 mm处发生屈服,榫头挤压接触处的木材逐渐进入塑性,柱脚管脚榫和柱头馒头榫也逐渐从卯口中拔出,荷载增长逐渐减缓,木构架抗侧刚度逐渐减小。在100 mm左右刚度急剧下降,之后缓慢下降直到加载到 450 mm达到峰值荷载。在达到峰值荷载对应位移后曲线接近水平,并保持荷载缓慢减少而位移继续增长。由此可见模型具有较高的水平承载能力和较好的延性变形能力。可确定模型的屈服位移和峰值位移分别约为 30 mm 和 450 mm。由此确定加载制度(图10),进行模型水平低周循环加载数值模拟。
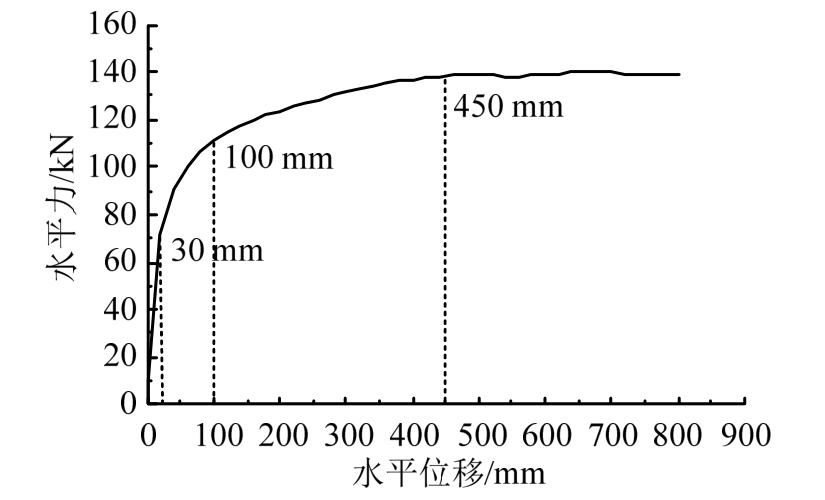
图9 水平单调加载的荷载-位移曲线
Fig.9 Load-displacement curve of horizontal monotonic loading
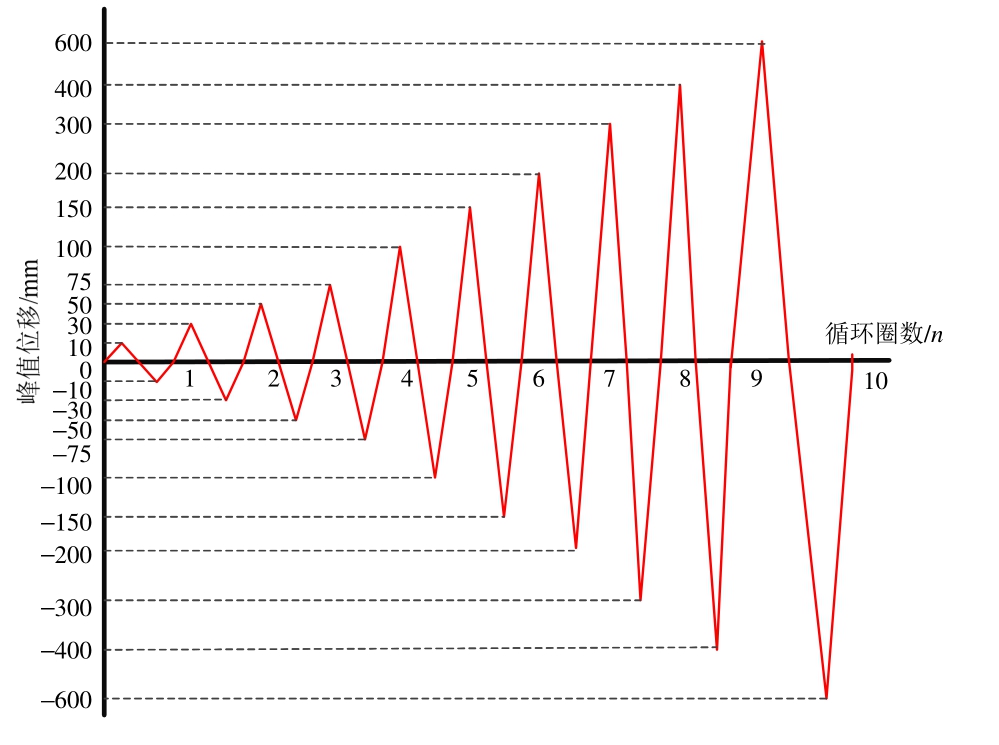
图10 加载制度
Fig.10 Loading process of the test
在竖向荷载作用下的单向水平力加载过程中,柱脚底面经历全截面受压、全截面偏压、临界抬升以及偏压抬升等工作状态。当水平荷载为零时,柱脚处于全截面均压或偏压状态,随水平位移增加,柱脚受压面减小。当水平位移为30 mm时,受压面约为柱截面一半。当柱头位移超过75 mm时,受压面主要在柱脚边缘。这与已有木柱拟静力试验研究结果[18]吻合较好,说明加载前期柱脚受压面迅速向柱脚边缘移动,而后期主要集中在柱脚边缘处。文献[18]中单根柱的拟静力试验及理论研究表明,由于柱脚与础石是面接触的受压变形,木柱的极限位移略小于半个柱径,而与础石为点接触的刚体柱极限位移为半个柱径。本文模型由于考虑了柱脚管脚榫和柱头馒头榫以及整体结构作用,受力现象与单根柱摇摆不同,在800 mm单调加载中,木柱位移达到781 mm,远比柱半径250 mm要大的多,实际上模型在加载到400 mm时,柱脚转动角度和柱头与斗拱之间夹角非常大,两节点处承压受力面积减少,变形加剧,受压破坏特别严重。柱脚在转动支承端部受到础石支承反力,而柱头受力端与柱脚相反,受到斗拱栌斗传递的局部集中压力。
文献[19]对古建木构的拟静力研究表明,整体构架的骨架曲线外包于摇摆木柱的骨架曲线,且曲线屈服处抗侧力与摇摆木柱的最大抗侧力接近,即整体构架的最大抗侧力一定大于摇摆木柱的抗侧力。本研究中木构架与摇摆木柱的最大抗侧力的差值取决于铺作层的抗力作用,而摇摆木柱的最大抗侧力在柱脚反力作用点和栌斗压力作用点趋于柱截面边缘时,大小约为 P=Nd/h,其中N为竖向作用力,d为柱径,h为柱高。本文中木构架N= 1100kN , d= 0.5m ,h=5m,则 P= 110kN 。本文木构架的最大抗侧力约为 140 kN,大于110 kN,滞回曲线屈服处抗侧力约为100 kN,与摇摆木柱的最大抗侧力110 kN接近,进而证明了本文数值分析结果的合理性。
3.2 柱脚节点变形特征
图11为模型在水平低周循环加载过程中的受力变形图。四根柱脚与础石接触端点在600 mm加载循环滞回圈的水平滑动位移变化曲线如图12所示。结合图13的柱脚偏转受力状态,柱脚底面支承点滑移量小于0.6 mm,证明柱脚底面发生转动而几乎没有发生滑移。这是由于柱脚管脚榫的约束作用,木柱仅发生绕柱脚与础石接触支承处的转动。在水平力作用下,柱脚管脚榫受到础石的约束而发生挤压和弯剪受力变形。当加载到最大位移800 mm时,柱脚抬升高度达到90 mm。
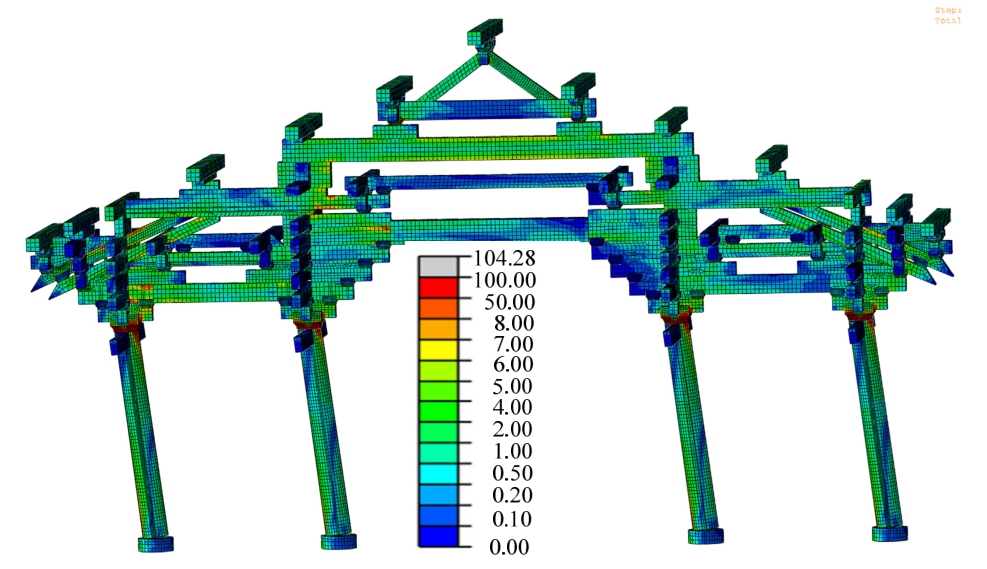
图11 水平低周反复加载木构架受力变形图
Fig.11 Stress and deformation diagram of wooden frame under repeated horizontal cyclic loading
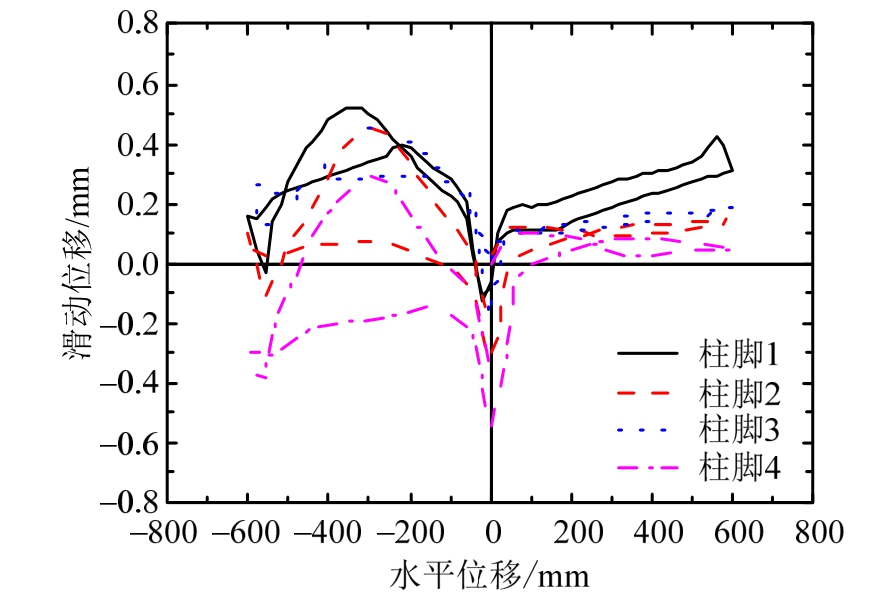
图12 柱脚与础石接触处的滑动位移
Fig.12 The sliding displacement of the contact surface of column foot and stone base

图13 柱脚1偏转受力形态
Fig.13 The rocking behaviour of the first column foot
图14为各级加载位移幅值的柱脚偏转受力变化状态。柱径为 588 mm,图中初始左边点(-294 mm,0)为柱脚最左侧,中间点(0,0)为柱截面中心,右边点(294 mm,0)为柱脚最右侧,可明显看出柱脚未发生滑移,转动角度和抬升高度均不断增大。
3.3 柱头-栌斗节点变形特征
柱头-栌斗受力状态如图15所示;柱头顶面与栌斗底面的相对受力位置变化状态如图16所示,其中C代表柱头,D代表斗拱栌斗,图中虚线表示栌斗底面转动抬升变化,实线表示柱头顶面转动抬升变化,左边点代表底面最左侧,右端点代表底面最右侧,两线在初始位置均为(-294 mm,0;294 mm,0)。可以看出随柱脚的转动和抬升增大,柱头也发生与柱脚同步的转动和抬升。柱头顶面最左端抬升达到84 mm,最右端仅比原水平高度下降3 mm。表明模型在水平力作用下,通过柱脚转动而抬升柱头以上的结构层做功,增大结构重力势能,在卸载时在重力势能作用下结构能够自复位而耗散能量。栌斗底面最左端随柱头的抬升而抬升,但抬升高度比柱头顶面略低,说明栌斗底面不断压屈而嵌入柱头顶面;栌斗底面最右端与最左端连线接近水平,但比最左端略低;栌斗底面与柱头顶面成一夹角,且夹角随柱头抬升而不断增大,说明数朵单独斗拱通过梁枋连接成铺作层后整体性能很强,斗拱底面最左端随柱头的抬升而抬升,并随斗拱底面最左端的抬升而发生铺作层整体抬升(图15)。值得注意的是,上部屋盖竖向荷载主要通过斗拱中部传递到栌斗底面中部,在其作用下,斗拱最右端发生向下位移,造成栌斗底面最右端比最左端略低。
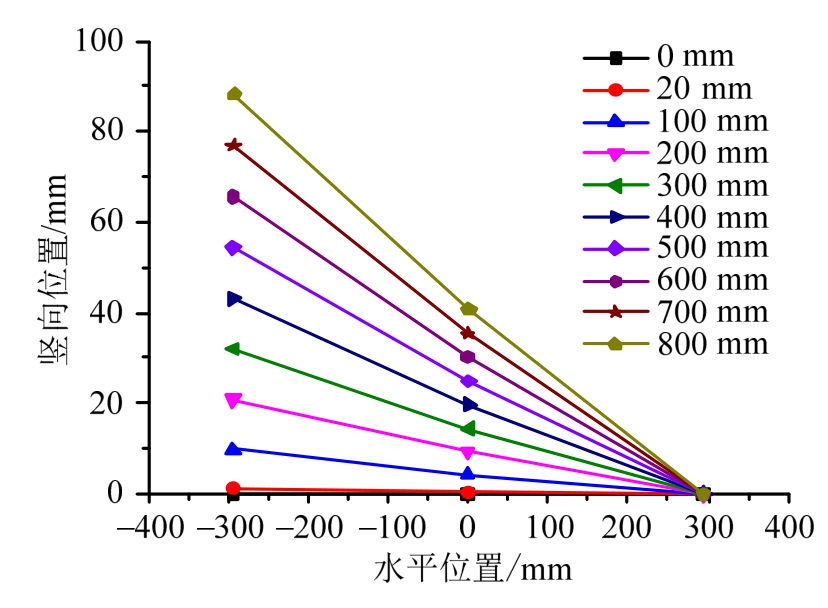
图14 柱脚1偏转受力的变化状态
Fig.14 Rotational deformation of the first column foot
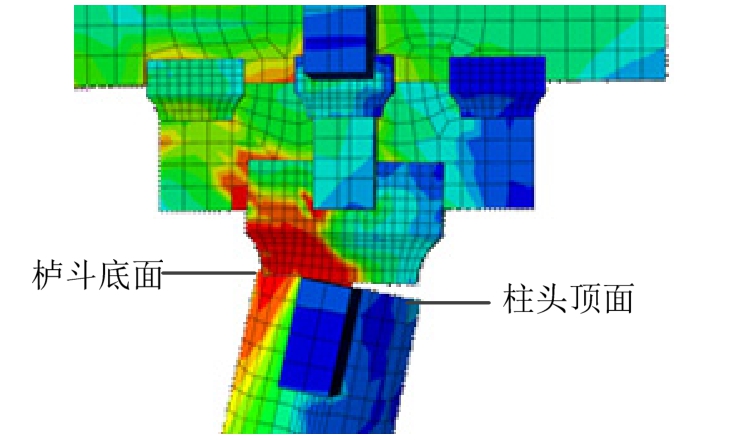
图15 柱头-栌斗节点受力状态
Fig.15 The deformation behaviour between column head and Lu-Dou brackets joints
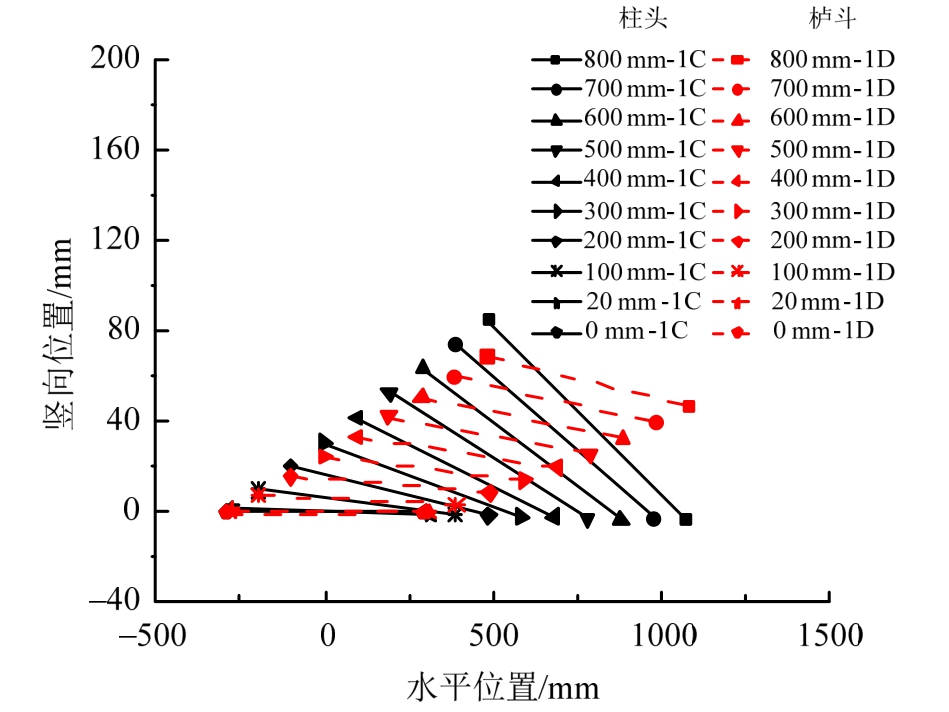
图16 柱头顶面与栌斗底面的相对位移变化状态
Fig.16 The displacement behaviour between column head and bottom of Lu-Dou
3.4 柱架摇摆变形特征
在各级位移幅值下,单根木柱与斗拱整体位移变化特征如图17所示。其中0 mm为未施加水平侧移时的位置,柱顶侧移与加载位移之间具有线性关系,柱顶位移随位移增加而同步增加。模型的整体水平位移主要是柱的水平侧移,斗拱随柱侧移而平移。在800 mm位移加载下,斗拱栌斗底面位移为781 mm,斗拱顶部位移为800 mm。斗拱在水平力作用下仅产生19 mm的相对剪切变形,变形现象不明显。图11中的整体模型变形图也表明柱的侧移较大。在各级位移幅值下,不同木柱与斗拱位移变化特征如图18所示。图例中1~4分别代表不同位置的木柱与斗拱。模型中柱顶位移、斗拱顶部位移在加载初期基本保持同步,两处的差值随加载位移增大逐渐增大但不显著,这主要是因为柱脚管脚榫和柱头馒头榫的榫头逐渐拔出,木构架整体性有所下降;加载后期梁与柱的弯曲变形逐渐增大,斗拱接触构件之间的暗榫挤压剪切严重变形,木构整体性严重下降。在斗拱铺作层的协同作用下,模型整体受力性能较好,柱网层转动抬升,铺作层整体抬升和水平移动,连接斗拱的梁枋发生轻微弯曲变形。

图17 木柱与斗拱位移变化特征
Fig.17 The displacement behaviour of one column and Dou-Gong

图18 不同木柱与斗拱位移变化特征
Fig.18 The displacement behaviour of all column and Lu-Dou
3.5 抗侧机理分析
加载初期,由于控制位移较小,柱脚抬升和构架模型摇摆现象不明显。随加载位移级别和循环次数的不断增加,模型在平面内的摇摆现象越来越显著。当加载位移达到30 mm时,柱脚开始抬升,出现摇摆现象。在构架摇摆过程中,各个柱脚均左右交替变换转动支点,发生明显抬升和木材压屈变形。当加载位移达到75 mm时,柱架摇摆现象显著,开始出现栌斗底面横纹压屈破坏(见图19)和暗销的拔出与剪切破坏(见图20)。加载位移达到 300 mm时,柱脚两侧转动支撑面发生压屈破坏。300 mm位移循环后回归水平位置时的柱脚受力变形图(图13)表明柱脚发生了不可恢复的塑性变形。当加载位移达到300 mm后,昂中部、明乳栿和草乳栿与斗拱连接端部,均开始出现弯拉弯压破坏趋势(见图21)。数值模拟水平加载结束后梁、柱以及斗拱组件基本保持完好,斗拱构件之间基本无相对变形。柱脚节点与柱头节点两侧产生严重的挤压塑性变形。栌斗整个底面产生严重压溃破坏,且破坏高度不断增大,最后上部的华拱也发生了受压破坏,是殿堂型木构架最主要的破坏形态。馒头榫与管脚榫的破坏形态为脱榫,破坏时存在显著的剪切变形。殿堂型木构架在水平荷载作用下,柱脚管脚榫、柱头馒头榫、栌斗、暗榫等相继发生破坏,加载后期木构架水平承载力不断下降,变形加剧,即将发生整体结构的倾覆破坏。
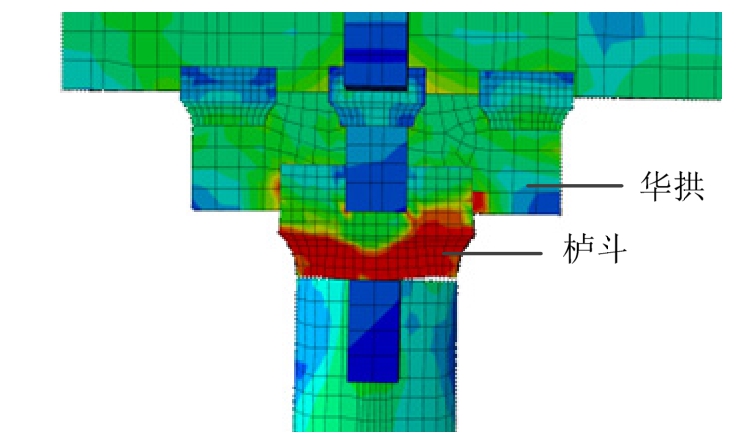
图19 栌斗的塑性不可恢复变形破坏
Fig.19 The plastic deformation of Lu-Dou
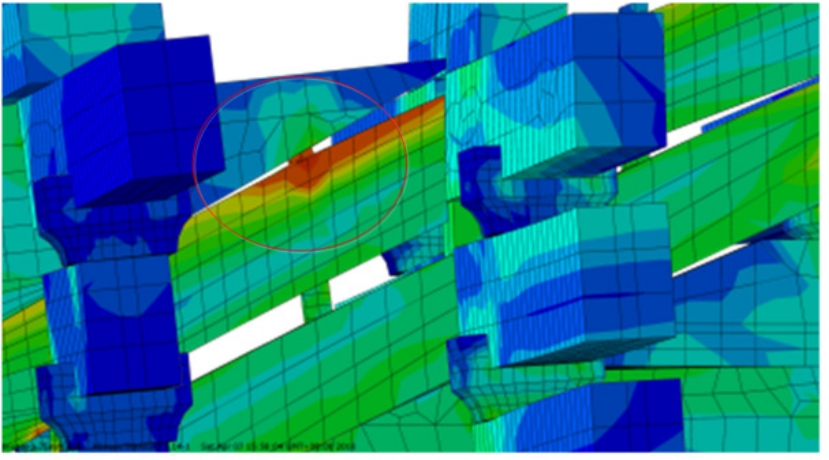
图20 暗榫拔榫与剪切破坏
Fig.20 The pull-out and shear failure of dowel
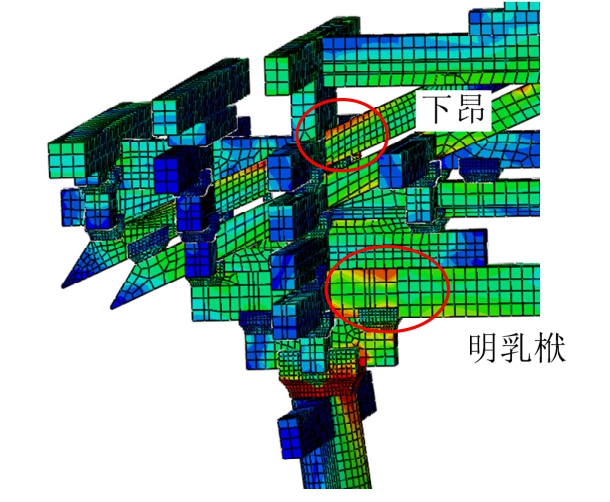
图21 昂中部和明乳栿端部的弯拉弯压破坏
Fig.21 The bending failure of Ang and Ming-ru-fu
4 结果及分析
4.1 滞回特性
殿堂型木构架模型加载点的水平荷载与位移滞回曲线左右两部分呈反对称S形(见图22),具有一定的“捏拢”效应,表明曲线受到较大的滑移影响;曲线两端比较饱满,反映出整体结构的初始变形能力较弱而后期塑性变形能力较强,能吸收较多的地震能量,比已有研究中亭榭四柱框架结构[3]和单根木柱[18]的耗能能力明显要大。观察滞回曲线的整体趋势,在各级位移循环过程中,加载时荷载-位移曲线基本一致,卸载时荷载位移曲线差别较大,位移级数越大,卸载段水平力越小。这主要是因为加载位移越大,结构塑性变形越多,结构整体抬升越高,存在不可恢复的变形和整体结构的回落恢复原位,导致卸载时水平力下降。
在加载初期, U<5 0 mm 时,滞回曲线基本呈线性发展,各曲线基本重合,滞回环较小;此时框架柱脚未抬升,卸载时基本没有残余变形,基本处在弹性阶段,抗侧刚度基本不变。这是由于柱脚受压面较大,柱脚应力未超过木材顺纹抗压强度,处于弹性阶段。随位移增加,当 U≥ 50 mm 时,滞回曲线开始呈非线性发展,滞回曲线面积增加,滞回环不再重合,出现捏拢现象;此时柱脚抬升,框架摇摆现象明显。说明在位移增大过程中,框架耗能能力增强,构件变形增加,构件受剪切挤压作用出现塑性残余变形。当位移U明显增大时,受压面集中在柱脚边缘,滞回曲线相对比较饱满,包络面积增加。在整个加载过程中,随循环次数增加滞回环面积相应增大。由滞回环斜率可知,当框架侧移较小时,曲线斜率较大,表明构件之间的相互作用较强;随位移增大,柱脚受压面集中在柱脚边缘,而栌斗受压面集中在柱顶边缘,两力形成的抵抗力偶不再增加,滞回曲线斜率逐渐降低,而后趋于平缓。正反向加载滞回曲线基本呈反对称,表明殿堂型木构架正反向受力性能基本一致。
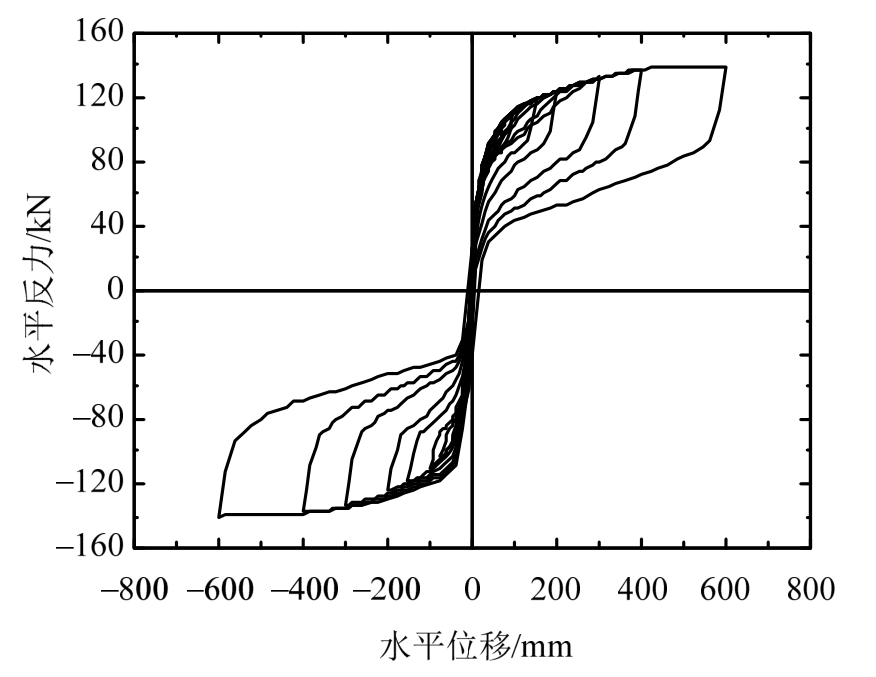
图22 滞回曲线
Fig.22 Hysteretic curve
骨架曲线呈反对称(见图23),与木材横纹受压的应力-应变曲线相似。在加载初始阶段,转动刚度较大,骨架曲线陡峭。当加载到30 mm附近时,骨架曲线产生屈服;超过30 mm后,随位移增加,骨架曲线增长速度减缓,抗侧刚度降低,水平作用力继续增大;当水平位移超过400 mm后,随位移继续增加,骨架曲线趋于水平,位移急剧增大。这是因为随位移增加,柱头随柱脚转动抬升而转动抬升,斗拱随柱头而发生抬升平动,继而整体结构产生抬升平动。当整体结构被抬升到最大高度后,结构发生严重倾斜,柱脚反力作用点和栌斗压力作用点趋于柱截面边缘,柱脚反力和栌斗压力构成的力偶达到最大后不断减小,竖向荷载的二阶距增加,增大了框架侧移的趋势,因此较小水平力就能引起较大的结构水平位移。
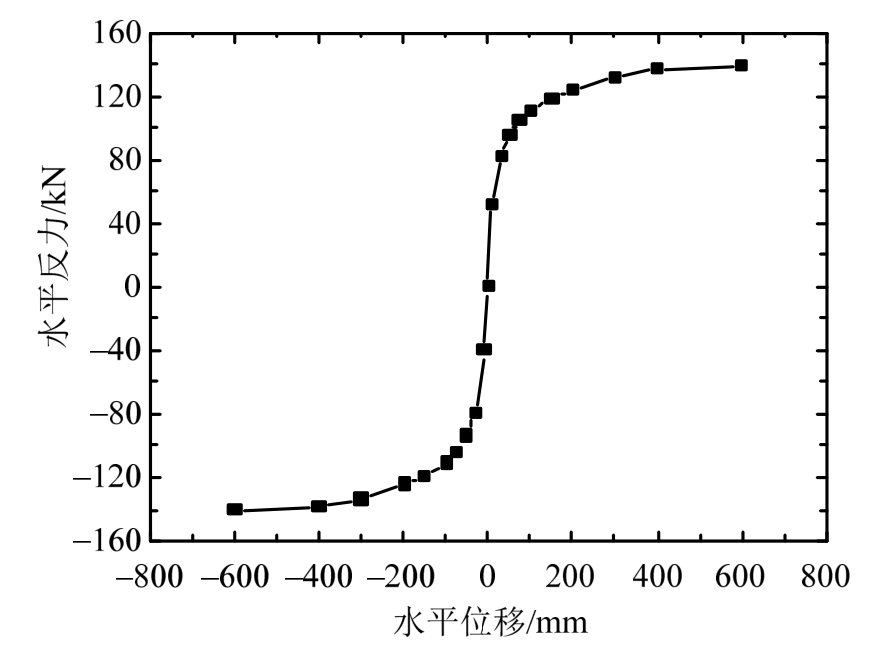
图23 骨架曲线
Fig.23 Skeleton curve
4.2 刚度退化与延性系数
模型转动刚度随水平位移和循环次数的增加而减小,产生刚度退化。延性系数u定义为各级循环位移加载正反向的极限位移绝对值之和除以正反向屈服位移绝对值之和,各级位移加载所对应的延性系数随刚度退化增大。为反映模型抗侧刚度的变化,通过计算各级循环位移加载正反向幅值点的荷载绝对值之和除以位移绝对值之和,求得模型割线刚度随延性系数的变化曲线(见图24)。图25为滞回曲线相邻加载幅值点连线的实时割线刚度随位移的变化曲线。模型初始抗侧刚度最大,并随加载位移增大不断变小。当位移达到100 mm之前,曲线下降较快,刚度退化较明显。当位移达到300 mm之后,曲线缓慢下降,刚度退化速率减慢。本文取骨架曲线线弹性段的转折点位移 30 mm为屈服位移,框架模型延性系数最高达到20,且最大位移时水平力为正值。框架模型从受力直到破坏,构件屈服后的塑性变形能力较大,承载能力较强,通过材料破坏、摩擦滑移、整体转动抬升来耗散能量,结构具有较好的延性和很好的耗能能力。
模型刚度退化主要是由柱脚的转动抬升、柱头的转动抬升和铺作层栌斗的抬升平动引起。随柱脚转动抬升增加,柱脚受压面由全截面受压变为部分截面受压,受压面逐渐变小,柱脚反力作用点由柱脚中心向柱脚一侧边缘偏移;柱头随柱脚转动抬升而同步转动抬升,栌斗受压面由全截面受压变为部分截面受压,受压面积也减小,与柱顶面的压力作用点由柱头顶面中心向柱头一侧边缘偏移,偏移方向与柱脚相反,柱脚反力与柱头压力构成一对力偶,力偶为抵抗弯矩,随位移增加力偶不断增加。此时柱头压力和柱脚反力作用点的偏移能引起木柱抵抗力偶快速增加,框架抗侧移刚度较大。竖向荷载不变,当柱脚受压面和栌斗受压面均靠近木柱边缘时,受压面的变化不再引起抵抗力偶的增加,相反栌斗底面和柱脚底面边缘的受压屈服导致两个受力点距离的不断减小,即力偶减小,抗侧刚度逐渐降低,出现刚度退化现象。同时在模型摇摆过程中,柱脚和栌斗底面残余变形等不可逆变形也会引起抗侧刚度的降低。当加载到最大位移时,框架仍具有一定抗侧移能力。
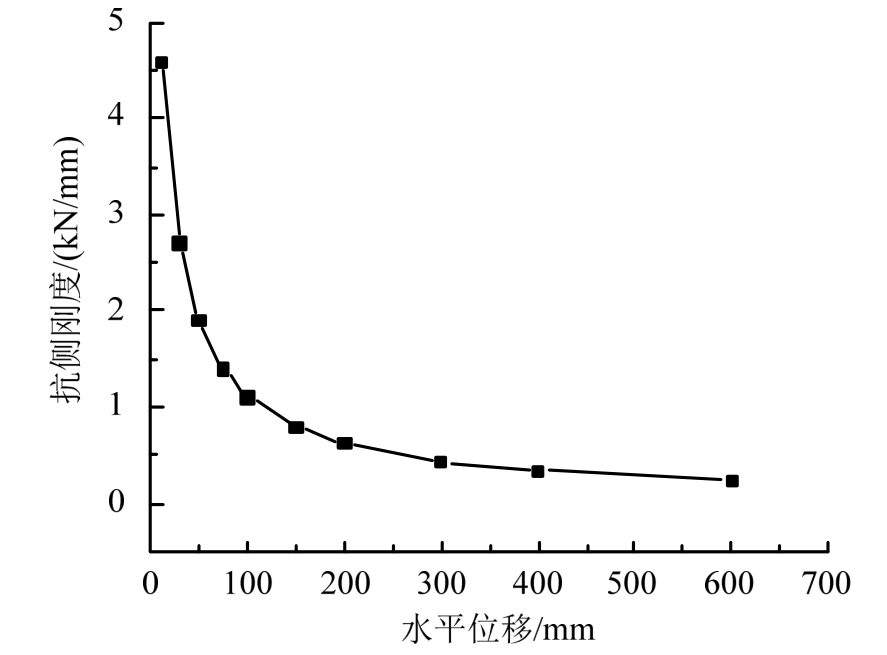
图24 整体模型刚度退化曲线
Fig.24 The stiffness degradation curve
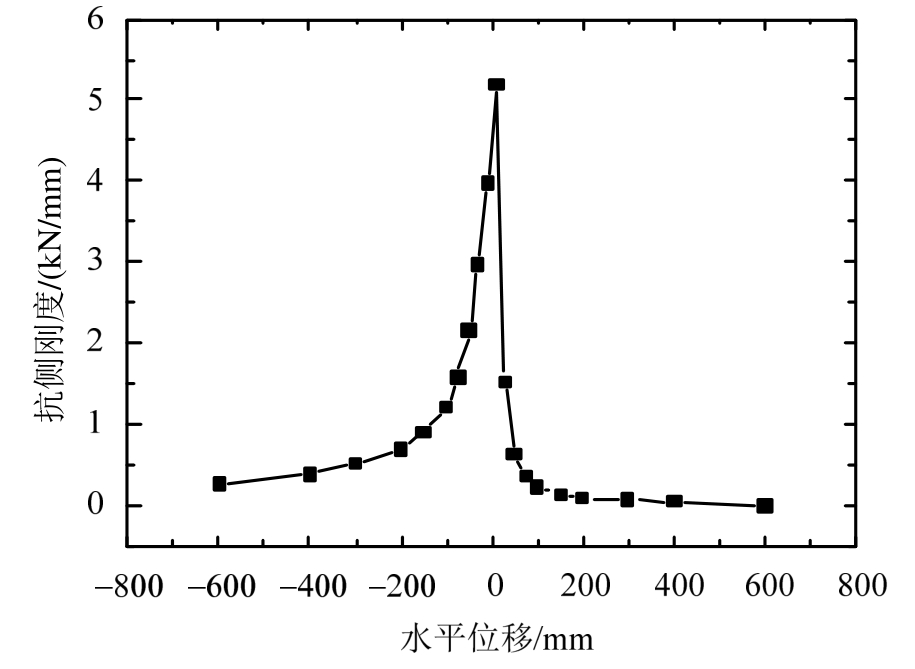
图25 相邻加载位移幅值点割线刚度
Fig.25 The secant stiffness of adjacent peak value of displacement
4.3 耗能特征与等效粘滞阻尼系数
每级加载位移累计消耗的能量如图26所示,其随位移增加而增大。能量消耗曲线由两段直线组成。100 mm为曲线转折点,表明加载到100 mm位移后构件耗能能力的增大源于不断积累的塑性变形。
根据图27所示的方法计算每级位移幅值对应滞回环的等效粘滞阻尼系数。由图28可知,其随位移增加而不断增大,耗能能力逐渐增强。在加载初始阶段,加载位移小于100 mm前,等效粘滞阻尼系数较小,接近于零。这是由于有限元模型构件组装无缝隙,在弹性阶段位移变形较小,耗能能力较弱。随位移增加,等效粘滞阻尼系数急剧增大。由于构件间发生摩擦滑移,暗榫发生剪切挤压,柱脚和柱头发生转动抬升,铺作层与屋架层的抬升和平动,柱脚和柱头栌斗的受压塑性变形等方式进行耗散能量,耗能快速增大。由于接触面滑动摩擦力不变,构件已经发生屈服或破坏,整体结构已经抬升到最大高度,等效粘滞阻尼系数增加势缓,继续加大位移将保持不变。加载到600 mm时最大值约为0.15,耗散能量曲线仍呈增大趋势。
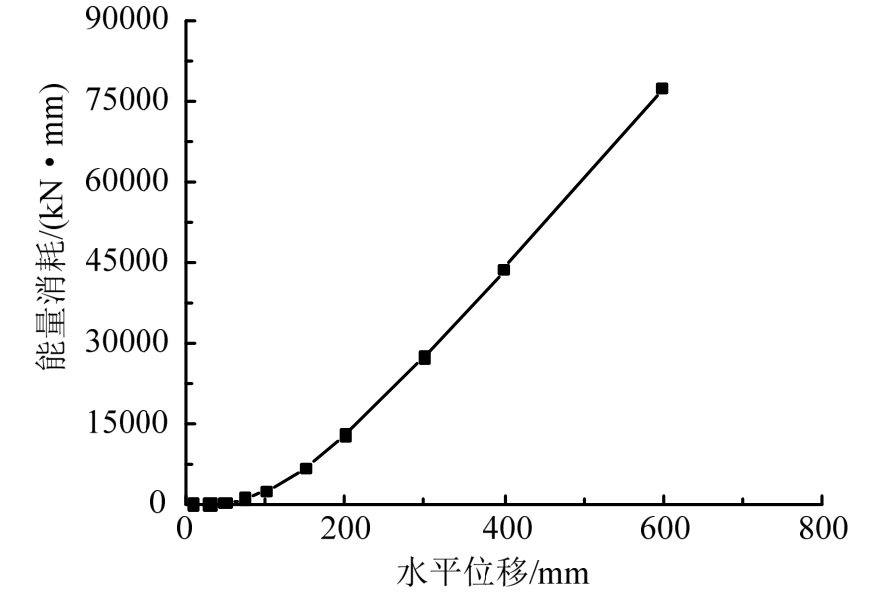
图26 累积能量消耗曲线
Fig.26 Curve of the accumulated energy dissipation
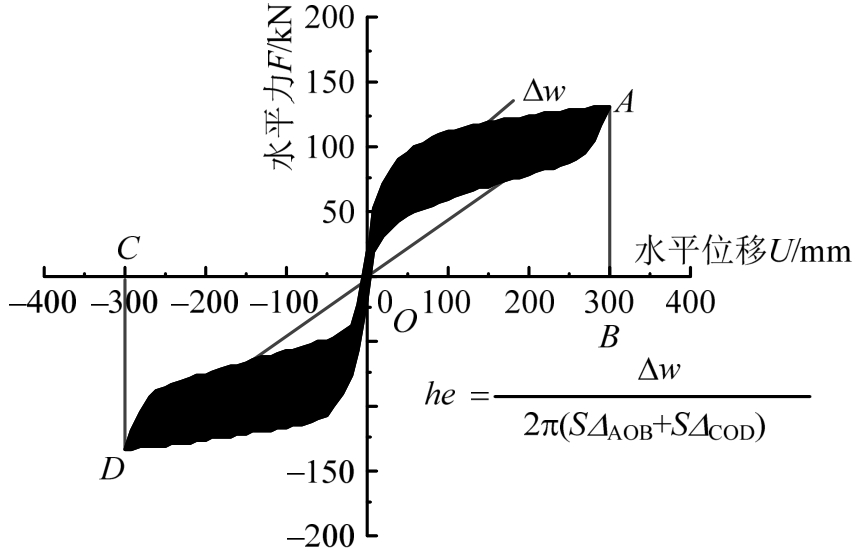
图27 等效粘滞阻尼系数计算方法
Fig.27 Calculation method of viscous damping ratio

图28 等效粘滞阻尼系数
Fig.28 Curve of viscous damping ratio
5 结论
(1)在水平低周反复荷载作用下,唐代殿堂型木构架柱脚转动抬升无滑移,栌斗底面随柱头抬升而升高,从而发生整体铺作层及屋架的抬升,木构架表现为转动抬升摇摆,铺作层如刚体般随柱的侧移而平移。
(2)木构架摇摆过程中,馒头榫与管脚榫发生脱榫和剪切变形,栌斗底面横纹压屈,暗榫、暗销发生拔出与剪切破坏,柱脚与柱头的转动边缘产生挤压破坏,明乳栿、草乳栿、斜昂构件均产生严重弯曲受力现象,铺作层与屋架层基本保持完好。
(3)殿堂型木构架的抗侧力-位移滞回曲线呈“S”形,具有显著捏拢效应,曲线两端较饱满。木构架初始抗侧刚度较大,屈服后刚度退化显著,通过柱脚节点和柱头-栌斗节点的塑性变形、构件接触面的摩擦滑移、整体转动抬升耗能;其消耗能量随位移增加而剧增,具有较好的延性和较高的耗能能力。
[1]高大峰.中国木结构古建筑的结构及其抗震性能研究[D].西安:西安建筑科技大学,2007.Gao Dafeng.A research on the structure and their aseismic characteristics of ancient chinese timber buildings [D].Xi’an:Xi’an University of Architecture and Technology,2007.(in Chinese)
[2]隋䶮,赵鸿铁,薛建阳,等.古建木构铺作层侧向刚度的试验研究[J].工程力学,2010,27(3):74―78.Sui Yan,Zhao Hongtie,Xue Jianyang,et al.Experimental study on lateral stiffness of Dougong layer in Chinese historic buildings [J].Engineering Mechanics,2010,27(3):74―78.(in Chinese)
[3]Chen J Y,Li T Y,Yang Q S,et al.Degradation laws of hysteretic behaviour for historical timber buildings based on pseudo-static tests [J].Engineering Structures,2018,156 (2018):480―489.
[4]陈春超.古建筑木结构整体力学性能分析和安全性评价[D].南京:东南大学,2016.Chen Chunchao.Integral mechanics property analysis and safety evaluation of ancient timber structures [D].Nanjing:Southeast University,2016.(in Chinese)
[5]刘妍,杨军.独乐寺辽代建筑结构分析及计算模型简化[J].东南大学学报(自然科学版),2007,37(5):887―891.Liu Yan,Yang Jun.Structural analysis and modeling simplification of Liao-dynasty structures in Dule Temple[J].Journal of southeast university.2007,37(5):887―891.(in Chinese)
[6]Lee Y W,Hong S G,Bae B S,et al.Experiments and analysis of the traditional wood structural frame [C]//The 14th World Conference on Earthquake Engineering,Beijing,China,2008.
[7]Ayala D F,Tsai P H.Seismic vulnerability of historic Dieh-Dou timber structures in Taiwan [J].Engineering Structures,2008,30(8):2101―2113.
[8]清华大学建筑设计研究院、北京清华城市规划设计研究院文化遗产保护研究所编著.佛光寺东大殿建筑勘察研究报告[M].北京:文物出版社,2011.Architectural design and Research Institute of Tsinghua University:Research Report on Building Investigation of the Main Hall of Fo-guang Temple [M].Beijing:Cultural Relics Publishing House,2011.(in Chinese)
[9]祁伟成.五台佛光寺东大殿[M].北京:文物出版社,2012.Qi Weicheng:The main hall of Wutai fo-guang temple[M].Beijing:Cultural Relics Publishing House,2012.(in Chinese)
[10]潘德华.斗栱(上册)[M].南京:东南大学出版社,2004.Pan Dehua.Dou-Gong (I)[M].Nanjing:Southeast University Publishing House,2004.(in Chinese)
[11]侯幼彬,李婉贞.中国古代建筑历史图说[M].北京:中国建筑工业出版社,2002.Hou Youbin,Li Wanzhen.The historical graph theory of ancient Chinese Architecture [M].Beijing:China Architecture & Building Press,2002.(in Chinese)
[12]马炳坚.中国古建筑木作营造技术[M].北京:科学出版社,1991:126―127.Ma Bingjian.Construction technology of Chinese ancient timber structure [M].Beijing:Science Press,1991:126―127.(in Chinese)
[13]陈志勇.应县木塔典型节点及结构受力性能研究[D].哈尔滨:哈尔滨工业大学,2011.Chen Zhiyong.Behaviour of typical joints and the structure of Yingxian wood pagoda [D].Harbin:Harbin Institute of Technology,2011.(in Chinese)
[14]《木结构设计手册》编辑委员会.木结构设计手册(第三版)[M].北京:中国建筑工业出版社,2005.The editorial board of the wooden structure design manual.Handbook for design of wood structure (The third edition)[M].Beijing:China Architecture & Building Press,2005.(in Chinese)
[15]刘大可.古建筑屋面荷载汇编(上)[J].古建园林技术,2001(3):58―64.Liu Dake.Load assembler of roofing of ancient building(The first volume)[J].Traditional Chinese Architecture and Gardens,2001(3):58―64.(in Chinese)
[16]刘大可.古建筑屋面荷载汇编(下)[J].古建园林技术,2001(4):56―63.Liu Dake.Load assembler of roofing of ancient building(The second volume)[J].Traditional Chinese Architecture and Gardens,2001(4):56―63.(in Chinese)
[17]贺俊筱,王娟,杨庆山.摇摆状态下古建筑木结构木柱受力性能分析及试验研究[J].工程力学,2017,34(11):50―58.He Junxiao,Wang Juan,Yang Qingshan.Theoretical and Experimental analysis on mechanical behavior of column in traditional timber structure during rocking [J].Engineering Mechanics,2017,34(11):50 ― 58.(in Chinese)
[18]He Junxiao,Wang Juan.Theoretical model and finite element analysis for restoring moment at column foot during rocking [J].Journal of Wood Science,2018,64(2):97―111.
[19]Masaki Maeno,Yoshiyuki Suzuki,Tatsuya Ohshita,et al.Seismic response characteristics of traditional wooden frame by full-scale dynamic and static tests [C]// The 13th World Conference on Earthquake Engineering,Vancouver,Canada,2004.