摘 要：界面粗糙度对岩石-混凝土界面断裂特性有重要影响。为研究不同粗糙度岩石-混凝土界面断裂特性，对岩石表面进行刻槽处理获得六种界面粗糙度，采用三点弯曲梁岩石-混凝土复合试件测量界面的断裂参数。运用数值方法计算了界面的起裂断裂韧度
并通过P-δ曲线计算界面的断裂能Gf。试验结果表明，所有试件都沿着界面发生破坏，说明岩石-混凝土界面相对于两侧材料属于薄弱面；采用界面刻槽的方式能够获得较大范围的粗糙度数值，当界面粗糙度Ra从0.676 mm增大到2.028 mm时，岩石-混凝土界面起裂断裂韧度
从0.362 MPa·m1/2增加到0.515 MPa·m1/2，提高了42.3%；界面断裂能Gf从17.928 N/m增加到47.802 N/m，提高了166.7%；同时
随着粗糙度的提高一直增大，而Gf随着粗糙度的提高先增大后趋于平缓。
岩石-混凝土界面力学性能薄弱，是众多建造在岩基上的混凝土建筑物的薄弱面，在外部荷载的作用下容易引起界面裂缝的萌生与扩展，因而受到了许多学者的关注[1―4]。与准脆性材料的断裂过程类似，岩石-混凝土界面的裂缝扩展也分为三个阶段：起裂，稳定扩展，失稳扩展。在运用虚拟裂缝模型研究准脆性材料的裂缝扩展过程时，描述裂缝前端应变软化行为的软化关系曲线是必不可少的参量，而断裂能是确定软化曲线重要的材料参数[5]。同时，双K断裂模型[6―7]在评判裂缝的起裂状态时使用了起裂断裂韧度这一断裂参数，能够准确的预估结构的起裂时间，而且基于起裂断裂韧度的裂缝扩展准则[8]在针对混凝土和界面的裂缝扩展研究中具有很强的适用性。因此，对岩石-混凝土界面的起裂断裂韧度和断裂能等断裂参数进行试验研究很有必要，这有助于进一步分析岩石-混凝土界面的断裂行为。
在岩石-混凝土界面断裂特性的试验研究方面，学者们已经做出了许多有益的工作。Kishen[9]进行了石灰岩-混凝土界面的楔入劈拉试验以研究界面的断裂能，试验结果表明界面峰值荷载是纯混凝土材料试件的61%，同时界面的断裂能只占混凝土试件断裂能的21%。陆超等[10]进行了不同缝高比情况下自然界面的岩石-混凝土三点弯曲梁试验，研究缝高比对界面应力强度因子和断裂能的影响，发现缝高比对界面断裂参数基本没有影响。Dong等[11]对岩石表面进行刻槽处理，研究了粗糙度对界面断裂参数的影响，试验结果表明界面断裂参数随着粗糙度的增大而提高，因此可以通过提高粗糙度来增强界面的抗裂性。李哲等[12]针对界面断裂特性研究的三点弯曲梁试验表明界面断裂能和断裂韧度均远小于两侧材料的断裂参数，说明界面相对于两侧介质属于薄弱层。既然界面断裂参数小于两侧介质，且随着界面粗糙度的增大而提高，那么其在界面粗糙度较大情况下的限值问题就成为一个值得探讨的问题。
本文采用三点弯曲梁试件和轴心受拉试件测量岩石-混凝土界面的断裂参数。对岩石表面进行刻槽处理获得六种界面粗糙度，以灌砂法量化粗糙度Ra。对复合试件进行三点弯曲梁试验测得起裂荷载(Pini)、荷载-裂缝口张开位移(P-CMOD)曲线和荷载-加载点位移(P-δ)曲线。运用计算界面应力强度因子的数值方法，结合起裂荷载 Pini，计算了界面的起裂断裂韧度Kini 1，并通过P-δ曲线计算界面的断裂能Gf。分别对粗糙度与起裂断裂韧度、粗糙度与断裂能进行拟合，得到了Kini 1与Gf随Ra的变化规律。
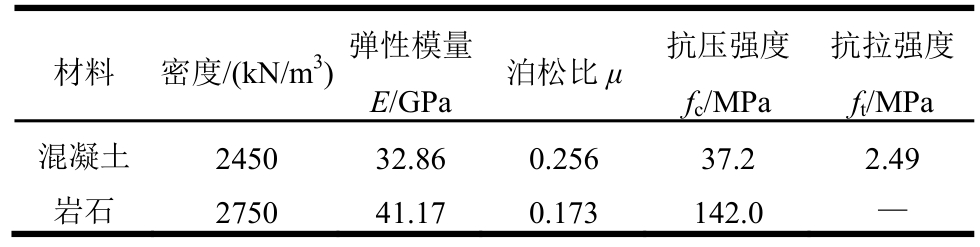
三点弯曲梁试验所用岩石-混凝土复合试件包含岩石和混凝土两种材料。其中岩石部分为花岗岩石材，取材自大连双塔石材加工厂，原材料在此加工厂制作成合适尺寸的试件后运送到实验室。混凝土材料强度设计等级为 C30，配合比为水泥∶砂子∶石子∶水=1∶2∶3.7∶0.6。其中，石子采用最大粒径为10 mm的瓜子石，砂子为普通河砂，水泥采用P.O.42.5普通硅酸盐水泥，由大连小野田水泥公司生产。岩石和混凝土材料的基本材料参数见表1。
表1 岩石和混凝土材料的基本材料参数
Table 1 Basic material parameters of rock and concrete materials
本批次试验包括三点弯曲梁复合试件、界面直拉试件。三点弯曲梁试件尺寸为100 mm×100 mm×500 mm，其中混凝土和岩石部分尺寸均为100 mm ×100 mm×250 mm。自然粘结界面高100 mm，包含70 mm的粘结段和30 mm的预制裂缝段。预制裂缝通过粘贴两片减摩片实现，减摩片尺寸为100 mm×30 mm，试件的具体尺寸和预制裂缝设置如图1所示。
图1 三点弯曲梁和直拉试件
Fig.1 The specimen of three point bending beam and tension specimen
为了研究界面粗糙度对复合界面断裂参数的影响，本次试验对岩石界面进行了刻槽处理[1]，刻槽工作在全自动化仪器上进行，以实现槽口尺寸的标准化。槽口深度3 mm，槽线均平行于对角线。本批次三点弯曲梁试件共包含六种界面粗糙度，分别为3×3、4×4、5×5、7×7、10×10和12×12。以3×3为例，数字3表示岩石表面侧边被平分成3份，各粗糙度界面如图2所示。
图2 界面粗糙度
Fig.2 Interface roughness
岩石表面经刻槽处理后，采用灌砂法量化岩石-混凝土界面的粗糙度，以定量评价其对界面断裂参数的影响。灌砂法是一种体积转化的方法，如图3所示，在处理后的岩石粗糙面上均匀铺撒细密的砂，填满刻槽并且不超过岩石初始表面，将槽口体积转化为可量测的细砂体积，以砂子体积除以岩石侧表面积就可得到界面粗糙度数值，如式(1)所示：
式中：A/mm2为岩石侧表面积；V/mm3为灌砂体积。
图3 灌砂法测量粗糙度
Fig.3 Roughness measurement by sand cone method
三点弯曲梁试验在250 kN电液伺服万能试验机(MTS)上进行，试验加载布置如图4所示，从上至下依次是10 t荷载传感器、加载头、复合梁和固定支座，支座间距400 mm，采用位移加载方式，加载速度0.024 mm/min。在预制裂缝缝尖位置对称布置四个格栅尺寸为10 mm×2 mm的电阻应变片监测加载过程中的缝尖应变数据，梁体侧面和底面布置夹式引伸仪量测加载点位移和裂缝口张开位移，试验数据通过IMC数据采集系统采集。
图4 三点弯曲梁试验加载装置
Fig.4 Loading device for three point bending test
岩石-混凝土界面直拉试验如图5所示。加持装置上带有球铰，可以避免拉拔过程中受力偏心的影响。试件两端通过建筑结构胶与加持装置牢固粘接，保证试验过程中不会出现松动。
图5 直拉试验
Fig.5 Tension test
如图6所示，六种界面粗糙度的岩石-混凝土复合梁在三点弯曲加载条件下均沿界面发生破坏，裂缝从预制裂缝缝尖处萌生并逐渐贯通整个界面，没有出现裂缝曲折发展进入两侧基体材料的情况。从界面的截断面来看，岩石部分基本保持完整，没有产生材料剥离破碎的现象，减摩片与岩石材料粘贴牢靠，说明预制裂缝尺寸符合预期要求；混凝土界面上非槽口部分较为光滑，而与岩石槽口对应部分基体材料发生剥离，这是因为岩石的抗拉强度远大于混凝土，说明采用的切槽方式对界面粘结性能具有重要的影响。
图6 三点弯曲梁的破坏模式及断面形式
Fig.6 Failure mode and fracture section of three point bending test
试验采用的加载速率为0.024 mm/min，在试验机刚度足够大的情况下，可以得到三点弯曲梁复合试件完整的P-δ曲线，如图7所示。
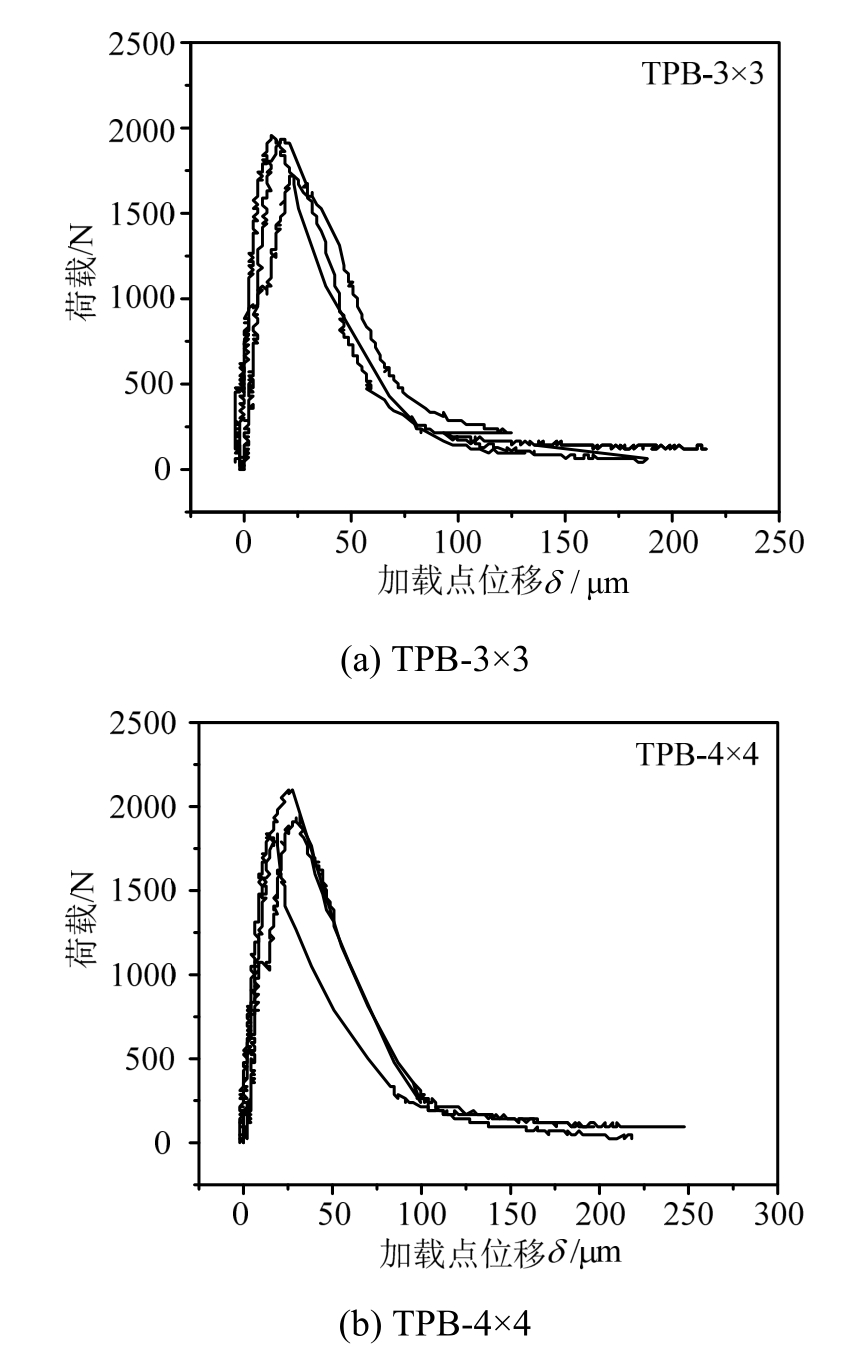
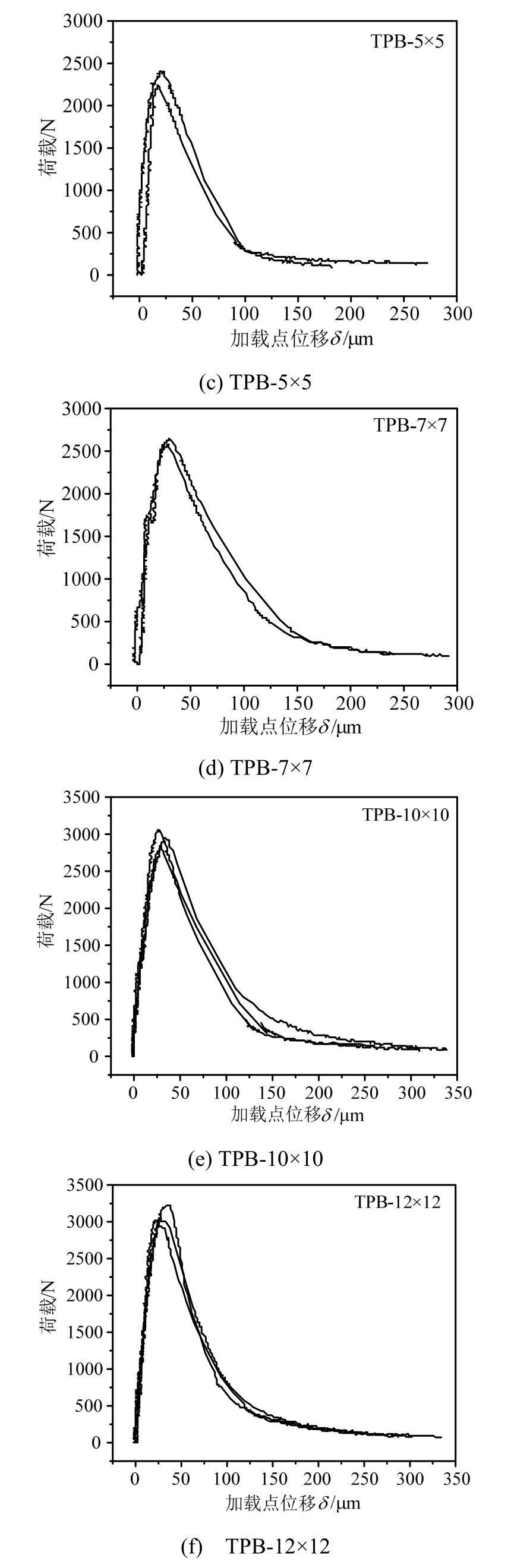
图7 三点弯曲梁P-δ曲线
Fig.7 P-δ curve of three point bending beam
与均质准脆性材料类似，岩石-混凝土界面受弯断裂的P-δ曲线由上升段和软化段组成，表现出显著的非线性和软化特征。在加载初期荷载较小，曲线斜率较大；随着荷载增大，P-δ曲线的斜率逐渐减小，说明复合梁的刚度逐渐降低，这是因为预制裂缝缝尖处已经有微裂缝萌生并扩展，继续加载到达峰值荷载后进入曲线软化段，荷载降低的同时δ显著增大。
三点弯曲梁复合试件中裂缝起裂时的状态对应着起裂荷载Pini和预制裂缝长度a0，由于a0已知为试验设定值，因此测定起裂断裂韧度的关键就是确定试件的起裂荷载。起裂荷载有诸多试验测定方法，如电阻应变片法[13]、声发射法[14]、光弹贴片法[15]等，基于实验室条件和试验便于实现等考虑，本试验采用了电阻应变片法测量起裂荷载。
从加载开始，布置在裂缝尖端的应变片数值不断增大，基本上呈线性增长，至某一荷载裂缝达到起裂状态，混凝土中聚集的能量得到释放，表现为应变片数值突降，曲线上出现“拐点”，此时对应的荷载即为起裂荷载，如图8所示，荷载-应变曲线中箭头指向点即为起裂荷载对应点。电阻应变片法意义明确，易于操作，测量结果也较为准确。
图8 TPB-3×3试件荷载-裂缝尖端应变曲线
Fig.8 Load-Strain curve of TPB-3×3 specimen
对于混凝土I型断裂，得到起裂荷载后可直接带入线弹性应力强度因子计算公式计算起裂断裂韧度，但对于界面断裂问题，由于缝尖应力状态的高度非线性以及两侧材料性质差异，难以运用解析方法分析计算裂尖应力强度因子，而需要借助有限元的方法进行定量计算。位移外推法[16]作为一种常用的计算界面应力强度因子的方法，不需要考虑界面裂尖应力振荡区内的数据，而是采用振荡影响区外的位移数值，具有较高的准确性。运用位移外推法时，先通过有限元方法计算缝尖附近的位移场，得到节点位移数值后，代入公式计算裂缝处节点的应力强度因子，并通过线性外推方法计算缝尖的应力强度因子，具体计算公式如式(2)所示：
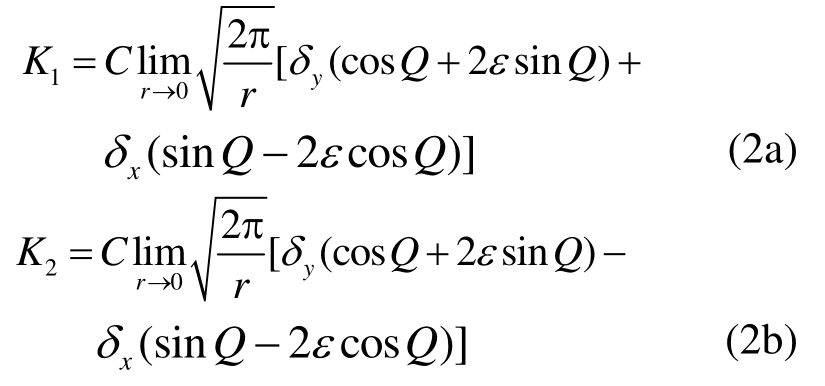
其中：
式中：Ei和νi分别表示弹性模量和泊松比。实际计算中，选取裂尖附近的的两对节点(a1,a2)和(b1,b2)，如图9所示，将裂缝表面两对节点之间的相对位移
代入式(2)计算各自的应力强度因子
然后由式(2)的线性插值公式计算裂缝尖端的应力强度因子K1和K2。
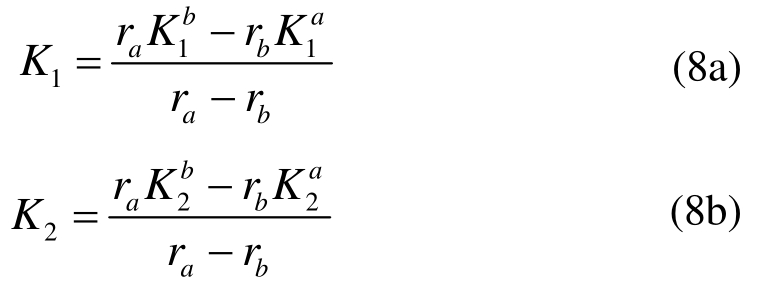
图9 位移外推法
Fig.9 Displacement extrapolation
结合试验测得的起裂荷载以及上文介绍的应力强度因子计算方法，便可以运用有限元软件ANSYS进行数值计算。计算时需要各粗糙度界面的抗拉强度值 ft。根据轴心受拉试件试验结果拟合得到ft与Ra的线性关系，见图10。
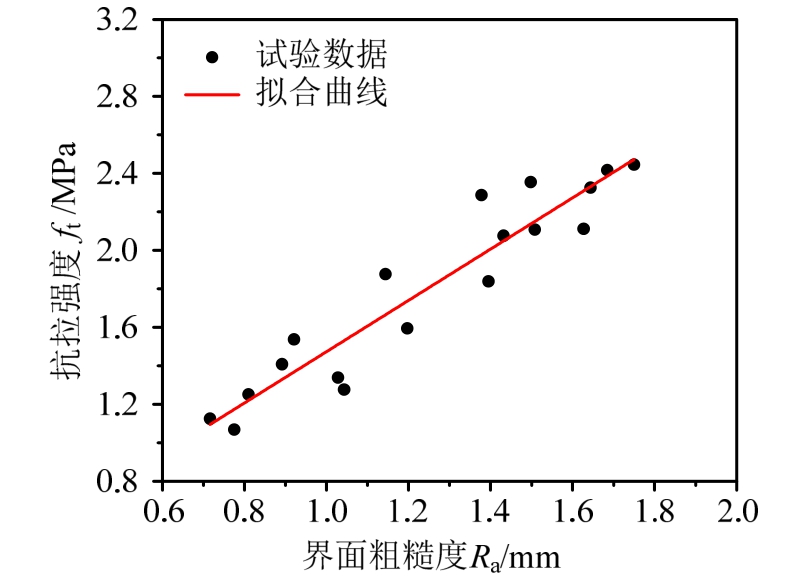
图10 粗糙度与界面抗拉强度线性拟合
Fig.10 Linear fitting between roughness and interface tensile strength
当粗糙度介于0.716～1.801的范围内，岩石-混凝土界面抗拉强度 ft随着粗糙度增大而提高，从1.068提高到2.445，提高了129%。两者的线性拟合公式为ft =1.326Ra+0.149，相关系数R2=0.882。
图11是二维有限元模型，采用PLANE 183单元，具有2维8节点和二次位移函数，能够较好地应对不规则模型的网格划分。模型尺寸和边界条件与实际试件保持一致，材料参数取试验实际测量结果。裂尖处进行了细密的网格划分以适应裂缝尖端复杂的应力场和位移场。在该模型上施加试验测得的起裂荷载计算
图11 三点弯曲梁有限元模型
Fig.11 Finete element model of three point bending beam
表2列出了不同工况下的岩石-混凝土界面粗糙度、起裂荷载、峰值荷载、起裂断裂韧度的试验与计算数据。由表2可知，本文采用的刻槽方式能够获得较大范围的粗糙度数值，且随着粗糙度的增大，试件的起裂荷载呈上升趋势，其中，试件TPB-5×5-3和 TPB-7×7-3由于加载机器操作原因没能得到完整的加载曲线，未纳入试验结果统计。Ⅱ型起裂断裂韧度
与Ⅰ型起裂断裂韧度
的比值在2%以内，可以近似认为岩石-混凝土界面三点弯曲梁试件为纯Ⅰ型断裂。
图12所示为界面粗糙度与Ⅰ型起裂断裂韧度的关系图。对试验得到的的数据点进行拟合，得到线性关系式
线性相关系数 R2为0.832。本试验的界面粗糙度Ra从0.676增加到2.028，界面Ⅰ型起裂断裂韧度
从0.362增加到0.515，提高了42.3%，且没有趋于平缓的趋势。
表2 三点弯曲梁试验与计算结果
Table 2 Three point bending beam test and calculation results
图12 粗糙度对界面起裂断裂韧度的影响
Fig.12 The effect of roughness on initial fracture toughness
在研究混凝土的断裂行为时，Hillerborg等[17]提出的虚拟裂缝模型具有重要的作用。在该模型中，断裂能是一项非常重要的断裂参数，其有助于确定断裂过程区软化曲线的形状，是运用数值方法进行断裂研究必不可少的参数[18―20]。断裂能Gf的定义是裂缝前端断裂过程区单位面积吸收的外力功，用公式表示为：
式中，σ(ω)表示软化曲线公式，也就是说断裂能等于软化曲线的下包络面积。由试验测得的荷载-加载点位移曲线可以计算断裂能的数值，同时需要考虑三点弯曲梁体自重的影响。计算过程中可以将梁体自重等效为一附加力，与外部荷载同时作用在梁上，即总荷载为P+mg。假设外部荷载做功全部用于裂缝向前扩展，且外部荷载、梁体自重与梁体变形处于同一方向，三点弯曲梁断裂能计算公式为：
式中：W0为外部荷载做的功，大小等于荷载-加载点位移曲线包络面积；δ0为三点弯曲梁受力破坏时刻对应的加载点位移，一般取加载曲线上对应于峰值荷载的5%的位移；D为试件高度；a0为预制裂缝长度；t为试件宽度；(D－a0)t即为初始韧带面积。断裂能计算结果如表3所示。
表3 三点弯曲梁断裂能
Table 3 Fracture energy of three point bending beam
根据表3的结果，随着粗糙度的提高，复合试件的断裂能逐渐增大，加载点位移也随之增加。同时，断裂能与加载点位移的变化趋势基本相同，这是因为外部荷载做的功绝大部分都用于裂缝的扩展，断裂能与加载点位移有对应关系，这一点从断裂能计算公式中也可得到验证。同时，从图13可以发现，界面断裂能数值随着粗糙度上升的过程中逐渐趋于平缓。如图13所示，转折点处的界面粗糙度为1.618，断裂能为44.139 N/m。
图13 粗糙度对界面能的影响
Fig.13 The effect of roughness on interface energy
本文进行了岩石-混凝土复合试件的三点弯曲梁试验和轴向拉伸试验，通过在岩石表面刻槽获得不同粗糙度，研究了界面粗糙度与界面起裂断裂韧度、断裂能的关系。根据本文的试验和分析结果，可得到以下结论：
(1)采用岩石表面刻槽的方式能够获得较大范围的粗糙度数值。在该种刻槽方式下，刻槽数量为12×12的试件截面槽口数量已到极限，该种刻槽方式的粗糙度限值在2左右。后续研究可以采用增加槽口深度的方法继续增加界面粗糙度。
(2)从三点弯曲梁复合试件的破坏形式看，所有试件都沿界面发生破坏，说明岩石-混凝土复合试件的界面相对于两侧材料属于薄弱面，在实际工程中应当加以重视。
(3)随着界面粗糙度Ra的增加，岩石-混凝土界面起裂断裂韧度
不断增大，而界面断裂能
先增大后保持不变。这表明，在本文研究的界面粗糙度范围内，
随着Ra的增加存在限值，而
随着Ra的增加未发现限值。
[1]Zhong H,Ooi E T,Song C,et al.Experimental and numerical study of the dependency of interface fracture in concrete–rock specimens on mode mixity [J].Engineering Fracture Mechanics,2014,124/125(9):287―309.
[2]Dong W,Wu Z,Zhou X.An experimental study on crack propagation at rock-concrete interface using digital image correlation technique [J].Engineering Fracture Mechanics,2017,171: 50―63.
[3]李哲,简政,黄松梅.岩石与混凝土 I—II复合型界面裂缝临界断裂曲线的研究[C]// 第6届全国结构工程学术会议论文集,广西,1997: 557―561.Li Zhe,Jian Zheng,Huang Songmei.Research on the critical fracture curve of rock-concrete interface crack[C]// Proceedings of the 6th National Conference on Structural Engineering,Guangxi,1997: 557―561.(in Chinese)
[4]Hussein M,Marion B,Madly L.Experimental study of the shear strength of bonded concrete-rock interfaces:surface morphology and scale effect [J].Rock Mechanics and Rock Engineering,2017(1): 1―25.
[5]王璀瑾,董伟,王强,等.混凝土 I型裂缝扩展准则比较研究[J].工程力学,2016,33(5): 89―96.Wang Cuijin,Dong Wei,Wang Qiang,et al.A comparative study on propagation criterion of Concrete mode I crack [J].Engineering Mechanics,2016,33(5):89―96.(in Chinese)
[6]Xu S,Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture,Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams [J].International Journal of Fracture,1999,98(2): 151―177.
[7]Choubey R K,Kumar S.Simplified equations for determining double-K fracture parameters of concrete for 3-point bending test [J].Fatigue ＆ Fracture of Engineering Materials ＆ Structures,2018,41(7): 1615―1626.
[8]Dong W,Wu Z,Zhou X.Calculating crack extension resistance of concrete based on a new crack propagation criterion [J].Construction ＆ Building Materials,2013,38(2): 879―889.
[9]Kishen J.Fracture of rock-concrete interfaces: laboratory tests and applications [J].ACI Structural Journal,2004,101(3): 325―331.
[10]陆超,何佳文,董伟.四点剪切条件下岩石-混凝土界面裂缝扩展过程研究[J].水利与建筑工程学报,2015,13(5): 83―89.Lu Chao,He Jiawen,Dong Wei.Study on the crack propagation of the rock-concrete interface under four-piont shear load [J].Journal of Water Resources and Architectural Engineering,2015,13(5): 83―89.(in Chinese)
[11]Dong W,Wu Z,Zhou X.Fracture mechanisms of rock-concrete interface: Experimental and numerical [J].Journal of Engineering Mechanics ASCE,2016,142(7):4016040.
[12]李哲,杨水成,张浩博.岩石与混凝土界面裂缝的断裂能及断裂韧度[J].水资源与水工程学报,1998,9(1):42―45.Li Zhe,Yang Shuicheng,Zhang Haobo.Fracture energy and fracture toughness of interfacial cracks between rock and concrete [J].Journal of Water Resources and Architectural Engineering,1998,9(1): 42―45.(in Chinese)
[13]徐晓良,杨树桐.钢筋混凝土少筋梁断裂特性试验研究[J].工程力学,2017,34(增刊)：239―243.Xu Xiaoliang,Yang Shutong.Experimental study on fracture behavior of lightly-reinforced concrete beam [J].Engineering Mechanics,2017,34(Suppl)：239―243.(in Chinese)
[14]Goszczyńska B,Świt G,Trąmpczyński W.Experimental validation of concrete crack identification and location with acoustic emission method [J].Archives of Civil ＆ Mechanical Engineering,2012,12(1)：23―28.
[15]董伟,何化南,吴智敏,等.光弹贴片法研究混凝土Ⅰ-Ⅱ复合型裂缝扩展过程[J].工程力学,2010,27(9)：41―48.Dong Wei,He Huanan,Wu Zhimin,et al.Experimental investigation on double-K fracture parameters for small size specimens in concrete.[J].Engineering Mechanics,2010,27(9)：41―48.(in Chinese)
[16]Chen L S,Kuang J H.A displacement extrapolation method for determining the stress intensity factors along flaw border [J].International Journal of Fracture,1992,57(4)：51―58.
[17]Hillerborg A,Modéer M,Petersson P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J].Cement and Concrete Research,1976,6(6)：773―781.
[18]Dong W,Wu Z,Zhou X.A comparative study on stress intensity factor-based criteria for the prediction of mixed mode I-II crack propagation in concrete [J].Engineering Fracture Mechanics,2018,197(11)：217―235.
[19]李冬,金浏,杜修力,等.考虑细观组分影响的混凝土宏观力学性能理论预测模型[J].工程力学,2019,36(5)：67―75.Li Dong,Jin Liu,Du Xiuli,et al.A theoretical prediction model of concrete macroscopic mechanical properties considering of the influence of mesoscopic composition[J].Engineering Mechanics,2019,36(5)：67―75.(in Chinese)
[20]董伟,肖魁,何化南,等.全级配混凝土 I型裂缝扩展全过程数值模拟[J].工程力学,2013,30(4)：228―234.Dong Wei,Xiao Kui,He Huanan,et al.Numerical simulation on complete process of model I crack propagation of fully-graded concrete [J].Engineering Mechanics,2013,30(4)：228―234.(in Chinese)
RESEARCH ON FRACTURE CHARACTERISTICS OF ROCK-CONCRETE INTERFACE WITH DIFFERENT ROUGHNESS
Abstract:The roughness of rock-concrete interface has significant effects on its fracture characteristics.To investigate the fracture characteristic of rock-concrete interface with different roughness,six kinds of interface roughnesses were prepared by mechanically cutting grooves on the rock surface and then standard three-point bending fracture tests were performed to measure the fracture parameters of rock-concrete interface.The initial fracture toughness
was computed by a numerical method,and interfacial fracture energy Gf was calculated by pertinent P-δ curve.Experimental results indicate that the final crack is along rock-concrete interface,which proves that the rock-concrete interface is unsubstantial compared with bilateral materials.When interfacial roughness changes from 0.676 mm to 2.028 mm,the initial fracture toughness of rock-concrete interface increases from 0.362 MPa·m1/2 to 0.515 MPa·m1/2 (increasing 42.3%)and the fracture energy of rock-concrete interface increases from 17.928 N/m to 47.802 N/m (increasing 166.7%).In addition,with the increase of the interfacial roughness,the initial fracture toughness increases continuously,while the mode I fracture energy increases first and remains unchanged.
王玉珏(1985―)，女，安徽人，硕士生，从事混凝土材料力学性能研究(E-mail: wangyujue@cribc.com);
赵馨怡(1993―)，女，陕西人，硕士生，从事混凝土材料撞击性能研究(E-mail: zhaoxinyi@cribc.com);
佘 吉(1992―)，男，江苏扬州人，硕士生，从事混凝土断裂力学研究(E-mail: sjfeel@126.com).