有限元模型分析是解决大型复杂结构受力性能和状态评估、抗风抗震模拟等的有效手段之一,由于结构的复杂性和相关参数的不确定性,建立能够反映结构实际受力的精准有限元模型十分困难。而有限元模型修正技术可以通过识别和优化不确定的参数,使建立的有限元模型能够极大程度反映实际结构受力[1-5]。
目前,有限元模型修正技术大致分为两类[2,6-9],第一类为非迭代法,第二类为迭代法,非迭代法由于在工程应用中的复杂性和不可操作性,应用不多;而迭代法由于物理意义明确,是通过修正选择的敏感参数,如结构的材料特性、截面特性等,使修正后的模型与工程结构响应误差最小,该法应用较为广泛。利用迭代法处理有限元模型修正问题,实际上是将有限元模型修正转换为有约束的非线性优化问题,优化时,目标函数可以理解为模型与试验之间的位移、频率、加速度等的残差,目标函数越小,说明模型与工程结构状态越接近,修正效果越好。因此,合理的算法选择是解决有限元模型修正问题的基本条件。传统的有约束非线性优化方法如牛顿法、拟牛顿法、一阶优化方法等,当非线性较强时,算法极易陷入局部最优解。对于当前复杂的工程结构模型,响应与参数之间的关系往往非线性程度较大,如若采用上述方法解决模型优化修正问题时,计算结果得不到保障。
智能优化算法可以有效避免传统优化方法不足,通过仿生技术可以有效提高算法效率。在处理工程问题中应用最为广泛的为遗传算法(GA),时常应用于工程结构模型修正[10-11],但与粒子群优化算法(PSO)相比,前者所需迭代次数较多会导致计算效率略低,而PSO已被证明能够以更少的迭代次数获得相同或较好的全局解[12-14]。其基本思想是通过粒子群的个体记忆和群体交流,增强群体全局搜索能力。但是标准粒子群优化在算法后期,由于粒子群聚集效应显著,导致群体的多样性丧失,如果目标函数非线性极强,标准粒子群算法也会陷入早熟或停滞,所以需引入改进措施,使群体在整个优化过程中保持种群多样性,增大寻找全局最优解的可能性。秦玉灵等[15]基于标准PSO、引入混沌搜索的分组PSO,对卫星结构进行有限元模型修正,修正结果证实了基于PSO算法的有效性和实用性;吴坛辉[16]和安玖臻[17]分别基于免疫算法和PSO的复合方法和标准PSO对虎门大桥进行模型修正和桥梁关键部位损伤识别;Perera和Fang等[18]基于PSO和GA方法应用于多目标的损伤识别中,综合运用两者的全局寻优和局部寻优能力;Shabbir和Omenzetter[19]结合PSO和小生镜技术,对某在役人行桥梁实施模型修正;。但是上述改进方法相对较为繁琐。
鉴于目前常用优化方法的优化效率和精度已无法满足日趋复杂化的结构模型修正问题,本文提出基于引入高斯白噪声扰动[20]的PSO(GMPSO)的有限元模型修正方法,该法可以有效改善修正过程效率,保证修正精度,同时改进方法更为便捷。由于鲜有GMPSO算法在工程结构有限元模型修正中的细致研究,有必要展开基于GMPSO的有限元模型修正方法研究,研究成果对该方法在复杂工程结构有限元模型修正中的应用提供参考。
本文主要讨论标准PSO及GMPSO算法在处理不同目标函数优化问题中的优缺点;理清基于GMPSO实施有限元模型修正的过程和各参数的物理意义,并利用该方法实施高维有损伤简支梁有限元模型修正和某在役桥梁结构模型修正,验证该优化方法作为模型修正方法的可行性。
1 PSO与GMPSO对比分析
1.1 标准PSO方法[15-19]
标准PSO算法中假设每一个微粒的位置和速度均为d维空间里的矢量,假设第i个粒子的位置和速度分别为Xi=[xi1,xi2,…,xid]和Vi=[vi1,vi2,…,vid],在每步迭代过程中,均会产生两个最优解,一个是粒子本身找到的最优解pbest,Pi=[pi1,pi2,…,pid]和全局最优解gbest,Pg=[pg1,pg2,…,pgd]。粒子根据以上两个最优解位置和式(1)、式(2)更新速度和位置,作为下一步迭代的初始值。

式中:t表示迭代步次;ω表示惯性权重;c1和c2为正的学习因子或加速因子;r1和r2为[0,1]上均匀分布的随机数,Δt可理解为单位时间1。流程图如图1所示,其基本流程如下:①随机初始化N个粒子的速度和位置,其中第i个粒子的速度和位置Vi和Xi,确定算法中权重惯性系数、学习因子和最大的迭代步数;②确定目标函数表达式,计算各粒子当前状态目标函数值,记录各粒子当前位置和目标函数值于pbest中,并择目标函数值最好的粒子,记录其位置和目标函数值于gbest中;③根据式(1)更新粒子速度,式(2)更新粒子位置,并注意粒子位置不要超越其上下限位置Xmax和Xmin;④计算更新后状态下各粒子的目标函数值,并与各粒子对应的pbest中目标函数值比对,如果优于pbest中记录的目标函数值,则刷新pbest存储,否则,进入step⑤;⑤选择当前所有粒子的pbest中目标函数值最好的粒子,如果目标函数值优于原始记录,则更新gbest存储为当前最好的目标函数值和其位置,否则进入step⑥;⑥在更新记录后的pbest和gbest中查看目标函数值是否满足终止条件或达到最大迭代步数,若满足,退出迭代,输出最优解的位置和其目标函数值,否则,返回step③。
1.2 高斯白噪声扰动粒子群优化算法(GMPSO)[20]
为提高种群多样性,协助部分粒子跳出局部最优解,基于GMPSO的算法应运而生。相较于其他改进方法之繁琐,GMPSO算法仅对粒子位置按变异概率施加高斯白噪声扰动,一般变异概率取值0.05~0.15,选中粒子按照下式进行变异:
式中,σ为高斯白噪声随机数,其余参数含义同前。
GMPSO算法基本步骤即在标准PSO方法步骤基础上,将原步骤③分解为3个过程,即:根据式(1)更新粒子速度;根据式(3)按照变异概率对粒子位置施加扰动更新粒子位置,并注意粒子位置不要超越其上下限位置Xmax和Xmin;根据式(2)更新粒子位置。流程图见图1。

图1 PSO(无虚线框)和GMPSO(含虚线框)流程图
Fig.1 The flowchart of PSO (without dashed box)and GMPSO (with dashed box)
2.3 标准PSO与GMPSO方法简单对比
为探究标准PSO和GMPSO算法的优化性能,即修正优化过程中的收敛速度和精度。图2和表1列出3组测试目标函数三维示意图和表达式,目标函数理论最优值精确解均为0,函数F1(Sphere)为单峰值函数,以验证PSO和GMPSO的精度;F2(Ackley)和F3(Rastrigrin)为典型复杂的非线性多峰函数,极值点较多,以检验算法的搜索能力。
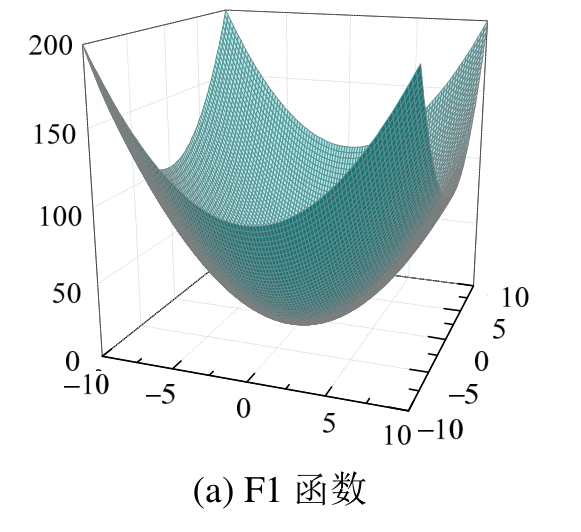

图2 各测试函数三维图
Fig.2 Three-D image of the four different test functions
表1 优化性能测试目标函数
Table 1 Test target functions for optimization ability

优化中,d取10,w取0.55,c1和c2取2,其中GMPSO算法中,高斯变异概率取0.1,粒子群总数均取60,最大迭代步数取300,终止条件要求为计算精度达到0.01或达到最大迭代步数。分析时,每中算法运行50次,若接近精确解,则记达优一次,如表2。图3给出各目标函数在PSO和GMPSO的一次优化过程,迭代步为横坐标,优化解为纵坐标。
由表2和图3可知,PSO和GMPSO在处理单峰函数时精度和效率均较好,且算法稳定性好,其中GMPSO效率有明显优势;在处理多峰函数时,PSO搜索能力逊于GMPSO,PSO几乎无法收敛,达优概率为0,而GMPSO达优概率仍为100%,且仍然保持较好的搜索效率。即GMPSO在处理单峰和多峰值目标函数时,均显示了较强的优化能力。
表2 基于PSO和GMPSO算法不同测试函数优化分析结果
Table 2 Optimization results of different test target functions based on PSO and GMPSO


图3 不同测试函数在PSO、GMPSO算法中的某一优化过程
Fig.3 One optimization process of different test functions in PSO and GMPSO algorithm
综上,GMPSO算法在处理复杂超高非线性目标函数时,仍能收敛于近似全局最优解,且保证较高的收敛速度,效率较高。因此,在处理诸如工程结构有限元模型优化修正过程中复杂的目标函数时,采用GMPSO处理优化修正问题,能够有效保证修正精度,同时提升计算效率。
2 基于高斯扰动粒子群优化(GMPSO)有限元模型修正方法验证
2.1 基于GMPSO有限元模型修正方法流程
在基于 GMPSO算法的有限元模型修正问题中,需要始终明确算法中各物理量与工程结构各物理量之间的对应关系。首先,将经过敏感性分析的高灵敏度参数设为待修正参数,将这些参数统一编入参数向量中,即P=[p1,p2,…,pd],此举将工程有限元结构离散为d维的空间向量来描述,一个参数向量即代表一个有限元结构状态。该参数向量可表述为粒子群算法中一个粒子的位置,优化过程中,每一个向量对应的元素变化数值可以理解为粒子群算法中粒子的速度,也即改变的步长。每一个粒子的位置对应一个参数变量,利用参数变量可以计算获得有限元结构响应,进而可以计算目标函数数值,即每一个粒子在该位置上的目标函数值,而后利用pbest和gbest选取步骤,完成GMPSO算法优化流程,直至目标函数值满足收敛条件。
当有限元模型修正完毕,需利用已有其他试验数据比对有限元计算结果。例如利用结构自振频率作为有限元模型修正的目标函数时,修正完成后,应对有限元模型与试验的振型MAC值进行计算,只有当MAC大于0.80时方认为振型匹配良好。
在基于GMPSO算法处理大型结构模型优化修正时,必须利用软件对模型作参数化处理,因此,可采用ANSYS的参数化建模平台,GMPSO算法流程可采用MATLAB软件进行编程,利用MATLAB与ANSYS参数化有限元模型交互访问,实现优化过程中目标函数的计算,也实现模块化便捷处理大型结构有限元模型修正过程。如图4所示基于GMPSO算法的有限元模型修正流程:1)确定目标函数,明确目标函数表达式与待修正参数之间的关系;2)调用ANSYS有限元模型实施参数敏感性分析,选择对目标函数中考虑的响应项敏感性高的参数为待修正参数;3)确定待修正参数组成参数向量作为粒子位置表达;4)运行MATLAB编制的GMPSO算法程序对参数进行优化,且每进行目标函数计算时,调用ANSYS参数化有限元模型计算对应粒子位置所表达参数状态下结构的响应,并与试验响应组合计算获得目标函数值,将之反馈至GMPSO程序中;5)获取修正后目标函数值最优的粒子位置,该粒子位置向量即为修正后的参数向量;6)修正后有限元模型与试验模型再一次比对,利用试验数据实施有限元模型验证。

图4 基于GMPSO算法的有限元模型修正一般流程
Fig.4 Flowchart of GMPSO algorithm applied in FE model updating process
2.2 算例1:高维变量损伤简支梁模型修正
2.2.1 简支梁模型介绍和修正主要步骤介绍
本节以一跨度为10 m的损伤简支梁为研究对象,基于GMPSO算法对其进行有限元模型修正,同时为验证GMPSO算法精度和效率,本节采用GA方法修正结果与之比对。该简支梁如图5所示,截面尺寸100 cm×100 cm,材料弹性模量取3.45×104 MPa,材料密度取2600 kg/m3,采用ANSYS参数化建模,选用Beam44梁单元模拟简支梁有限元模型,其中单元数10个,节点11个。在该数值算例中,考虑使用降低部分单元截面惯性矩的方法来模拟简支梁局部损伤,并将局部损伤简支梁动力特性数据作为实测数据,即“试验”数据,再分别利用GMPSO和GA算法,修正各截面惯性矩参数,变量维度为10,修正后有限元模型和该“试验”模型需保持一致。

图5 简支梁数值算例
Fig.5 Simply supported beam as a simulation example
假设简支梁在梁单元3和8出现局部损伤,其截面惯性矩均下降为原始值的70%,其余梁单元截面特性不变,由此,可以获得简支梁模型前 10阶“试验”自振频率,此时对照“试验”和初始有限元(无损伤简支梁模型)前10阶自振频率,如表3,前5阶频率中,第1阶为竖弯频率,第2阶为横弯频率,第3阶、第4阶为竖弯频率,第5阶为横弯频率,其中1阶频率误差值为4.21%,所有频率最大误差值为5.92%,较多频率集中在5%附近,但振型MAC值对应良好,如果对于工程结构而言,试验与有限元模型能够达到如此精度,无需再进行模型修正,但对于数值简支梁而言,因模型十分简单,也不存在相关假设或建模造成误差,更不存在实际工程结构建造过程出现误差,所以5.92%的误差对于简支梁数值模型来说,误差偏大,需进行有限元模型修正,以获得精准模型。
基于GMPSO算法的有限元模型修正过程参照上一小节,将该修正划分为以下几个步骤:
1)明确目标函数选择简支梁前2阶竖弯和前2阶横弯自振频率“试验”与有限元模型结果残差之和;2)为简化分析,这里不进行各个物理参数的敏感性分析,以10个梁单元各自的截面惯性矩为修正参数;3)粒子的位置可以描述为10个截面惯性矩组成的参数向量,为方便起见,对参数向量统一进行无量纲处理,即无损伤简支梁待修正参数向量为单位向量[1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0]T,而损伤简支梁修正后参数向量精确解应为[1.0,1.0,0.7,1.0,1.0,1.0,1.0,0.7,1.0,1.0]T;4)运行MATLAB编制的GMPSO算法程序对待修正参数进行优化,每计算目标函数值时,需计算各粒子位置对应的简支梁上述4阶自振频率,并与“试验”上述4阶自振频率组合为残差之和的形式,得到目标函数值,反馈到GMPSO程序中;5)获取目标函数值最优的粒子位置作为优化修正获得的参数向量;6)修正后有限元模型与试验模型比对验证,此时可利用简支梁“试验”其余6阶自振频率与修正后有限元模型进行比对,检验是否获得精准模型。
2.2.2 基于GMPSO与GA的简支梁修正结果对比
基于GA的有限元模型修正方法,参照基于GMPSO的有限元模型修正方法,在④步改调用GMPSO算法程序为调用GA优化算法,其余步骤保持一致。
表3 简支梁数值模型前10阶自振特性“试验”值、初始模型值、优化修正模型值
Table 3 First ten vibration properties of test,initial and updated model of simulation beam
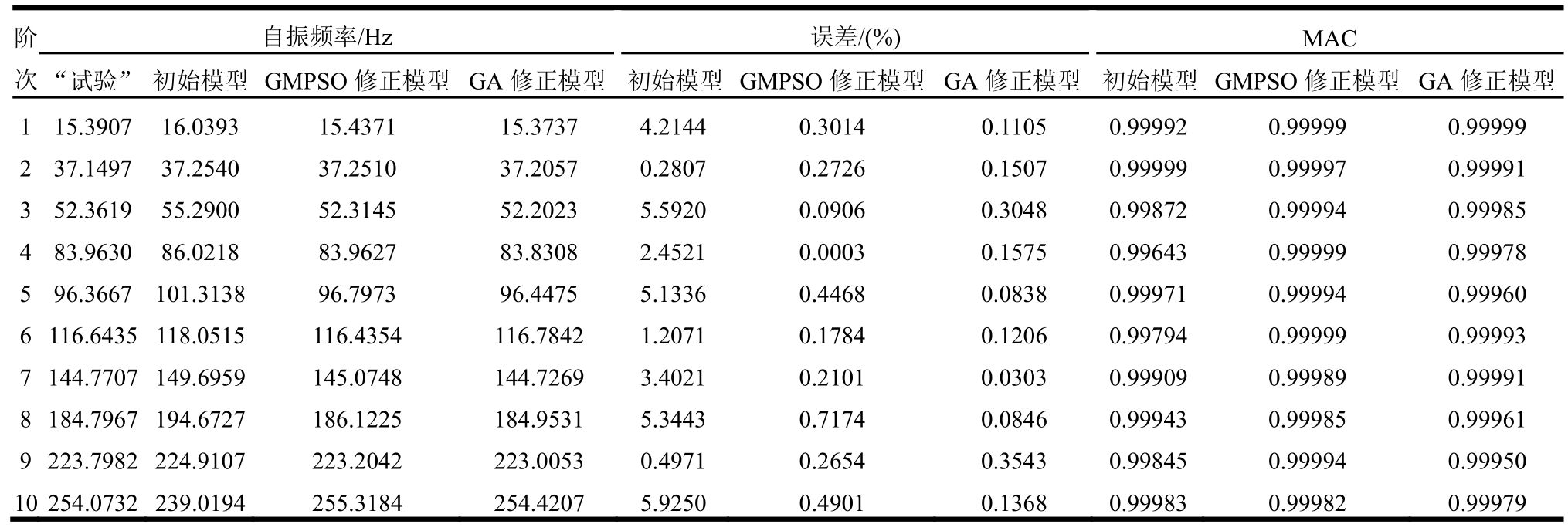
注:表3中误差=|初始模型(或修正模型)-“试验”|/“试验”×100%。
在GMPSO算法程序中,粒子群数目为60,w取0.55,c1和c2取2,高斯变异概率取0.1,最大迭代步数取60步,搜索中各无量纲变量的上下维度均为[0.6,1.1]之间,取3次(单次优化过程约为3 h)结果的算术平均值为最终优化值,获得参数向量优化结果为[0.991000,0.945038,0.716789,0.977679,1.004560,1.037201,0.981879,0.729190,0.980079,1.033601]T;在GA算法程序中,粒子群数目和最大迭代步数同前,交配概率0.8,变异概率0.2,各无量纲变量的上下维度不变,取3次(单次优化过程时间与基于GMPSO算法接近)基于GA的有限元模型修正结果的算术平均值为最终优化值,获得待修正参数向量优化最终结果为[0.964357,0.984285,0.679746,0.973309,1.037971,0.963432,1.022584,0.720168,1.012278,1.053255]T。
如图6,比对基于不同算法修正后各截面惯性矩参数值与精确解结果显示,各参数精确解与优化解误差基本控制在5%,表3列出基于不同修正方法获得的简支梁优化后模型的前10阶自振频率,经过模型验证,除简支梁前2阶竖弯和前2阶横弯自振频率,其余6阶自振频率误差也相应下降,最大误差仅为0.72%,其余误差也较多波动于0.2%附近,各阶MAC值均吻合良好,几乎全部达到1,说明基于GMPSO算法的有限元模型修正方法与基于GA的有限元模型修正方法的修正精度一致,修正后模型均能精确地反映“试验”模型。以其中一次修正过程为例,基于GMPSO和基于GA的有限元模型修正方法迭代过程如图7,当选取误差精度为1×10-5时,基于GMPSO的模型修正方法仅需25次迭代即可达标,而基于GA的有限元模型修正方法需要57次迭代,显然在满足相同精度要求的条件下,基于GMPSO的有限元模型修正方法较常用的基于GA的有限元模型修正方法需要的迭代步少,效率更高,当修正过程中,一次迭代所需时间较长时,尽量减小迭代步可以快速提升计算效率。

图6 简支梁各截面惯性矩参数精确值与修正后数值
Fig.6 Accuracy and updated value of every section moment inertia parameter

图7 基于不同有限元模型修正方法的一次优化迭代过程
Fig.7 Iteration process of different model updating methods
2.3 算例2:某在役桥梁结构模型修正
本节以某在役自锚式悬索桥为工程背景,该桥跨径为53 m+112 m+53 m=218 m,桥面宽52 m。主梁为预应力混凝土双边箱截面,边箱采用单箱三室,标准段高度为2.8 m,材料采用C50混凝土;桥塔由主塔和副塔组成,门形框架,主塔桥面以上(含塔尖)高度为45 m,材料为C40混凝土;主缆缆心横向间距为31.7 m,主跨矢跨比为1/5.276;吊杆标准间距为5 m,全桥吊杆共37对,2边跨各8对,主跨21对。桥梁整体图和标准断面如图8所示。
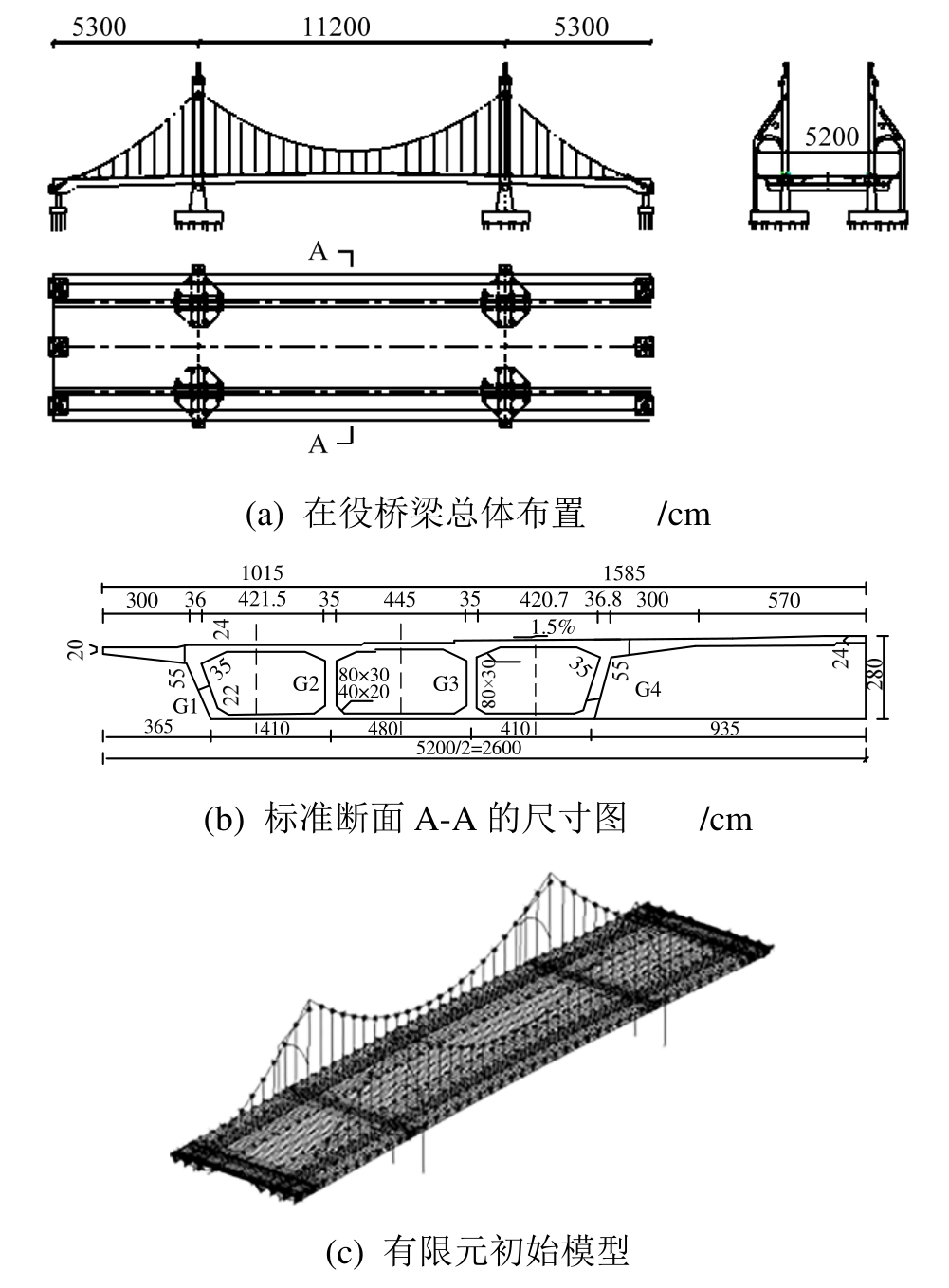
图8 在役桥梁总体布置、标准截面尺寸和有限元初始模型 /cm
Fig.8 General layout,standard section and FE model of the in-serviced bridge
基于ANSYS平台建立该自锚式悬索桥三维有限元模型,其中主梁、横梁、桥塔均简化为空间梁单元(Beam44),考虑到箱梁宽跨比较大,基于梁格理论将双箱纵梁划分为8片梁格,主缆及吊杆采用空间杆单元(Link10),索夹、主鞍座及二期恒荷载均已转换为质量单元(Mass21)。桥塔与主梁以及主梁与基础之间的约束均采用弹簧单元(Combine14),其中,左塔与主梁仅约束纵向位移,释放横向位移;右塔与主梁释放纵横向位移;主梁与基础间除主梁中轴线上支座约束横向位移,释放纵向位移外,其余支座纵横向位移均释放。塔底按照固结处理。全桥有限元模型共15530个节点,20875个单元。初始模型主梁前5阶自振频率和环境激励试验测试频率比对如表4,除横弯频率误差较小,为3.08%外,其余各阶频率误差均较大,2阶和3阶竖弯频率误差高至38.60%和38.08%,需要对其进行模型修正。
基于GMPSO的有限元模型修正过程同样参照上一小节,将该修正划分为以下几个步骤:1)明确目标函数选择在役桥梁主梁前5阶自振频率与有限元模型结果残差、主跨跨中与边跨跨中竖向位移与模型计算结构残差之和;2)经过敏感性分析结果,修正参数取将主梁、主塔、主缆、吊杆材料弹性模量,主梁材料密度,主梁截面竖向、横向、扭转惯性矩,主塔截面惯性矩,主梁、主塔截面面积,二期恒载和环境温度作为13个敏感参数;3)粒子的位置可以描述为13个参数组成的向量,为方便起见,对参数向量统一进行无量纲处理,并将各参数作归一化处理(修正参数=过程值/初始值)作为修正参数,即对于初始有限元,其参数向量可表达为[1,1,1,1,1,1,1,1,1,1,1,1,1]T;4)运行MATLAB编制的GMPSO算法程序对待修正参数进行优化,每计算目标函数值时,需计算各粒子位置对应的主梁前5阶自振频率和中跨与边跨跨中竖向位移,并与试验相对应结果的残差之和作为目标函数值,反馈到GMPSO程序中;5)获取目标函数值最优的粒子位置作为优化修正获得的参数向量;6)修正后有限元模型与试验模型比对验证,可对比其各主要频率是否达到修正要求。
在GMPSO算法程序中,粒子群数目为100,w取0.55,c1和c2取2,高斯变异概率取0.1,最大迭代步数取100步,搜索中各无量纲变量的上下维度均为[0.7,1.3]之间,取3次优化结果的算术平均值为最终优化值,获得待修正参数向量优化最终结果为[1.289907,1.280233,1.029669,1.011077,1.289467,1.230214,1.272362,1.177837,0.910527,0.804750,0.829647,1.059665,1.103798]T。修正后模型的主梁频率值以及其与试验值的对比如表4所示。
由表4可知,各阶频率与试验值误差修正后均大幅下降,误差控制在9%以内,从MAC数值来看,振型吻合度均较好。综上数据说明,基于 GMPSO的有限元修正方法可获得较为精准的在役桥梁有限元模型。
表4 在役桥梁主梁自振频率修正前后对比
Table 4 Comparison of main girder vibration frequencies of the in-serviced bridge before and after model updating

注:表4中误差=|模型频率-试验频率|/试验频率×100%
3 结论
传统有限元模型修正优化方法效率低、精度不高,基于智能优化的改进PSO模型修正方法可有效提升效率,保证精度。鉴于目前基于改进PSO有限元模型修正研究较少且相关改进方法较为繁琐,本文提出基于GMPSO的高效有限元模型修正方法,并对其展开研究和验证。GMPSO相较于其他改进法,因仅引入高斯白噪声对PSO进行局部扰动,简单便捷,且效率提升显著。通过PSO与GMPSO全局搜索能力的对比以及基于GMPSO的简支梁模型和在役桥梁结构模型修正,得到以下结论:
(1)基于不同寻优难度的测试函数寻优结果显示,在经简便改进后的GMPSO方法较改进前寻优效率得到显著提升,寻优所需迭代步较少,全局寻优能力增强;
(2)基于GMPSO的模型修正方法在高维损伤简支梁模型修正中应用结果显示,相较于基于GA的有限元模型修正方法,当选取误差精度为1×10-5时,基于GMPSO的有限元模型修正方法仅需25次迭代即可达标,而基于GA的有限元模型修正方法需要57次迭代,即在保证修正精度条件下,所提方法修正效率得到显著提升,有效验证该方法在高维复杂工程结构模型修正中的应用可行性。
(3)基于GMPSO的模型修正方法在桥梁结构模型修正中的应用结果显示,修正后桥梁主梁各阶频率与试验值误差均大幅下降,均控制在9%以内,有效验证了该方法在结构有限元模型修正中的应用可行性。
[1]Li J H,Li A Q,Feng M Q.Sensitivity and reliability analysis of a self-anchored suspension bridge [J].Journal of Bridge Engineering,2013,18(8):703―711.
[2]Xia Z Y,Li A Q,Li J H,et al.FE model updating on an in-service self-anchored suspension bridge with extra-width using hybrid method [J].Applied Sciences,2017,7(2):191.
[3]王浩,王付全,李爱群,等.大跨度缆索支撑桥梁分阶段有限元模型修正[J].工程力学,2009,26(10):111―116.Wang Hao,Wang Fuquan,Li Aiqun,et al.Multi-phase FE model updating on long-span cable-supported bridges[J].Engineering Mechanics,2009,26(10):111―116.(in Chinese)
[4]韩建平,骆勇鹏,郑沛娟,等.基于响应面的刚构-连续组合梁桥有限元模型修正[J].工程力学,2013,30(12):85―90.Han Jianping,Luo Yongpeng,Zheng Peijuan,et al.Finite element model updating for a rigid frame-continuous girders bridge based on response surface method [J].Engineering Mechanics,2013,30(12):85 ― 90.(in Chinese)
[5]Cismaşiu C,Narciso A C,Amarante dos Santos F P.Experimental dynamic characterization and finiteelement updating of a footbridge structure [J].Journal of Performance of Constructed Facilities,2015,29(4):04014116.
[6]宗周红,高铭霖,夏樟华.基于健康监测的连续刚构桥有限元模型确认(I)—基于响应面法的有限元模型修正[J].土木工程学报,2011,44(2):90―98.Zong Zhouhong,Gao Minglin,Xia Zhanghua.Finite element model validation of the continuous rigid frame bridge based on structural health monitoring part I:FE model updating based on the response surface method[J].China Civil Engineering Journal,2011,44(2):90―98.(in Chinese)
[7]蒋运忠,周云,谢利民.基于应用程序交互访问技术的桥梁有限元模型修正研究[J].工程力学,2015,32(9):174―182.Jiang Yunzhong,Zhou Yun,Xie Limin.Research on updating finite element model for bridge based on application programming interface technique [J].Engineering Mechanics,2015,32(9):174―182.(in Chinese)
[8]郭力,李兆霞,高效伟.基于复域灵敏度分析的静力模型修正方法研究[J].工程力学,2010,27(8):100―106.Guo Li,Li Zhaoxia,Gao Xiaowei.Static model updating method via complex domain sensitivity analysis [J].Engineering Mechanics,2010,27(8):100―106.(in Chinese)
[9]刘纲,罗钧,秦阳,等.基于改进 MCMC 方法的有限元模型修正研究[J].工程力学,2016,33(6):138―145.Liu Gang,Luo Jun,Qin Yang,et al.A finite element model updating method based on improved mcmc method [J].Engineering Mechanics,2016,33(6):138―145.(in Chinese)
[10]Deng L,Cai C S.Bridge model updating using response surface method and genetic algorithm [J].Journal of Bridge Engineering,2010,15(5):553―564.
[11]何浩祥,闫维明,王卓.基于子结构和遗传神经网络的递推模型修正方法[J].工程力学,2008,25(4):99―105.He Haoxiang,Yan Weiming,Wang Zhuo.Stepwise model updating method based on substructures and GA-ANN [J].Engineering Mechanics,2008,25(4):99―105.(in Chinese)
[12]Do D M,Gao W,Song C,et al.Dynamic analysis and reliability assessment of structures with uncertain-butbounded parameters under stochastic process excitations[J].Reliability Engineering & System Safety,2014,132:46―59.
[13]Gholizadeh S,Moghadas R K.Performance-based optimum design of steel frames by an improved quantum particle swarm optimization [J].Advances in Structural Engineering,2014,17(2):143―156.
[14]Nanda B,Maity D,Maiti D K.Crack assessment in frame structures using modal data and unified particle swarm optimization technique [J].Advances in Structural Engineering,2014,17(5):747―766.
[15]秦玉灵,韩增尧,邹元杰,等.基于粒子群优化算法的整星有限元模型修正方法[J].航天器环境工程,2015,32(3):243―246.Qin Yuling,Han Zengyao,Zou Yuanjie,et al.PSO-based satellite model updating method [J].Spacecraft Environment Engineering,2015,32(3):243―246.(in Chinese)
[16]吴坛辉.基于免疫粒子群优化算法的结构动力模型修正[D].南京:南京理工大学,2009:29―51.Wu Tanhui.Structural dynamic model updating based on immune PSO algorithm [D].Nanjing:Nanjing University of Science and Technology,2009:29―51.(in Chinese)
[17]安玖臻.基于粒子群优化算法的结构有限元模型修正[D].西安:长安大学,2013:44―49.An Jiuzhen.Based on particle swarm optimization algorithm for finite element model updating [D].Xi’an:Chang’an University,2013:44―49.(in Chinese)
[18]Perera R,Fang S E,Ruiz A.Application of particle swarm optimization and genetic algorithms to multiobjective damage identification inverse problems with modelling errors [J].Meccanica,2010,45(5):723―734.
[19]Shabbir F,Omenzetter P.Particle swarm optimization with sequential niche technique for dynamic finite element model updating [J].Computer-Aided Civil And Infrastructure Engineering,2015,30(5):359―375.
[20]廖振兴,钟伟民,钱峰.基于高斯白噪声扰动变异的粒子群优化算法[J].华东理工大学学报(自然科学版),2008,34(6):859―863.Liao Zhenxing,Zhong Weimin,Qian Feng.Particle swarm optimization algorithm based on mutation of Gaussian white noise disturbance [J].Journal of East China University of Science and Technology (Natural Science Edition),2008,34(6):859―863.(in Chinese)