同地震荷载作用,风荷载是一种重要的工程环境荷载。风速和风向是风荷载的主要特性,其对高层建筑、大跨空间结构以及桥梁等柔性结构的性能分析、设计和选型具有重要影响。有关风速的概率分布研究中,通常以极值风速作为变量建立概率模型[1-4]。目前,常用于描述风速概率分布的模型有极值 I型(Gumbel)分布、极值 II型(Frechet)分布、极值III型(Weibull)分布、广义极值分布、正态分布、对数-Weibull混合分布以及三参数正态-对数正态混合分布等[1,3]。虽然上述极值风速概率模型的理论不一,但均未考虑风向角的影响;研究表明,忽略风向的影响可能会导致高估结构的风荷载[5-6]。目前针对连续型风向角概率分布的研究成果相对较少[7-12],且不存在普遍适用的数学模型和计算理论;常用的概率模型有均匀分布、缠绕正态分布以及von Mises分布等[13]。此外,还可利用三角级数将离散的风向频度函数连续化,如,截断傅里叶级数和谐波函数[8,14]。然而,利用三角级数拟合风向的方法需要对所有风向的风速进行拟合,计算量较大;且该方法只是形式上将风向频度函数连续化,本质上仍离散。
研究表明[15-18],风向对结构在强风作用下的动力响应具有重要影响。因此,建立能够同时反映极值风速和风向效应的联合概率密度函数(Joint probability density function,简称JPDF),对精确计算结构风荷载以及进行结构抗风设计等具有重要的实际意义。针对风速风向联合作用的研究方法主要包括平稳随机过程法、最大风向系数法和联合概率分布法[19]。其中,联合概率分布法是研究风速风向联合概率模型最为常用和有效的方法。传统的联合概率分布法假设风速和风向是完全独立的随机变量,通过各向同性高斯分布[10]、各向异性高斯分布[11]或者各向异性对数高斯分布[13]建立风速和风向的联合概率分布。然而,研究表明风速和风向不是完全相互独立的随机变量[20];因此,传统的风速风向联合概率模型的建立方法是不合理的。Johnson和 Wehrly[9]基于熵最大原理提出了角度-线性(Angular-linear,AL)模型,并将其应用到风速风向联合概率分布的研究中。在该方法中,风速概率密度函数可由常用的分布模型来描述,而风向概率密度函数可由混合von Mises分布拟合得出。Carta等[21]对 AL模型进行了改进,提出利用混合 Normal-Weibull分布来描述风速的概率分布,并给出了AL模型中参数初始值的计算方法。文献[22―23]在Carta等研究的基础上,分析了我国部分地区的风速风向联合概率密度函数。然而,由于AL模型中涉及到三角函数的指数形式以及改进的第I类零阶Bessel函数,导致其计算过程比较复杂。Johnson等[24]假设风速风向的相关系数为 0.25,并通过Farlie-Gumbel-Morgenstern(FGM)模型对风速风向的联合概率分布直接进行了描述[25]。但实际,风速和风向的相关性并不确定,且在某些地区风速风向的相关系数远小于 0.25[26]。文献[27]通过假设风速概率分布中的参数和风向频度函数的变化均服从谐波函数,基于乘法定理导出了风速风向联合概率密度函数。Li等[28]针对建立风速风向联合概率模型传统方法中存在的缺陷,提出高效准确的基于Copula函数的联合概率模型分析方法。目前,国内针对风速风向联合分布的研究主要集中于某一特定方法进行研究,缺乏不同方法间适用性的对比研究。
该文以中国气象局气象数据中心提供的大理地区风速日值数据资料为例,利用谐波函数和混合von Mises分布对风向概率密度函数进行拟合,并分别基于乘法定理和AL模型导出大理地区风速风向联合概率分布,根据决定系数(Determinant coefficient,R2)和均方根误差(Root mean squared error,RMSE)对由两种方法得到的JPDF进行拟合优度检验。最后,利用基于AL模型得到的风速风向联合分布模型对大理地区 50年重现期的极值风速进行了预测。本文工作对风速风向联合概率分布模型的研究,并进一步指导规范中相应条文的修订及合理利用气象数据中心提供的风速数据资料具有一定的指导意义。
1 数据来源与分析
大理国家气候观象台位于大理市的苍山洱海之间,地处云贵高原,且受孟加拉湾西南季风带的影响,导致该地区遭受潜在风灾的可能性较大。中国气象局气象数据中心(http://data.cma.cn/)提供全国824个基准、基本气象站1951年1月以来的风速资料日值数据集,但 1971年之前的风速数据仅包含平均风速。因此,本文选取了 1971年1月1日~2017年4月 30日期间大理气象站记录的全部10 m高度处的日最大风速(日最大风速是指每天10 min平均风速样本中的最大值)和相应的风向记录(0°表示正北方向,以22.5°为间隔、顺时针为正,共16个方位,如图1所示)。除去因设备维修等原因未记录的数据,总计16561个数据样本,表1统计了风速数据样本在16个风向区间内的频数p(θ)。理想的风速数据应该是所有风向的日最大风速,然而气象站仅给出了当日 16个风向中数值最大的风速。图2和图3分别示意了由实测数据得到的风速频度散点图和风向玫瑰图,可以看出,日最大风速主要集中在0 m/s~20 m/s以内,对应发生频度较大的风向有E、ESE、SSE、WSW、W和WNW,这表明大理地区并不存在特定的主风向,因此有必要研究该地区风速风向的联合概率模型。
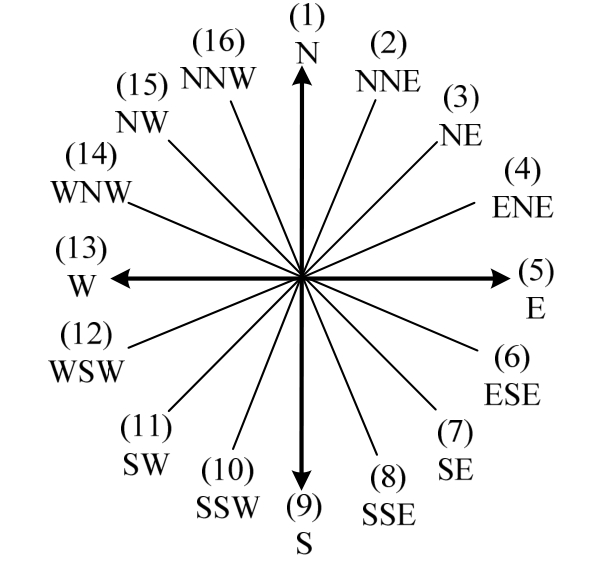
图1 风向分布图
Fig.1 Schematic of wind direction
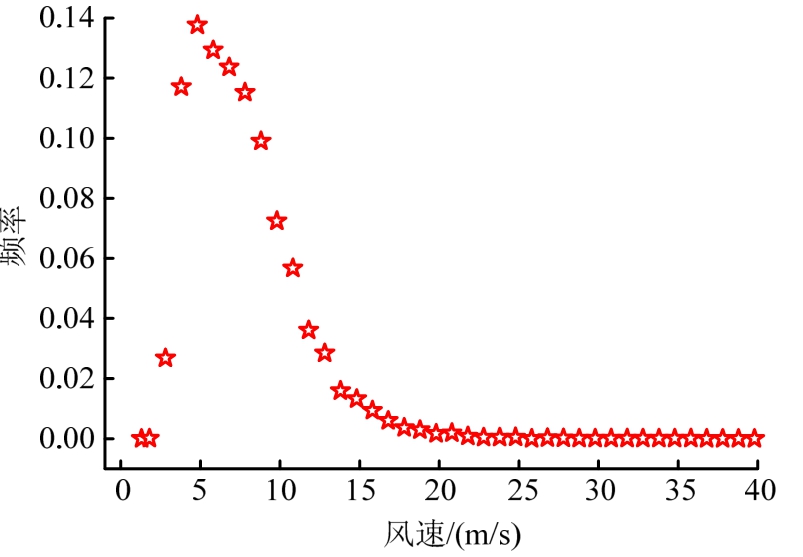
图2 风速分布散点图
Fig.2 Scatter distribution of wind speed
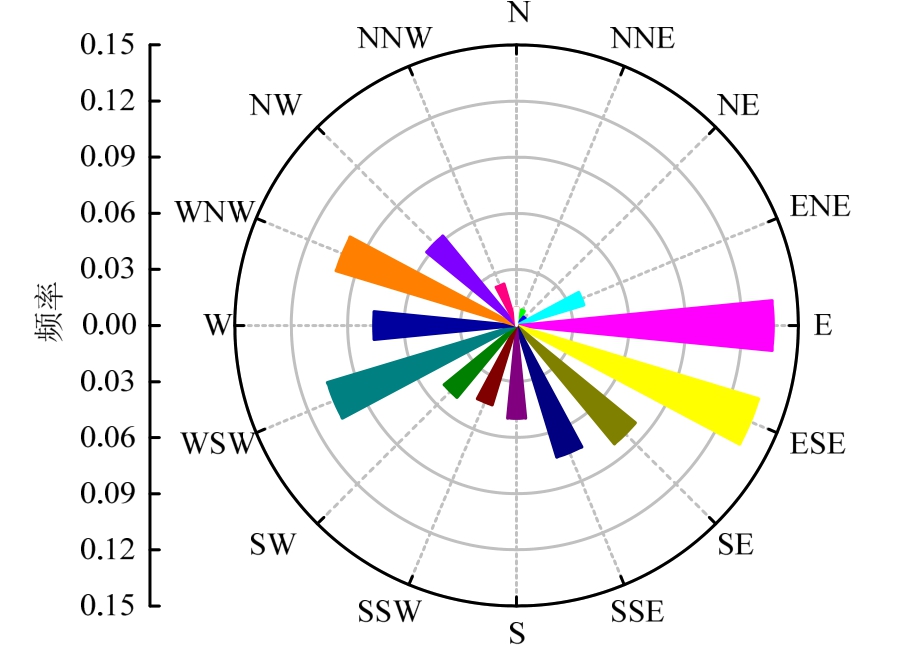
图3 风向玫瑰图
Fig.3 Wind rose map
2 风速概率分布
关于风速分布模型的研究成果较多,主要包括用于拟合单峰数据和多峰数据的分布模型[1,3]。当前,我国现行规范[29]选用Gumbel分布来描述风速概率分布,美国采用 Frechet分布,而加拿大则采用 Weibull分布。由此可以发现,目前并不存在最优的风速概率分布,而且样本数据的差异也会导致风速最优分布模型有所不同[30-31]。本文分别采用Gumbel分布、Frechet分布、三参数Weibull-3分布和双参数Weibull-2分布描述大理地区全风向和16个风向区间的风速概率分布,结果列于表1。篇幅所限,本文仅给出上述四种概率模型对全风向风速概率分布的拟合曲线,如图4所示。

图4 典型风速概率密度函数的比较
Fig.4 Comparison with typical distributions of wind speed
由表1给出的拟合结果可知,对全风向风速数据而言Weibull-2分布、Frechet分布、Weibull-3分布和Gumbel分布对全风向风速的拟合优度依次增强,此结论与文献[2]中给出的结论基本一致,即Weibull分布和Gumbel分布对于风速的拟合效果优于Frechet分布。从图4可直观看出,Weibull-2分布和 Weibull-3分布的拟合结果比较接近,对低风速段(0 m/s~5 m/s)拟合结果偏大,而对高风速段(10 m/s~20 m/s)拟合结果偏低;Frechet分布仅对低风速段拟合效果较好;与其它三类概率模型相比,Gumbel分布对低风速段拟合结果略微偏高,而对其它段风速拟合结果较好。并且Weibull分布的尾部长度属于有限有界型,这与风速有限无界的特性相冲突[2]。因此,本文决定选用 Gumbel分布来研究风速风向联合概率分布。
表1 大理1971年~2017年风速概率分布的参数估计结果
Table 1 Parameters identification results for the distributions of wind speeds from 1971~2017 in Dali

注:a、b和c分别表示位置、比例和形状参数。
3 风速风向联合概率分布
与风速数据相比,风向区间的记录较少(我国的气象站仅记录16个风向区间),因此风向概率分布的离散性较强。离散型风向分布的连续化比较困难,这也是制约风速风向联合概率分布研究发展的重要因素。目前离散的风向分布连续化的途径主要有:一是利用三角级数(如傅里叶级数、谐波函数)对风向频度函数进行拟合,二是通过混合von Mises分布来描述风向概率密度函数。本文分别基于上述两种方法以大理地区为例对其风向概率分布模型进行研究,并由此建立该地区的风速风向联合概率分布。
3.1 基于谐波函数与乘法定理的方法
基于谐波函数与乘法定理的风速风向联合概率分布的方法需引入以下四个假定[32]:1)任意指定风向区间的风速样本服从相同概率分布;2)不同风向区间风速样本的概率分布参数由该风向区间的风速样本回归得到;3)不同风向区间风速概率分布的相关性由实测风速数据反映;4)风速概率分布的参数及风向频度函数的变化满足谐波函数。基于乘法定理,风速风向的联合概率分布函数可表示为[33]:
式中:p(θ)为风向频度函数,反映风速在各风向区间分布情况;f(θ)为风向的概率密度函数;Δθ/rad为实测风向数据的间隔,本文统一取 0.393 rad(即![]() 为各个风向区间的风速概率分布函数,风速数据间隔取Δv=1 m/s。由概率分布函数和概率密度函数的关系,风速风向的联合概率密度函数可表示为:
为各个风向区间的风速概率分布函数,风速数据间隔取Δv=1 m/s。由概率分布函数和概率密度函数的关系,风速风向的联合概率密度函数可表示为:
根据假定 4),Gumbel分布的位置参数 a(θ)和尺度参数 b(θ)以及概率密度 f(θ)在圆周上的变化满足谐波函数[13],即:
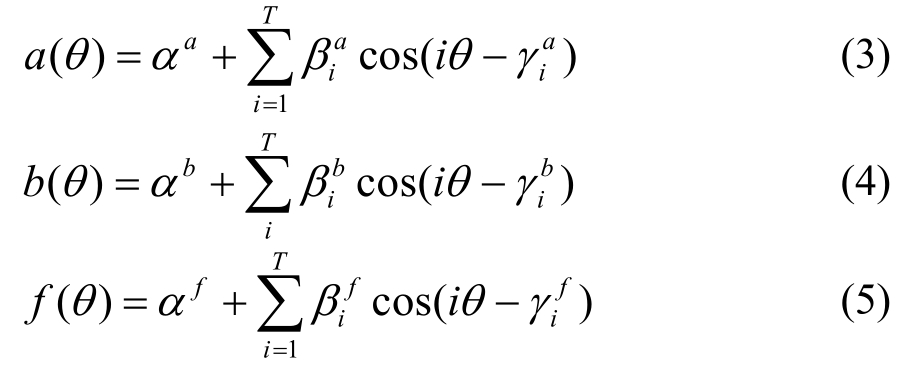
式中:α、β和γ为待定系数;T为谐波函数的阶数,作者探讨了谐波函数的阶数对其拟合优度的敏感性,分析表明,三阶谐波函数具有最优的拟合效果。利用式(3)~式(5)分别对表1中Gumbel模型的参数及风向概率密度进行拟合,参数识别结果列于表3,拟合曲线绘于图5。由表2中的参数拟合结果以及图5的拟合曲线不难看出,由谐波函数拟合得到的结果并不理想。
表2 谐波函数拟合结果
Table 2 Fitting results of harmonic functions
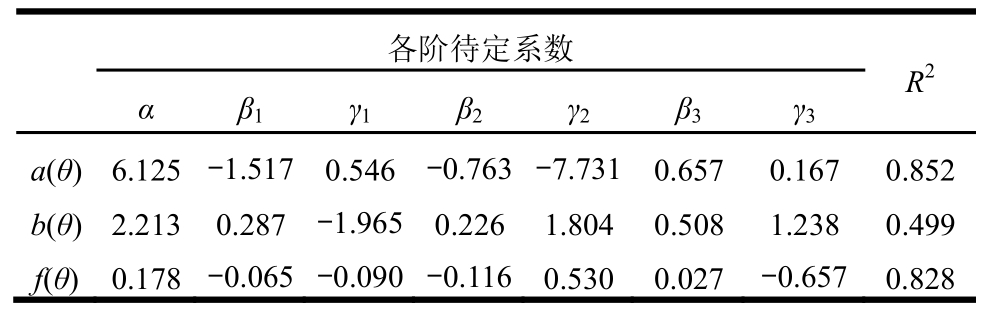

图5 参数的谐波函数拟合曲线
Fig.5 Harmonic function fitting curves of parameters
3.2 基于混合von Mises分布与AL模型的方法
Johnson和 Wehrly[9]基于熵最大原理推导了表示角度-线性(Angular-Linear)分布的模型,并将其用于描述风速风向的联合概率分布,其联合概率密度函数为:
式中:f(v)为全风向风速概率密度函数,可由Gumbel分布描述,参数拟合结果如表1所示;f(θ)为风向概率密度函数,可由混合von Mises分布描述,其概率密度函数为:
式中:N为混合von Mises分布的阶数,通常根据风向概率密度分布直方图的峰值数进行初步判断,Carta等[21]提出,混合模型的拟合优度会随阶数 N的增加而提高,但当N>6时,阶数的增加对于拟合优度提高的贡献甚微;θ表示风向角,0≤θ<2π;µi为位置参数,表示平均风向,0≤µi<2π;ki是尺度参数,ki≥0;ωi为各阶von Mises分布的权重系数,其满足:![]() 为零阶修正的第I类Bessel方程[21]。
为零阶修正的第I类Bessel方程[21]。
基于MATLAB平台的fittype( )函数对风向概率密度进行非线性拟合时,需要输入各参数的初始值,并且准确的参数初始值能显著提高拟合精度和效率[33]。为确定N阶混合von Mises模型中的参数的初始值,需要将观测到的风向数据分成以下N组:![]() N阶混合von Mises的权重系数ωi可表示为
N阶混合von Mises的权重系数ωi可表示为![]() Carta等[21]和 Li等[28]提出了确定µi和ki的详细步骤,本文在此不再赘述,仅给出其计算公式:
Carta等[21]和 Li等[28]提出了确定µi和ki的详细步骤,本文在此不再赘述,仅给出其计算公式:

式中,si和ci可表示为:

由图5(a)可知,风向概率密度直方图至少有 3个峰值,因此阶数N≥3。并且,当N取6时,混合von Mises分布中共有18个未知参数需要确定,即至少18组数据才能满足需求,而本文仅有16组数据。因此,本文取N为3、4和5,分别对风向概率密度直方图进行拟合,拟合结果列于表3。由表中拟合结果可以发现,5阶和4阶von Mises分布的拟合结果一致,且优于3阶模型,因此,本文采用4阶von Mises分布对风向概率密度进行拟合,拟合曲线如图6所示,并将谐波函数的拟合结果也绘于图6。显然,4阶von Mises分布对风向概率密度函数的拟合效果要优于谐波函数。

图6 风向圆周分布模型拟合曲线与实测数据对比
Fig.6 Distribution comparison of circumferential distribution models and measured data for wind directions
表3 各阶混合von Mises模型的参数拟合值
Table 3 Numerical values of the parameters of the von Mises mixture model
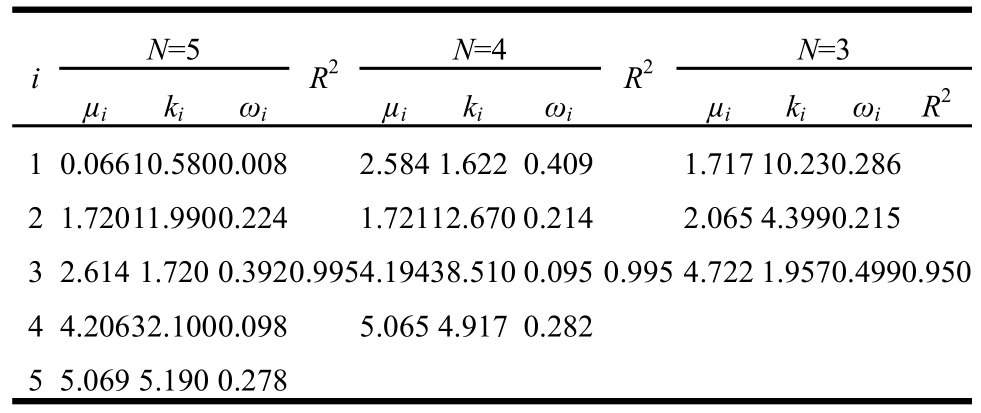
表4 g(ζ)的参数拟合值
Table 4 Fitting values of the parameters of g(ζ)
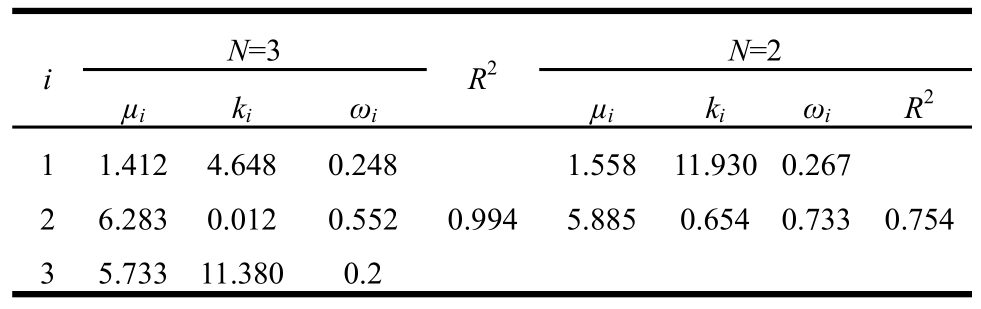
AL模型中的参数 ζ为角度变量,可由式(11)确定。其中,g(ζ)是参数 ζ的概率密度函数,由混合von Mises分布进行拟合得到,本文选用2阶和3阶von Mises分别对其进行拟合[13,26],拟合结果列于表4。
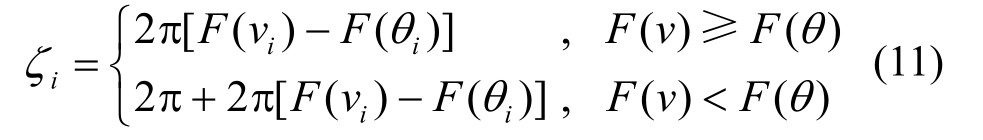
式中,F(vi)和F(θi)分别为风速和风向的累积概率。由表4中的拟合结果可知,3阶von Mises分布对ζ的拟合效果明显优于2阶模型。得到风速、风向和角度变量的概率密度函数后,便可根据AL模型直接确定风速风向联合概率密度函数。
3.3 预测值与实测值的对比
对大理地区的实测风速数据进行分组,计算落在风速区间![]() 及风向区间
及风向区间![]() 内的风速数据点数tij。实测风速风向的联合概率分布可表示为
内的风速数据点数tij。实测风速风向的联合概率分布可表示为![]() 其中,Nt为实测风速样本数。由统计基本理论可知,风速风向联合概率密度的实测值表示为:
其中,Nt为实测风速样本数。由统计基本理论可知,风速风向联合概率密度的实测值表示为:

根据实测数据,计算矩形区域v∈[0,40]和θ∈[0,360]内27×16个离散点的风速风向联合概率分布实测值,并将其等值线及由本文两种方法得到的风速风向联合概率分布预测值的等值线绘于图7。不难看出,基于混合von Mises分布与AL模型的方法得到的预测值对实测值的拟合效果更好。为进一步对比基于谐波函数与乘法定理的方法和基于混合von Mises分布与AL模型的方法得到风速风向的JPDF的拟合优度,通过R2和RMSE检验两种方法的拟合优度。其中,R2趋于1,RMSE接近于零,说明拟合效果好。基于谐波函数与乘法定理的方法导出的风速风向联合概率密度函数的拟合结果为:R2=0.539,RMSE=0.007;而基于混合von Mises分布与AL模型的方法得到的联合概率密度函数的拟合结果为:R2=0.772,RMSE=0.005。此外,将由上述两种方法得到的JPDF预测值与实测的等值线绘于图8。由图8可直观发现,基于混合 von Mises分布与AL模型的方法得到的JPDF可以很好的捕捉到实测JPDF的变化趋势,而基于谐波函数与乘法定理的方法得到的JPDF在风向11处附近断开,即由该方法得到的JPDF不连续。显然,基于混合von Mises分布与AL模型方法得到的联合概率分布更适合于描述大理地区的风速风向联合概率密度函数,在接下来的研究中仅考虑该方法。
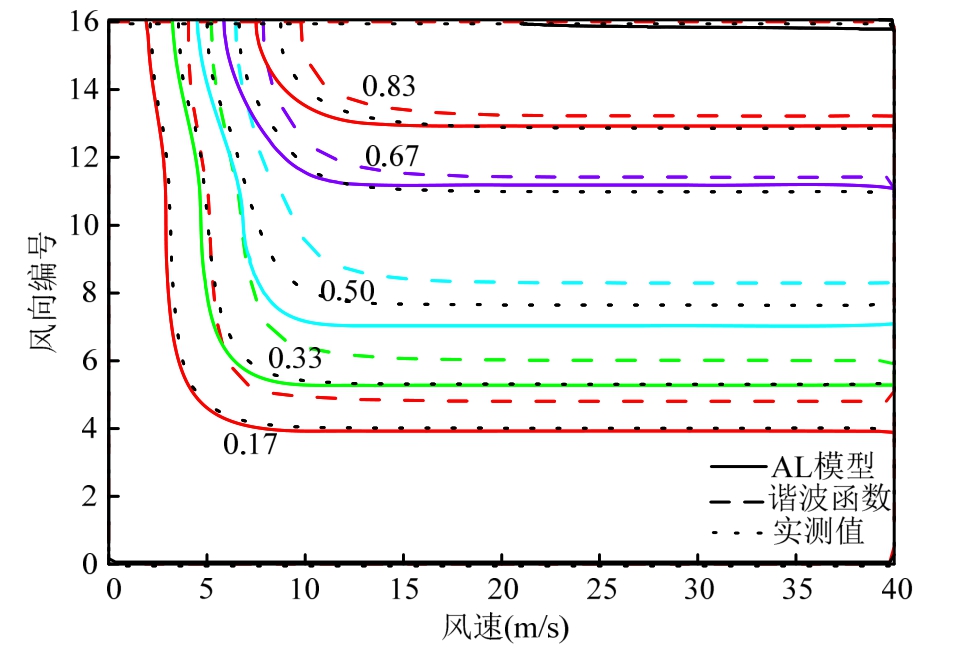
图7 风速风向联合概率分布实测值与预测值的对比
Fig.7 Comparison of measured and predicted values of joint distribution of wind speed and direction

图8 风速风向联合概率密度实测值与预测值的对比
Fig.8 Comparison of measured and predicted values of JPDF of wind speed and direction
风速风向联合概率密度的预测值的误差主要来自两方面:1)AL 模型中的 g(ζ)、f(v)和 f(θ)均需拟合得到,这势必会造成误差的累积;2)AL模型中的风速概率密度 f(v)是由 Gumbel分布对全风向风速拟合得到的,而由第2节研究结果可知各风向的最优风速分布模型有所差异。
4 基于风速风向联合分布的极值风速应用
以大理地区为例,取极值风速的重现期R,则该风速的超越概率为1/R。由于重现期R以年为单位,而本文采用的风速记录为日值数据,因此,将R换算成以天为单位,即实际重现期为 365 R。已知风速风向的联合概率密度函数,由概率论基本理论可知,任意给定风向风速分布的条件概率为:
其中,fθ(θ)表示 f(v,θ)关于 θ 的边缘概率密度,可表示为:
由重现期与超越概率的关系可知:
按传统方法不考虑风向的影响,根据第2节得出的大理地区全风向风速概率分布函数,即Gumbel分布模型计算该地区 50年重现期的极值风速为31.1 m/s。而基于风速风向联合概率分布计算的 E方向50年重现期的极值风速为23.1 m/s,比不考虑风向影响的极值风速小25.7%,因此有必要考虑风向对风速的影响。应该指出,AL模型中的角度变量ζ的概率密度函数g(ζ)是关于风速和风向的函数,这导致式(14)难以获得解析解,通常需要大量的迭代计算才能获得相应重现期的极值风速,这极大限制了该方法的应用。
5 结论
本文以大理国家气候观象台站监测的1971年1月以来的风速风向日值数据为研究对象。首先,探讨了描述风速分布规律的最优概率模型;其次,分别采用谐波函数和混合von Mises分布对风向概率密度进行拟合,并基于乘法定理和AL模型分别导出风速风向的联合概率密度函数;最后,基于风速风向联合概率模型对大理地区 50年重现期的极值风速进行了预测。主要结论如下:
(1)本文选用Gumbel分布、Frechet分布、三参数Weibull分布和双参数Weibull分布分别对全风向风速和 16个风向的风速进行了拟合,综合分析表明,Gumbel分布能更好地描述大理地区的风速分布规律。
(2)与谐波函数相比,混合von Mises分布更适合用于描述风向概率密度。基于混合von Mises分布与AL模型方法得到的风速风向联合概率密度函数的优度,明显优于基于谐波函数与乘法定理方法得到的联合概率分布。
(3)考虑风向影响得到的极值风速明显小于不考虑风向影响时的计算结果。因此,在对结构进行性能分析、设计以及风能资源评估等工作时,需考虑风速风向的联合作用。值得注意的是,本文的研究结论是根据大理地区实测风速数据得到的,并不完全适用于其他地区。但本文的研究工作对指导其他地区风速风向联合概率分布的研究及指导规范中相应条文的修订具有重要意义。
[1]Carta J A,Ramírez P,Velázquez S.A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands [J].Renewable & Sustainable Energy Reviews,2009,13(5):933―955.
[2]李宏男,王杨,伊廷华.极值风速概率方法研究进展[J].自然灾害学报,2009,18(2): 15―26.Li Hongnan,Wang Yang,Yi Tinghua.Advance in research on extreme wind speed models [J].Journal of Natural Disasters,2009,18(2): 15―26.(in Chinese)
[3]Zhou J,Erdem E,Li G,et al.Comprehensive evaluation of wind speed distribution models: A case study for North Dakota sites [J].Energy Conversion & Management,2010,51(7): 1449―1458.
[4]陈朝晖,汤海涛.基于Monte-Carlo法的极值风速模型研究[J].工程力学,2009,26(增刊1): 193―197.Chen Zhaohui,Tang Haitao.The extreme wind speed predicting model of typhoon by using monte carlo method [J].Engineering Mechanics,2009,26(Suppl 1):193―197.(in Chinese)
[5]Simiu E,Heckert N A.Ultimate wind loads and direction effects in non-hurricane and hurricane-prone regions [J].Environmetrics,2015,9(4): 433―444.
[6]王浩,徐梓栋,陶天友,等.基于 2008―2015年实测数据的苏通大桥风速风向联合分布分析[J].东南大学学报(自然科学版),2016,46(4): 836―841.Wang Hao,Xu Zidong,Tao Tianyou,et al.Analysis on joint distribution of wind speed and direction on sutong bridge based on measured data from 2008 to 2015 [J].Journal of Southeast University (Natural Science Edition),2016.46(4): 836―841.(in Chinese)
[7]Smith O E.An application of distributions derived from the bivariate normal density function [C].Honolulu,AMER Meteorological Soc,1971: 162―168.
[8]Jones R H.Fitting a circular distribution to a histogram[J].Journal of Applied Meteorology,1976,15(1): 94―98.
[9]Johnson R A,Wehrly T E.Some angular-linear distributions and related regression models [J].Journal of the American Statistical Association,1978,73(363):602―606.
[10]Mcwilliams B,Newman M M,Sprevak D.The probability distribution of wind velocity and direction[J].Wind Engineering,1979,3(4): 269―273.
[11]Weber R.Estimator for the standard deviation of wind direction based on moments of the cartesian components[J].Journal of Applied Meteorology,1991.30(9): 1341―1353.
[12]Wehrly T E.Statistical analysis of circular Data [J].Technometrics,1993,37(2): 229―230.
[13]Erdem E,Shi J.Comparison of bivariate distribution construction approaches for analysing wind speed and direction data [J].Wind Energy,2011,14(1): 27―41.
[14]Coles S G,Walshaw D.Directional modelling of extreme wind speeds [J].Applied Statistics,1994,43(1): 139―157.
[15]Wen Y K.Wind direction and structural reliability [J].Journal of Structural Engineering,1983,109(4):1028―1041.
[16]张春涛,李正良,范文亮,等.考虑风向风速联合分布的输电塔线体系风振疲劳研究[J].工程力学,2013,30(3): 315―322.Zhang Chuntao,Li Zhengliang,Fan Wenliang,et al.Study on wind-induced fatigue of transmission tower-line coupled system considering the joint distribution of wind speed and wind direction [J].Engineering Mechanics,2013,30(3): 315―322.(in Chinese)
[17]杨风利.角钢输电铁塔横担角度风荷载系数取值研究[J].工程力学,2017,34(4): 155―164.Yang Fengli.Study on skewed wind load factor on cross-arms of angle steel transmission towers under skewed wind [J].Engineering Mechanics,2017,34(4):155―164.(in Chinese)
[18]Zheng Xiaowei,Li Hongnan,Li Chao.Damage probability analysis of a high-rise building against wind excitation with recorded field data and direction effect[J].Journal of Wind Engineering and Industrial Aerodynamics,2019,184: 10―22.
[19]Simiu E,Scanlan R H.Wind effects on structures [M].New York: Wiley,1996: 301―317.
[20]Basile S,Burlon R,Morales F.Joint probability distributions for wind speed and direction.A case study in Sicily [C].New York: IEEE,2016: 1591―1596.
[21]Carta J A,Bueno C,Ramírez P.Statistical modelling of directional wind speeds using mixtures of von mises distributions: Case study [J].Energy Conversion & Management,2008,49(5): 897―907.
[22]董胜,林逸凡.固定测站的风向风速联合分布研究[J].工程力学,2016,33(6): 234―241.Dong Sheng,Lin Yifan.Study of joint probabilistic distribution of wind speed and direction at a fixed observation station [J].Engineering Mechanics,2016.33(6): 234―241.(in Chinese)
[23]林涛涛,陈隽,李想,等.基于连续型风速风向联合概率分布的风致结构疲劳分析方法研究[J].振动与冲击,2012,33(12): 48―52,105.Lin Taotao,Chen Juan,Li Xiang,et al.Analysis method for wind-induced structural fatigue based on continuous JPDF [J].Journal of Vibration and Shock, 2012,33(12):48―52,105.(in Chinese)
[24]Johnson R A,Evans J W,Green D W.Some bivariate distributions for modeling the strength properties of lumber [J].Mechanical Systems & Signal Processing,1999,6(3): 251―260.
[25]Schucany W R,Parr W C,Boyer J E.Correlation structure in farlie-gumbel-morgenstern distributions [J].Biometrika,1978.65(3): 650―653.
[26]Carta J A.Ramírez P,Bueno C.A joint probability density function of wind speed and direction for wind energy analysis [J].Energy Conversion & Management,2008,49(6): 1309―1320.
[27]Xu Y L,Chen J,Ng C L,et al.Occurrence probability of wind-rain-induced stay cable vibration [J].Advances in Structural Engineering,2008,11(1): 53―69.
[28]Li Hongnan,Zheng Xiaowei,Li Chao.Copula-based joint distribution analysis of wind speed and direction [J].Journal of Engineering Mechanics,2019,145(5):04019024.
[29]GB 50009―2012,建筑结构荷载规范[S].北京: 中国建筑工业出版社,2012.GB 50009―2012,Load code for the design of building structures [S].Beijing: China Architecture & Building Press,2012.(in Chinese)
[30]Xiao Y Q,Li Q S,Li Z N,et al.Probability distributions of extreme wind speed and its occurrence interval [J].Engineering Structures,2006,28(8): 1173―1181.
[31]范文亮,李正良,张培.风向风速的联合概率结构建模[J].土木工程学报,2012,45(4): 81―90.Fan Wenliang,Li Zhengliang,Zhang Pei.Modeling of the joint probabilistic structure of wind direction and speed [J].China Civil Engineering Journal,2012,45(4):81―90.(in Chinese)
[32]陈隽,赵旭东.总体样本风速风向联合概率分析方法[J].防灾减灾工程学报,2009.29(1): 63―70.Chen Jun,Zhao Xudong.Analytical method of joint probability density function of wind speed and direction from parent population [J].Journal of Disaster Prevention and Mitigation Engineering,2009,29(1): 63―70.(in Chinese)
[33]Lange B,Højstrup J.Evaluation of the wind-resource estimation program WAsP for offshore applications [J].Journal of Wind Engineering & Industrial Aerodynamics,2001,89(3): 271―291.