结构振动控制技术可以有效抑制结构在风、地震等多种外部激励作用下产生的动力响应，按其控制方式的不同可分为被动控制、主动控制、半主动控制及混合控制[1－4]。其中，通过在结构中附设消能减震(振)装置或者调谐减震(振)装置进行被动控制是目前应用最为广泛的一种结构振动控制方式，其主要通过在结构中增设质量、阻尼、弹簧这三类基本力学元件(一类或多类)来实现改变结构动力特性、降低结构动力响应的目的。在这三类基本力学元件中，阻尼和弹簧是两端点力学元件，其端部出力分别与其两端点间的相对速度和相对位移有关；而质量(如调谐质量阻尼器中的质量块、调谐液体阻尼器中的液体等[5－10])则是一种单端点力学元件(图1)。由于两端点力学元件弹簧(刚度)和阻尼元件便于在结构中安装，因此基于这两类力学元件的减震(振)装置在结构振动控制领域被广为使用。而质量元件作为一种单端点装置，为达到预期控制效果所需体量大，因此不便安装，同时在结构中附加质量后也将导致附加的动力效应。
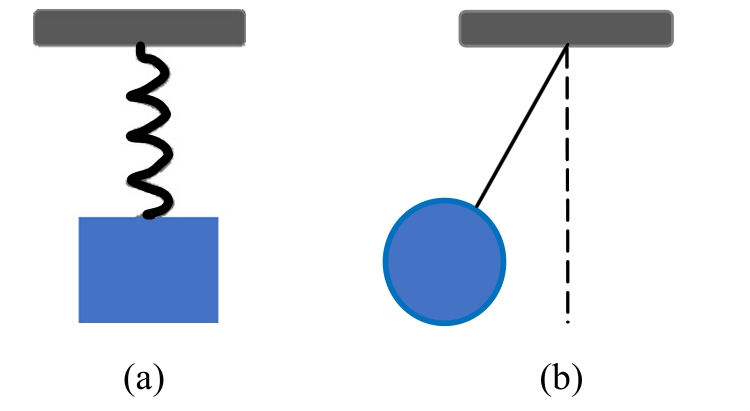
图1 单端点惯性元件—质量
Fig.1 One-terminal inertial element—mass
21世纪初，日本东北大学Inoue和Ikago团队[11－15]提出利用两端点惯性原理的结构减震(振)装置，并对其惯性增效和阻尼增效原理进行了系统化研究；英国学者Smith团队[16]通过力学与电学间的力-电流类比[17]，提出以“Inerter”(对应于电学中的电容)来命名两端点惯性元件，从理论角度概括了惯容元件(两端点惯性元件)的原理。与传统质量元件(单端点惯性元件)不同，惯容的出力与其两端点间的相对加速度相关(图2)，其出力与两端相对加速度的比值称为惯容系数(Inertance)：
图2 两端点惯性元件—惯容
Fig.2 Two-terminal inertial element—inerter
式中：p为惯容力；min为惯容系数(量纲等同质量，也称惯质或者表观质量)；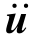
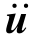1、2分别为惯容两个端点的加速度。
与传统质量元件相比，惯容元件的优势在于：调整结构惯性特性时不仅限于单端点连接(如调谐质量阻尼器的悬挂等方式)，还可以采用与普通消能器相同的层间安装方式，这样可以更灵活有效地实现改变结构惯性和调谐的目的。从目前已有的惯容装置来看，其产生的惯容系数可以远大于其自身的物理质量[18]，即惯容可以在基本不改变结构物理质量的前提下实现惯性特征的调整，而且惯容所增大的惯性并不会增加结构所受的地震作用，这个特点是惯容的另一个显著优势。
为更好地利用惯容实现结构减震(振)的目的，需要有消能装置(阻尼器)的配合。惯容与消能装置共同工作时能有效提高后者的能量耗散效率，这种耗能增益特性一方面源于惯容实现机制对等效黏滞系数的放大，另一方面是惯容-弹簧串联体系可以放大其内部自由度的变形，若将消能装置与惯容-弹簧串联体系中的某一元件并联，则可同时放大消能装置的变形，进而提高耗能效率。惯容系统的这一特点使其能够适用于结构相对变形较小的情形。
本文将从惯容的实现机理、惯容减震(振)系统的性能、惯容减震(振)结构体系的分析设计三个方面介绍、论述惯容的原理及其在减震(振)控制领域的发展历程与研究现状，总结惯容减震(振)结构体系的设计方法，同时指出有待进一步研究的方向，以促进惯容减震(振)系统理论研究的进一步成熟，并推进其在实际工程中的广泛应用。
1 惯容的实现机制
惯容的两端点惯性特征主要通过改变装置部件的运动形式来实现，如平动-转动的转换[19]、速度(流速)[20]的改变等方式。其中以平动-转动转换装置最为多见，其利用了机械工程中用于改变运动形式的传动装置，故此类惯容又称机械式惯容。机械式惯容的惯容系数本质上是转动惯量进行等效平动化的宏观参数。平动-转动转换装置应用于结构振动控制可追溯到20世纪80年代[21－23]提出的作为管道支承的缓冲器，该装置利用滚珠螺杆把平动转化为转动，设备正常运行时(低速相对运动)允许自由变形；当遭遇动力作用时(地震或冲击)，内置旋转质量将提供惯性力限制管道发生过大的变形。之后日本学者[19,24]提出了类似的装置实现了对黏滞阻尼器有效阻尼的放大，但两端点惯容原理并没有明确提出。Inoue和Ikago团队[11－15]及Smith团队[16]的学者对此类装置的实现机制理论化后，类似装置开始以两端点“惯容”元件为名出现在文献中。除了滚珠螺杆机构外，目前见诸文献的惯容实现机构还有齿轮齿条机构[16,25－26]、液压机构[27－30]、电磁机构[31－36]等。除上述常见惯容机制外，聂佳梅等[37]提出了几种新型惯容器，包括以封装质量惯性为特征的惯容器和扭转惯容器，具体有杠杆质量惯容器、少齿差行星齿轮扭转惯容器、摆线钢球扭转惯容器等。下面简要介绍几种典型惯容实现机制及其惯容系数的理论计算表达式。
1.1 滚珠螺杆式惯容
目前经典的惯容实现机制之一是滚珠螺杆机制。Inoue 和 Ikago 团队[14－15,18,38－40]对其进行了系统性的研究，并出版了第一部关于惯容减震(振)系统的学术专著[14]。滚珠螺杆惯容器将其两端点间直线相对运动转化为飞轮的高速旋转运动[18](图3)。滚珠螺杆体系将轴向平动加速度转换为旋转加速度，由于飞轮转动惯量的存在，元件将产生惯性作用力。从宏观运动形式来看，惯容元件发生的是轴向平动变形，故采用轴向平动加速度和惯容系数来直观描述其力学特性。但惯容系数产生的本质是转动惯性力的平动等效。由于飞轮的转动惯量产生的惯性作用远大于其物理质量的惯性作用，故该装置可以使用较小的物理质量产生较大的惯性力，达到惯性增效的效果，即惯容系数远大于实际物理质量。此特性在结构控制中有相当重要的作用，可以显著减小附加子系统的实际质量和体量，以节省空间和方便施工。
滚珠螺杆惯容器中，若螺杆导程为Ld，飞轮转动惯量为I，实际质量为m0，外直径为ro，内直径为 ri，则惯容器出力可以表示如下[18]：
图3 滚珠螺杆惯容机制原理示意图与实物图[11,13,25]
Fig.3 Schematic drawing and real photo of inerter using ball screw mechanism
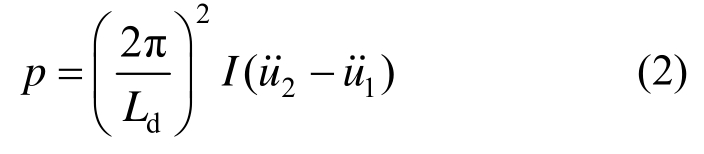
对比式(1)，可以得到滚珠螺杆惯容器的惯容系数表达式：
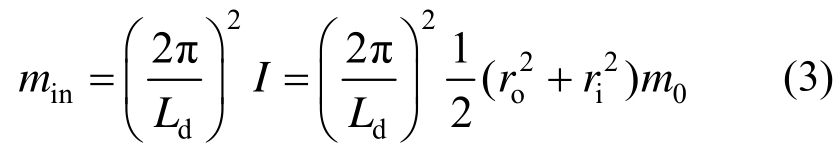
1.2 齿轮-齿条式惯容
Smith[16]在解释惯容原理时，构造了一个简单的实现机制：齿轮齿条机制[16,26]，即通过齿条、小齿轮和大齿轮的啮合传动，带动飞轮转动(图4)，从而提供较大的惯容系数。
图4 齿轮-齿条惯容机制原理示意图与实物图[25]
Fig.4 Schematic drawing and real photo of inerter using gear-rack mechanism
若与齿条啮合的小齿轮半径为 r1，大齿轮半径为 r2，与飞轮同轴的小齿轮半径为 r3，飞轮转动惯量为 I，则齿轮齿条惯容器的惯容系数：
1.3 液压式惯容
惯容还可以通过液压机制来实现[28](图5)。液缸外围设置螺旋管道，活塞在缸内运动时将驱动缸中液体通过外围螺旋管道，由于管道直径远小于缸体直径，管道内流体速度相较于活塞速度得以放大。通过扩大活塞面积或减小通道截面积可以进一步放大该装置的惯容系数[27,29－30]。
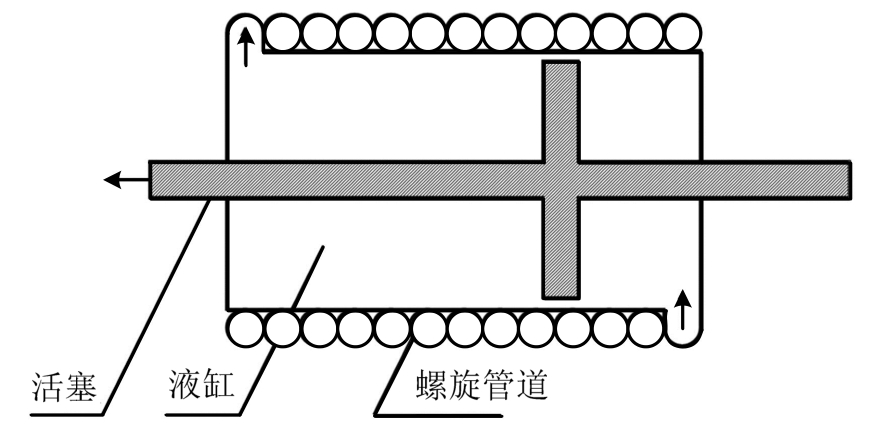
图5 液压式惯容原理示意图[28]
Fig.5 Inerter using hydraulic mechanism
假定液缸截面积(或活塞工作面积)为A1，螺旋管道截面积为 A2，管道长度为 l，液体密度为 ρ；两端等大反向的力为 p，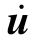
1、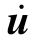2分别为两端速度。假设液体在螺旋管道中的平均速度为 v，根据流量相等可得：
螺旋管道中液体能量为
那么理想惯容器储存能量应为
令二者相等，得液压惯容器的惯容系数为：
1.4 电磁式惯容
电磁感应系统也可以产生惯容的两端点惯性特性[31,32,34－36]，如图6所示，在减震装置中加入了线性电机等电磁传感器。电机轴移动时，感应线圈两端产生电压差，电压差与其两端相对速度成比例。若线圈周围电路闭合，则根据洛伦兹原理，电磁传感器将产生与电流强度成比例的力。由电容、电感和电阻以特定方式组装而成的电路，通过电磁效应可以在装置的机械部分产生等效的惯容行为。该装置易于实现，通用性强，损失较小，可用于结构振动控制及健康监测。Gonzalez-Buelga等[31]在该装置中引入能量收集系统以储存电路中的能量。Wang等[36]通过对比研究说明了电磁机制具有一定优越性。Høgsberg等[33]提出在该系统中引入力反馈机制控制的主动作动器可以实现混合控制。
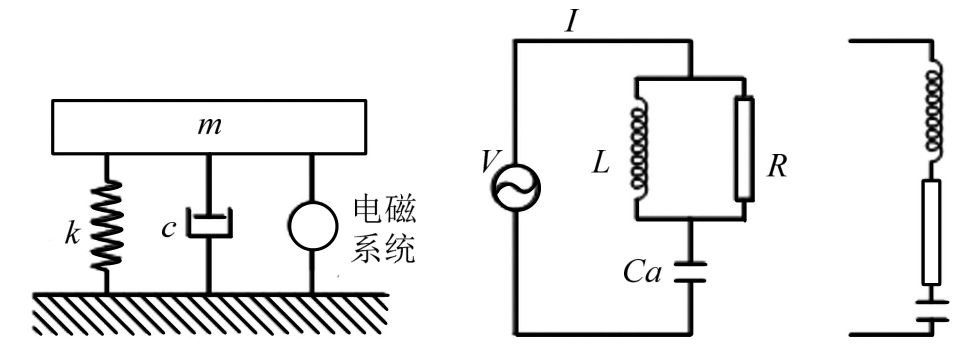
图6 电磁机制惯容原理示意图[32]
Fig.6 Mechanism of electromagnetic inerter
2 惯容减震(振)系统
2.1 惯容减震(振)系统的概念与基本类型
惯容元件自身仅具备惯性调整和能量转移的功能，为更有效地实现减震(振)控制的目的，常常需要将惯容与弹簧、耗能元件(阻尼器)等力学元件相连接以协同工作。由于惯容、弹簧和耗能装置分别对应动力学运动方程的质量项、刚度项和阻尼项，这已构成了一个完整的动力学系统，故本文将含有惯容、弹簧和耗能元件的振动控制装置称为惯容减震(振)系统(简称惯容系统)。惯容减震(振)系统的减震(振)原理可以从以下两方面来论述：1)惯容和弹簧可以调节结构的惯性和刚度特性，即通过调频以避免主结构与外部激励的共振；2)作为一个完整的动力学系统，惯容减震(振)系统内部的振动与主体结构并不同步，这种异步振动可以使惯容系统内部耗能装置的有效变形得以放大，从而起到耗能增效的作用以进一步抑制响应。具备调谐机制和能量耗散增效机制的惯容系统根据力学元件的拓扑连接形式的不同可组合出不同类型。在只包含一个惯容元件、一个弹簧和一个耗能元件的前提下，三种典型的基本惯容系统为[41－42]：串联型惯容系统(SIS)，混联 I型惯容系统(SPIS-I)和混联 II型惯容系统(SPIS-II)，见图7。
2.2 汽车、机械领域的惯容减震(振)系统
尽管惯容系统在土木领域的出现略早于机械领域[19,24]，但机械领域较早地对其展开了系统性研究。惯容在机械领域的首次实际应用是 F1赛车的悬架系统[43]，并被证实显著提高了车辆的性能[44－46]。随后，惯容在机械领域开始得到关注。Evangelou等[47]将惯容引入转向补偿器，以改善高性能摩托车的动力特性，并提出了该系统的设计及优化方法。Wang等[48]讨论了摩擦、间隙和弹性效应等惯容的非线性特性对车辆悬架性能的影响。该团队还研究了安装惯容的列车悬架系统，表明惯容可以有效改善列车悬架系统的性能[49]；另外，他们还将惯容引入光学平台[50]以抑制地面干扰产生的响应，也被证明是有效的。陈龙等[51]研究了一种两级串联型“惯容-弹簧-阻尼”车辆ISD悬架系统，通过分析证实了该系统具有良好的动态性能，可以有效抑制车身共振，改善乘坐舒适性及行驶安全性。杨晓峰等[52]研究了含有惯容的动力吸振器与主系统的连接方法与耦合关系，提出了车辆ISD悬架结构设计方法。Chen等[53]提出了基于灵敏度分析和量子遗传算法的车辆悬架系统参数优化方法。Shen等[54]提出了一种流体惯容器，研究了其非线性特征，并建立非线性模型，基于量子遗传算法对悬架系统刚度和阻尼系数进行了优化。Dong等[55]通过仿真模拟，观察和分析了引入惯容系统的飞机起落架的性能，发现在一定参数下其性能得到了改善，而参数不当则会引入额外的不稳定性。Liu等[56]研究了安装惯容系统的飞机起落架的非线性效应。Papageorgiou等[57]对比研究了滚珠螺杆惯容器和齿轮齿条惯容器，通过测试对装置的不稳定性进行观察和解释；该团队还对滚珠螺杆惯容器和齿轮齿条惯容器进行了实物测试[25]。
图7 惯容系统基本类型
Fig.7 Mechanical layouts of inerter systems
在机械领域，除了上述用于被动控制的惯容系统，在半主动控制中惯容系统也有相关应用。Chen等[58－59]提出半主动惯容系统的形式，Hu等[60]据此提出了一种新型的基于半主动惯容的自适应调谐减振器，其通过将惯容器中的固定惯性飞轮替换为可控惯性飞轮，实现了对惯容系数的半主动控制。针对此半主动控制惯容设备提出了基于频率跟踪和相位检测的两种控制方法。随后通过试验证明了该系统可以有效减振，并对主系统参数的变化有良好的适应性。
2.3 土木领域的惯容减震(振)系统
2.3.1 惯容减震(振)系统的雏形—旋转质量黏滞阻尼器
20世纪70年代开始两端点的惯性机制的利用就已经开始在土木工程领域萌芽[20]。90年代末，Arakaki等[19,24]使用滚珠螺杆机构对黏滞阻尼元件的阻尼力进行放大，以更高效地对结构的地震响应进行控制。由于当时“惯容”作为基本力学元件的概念未广泛传播，该装置被称为旋转阻尼系统(RD)，但其实质上利用的也是惯容的耗能增效原理。同一时期，采用了惯容放大机制的黏滞阻尼器还被称为旋转质量阻尼器(GMD)[61]或惯性质量阻尼器(IMD)[62]。Saito等[63]研究了附加GMD的单自由度结构，并讨论了其应用于多自由度隔震结构的可能性。Hessabi等[64]研究了GMD安装位置和数量对其减震(振)效果的影响，同时发现 GMD在控制最大底部剪力方面有良好的效果。此外，Hessabi等[65]还提出了一种GMD-黏滞阻尼-支撑系统，简称为 GVB系统，并证实该系统可以进一步提高体系的减震(振)性能。Wang等[66]提出一种基于惯容的建筑悬架体系，其实质为设置惯容系统的竖向隔震体系。Saitoh[67]研究了三种附加 GMD的隔震结构的动力性能，基于理想化模型提出了结构设计参数的解析表达式。Takewaki等[68]通过对安装IMD装置结构的研究，发现虽然加速度响应及底部剪力得到了控制，但结构最大层间位移角可能有所增加。Hwang等[69]提出将肘节式支撑与旋转惯性阻尼器(RID)相结合，以放大结构变形，提高阻尼器的耗能效率。
2.3.2 首个完整意义上的惯容减震(振)系统—调谐黏滞质量系统
Inoue 和 Ikago 团队[12－13,18,70－74]将飞轮惯性放大机制和调谐机制引入旋转黏滞阻尼器，提出了一种新的减震(振)装置，称为调谐黏滞质量阻尼器(TVMD)，该装置的力学拓扑形式等同于图7中的混联II型惯容系统(SPIS-II)，其中阻尼耗能装置采用黏滞阻尼元件，这是土木工程领域首次出现的完整意义上的惯容减震(振)系统。针对新装置的机理提出了优化设计方法，考虑了对直接作用于主结构质量的强迫谐波振动的变形响应因子进行控制(基于变形的优化)、对作用于系统基础的谐波干扰的位移放大系数及加速度放大系数进行控制(基于位移和加速度的优化)，随后基于一个单自由度体系的振动台试验证明了所提出的设计方法的有效性。此外，Saito等[70]证明了惯容系统中阻尼元件的最优阻尼系数和弹簧元件的最优刚度可以由惯质比(惯容系数与主结构质量之比)唯一确定。Arai等[72]对黏滞阻尼器(VD)、黏滞质量阻尼器(VMD)和 TVMD进行了比较研究，发现在相同的阻尼比下 TVMD对结构振动控制最有效。另外，还对附加 TVMD的结构进行了缩尺振动台试验及非线性时程分析。Kida等[73]对附加TVMD的结构进行了足尺振动台试验，进一步验证了其在结构振动控制方面的效果。Ikago等[15,18]基于Den Hartog的定点理论[5]提出了一种简单的TVMD减震(振)控制系统的设计方法，并进行缩尺振动台试验，通过比较发现在附加阻尼比相同时，TVMD系统比传统 VD、VMD更有效。Sugimura等[75]将TVMD应用于日本的钢结构建筑，证明 TVMD系统可以使结构获得更大的惯性，并放大了对地震响应控制起主导作用的一阶模态的阻尼；结合黏滞阻尼器可以放大任意阶模态的阻尼，得到更好的地震响应控制效果。Ikago等[40,76]讨论了 TVMD 用于地震响应控制时的结构模态响应特性，并发现 TVMD可以用于控制结构的高阶模态响应[77]。
由于解析法进行惯容系统参数优化设计需要假定结构固有阻尼比为 0，这可能会造成误差。鉴于此，李超等[78]基于遗传算法提出了一种更通用TVMD参数优化方法，以获得更合理的设计参数。阎武通等[79]将TVMD应用于斜拉桥减震(振)控制，提出多 TVMD控制装置参数优化方法，并以实际结构为控制对象，提出相应控制方案并验证TVMD控制效果。裴星洙等[80]分析了附加 TVMD的多层钢框架，基于能量平衡方程推导了地震响应预测公式，并提出能量分散系数的简化计算公式，为阻尼器初步设计提供了快捷的方案。Asai等[81]将TVMD系统安装在高层建筑的伸臂桁架和外立柱之间，以放大 TVMD系统两端的相对运动，进而提高其减震(振)效果。
上述 TVMD系统可以用较小的实际质量获得较大的惯性力，但惯容系数的增加可能导致附加系统对主结构上产生过大的附加内力。因此，Kida等[38,73－74]将TVMD进行了改进，附设摩擦装置以避免 TVMD产生过大的内力，即限力调谐黏滞质量阻尼器(FRTVMD)(图8)，并通过单自由度结构说明了限力机制可以在保证减震(振)效果的同时有效限制控制力的大小；同时发现了结构在受长周期地面运动作用时应用FRTVMD的优势。此后，Ikenaga等[82]对FRTVMD进行了振动台试验，验证了其结构响应控制效果。Nakaminami等[83]将FRTVMD应用于隔震结构，采用非线性时程分析方法验证了将FRTVMD用于隔震结构并控制最大阻尼力的可能性，最后提出了一种实用设计方法。在限力机制的研究方面，Ikenaga等[84]又提出了一种使用Bingham流体进行力限制的方法，并将其应用在基础隔震建筑中。
图8 力限制调谐黏滞质量阻尼器(FRTVMD)[74]
Fig.8 Force restriction tuned viscous mass damper(FRTVMD)
2.3.3 调谐惯容系统
Lazar等[85－87]研究了调谐惯容阻尼器(TID)振动控制系统的性能，其中TMD的质量块由安装在多层建筑物的相邻楼层支撑上的惯容器所取代，使用TID取代传统TMD可以实现质量和减振效果的放大。TID的力学拓扑形式等同于图7中的混联I型惯容系统(SPIS-I)。Lazar等[89－89]、Sun 等[90]研究了TID在振动控制中的应用，并提出了近似的参数设计方法。Luo等[91]将具有不同连接方式的惯容系统用于桥索减振，提出TID系统在研究的四种系统中最具优势。Zhang等[92]研究了不同的惯容系统拓扑结构[93]，并提出TID有利于降低成本以及阻尼器尺寸。Gonzalez-Buelga等[94]对 TID系统非线性特性进行了研究，并进行了试验验证。Domenico等[95]将TID附加到基础隔震层，进行优化设计，同时研究了场地土条件对TID参数的影响，并通过时域分析验证该结构的有效性；此外，对于隔震结构，Domenico等[96]进行了不同惯容减震(振)系统与传统TMD的对比研究，说明了惯容减震(振)系统在隔震结构中的优越性。Wen等[97]采用H2优化方法对安装多个TVMD或TID的多自由度结构进行了地震作用下的优化设计。
2.3.4 惯容减震(振)系统与调谐质量阻尼器的组合
Garrido等[98]将TVMD设置在传统TMD中，提出了一种改进的 TMD，称为旋转惯性双调谐质量阻尼器(RIDTMD)(图9)，其中传统黏滞阻尼器由TVMD取代。在质量比相同的条件下，激振频率与共振频率相近时，RIDTMD比传统TMD更有效。
图9 旋转惯性双调谐质量阻尼器(RIDTMD)[98]
Fig.9 Rotational inertia double-tuned mass damper(RIDTMD)
Marian等[99－102]将惯容设置在 TMD 体系中，提出了被称为调谐质量阻尼惯容器(TMDI)的系统(图10)，经优化设计的TMDI系统在减小位移响应方面的表现优于经典 TMD。Pietrosanti等[103]分析了TMDI系统性能，在白噪声输入下用三种不同方法对该系统进行参数优化，进行敏感性分析，证明TMDI系统比传统TMD系统具有更优异的性能。Giarails等[104]对有色噪声激励下具有TMDI的线性多自由度体系进行分析，考虑了结构模型和地震激励的不确定性，提出对于不确定的地震激励，TMDI比传统TMD更具有鲁棒性；此外，Giarails等[101]还将TMDI应用于高层结构，研究了其对减少由涡旋效应引起的高层建筑横风向风振响应的有效性，指出相比传统TMD，TMDI可以减小附加质量并更有效地控制顶层加速度响应，以满足结构设计中的舒适度指标。Domenico等[105]将TMDI应用于基础隔震结构，提出将TMDI附加到隔震层上可以有效减少隔震层位移、底部剪力及上部结构层间位移角。Jin等[106]对比研究了两种TMDI连接形式，进行优化设计，并分析了TMD质量比和惯容惯质比对系统性能的影响。Ruiz等[107]通过响应分析对地震风险进行量化，并据此提出了一种TMDI的设计优化方法。
2.3.5 其他类型惯容减震(振)系统
张瑞甫等[108]提出将惯容元件和阻尼元件串联(SVMD)用于隔震结构(图11)，这与TVMD中黏滞元件与质量元件并联的连接方式不同。罗浩等[109]对该系统进行了结构响应分析和优化设计，对比研究了将该系统应用于隔震建筑结构的优越性。
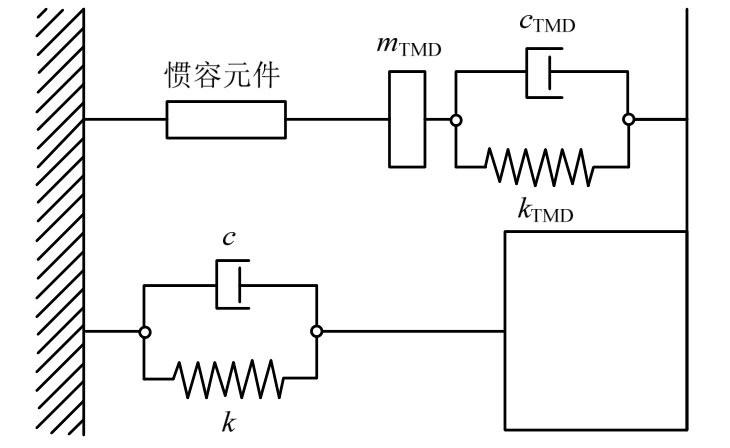
图10 谐质量阻尼惯容器(TMDI)[100]
Fig.10 Tuned mass damper inerter(TMDI)
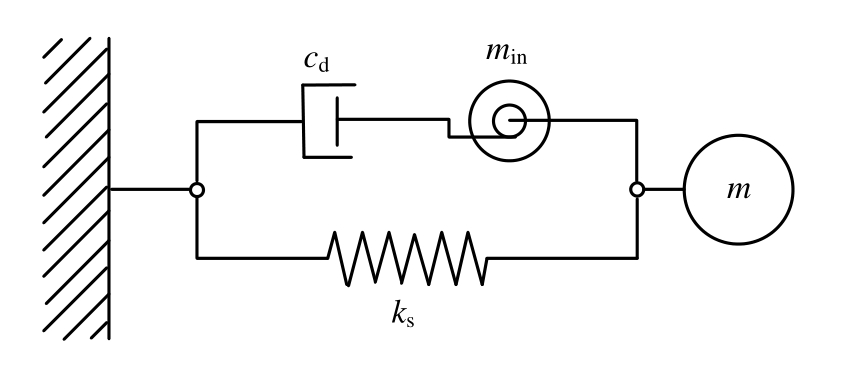
图11 串联黏滞质量阻尼器(SVMD)[108]
Fig.11 Series viscous mass damper (SVMD)
Ohtake等[110]将滚珠螺杆机构与发电机结合，用于结构振动控制。在此基础上，Nakamura等[111]提出了一种带有旋转惯性质量的新型电磁惯性质量阻尼器(EIMD)。在该系统中，滚珠螺杆机构产生较大的惯性力，发电机产生可变阻尼力。随后其进行了足尺振动台试验，分析表明该系统能够减少层间位移角和加速度，且在减小加速度响应方面优于传统阻尼器。
Hatanaka等[112－113]提出了一种新型液压惯容系统，称为紊流液压惯容系统，并研究了配置该系统的单层框架结构的响应特性。Asai等[114]提出将调谐惯性质量电磁传感器引入能量收集系统，通过优化以最大化地从静态随机扰动中收集能量。
Faraj等[115]提出了一种调节惯容器惯性质量的方法。Brzeski等[116－117]在齿轮齿条惯容机制中加入可调无级变速箱，实现了惯性的调节，并利用该装置改造了传统 TMD，使其可以在更宽的频带内减震(振)。此外，该团队还对加入惯容系统的TMD进行深入研究，具体探究了惯质比、黏滞阻尼、干摩擦及缝隙对减震(振)效果的影响[118]。
赵志鹏等[119]提出一种非速度依赖型阻尼惯容系统，相较于传统的黏滞阻尼惯容系统提高了耗能效率。针对风振控制，Zhang等[120]提出了一种调谐并联惯性质量系统(TPIMS)。班鑫磊等[121]基于惯容原理提出了一种拉索式旋转电涡流惯容系统，研究了其力学模型并分析了频域响应。此外，惯容的质量增效机制也为负刚度装置的开发提供了便利[18,122]，Lu等[123]在研究桥索减振时，采用了一种黏滞惯性质量消能器作为负刚度装置。基于调谐质量类的颗粒阻尼控制装置，Zhao等[124]提出了耗能效率更高的颗粒阻尼惯容减震(振)系统(PIS)。
2.3.6 惯容减震(振)结构的设计与应用
在惯容减震(振)结构设计方面，初期的设计方法均基于定点理论展开，未考虑主结构的阻尼，也未考虑全局优化和控制成本等问题。张瑞甫及其团队[78,108－109,120,125－129]对设置惯容减震(振)系统的结构提出了基于需求和减震(振)效率的设计思想，探索出更为有效实用的设计方法。张瑞甫等[109,125]利用惯容器和橡胶支座提出了一种混合控制系统，对储罐进行隔震控制，该系统可以有效降低液面晃动响应、储罐底部剪力以及倾覆力矩；并研究了惯容系统力学元件的拓扑形式对储罐减震(振)效果的影响，基于储液罐的目标性能提出了优化设计方法[126,130]。赵志鹏等[131]提出了使用SPIS-II型惯容系统的隔震建筑结构基于需求的设计方法。张瑞甫等[120]对风电塔使用调谐并联惯性质量系统(TPIMS)进行了减震(振)控制研究，在参数研究的基础上基于需求和减震(振)效率提出优化设计方法，证明了该系统在控制风电塔地震响应方面的有效性，且与传统调谐质量阻尼器相比可减小所需附加物理质量。张璐琦[132]提出利用惯容系统的耗能增效和结构高阶模态调谐机制，将惯容系统设置在抗震墙结构的连梁位置，以提高这类结构的减震(振)效率。赵志鹏等[119]针对非速度依赖型阻尼惯容系统，提出了单自由度结构使用该装置的基于需求的优化设计方法。曹嫣如等[129,133]使用一种惯容系统代替传统调谐质量阻尼器，研究其在高层结构风振控制中的作用，证明使用惯容系统可以在确保减震(振)效果的同时显著降低附加物理质量。Pan等[127]对安装惯容减震(振)系统的单自由度结构进行了参数研究，并提出了新的参数优化策略，考虑了结构的固有阻尼及控制成本，相较于以往基于定点理论的设计方法而言更为合理。为了使设计结果更为可靠，Pan等[126]基于随机振动理论推导了惯容单自由度体系随机响应的解析表达式，并基于此提出了以响应减震(振)比作为设计指标、以响应极值条件作为参数优化条件的设计方法，并提供了经验拟合公式以便工程应用。Chen等[128]研究了土-结构相互作用对惯容减震(振)结构的影响，并提出了相应的参数优化设计方法。Zhao等[124]对使用颗粒阻尼惯容减震(振)系统的结构提出了基于需求的优化设计方法。Pan等[134]还考察了随机地震激励对设置惯容系统的单自由度体系的响应变化规律的影响并给出设计建议。
在实际工程应用方面，世界上首次使用惯容减震(振)系统的土木工程结构是仙台 NTT公司大楼(图12)[75]。该建筑为钢框架结构，为控制地震响应而采用减震(振)系统。x方向上低层(1层～4层)设置黏滞阻尼器，高层(5层～14层)则设置TVMD减震(振)系统。采用改进的定点理论[18]设计系统参数，通过支撑将减震(振)系统与主结构进行连接。该TVMD减震(振)系统将一个实际质量为560 kg的两端点质量元件放大为5400 t的等效质量，体现了惯容的质量放大机制。分析表明惯容系统有效增大了对地震响应起主导作用的第一振型阻尼，另外高阶振型阻尼也可以提高；通过限力机制可以在保证控制效果的同时有效限制减震(振)系统的出力。
图12 首个利用惯容系统的土木工程结构——日本仙台NTT公司大楼
Fig.12 The first civil engineering structure with inerter system—NTT building in Sendai,Japan
3 惯容减震(振)结构体系的分析与设计
3.1 惯容减震(振)结构体系的运动方程
3.1.1 单自由度结构
经典单自由度结构在外部激励p(t)作用下的运动方程可以如下表示：
式中：m、c、k分别为单自由度结构质量、阻尼、刚度；u、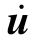、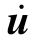分别为主结构位移、速度、加速度。当结构受到地震作用时，取p(t)=-mag，其中ag为地面运动加速度。
在单自由度体系中设置惯容减震(振)系统后(如图13)，体系的运动方程可写为：
式中，FIS为惯容系统出力，由于惯容系统会带来额外的自由度，因此还需要附加方程才能完全描述体系的运动。三种基本的惯容系统(采用线性黏滞阻尼器作为耗能装置)对应的FIS表达式及对应附加方程分别为：
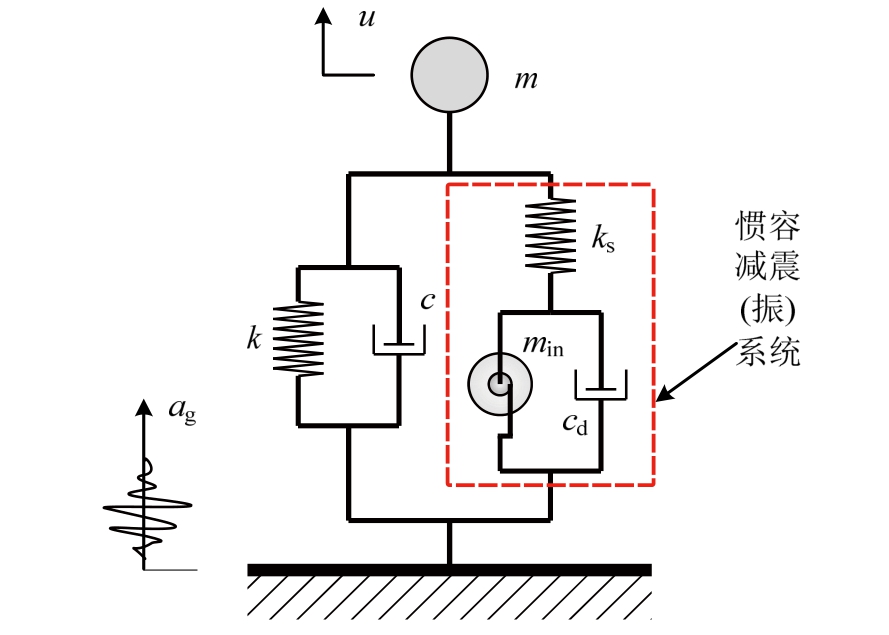
图13 安装惯容减震(振)系统的单自由度体系示意图
Fig.13 Single-degree-of-freedom structure with inerter system
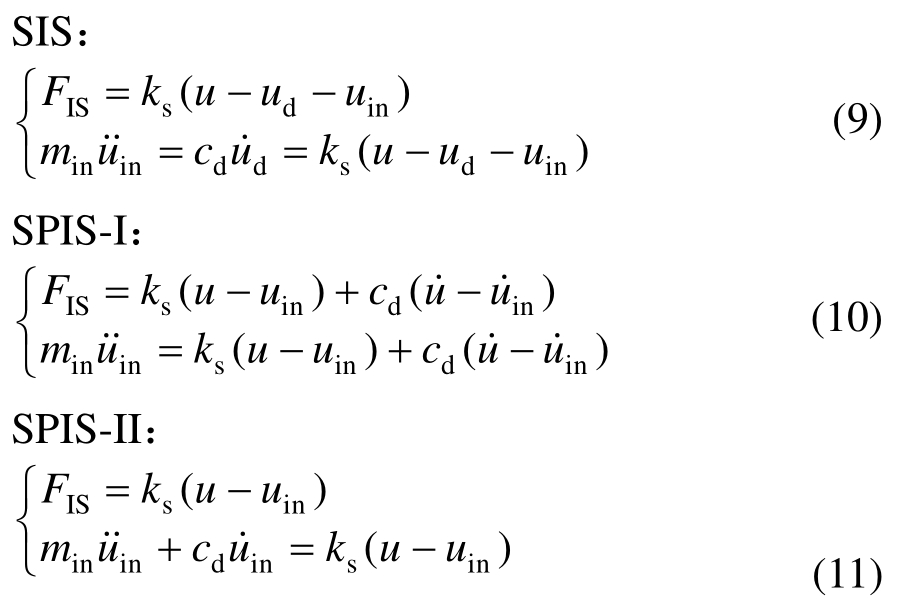
式中：ks为惯容系统中弹簧的刚度；min为惯容系数；cd为惯容系统中耗能装置的黏滞阻尼系数；u为主结构位移；ud为惯容系统中阻尼元件两端相对位移；uin为惯容元件两端相对位移。
3.1.2 多自由度结构
多自由度体系在外部激励P(t)作用下的运动方程可以如下表示：
式中：Mp、Cp、Kp分别为多自由度结构质量矩阵、阻尼矩阵、刚度矩阵；u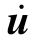p、p、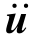p分别为主结构各层位移向量、速度向量、加速度向量。若结构为N自由度，则式中
当结构受到地震作用时，外部激励
其中，Ep=(11…11)T，ug为地面位移。
在多自由度体系中设置惯容减震(振)系统，体系运动方程矩阵表达式如下：
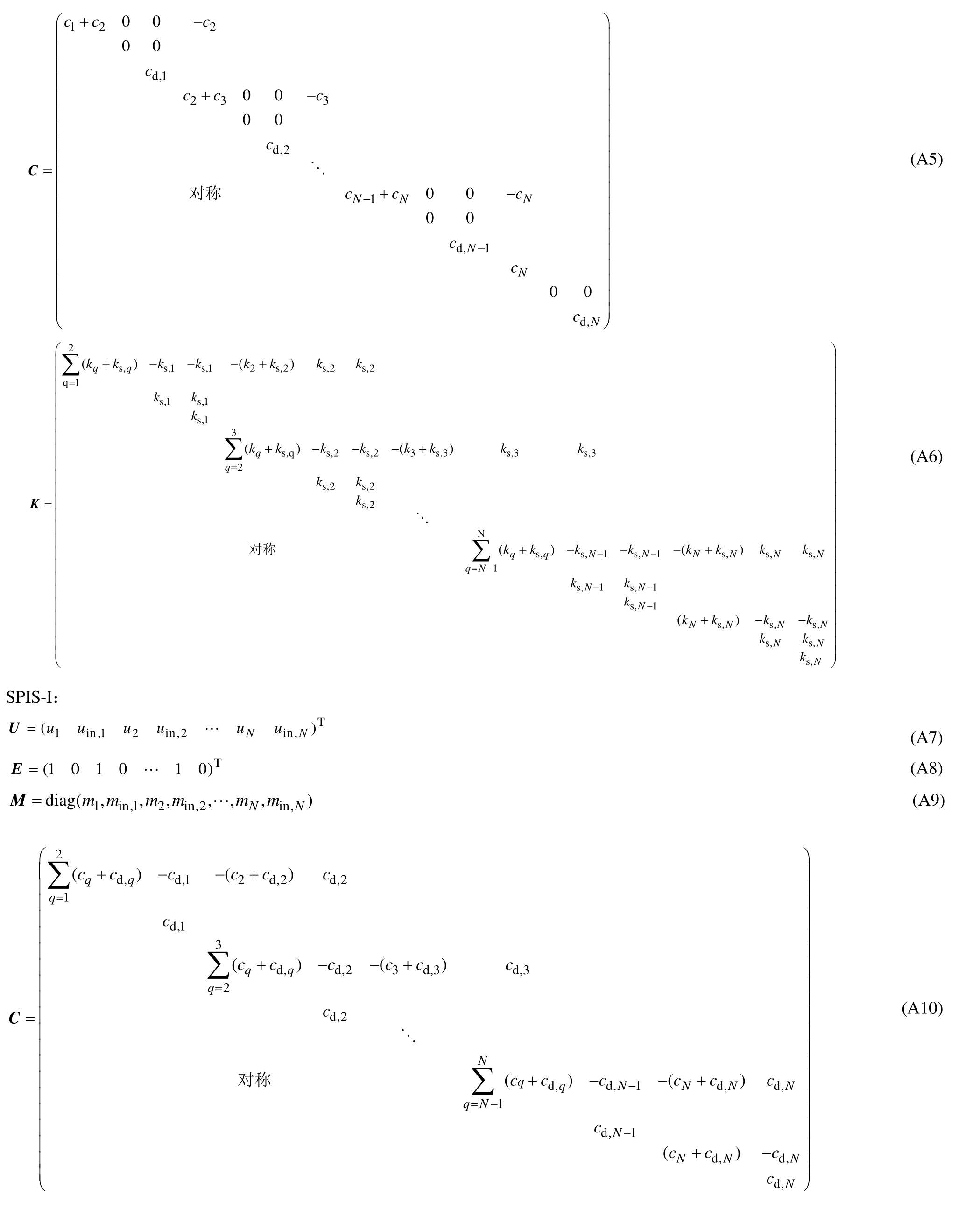
式中：M、C、K分别为设置惯容减震(振)系统后多自由度结构的质量矩阵、阻尼矩阵、刚度矩阵；U表示各自由度的位移响应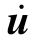；设置惯容减震(振)系统后，结构各层自由度除原有的各层质量产生外，还产生了惯容系统内相关元件的自由度，根据所设置惯容系统的不同形式，矩阵表达式也有所区别。对于不同惯容减震(振)系统，上述矩阵表达式的具体形式在附录中给出。
图14绘制了各层均设置SPIS-II的示意图，图中，min,n、cd,n、ks,n(n=1,2,…,N)分别为各层安装的惯容减震(振)系统的惯容系数、黏滞阻尼系数和弹簧刚度。
3.2 惯容减震(振)结构体系的响应求解
求解惯容减震(振)结构体系响应主要有两种基本思路：1)选择足够多的动力激励时程，采用逐步积分法，对运动方程进行直接求解；2)选择能代表动力激励频谱特性的输入功率谱模型，进行随机响应求解。具体而言，对于简单结构，可以通过编写数值求解程序进行求解；对于复杂结构，宜借助结构分析设计软件进行相应求解。对于通用有限元软件，目前商用软件中尚缺少惯容相关单元，可通过子程序接口进行二次开发，或在软件内建立圆盘-刚臂机构(如图15所示)以模拟惯容的特殊力学行为。
图14 安装SPIS-II惯容系统的多自由度体系示意图
Fig.14 Multi-degree-of-freedom structure with SPIS-IIs
图15给出的是SPIS-II惯容系统的圆盘-刚臂模拟示意图。当图中圆盘的转动惯量
且刚杆长度l很大时，其力学行为等价于惯容系数为min的惯容器。圆盘-刚臂机构源于惯容元件的平动-转动转换机理[18]，是一种在通用有限元软件中模拟惯容系统的有效手段。
3.3 惯容减震(振)结构体系的参数设计方法
与惯容系统的组成部件相对应，一个基本惯容系统包含三个关键参数：惯容系数 min、惯容系统弹簧刚度ks、惯容系统阻尼系数cd。本文建议采用表1中三个无量纲量作为惯容系统的设计参数。
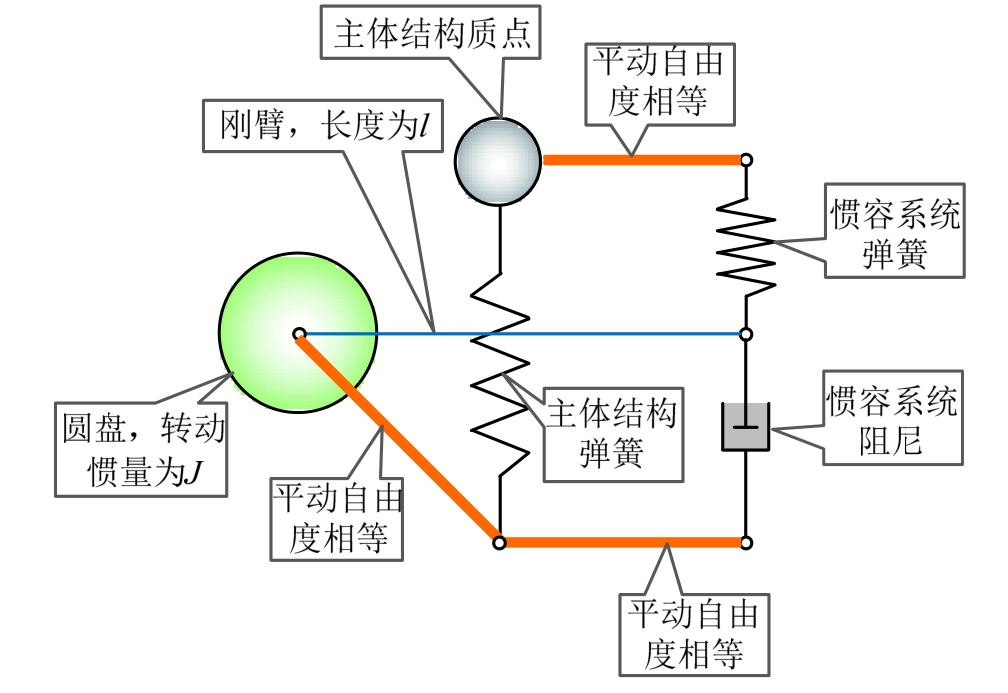
图15 用圆盘-刚臂机构模拟惯容机理
Fig.15 Wheel-rigid-beam system for the simulation of inerter
对于设计过程中上述参数的确定，已有多位学者提出了不同的方法。Ikago等[18]基于Den Hartog定点理论[5]，分别对安装惯容系统的单自由度结构和多自由度结构提出了相应的惯容系统设计方法。对于单自由度主结构，在确定了惯质比之后，刚度比和名义阻尼比可以通过以下公式获得：
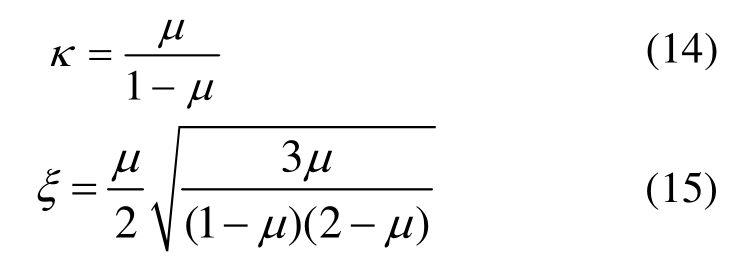
表1 惯容系统基本设计参数
Table 1 Fundamental design parameters of inerter system
对于多自由度结构，Ikago等[77]提出假定结构每层的附加惯容系数与层刚度成正比，通过等效单自由度，使用改进的定点理论，获得各层需要的惯容系统各部分参数。
结合定点理论[5]，Hu等[41]对安装不同惯容减震(振)系统的单自由度体系进行了优化，并提出了相应的设计方法。
基于Den Hartog定点理论[5]，Pan等[126]针对安装有SIS、SPIS-I、SPIS-II这三种基本惯容减震(振)系统的单自由度结构，推导了附加系统调谐刚度比与名义阻尼比的解析表达式，如表2所列。表达式的详细推导过程在文献[127]中有具体阐述。
基于定点理论得出的设计公式较为简单，但其推导过程并未考虑主结构的固有阻尼和外部激励特性，亦未考虑结构性能目标或要求，因此具有一定局限性。对此，张瑞甫等[109,120,126－127]在2014年提出基于性能需求的惯容系统设计理念，并进行了相关研究。Pan等[127]针对定点理论的缺陷，提出以满足结构性能为前提、以代价最小为目标的设计思路，以均方随机位移响应反映结构性能，以惯容减震(振)系统均方力响应作为结构成本控制依据，同时限制惯容减震(振)系统的黏滞阻尼，以使得惯容减震(振)系统中的惯容元件在结构振动控制中起主导作用。该优化设计方法可以写成如下的数学表达式：
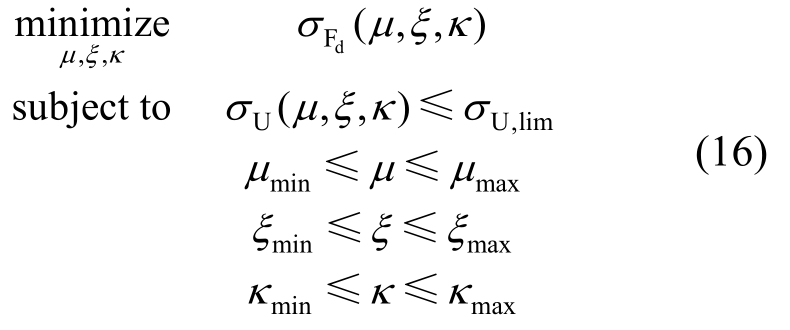
式中：σU,lim 为σU最大容许值，即结构性能指标；下标min、max分别代表对应变量可取的最小值、最大值。
上述优化问题可采用常见数值优化算法求解，但数值优化算法可能会带来数值稳定性等问题。为了提高设计过程的可靠性，Pan和Zhang[126]提出了基于随机响应解析表达式的设计方法，该方法以响应减震(振)比作为设计目标，引入响应极值条件建立方程组进行设计参数求解，同时，该方法也考虑了结构固有阻尼、不同外部激励形式等因素。据文中定义[126]，随机响应减震(振)比为减震(振)结构的均方根响应与原结构均方根响应之比：
表2 基于定点理论的单自由度结构安装惯容减震(振)系统参数
Table 2 Parameter expressions for an SDOF structure with an inerter system under fixed-point theory
注：*与上述Ikago等[18]提出的表达式相同。
images/BZ_30_914_2796_1018_2874.pngimages/BZ_30_1039_2938_1161_2974.pngimages/BZ_30_882_2896_1166_2976.pngimages/BZ_30_887_2997_1072_3076.png
设计时，可先根据结构性能需求确定目标减震(振)比，若要满足性能需求则应使结构实际响应减震(振)比与目标响应减震(振)比相等，即：
考虑参数优化，引入位移响应极值条件和出力响应极值条件：
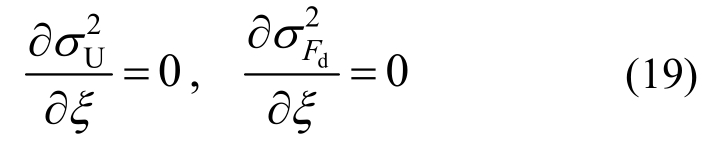
式(18)、式(19)可以整理为关于μ、ξ、κ的方程组，求解即可得相应参数。
为使设计更为简便，文献[126]中提供了白噪声激励下惯容系统的经验设计公式，其中相关参数取值参见表3：
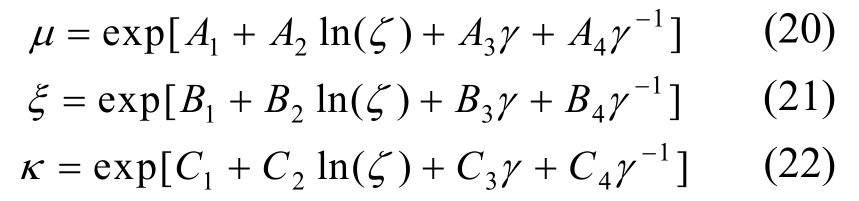
表3 单自由度结构中不同惯容系统半解析半经验设计公式参数取值
Table 3 Values of the coefficients in the semi-analyticalempirical design formulae for SDOF structures with respect to the type of inerter system
4 结论与展望
4.1 结论
本文以惯容系统为研究对象，综合了国内外大量学者的研究成果，全面介绍了惯容的实现机理、惯容减震(振)系统性能、惯容减震(振)结构体系的分析设计方法，阐述了惯容的原理及其在减震(振)控制领域的发展历程与研究现状，并得出以下结论：
(1)相比于传统减震(振)系统，惯容减震(振)系统具有如下优势：
惯容的出现为结构惯性调整提供了新的方式，即可在层间或结构内部两节点间安装。这改变了为提供惯性进行减震(振)只能通过悬挂质量来实现的局面，使得结构惯性调整及调谐更为灵活；
惯容实现机理以及惯容元件对相连消能元件的变形放大作用，使得惯容减震(振)系统中消能元件的耗能效率得到有效提高，进而使其能适用于结构内部变形较小情形下的减震(振)控制；
惯容装置可以实现远大于其物理质量的惯容系数，因此其调整结构惯性特征时基本不会改变结构物理质量。在外部动力激励下，特别是在地震激励下，这一特点使其并不会增加结构体系所受的地震作用。
(2)惯容减震(振)结构体系的响应分析求解，可以根据条件和需要选用时域分析或频域分析方法，计算手段主要有编制计算程序和使用有限元软件。在使用有限元软件时，由于目前尚无现成惯容单元，故需进行合理的等效模拟或进行二次开发。
(3)所提出的针对惯容减震(振)结构体系的设计方法中，早期出现的以定点理论为基础的方法，普遍具有定点理论的局限性，如忽略主结构固有阻尼、未考虑结构性能等。对此，近年来学者提出了以性能需求为导向的惯容减震(振)结构体系实用设计方法。
4.2 展望
对于惯容以及惯容减震(振)结构体系，尚有以下问题有待进一步深入研究：
(1)根据惯容的基本力学原理，在现有装置的基础上进行改进或开发新的装置。目前的惯容装置大多集中于平动-转动转换的机械机制，可考虑基于其他物理现象和原理开发非转动类、非机械类惯容以更利于实际应用。
(2)研究惯容减震(振)系统与主体结构的连接构造，使该系统更加经济实用，能够更加广泛地应用于实际工程。
(3)目前对于惯容减震(振)系统优化设计方法的研究主要以经典单自由度、多自由度体系为载体，如今随着超高层、大跨及其他特殊结构的大量涌现，如何在这些复杂结构中应用惯容减震(振)系统需要进一步研究。
(4)目前已有惯容减震(振)系统相关的研究中，理论研究占比较高，而试验研究相对不足。因此尚需更多细致深入的试验研究来确保惯容减震(振)系统的可靠性。
附录：
安装不同惯容减震(振)系统的多自由度体系运动方程：
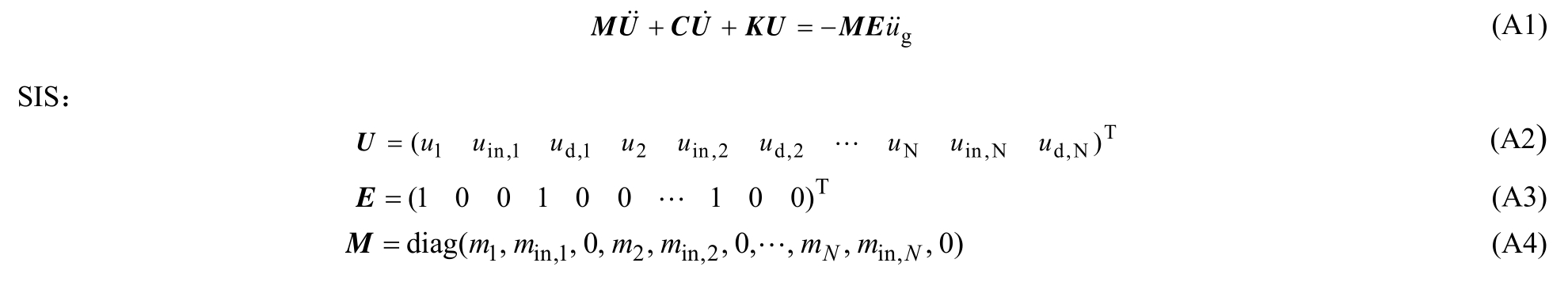
[1]Soong T T,Spencer B F.Supplemental energy dissipation: state-of-the-art and state-of-the practice [J].Engineering Structures,2002,24(3): 243―259.
[2]Hao L F,Zhang R F.Structural safety redundancy-based design method for structure with viscous dampers [J].Structural Engineering and Mechanics,2016,59(5):821―840.
[3]Zhang R F,Wang C,Pan C,et al.Simplified design of elastoplastic structures with metallic yielding dampers based on the concept of uniform damping ratio [J].Engineering Structures,2018,176: 734―745.
[4]Hao L F,Zhang R F,Jin K.Direct design method based on seismic capacity redundancy for structures with metal yielding dampers [J].Earthquake Engineering ＆ Structural Dynamics,2018,47(2): 515―534.
[5]Den Hartog J P.Mechanical vibrations [M].4th.New York: Dover,1956.
[6]Fujino Y,Sun L,Pacheco B M,et al.Tuned liquid damper (TLD)for suppressing horizontal motion of structures [J].Journal of Engineering Mechanics,1992,118(10): 2017―2030.
[7]滕军,刘季.高耸结构顺风向调谐质量阻尼振动控制系统优化设计[J].建筑结构,1995(7): 7―13.Teng Jun,Liu Ji.Optimal design of TMD system for along-wind dynamic response control of high-rise buildings [J].Building Structure,1995(7): 7―13.(in Chinese)
[8]刘季,李惠.底层柔性建筑和液压质量控制系统(Hms)的抗震优化设计方法[J].工程力学,1996,13(3):61―68.Liu Ji,Li Hui.Optimal design method for flexible first story building and hydraulic-mass control system [J].Engineering Mechanics,1996,13(3): 61―68.(in Chinese)
[9]Sadek F,Mohraz B,Taylor A W,et al.A method of estimating the parameters of tuned mass dampers for seismic applications [J].Earthquake Engineering ＆ Structural Dynamics,1997,26(6): 617―635.
[10]楼梦麟,韩博宇.高层建筑环境振动TLD控制研究[J].工程力学,2015,32(增刊1): 184―190.Lou Menglin,Han Boyu.Research on TLD control to environmental vibration of high-rise buildings [J].Engineering Mechanics,2015,32(Supll 1): 184―190.(in Chinese)
[11]Saito K,Toyota K,Nagae K,et al.Dynamic loading test and its application to a high-rise building of viscous damping devices with amplification system [C].Proceedings of the Third World Conference on Structural Control,Como,Italy,2002.
[12]斉藤賢二,井上範夫.慣性接続要素を利用した粘性ダンパーをもつ制振構造の最適応答制御に関するー考察: 最適設計システムにおける線形粘性要素の等価非線形粘性要素への置換法[J].日本建築学会技術報告集,2007,13(26): 457―462.Saito K,Inoue N.A study on optimum response control of passive control systems using viscous damper with inertial mass: substituting equivalent nonlinear viscous elements for linear viscous elements in optimum control systems [J].Journal of Architecture and Building Science,2007,13(26): 457―462.(in Japanese)
[13]斉藤賢二,栗田哲,井上範夫.慣性接続要素を利用した線形粘性ダンパーによる一質点構造の最適応答制御とKelvinモデル化手法に関する考察[J].構造工学論文集,2007,53B: 53―66.Saito K,Kurita S,Inoue N.Optimum response control of 1-DOF system using linear viscous damper with inertial mass and its Kelvin-type modeling [J].Journal of Structural Engineering,2007,53: 53―66.(in Japanese)
[14]Inoue N,Ikago K.Displacement control design of buildings: design method of long-period seismic isolation buildings against earthquake [M].Tokyo,Japan:Maruzen Publishing,2012.
[15]Ikago K,Sugimura Y,Saito K,et al.Simple design method for a tuned viscous mass damper seismic control system [C].Proceedings of the 15th World Conference on Earthquake Engineering,Lisbon,Portugal,2012.
[16]Smith M C.Synthesis of mechanical networks: the inerter [J].IEEE Transactions on Automatic Control,2002,47(10): 1648―1662.
[17]Firestone F A.A new analogy between mechanical and electrical systems [J].Journal of the Acoustical Society of America,1933,4(3): 249―267.
[18]Ikago K,Saito K,Inoue N.Seismic control of single-degree-of-freedom structure using tuned viscous mass damper [J].Earthquake Engineering ＆ Structural Dynamics,2012,41(3): 453―474.
[19]新垣忠志,黒田英二,有馬文昭,等.ボールネジを用いた制震装置の開発: その 1 制震チューブ·制震ディスクの性能試験[J].日本建築学会技術報告集,1999,5(8): 239―244.Arakaki T,Kuroda H,Arima F,et al.Development of seismic devices applied to ball screw : Part 1 Basic performance test of RD-series [J].Journal of Architecture and Building Science,1999,5(8): 239―244.(in Japanese)
[20]Kawamata S.Development of a vibration control system of structures by means of mass pumps [R].Tokyo,Japan:Institute of Industrial Science,University of Tokyo,1973.
[21]Severud L K,Summers G D.Design considerations for mechanical snubbers [R].Richland,WA (USA): Hanford Engineering Development Lab.,1980: 1―15.
[22]Kawaguchi O,Kanoh T,Akino K,et al.Research and development of seismic restraint snubbers(I)[J].Transactions of the Atomic Energy Society of Japan,1991,33(1): 76―89.
[23]Nims D K,Kelly J M.Experimental study of mechanical pipe snubber seismic behavior [J].Asme Trans Journal of Pressure Vessel Technology,1997,119(3): 384―388.
[24]新垣忠志,黒田英二,有馬文昭,等.ボールネジを用いた制震装置の開発: その 2制震チューブの減衰性能とその評価法[J].日本建築学会技術報告集,1999,5(9): 265―270.Arakaki T,Kuroda H,Arima F,et al.Development of seismic devices applied to ball screw: Part 2 Performance test and evaluation of RD-series [J].Journal of Architecture and Building Science,1999,5(9): 265―270.(in Japanese)
[25]Papageorgiou C,Smith M C.Laboratory experimental testing of inerters [C].Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference 2005,Seville,Spain,2005: 3351―3356.
[26]Makris N,Kampas G.Seismic protection of structures with supplemental rotational inertia [J].Journal of Engineering Mechanics,2016,142(11): 04016089-1―04016089-28.
[27]Kawamata S.Liquid type mass damper with elongated discharge tube [P].United States: 4,872,649,1989.
[28]Smith M C,Houghton N E,Long P J G,et al.Force-controlling hydraulic device [P].United States:8,881,876,2011.
[29]Wang F C,Hong M F,Lin T C.Designing and testing a hydraulic inerter [J].Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2011,225(1): 66―72.
[30]Swift S J,Smith M C,Glover A R,et al.Design and modelling of a fluid inerter [J].International Journal of Control,2013,86(11): 2035―2051.
[31]Gonzalez-Buelga A,Clare L R,Neild S A,et al.An electromagnetic vibration absorber with harvesting and tuning capabilities [J].Structural Control ＆ Health Monitoring,2015,22(11): 1359―1372.
[32]Gonzalez-Buelga A,Clare L R,Neild S A,et al.An electromagnetic inerter-based vibration suppression device [J].Smart Materials and Structures,2015,24(5):055015-1―055015-10.
[33]Høgsberg J,Brodersen M L,Krenk S.Resonant passive-active vibration absorber with integrated force feedback control [J].Smart Materials ＆ Structures,2016,25(4): 047001-1―047001-8.
[34]Høgsberg J,Krenk S.Calibration of piezoelectric RL shunts with explicit residual mode correction [J].Journal of Sound ＆ Vibration,2016,386: 65―81.
[35]Høgsberg J,Krenk S.Accurate calibration of RL shunts for piezoelectric vibration damping of flexible structures[C].Proceedings of the 27th International Conference on Adaptive Structures and Technologies,Lake George,New York,USA,2016: 1―11.
[36]Wang F C,Chen Y C,Lee C H.Design and optimization of inerter layouts for a multi-layers building model [C].Society of Instrument and Control Engineers of Japan(SICE),2016 55th Annual Conference of the.IEEE,2016: 1076―1081.
[37]聂佳梅,张孝良,江浩斌,等.惯容器模型结构探索[J].机械设计与研究,2012,28(1): 29―32.Nie Jiamei,Zhang Xiaoliang,Jiang Haobin,et al.Research on the inerter structure [J].Machine Design and Research,2012,28(1): 29―32.(in Chinese)
[38]Kida H,Ikago K,Inoue N.Applicability of force-restricted tuned viscous mass dampers to high-rise buildings subjected to long-period ground motions [C].Proceedings of the 15th World Conference on Earthquake Engineering,Lisbon,Portugal,2012.
[39]Nakamura Y,Hanzawa T,Isoda K.Performance-based placement design of tuned inertial mass dampers [C].Proceedings of 13th World Conference on Seismic Isolation,Energy Dissipation and Active Control of Structures,Sendai,Japan,2013:1―8.
[40]Ikago K,Sugimura Y,Saito K,et al.Modal response characteristics of seismic controlled MDOF shear building using tuned viscous mass dampers [J].Journal of Structural and Construction Engineering,2014,79(697): 367―374.(in Japanese)
[41]Hu Y L,Chen M Z Q,Shu Z,et al.Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution [J].Journal of Sound and Vibration,2015,346: 17―36.
[42]Krenk S,Høgsberg J.Tuned resonant mass or inerter-based absorbers: unified calibration with quasi-dynamic flexibility and inertia correction [J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,2016,472(2185): 20150718.
[43]Chen M Z Q,Papageorgiou C,Scheibe F,et al.The missing mechanical circuit element [J].IEEE Circuits and Systems Magazine,2009,9(1): 10―26.
[44]Smith M C,Wang F C.Performance benefits in passive vehicle suspensions employing inerters [J].Vehicle System Dynamics,2004,42(4): 235―257.
[45]Shen Y J,Chen L,Yang X F,et al.Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension [J].Journal of Sound and Vibration,2016,361: 148―158.
[46]Hu Y L,Chen M Z Q,Sun Y H.Comfort-oriented vehicle suspension design with skyhook inerter configuration [J].Journal of Sound and Vibration,2017,405: 34―47.
[47]Evangelou S,Limebeer D J N,Sharp R S,et al.Mechanical steering compensators for high-performance motorcycles [J].Journal of Applied Mechanics,Transactions ASME,2006,74(2): 332―346.
[48]Wang F C,Su W J.Inerter nonlinearities and the impact on suspension control [C].American Control Conference,Seattle,WA,USA,2008: 3245―3250.
[49]Wang F C,Liao M K,Liao B H,et al.The performance improvements of train suspension systems with mechanical networks employing inerters [J].Vehicle System Dynamics,2009,47(7): 805―830.
[50]Wang F C,Wu S Y.Vibration control of an optical table employing mechatronic inerter networks [J].Journal of Vibration and Control,2016,22(1): 224―234.
[51]陈龙,张孝良,聂佳梅,等.基于半车模型的两级串联型ISD悬架性能分析[J].机械工程学报,2012,48(6):102―108.Chen Long,Zhang Xiaoliang,Nie Jiamei,et al.Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model [J].Journal of Mechanical Engineering,2012,48(6): 102―108.(in Chinese)
[52]杨晓峰,沈钰杰,陈龙,等.基于动力吸振理论的车辆ISD悬架设计与性能分析[J].汽车工程,2014,36(10):1262―1266,1277.Yang Xiaofeng,Shen Yujie,Chen Long,et al.Design and performances analysis of vehicle ISD suspension based on dynamic vibration absorber theory [J].Automotive Engineering,2014,36(10): 1262―1266,1277.(in Chinese)
[53]Chen L,Liu C,Liu W,et al.Network synthesis and parameter optimization for vehicle suspension with inerter [J].Advances in Mechanical Engineering,2016,9(1): 1687814016684704-1―1687814016684704-7.
[54]Shen Y,Chen L,Liu Y,et al.Modeling and optimization of vehicle suspension employing a nonlinear fluid inerter[J].Shock and Vibration 2016: 2623017-1―2623017-9.
[55]Dong X,Liu Y,Chen M Z Q.Application of inerter to aircraft landing gear suspension [C].The 34th Chinese Control Conference,Hangzhou,China,2015: 2066―2071.
[56]Liu Y,Chen M Z Q,Tian Y.Nonlinearities in landing gear model incorporating inerter [C].International Conference on Information and Automation,Lijiang,China,2015: 696―701.
[57]Papageorgiou C,Houghton N E,Smith M C.Experimental testing and analysis of inerter devices [J].Journal of Dynamic Systems,Measurement,and Control,2008,131(1): 011001-1―011001-11.
[58]Chen M Z Q,Hu Y,Li C,et al.Semi-active suspension with semi-active inerter and semi-active damper [C].The 19th World Congress of the International Federation of Automatic Control,Cape Town,South Africa,2014:11225―11230.
[59]Chen M Z Q,Hu Y,Li C,et al.Application of semi-active inerter in semi-active suspensions via force tracking [J].Journal of Vibration and Acoustics,2016,138(4): 041014:1―11.
[60]Hu Y,Chen M Z Q,Xu S,et al.Semiactive inerter and its application in adaptive tuned vibration absorbers [J].IEEE Transactions on Control Systems Technology,2016,25(1): 294―300.
[61]Kuroda H,Arima F,Baba K,et al.Principles and characteristics of viscous damping devices(gyro-damper),the damping forces which are highly amplified by converting the axial movement to rotary one [C].The 12th world conference on earthquake engineering,Auckland,New Zealand,2000.
[62]Furuhashi T,Ishimaru S.Mode control seismic design with dynamic mass [C].The 14th World Conference on Earthquake Engineering,Beijing,China,2008.
[63]Saito K,Yogo K,Sugimura Y,et al.Application of rotary inertia to displacement reduction for vibration control system [C].The 13th World Conference on Earthquake Engineering,Vancouver,Canada,2004.
[64]Hessabi R M,Mercan O.Application of gyro-mass dampers to mitigate the seismic failure in soft first story buildings[C].Proceedings of Structures Congress 2015,Portland,Oregon,2015: 2032―2043.
[65]Hessabi R M,Mercan O.Investigations of the application of gyro-mass dampers with various types of supplemental dampers for vibration control of building structures [J].Engineering Structures,2016,126: 174―186.
[66]Wang F C,Hong M F,Chen C W.Building suspensions with inerters [J].Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science,2010,224(C8): 1605―1616.
[67]Saitoh M.On the performance of gyro-mass devices for displacement mitigation in base isolation systems [J].Structural Control ＆ Health Monitoring,2012,19(2):246―259.
[68]Takewaki I,Murakami S,Yoshitomi S,et al.Fundamental mechanism of earthquake response reduction in building structures with inertial dampers [J].Structural Control ＆ Health Monitoring,2012,19(6):590―608.
[69]Hwang J S,Kim J,Kim Y M.Rotational inertia dampers with toggle bracing for vibration control of a building structure [J].Engineering Structures,2007,29(6):1201―1208.
[70]斉藤賢二,杉村義文,井上範夫.慣性接続要素を利用した粘性ダンパーによる制振構造の応答制御に関する一考察[J].構造工学論文集,2008,54(B): 635―648.Saito K,Sugimura Y,Inoue N.A study on response control of a structure using viscous damper with inertial mass [J].Journal of structural engineering,2008,54(B):635―648.(in Japanese)
[71]Saito K,Sugimura Y,Nakaminami S,et al.Vibration tests of 1-story response control system using inertial mass and optimized softy spring and viscous element[C].The 14th World Conference on Earthquake Engineering,Beijing,China,2008.
[72]Arai T,Aburakawa T,Ikago K,et al.Verification on effectiveness of a tuned viscous mass damper and its applicability to non-linear structural systems [J].Journal of Structural ＆ Construction Engineering,2009,645(74):1993―2002.
[73]木田英範,中南滋樹,斉藤賢二,五十子幸樹,井上範夫.実大加振実験に基づく同調粘性マスダンパーの解析モデルに関する検証[J].構造工学論文集,2010,56B: 137―146.Kida H,Nakaminami S,Saito K,et al.Verification in analysis model of tuned viscous mass damper based on full-scale dynamic tests [J].Journal of Structural Engineering,2010,56B: 137―146.(in Japanese)
[74]木田英範,渡邉義仁,中南滋樹,田中久也,杉村義文,斉藤賢二,五十子幸樹,井上範夫.軸力制限機構付き同調粘性マスダンパーの実大加振実験とその解析的検証[J].日本建築学会構造系論文集,2011,76(665): 1271―1280.Kida H,Watanabe Y,Nakaminami S,et al.Full-scale dynamic tests of tuned viscous mass damper with force restriction mechanism and Its analytical verification [J].Journal of Structural and Construction Engineering,2011,76(665): 1271―1280.(in Japanese)
[75]Sugimura Y,Goto W,Tanizawa H,et al.Response control effect of steel building structure using tuned viscous mass damper [C].The 15th World Conference on Earthquake Engineering,Lisbon,Portugal,2012.
[76]Shinjo T,Ikenaga M,Ikago K,et al.Optimum response control of multi-degree-of-freedom seismic control system incorporated with concentratedly arranged tuned viscous mass dampers [J].Journal of Structural and Construction Engineering,2015,80(715): 1393―1402.
[77]Ikago K,Sugimura Y,Saito K,et al.Modal response characteristics of a multiple-degree-of-freedom structure incorporated with tuned viscous mass dampers [J].Journal of Asian Architecture ＆ Building Engineering,2012,11(2): 375―382.
[78]李超,张瑞甫,赵志鹏,等.调谐黏滞质量阻尼器基于遗传算法的参数优化研究[J].结构工程师,2016,32(4): 124―131.Li Chao,Zhang Ruifu,Zhao Zhipeng,et al.Optimum study of tuned viscous mass dampers based on genetic algorithm [J].Structural Engineers,2016,32(4): 124―131.(in Chinese)
[79]阎武通,韩冰,文永奎.新型调谐黏滞质量阻尼器对斜拉桥的减震控制分析[J].土木工程学报,2016(增刊1): 66―71.Yan Wutong,Han Bing,Wen Yongkui.Seismic control analysis of cable-stayed bridge based on tuned viscous mass damper [J].China Civil Engineering Journal,2016(Suppl 1): 66―71.(in Chinese)
[80]裴星洙,邱吉祥,伏恬甜.基于能量法的调谐黏性质量阻尼器地震响应预测式研究[J].振动与冲击,2017,36(19): 29―35.Pei Xingzhu,Qiu Jixiang,Fu Tiantian.Optimization design method for tuned viscous mass dampers based on the energy balance principle [J].Journal of Vibration and Shock,2017,36(19): 29―35.(in Chinese)
[81]Asai T,Ikago K,Araki Y.Outrigger tuned viscous mass damping system for high-rise buildings subject to earthquake loadings [C].6th International Conference on Advances in Experimental Structural Engineering,University of Illinois,Urbana-Champaign,United States,2015: 1―11.
[82]池永昌容,由川太一,長瀬拓也,等.軸力制限機構付き同調粘性マスダンパー制振システムの振動台実験[J].日本建築学会技術報告集,2012,18(39): 437―440.Ikenaga M,Yoshikawa T,Nagase T,et al.Shaking table test of seismic control system using force restricted tuned viscous mass damper [J].AIJ Journal of Technology and Design,2012,18(39): 437―440.(in Japanese)
[83]Nakaminami S,Ikago K,Inoue N,et al.Response characteristics of a base-isolated structure incorporated with a force-restricted viscous mass damper [C].The 15th World Conference on Earthquake Engineering,Lisbon,Portugal,2012.
[84]池永昌容,五十子幸樹,井上範夫.粘性要素を軸力制限機構に用いた粘性マスタンパーの免震構造物への適用性[J].日本建築学会構造系論文集,2015,80(714): 1251―1260.Ikenaga M,Ikago K,Inoue,N.Feasibility of viscous mass damper with bingham fluid origined force restriction mechanism for base-isolated structure [J].Journal of Structural ＆ Construction Engineering,2015,80(714): 1251―1260.(in Japanese)
[85]Lazar I F,Neild S A,Wagg D J.Using an inerter-based device for structural vibration suppression [J].Earthquake Engineering ＆ Structural Dynamics,2014,43(8): 1129―1147.
[86]Lazar I F,Neild S A,Wagg D J.Inerter-based vibration suppression systems for laterally and base-excited structures [C].Proceedings of EURODYN 2014-9th International Conference on Structural Dynamics,Porto,Portugal,2014: 1525―1530.
[87]Lazar I F,Neild S A,Wagg D J.Design and performance analysis of inerter-based vibration control systems [C].Dynamics of Civil Structures,Volume 4: Proceedings of the 32nd IMAC,2014: 493―500.
[88]Lazar I F,Neild S A,Wagg D J.Performance analysis of cables with attached tuned-inerter-dampers [C].Conference Proceedings of the Society for Experimental Mechanics Series,2015: 433―441.
[89]Lazar I F,Neild S A,Wagg D J.Vibration suppression of cables using tuned inerter dampers [J].Engineering Structures,2016,122: 62―71.
[90]Sun L M,Hong D X,Chen L.Cables interconnected with tuned inerter damper for vibration mitigation [J].Engineering Structures,2017,151: 57―67.
[91]Luo J,Jiang J Z,Macdonald J H G.Damping performance of taut cables with passive absorbers incorporating inerters [C].Journal of Physics:Conference Series 744,2016: 012046.
[92]Zhang S Y,Jiang J Z,Neild S.Passive vibration suppression using inerters for a multi-storey building structure [C].Journal of Physics: Conference Series 744,2016: 012044-1―012044-9.
[93]Zhang S Y,Jiang J Z,Neild S.Optimal configurations for a linear vibration suppression device in a multi-storey building [J].Structural Control ＆ Health Monitoring,2017,24(3): e1887-1―e1887-17.
[94]Gonzalez-Buelga A,Lazar I F,Jiang J Z,et al.Assessing the effect of nonlinearities on the performance of a tuned inerter damper [J].Structural Control ＆ Health Monitoring,2017,24(3): e1879.
[95]Domenico D D,Impollonia N,Ricciardi G.Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper [J].Soil Dynamics ＆ Earthquake Engineering,2018,105: 37―53.
[96]De Domenico D,Ricciardi G.Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study [J].Structural Control and Health Monitoring,2018,25(10):e2234.
[97]Wen Y,Chen Z,Hua X.Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures [J].Journal of Structural Engineering,2016,143(4): 04016207-1―04016207-11.
[98]Garrido H,Curadelli O,Ambrosini D.Improvement of tuned mass damper by using rotational inertia through tuned viscous mass damper [J].Engineering Structures,2013,56: 2149―2153.
[99]Marian L,Giaralis A.Optimal design of inverter devices combined with TMDs for vibration control of buildings exposed to sto- chastic seismic excitations [C].Safety,Reliability,Risk and Life-Cycle Performance of Structures and Infrastructures-Proceedings of the 11th International Conference on Structural Safety and Reliability,New York,USA,2013: 1025―1032.
[100]Marian L,Giaralis A.Optimal design of a novel tuned mass-damper–inerter (TMDI)passive vibration control configuration for stochastically support-excited structural systems [J].Probabilistic Engineering Mechanics,2014,38(SI): 156―164.
[101]Giaralis A,Marian L.Use of inerter devices for weight reduction of tuned mass-dampers for seismic protection of multi-story building: the Tuned Mass-Damper-Interter(TMDI)[C].Active and Passive Smart Structures and Integrated Systems,Las Vegas,Nevada,United States,2016: 97991G-1―97991G-10.
[102]Marian L,Giaralis A.The tuned mass-damper-inerter for harmonic vibrations suppression,attached mass reduction,and energy harvesting [J].Smart Structures and Systems,2017,19(6): 665―678.
[103]Pietrosanti D,De Angelis M,Basili M.Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI)[J].Earthquake Engineering ＆ Structural Dynamics,2017,46(8): 1367―1388.
[104]Giaralis A,Taflanidis A A.Optimal tuned mass-damperinerter (TMDI)design for seismically excited MDOF structures with model uncertainties based on reliability criteria [J].Structural Control ＆ Health Monitoring,2018,25(2): e2082.
[105]De Domenico D,Ricciardi G.An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI)[J].Earthquake Engineering ＆ Structural Dynamics,2018,47(5): 1169―1192.
[106]Jin X,Chen M Z Q,Huang Z.Minimization of the beam response using inerter-based passive vibration control configurations [J].International Journal of Mechanical Sciences,2016,119: 80―87.
[107]Ruiz R O,Giaralis A,Taflanidis A,et al.Risk-informed optimization of the tuned mass-damper-inerter (TMDI)for seismic protection of buildings in Chile [C].The 16th World Conference on Earthquake Engineering,Santiago,Chile,2017.
[108]张瑞甫.储液罐地震响应控制研究[R].上海: 同济大学,2014.Zhang Ruifu.Research on seismic response analysis of base-isolated vertical tank [R].Shanghai: Tongji University,2014.(in Chinese)
[109]罗浩,张瑞甫,翁大根,等.一种旋转黏滞质量阻尼器对结构响应的控制研究[J].防灾减灾工程学报,2016,36(2): 295―301,308.Luo Hao,Zhang Ruifu,Weng Dagen,et al.Study of a series viscous mass damper in the control of structural response [J].Journal of Disaster Prevention and Mitigation Engineering,2016,36(2): 295―301,308.(in Chinese)
[110]Ohtake T,Sunakoda K,Matsuoka T.Study on vibration control device using power generator [C].ASME PVP2006/ICPVT-11 Conference,Vancoucer,BC,Canada,2006,73: 185―189.
[111]Nakamura Y,Fukukita A,Tamura K,et al.Seismic response control using electromagnetic inertial mass dampers [J].Earthquake Engineering and Structural Dynamics,2014,43(4): 507―527.
[112]畑中友,船木尚己.慣性質量効果を有する液流ダンパーを用いた1層フレーム試験体の振動応答特性[J].構造工学論文集,2017,63B: 205―211.Hatanaka T,Funaki N.Experimental study on dynamic behavior of test frame passively controlled by liquid damper with inertia mass effect [J].Journal of Structural Engineering,2017,63B: 205―211.(in Japanese)
[113]畑中友,薛松濤,船木尚己.慣性質量効果を有する液流ダンパーを用いた 1層骨組の振動応答特性[C].第15回日本地震工学シンポジウム,仙台,2018.Hatanaka T,Xue S T,Funaki N.Dynamic behavior of single story frame passively controlled by liquid damper with inertia mass effect [C].The 15th Japan Earthquake Engineering Symposium,Sendai,Japan,2018.(in Japanese)
[114]Asai T,Araki Y,Ikago K.Energy harvesting potential of tuned inertial mass electromagnetic transducers [J].Mechanical Systems and Signal Processing,2017,84(Part A): 659―672.
[115]Faraj R,Holnickiszulc J,Knap L,et al.Adaptive inertial shock-absorber [J].Smart Materials ＆ Structures,2016,25(3): 035031.
[116]Brzeski P,Kapitaniak T,Perlikowski P.Novel type of tuned mass damper with inerter which enables changes of inertance [J].Journal of Sound ＆ Vibration,2015,349: 56―66.
[117]Brzeski P,Lazarek M,Perlikowski P.Experimental study of the novel tuned mass damper with inerter which enables changes of inertance [J].Journal of Sound and Vibration,2017,404: 47―57.
[118]Brzeski P,Perlikowski P.Effects of play and inerter nonlinearities on the performance of tuned mass damper[J].Nonlinear Dynamics,2017,88(2): 1―15.
[119]赵志鹏,张瑞甫,潘超.一种用于结构减震的金属屈服型惯容系统[C].第十届全国地震工程学术会议,上海,2018.Zhao Zhipeng,Zhang ruifu,Pan Chao.An inerter system with metallic yielding element for vibration mitigation[C].10th CNCEE,Shanghai,China,2018.(in Chinese)
[120]Zhang R F,Zhao Z P,Dai K S.Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system [J].Engineering Structures,2019,180：29―39.
[121]班鑫磊,谢丽宇,薛松涛,等.拉索式旋转电涡流阻尼器的理论模型及频域响应分析[J].地震工程学报,2018,40(5)：941―945.Ban Xinlei,Xie Liyu,Xue Songtao,et al.Theoretical model and analysis of the frequency response of a rotational eddy current damper with cable bracing [J].China Earthquake Engineering Journal,2018,40(5)：941―945.(in Chinese)
[122]Luo H,Chong C,Higano H,et al.Development of an inerter-spring-damper device for the protection of long-period structures subjected to extreme seismic events [C].Proceedings of the 16th International Symposium on New Technologies for Urban Safety of Mega Cities in Asia,Sendai,Japan,2017.
[123]Lu L,Duan Y F,Spencer B F,et al.Inertial mass damper for mitigating cable vibration [J].Structural Control ＆ Health Monitoring,2017,24(10)：e1986.
[124]Zhao Z P,Lu Z,Zhang R F.A particle inerter system for structural seismic response mitigation [J].Journal of the Franklin Institute,2019― doi：https：//doi.org/10.1016/j.jfranklin.2019.02.001.
[125]Luo H,Zhang R F,Weng D G.Mitigation of liquid sloshing in storage tanks by using a hybrid control method [J].Soil Dynamics and Earthquake Engineering,2016,90：183―195.
[126]Pan C,Zhang R F.Design of structure with inerter system based on stochastic response mitigation ratio [J].Structural Control and Health Monitoring,2018,25(6)：e2169.
[127]Pan C,Zhang R F,Luo H,et al.Demand-based optimal design of oscillator with parallel-layout viscous inerter damper [J].Structural Control ＆ Health Monitoring,2018,25(1)：e2051.
[128]Chen Q J,Zhao Z P,Zhang R F,et al.Impact of soilstructure interaction on structures with inerter system [J].Journal of Sound and Vibration,2018,433：1―15.
[129]Xia Y Y,Zhang R F,Friswell M I,et al.Suppression of the wind-induced vibration of high-rise buildings with inerter systems [C].International Conference on Noise and Vibration Engineering,Leuven,Belgium,2018：4223―4234.
[130]赵志鹏,潘超,郝霖霏,等.基于性能目标的储液罐安装惯容系统设计方法[C].第十届全国地震工程学术会议,上海,2018.Zhao Zhipeng,Pan Chao,Hao Linfei,et al.Performance-based optimum design of storage tank with inerter system [C].10th CNCEE,Shanghai,China,2018.(in Chinese)
[131]赵志鹏,潘超,吴敏君,等.基于性能需求的安装惯容系统隔震结构设计方法[C].第264场中国工程院科技论坛暨第十届全国防震减灾工程学术研讨会,成都,2018.Zhao Zhipeng,Pan Chao,Wu Minjun,et al.Performance-oriented optimal design of base-isolated structure with ineter system [C].264th China Engineering Science and Technology Forum and the 10th National Conference on Earthquake Disaster Prevention and Mitigation Engineering,Chengdu,China,2018.(in Chinese)
[132]张璐琦.惯容减震系统在抗震墙结构中的应用研究[D].上海：同济大学,2018.Zhang Luqi.Research on the application of shear wall structure with the inerter system [D].Shanghai：Tongji University,2018.(in Chinese)
[133]曹嫣如.具有惯容系统结构的风振控制研究[D].上海：同济大学,2018.Cao Yanru.Study on wind-induced vibration control of structures with inerter system [D].Shanghai：Tongji University,2018.(in Chinese)
[134]潘超,张瑞甫,王超,等.单自由度混联Ⅱ型惯容减震体系的随机地震响应与参数设计[J].工程力学,2019,36(1)：129―137,145.Pan Chao,Zhang Ruifu,Wang Chao,et al.Stochastic seismic response and design of structural system with series-parallel-II inerter system [J].Engineering Mechanics,2019,36(1)：129―137,145.(in Chinese)