飞行器在飞行过程中会产生多种类型的噪声，如发动机的工作噪声、附面层气流脉动压力引起的脉动噪声、进气道的吸气噪声等。高强度噪声激励将引起结构的剧烈声振响应，在薄弱部位引起疲劳破坏。根据有关设计标准，噪声声强大于130 dB时，就必须考虑结构的声疲劳问题[1]。
相比于一般飞行器，高速飞行器所受的噪声激励分布频带宽，局部声强大，如在进气道唇口及冲压发动机燃烧室等部位可达180 dB以上[2-3]，在结构强度设计时，必须考虑高频声振耦合激励所引起的结构疲劳。经典的结构疲劳寿命分析方法主要为时域法[4-5]、频域法[6-7]。其中时域法依靠准确的应力时域曲线以对应力幅值和均值进行循环计数，频域法则根据有限元分析或试验得到的应力功率谱曲线获得应力幅值概率密度函数。近年来，随着计算流体力学(CFD)的发展，已可以通过数值计算方法得到复杂外形结构的较为精确的高频脉动压力分布[8-9]，但是有限元、边界元等经典数值计算方法仍然难以据此准确给出高频随机激励下的结构响应；而高速飞行器工况复杂、环境严苛，目前也难以通过试验获取其真实的结构应力时、频域信息。由于无法提供足够精确的应力分布参数，传统的结构疲劳寿命分析方法在处理高速飞行器声振耦合所引起的结构疲劳问题时受到了极大地限制。
统计能量方法(SEA)基于功率流理论，将高频段划分为若干倍频程，通过建立在各倍频程内的子系统能量平衡关系对结构响应进行求解，克服了有限元、边界元等确定性数值算法处理高频问题时计算成本高、对结构细节过于敏感的缺陷，已经成为目前最主流的高频声振问题分析方法[10-12]。然而在采用统计能量分析给出倍频程内的均方速度或均方应力后，仍然不能获得结构危险点的应力功率谱，因此其计算结果难以直接应用于结构疲劳寿命分析中。
Wang等[12]的研究指出，当倍频程内应力均方值确定后，Park等[13]提出的五种基本形式的应力谱可以简化为平谱曲线，并据此构造出整个分析频带内的功率谱曲线，提出了一种基于统计能量分析的高频声振疲劳寿命计算方法，计算结果与试验吻合较好。
本文考虑到工程实践中真实复杂的应力谱分布特性，不再采用以上基于五种特定应力谱分布形式给出的等效平谱方法，而是引入模态间隔的Poisson和Rayleigh分布假设，生成符合真实结构模态分布特性的频域随机模态空间，给出了一种基于模态能量叠加的高频应力谱曲线构造方法，进一步采用Dirlik应力幅值概率模型进行大量Monte Carlo模拟试验，得到结构疲劳寿命。作为工程应用实例，对飞行器蒙皮壁板受到强噪声激励下的结构疲劳寿命进行了预测，并讨论了蒙皮厚度以及阻尼对疲劳寿命的影响。
1 基于应力谱的频域疲劳损伤计算方法
结构受到随机激励时，通常情况下难以采用时域方法直接预测疲劳寿命；而频域法采用应力谱的谱参数描述应力响应的幅值概率密度，可以估算出结构的疲劳寿命。
目前主要的幅值概率密度模型包括Rayleigh模型、Wirsching模型以及Dirlik模型等。大量的试验结果表明，相比于其它模型，Dirlik模型对于宽带分布的应力过程预测更为精确，已经成为目前工程应用中最主流的宽带应力过程疲劳损伤估算方法[12]。
对于已知单边应力谱为Gσ(f)的应力过程，Dirlik模型给出幅值为S的峰值出现的概率密度为：
式中：
对常见的合金材料，可认为其S-N曲线符合幂指数模型：
根据Miner线性累积损伤理论，循环应力连续变化的情况下结构的累积损伤度为：
E[D]Dir=1时，即可认为结构发生疲劳破坏，对应N即为结构的疲劳寿命。
2 基于统计能量分析的高频应力谱构造方法
虽然Dirlik模型可以给出较为精确的随机振动疲劳寿命，但对于受脉动激励的飞行器壁板结构，其应力功率谱Gσ(f)仍然难以直接得到，特别是本文关注的高频应力功率谱。因此，如何由统计能量分析得到的飞行器壁板结构应力均方响应，获得结构危险点的应力功率谱，是结构高频疲劳分析的关键。鉴于高频激励响应和结构固有特性的随机性，本文引入宽频模态间隔的Poisson和Rayleigh分布假设，生成符合模态分布特性的频域随机模态空间，并基于模态能量叠加方法构造结构危险点的应力谱曲线。
2.1 倍频程内的最大应力分布
受到高频脉动噪声激励的板壳结构，采用统计能量分析可以给出其在中心频率为fc、平均模态密度为n(fc)的分析频带(倍频程)内的均方位移响应＜u2＞x,t。结构在倍频程内最大位移响应的密集程度可以用统计响应集中因子Rs表征[10]：
式中：η为结构的内损耗因子；δf=1/n(fc)为平均模态频率间隔；Δf为倍频程带宽；φmax为通过模态质量正则化得到的振型幅值，对于二维板壳振型，φmax=2。
可以得到点x处的均方最大应变与均方最大应力为[10]：
式中：
为点x处的均方速度；
为材料的拉伸波速；E、ρ分别为结构的弹性模量和密度。联立式(5)和式(6)即可给出最大应力点在频带内的应力均方值。
2.2 倍频程内的模态分布
Lyon与DeJong[11]假设结构的高频模态在频域中随机分布，同时各模态之间相互独立，从而给出了倍频程内模态间隔的概率密度Poisson分布：
式中，δω为相邻两阶固有频率之间的间隔，
为平均模态圆频率间隔。
Stratonovich[14]引入随机矩阵理论的单阶高斯正交总体分布特性，认为模态频率间隔在频域内为Rayleigh分布，从而模态间隔的概率密度函数为：
2.3 基于模态能量叠加的应力谱构造方法
一般线性结构第i阶模态引起的响应速度功率谱分布如下[15]：
式中：ωi为第i阶模态的圆频率；
为第i阶模态响应功率谱的系数；
为第i阶模态的速度响应谱峰值。
在全频带内第i阶模态响应的能量密度为：
对于线性小阻尼结构，单阶模态响应的主要成分集中在模态频率附近，将式(10)代入式(11)可得：
可知最大应力点由第i阶模态响应引起的振动能量密度为：
式中：
为最大应力点处第i阶模态的速度响应的时间均方值；
为整个子系统对第i阶模态速度响应对时间和空间的均方根；
为子系统由第i阶模态响应引起的平均能量密度。
Lyon与DeJong[11]认为高频段倍频程内所有模态能量相等，因此第i阶模态的模态能量为：
式中：Etot=M＜v2＞x,t为子系统在倍频程内的总能量；M为子系统总质量；N=n(f )Δf为蒙皮壁板结构在倍频程内的模态数；S=M/(ρh)为均质等厚板壳结构的表面积，h为板厚。联立式(12)、式(13)和式(14)可以给出系数
由式(6)和式(15)即可给出危险点的单阶模态应力谱：
倍频程内共有N阶模态，故倍频程内的功率谱密度为：
在生成符合Poisson或Rayleigh分布的模态频率空间后，引入式(17)可构造出倍频程内的应力谱函数，采用Dirlik方法即可估算结构的疲劳寿命；由于生成的模态频率具有随机性，本文进行了多次Monte Carlo模拟试验以验证本方法的精度以及收敛性。采用本文方法计算结构高频声振疲劳寿命的流程如图1所示。
图1 高频声振疲劳寿命分析流程
Fig.1 Flow chart of fatigue life estimation for vehicle-plates excited by high frequency fluctuations
3 飞行器疲劳寿命计算
某高速飞行器在以高马赫数巡航时，飞行器上某壁板参数如表1所示[16]，其中，S为壁板面积，h为壁板厚度，ρ为材料密度，E为弹性模量，k、C分别为名义应力法中的疲劳强度指数、疲劳强度系数。采用CFD方法可以得到其高频脉动噪声的时域变化数据。图2为CFD得到的噪声声压在该壁板的分布，可见壁板结构所受到的局部声压超过180 dB，平均声压超过175 dB。表2给出了对时域声压数据处理后各倍频程内的声压均方根prms以及通过统计能量分析给出的在该噪声激励下的壁板响应数据。
图3给出了分别采用Poisson和Rayleigh模态空间分布单次模拟生成的应力谱Sσ，500次Monte Carlo试验完成后的平均应力谱Sσa，以及Wang等[12]采用的应力平谱Sσw。可见，采用本文方法模拟给出的单次应力谱曲线Sσ出现多个峰值，体现了模态间隔对于应力频域分布特性的影响；Sσ在倍频程交界处光滑连续；当相邻倍频程均方应力接近时，平均后的应力谱曲线Sσa较接近Sσw；而当相邻倍频程之间均方应力差距较大时，Sσa为平滑下降或上升的曲线，与出现阶跃突变的Sσw差异明显。考虑到工程实际中一般的应力谱曲线均为连续变化，因此本文方法构造的应力谱曲线具有更好体现真实应力频域分布特性的能力。
图4给出了分别采用Poisson和Rayleigh模态分布进行单次Monte Carlo模拟试验获得的疲劳寿命Ts、前N次Monte Carlo模拟试验结果的平均值TN，根据2000次试验给出的平均应力谱Sσa计算得到的疲劳寿命Tp和采用Wang等[12]文中方法给出的疲劳寿命Tw。
图2 分析壁板的声压级分布(dB 参考值：2×10-5 Pa)
Fig.2 SPL Distribution on the considered panel(dB Ref: 2×10-5 Pa)
表1 矩形薄板参数
Table 1 Parameters of the rectangular plate
S h/m 3/(kg/m)/m2ρ E/Pa v k C 0.55 0.003 2800 7.2×1010 0.3 1.865 1×109.98
表2 壁板的倍频程参数
Table 2 Octave parameters of the panel
fc/Hz prms/Pa3 rms/(10m/s)v× fc-模态N 1000 4678 573 14 1250 5030 481 18 1600 5704 439 23 2000 6054 387 29 2500 6541 364 36 3150 6649 375 45 4000 5961 617 57 5000 833.2 77.4 72 6300 471.7 25.3 91
由图3和图4可见，虽然采用不同的模态空间分布假设会导致Sσa分布出现差异，但是随着模拟次数的增加，两种模态空间假设给出的Tn均越来越逼近于Ta，表明本文提出的方法具有良好的计算稳定性，且两者给出的Ta非常接近，均略大于Wang等[12]文中方法给出的疲劳寿命Tw。
图3 应力谱分布
Fig.3 PSD of stress
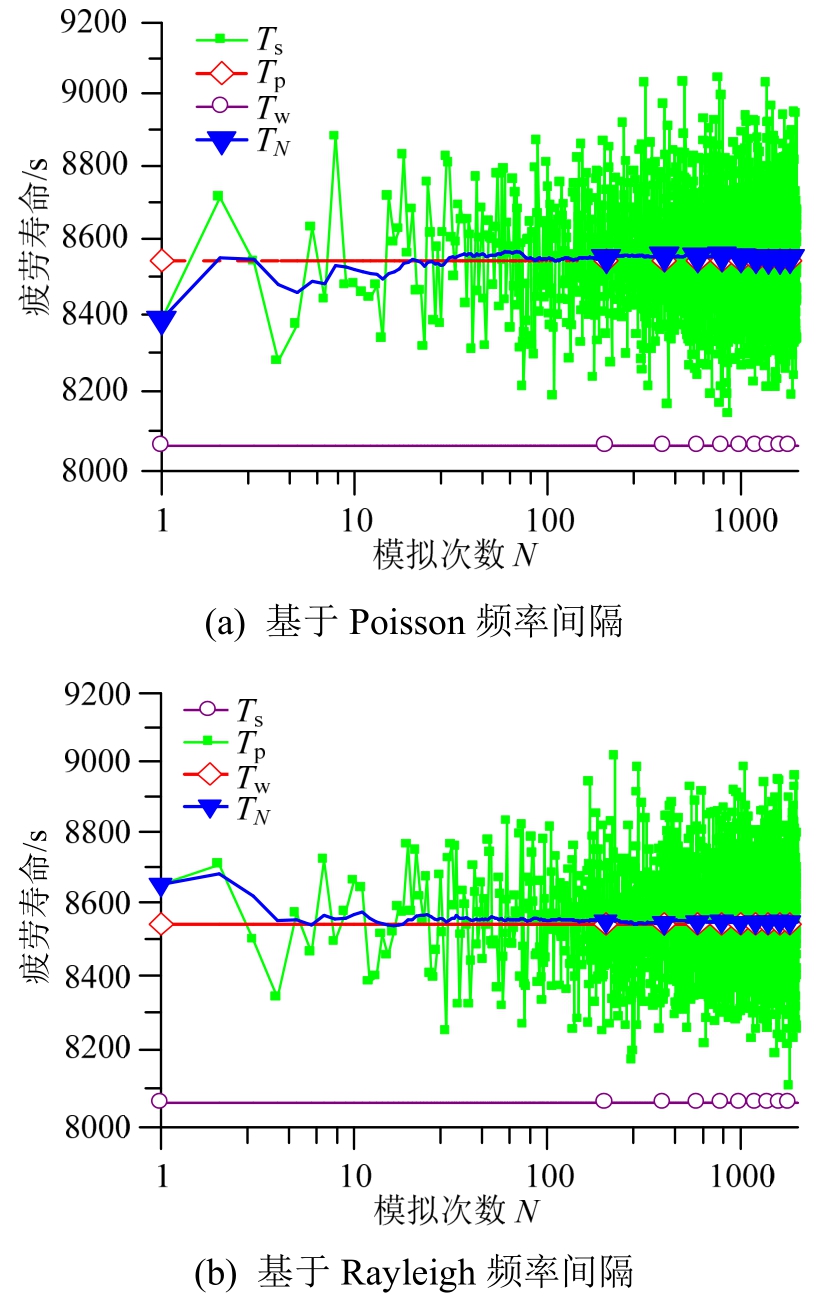
图4 壁板疲劳寿命
Fig.4 Fatigue life of the panel
为验证本文方法的收敛性，以不同的Monte Carlo模拟次数N进行了多次计算。图5以N为10000次时得到的疲劳寿命TNmax作为归一化参考，给出了归一化后的N从1增加至10000过程中计算结果TN/TNmax的变化曲线。
由图5可见，随着N增加，计算结果趋向于稳定，表明本方法具有良好的收敛性。若当N≥Ncov时，TN与Tp的相对误差
恒成立，即可认为模拟次数达到Ncov时计算结果达到收敛。采用两种模态空间分布假设计算所需的收敛次数Ncov以及其他相关的计算结果见表3。
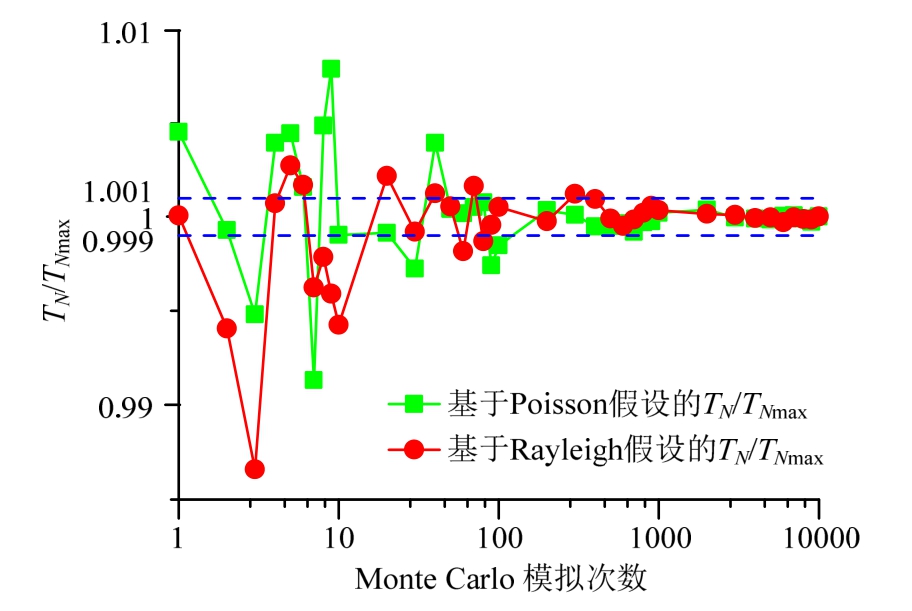
图5 归一化疲劳寿命与Monte Carlo试验次数N的关系
Fig.5 Normalized fatigue life with different number of Monte Carlo tests
表3 疲劳寿命计算结果
Table 3 Results of the fatigue life calculation
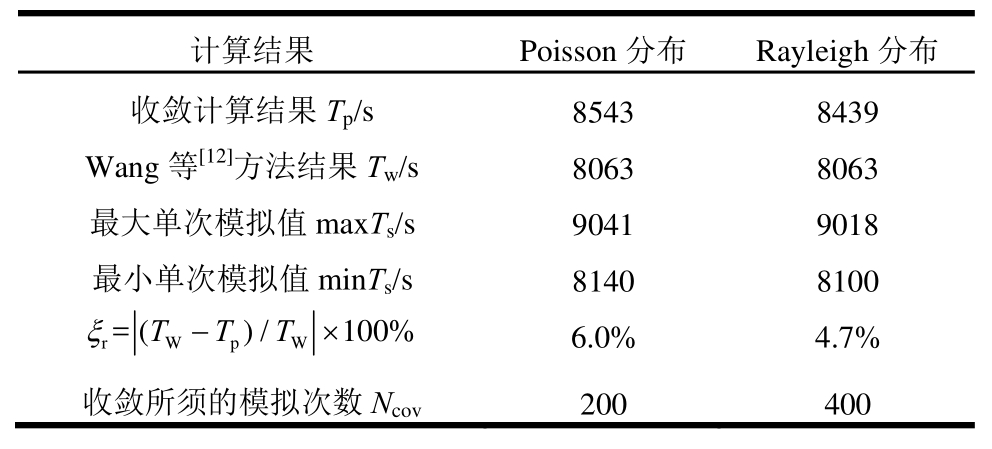
计算结果 Poisson分布 Rayleigh分布收敛计算结果Tp/s 8543 8439 Wang等[12]方法结果Tw/s 8063 8063最大单次模拟值maxTs/s 9041 9018最小单次模拟值minTs/s 8140 8100 ξ-× 6.0% 4.7%收敛所须的模拟次数Ncov 200 400 rWpW=()/100%TTT
通过以上数值计算可以得到以下结论：
1)本文方法与采用Wang[12]等方法的计算结果相对偏差不超过6%，对于疲劳寿命预报而言，可以认为两种算法给出的结果已经相当接近，证明本文方法精确有效；
2)采用Poisson或Rayleigh模态分布假设计算得到的疲劳寿命基本相同，但前者的收敛速度更快，因此在后续研究中，将基于Poisson假设给出频率空间分布，以基于200次Monte Carlo试验给出的应力谱均值的计算结果作为疲劳寿命的预报结果。
4 飞行器壁板参数设计对结构疲劳寿命的影响
几何、材料参数如表1所示的飞行器壁板结构在巡航状态下受到脉动噪声激励如表4所示，通过附加阻尼材料可使蒙皮内损耗因子η在2×10-3至2×10-1之间调整。设计中要求在严格控制壁板重量的前提下，合理调整附加阻尼使该壁板至少工作2×105 s而不发生疲劳破坏。
表4 脉动噪声声压谱
Table 4 Fluctuation sound pressure spectrum
fc/Hz 100012501600 2000 2500 31504000 p 468 503 570 605 654 664 596 rms/Pa
图6为计算给出的疲劳寿命T随不同板厚h以及内损耗因子η的变化关系，可以得到以下结论：
1)内损耗因子相同时，总体上疲劳寿命随着板厚的增加而增加；但是当激励声压谱一定时，板厚增加将使平板的临界频率靠近激励频段，使声场对平板的输入功率明显增大，因此会出现疲劳寿命极值。
2)板厚相同时，疲劳寿命随着内损耗因子的增加先升高，此后到达极值并开始下降。出现这种状况的主要原因在于，初期阻尼增大使应力均方值
减小，从而降低了危险点的应力水平，提高了疲劳寿命；此后η继续增大，由式(5)和式(15)可看出统计响应集中因子Rs和危险点的单阶模态振幅
也会提高，此时虽然子系统的均方响应下降，但是由于应力集中，危险点的应力水平仍然在升高，导致结构疲劳寿命下降。
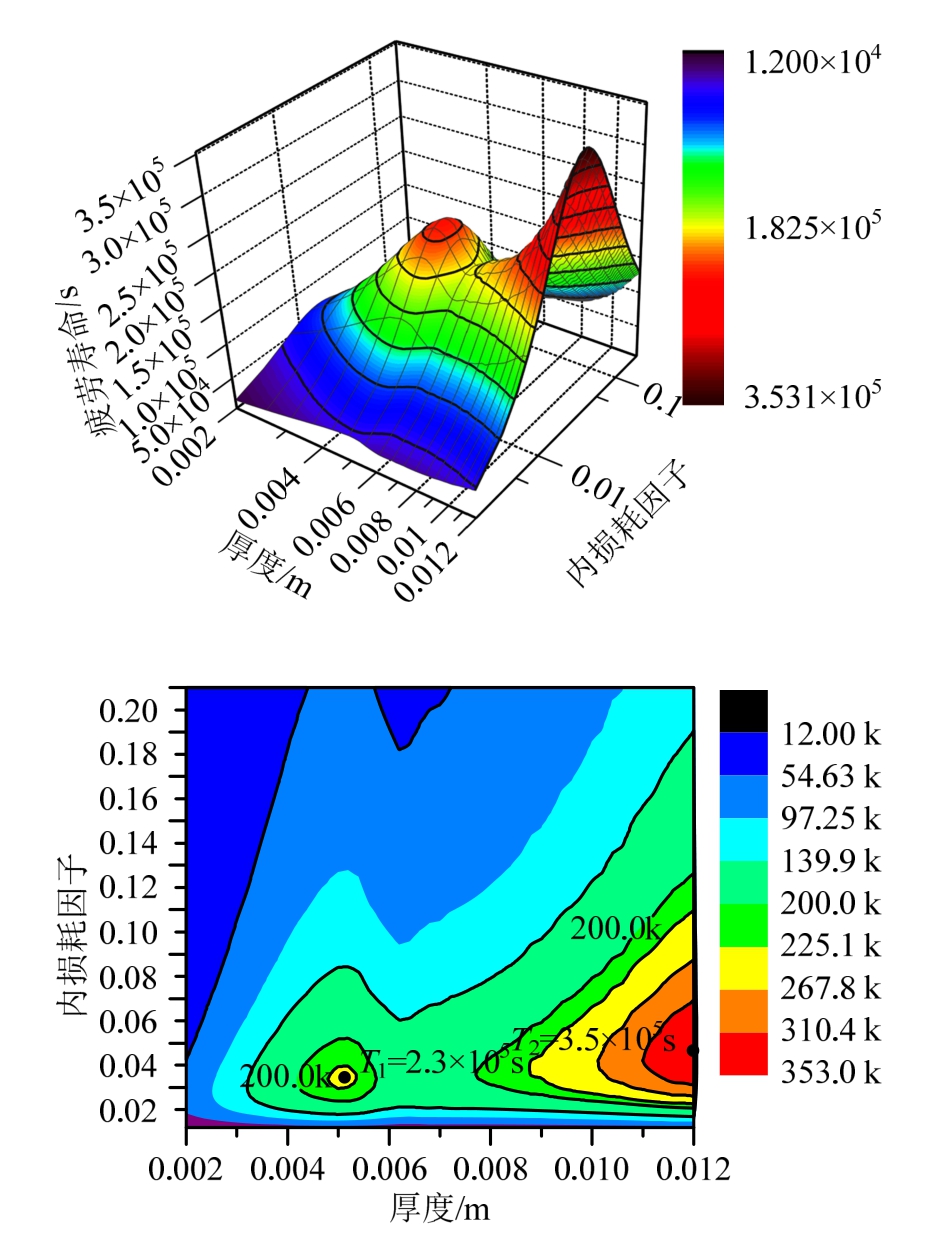
图6 不同厚度与内损耗因子的壁板疲劳寿命
Fig.6 Fatigue life of the panel with different h and η
3)由图5(b)可知，在整个设计平面2×105 s包线范围内的设计参数均满足要求。但显然h=0.005 m，η=0.024时出现的极值点T1是满足设计要求的局部最优解，相比于非极值区域2.25×105 s包线以上的解，极值点T1可节约质量(厚度)40%以上。
由计算结果可知，在高速飞行器的设计阶段，应当针对高频脉动噪声场的频谱特性合理选择蒙皮厚度及阻尼参数。过大的阻尼可能会引起统计响应集中因子增大从而降低疲劳寿命，而适当的厚度可以在脉动噪声较强的频带降低结构与声场的耦合性能，更可以节省宝贵的载荷质量。
5 结论
本文结合高速飞行器强度设计中的实际问题，引入统计能量方法以及Rayleigh、Poisson模态空间分布假设，并与已有方法解对比验证了其正确性。论文提出基于模态能量叠加的高频应力谱构造方法，并进一步给出了采用Dirlik应力幅值概率模型的结构疲劳寿命Monte Carlo模拟方法。
本文根据统计能量给出的结构响应预测疲劳寿命，考虑到了倍频程内模态分布特性对于应力谱的影响，生成的应力谱曲线物理含义明确，计算收敛速度快，稳定性良好；由算例仿真可以看出，计算结果精确可靠。在此基础上，研究了激励声压谱一定的情况下结构阻尼及厚度对飞行器板壳结构疲劳寿命的影响，计算结果表明，在设计域内可能存在使疲劳寿命达到极大值的局部最优解。
由于需要进行多次Monte Carlo模拟，本方法的计算时间较长，在以后的研究中，仍须通过引入收敛速度更快、更精确的模态空间分布假设，对算法进行更深入的研究与验证。
[1]张正平, 任方, 冯秉初.飞机噪声技术研究-工程解决方法[J].航空学报, 2008, 29(5):1207―1212.Zhang Zhengping, Ren Fang, Feng Binchu.Noise task of aircraft-resolve in engineering [J].Acta Aeronautica et Astronautica Sinica, 2008, 29(5):1207―1212.(in Chinese)
[2]Paul L M, Vincent L R, Laut T N.NASA hypersonic flight demonstrators: overview status and future plans[R].Acta Astronautica, 2004, 55(3): 619―630.
[3]郭静, 吴振强, 方伟, 等.热噪声复合环境下飞行器结构动响应预示技术研究进展[J].强度与环境, 2014,41(6): 1―10.Guo Jing, Wu Zhenqiang, Fang Wei, et al.Review of study on prediction of dynamic response for aerocraft structure under a combination of thermal and acoustic environments [J].Structure and Environmental Engineering, 2014, 41(6): 1―10.(in Chinese)
[4]Marsh Gabriel, Wignall Colin, Thies Philipp, et al.Review and application of rainflow residue processing techniques for accurate fatigue damage estimation [J].Internation Journal of Fatigue, 2016, 82(3): 757―765.
[5]方吉, 李季涛, 王悦东, 等.基于随机振动理论的焊接结构疲劳寿命概率预测方法研究[J].工程力学, 2016,33(3): 24―30.Fang Ji, Li Jitao, Wang Yuedong, et al.Research on fatigue life probability prediction method of welded sturcture based on random vibration theory [J].Engineering Mechanics, 2016, 33(3): 24―30.(in Chinese)
[6]周亚东, 吴邵庆, 李彦斌, 等.变温条件下热结构的声疲劳寿命评估[J].工程力学, 2015, 32(10): 220―225.Zhou Yadong, Wu Shaoqing, Li Yanbin, et al.Acoustic fatigue life assesement of hot structures under viriable temperature conditions [J].Engineering Mechanics,2015, 32(10): 220―225.(in Chinese)
[7]Schütz W.Fatigue life prediction of aircraft structures-past, present and future [J].Engineering Fracture Mechanics, 1974, 6(4): 745―762.
[8]Sun Y, Fattah R, Zhong S, et al.Stable time-domain CAA simulations with linearised governing equations [J].Computers & Fluids, 2018, 167(1): 187―195.
[9]Titchener N，Babinsky H.Shock wave/boundary-layer interaction control using a combination of vortex generators and bleed [J].AIAA Journal, 2013, 51(5):1221―1233.
[10]姚德源, 王其政.统计能量分析原理及其应用[M].北京: 北京理工大学出版社, 1995.Yao Deyuan, Wang Qizheng.Theory and application of statistical energy analysis [M].Beijing: Beijing Institue of Technology Press, 1995.(in Chinese)
[11]Lyon R H, DeJong R G.Theory and application of statistical energy analysis [M].2nd ed.Cambridge, MA:MIT Press, 1998.
[12]Wang Y Y, Chen H B, Zhou H W.A fatigue life estimation algorithm based on statistical energy analysis in high-frequency random processes [J].International Journal of Fatigue, 2016, 83(2): 221―229.
[13]Park J B, Choung J, Kim K S.A new fatigue prediction model for marine structures subject to wide band stress process [J].Ocean Engineering, 2014, 76(15): 144―151.
[14]Stratonovich R L.Topics in the theory of random noise[M].New York: Gordon and Breach, 1963.
[15]Davy J L.The relative variance of the transmission function of a reverberation room [J].Journal of Sound and Vibration, 1981, 77(4): 455―479.
[16]Yahr G T.Fatigue design curves for 6061―T6 aluminum [J].Journal of Pressure Vessel Technology,1993, 119(2): 211―215.