工程结构在地震、强风等强动力荷载作用下往往会在不同的时刻和不同的部位出现不同程度的损伤，基于结构的外激励和动力响应信息对结构损伤的发生发展过程进行识别，进而对其性能，特别是剩余承载力和剩余寿命进行预测具有重要意义。目前基于结构模态和频率的结构损伤识别方法严格来讲适用于线性系统，而且通常通过结构刚度的变化描述损伤。土木工程结构一般具有体量大且建筑材料多样和结构形式复杂的特点，在地震等动力荷载作用下的完整的动力响应测量难以实现，且动力响应测量难免受到测量噪声的影响。此外，土木工程材料和结构形式的多样性和复杂性使得实际工程结构的恢复力模型的参数化形式的事先获得也存在较大困难。而且，结构活荷载的存在使得结构质量的识别成为必要，因为结构质量直接影响结构刚度或者恢复力的识别结果。因此，研究结构动力响应测量不完备条件下，不依赖于结构非线性行为的参数化模型的恢复力以及质量识别方法具有重要意义。
近年来，国内外学者借助卡尔曼滤波类算法实现了动力响应不完备情况下动力系统的识别。Hoshiya和Saito[1]提出全局迭代的扩展卡尔曼滤波(Extended Kalman filter with weighted global iteration, EKF-WGI)。在此基础上，王祥建[2]结合记忆衰退技术提出记忆衰退全局迭代扩展卡尔曼滤波(Extended Kalman filter with memory fading technique and weighted global iteration method,EKF-MF-WGI)，提高识别精度和收敛速度。
针对输入未知或部分未知的情况，Xu和He等[3-4]在开展基于最小二乘的加权自适应迭代算法识别线性系统结构参数和未知部分激励的基础上，将其扩展到非线性结构中。Yang等[5]结合自适应技术发展了递进最小二乘法，识别了未知激励和时变参数。为了进一步减少算法对系统响应信息的依赖性，Xu等[6]将自适应加权迭代的子结构技术和加权全局迭代的扩展卡尔曼滤波算法(Extended Kalman filter，EKF)相结合，实现线性参数识别和未知激励识别。Lei等[7-8]在EKF算法中利用递进最小二乘法实现部分响应下的结构参数和未知激励的识别。
地震动识别是地震工程十分重要的课题，李杰等[9-10]基于结构动力响应，利用统计平均法迭代识别了结构物理参数，进而得到地震动输入。冯新等[11]提出一种仅利用结构顶端三个自由度响应识别地震激励和结构参数的两阶段方法。王晓燕等[12]利用统计平均算法和EKF实现了地震动反演，算法具有较好的抗噪性。Das等[13]首先利用子结构内部的已知响应识别未知地震力，随后通过广义迭代最小二乘卡尔曼滤波方法识别结构刚度损伤。谢献忠等[14]将一种分解反演算法或统计平均算法与子结构技术结合，识别了剪切结构和桁架结构的物理参数，并同时反演了地震荷载。王祥建等[15]将记忆衰退扩展卡尔曼滤波和统计平均法结合，识别了地震激励及结构参数，随后根据单元变化率判断损伤位置和损伤程度。以上地震动反演问题的研究大多局限于线性系统，目前国内外都很少涉及到地震作用下非线性系统的识别问题。然而，工程结构在地震等强荷载作用下的损伤发生发展往往会呈现典型的非线性特征，而且其非线性行为的参数化模型很难准确实现已知。研究地震动作用下结构恢复力的非参数化模型的一般化识别方法具有重要意义。
对非线性动力系统的非参数化识别研究方面，Masri和Caughey[16]提出恢复力曲面法，将系统恢复力利用切比雪夫正交多项式表征，实现恢复力的非参数化识别。许斌等[17]基于实测动力响应，通过等效线性理论实现了结构非线性恢复力免模型识别。Xu等[18-20]提出了利用幂级数多项式和切比雪夫多项式识别不同非线性模型的非线性恢复力，并通过带有不同非线性构件的剪切框架结构的试验以及数值模拟验证了该算法的有效性。何明煜[21]将等效线性理论、幂级数多项式分别与EFK和无迹卡尔曼滤波(Unscented Kalman filter，UKF)相结合，提出了部分输出未知下非线性恢复力的两阶段非参数化识别方法。但是，目前的大多数系统识别方法均假设质量已知。而结构质量的误差将引起结构刚度等物理参数以及恢复力识别误差。许斌等[22]提出了利用切比雪夫多项式和UKF识别结构质量和滞回特性的方法，但仍需要已知激励信息。对地震激励未知情况下的非线性行为以及质量识别有待进一步研究。
针对以上结构行为的非线性、激励与部分质量以及部分动力响应未知的问题，本文提出一种地震激励下非线性系统恢复力及质量的非参数化识别方法。该方法仅需要已知部分自由度的响应和质量信息，识别出结构恢复力、质量以及未知地震加速度信息。首先，根据部分已知结构响应和质量，结合用于表征非线性恢复力的幂级数多项式，实现非线性系统的地震加速度识别。其次，结合等效线性化方法与EKF-MF-WGI方法识别结构未知质量及响应。基于完整的输入输出信息，通过幂级数多项式识别系统的层间恢复力。通过在一个多层剪切结构的模型中引入磁流变阻尼器(Magnetoreheological, MR)模拟非线性行为，对比无噪声和4%噪声下的识别结果，验证了所提出方法的有效性和抗噪性。
1 非线性结构地震加速度、恢复力与质量识别方法
1.1 非线性恢复力的幂级数多项式表述
在地震作用下一个n自由度非线性动力系统的运动平衡方程可表达为：
式中：M为质量矩阵；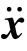
(t)为加速度响应；Rnon(t)为体系非线性恢复力；
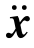g(t)为地面加速度。
在本文中，利用幂级数多项式表述结构非线性恢复力，将体系的非线性恢复力仅用层间相对速度和相对位移以及幂级数多项式系数形式表示，避免使用任何参数化的非线性恢复力模型。非线性恢复力通过幂级数多项式表述如下：
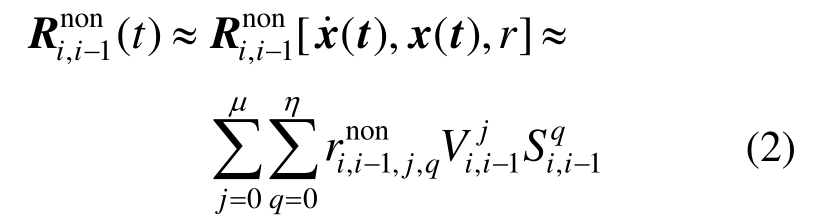
式中：
分别表示结构速度位移响应。
表示第i和第i-1个自由度的层间恢复力；
为幂级数多项式系数；μ和η为整数，本文取μ+η=3(μ+η≠0)，Vi,i-1和Si,i-1为自由度i与i-1间的相对速度和相对位移。
根据式(1)和式(2)，对应第i个自由度的平衡方程可表示为：
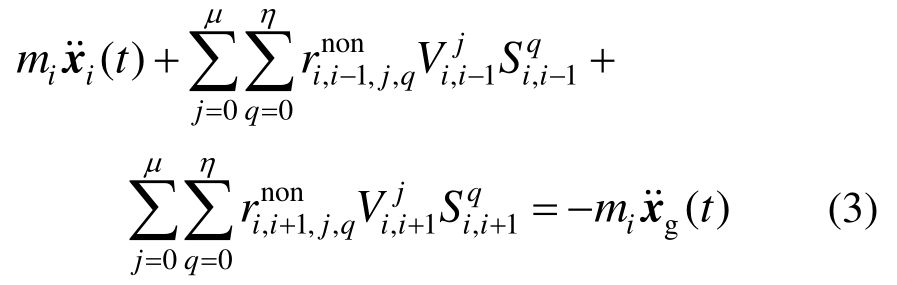
在地震加速度、结构响应及质量完全已知的前提下，利用最小二乘法可识别幂级数多项式系数，从而得到非线性系统各个自由度之间的层间恢复力。
1.2 非线性系统的地震加速度识别
实际工程中往往难以获得所有自由度的质量及响应信息，但是可以根据需要获得部分自由度的信息。借鉴文献[11]所提出的地震动反演算法，对于一个n自由度非线性系统，假设结构第n、第n-1和第n-2个自由度的响应和第n、第n-1个自由度的质量已知，根据式(1)与式(2)可得：
由牛顿第三定律可得：
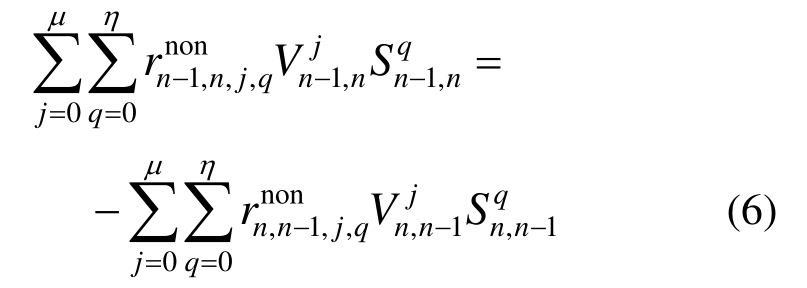
因此，联立式(4)～式(6)可得：
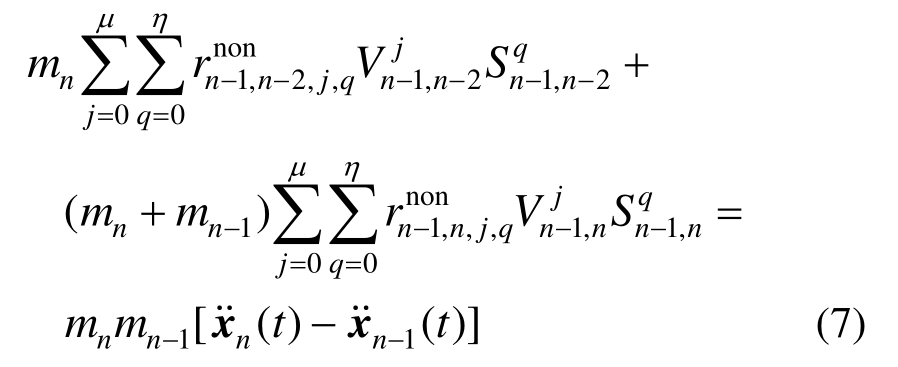
利用最小二乘算法可识别出上式幂级数多式项系数，进而根据式(5)求得未知地面加速度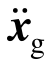
。
1.3 基于等效线性化的EKF-MF-WGI
通常情况下，结构发生损伤或非线性行为的位置是未知的，本文将等效线性理论和质量参数引入EKF状态向量中，实现在结构损伤位置未知情况下的非线性行为的定位和识别以及质量识别。同时利用EKF-MF-WGI提高识别精度和收敛速度。
根据等效线性理论，式(1)可以表示为：
式中：ME、CE、KE分别为结构等效质量矩阵、刚度矩阵和阻尼矩阵。一般认为，在损伤的发生发展过程中结构质量未发生明显变化，因此，结构质量矩阵M可取式(3)中的识别值ME。
将引入等效线性系统质量、刚度和阻尼矩阵引入EFK的状态向量中，如下式所示：
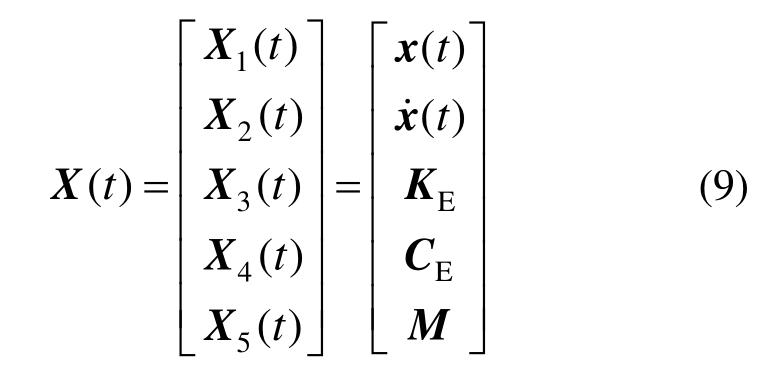
不考虑参数时变，可得：
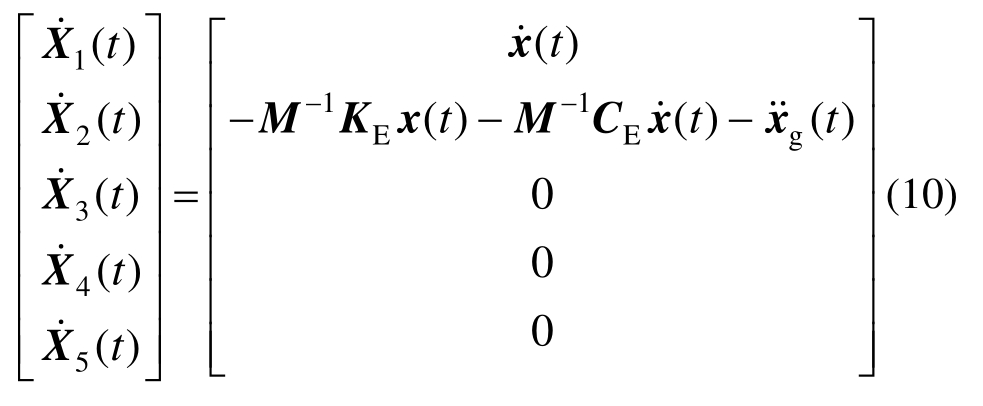
式(10)可以改写为：
以已知加速度信息为观测向量，则观测方程可表示为：
式中：y(k)为t=Δt×k时刻的观测向量(Δt为采样时间步长)；v(k)为均值为零、协方差为R的噪声向量。
根据状态向量和观测方程，EKF识别过程如下：
1)状态预测
2)误差协方差方程
式中：
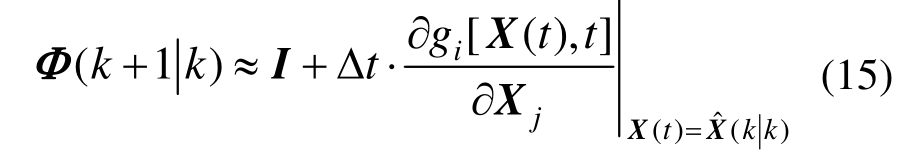
3)增益矩阵
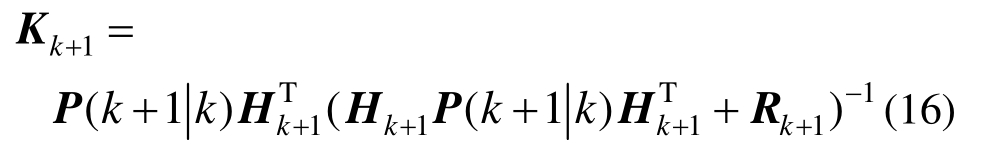
式中：
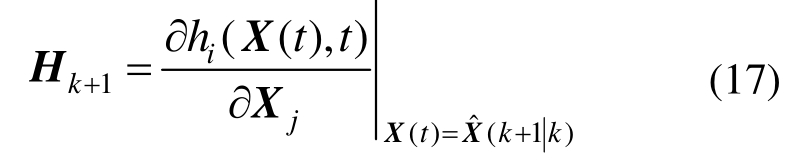
4)状态滤波方程
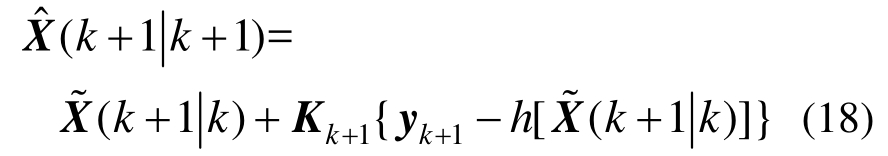
5)误差协方差方程：
6)令k=k+1，迭代循环直至k=l(l表示采样时间tl的最终时刻)。至此，一次EKF迭代过程完成。
为了得到更为准确的识别结果，根据EKF-WGI方法[1]，将识别的状态向量和误差协方差加权后作为初始值继续迭代。在第二次全局迭代中，状态向量和误差协方差可以设定为：
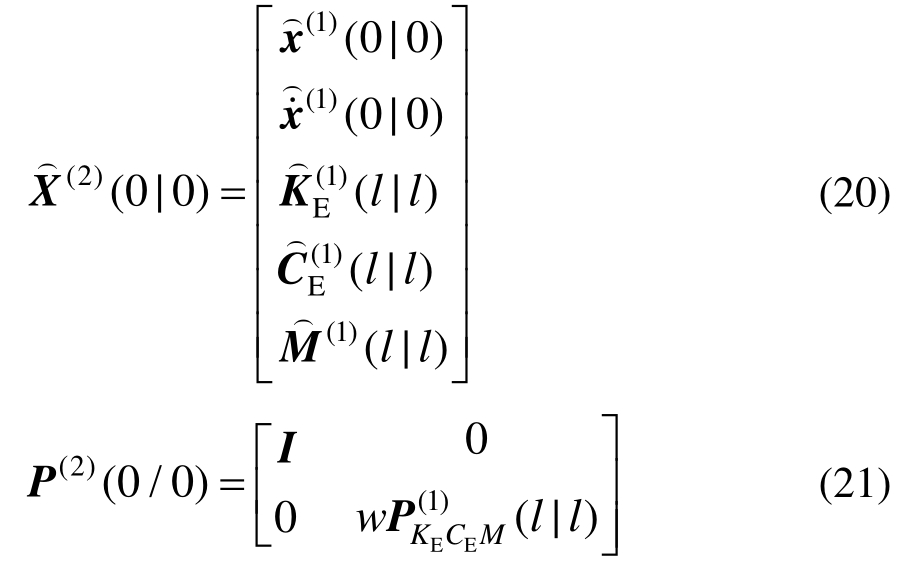
上标(2)代表第二次全局迭代，w为权重系数。
分别代表第一次迭代的等效刚度、阻尼、质量和误差协方差矩阵参数部分最终时刻的识别值。I为单位矩阵。重复全局迭代过程直到满足收敛条件。
EKF在计算模型不精确和噪声干扰等情况下容易出现滤波发散，利用记忆衰退滤波技术[2]可加大新数据对滤波的影响权重，减少旧数据对识别结果的不良影响。通过将式(14)做如下处理得以实现：
式中，G为记忆衰退权重系数，文献[2]提出的取值范围为
基于预估的未知质量、部分已知响应信息和识别的地面加速度，通过EKF-MF-WGI方法可识别结构质量和完整的速度位移响应。未知加速度可由相应的速度响应对时间求导得到。在本文中，设定前后两次识别的质量识别误差不超过1 kg为收敛标准，若满足误差要求，则终止循环，否则将质量识别值作为初始值继续循环。
1.4 识别算法步骤
所提出识别方法的步骤如下：
1)根据部分已知输出和质量信息识别地震动激励；
2)预估未知质量，设定权重系数w、G；
3)利用EKF-MF-WGI方法识别结构未知质量和输出信息；
4)根据完整输出信息，利用幂级数多项式识别系统非线性恢复力。
2 数值算例
2.1 计算模型
为了研究算法有效性，考虑一个7层集中质量剪切结构，在第4层引入一个磁流变阻尼器MR模拟结构非线性行为，如图1所示。结构各层质量为200 kg，线性刚度为
阻尼为150 N·s/m。
假设结构第5层、6层、7层的响应和第1层、3层的加速度已知，第6层、7层质量已知，其余层的质量和响应未知。基底地震作用输入采用Friuli地震波，时长为20 s，采样时间间隔为0.01 s，如图2所示。基底地震作用下非线性结构的动力响应采用Newmark-β计算。MR阻尼器恢复力采用Dahl模型[23]，其表达式为：
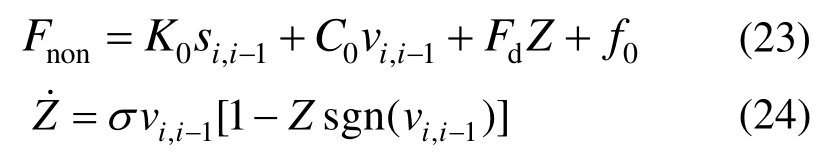
式中：Fnon为MR阻尼器的恢复力；K0、C0、Fd、f0、σ为模型参数；Z为无量纲滞回量。各参数取值为：K0=30 N/m,C0=600 N·s/m,Fd=50 N，σ=500 s/m，f0=0。
在本文中，假设预估的未知质量为真实值的70%，权重系数w=100，G=1.005。表征层间非线性恢复力的幂级数多项式的基函数为：
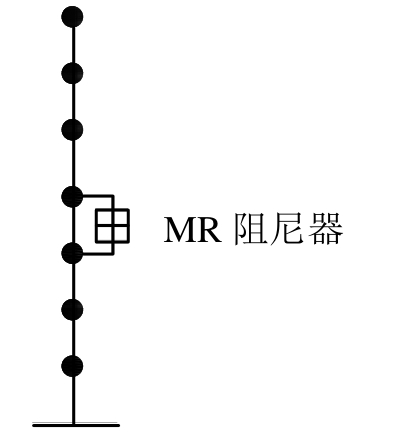
图1 计算模型
Fig.1 Numerical model
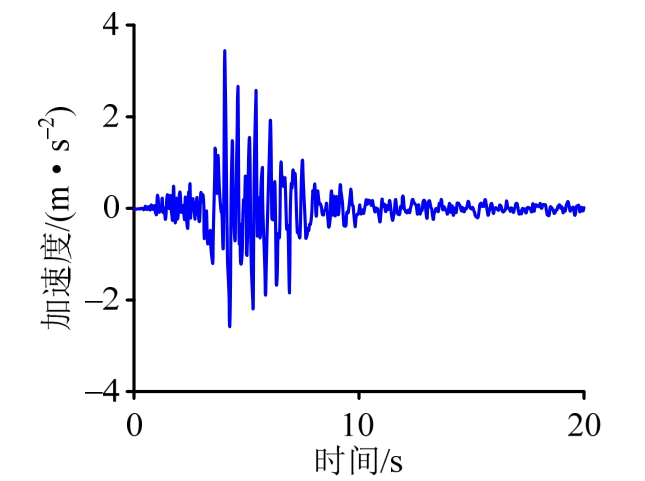
图2 Friuli 地震波
Fig.2 Friuli earthquake wave
2.2 工况1：无测量噪声
假设已知动力响应未受噪声影响，利用5层、6层、7层的输出信息和6层、7层的质量，通过式(7)和式(5)识别未知地震加速度。识别的地面加速度时程和真实值对比如图3所示，二者几乎重合，说明本文所提出的非线性系统地震动输入识别方法在无噪声测量噪声影响时识别效果可靠。
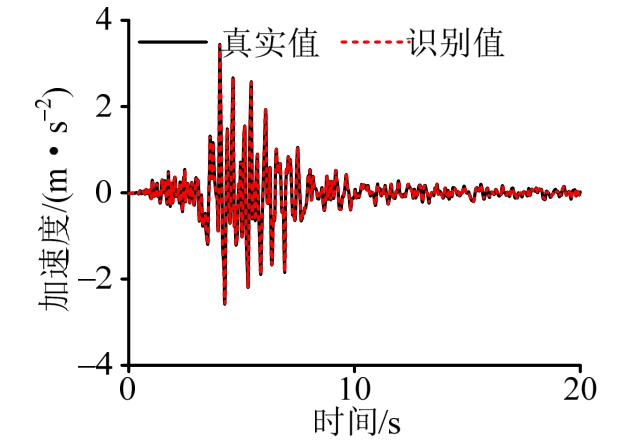
图3 地面加速度识别结果(无噪声)
Fig.3 Identified result of ground acceleration(noise free)
基于已识别的地面加速度，利用记忆衰退全局迭代扩展卡尔曼滤波对结构未知质量和响应进行识别，结构未知质量和等效线性参数如表1所示。
表1 质量和等效线性参数识别结果
Table 1 Identified mass and equivalent linear parameters
层数 质量/kg 等效刚度/(kN/m)等效阻尼/识别值 误差/(%)(kNsm-)··1第1层 201.9 0.95 23.9 0.24第2层 197.2 1.40 23.5 0.10第3层 196.3 1.85 24.4 0.15第4层 202.3 1.15 25.5 1.25第5层 203.5 1.75 23.5 0.12第6层 — — 23.7 0.13第7层 — — 24.2 0.17
从表1可知，在30%的质量初始误差下，质量识别结果的相对误差在2%以内。对比等效线性参数识别值与真实值，发现结构第4层阻尼值发生了较大变化，说明第4层耗能较大，为非线性发生位置，这与MR阻尼器作用于第4层相符。
图4为各层质量识别迭代过程。为了研究记忆衰退技术对算法的影响，同时给出了EKF-WGI算法的质量识别迭代过程(记忆衰退滤波因子G=0)。结果表明，记忆衰退技术能够有效地提高算法的识别精度和收敛速度，增加算法的稳定性。
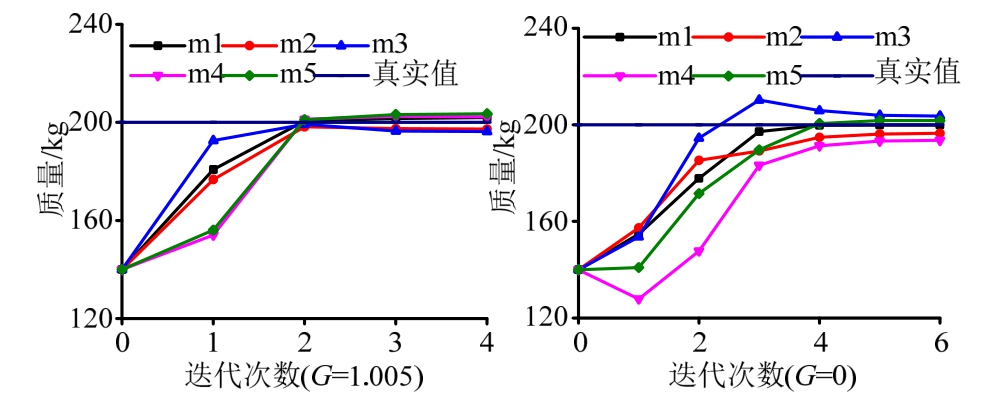
图4 质量识别迭代过程比较
Fig.4 Comparison of the iterative procedure of mass identification
图5和图6分别给出了第2层、第3层速度位移和第4层加速度响应识别与模拟值的比较，可见未知响应识别与理论值十分接近。
图5 结构第2层、第4层位移、速度响应识别结果
Fig.5 Identified structural displacement, velocity of the second and fourth floors
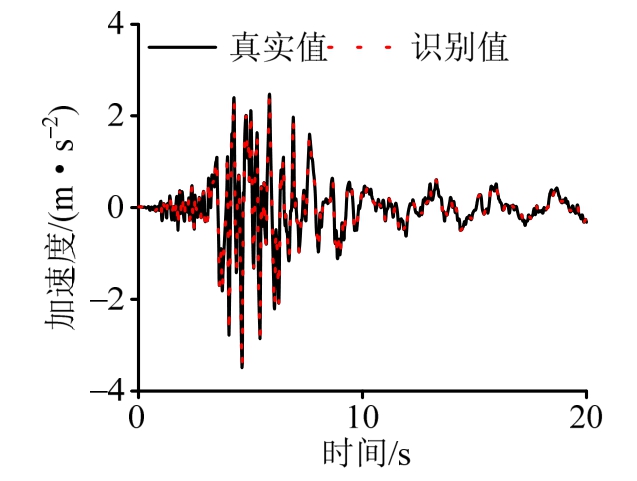
图6 结构第4层加速度响应识别结果
Fig.6 Identified structural acceleration of the fourth floor
基于完整的结构响应，利用幂级数多项式识别出非线性层的非线性恢复力
其表达式如下。
值得注意的是，本文识别的总非线性恢复力包含有线弹性恢复力、粘滞阻尼力以及非线性构件MR的恢复力。在识别的层间恢复力中减去线弹性恢复力和粘滞阻尼力得到阻尼器的恢复力，并与真实值对比。图7所示为MR恢复力识别值与真实值的对比。可以看出，在质量初始误差较大的条件下本文方法可较好地识别阻尼器的非线性恢复力。
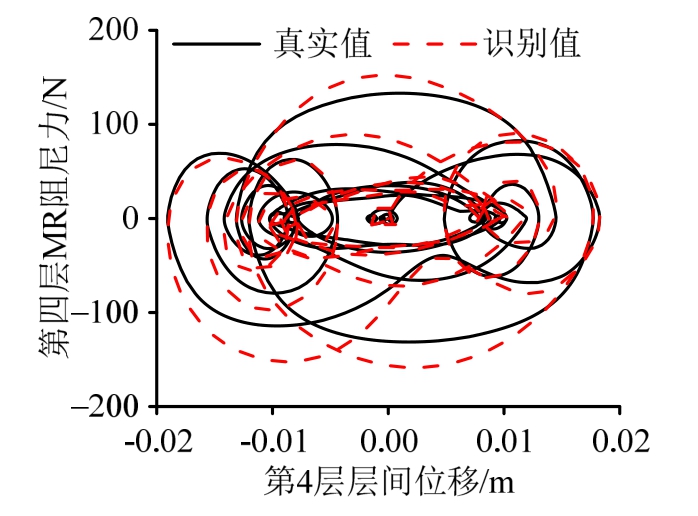
图7 MR阻尼力识别值(无噪声)
Fig.7 Identified MR damper force(noise free)
2.3 工况2：4%测量噪声
实际中测量数据不可避免地会受到噪声污染，为了研究算法的抗噪性，向已知的动力响应信号中加入信噪比为4%的白噪声，利用非线性系统地震动加速度识别方法所识别的地面加速度时程与实际地震加速度的对比如图8所示。
图9给出了两种工况下识别的地震加速度时程误差比较。可以看出，测量噪声对地面加速度识别结果有一定影响，由式(5)所识别的地面加速度不可避免地受到顶层加速度的量测噪声的影响。但是，在受噪声影响情况下，对地震激励加速度的识别结果与实际地震动加速度吻合较好。
图8 地面加速度识别结果(4%噪声)
Fig.8 Identified result of ground acceleration(4% noise)
图9 地面加速度识别误差比较
Fig.9 Error comparison of identified ground accelerations
基于地面加速度时程的识别结果，质量识别结果以及其迭代过程分别如表2和图10所示。在质量有30%的初始误差和4%的测量噪声情况下，质量识别结果的最大误差仅为2.4%。对比无噪声影响下的质量识别结果，说明噪声对质量识别结果影响不大。此外，从图10所示，质量识别结果能够在有限次迭代后即可收敛。
表2 质量识别结果(4%噪声)
Table 2 Mass identification results(4% noise)
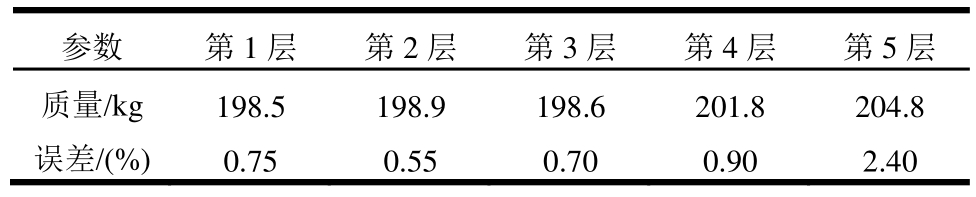
参数 第1层 第2层 第3层 第4层 第5层质量/kg 198.5 198.9 198.6 201.8 204.8误差/(%)0.75 0.55 0.70 0.90 2.40
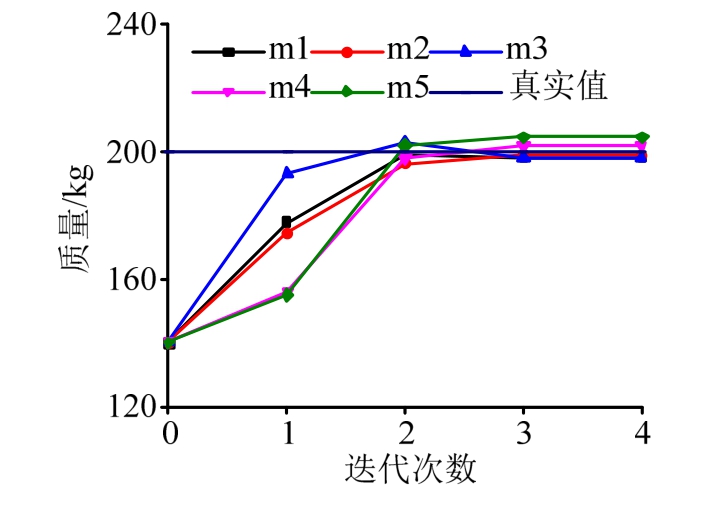
图10 质量迭代识别图(4%噪声)
Fig.10 Iteration of mass identification(4% noise)
同样地，利用幂级数多项式可得到第四层的总非线性恢复力，通过减去弹性恢复力和粘滞阻尼力得到MR阻尼力的恢复力与真实值的对比如图11所示。结构第四层的层间恢复力的幂级数多项式的表达式如式(27)所示。
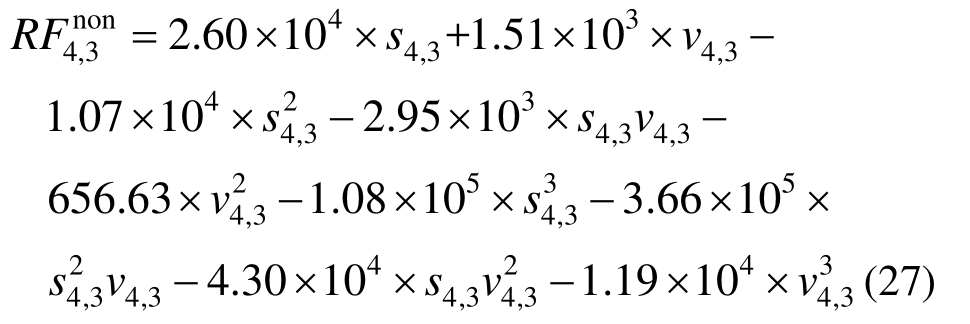
图11 MR阻尼力识别值(4%噪声)
Fig.11 Identified MR damper force(4% noise)
结果表明，本文算法在质量初始误差较大以及存在测量误差情况下仍能对结构非线性恢复力、质量以及地震加速度进行有效识别。
3 结论
本文结合记忆衰退全局加权迭代扩展卡尔曼滤波和幂级数多项式，提出了一种地震激励未知下的结构质量、非线性恢复力以及地震加速度的非参数化识别方法。该方法只需要已知结构部分动力响应输出和部分质量信息。并通过非线性系统的数值模拟验证了该方法的可行性。
在数值算例中，将MR阻尼器引入到一个7层的集中质量剪切型结构构成非线性系统。在无噪声和4%测量噪声两种工况下，对结构质量和MR阻尼器恢复力以及地震加速度进行了识别。结果表明，即使测量噪声对地震加速度识别结果有一定的影响，该方法仍然能够较好地识别质量和非线性恢复力，具有较强的适用性和抗噪性。
本文提出的地震激励未知下结构质量和系统非线性恢复力的非参数化识别方法，可以识别出结构构件非线性发生发展过程，所识别的非线性恢复力定量计算结构构件的耗能等，并且不需要已知非线性行为的参数化模型，具有一般性。能够为震后损伤识别和状态评估提供有效的方法。此外，不同于传统基于动力特征值识别结构刚度的方法，本方法所得到的不同时刻结构的损伤发生发展过程的结果可以更加直观反应结构在地震作用下的损伤模式的变化过程，更有助于了解在地震作用下结构层次不同构件不同时刻的损伤状况，为研究结构破坏模式的演化提供帮助。
[1]Hoshiya M, Saito E.Structural identification by extended Kalman filter [J].Journal of Engineering Mechanics,1984, 110(12): 1757―1770.
[2]王祥建.土木工程中的物理参数时域识别及地震动反演研究[D].哈尔滨：中国地震局工程力学研究所,2011.Wang Xiangjian.Study on parameter identification of civil engineering in time domain and inversion of ground motion [D]Harbin: Institute of Engineering Mechanics,China Earthquake Administration, 2011.(in Chinese)
[3]Xu B, He J, Rovekamp R, et al.Structural parameters and dynamic loading identification from incomplete measurements: Approach and validation [J].Mechanical Systems and Signal Processing, 2012, 28: 244―257.
[4]He J, Xu B, Masri, S F.Restoring force and dynamicloadings identification for a nonlinear chain-like structure with partially unknown excitations [J].Nonlinear Dynamics, 2012, 69(1/2): 231―245.
[5]Yang J N, Pan S W, Lin S.Least-squares estimation with unknown excitations for damage identification of structures [J].Journal of Engineering Mechanics, 2007,133(1): 12―21.
[6]Xu B, He J.Substructural parameter and dynamic loading identification with limited observations [J].Smart Structures and Systems, 2015, 15(1): 169―189.
[7]Lei Y, Wu Y, Li T.Identification of non-linear structural parameters under limited input and output measurements[J].International Journal of Non-Linear Mechanics,2012, 47(10): 1141―1146.
[8]Lei Y, Jiang Y Q, Xu Z Q.Structural damage detection with limited input and output measurement signals [J].Mechanical Systems and Signal Processing, 2012, 28(5):229―243.
[9]李杰, 陈隽.结构参数未知条件下的地震动反演研究[J].地震工程与工程振动, 1997, 17(3): 27-35.Li Jie, Chen Jun.Inversion of ground motion with unknown structural parameters [J].Earthquake Engineering and Engineering Vibration.1997, 17(3):27―35.(in Chinese)
[10]李杰, 陈隽.子结构物理参数识别与输入地震动的复合反演研究[J].振动与冲击, 1998, 17(1): 58―62.Li Jie, Chen Jun.Study on composite inversion of ground motion and substructural parameter and identification [J].Journal of Vibration and Shock, 1998, 17(1): 58―62.(in Chinese)
[11]冯新, 周晶, 陈健云.一种结构参数的两阶段方法[J].计算力学学报, 2002, 19(2): 222―227.Feng Xin, Zhou Jing, Chen Jianyun.A two-stage method for identification of structural parameter [J].Chinese Journal of Computational Mechanics, 2002, 19(2): 222―227.(in Chinese)
[12]王晓燕, 黄维平, 李华军.地震动反演及结构参数识别的EKF算法[J].工程力学，2005, 22(2): 20―23.Wang Xiaoyan, Huang Weiping, Li Huajun.Inversion of ground motion and identification of structural parameters by EKF [J].Engineering Mechanics, 2005, 22(2): 20―23.(in Chinese)
[13]Das A K, Haldar A.Health assessment of structural exposed to seismic excitations [J].Iset Journal of Earthquake Technology, 2011, 48(1): 11―27.
[14]谢献忠, 易伟建.结构物理参数时域识别的子结构研究方法[J].工程力学, 2005, 22(5): 94―98.Xie Xianzhong, Yi Weijian.Substructure method for parameter estimation in time domain [J].Engineering Mechanics, 2005, 22(5): 94-98.(in Chinese)
[15]王祥建, 万鹏, 崔杰.基于三阶段法的结构损伤识别研究[J].世界地震工程, 2015, 31(4): 50-57.Wang Xiangjian, Wang Peng, Cui Jie.Structural damage identification based on the three-stage method [J].World Earthquake Engineering, 2015, 31(4): 50―57.(in Chinese)
[16]Masri S F, Caughey T K.A nonparametric identification technique for nonlinear dynamic problems [J].Journal of Applied Mechanics.1979, 46(3): 433―447.
[17]许斌, 贺佳.基于实测时间序列的非线性系统恢复力识别[J].中国工程科学, 2011, 13(9): 76―82.Xu Bin, He Jia.Nonlinear restoring force identification based on measured time series [J].Engineering Science,2011, 13(9): 76―82.(in Chinese)
[18]Xu B, He J, Masri S F.Data-based identification of nonlinear restoring force under spatially incomplete excitations with power series polynomial model [J].Nonlinear Dynamics, 2012, 67(3): 2063―2080.
[19]许斌, 辛璐璐, 贺佳.基于切比雪夫多项式模型的多自由度结构非线性恢复力时域识别[J].工程力学,2014, 31(11): 99―109.Xu Bin, Xin Lulu, He Jia.Time domain nonlinear restoring force identification for MDOF structures with Chebyshev polynomial meodel [J].Engineering Mechanics, 2014, 31(11): 99―109.(in Chinese)
[20]Xu B, He J, Dyke S J.Model free nonlinear restoring force identification for SMA dampers with double Chebyshev polynomials: Approach and Validation [J].Nonlinear Dynamics, 2015, 82(3): 1507―1522.
[21]何明煜.部分观测下基于模型或数据的结构非线性的识别方法[D].厦门: 厦门大学, 2014.He Mingyu.Model based or data based approaches for the identification of structural nonlinearity with limited output measurement [D].Xiamen: Xiamen University,2014.(in Chinese)
[22]许斌, 王云.利用部分加速度测量的结构滞回特性免模型识别[J].工程力学, 2018, 35(2): 180―187.Xu Bin, Wang Yun.Model free structural hysteretic behavior identification with limited acceleration measurement [J].Engineering Mechanics, 2018, 35(2):180―187.(in Chinese)
[23]周强, 瞿伟廉.磁流变阻尼器的两种力学模型和试验验证[J].地震工程与工程振动, 2002, 22(4): 144―150.Zhou Qiang, Qu Weilian.Two mechanic models for magneto-rheological damper and corresponding test verification [J].Earthquake Engineering and Engineering Vibration, 2002, 22(4): 144―150.(in Chinese)