多次历史震害表明,土体在遭遇较大地震动作用时会表现为非线性特性[1-5]。土体非线性行为会随着剪应变不断增加,而土体剪切模量不断减小,阻尼不断增大。国内外学者提出了不同的本构模型来考虑土体非线性,并且编制了场地土层地震反应分析计算程序[6-21]。其中,一维传统等效线性化方法是一种频率无关的方法(以下简称“频率无关方法”)[6],它具有计算量小和所需参数少的优点,关键是其参数可以通过动三轴或共振柱试验获得,并且等效线性化方法与相应的参数之间的精度能够相互匹配,而不像其它非等效的非线性方法,用静力实验得到的静力参数去替代动力参数,由此产生很大的误差。而这种动静力参数之间的误差经常会大于等效线性与非线性方法之间的误差。由于等效线性方法和模型参数之间相互匹配,因而得到了广泛应用,并且被国家标准《工程场地地震安全性评价》(GB 17741―2005)推荐使用。
频率无关方法假定土体剪切模量和阻尼比与加载频率无关。然而,室内试验结果表明加载频率对土体剪切模量和阻尼比有较大影响[22-30],而地震动又是由不同频率成分的分量构成的,因此等效线性化方法应该考虑土体动参数频率相关特性。国内外不少学者[14-16,18,21]提出频率相关等效线性化方法,但这些方法不能反应土体动参数受加载频率影响的真实物理过程。通常这类方法假定剪应变-频率的关系表达式和速度-频率的关系表达式相同,但文献[19]指出这一假定不适合水平成层介质。
频率无关方法要求输入的动参数为土体剪切模量比和阻尼比随剪应变的变化而变化的关系曲线以及土体剪切波速值。前者一般通过室内动三轴或共振柱试验获得,后者一般通过现场地球物理测试获得。这就涉及到实验所得到的频率相关的关系曲线与地震动不同频率分量之间的相互协调问题。即土层动力反应分析应该考虑某一确定频率下土体动参数与地震动相应频率下的分量的协调问题。鉴于此,本文在国内外不同学者给出的加载频率对土体剪切模量和阻尼比影响规律的试验结果的基础上,对数据进行回归统计分析,尝试建立了剪切模量-频率和阻尼比-频率的定量关系式;并结合等效线性化模型所需的土动力参数,推导给出了地震动不同频率分量作用下规准化的频率相关土体剪切模量及其阻尼比随剪应变的变化而变化的关系式;借鉴袁晓铭等[19]给出的频率相关等效线性化方法,建立了考虑双频率参数的频率相关等效线性化方法。采用本文方法和频率无关方法对单覆盖层均质线性场地和多层覆盖层非线性场进行了不同工况下土层地震反应分析计算,揭示试验室土动力性能参数测试频率Rf和剪切波速测试频率f(vs)对场地地震响应影响规律,为场地地震反应提供了技术支持。
科学确定场地地震动参数是保证重大工程地震安全的前提[31-36]。本文方法能够考虑试验室土动力性能参数测试频率Rf和剪切波速测试频率f(vs)对土层地震反应的影响,能够处理这2个关系之间的频率协调问题,并可相对真实地分析土层的地震反应。这种方法中土动参数和频率无关方法的参数保持了一致,即均要求输入剪切模量比和阻尼比随应变的变化曲线、剪切波速和土体密度;所不同之处在于增加了Rf 和f(vs)两个参数的输入。但总体上仍然延续了传统方法所需动参数少的优点。
1 频率相关等效线性化方法
1.1 频率相关土体动本构模型
土动剪切模量和阻尼比是场地地震反应分析最重要的动力参数,国内外不同学者针对加载频率对土体动剪切模量比和阻尼比影响规律开展了试验研究。
Kim等[22]利用扭剪仪和共振柱对压实路基土和粘性土开展了试验研究,应变控制在0.001%和0.01%之间,加载频率控制在0.05 Hz和100 Hz之间,采用扭剪仪进行10 Hz以下频率加载,共振柱进行10 Hz以上频率加载。试验结果表明剪应变为0.001%和0.01%水平下的土体剪切模量随着加载频率的增加而增加,并且呈现出对数线性规律。为了更好的表示剪切模量和阻尼比与加载频率的关系,将剪切模量和阻尼比分别以0.5 Hz水平下的剪切模量值G(0.5)和阻尼比D(0.5)为基准进行规准化处理(以下分别简称“规准化剪切模量比”和“规准化阻尼比”)。两种应变水平下的规准化剪切模量比与加载频率变化规律曲线如图1所示,通过图1可以看出,两者呈现出基本一致的对数线性比例关系。规准化阻尼比与加载频率变化规律曲线如图2所示,通过图2可以看出,当加载频率大于2 Hz时,阻尼比随着频率的增加而增加;加载频率低于2 Hz时,阻尼比则变化很小。
Darendeli等[24]利用扭剪仪和共振柱实验研究了应变幅值范围处于0.0001%和0.01%之间,频率1 Hz~100 Hz之间的粘土剪切模量和阻尼比变化规律:规准化剪切模量比与加载频率关系式可近似表达为对数线性关系,加载频率增加一个数量级,剪切模量大约有接近10%的增长。规准化阻尼比随频率增加而增加的速率高于剪切模量比,频率增加一个数量级,阻尼比则大约增加50%左右。限于篇幅问题,本文没有给出相应的曲线图,读者可参考相关文献(以下Rix等[25]、徐学燕等[29]、李瑞山等[30]研究成果同样没有给出曲线图)。
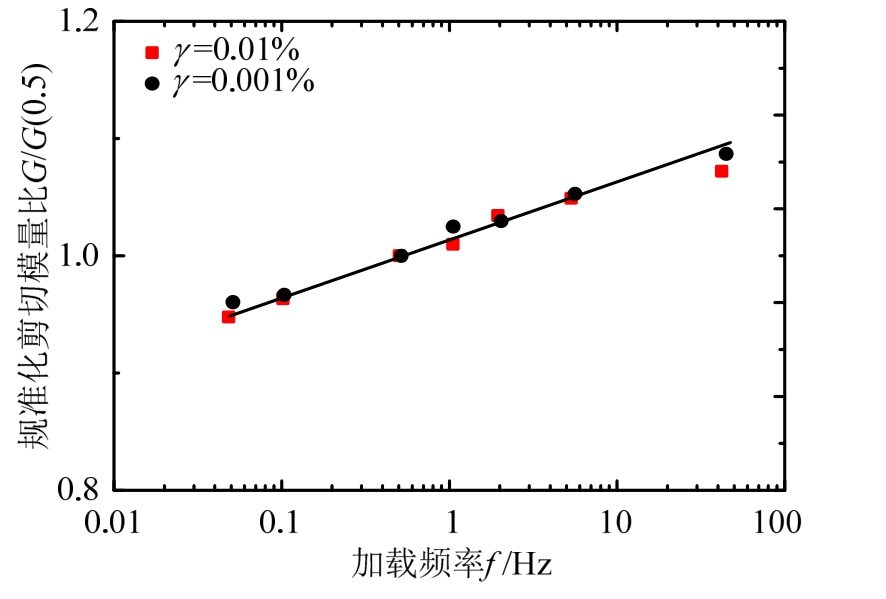
图1 规准化剪切模量比与加载频率变化规律曲线[22]
Fig.1 Variation of normalized shear modulus with variation in loading frequency
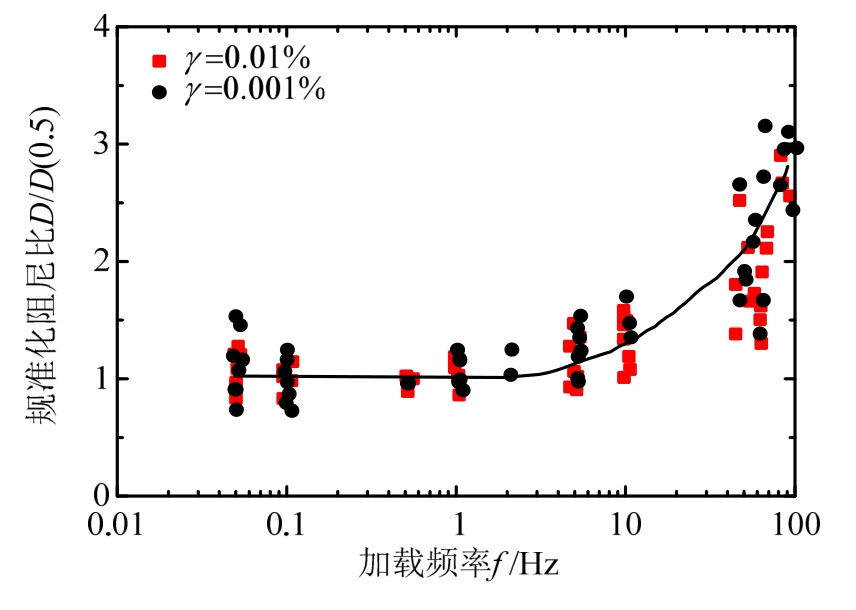
图2 规准化阻尼比与加载频率变化规律曲线[22]
Fig.2 Variation of normalized damp ratio with variation in loading frequency
Rix等[25]利用非共振方法对粘性土进行了试验研究,试验应变幅值为8×10-6,加载频率在0.01 Hz~30 Hz之间。规准化剪切模量比随着加载频率的增加单调增加,基本呈现出对数线性关系。规准化阻尼比与加载频率的变化规律则比较复杂:在0.5 Hz以下,阻尼比随着加载频率增加而降低;在0.5 Hz以上,阻尼比则随着加载频率的增加而增加。
徐学燕等[29]利用动三轴试验仪对青藏高原冻土带的不同温度下的粉质粘土进行了加载频率分别为0.1 Hz、1 Hz和5 Hz情况下的动力性能研究,规准化剪切模量比随着加载频率的增加而增加,同样其关系式可近似为对数线性关系。规准化阻尼比与加载频率关系式也可近似为对数线性关系,但阻尼比随着加载频率增加而减少。
李瑞山等[30]利用DYNYYS动三轴仪,研究了0.1 Hz~5 Hz范围内加载频率对粘土动剪切模量和阻尼比的影响,试验结果表明粘性土动剪切模量随着加载频率的增加而增加,而且呈现出良好的线性相关性,其规准化剪切模量比与加载频率的关系也可近似用对数线性关系描述。阻尼比随着加载频率的增大而减小,也呈现出良好的线性相关性,同样,规准化阻尼比与加载频率的关系也可近似为对数线性关系。
由以上国内外试验研究结果可以看出,加载频率对土体动剪切模量和阻尼比有较大影响,但影响的幅度还没有统一认识,到目前为止还没有明确的函数关系式来科学描述加载频率对土体动剪切模量和阻尼比的影响规律。因此,本文对上述学者给出的试验结果进行了统计回归,首次分别给出了规准化剪切模量比和规准化阻尼比与加载频率的关系式。
规准化剪切模量与加载频率数据统计回归结果如图3所示,通过图3可以看出,除了李瑞山等[30]试验结果有一定的离散性之外,其余试验给出的不同剪应变应幅值下的规准化剪切模量比与加载频率结果整体上均呈现出同一对数线性关系,其回归关系式可表达为:
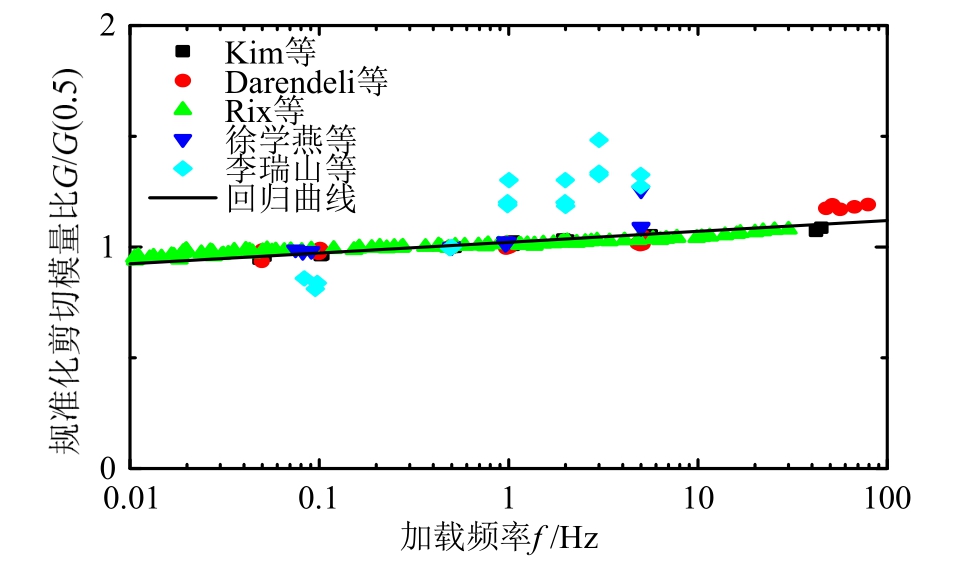
图3 规准化剪切模量比与加载频率统计回归结果
Fig.3 The data regression results for variation of normalized shear modulus with variation in loading frequency
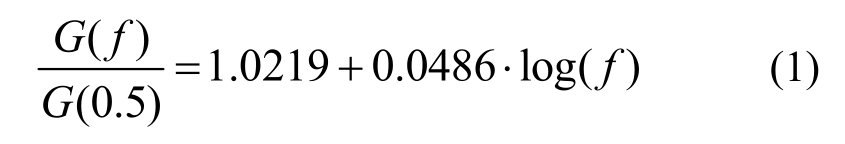
频率无关方法通常采用动力学试验给出的归一化的剪切模量比和阻尼比与剪应变关系曲线作为输入,不考虑加载频率对动剪切模量影响情况下的剪切模量求解方程如下:

式中:Gmax是剪切模量最大值,可以通过![]() 得到,其中ρ为土体密度,vs为剪切波速值,vs通常通过地球物理方法获得;G/Gmax(γ)为归一化的剪切模量比与剪应变变化关系曲线,通常通过室内动三轴或共振柱试验获得。假定地球物理方法测试剪切波速vs的频率为f(vs),动三轴或共振柱试验测试G/Gmax(γ)曲线的加载频率为Rf,通常情况下,f(vs)与Rf并不相等,因此,如果考虑加载频率对动剪切模量的影响,式(2)已经不适用,下面给出了考虑频率参数协调的频率相关动剪切模量求解过程。
得到,其中ρ为土体密度,vs为剪切波速值,vs通常通过地球物理方法获得;G/Gmax(γ)为归一化的剪切模量比与剪应变变化关系曲线,通常通过室内动三轴或共振柱试验获得。假定地球物理方法测试剪切波速vs的频率为f(vs),动三轴或共振柱试验测试G/Gmax(γ)曲线的加载频率为Rf,通常情况下,f(vs)与Rf并不相等,因此,如果考虑加载频率对动剪切模量的影响,式(2)已经不适用,下面给出了考虑频率参数协调的频率相关动剪切模量求解过程。
根据式(1)可得Gmax(Rf)为:
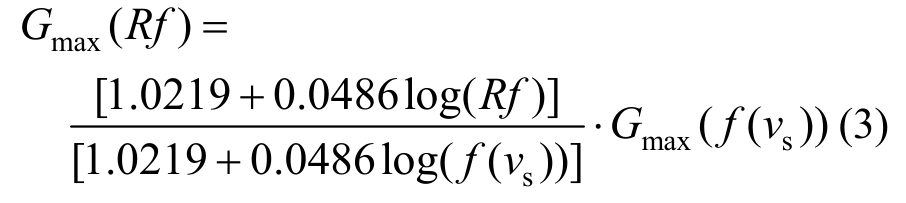
同样由式(1),可得到地震动频率f作用下的G(f )为:
将式(4)两边同时除以Gmax(Rf)可得:

频率f作用下与剪应变幅值γ相对应的剪切模量为:
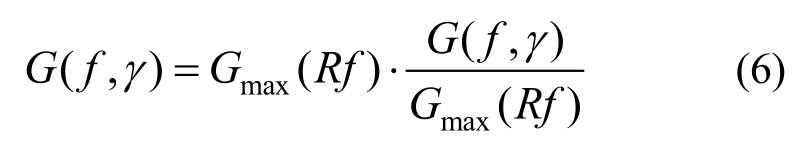
将式(3)和式(5)代入式(6)可得G(f,γ)表达式为:
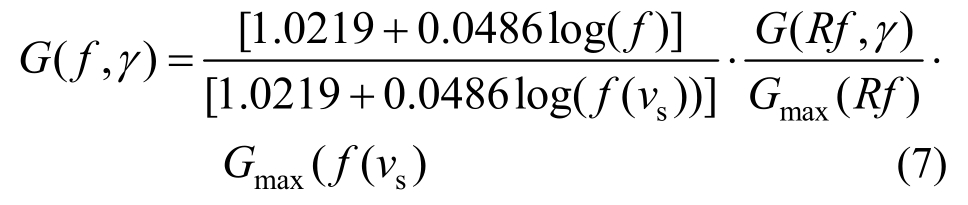
式(7)右边项中,地震动频率f、波速测试频率f(vs)和试验室土体动力性能测试频率Rf下归一化剪切模量比随剪应变变化曲线G(Rf, γ)/Gmax(Rf)均为已知,![]() 也为已知量,因此,地震动频率f下的土体动剪切模量可由式(7)求出。
也为已知量,因此,地震动频率f下的土体动剪切模量可由式(7)求出。
规准化阻尼比与加载频率试验数据统计结果如图4所示,回归曲线在10 Hz以内吻合较好,高于10 Hz的情况下,试验数据和回归曲线有一定的离散性。图4给出的回归关系式可表达为:
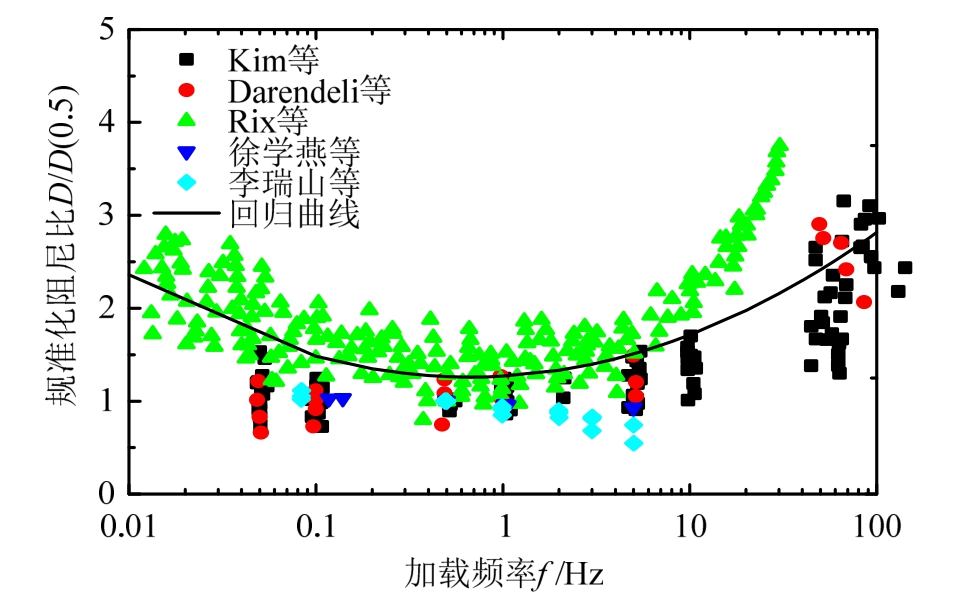
图4 规准化阻尼比与加载频率统计回归结果
Fig.4 The data regression results for variation of normalized damping ratio with variation in loading frequency
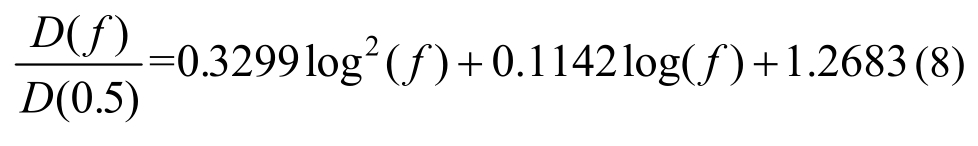
同推导地震动频率f作用下剪切模量取值公式类似,也可得到地震动频率f作用下与剪应变幅值γ相对应的阻尼比求解公式:
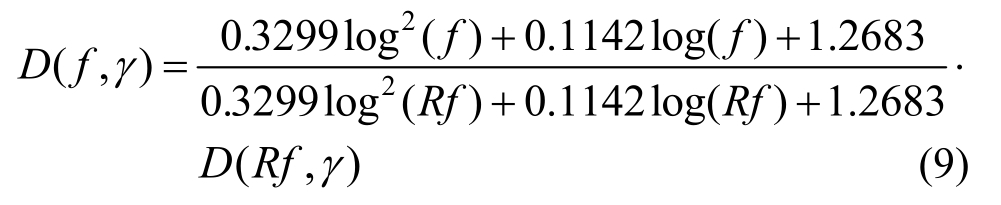
通过式(9)可以看出,地震动频率f下阻尼比与频率f、室内试验测试频率Rf和室内试验给出的阻尼比与剪应变变化关系曲线D(Rf)有关,而且均为已知,因此,通过式(9)可以得到地震动频率为f 的阻尼比D(f )。
1.2 频率相关等效线性化方法
等效线性化方法主要是基于传递函数的概念建立各计算土层之间的关系,然后进行迭代,直到剪切模量和阻尼比满足误差要求为止。频率相关方法是建立在频率无关方法的基础上,下面给出了频率相关方法的建立过程。
假定某一维水平成层场地相邻两层j层和j+1层之间的波幅系数表达式如下:
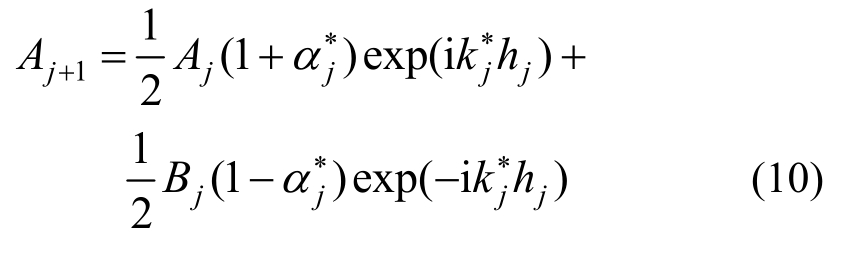
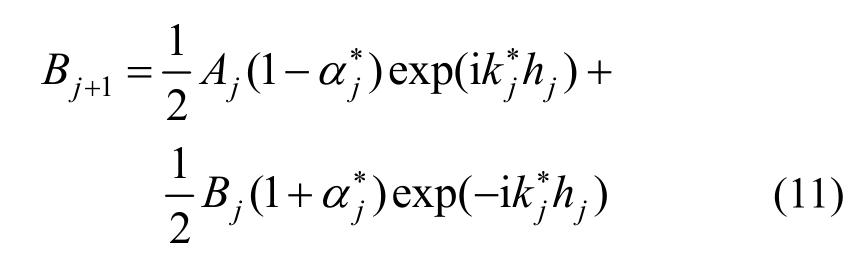
式中,Aj+1和Bj+1分别为第j+1层土介质内上行和下行波的波幅系数,基于小应变假定情况下定义的![]() 和
和![]() 如下所示:
如下所示:
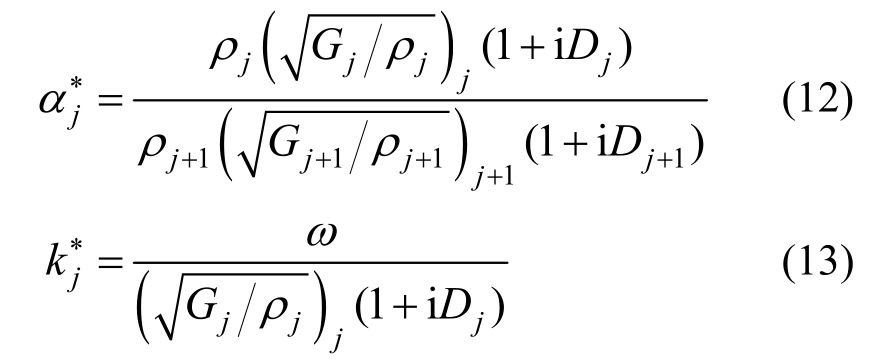
式中:ω=2πf,G和D为未考虑加载频率影响的剪切模量和阻尼比,如果考虑加载频率的影响,只需将G和D替换为与加载频率f相应的G(f)和D(f)即可。本文方法的计算步骤与频率无关方法基本一致,本文不进行详细论述,具体可参考文献[6]。
本文方法与频率无关方法相比,只是增加了计算频率相关动剪切模量和阻尼比的步骤,由于等效线性化方法计算量主要集中在计算每个子层的传递函数、求解每个子层中点位置处的剪应变时程和迭代判断是否满足精度要求上,本文方法并没有实质性的增大计算量,继承了频率无关方法计算量小的优点。在对场地土的最终等效参数方面,频率无关方法将场地等效成剪切模量为Gj、阻尼比为Dj的线性场地,本文方法则存在N组等效剪切模量G(fi )和阻尼比D(fi ),其中i=1, 2,..., N,N为输入地震动频率分量数,能够反映土体在不同频率荷载作用下呈现出不同土动参数的特性。
2 算例
2.1 线性场地算例
为了更清晰的表达频率无关方法和频率相关方法的区别与联系,采用两种方法对某一单层土覆盖层均质线性场地的传递函数进行了计算,并对计算结果进行了分析讨论。单层土覆盖层场地计算模型如图5所示,其中h为单覆盖层厚度,X(t)和Y(t)分别为基岩露头和土层场地的地表地震动时程,X(f )和Y(f )分别为X(t)和Y(t)的傅里叶变换形式。
根据文献[37],SH波入射下图5所示模型的传递函数表达式为:
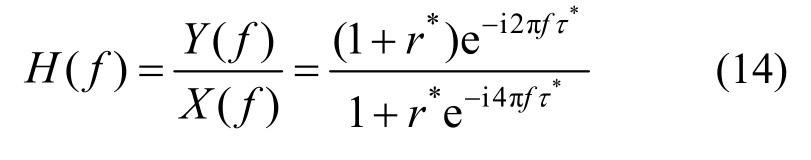
式中:r*和τ*分别为复反射系数和复传播时间,且r*=(4Qr-i(1-r))/(4Q+i(1-r)),τ*=(2Q/(2Q+i))τ,其中r和τ分别为反射系数和传播时间,分别可由如下公式求得:r=(ρrvr-ρsvs)/(ρrvr+ρsvs),τ=(h/vs),ρr和ρs分别为基岩和土层密度,vr和vs分别为基岩和土层剪切波速,Q为土层品质因子,且Q=1/(2D)。文献[37]对式(14)进行复数求模,并作了简化处理,给出了传递函数的近似精简表达式如下:
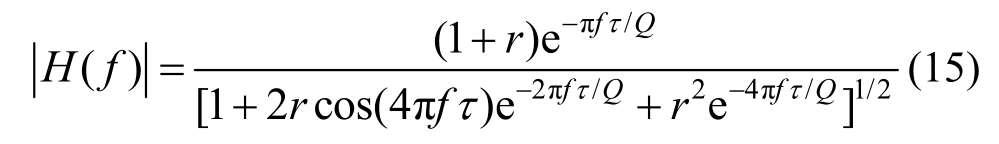
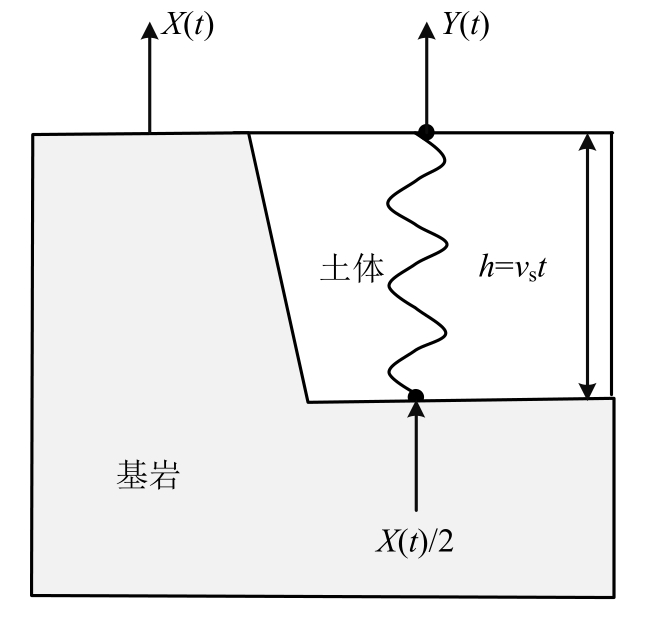
图5 一维单层土覆盖层场地计算模型
Fig.5 The one-dimensional single soil layer over bedrock model
根据式(3),并联合![]() 可得vs(f )表达式为:
可得vs(f )表达式为:

式中,f(vs)为波速测试频率。同样,根据式(9),并联合Q(f )=1/(2D( f ))可得:
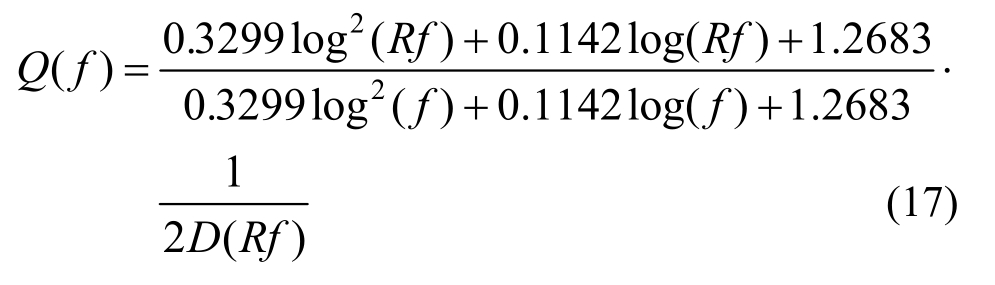
假定覆盖层场地为粉质粘土场地,覆盖层厚度H=30 m,粉质粘土剪切波速沿深度变化公式采用文献[38]给出的结果:
本文采用中心点H=15 m处的剪切波速近似代表整个覆盖层的等效波速,粉质粘土阻尼比采用文献[38]给出的小应变γ=0.5×10-5情况下的阻尼比测试结果,即D(Rf )=0.012。根据文献[17, 39]总结的波速测试频率范围和动三轴、共振柱测试频率范围,构造两组不同频率组合的工况进行传递函数计算:1)假定动三轴测试频率Rf取值0.1 Hz、1 Hz、10 Hz,剪切波速测试频率f(vs)取值1 Hz、5 Hz、10 Hz,共计9种工况;2)假定共振柱测试频率Rf取值20 Hz、50 Hz、100 Hz,剪切波速f(vs)取值1 Hz、5 Hz、10 Hz,共计9种工况。
图6给出了上述频率组合和频率无关方法的传递函数计算结果,通过图6可以看出,室内土样动力试验测试频率Rf值对本文方法和频率无关方法得到的波峰峰值大小关系影响较大。对于Rf <20 Hz的情况,频率无关方法得到的峰值大多数情况下高于本文方法得到的峰值;对于Rf >20 Hz的情况,频率无关方法得到的峰值大多数情况下低于本文方法得到的峰值。波速测试频率f(vs)对波峰影响相对较小,但对波峰出现的位置有较大影响。

图6 两种方法两组工况下传递函数计算结果
Fig.6 The simulation results of transfer function between two methods under six cases
为了定量分析两种方法的差别,表1给出了两种方法得到的传递函数6个波峰所对应的频率差δi,本文δi定义为频率无关方法第i(i=1,2,...,6)个波峰对应的频率值ft(i)与本文方法同一个波峰对应的频率值fr(i)之差,即δi= ft(i)- fr(i)( i=1,2,...,6)。由表1可知:低频段波峰所对应的频率差相对较小,高频段对应的频率差相对较大;随着f(vs)增大,频率差的绝对值总体上呈现出逐渐变小的趋势。
表1 两种方法不同f(vs)下不同波峰对应频率差
Table 1 Peak frequency difference between the peaks of transfer function for two methods under different f(vs)
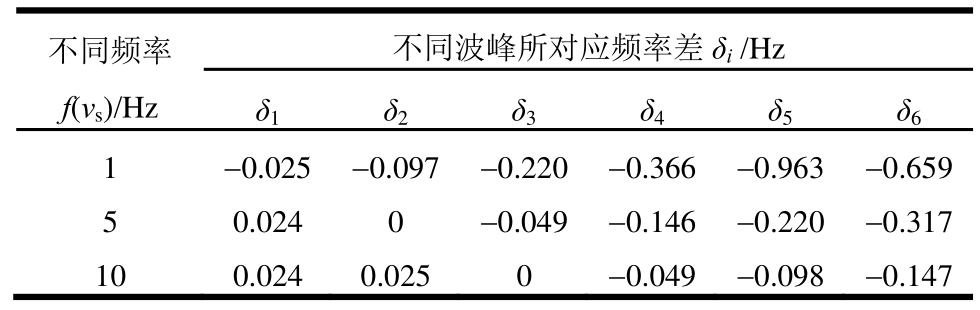
注:由于Rf对波峰位置没有影响,因此表中没有给出Rf值。
不同频率f(vs)/Hz不同波峰所对应频率差δi /Hz δ1 δ2 δ3 δ4 δ5 δ6 1 -0.025-0.097-0.220 -0.366 -0.963-0.659 5 0.0240 -0.049 -0.146 -0.220-0.317 10 0.0240.0250 -0.049 -0.098-0.147
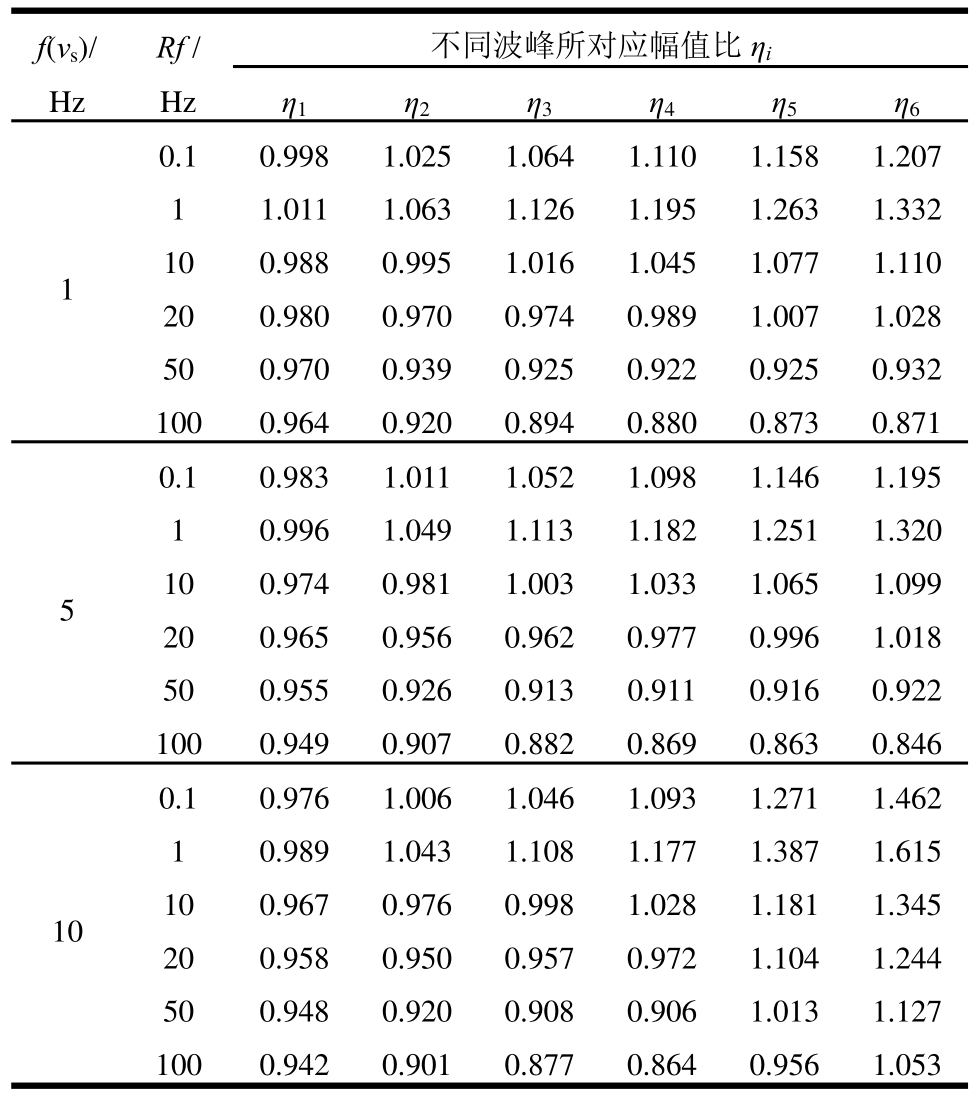
本文还定义了幅值比ηi以分析室内土体动力测试频率Rf对传递函数波峰幅值的影响,定义思路同频率差δi类似,频率无关方法第i(i=1,2,...,6)个波峰对应的传递函数幅值H(f )it与本文方法同一个波峰对应的传递函数幅值H(f )ir之比,即ηi=H(f )it/H(f )ir( i=1,2,...,6)。不同频率下两种方法各个波峰幅值比ηi如表2所示,通过表2可以看出,频率Rf对波峰幅值比ηi的大小起主要作用,幅值比总体处于0.846~1.615之间。
综合本节算例可以看出,f(vs)对传递函数波峰峰值影响影响较小,Rf影响较大,主要是由于f(vs)对剪切波速的影响较小,Rf对品质因子影响较大。图7和图8分别给出了不同f(vs)和Rf下剪切波速和品质因子与频率f变化曲线。由图7和图8可知,在传递函数波峰对应的频率处,3种不同f(vs)取值下的频率相关与频率无关剪切波速相差不超过3%,6种不同Rf取值下的频率相关与频率无关品质因子最大相差接近100%,因此Rf对传递函数影响较大。由图8还可判断出f取值13.8 Hz(传递函数第四个波峰对应频率)处的不同Rf值下的品质因子与频率无关品质因子的关系,Rf取值0.1 Hz、1 Hz和10 Hz工况下品质因子小于频率无关方法,因此计算得到的传递函数小于频率无关方法;Rf取值20 Hz、50 Hz和100 Hz工况下品质因子大于频率无关方法,因此计算得到的传递函数大于频率无关方法。建议在土样动力性能测试频率Rf<20 Hz,以尽量使得频率无关方法计算的结果偏于保守。
表2 两种方法不同频率下传递函数波峰对应幅值比
Table 2 Ratio between the peak amplitudes of transfer function for two methods
f(vs)/Rf / 不同波峰所对应幅值比ηi Hz Hz η1 η2 η3 η4 η5 η6 0.1 0.998 1.025 1.064 1.110 1.158 1.207 1 1 1.011 1.063 1.126 1.195 1.263 1.332 10 0.988 0.995 1.016 1.045 1.077 1.110 20 0.980 0.970 0.974 0.989 1.007 1.028 50 0.970 0.939 0.925 0.922 0.925 0.932 100 0.964 0.920 0.894 0.880 0.873 0.871 0.1 0.9831.0111.052 1.098 1.1461.195 5 1 0.9961.0491.113 1.182 1.2511.320 10 0.9740.9811.003 1.033 1.0651.099 20 0.9650.9560.962 0.977 0.9961.018 50 0.9550.9260.913 0.911 0.9160.922 100 0.9490.9070.882 0.869 0.8630.846 0.1 0.976 1.006 1.046 1.093 1.271 1.462 10 1 0.989 1.043 1.108 1.177 1.387 1.615 10 0.967 0.976 0.998 1.028 1.181 1.345 20 0.958 0.950 0.957 0.972 1.104 1.244 50 0.948 0.920 0.908 0.906 1.013 1.127 100 0.942 0.901 0.877 0.864 0.956 1.053
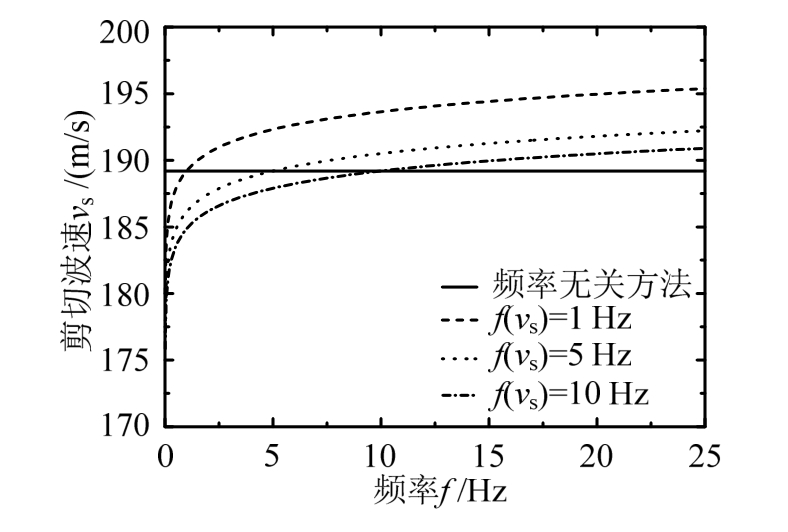
图7 不同f(vs)值下剪切波速计算结果
Fig.7 The calculation results of shear wave velocity under different f(vs)values
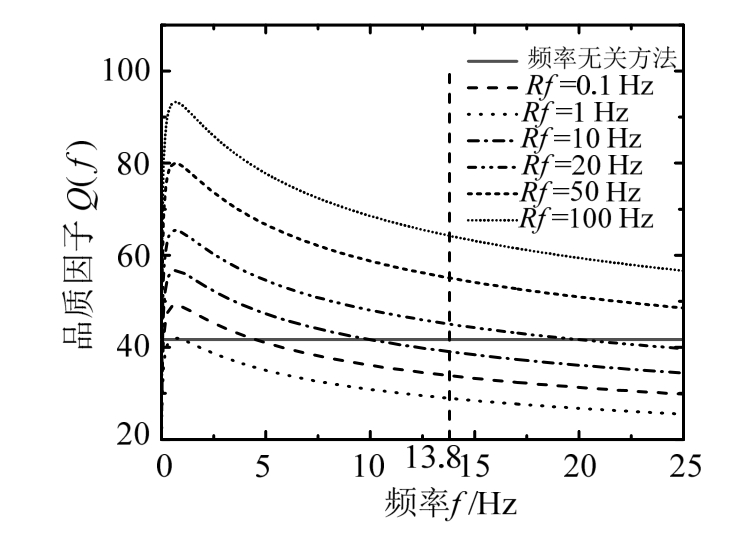
图8 不同Rf值下品质因子计算结果
Fig.8 The calculation results of quality factor under different Rf values
2.2 非线性场地算例
本节构造了覆盖层厚度为60 m的非线性场地计算模型,分别选取高频成分和低频成分丰富的两条地震动作为输入,采用本文方法和频率无关方法进行了场地土层动力反应分析计算。本节首先对峰值加速度0.30 g地震动作用下两种方法计算结果进行了对比分析,然后又研究了不同强度地震动输入对两种方法计算结果的影响规律。计算场地模型假定由单一粘性土构成,粘性土剪切波速随深度的变化关系采用式(18)给出的关系式。粘性土和基岩室内试验测得的动剪切模量比和阻尼比随剪应变的变化关系采用了文献[38]给出的结果,如表3所示。
表3 粘性土和基岩的剪切模量比和阻尼比值
Table 3 G/Gmax-γ and D-γ curves for sands and rock
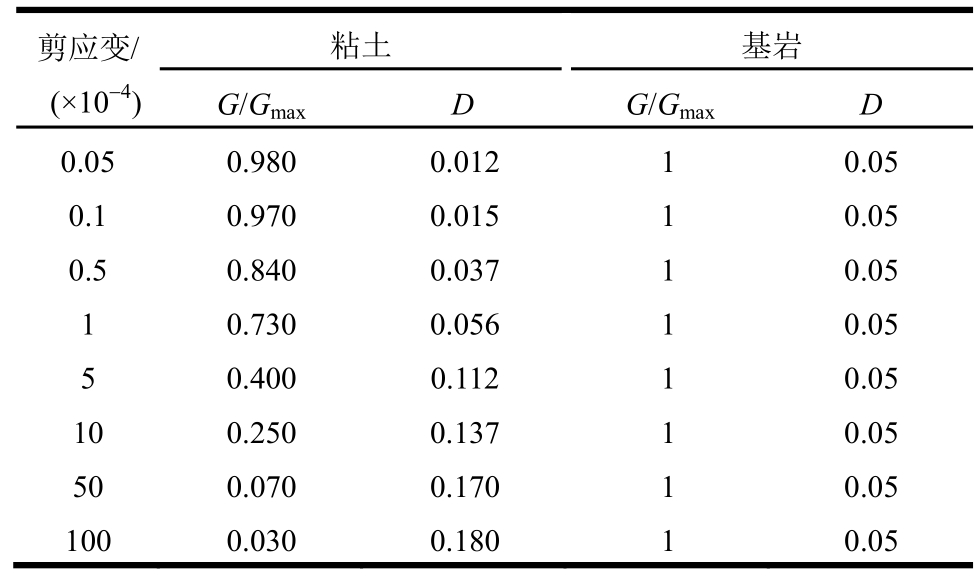
剪应变/(×10-4)粘土 基岩G/Gmax D G/Gmax D 0.05 0.980 0.012 1 0.05 0.1 0.970 0.015 1 0.05 0.5 0.840 0.037 1 0.05 1 0.730 0.056 1 0.05 5 0.400 0.112 1 0.05 10 0.250 0.137 1 0.05 50 0.070 0.170 1 0.05 100 0.030 0.180 1 0.05
考虑到计算量和文章篇幅,本算例Rf取1 Hz和50 Hz分别代表动三轴和共振柱测试频率,f(vs)取1 Hz和10 Hz覆盖波速测试频率主要范围。地震动输入分别选取高频成分相对比较丰富的Northern Calif-07地震记录和低频成分相对比较丰富的Taiwan SMART1(45)地震记录[40],峰值加速度统一标定为0.30 g,地震动时程详细信息如表4所示,加速度时程曲线和归一化傅立叶幅值谱分别如图9和图10所示。
表4 地震动时程信息表
Table 4 Information about earthquake ground motion

地震名称 发生时间震级 台站名称 震中距/km Northern Calif-07 1975 06 075.2 Cape Mendocino34.7 Taiwan SMART1(45)1986 11 147.3 SMART1 I01 56.2

图9 加速度时程曲线
Fig.9 Acceleration time history curves

图10 傅里叶幅值谱曲线
Fig.10 Fourier amplitude spectra curves
1)0.30 g峰值加速度地震动输入
0.30 g地震动强度输入下采用两种方法得到的场地地表加速度反应谱如图11所示,通过图11可以看出,两种方法计算得到的反应谱形状基本一致,只是幅值有所区别。对于Rf=50 Hz的两种工况,两种地震动输入下的反应谱值明显高于其他工况和频率无关方法下的反应谱值,而且Rf=50 Hz两种工况下的反应谱值比较接近。对于Rf=1 Hz的两种工况,其反应谱值与频率无关方法反应谱值的关系与地震动输入有关,Northern Calif-07地震作用下频率无关方法计算得到的反应谱值明显高于Rf=1 Hz两种工况下的反应谱值,Taiwan SMART1(45)地震作用下频率无关方法计算得到的反应谱值则略高于Rf=1 Hz两种工况下的反应谱值,差别相对较小。
为了对两种方法不同工况下得到的地表峰值加速度进行定量分析,本文定义放大率ξ如下:放大率=(本文方法结果-频率无关方法结果)/频率无关方法结果。表5给出了两种方法不同工况下地表峰值加速度和放大率计算结果。通过表5可以看出,Rf=50 Hz和f(vs)=1 Hz工况下的峰值加速度和放大率最大,放大率最大为46.2%,Rf=1 Hz和f(vs)=10 Hz工况下的峰值加速度和放大率最小,放大率最小为-20.3%。
综合图11和表5可以看出,Rf=50 Hz工况下的反应谱值最高,这表明Rf 对加速度反应谱计算结果起决定性作用,而f(vs)对计算结果的影响较小。
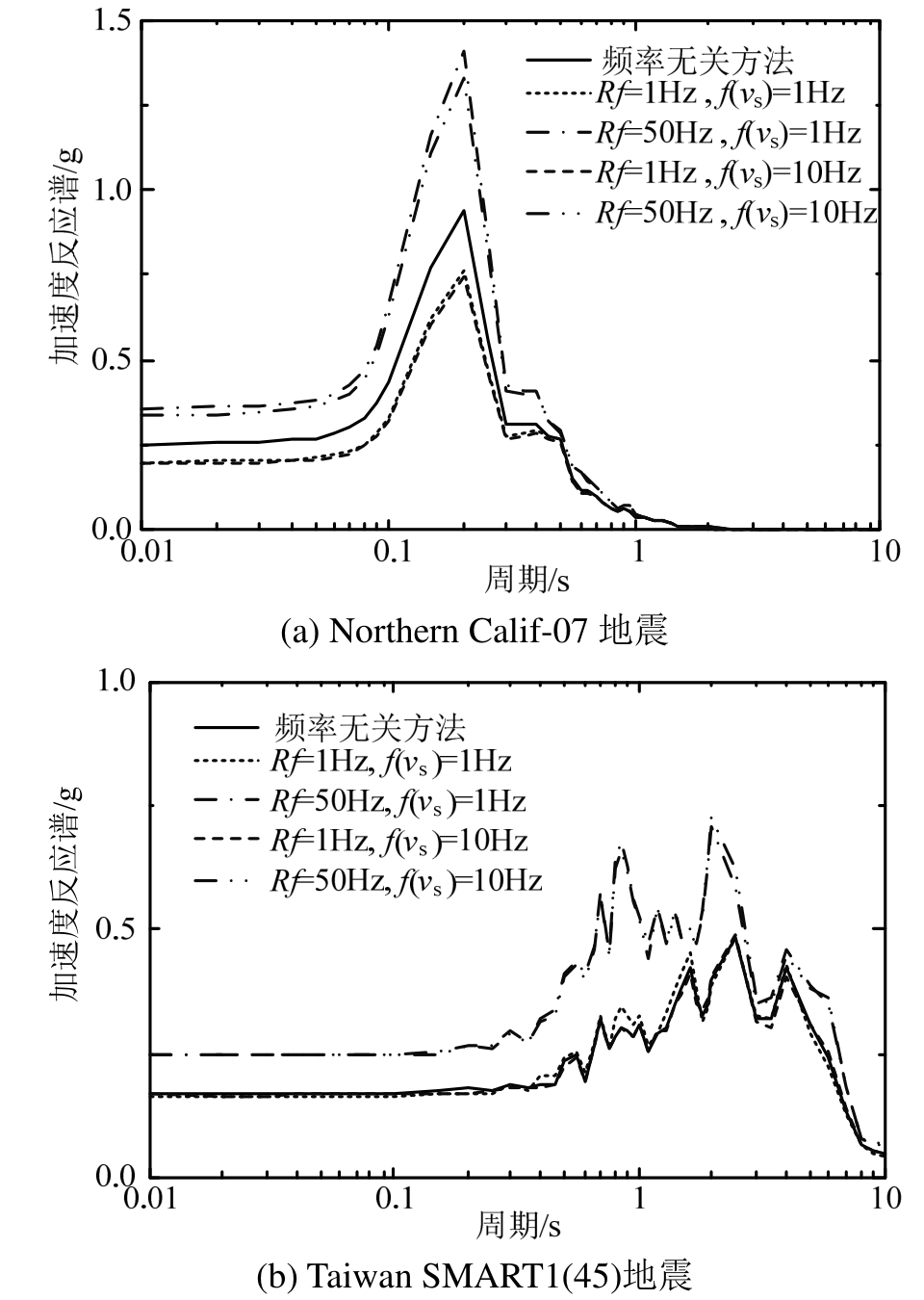
图11 两种方法得到的地表加速度反应谱
Fig.11 Acceleration response spectrum of ground surface for the site obtained by two methods
2)不同强度地震动输入
表6和表7给出了两种方法不同强度地震动输入下不同工况地表峰值加速度和放大率计算结果。由表6和表7可知无论何种地震动强度输入下,Rf值越高,地表峰值加速度和放大率越大。输入地震动频率成分不同,两种方法计算结果差异程度也不同。这与0.30 g强度地震动输入下认识基本一致。另一方面,总体上来看,随着地震动输入强度的增大,土体呈现出越来越强的非线性,两种方法计算结果的差异呈现出越来越大的趋势。
表5 两种地震作用下地表峰值加速度和放大率计算结果
Table 5 Surface results of peak ground acceleration and amplification ratio under two earthquake

地震作用 频率无关方法 Rf=1 Hz f(vs)=1 Hz Rf=50 Hz f(vs)=1 Hz Rf=1 Hz f(vs)=10 Hz Rf=50 Hz f(vs)=10 Hz PGA/g PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)Northern Calif-07 0.251 0.200 -20.3 0.357 42.2 0.195 -22.3 0.339 35.1 Taiwan SMART1(45)0.169 0.164 -3.0 0.247 46.2 0.166 -1.8 0.242 43.2
表6 Northern Calif-07地震作用下不同输入强度地表峰值加速度和放大率计算结果
Table 6 Surface results of peak ground acceleration and amplification ratio for sites with different strength of input ground under Northern Calif-07 earthquake
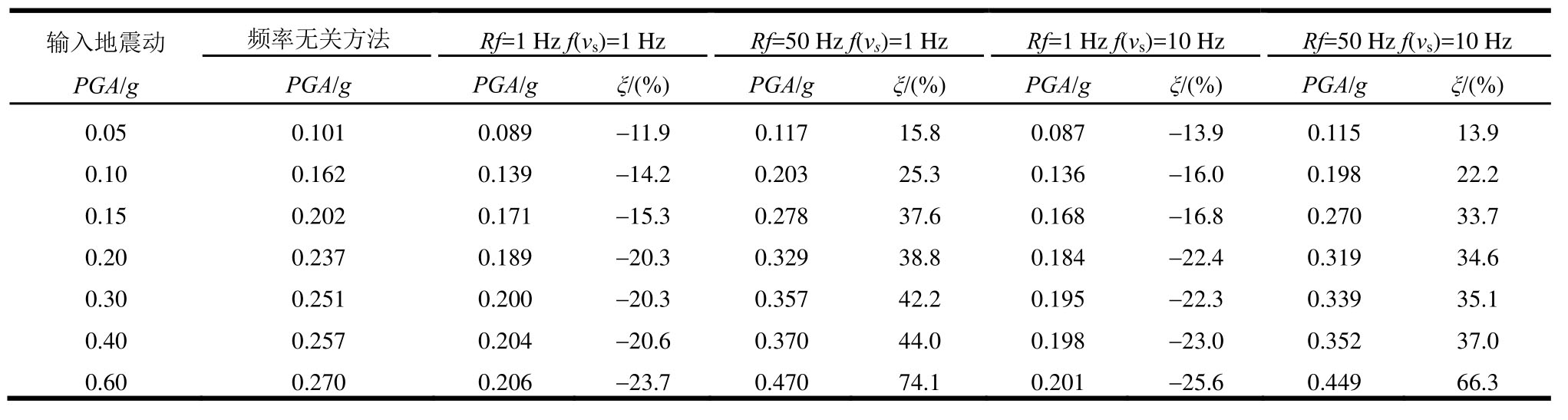
输入地震动PGA/g频率无关方法 Rf=1 Hz f(vs)=1 Hz Rf=50 Hz f(vs)=1 Hz Rf=1 Hz f(vs)=10 Hz Rf=50 Hz f(vs)=10 Hz PGA/g PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)0.05 0.101 0.089 -11.9 0.117 15.8 0.087 -13.9 0.115 13.9 0.10 0.162 0.139 -14.2 0.203 25.3 0.136 -16.0 0.198 22.2 0.15 0.202 0.171 -15.3 0.278 37.6 0.168 -16.8 0.270 33.7 0.20 0.237 0.189 -20.3 0.329 38.8 0.184 -22.4 0.319 34.6 0.30 0.251 0.200 -20.3 0.357 42.2 0.195 -22.3 0.339 35.1 0.40 0.257 0.204 -20.6 0.370 44.0 0.198 -23.0 0.352 37.0 0.60 0.270 0.206 -23.7 0.470 74.1 0.201 -25.6 0.449 66.3
表7 Taiwan SMART1(45)地震作用下不同输入强度地表峰值加速度和放大率计算结果
Table 7 Surface results of peak ground acceleration and amplification ratio for sites with different strength of input ground under Taiwan SMART1(45)earthquake
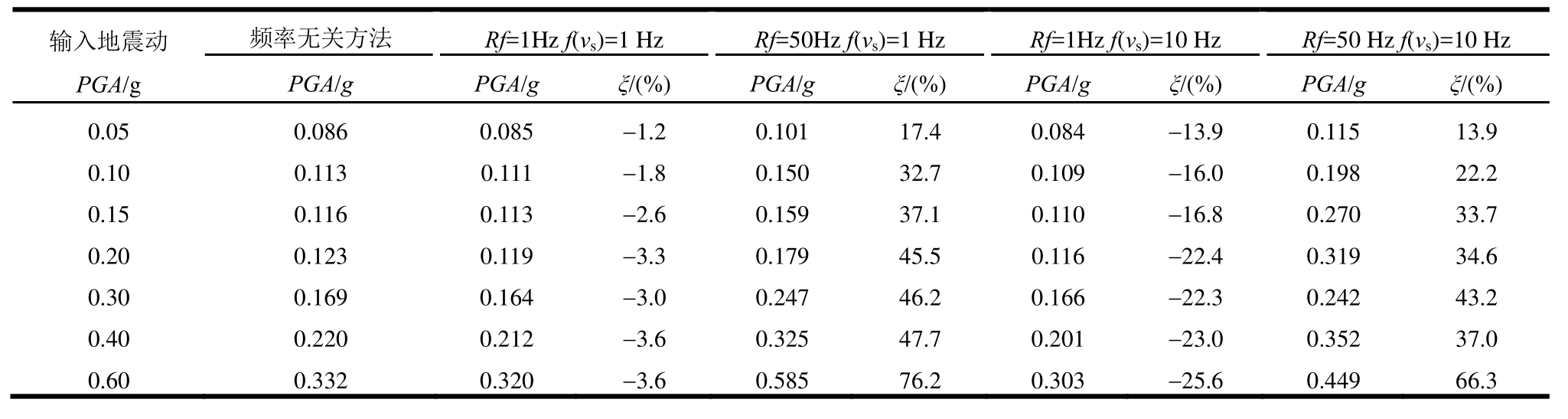
输入地震动PGA/g频率无关方法 Rf=1Hz f(vs)=1 Hz Rf=50Hz f(vs)=1 Hz Rf=1Hz f(vs)=10 Hz Rf=50 Hz f(vs)=10 Hz PGA/g PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)PGA/g ξ/(%)0.05 0.086 0.085 -1.2 0.101 17.4 0.084 -13.9 0.115 13.9 0.10 0.113 0.111 -1.8 0.150 32.7 0.109 -16.0 0.198 22.2 0.15 0.116 0.113 -2.6 0.159 37.1 0.110 -16.8 0.270 33.7 0.20 0.123 0.119 -3.3 0.179 45.5 0.116 -22.4 0.319 34.6 0.30 0.169 0.164 -3.0 0.247 46.2 0.166 -22.3 0.242 43.2 0.40 0.220 0.212 -3.6 0.325 47.7 0.201 -23.0 0.352 37.0 0.60 0.332 0.320 -3.6 0.585 76.2 0.303 -25.6 0.449 66.3
3 结论
(1)本文对国内外学者给出的加载频率对土动剪切模量和阻尼比试验结果进行了统计回归,得到了动剪切模量和阻尼比与加载频率的关系式。参照频率无关方法土动参数的输入形式,推导了频率相关剪切模量比和阻尼比与剪应变关系式如式(7)和式(9)所示,并对频率无关等效线性化方法进行了改进,建立了考虑频率参数协调的频率相关等效线性化方法。
(2)采用两种方法对30 m厚单层粉质粘土覆盖层线性场地的传递函数进行了分析计算,计算结果表明,Rf对传递函数波峰幅值起决定性作用,f(vs)则对波峰所对应的频率值有较大影响。
(3)选取频谱成分不同的两条地震记录,采用两种方法对60 m厚的粉质粘土场地遭受不同强度地震作用下进行了非线性场地地震反应分析。计算结果表明:Rf值对峰值加速度和反应谱值影响较大,f(vs)值影响较小;地震动频率成分不同,两种方法计算结果的差异程度也有所不同。
(4)综合本文计算结果以及动三轴和共振柱通常的测试频率范围,可得出如下结论:动三轴测试频率Rf值一般较小,频率无关方法得出的结果通常偏高;共振柱测试频率Rf值一般较大,频率无关方法得出的结果偏低。建议土体动力非线性参数测试报告提供Rf值,并采用本文方法和频率无关方法进行土层地震反应分析计算,综合分析给出场地设计地震动参数。
[1]Chin B H, Aki K.Simultaneous study of the source, path,and site effects on strong ground motion during the 1989 Loma Prieta earthquake: a preliminary result on pervasive nonlinear site effects [J].Bulletin of the Seismological Society of America, 1991, 81(5): 1859-1884.
[2]Field E H, Johnson P A, Beresnev I A, et al.Nonlinear ground-motion amplification by sediments during the 1994 Northridge earthquake [J].Nature, 1997,390(6660): 599-602.
[3]Beresnev I A, Atkinson G M.Stochastic finite-fault modeling of ground motions from the 1994 Northridge,California, earthquake.I.Validation on rock sites [J].Bulletin of the Seismological Society of America, 1998,88(6): 1392-1401.
[4]Kwok A O L, Stewart J P, Hashash Y M A.Nonlinearground-response analysis of Turkey flat shallow stiff-soil site to strong ground motion [J].Bulletin of the Seismological Society of America, 2008, 98(1): 331-343.
[5]Elia G, Rouainia M, Karofyllakis D, et al.Modelling the non-linear site response at the LSST down-hole accelerometer array in Lotung [J].Soil Dynamics and Earthquake Engineering, 2017, 102: 1-14.
[6]Schnabel P B, Lysmer J, Seed H B.SHAKE: A computer program for earthquake response analysis of horizontally layered sites [R].EERC Report 72-12, Berkeley,University of California, Berkeley, 1972.
[7]Streeter V L, Wylie E B, Richart F E.Soil Motion computations by characteristics method [J].ASCE Journal of the Geotechnical Engineering Division, 1974,100(3): 247-263.
[8]Lee M K W, Finn W D L.DESRA-1 Program for the dynamic effective stress response analysis of soil deposits including liquefaction evaluation [R].Soils Mechanics No.36, Vancouner, Department of Civil Engineering, University of British Columbia, Canada,1975.
[9]Idriss I M, Dobry R M, Doyle E H, et al.Behavior of soft clays under earthquake loading conditions [C].Houston,ASCE Offshore Technology Conference, 1976: 605-616.
[10]Joyner W B.A fortran program for calculating nonlinear seismic ground response [R].Reston: US Geological Survey, 1977: 77-671.
[11]Lam I, Tsai C-F, Martin G R.Determination of site dependent spectra using nonlinear analysis [C].San Francisco, Second International Conference on Microzonation, 1978: 1089-1104.
[12]Lee M K W, Finn W D L.DESRA-2: Dynamic effective stress response analysis of soil deposits with energy transmitting boundary including assessment of liquefaction potential [R].Soils Mechanics No.36,Vancouner: Department of Civil Engineering, University of British Columbia, Canada, 1975.
[13]李小军.非线性土层地震反应分析的一种方法[J].华南地震, 1992, 12(4): 1-8.Li Xiaojun.A method for analyzing seismic response of nonlinear soil layers [J].South China Journal of Seismology, 1992, 12(4): 1-8.(in Chinese)
[14]Kausel E, Assimaki D.Seismic simulation of inelastic soils via frequency-dependent moduli and damping [J].Journal of Engineering Mechanics, 2002, 128(1): 34-47.
[15]Yoshida N, Kobayashi S, Suetomi I.Equivalent linear method considering frequency dependent characteristics of stiffness and damping [J].Soil Dynamics and Earthquake Engineering, 2002, 22(3): 205-222.
[16]蒋通, 邢海灵.水平土层地震反应分析考虑频率相关性的等效线性化方法[J].岩土工程学报, 2007, 29:218-224.Jian Tong, Xing Hailing.An equivalent linear method considering frequency-dependent soil properties for seismic response analysis [J].Chinese Journal of Geotechnical Engineering, 2007, 29: 218-224.(in Chinese)
[17]Park D P, Hashash Y M A.Rate-dependent soil behavior in seismic site response analysis [J].Canadian Geotechnical Journal, 2008, 45(4): 454-469.
[18]王伟, 刘必灯, 周正华, 等.刚度和频率相关的等效线性化方法[J].岩土力学, 2010, 31: 3928-3933.Wang Wei, Liu Bideng, Zhou Zhenghua, et al.Equivalent linear method considering frequency dependent stiffness and damping [J].Rock and Soil Mechanics, 2010,31(12): 3928-3933.(in Chinese)
[19]袁晓铭, 李瑞山, 孙锐.新一代土层地震反应分析方法[J].土木工程学报, 2016, 49(10): 95-102.Yuan Xiaoming, Li Ruishan, Sun Rui.A new generation method for earthquake response analysis of soil layers[J].China Civil Engineering Journal, 2016, 49(10): 95-102.(in Chinese)
[20]张季, 梁建文, 巴振宁.水平层状饱和场地地震响应分析的等效线性化方法[J].工程力学, 2016, 33(10):52-61.Zhang Ji, Liang Jianwen, Ba Zhenning.Equivalent linear analysis of seismic response of horizontally layered fluid-saturated poroelastic half-space [J].Engineering Mechanics, 2016, 33(10): 52-61.(in Chinese)
[21]Huang D, Wang G, Wang C, et al.A modified frequency-dependent equivalent linear method for seismic site response analyses and model validation using kik-net borehole arrays [J].Journal of Earthquake Engineering, 2018, 3: 1-18.
[22]Kim D S, Stokoe K H, Hudson W R.Deformational characteristics of soils at small to intermediate strains from cyclic tests [R].Austin: University of Texas at Austin, 1991: 73-80.
[23]Shibuya S, Mitachi T, Fukuda F, et al.Strain rate effects on shear modulus and damping of normally consolidated clay [J].Geotechnical Testing Journal, 1995, 18(3):365-375.
[24]Darendeli M B.Development of a new family of normalized modulus reduction and material damping curves [D].Austin: Department of Civil Engineering,University of Texas at Austin, 2001.
[25]Rix G J, Meng J W.A non-resonance method for measuring dynamic soil properties [J].Geotechnical Testing Journal, 2005, 28(1): 1-8.
[26]Meng J W, Earthquake ground motion simulation with frequency-dependent soil properties [J].Soil Dynamics and Earthquake Engineering, 2007, 27(3): 234-241.
[27]Khan Z H, Cascante G, El Naggar M H, et al.Measurement of frequency-dependent dynamic properties of soils using the resonant-column device [J].Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(9): 1319-1326.
[28]黎冰, 高玉峰, 丰土根.振动频率对LCES动力特性的影响分析及其机理初探[J].岩土力学, 2008, 29(10):2731-2734.Li Bin, Gao Yufeng, Feng Yugen.Cyclic loading frequency effect and mechanism of lightweight clay-EPS beads soil [J].Rock and Soil Mechanics, 2008, 29(10):2731-2734.(in Chinese)
[29]徐学燕, 陈亚明.冻土的动力特性研究及其参数确定[J].岩土工程学报,1998, 20(5): 77-81.Xu Xueyan, Chen Yaming.Research on dynamic characters of frozen soil and determination of its parameters [J].Chinese Journal of Geotechnical Engineering, 1998, 20(5): 77-81.(in Chinese)
[30]李瑞山, 陈龙伟, 袁晓铭, 等.荷载频率对动模量阻尼比影响的试验研究[J].岩土工程学报, 2017, 39(1):71-80.Li Ruishan, Chen Longwei, Yuan Xiaoming, et al.Experimental study on influences of different loading frequencies on dynamic modulus and damping ratio [J].Chinese Journal of Geotechnical Engineering, 2017,39(1): 71-80.(in Chinese)
[31]卢啸, 陆新征, 李梦珂, 等.地震作用设计参数调整对框架结构抗震设计及安全性的影响[J].工程力学,2017, 34(4): 22-31.Lu Xiao, Lu Xinzheng, Li Mengke, et al.Influence of seismic action adjustments on seismic design and safety of RC frames [J].Engineering Mechanics, 2017, 34(4):22-31.(in Chinese)
[32]朱志辉, 杨乐, 王力东, 等.地震作用下铁路斜拉桥动力响应及行车安全性研究[J].工程力学, 2017, 34(4):78-87.Zhu Zhihui, Yang Le, Wang Lidong, et al.Dynamic responses and train running safety of railway cable-stayed bridge under earthquakes [J].Engineering Mechanics, 2017, 34(4): 78-87.(in Chinese)
[33]Kiani J, Pezeshk S.Sensitivity analysis of the seismic demands of RC moment resisting frames to different aspects of ground motions [J].Earthquake Engineering &Structural Dynamics, 2017, 46(15): 2739-2755.
[34]孙小云, 韩建平, 党育, 等.地震动持时对考虑梁柱节点区不同破坏模式RC框架的地震易损性影响[J].工程力学, 2018, 35(5): 193-203.Sun Xiaoyun, Han Jianping, Dang Yu, et al.Effect of ground motion duration on seismic fragility of RC frames with different beam-column joint failure modes[J].Engineering Mechanics, 2018, 35(5): 193-203.(in Chinese)
[35]张锐, 成虎, 吴浩, 等.时程分析考虑高阶振型影响的多频段地震波选择方法研究[J].工程力学, 2018,35(6): 162-172.Zhang Rui, Cheng Hu, Wu Hao, et al.Multi-band matching method for selection of group motions in time-history analysis considering higher modes effects[J].Engineering Mechanics, 2018, 35(6): 162-172.(in Chinese)
[36]Molazadeh M, Saffari H.The effects of ground motion duration and pinching-degrading behavior on seismic response of SDOF systems [J].Soil Dynamics and Earthquake Engineering, 2018, 114: 333-347.
[37]Safak E.Discrete-time analysis of seismic site amplification [J].Journal of Engineering Mechanics,1995, 121(7): 801-809.
[38]廖振鹏.地震小区划-理论与实践[M].北京: 地震出版社, 1989: 134-140.Liao Zhenpeng.Seismic microzonation: theory and practice [M].Beijing: Seismological Press, 1989: 134-140.(in Chinese)
[39]Meng J.Earthquake ground motion simulation with frequency-dependent soil properties [J].Soil Dynamics and Earthquake Engineering, 2007, 27(3): 234-241.
[40]Pacific Earthquake Engineering Research Center.PEER Ground Motion Database [DB].http://ngawest2.berkeley.edu/.2017-06-28.