非饱和土体由固、液、气三相组成，是一种非常复杂的多孔介质材料。在人类活动(如输油管道、地源热泵、核废料处置等)的影响下，势必会引起土体内部的热量传输和水分迁移。然而土体的热量传输和水分迁移间存在着相互耦合作用关系，热量传输产生的温度梯度驱使土体中的水分迁移，从而改变其含水率。而含水率的变化又会影响土体的物理特性(热扩散系数、密度、饱和度等)，从而导致土体中热量传输及温度分布发生变化。与此同时，热量传输与水分迁移过程又会在土体中产生附加应力并发生变形，从而影响到地基的承载力和稳定性，引起一系列的工程病害或安全隐患[1-2]。因此，研究非饱和土体中的水热耦合关系，具有非常重要的现实意义和工程应用价值。
国内外学者从不同角度采用解析方法、试验研究、数值模拟等主要研究手段，对非饱和土体的水热耦合作用机制，开展了大量的研究工作，并取得了较好的进展。其中数值模拟技术主要通过设定边界条件，采用数值方法求解描述复杂物理现象的水热耦合控制方程，能够较好的解决实际问题，并在工程界得到了极大的重视。白冰等[1]对半无限体自由作用平面热源条件下，非饱和介质内温度场及体积含水率的分布特征进行了数值积分求解。陈佩佩等[2]基于光滑粒子法，对非饱和土中热量传输及水分迁移的规律进行了数值计算。Selvadruai[3]采用有限单元法求解了粘土障中的水热耦合控制方程。郭庆荣等[4]依据土壤非恒温及水热耦合运移的特征，建立了水热耦合运移的数学模型，并模拟了农田土壤湿度及温度的时空变化特征。毛卫南等[5]考虑土体冻结过程的冰水相变，建立了一维水热耦合数学模型，并分别采用有限差分和有限元法对该模型进行了离散化处理。Liu等[6]采用有限差分法数值求解了含有干燥表面层土体中的水热耦合问题，并分析了自然条件下温度场与水分场的瞬态分布。Gan[7]基于土体中的水热耦合作用机制，模拟了地热交换器作用下，不同埋深及地质条件对地层热量传输的影响。然而，针对于非饱和土体的水热耦合模型研究，常规的宏观数值模拟方法(有限差分法、有限单元法、有限体积法等)往往基于宏观连续方程的离散化处理，通常只能考虑热量传输对水分迁移的影响，而难以同时模拟水分迁移作用导致土体热物理参数的瞬态变化。
近30年发展起来的格子Boltzmann方法(LBM)，是一种介于宏观和微观之间的介观数值模拟方法，它不考虑物体内部单个分子之间相互作用，而是把所有分子的运动看成一个整体，在反映物质宏观形态的同时，也能展现出其对应的微观运动规律。与传统的数值方法相比，该方法具有微观背景且物理概念清晰、易于处理复杂边界、算法简单易于实现等优点，在多相流、多场耦合问题、多孔介质内的流动与传热等传统数值方法受限的研究领域，具有独特的优势。基于此，陈黎[8]基于LBM研究了微细多孔介质内的气液两相流动过程。Lin等[9]发展了LBM的流动与传热模型，并模拟了相变材料自然对流和熔融的相互作用问题。Gao等[10]将体积热容和一个新参数引入到LBM的温度平衡态分布函数中，提出了一种模拟多孔介质中耦合传热的数值模型。田智威等[11]基于LBM将多孔介质模型与反应迁移模型耦合，研究了含喉部裂隙介质中CO2的反应迁移规律。刘克同等[12]基于LBM进行了桥梁主梁断面气动导数的大涡模拟仿真。然而，对于不同研究领域的多场耦合问题，各场自身的演化机制及相互之间的耦合作用存在较大差异。为了研究非饱和土体的水热耦合过程，基于格子Boltzmann方法中的D2Q5模型，采用双分布函数分别模拟温度场及水分场，建立了相应的数值模型，并结合半无限空间的水热耦合问题，验证了该模型的有效性。最后考虑耦合作用模式、热源温度及土体孔隙率等因素的影响，讨论了非饱和土体温度场及水分场的演化规律及其耦合作用机制。
1 水热耦合数学模型
1.1 基本假定
为简化计算，针对热源作用下非饱和土体的水热耦合过程，作以下基本假定：
1)忽略非饱和土体各组分结构性的影响，将其视作为连续、均质、各向同性的理想状态多孔介质；
2)土体中水分迁移以液态形式进行，且不考虑水分的相变及重力项的影响；
3)忽略水热耦合过程对非饱和土体孔隙结构的影响以及由此引起的体积变形；
4)不考虑土体孔隙中水分迁移的实际过程，将体积含水率作为评价水分迁移的指标。
1.2 数学方程
在热源影响下，非饱和土体的二维水热耦合控制方程可表述为：温度场：
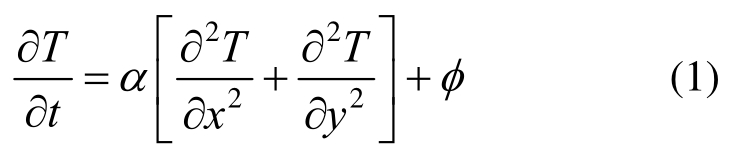
水分场：
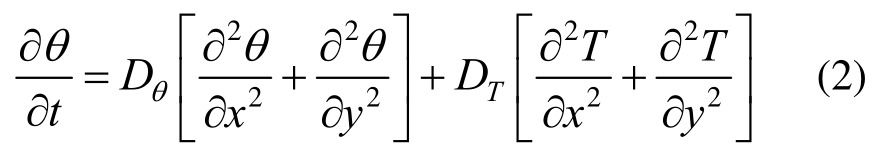
式中：T为土体的温度；t为时间；θ为非饱和土体的体积含水率；Dθ为水分扩散系数；DT为温度诱致水分扩散系数；α为土体的等效热扩散系数，α=k/(ρC)，ρ为等效密度，C为等效比热容，k为等效热传导系数；φ为热源强度，φ=q/ρC，q为热源。
考虑非饱和土体中土颗粒、水分、空气各相体积分数的影响，等效热物理参数可表示为[13-14]：
等效体积热容：
等效导热系数：
等效热扩散系数：
式中：n、ε分别为非饱和土体中的孔隙率和体积含水率；下标s、w、g分别表示为固体土颗粒、水分及空气。
对于非饱和土体中水分场与温度场间的耦合作用关系，由式(2)右侧第二项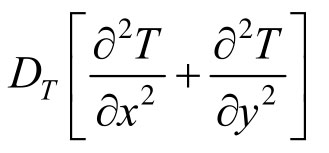
可知，土体中水分场的分布和演化受温度场制约；同时，由于水分迁移导致土体中局部体积含水率发生改变，致使土体的等效热扩散系数(可由式(5)求得)变化，从而影响其温度场的发展演化。
2 格子Boltzmann模型
为了研究热源作用下非饱和土体的水热耦合作用机制，基于格子Boltzmann方法，采用微观变量温度和体积含水率的分布函数分别表征宏观温度和体积含水率，并考虑非饱和土体中两者间的耦合作用，对各自的演化过程进行数值模拟。
2.1 温度场演化的格子Boltzmann方程
DnQb模型(n为维数，b为离散速度个数)是LBM中应用最为广泛的基本模型，本文选择D2Q5模型(如图1所示)对温度场的演化进行数值计算。
图1 D2Q5模型
Fig.1 D2Q5 model
基于D2Q5模型，相应的格子Boltzmann方程可表示为：
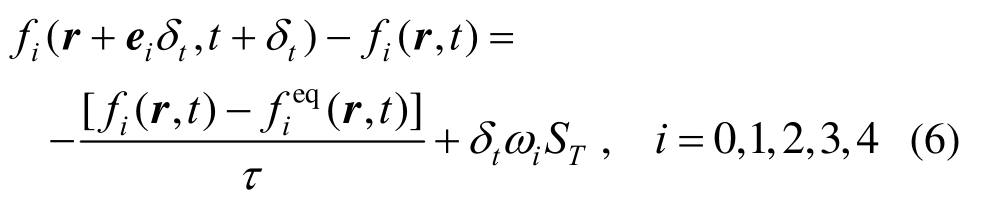
式中：fi(r,t)为t时刻在节点r处沿i方向的温度分布函数；τ为无量纲的弛豫时间，为了保证数值计算的稳定性与准确性，τ的取值宜控制0.5～2.0之间[15]。ei为离散速度，由5个方向上的速度向量构成如下集合：
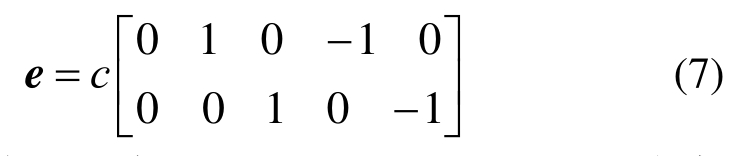
式中，c为格子速度c=δx/δt，δx、δt分别为离散的格子步长和时间步长，为便于计算通常取为δx=δt=1。
(r,t)为平衡态分布函数，可表示为：
ω为权系数，对于D2Q5模型，其值为：
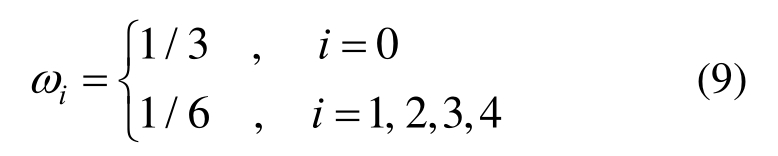
ST为源项，由式(1)可知：
采用Chapman-Enskog多尺度展开方法，可以将格子Boltzmann方程式(6)还原为宏观的热传导方程式(1)。同时，得到宏观温度与温度分布函数间的关系，以及土体等效热扩散系数α与无量纲弛豫时间τ的表达式为：
2.2 水分场演化的格子Boltzmann方程
与温度场演化过程相类似，非饱和土体体积含水率的格子Boltzmann方程可表示为：
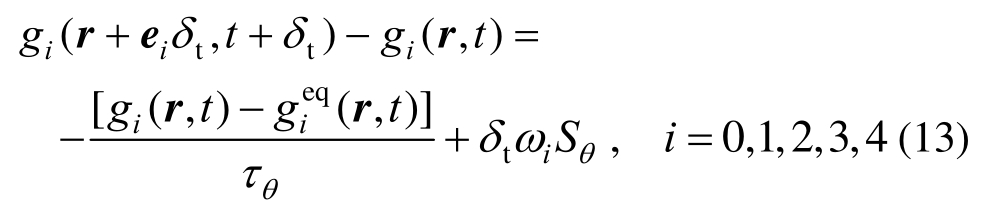
平衡态分布函数
为：
根据式(2)，源项Sθ可表示为：
为简化计算，对源项Sθ采用二阶中心差分近似求解二阶导数，则式(15)可离散为：
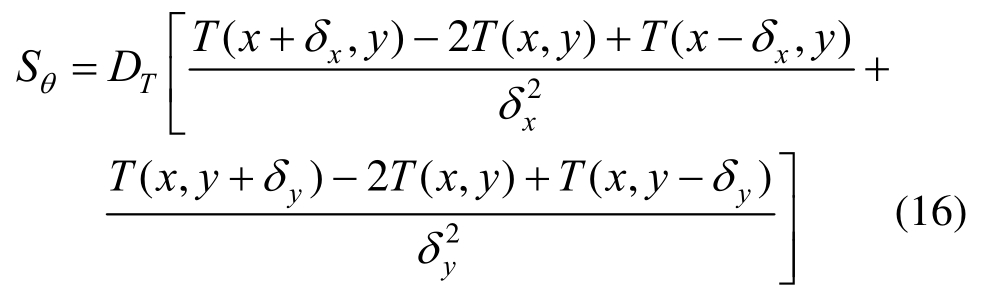
非饱和土体的水分扩散系数Dθ与无量纲弛豫时间τθ的关系为：
土体体积含水率与其分布函数间的关系为：
2.3 边界条件处理
对于恒温边界和绝热边界，采用Guo等[16]提出的非平衡态外推格式进行处理。将边界节点的分布函数分为平衡态(feq )和非平衡态(fneq)两部分，对于平衡态部分，可由式(8)求得，即：
恒温边界：
绝热边界：T(O,t)=T(B,t)，
ωiT(O,t)而非平衡态部分则由与之相邻的节点代替，故边界节点的分布函数可表示为：
式中：fi(O,t)为边界节点的温度分布函数；fi(B,t)为与边界相邻节点的温度分布函数。
对于恒热流密度边界条件，即：
采用有限差分对其进行近似处理，可表示为：
即：
对于D2Q5模型，当左侧为热源边界时，其未知的温度分布函数f1(x,y)可以表示为：
同理，对于体积含水率所对应的边界条件，采用与温度场相似的方法进行处理。
2.4 单位转换
将无量纲参数作为联系格子单位与实际物理单位的桥梁，实现两者之间的单位换算。具体的无量纲参数如下：
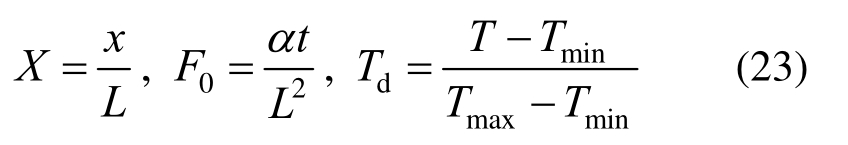
式中：L为特征长度；X为无量纲的长度；F0为无量纲时间；Td为无量纲温度。
对于格子单位与物理单位中时间的对应关系，根据式(23)的无量纲时间F0可表示为：
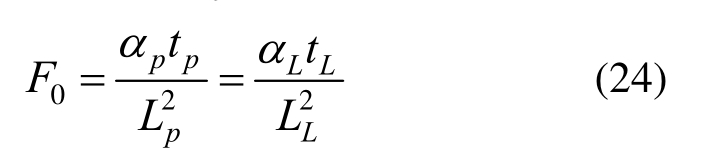
式中，下标p、L分别代表物理单位和格子单位的参数，其中tL=Nδt ，N为计算时步数。
当δt取为1时，物理时间与格子计算时步的对应关系为：
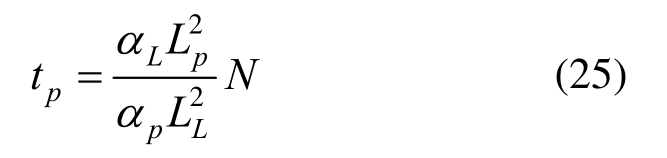
同理，可以求得温度T、长度x、热扩散系数α等物理量，在两个单位系统下的对应关系。
3 算法验证
为验证本数值算法的准确性，编制了相应的计算程序，并求解了恒定热源作用下半无限空间内的水热耦合问题，计算模型如图2所示。土体的初始温度Ti=20℃，在模型左侧x=0处设置恒定热源，其热源强度为φ0=2.7×10-4℃/s。土体的物理参数取值分别为[2]：热扩散系数α=5.0×10-7m2/s，温度诱致水分扩散系数DT=1.0×10-8m2/(s·℃)，初始体积含水率θi=0.267，水分扩散系数Dθ=1.5×10-6m2/s。
图2 半无限空间水热耦合问题示意图
Fig.2 Diagram of moisture-heat coupling problem in the semi-infinite space
为了与文献[2]中的计算结果进行对比，采用单向耦合模式(只考虑温度场对水分迁移的影响)对土体的水热耦合过程进行了数值计算。图3为不同时刻土体中温度场及水分场的本文解与文献[2]中S P H解的对比。由图可知，无论是温度场还是水分场，在不同时刻本文的L B M数值解均与文献[2]中的S P H解吻合较好，这充分证明了本计算模型在处理水热耦合问题方面的有效性。
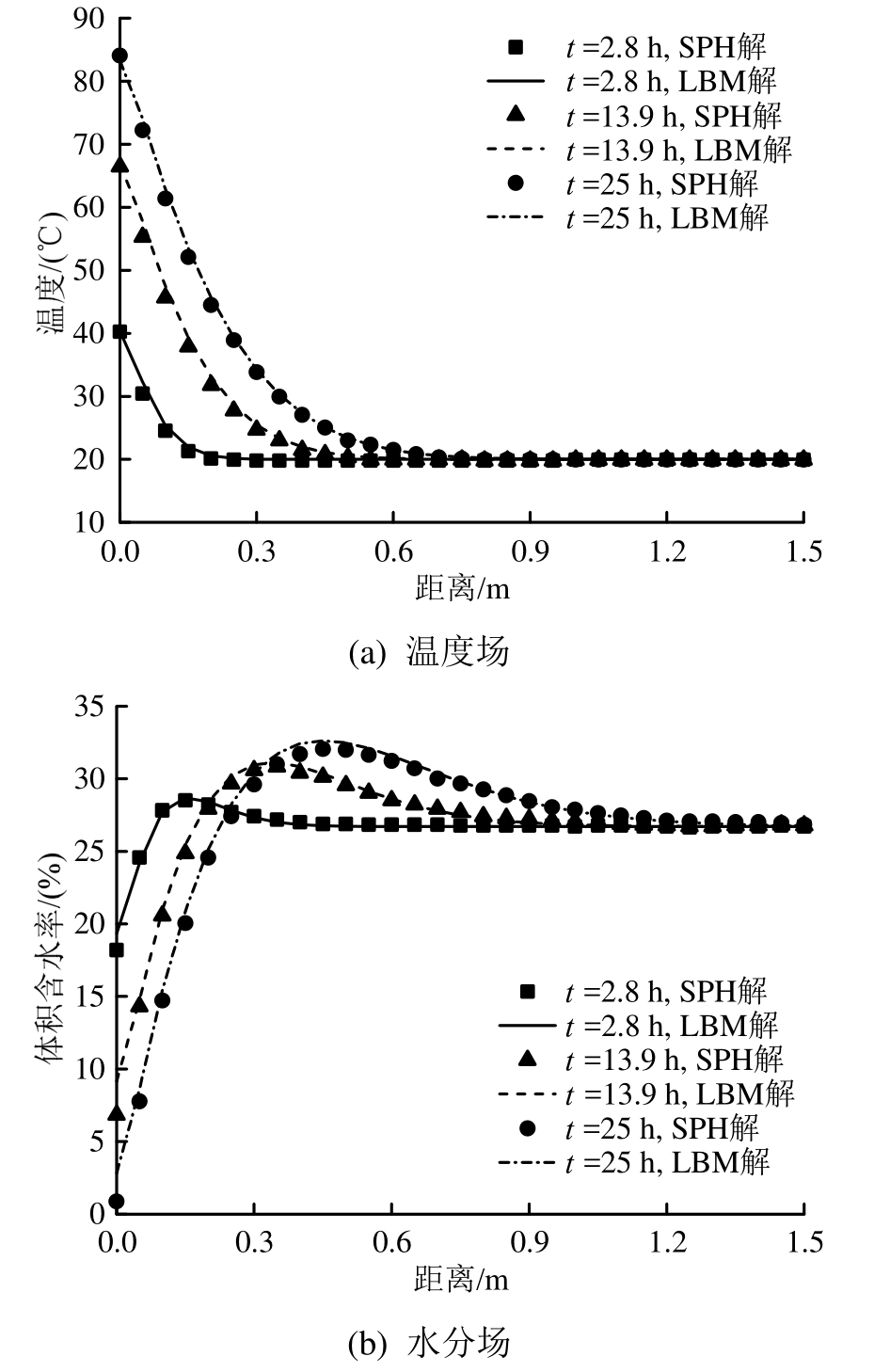
图3 不同时刻本文解与SPH解的对比
Fig.3 Comparison between the solution in this paper and SPH solution at different times
4 分析讨论
为研究水热耦合作用模式、恒温热源及土体孔隙率等因素对非饱和土体水热耦合作用机制的影响，采用本文提出的水热耦合模型对各影响因素进行分析讨论。假定非饱和土体为亚粘土层[17]，初始孔隙率n=0.45，初始温度为20 ℃，初始体积含水率ε=30%，水分扩散系数
温度诱致水分扩散系数
土体的热物理参数见表1。计算模型如图2所示，为便于分析，在模型左侧设置恒温热源，T0=80℃。
表1 非饱和土体各组分的热物理参数
Table 1 The thermal physical parameters of each component of unsaturated soil
土体组分 ρ/(kg/m3)C/(kJ/(kg·℃))kW/(m·℃)亚粘土 2215 0.85 1.62水分 1000 4.18 0.56空气 1.29 1.005 0.026
4.1 不同耦合模式对水热耦合过程的影响
为分析传统单向耦合(仅考虑温度变化对水分迁移的影响)及双向耦合(同时考虑水分迁移对热扩散系数的影响)两种模式下，非饱和土体水分场及温度场的演化规律，对于恒温作用下土体温度场及水分场的分布情况进行了数值计算，计算结果如图4所示。由图4可知，双向耦合模式下非饱和土体的传热速度比单向耦合模式快，且随着时间的推移，两者间的差异愈发显著，在传热30 h后，两者的最大温差达3.6 ℃。与单向耦合相比，双向耦合模式下土体的局部等效热扩散系数受到水分迁移的影响较大，从而影响了土体的导热能力。同时，两种耦合模式下土体中的体积含水率均呈现出先增大后减小的趋势，但随着土体与热源距离的变化，两者在局部有所差异。由式(2)可知，非饱和土中的水分迁移主要由自身水分扩散和温度诱致水分扩散两部分组成。在温度梯度较大的位置(传热初期热源附近)，温度诱致水分扩散占主导；而在温度梯度较小的地方，则以自身的水分扩散为主。此外，在距离热源稍近的位置，双向耦合模式下土体的传热速度较快，水分迁移速率迅速，体积含水率下降也较快；由于受到热源附近水分迁移的影响，在距热源稍远位置处，土体的体积含水率略有增加，且双向耦合模式下增加幅度稍大。
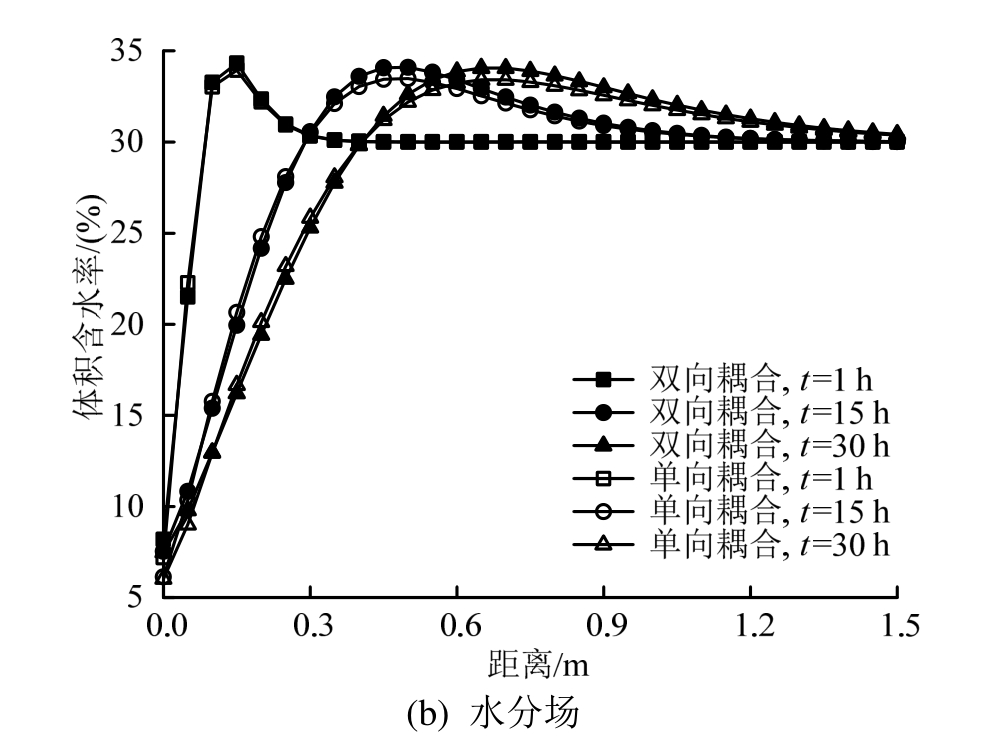
图4 不同耦合模式下温度场与水分场的分布趋势
Fig.4 Distribution of temperature field and moisture field under different coupling modes
4.2 不同恒温热源对水热耦合过程的影响
为研究不同恒温热源对非饱和土体温度场及水分场的影响，在热源温度T0分别为40 ℃、60 ℃、80 ℃情况下，分别讨论了不同时刻土体中水分场及温度场的变化趋势，如图5所示。从图5可以看出，热源温度越高，其附近土体中的初始温差越大，热量传递速度越快。同时，随着热源温度的增大，水分迁移受温度的影响越大，土体体积含水率的变化也越剧烈。在15 h～30 h时间内，温度升高快的位置，其体积含水率的变化也较快。热源温度为40 ℃、60 ℃、80 ℃时，均在0.3 m的位置处温度升高最快，分别升高11.4 ℃、7.2 ℃、3.4 ℃；相应位置处所对应的体积含水率分别下降5.3%、3.4%、1.6%。
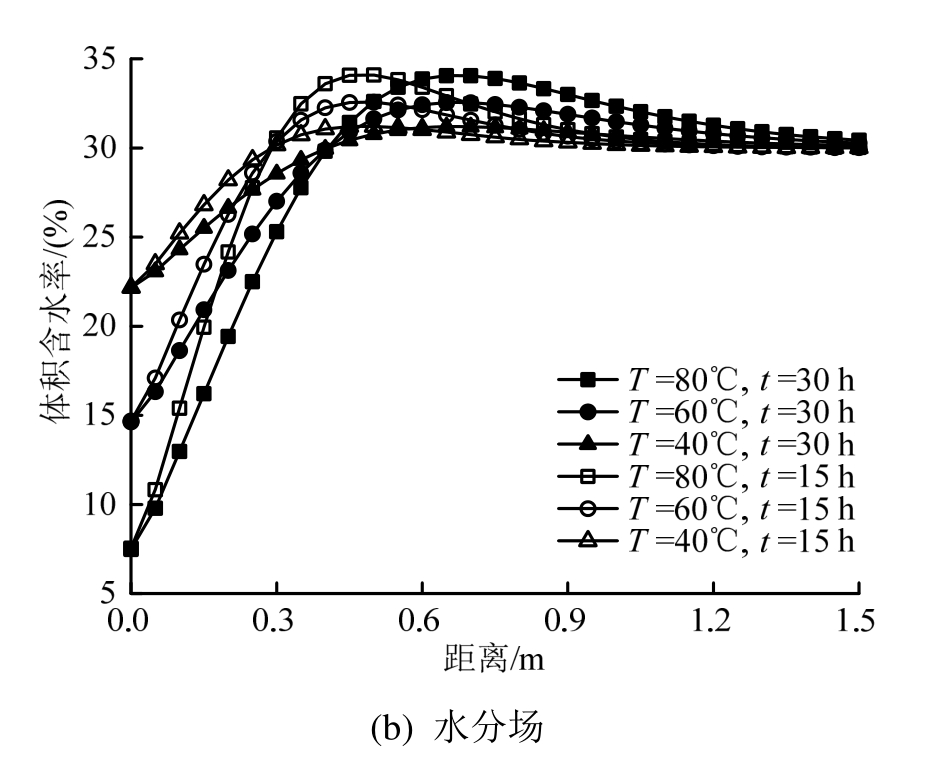
图5 不同恒温热源时温度场与水分场的分布趋势
Fig.5 Distribution of temperature field and moisture field under different heat source temperatures
4.3 不同孔隙率对水热耦合过程的影响
为分析非饱和土体孔隙率对其温度场及水分场演化的影响，在保持初始体积含水率为30%不变的情况下，将孔隙率分别设定为0.35、0.50，并计算了土体温度场及体积含水率的变化规律，如图6所示。由式(5)计算得到孔隙率分别为0.35、0.50，初始体积含水率均为30%时，非饱和土体的初始等效热扩散系数分别为4.93×10-7m2/s、4.48×10-7m2/s。在水热耦合作用下，两者虽发生变化，但温度仍以孔隙率为0.35的土体升高速度稍快。由于等效热扩散系数较为接近，使得温度分布也相差不大。从水分场的发展趋势来看，当初始体积含水率一定时，孔隙率较大的土体，其体积含水率也变化较快。然而，由于两种土体的温度分布相近，从而导致其体积含水率也相差不大。
图6 不同孔隙率时温度场与水分场的分布趋势
Fig.6 Distribution of temperature field and moisture field under different porosity
5 结论
(1)基于格子Boltzmann方法，采用双分布函数分别模拟温度场与水分场的演化过程，提出了非饱和土体的水热耦合模型。采用该模型对半无限空间的水热耦合问题进行了数值求解，并将计算结果与文献中的SPH解进行了分析对比，验证了本计算模型的可靠性。
(2)对于水热耦合模型，由于传统的单向耦合模式未考虑水分迁移对非饱和土体的热扩散系数的影响，无法确定其热物理特性的瞬态变化，导致温度场的整体分布有所偏差，本文提出的双向耦合模式更具合理性。
(3)在恒温热源作用下，不同热源温度对土体温度场及水分场的演化均会产生较大影响，热源温度越高，其附近土体中的初始温差越大，热量传递速度越快。同时，在非饱和土体温度升高较快的位置，体积含水率也相应的变化较快。
(4)在相同热源作用下，当初始体积含水率一定时，对于孔隙率分别为0.35和0.5的两种非饱和土，孔隙率较小的土体，温度升高速度较快，但总体差别不大，从而使得两者体积含水率分布也较为接近。
[1]白冰, 刘大鹏.非饱和介质中热能传输及水分迁移的数值积分解[J].岩土力学, 2006, 27(12): 2085-2089.Bai Bing, Liu Dapeng.Numerical integral solutions of heat transfer and moisture transport in unsaturated porous media [J].Rock and Soil Mechanics, 2006, 27(12):2085-2089.(in Chinese)
[2]陈佩佩, 白冰.非饱和土中温度引起水分迁移的光滑粒子法数值模拟[J].工程力学, 2016, 33(4): 150-156.Chen Peipei, Bai Bing.SPH numerical simulation of moisture migration caused by temperature in unsaturated soils [J].Engineering Mechanics, 2016, 33(4): 150-156.(in Chinese)
[3]Selvadurai A P S.Heat-induced moisture movement in a clay barrier Ⅱ.Computational modelling and comparison with experimental results [J].Engineering Geology, 1996, 41(1): 219-238.
[4]郭庆荣, 李玉山.非恒温条件下土壤中水热耦合运移过程的数学模拟[J].中国农业大学学报, 1997, 2(增刊1):33-38.Guo Qingrong, Li Yushan.Mathematical simulation of heat ans water coupling flow in soil under unsteady temperature [J].Journal of China Agricultural University,1997, 2(Suppl 1): 33-38.(in Chinese)
[5]毛卫南, 刘建坤.不同离散化方法在正冻土水热耦合模型中的应用[J].工程力学, 2013, 30(10): 128-132.Mao Weinan, Liu Jiankun.Different discretization method using coupled water and heat transport mode for soil under freezing conditions [J].Engineering Mechanics, 2013, 30(10): 128-132.(in Chinese)
[6]Liu B C, Liu W, Peng S W.Study of heat and moisture transfer in soil with a dry surface layer [J].International Journal of Heat and Mass Transfer, 2005, 48(21): 4579-4589.
[7]Gan Guohui.Dynamic thermal performance of horizontal ground source heat pumps-The impact of coupled heat and moisture transfer [J].Energy, 2018, 152: 877-887.
[8]陈黎.能源与环境学科中的多尺度多物理化学耦合反应输运过程数值模拟研究[D].西安: 西安交通大学,2013.Chen Li.Numerical investigation of multiscale multiple physicochemical coupled reactive transport processed in energy and environmental discipline [D].Xi’an: Xi’an Jiaotong University, 2013.(in Chinese)
[9]Lin Qi, Wang shugang, Ma zhenjun, et al.Lattice Boltzmann simulation of flow and heat transfer evolution inside encapsulated phase change materials due to natural convection melting [J].Chemical Engineering Science,2018, 189: 154-164.
[10]Gao Dongyan, Chen Zhenqian, Chen Linghai, et al.A modified lattice Boltzmann model for conjugate heat transfer in porous media [J].International Journal of Heat and Mass Transfer, 2017, 105: 673-683.
[11]田智威, 谭云亮.含喉部裂隙介质CO2反应迁移的格子Boltzmann模拟研究[J].岩土力学, 2017, 38(3):663-671.Tian Zhiwei, Tan Yunliang.Lattice Boltzmann simulation of CO2 reactive transport in throat fractured media [J].Rock of Soil Mechanics, 2017, 38(3): 663-671.(in Chinese)
[12]刘克同, 汤爱平, 曹鹏.桥梁气动导数的格子Boltzmann大涡模拟仿真[J].工程力学, 2015, 32(5):111-119.Liu Ketong, Tang Aiping, Cao Peng.Large eddy simulation of the aerodynamic derivatives of bridge using lattice Boltzmann method [J].Engineering Mechanics, 2015, 32(5): 111-119.(in Chinese)
[13]刘建刚, 刘泉, 周冬冬, 等.地下水横向水平流速对人工水平冻结壁形成的影响[J].应用基础与工程科学学报, 2017, 25(2): 258-265.Liu Jiangang, Liu Quan, Zhou Dongdong, et al.Influence of groundwater transverse horizontal flow velocity on the formation of artificial horizontal freezing wall [J].Journal of Basic Science and Engineering, 2017, 25(2):258-265.(in Chinese)
[14]夏锦红, 陈之祥, 夏元友, 等.不同负温度条件下冻土导热系数的理论模型和试验验证[J].工程力学, 2018,35(5): 109-117.Xia Jinhong, Chen Zhixiang, Xia Yuanyou, et al.Theoretical model and experimental verification on thermal conductivity of frozen soil under different negative temperature conditions [J].Engineering Mechanics, 2018, 35(5): 109-117.(in Chinese)
[15]Wang Moran, Wang Jinku, Pan Ning, et al.Mesoscopic predictions of the effective thermal conductivity for microscale random porous media [J].Physical Review E,2007, 75(3): 036702-1-036702-10.
[16]Guo Zhaoli, Zheng Chuguang, Shi Baochang.Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method [J].Chinese Physics, 2002, 11(4): 366-374.
[17]Song Wenyu, Zhang Yaning, Li Bingxi, et al.A lattice Boltzmann model for heat and mass transfer phenomena with phase transformations in unsaturated soil during freezing process [J].International Journal of Heat and Mass Transfer, 2016, 94: 29-38.