火/核电厂大型冷却塔普遍采用钢筋混凝土双曲线型旋转壳冷却塔结构。自然通风冷却塔堪称世界上最大的钢筋混凝土壳体结构，对风荷载的作用尤为敏感。1965年英国渡桥电厂的冷却塔风毁事故引发了各国学者对冷却塔风致稳定性能的研究热潮。表1列举了双曲壳体稳定性的代表性研究进展。
表1 双曲旋转壳体稳定性研究回顾
Table 1 Review on the stability of hyperbolic shells
文献 时间 研究方法 研究内容Krivoshapko[1] 1966 模型试验 考虑重力作用下的双曲壳体稳定极限荷载Der等[2] 1968 模型试验 考虑环向风荷载作用下双曲壳体整体稳定性Mungan[3] 1976 模型试验有限单元法 采用静水压力模拟风压分布，结合有限单元法分析双曲壳体的局部稳定性Krätzig等[4] 1983 理论方法有限单元法 双曲壳体初始几何缺陷对稳定性能的影响Agapov[5] 2000 有限单元法 考虑大变形以及材料非线性时双曲壳体、环基、土体联合作用下的稳定性Sabouri-Ghomi等[6] 2006 有限单元法 加劲环的数量、位置和尺寸等参数的优化对双曲壳体稳定性能的影响张军锋[7] 2015 有限单元法 采用线性分支点屈曲算法对Mungan试验结果进行比较分析
在众多学者的研究当中，Der(1968)及Mungan(1976)两位学者分别提出的双曲旋转壳体整体稳定公式与局部稳定验算公式被中、德、英多国水工行业规范[8-12]采纳并沿用至今。1973年以前国内外对大型冷却塔结构的理论分析大部分是基于旋转壳体的无矩理论，鉴于这种方法忽略壳体平衡方程中弯矩与横向剪力效应，不能准确反映壳体实际受力状态，亦被归结为渡桥电厂风毁事故的原因之一。由于计算荷载模式的简化，早期的有限单元法与模型试验结果的差异也相对较大[13]：对于环氧树脂材料模型而言，有限元计算结果比实验高出50%～80%；对于铜质模型而言，有限元计算结果则高于实验结果100%～120%。早期对于冷却塔局部稳定性的设计方法多以物理模型实验为主要依据，辅以理论计算。比较典型的就是国内外水工行业规范[8-12]通用的局部稳定验算公式。局部稳定验算公式是冷却塔壁厚与线型设计的控制因素，直接影响着冷却塔工程的安全性与经济性。
随着国家电力建设的飞速发展，冷却塔作为其中的一项重要设施也面临着塔筒几何线型多样化并超出既有公式适用范围的问题[14]。由于局部稳定验算公式形成过程的缺陷，既有局部稳定性公式已不再适用于新型超大双曲壳结构，我国局部稳定安全系数取KB存在偏于保守的嫌疑。相比之下，欧美规范已放弃采用局部稳定性验算作为冷却塔抗风设计的强制性条款，即便是在同等条件下局部稳定安全系数取3.0左右亦可展开工程设计。亟需重新认识我国在建超规范冷却塔局部稳定性验算公式。目前，有限单元法对壳体稳定性的分析计算能力已有了长足的发展，线弹性范围内壳单元的模拟精度基本满足工程需求。为了评价水工规范局部稳定公式对超规范限定的双曲壳体冷却塔的适用性和合理性，有必要对规范中的局部稳定公式的形成过程进行有限元再分析，着重针对仅考虑早期均布压力加载试验条件环向临界压应力 σ110的分析形成过程中模型试验荷载模式的局限性展开讨论。提出了环向荷载以风压形式单独作用下的环向应力临界荷载计算公式，并拟合得到修正后的局部稳定验算公式用于工程实践。图1示意了主要研究思路和流程。
1 规范局部稳定公式来源
1976年Mungan通过线性分支点屈曲理论结合静水压力模型试验修正的方法首次得到了局部稳定验算方法[3](亦称为BSS方法：Buckling Stress State)。1979年的德国冷却塔建规范[12](VGB-610 Ue 2010)便将BSS法收录其中作为大型双曲线型冷却塔建设的稳定性验算准则。英国冷却塔建设规范[9](BS4485)以及中国冷却塔建设规范[8](GB/T 50102―2003)均借鉴了德国规范所采用的BSS公式，并一直沿用至今。
图1 研究工作流程图
Fig.1 General layouts of the research
1.1 试验过程
试验所采用的模型尺寸如图2所示，高度120 cm、底部直径60 cm、喉部直径40 cm，模型材料为环氧树脂，共制作了壁厚分别为1.3 mm、1.4 mm以及1.5 mm的三种模型。试验研究发现对称结构的双曲旋转壳体模型喉部的应力状态与冷却塔结构的双曲旋转壳模型相比差异较小，为了试验加载方便，采用了如图2所示的对称双曲壳体结构。试验模型被放置在密闭的水压容器中，环向水压与轴向的压力组合可以得到不同的应力状态。密闭容器外接气泵，通过改变水面的气压分布得到不同环向均布静水压力，模型上端千斤顶实现轴向的荷载变化，由此可以实现轴向与环向荷载的任意组合。密闭容器外部的水体分布使得屈曲发生过程减缓，以便在观察到第一个屈曲谐波时能及时卸载，试验能够实现模型的反复利用。通过模型喉部位置的应变片测量数据可以得到屈曲临界荷载作用下不同的环向和子午向应力组合。
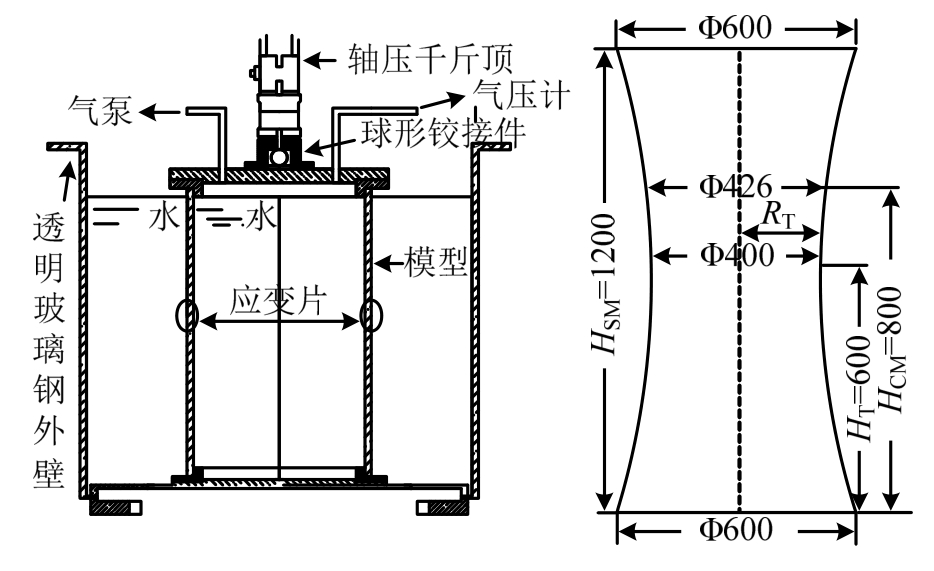
图2 实验装置和模型 /mm
Fig.2 The experimental device and the physical model
1.2 试验推荐公式
式(1)～式(3)为Mungan提出的局部稳定方法，属基于线性分支点理论经试验结果修正的方法。
环向临界应力：
子午向临界应力：
双向应力拟合公式：
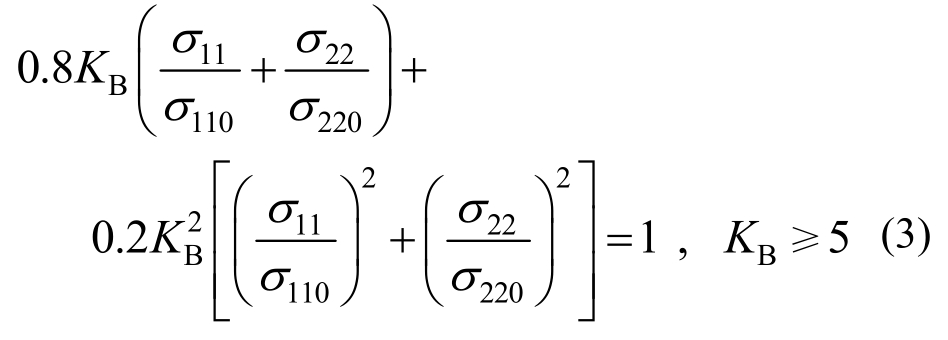
式中：E为弹性模量；v为材料泊松比；t和RT分别为壳体喉部壁厚与半径；FG是考虑双曲线型和边界条件的计算因子；φ是考虑试验结果与线性分支点理论结果误差的修正因子；σ110、σ220是塔筒各点环向和子午向临界压应力；σ11、σ22是塔筒各点环向和子午向应力，以压应力为正，拉应力为负；KB是局部稳定计算所需的安全因子。
前国际空间结构和薄壳学会(IASS)主席Medwadowski在对壳体稳定问题的系统阐述中介绍了Mungan的BSS方法，认为BSS方法不仅可以用于冷却塔壳体结构，还可以用于普通的混凝土壳体屋面结构的稳定性评价[15]。
通过对BSS公式的形成过程的研究可以发现，公式只关注模型喉部位置的应力状态，当应用到实际冷却塔稳定性验算中会出现如表2列举的与试验条件不相符的地方。本研究主要针对其中的冷却塔风荷载模式模拟以及试验与实际边界条件的差异展开。
表2 局部稳定验算公式修正因素
Table 2 Correction factors of local stability check formula
因素 备注风荷载模式的模拟不足试验模型采用环向均布静水压力来模拟实际环向荷载，对于实际环向非均匀分布风荷载的作用不能准确反映理论与试验结果差异公式针对不同的子午线型采取了相同的φ作为修正系数，忽略数值解与实验解值之间误差受子午线型的影响边界条件的差异公式中对边界条件的修正只是模拟了试验条件的特定边界条件，试验边界条件与冷却塔边界条件有较大差异模型试验荷载模式与实际差异公式试验模型处于二维双向受力状态，与实际冷却塔结构在自重和风荷载作用下处于三维受力状态不一致旋转壳线型和壁厚与实际差异工程应用过程中壳体多采用分段线性线型，且壁厚并非与试验一致，采用渐变壁厚
2 结构有限元分析
2.1 线性特征值屈曲
BSS公式只适用于弹性范围，对于完善结构第一类稳定问题中分支点屈曲问题的结构有限元分析通常采用特征值屈曲分析法。特征值屈曲分析可以归结为一个有关于整体刚度矩阵以及与几何刚度矩阵的特征值求解问题：
式中：Ke为整体弹性刚度矩阵；Kg(P0)为考虑荷载P0影响的几何刚度矩阵；Ve为屈曲模态；λc为屈曲荷载放大因子。
特征值屈曲的表达式(4)表明屈曲模态Ve为整体刚度矩阵与几何刚度矩阵比值的分布状态，屈曲模态最大的区域也是结构稳定性能最为薄弱的区域。
2.2 试验边界条件模拟
对比发现：Mungan在设计模型试验时只关注塔筒最危险区域的应力状态，即认为喉部位置为屈曲分析的控制位置，而线性分支点理论则是通过整体弹性刚度与几何刚度之间的比值关系来判定。在壳体有限元建模时需要使壳体在环向均布压力下的屈曲模态最大区域与试验条件下关注的位置相吻合，并且BSS法应用于冷却塔壳体稳定性验算时需要考虑到底支柱的影响(如图3)。
线性分支点屈曲理论分析结果对边界条件的选择比较敏感，通过改变壳体上端和下端边界的约束条件特征值屈曲模态会发生变化。为了再现Mungan当时的实验状态，选择的壳体边界条件为约束试验模型顶端转动自由度ROTX、ROTY、ROTZ以及模型底部完全固结。如图3(a)所示，此时壳体屈曲模态与试验条件类似，最大模态位移出现在壳体喉部位置附近。
图3 有限元模型
Fig.3 Finite element models
2.3 有限元模型验证
为了定量地评价所建立的有限元模型与Mungan试验模型的相似性，可以利用特征值屈曲法对Mungan施加环向均压时的边界条件进行模拟计算，以得出环向均压作用下各线型的环向极限应力。从式(1)可以看出，计算壳体极限应力状态时，双曲壳体线型的变化主要体现在计算因子FG11中[16]。图4给出了Mungan的BSS公式中所推荐的不同双曲线型计算因子FG11以及根据以上建立的有限元模型计算得出的FG11取值之间的对比。
图4 BSS公式环向极限应力修正系数FG11对比
Fig.4 Comparison of circumferential ultimate stress correction factor FG11 of BSS formula
图4中的数据对比表明：在环向均布压力作用下，计算所得的各线型双曲壳体环向极限应力与Mungan的实验值较为接近，环向极限应力随着壳体喉部半径与喉部高度比值的增大而增大，随着壳体喉部半径与底部半径比值的增大而减小，所建立的有限元模型能够较好地模拟Mungan的试验模型。
在Mungan的试验过程中壳体底部进行固结处理，稳定验算公式也是在此基础上得出。但当BSS公式用于冷却塔的稳定性能验算时必须考虑到底支柱边界条件的差异，本研究同时建立了如图5(b)所示带有底支柱的壳体模型。在施加环向风压时有无底支柱对壳体的屈曲模态影响较小如图5(b)、图5(c)所示。
图5 失稳模态
Fig.5 Buckling modes
以上算例双曲壳体与Mungan试验模型保持一致，壁厚2 mm，高820 mm，零米直径600 mm，出口直径426 mm，喉部直径400 mm；均压指模拟实验状态下表面的静水压力；非均布风压代表平均风压分布满足
取值见表3。
表3 平均风压分布系数取值
Table 3 Parameters of average wind pressure distribution
参数取值 分布曲线α0 α1-0.4426 0.2451 α2 α3images/BZ_150_972_2362_1152_2451.png0.6752 0.5356 α4 α5 0.0615 -0.1384 α6 α7 0.0014 0.0650
通过屈曲荷载作用下喉部位置环向临界应力的对比(图6)可以发现有无底支柱对壳体喉部位置环向临界应力的影响可以忽略。综上分析，下文对冷却塔稳定性分析所建立的有限元模型均选择无底支柱上端约束转动的边界条件。
图6 有无底支柱环向极限应力对比
Fig.6 Comparison of circumferential ultimate stress with or without bottom-supported pillars
2.4 环向临界应力修正
针对上文提出的环向荷载的不合理性，计算了各个线型壳体在风压荷载单独作用下的环向临界应力。最终在BSS环向临界应力计算基础上提出了改进的环向临界应力计算公式(5)，均压与风压的修正主要体现在计算因子
上，具体取值见表4。
改进BSS法环向临界应力：
表4给出的环向极限应力修正系数可以看出，各个线型的环向临界应力相比于均压作用在非均布风压作用下均有所提高，且修正前FG11与修正后的
变化趋势较为一致，环向临界应力都随着喉部半径与底部半径的比值的增大而降低。表明当壳体线型从双曲线型向圆柱壳体线型变化时，壳体的不稳定性逐渐增加，这也从侧面反映了大型冷却塔设计时采用双曲线型壳体而不采用圆柱壳体的合理性。
2.5 组合应力状态拟合
Mungan所提出的局部稳定验算公式是一个理论结合试验修正的计算公式，这一点正体现在单轴临界应力计算式(1)、式(2)的修正参数φ11与φ22当中。仅仅通过均压作用与风压作用下的环向极限应力差异来对BSS公式进行修正并不能全面地反映风压作用情况下双曲壳体稳定性能的变化，按照Mungan的应力状态理论，冷却塔结构工程应用应更加关注双向应力状态的关系表达式。为此，Mungan经过大量的双向应力试验，在此基础上拟合得出了双曲壳体双向应力之间的关系式，参见式(3)。
对于环向施加风压的壳体，当发生屈曲时与环向施加均压相比的双向应力状态关系式是不一致的。为了量化这种关系在提出环向临界应力修正后进行了环向与轴向荷载同时作用下的屈曲计算。与试验状态相似，轴向加载通过壳体上端施加竖直向下的荷载来实现。由于不同荷载组合状态下的屈曲模态有所不同，选取屈曲模态最大点的应力状态作为临界屈曲组合应力，归一化的双向应力状态如图7所示。
表4 改进前后BSS公式环向极限应力修正系数对比
Table 4 Comparison of circumferential ultimate stress correction factor of BSS formula before and after correction
?
图7 双向应力状态拟合公式
Fig.7 Bidirectional stress state fitting formula
最后给出完整的考虑风荷载作用的修正BSS法表达式(6)～式(8)，其中子午向临界应力保持不变，
取值见表4其余计算参数定义规则均与BSS法相同。式(8)为双曲壳体环向风荷载与轴向荷载同时作用下的双向应力之间的关系式，公式采用BSS法中以应力组合的一次与二次项的方法拟合保留了表达式的简洁性。
环向临界应力：
子午向临界应力：
双向应力拟合公式：
3 改进BSS法工程运用
为了更加具体地评价经过改进BSS法与原BSS法之间的差异性，最后选取了一座具体的双曲线型冷却塔[17]进行稳定性验算。选择的算例塔高222.00 m，底部直径164.52 m，出口直径129.21 m，喉部直径123.43 m，喉部模板标高166.40 m，喉部壁厚0.37 m；基本风压0.45 kPa，塔筒内风压系数相对于塔顶来流风压取-0.5，地貌类型为B类地貌，风剖面幂指数α=0.15。本算例塔高度已经远超出规范165 m的高度限制属于超大型冷却塔，建立的有限元模型如图8所示。其中，塔筒采用SHELL63空间壳单元模拟，底支柱与环基采用BEAM188空间梁单元模拟，地基等效土弹簧采用COMBIN14单元模拟；与旋转壳体稳定性前期研究不同的是计入渐变壁厚的实际影响，参见图8(c)。
图8 冷却塔有限元建模
Fig.8 Finite element modeling of the cooling tower
图9给出了分别按照BSS法与改进BSS法给出的设计风荷载作用下每层模板高度最小稳定系数KB分布。需要明确的是，由于研究过程只是关注了双向受压荷载作用下的稳定性，故计算过程中压应力取正值且拉应力取零值[7]。总体来看两者的结果变化趋势相近，但BSS法与改进BSS法相比较为保守。以上两者之间的不同点从改进BSS公式与原BSS公式之间的差异亦可看出：相比于环向施加的均布压力，环向施加风压分布压力使得塔筒的环向临界屈曲荷载明显增加；同时从双向应力状态关系的拟合曲线可以看出改进BSS法能比原BSS法包络更多的应力变化范围。以上两点的共同作用导致了冷却塔在符合实际情况的风荷载作用下整体局部稳定性能比较明显地提高，这点从改进BSS法与BSS法推荐拟合公式之间的变化也可以看出，对于一个关于KB的常数项为-1的一元二次方程在增加二次项系数同时减少一次项系数(拟合公式中推荐的一次项系数、二次项系数均为正值)其正根KB必然会有所增加。图9展示的计算结果表明：经改进BSS法计算得出的局部稳定安全因子都符合规范规定的KB≥5的要求。
图9 改进BSS法与BSS法各高度最小稳定安全因子
Fig.9 Minimum stable safety factor of BSS method and modified BSS method at each height
4 结论
分析了目前国内外广泛应用于冷却塔壳体稳定性验算的BSS公式的来源；采用有限元数值计算分析了双曲旋转壳体在单向和双向应力状态下的临界荷载，并给出更加符合实际风荷载作用情况的修正BSS法用于冷却塔风致稳定性验算工作。具体结论如下：
(1)现行规范中推荐的局部稳定验算法存在环向风压模拟不足的缺点，环向施加风压与公式形成的实验在施加的环向均布荷载的屈曲模态存在较大差异；
(2)双曲壳体稳定验算公式BSS法运用到冷却塔塔筒稳定性验算当中时，底支柱的影响可以忽略不计；
(3)对于目前的超规范冷却塔局部稳定性验算推荐使用本文修正后的BSS法，与修正BSS法相比BSS法显得较为保守。
本文研究工作在非均布风压作用下实施，修正前后的BSS公式都是针对无干扰风荷载作用下的双曲壳体稳定问题，而实际情况下大型双曲壳体结构群体干扰效应较为明显，风压分布变化非常复杂，未来研究工作拟针对双曲壳体结构在干扰条件下的非均布、非对称复杂风压条件[18]下的局部稳定问题展开有限元计算并适时开展风洞模型试验研究。
[1]Krivoshapko S N.Static, vibration, and buckling analyses and applications to one-sheet hyperboloidal shells of revolution [J].Applied Mechanics Review,2002, 55(3): 241―270.
[2]Der T J, Filder R.A model study of the buckling behavior of hyperbolic shells [C].London: Proceedings of the 4th Institution of Engineering, 1968, 41(1): 105―118.
[3]Mungan I.Buckling stresses of hyperboloidal shells [J].Journal of Structural Division, 1976, 80(2): 2005―2020.
[4]Krätzig WB, Wittek U, Basar Y.Buckling of general shells-theory and numerical analysis [C].Cambridge:Cambridge University Press, 1983, 377―394.
[5]Agapov V P.Finite element method in statics dynamics and stability of spatial thin-walled stiffened constructions[C].Moscow, ASV izd-vo, 2000: 156―157.
[6]Sabouri-Ghomi S, Kharrazi M H K, Javidan P.Effect of stiffening rings on buckling stability of r.c.hyperbolic cooling towers [J].Thin-Walled Structures, 2006, 44(2):152―158.
[7]张军锋.双曲壳体冷却塔局部稳定检算方法研究[J].建筑结构, 2015, 79(2): 51―56.Zhang Junfeng.Study on local stability method of hyperboloidal shell cooling towers [J].Building Structure, 2015, 79(2): 51―56.(in Chinese)
[8]GB/T 50102―2003, 工业循环水冷却设计规范[S].北京: 中国计划出版社, 2003.GB/T 50102―2003, Code for design of cooling for industrial recalculating water [S].Beijing: Chinese Planning Press, 2003.(in Chinese)
[9]BS 4485, Part 4 code of practice for structural design and construction-water cooling towers [S].London: British Standard Institution, 1996.
[10]IASS, Recommendations for the design of hyperbolic or other similarly shaped cooling towers [S].Belgium,Working Group No.3, 1977.
[11]IASS, Recommendations for the design of hyperbolic or other similarly shaped cooling towers [S].Spain,Working Group No.3, 1979.
[12]VGB-Guideline: Structural design of cooling tower-technical guideline for the structural design,computation and execution of cooling towers(VGB-R 610Ue)[S].Essen: BTR Bautechnik bei Kühltürmen,2005.
[13]Abel J F, Billington D P, Nagy D A, et al.Buckling of cooling towers [J].Journal of Structural Division, 1982,10(ST10): 2162―2174.
[14]Zhang J F, Ke S T, Zhao L, et al.Re-recognition of the BSS approach for hyperboloidal cooling towers [C].In Cooling Towers.6th Int.Symp.on Cooling Towers ISCT2012, Harte, R.and Meiswinkel, R.(eds.).Cologne,2012, 291―298.
[15]张军锋, 葛耀君, 赵林.基于风洞试验的双曲冷却塔静风整体稳定研究[J].工程力学, 2012, 29(5): 68―77.Zhang Junfeng, Ge Yaojun, Zhao Lin.Study on global aerostatic stability of hyperboloidal cooling towers based on the wind tunnel tests [J].Engineering Mechanics,2012, 29(5): 68―77.(in Chinese)
[16]Mungan I.Buckling of reinforced concrete cooling tower shells: BSS approach [J].Structural Journal, 1982, 79(5):387―391.
[17]Zhao L, Ge Y J.Wind loading characteristics of super-large cooling towers [J].Wind and Structures,2010, 13(3): 257―273.
[18]展艳艳, 赵林, 梁誉文, 等.大型冷却塔群塔组合(六塔双列)风致干扰准则综合评价[J].工程力学, 2017,34(11): 66―76.Zhan Yanyan, Zhao Lin, Liang Yuwen, et al.Comprehensive assessment of wind-induced interference criteria about large cooling towers with typical six-towers double-columns arrangements [J].Engineering Mechanics, 2017, 34(11):66―76.(in Chinese)