地震时造成人员伤亡,经济损失的主要原因是建筑物倒塌、破坏,将抗震可靠度理论应用于实际工程中,对结构的地震风险性、地震易损性及地震危险性进行分析,可以得到当地震动的加速度峰值不同时,结构发生各级破坏的概率,既可以有针对性的提高抗震性能又能为地震损失估计提供依据[1-2]。“整体可靠度”理论最早由国外学者Liu和Der Kiureghian[3]提出,分析了平面刚架结构的整体可靠度与灵敏度问题;Au和Bech[4]采用重要抽样法解决了线性结构的首次超越难题。宋鹏彦[5]针对地震作用下单榀框架的抗竖向连续倒塌性能提出了整体可靠度分析方法。隔震结构在近年来的几次地震中均表现出良好的抗震性能,隔震技术的应用越来越广泛,研究者将可靠度思想运用于分析隔震结构的抗震性能,杜东升等[6]建立隔震结构的损伤模型,得到损伤指数的统计参数和概率密度函数,然后根据极值分布理论计算损伤指数超过不同性能水准的可靠度。以上研究说明,从可靠度理论分析基础隔震技术可明显提高结构的抗侧向增量倒塌能力,但未分析地震作用下,隔震结构的竖向连续倒塌性能;地震的三水准设防一直是我国建筑结构抗震设计的基本原则[7],但该规范的倒塌仅对“侧向增量倒塌”的变形量进行控制,没有考虑到结构在受到水平荷载作用竖向构件发生损伤甚至缺失后,结构发生局部竖向连续倒塌的可能,而该方面的研究近期才受到工程人员的关注[8]。
对于基础隔震结构,当下部某个隔震支座失效后,损伤部位周围的隔震支座不能提供足够的抗侧力[9],可能会对结构的抗竖向连续倒塌带来更为不利的影响。因此,研究基础隔震结构的竖向连续倒塌显得尤为必要。
本文首先建立地震作用下隔震支座的损伤模型,利用整体可靠度理论分析隔震结构发生竖向连续倒塌的概率。
1 地震作用下结构最易失效隔震支座的判别
1985年,Park和Ang[10]提出了基于地震弹塑性变形和累积滞回耗能线性组合的构件损伤模型,该模型适用于上部结构构件,但对于隔震支座,该模型无法反映隔震支座的压剪及拉压特性对其损伤的影响,杜东升等[6]结合隔震层的拉压特性、弹塑性变形和累积滞回耗能,提出了隔震层的损伤模型,如式(1)所示。
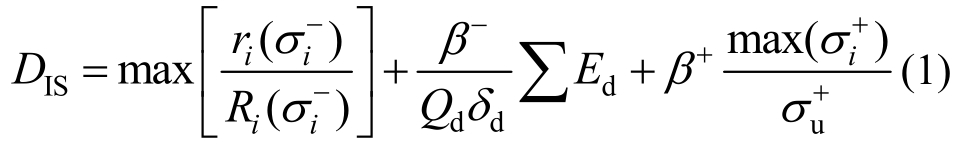
式中,参数的具体含义及计算方法参见文献[6]。
文中将式(1)转换为单个隔震支座的损伤模型,如式(2)所示。利用该公式将地震作用下,损伤指数最大的隔震支座作为最易失效的隔震支座。
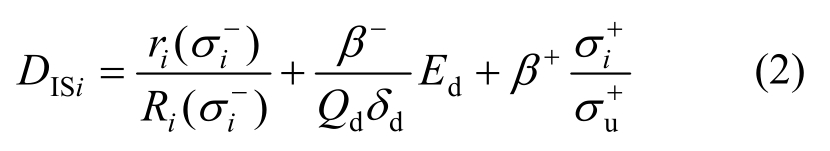
式中:DISi为单个隔震支座的损伤指数;Ed为单个隔震支座的累积滞回耗能。
本文采用式(2)计算隔震支座的损伤指数,将损伤指数最大的隔震支座确定为结构的最易失效隔震支座。
2 损伤整体结构竖向连续倒塌可靠度分析
结构的竖向连续倒塌分析方法可分为静力线性分析、静力非线性分析、动力线性分析、动力非线性分析四种方法[11-12],损伤结构连续倒塌分析是一个复杂的动力效应问题,动力非线性分析能反映结构在构件失效后,剩余结构的真实情况,所以采用非线性动力分析方法来研究结构的倒塌性能是最合适的。因此,文中采用竖向随机动力分析方法分析结构竖向连续倒塌。
2.1 竖向随机动力增量分析方法步骤
1)确定损伤隔震结构的不确定性参数。
2)利用拉丁超立方抽样,对结构的样本点进行抽样。
3)针对其中一组样本点,移除初始失效隔震支座,并对结构进行非线性动力分析。
根据GSA2003[13]规定,在进行结构连续倒塌分析时,可根据以下步骤模拟结构的失效过程。
① 将基本荷载作用于原结构上,利用式(3)计算P0;
② 拆失效隔震支座,将P0反向施加在失效支座处;
③ 对损伤结构进行分析,确定周期;
④ 为了模拟构件瞬间失效的过程,使P0在小于T/10 s内衰减到零,如图1所示。
式中:D为恒载;L为活载。
4)对荷载组合D+0.25L进行调幅。
5)将每次分析的峰值位移和荷载调幅系数记录下来,绘制成竖向IDA曲线。
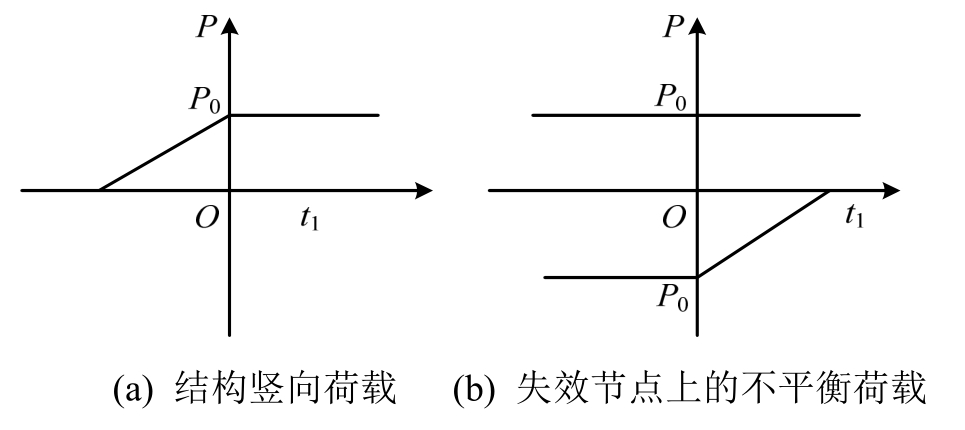
图1 荷载时程曲线
Fig.1 Load time-history curve
根据新版的DoD2010[14]的相关规定,本文认为结构发生损伤后,当剩余结构的变形超过承重构件的变形能力极限时,结构即发生竖向连续倒塌。
2.2 结构整体连续倒塌易损性分析方法
在对结构进行整体连续倒塌易损性分析时,利用竖向随机IDA方法计算损伤结构的荷载系数α的界限值,且将α作为强度参数IM,利用式(4)获得结构的失效概率。
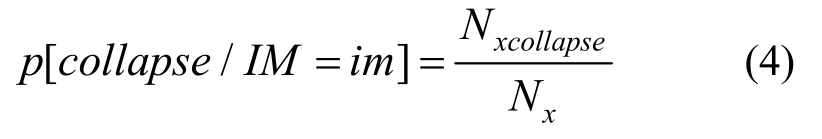
式中:Nxcollapse为结构发生倒塌的数量;Nx为结构样本总数。
2.3 结构整体竖向连续倒塌可靠度分析方法
1)利用2.1节得到的α(D+0.25L),作为该样本的极限承载力,则样本在基本荷载作用下的竖向连续倒塌极限状态方程为:
当某个支座发生损伤后,Z > 0时,由于损伤跨的极限承载力小于作用于损伤跨的竖向荷载,结构可能会发生竖向连续倒塌;Z≤0时,结构不会发生竖向连续倒塌。
2)利用2.1节得到的结构倒塌荷载系数及改进的罗森布鲁斯法[15],计算式(5)所对应的功能函数的前四阶矩统计参数。
利用改进的罗森布鲁斯法计算得到的前四阶原点距,如式(6)~式(9)所示。
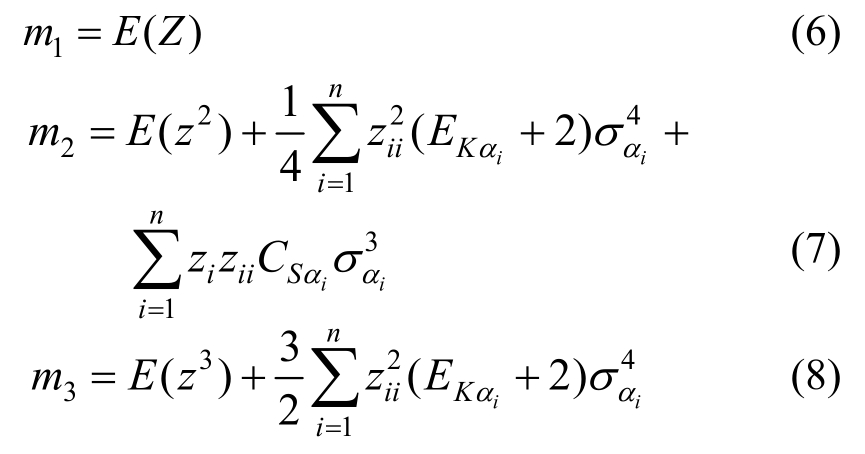
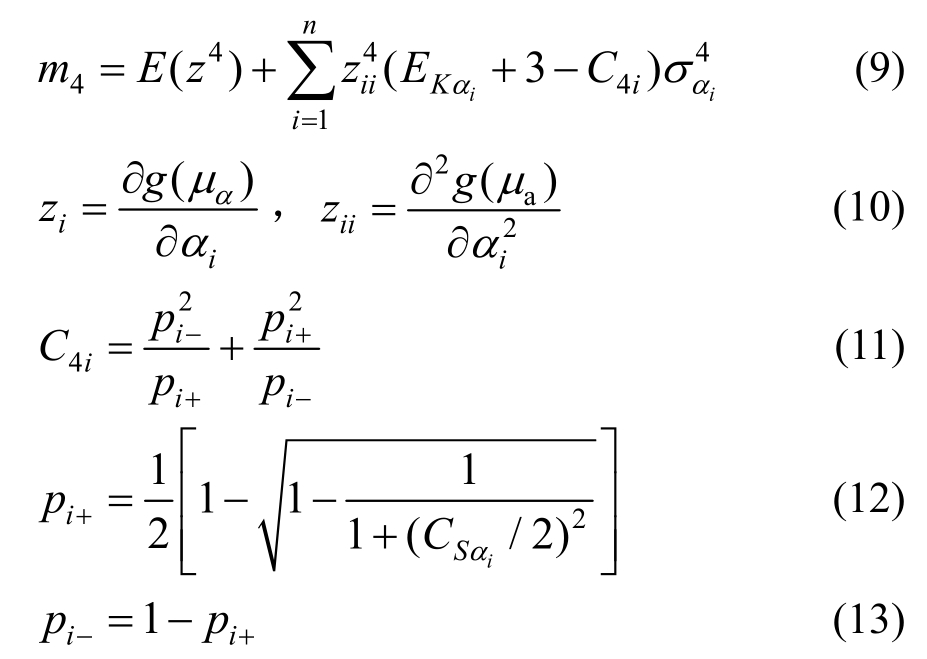
式中:m1、m2、m3和m4为Z的前四阶原点距;EKαi和CSαi为α的峰度系数和偏度系数;μα为α的均值;E(Z)为Z的均值。
根据式(6)~式(9)及中心距与原点距的基本概念,计算结构的前四阶中心距。
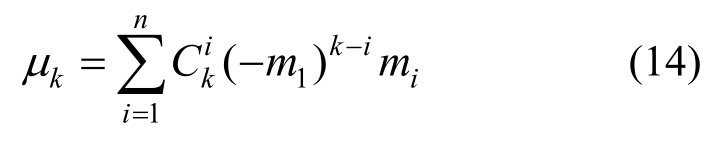
根据Z的前四阶中心距的计算结构,可得到Z的前四阶矩的平均值、变异系数、偏度系数和峰度系数。
3)采用二次四阶矩法计算结构的整体失效概率。以Z的前四阶矩统计参数为约束,由最大熵原理确定Z的最大熵分布,最后通过数值积分求得结构的失效概率[16-17]。
将功能函数Z变换为标准化随机变量R,即式(15)。
R的前四阶矩统计参数为R(0, 1, CrZ, EKZ),其最大熵概率密度函数如式(16)所示。
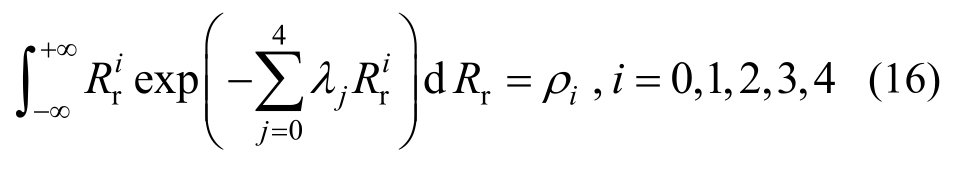
其中:ρ0=1,ρ1=0,ρ3=CSZ,ρ4=KSZ+3;EKZ和CrZ为功能函数Z的峰度系数和偏度系数;在解出λi后,可利用式(17)计算结构的失效概率。
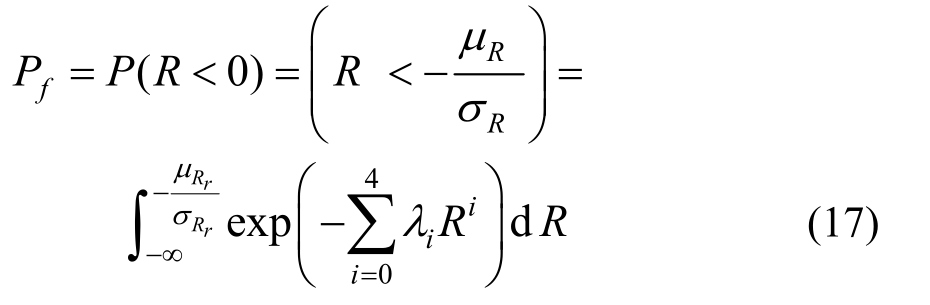
式中:Pf为结构的失效概率;μR为R的均值;σR为R的方差。
4)由于实际工程问题较为复杂,结构的功能函数服从正态分布的可能性较小,但当结构的失效概率较大时,可通过假定结构功能函数服从正态分布简化计算,如式(18)所示。
因此,结合上文提出的改进的罗森布鲁斯法,利用最大熵原理求出结构在竖向荷载作用下的失效概率。
3 算例分析
本文以一钢混框架-剪力墙结构为例,抗震设防类别为乙类,场地类别为二类,分组为三组,烈度为8度,利用文献[18]中的隔震设计方法,对结构进行设计,最终隔震支座布置结果如图2所示。结构的基本信息如表1所示。梁、柱构件的非线性行为采用FAMA Beam和FAMA Column模拟。墙单元的非线性行为采用纤维单元模拟。

图2 结构平面图
Fig.2 Plan layout of structure
表1 结构基本参数
Table 1 Parameters of structures
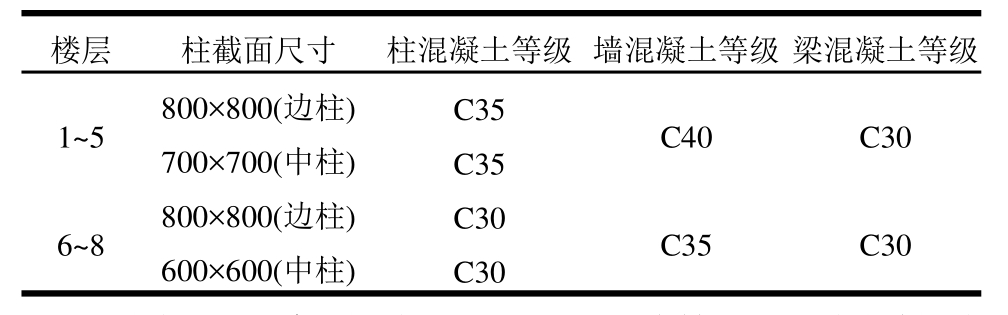
楼层 柱截面尺寸 柱混凝土等级 墙混凝土等级 梁混凝土等级1~5 800×800(边柱)C35 C40 C30 700×700(中柱)C35 6~8 800×800(边柱)C30 C35 C30 600×600(中柱)C30
选择20条地震动记录,对结构进行弹塑性时程分析,并且将20条地震动的峰值加速度调至400 gal,为了反映地震动的离散性,图3给出20条地震记录的弹性加速度反应谱。
3.1 地震作用下结构最易失效隔震支座的判别
根据地震作用下结构最易失效隔震支座的判别方法即式(2),计算罕遇地震作用下所有隔震支座的损伤指数,如表2所示。
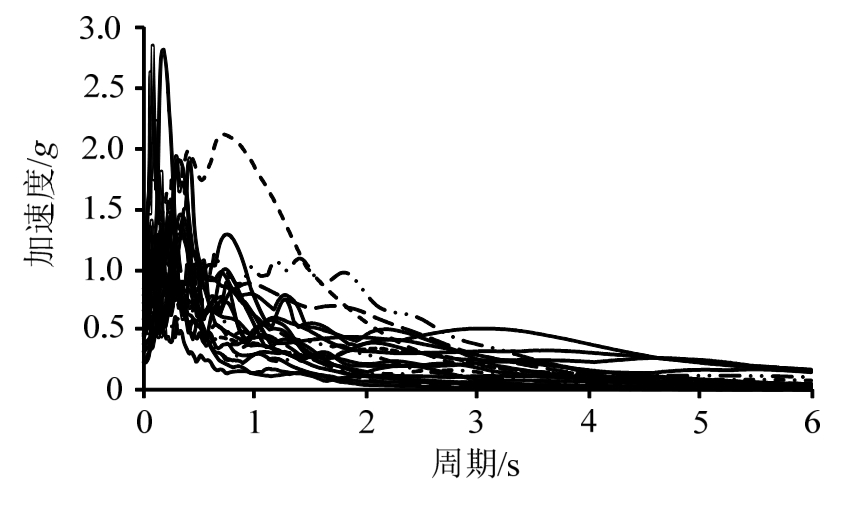
图3 地震波反应谱
Fig.3 Response spectra of ground motion records
表2 隔震支座损伤指数
Table 2 Damage index of base isolators

注:支座编号如图2中B3支座为例进行统一编号。
支座编号 损伤指数 支座编号 损伤指数A1 0.932 C4 0.617 A2 0.747 C5 0.705 A3 0.720 C6 0.813 A4 0.712 C7 0.775 A5 0.777 D1 0.738 A6 0.645 D2 0.631 A7 0.827 D3 0.624 B1 0.792 D4 0.713 B2 0.727 D5 0.705 B3 0.624 D6 0.743 B4 0.617 D7 0.801 B5 0.705 E1 0.739 B6 0.701 E2 0.729 B7 0.698 E3 0.722 C1 0.747 F1 0.715 C2 0.727 F2 0.810 C3 0.623 F3 0.722
表中加粗斜体为剪力墙下隔震支座,从表中可以看出,在地震作用下,剪力墙下隔震支座损伤指数普遍大于框架柱下隔震支座的损伤指数,说明对于基础隔震框剪结构,相较于框架柱,剪力墙下隔震支座更容易发生破坏。
从表2还可以看出,在地震作用下,剪力墙下损伤指数最大的隔震支座,即最容易损伤的隔震支座为A1,从图2可以看出隔震支座A1和B1在同一片剪力墙下,当A1失效时B1会随之失效;框架柱下损伤指数最大的隔震支座是A2,鉴于以上结果,文中之后在讨论剪力墙下隔震支座失效后损伤结构的竖向连续倒塌时,将隔震支座A1、B1作为失效隔震支座。在讨论框架柱下隔震支座失效后结构的竖向连续倒塌时,将隔震支座A2作为失效隔震支座。
3.2 结构样本点的形成
描述结构不确定性的方法有基于数理统计的概率模型,以及近年发展起来的基于凸集理论的非概率凸模型。对于上部结构的基本随机变量可参见文献[19―21]。
概率模型需大量样本的存在、或事件具有可重复性为基本前提来得到完整的概率分布信息。而非概率的凸模型在不确定信息量较少的情况下,尽管不知道参数的概率分布函数,但可以根据已有资料确定参数不确定性的幅度或界限,并将其界限采用区间集、椭球集等凸集进行描述。目前针对隔震支座力学性能随机变量概率分布情况的研究还较少,因此,本文采用凸集模型描述隔震支座的随机性。
表3 支座的基本随机变量
Table 3 Basic random variables of base isolator

支座类型 不确定性变量 均值 偏差/(%)标准化变量凸模型描述LRB 700屈服力/kN 123.1 20 M1 22屈服前刚度/(kN/m)11800 20 M2屈服后刚度/(kN/m)1180 20 M2 LRB 800 M+M≤121 M+M≤屈服前刚度/(kN/m)12760 20 M4屈服力/(kN)160.3 20 M3 22 341屈服后刚度/(kN/m)1276 20 M4屈服力/kN 203.5 20 M5 LRB 900 M+M≤屈服前刚度/(kN/m)13847 20 M6 22 561屈服后刚度/(kN/m)1384 20 M6
3.3 损伤结构的竖向连续倒塌易损性分析
根据3.1节所述,在讨论框架柱下隔震支座失效后结构的竖向连续倒塌时,将隔震支座A2作为失效隔震支座。在讨论剪力墙下隔震支座失效后损伤结构的竖向连续倒塌时,将隔震支座A1、B1作为失效隔震支座。根据2.1节所述的竖向随机动力增量分析方法,绘制竖向IDA曲线如图4所示。
从图4(a)可以看出,随着节点竖向位移的增加,荷载系数逐渐增大,在达到峰值后,荷载系数几乎不再增大,而节点竖向位移迅速增大,此峰值体现了结构的整体抗连续倒塌的能力,文中将此荷载系数峰值作为结构抗连续倒塌的荷载系数极限值,当结构达到梁机制承载力极限后,由于后续悬链线机制的存在,结构会存在荷载系数几乎不再增加,而位移迅速增大的阶段。
从图4(b)可以看出,随着节点竖向位移的增加,荷载系数逐渐增大,不同于4(a)的是随着节点位移的增大,荷载系数的增大速度变慢,但也有一定的增幅,直到结构发生倒塌,这是由于,A1、B1在结构的角部,其仅有梁机制阶段。因此,当结构达到梁机制阶段的最大承载力后,结构发生竖向连续倒塌。

图4 随机IDA曲线
Fig.4 Random IDA Curves
根据2.2节中结构竖向连续倒塌失效概率的计算方法及文中对结构发生竖向连续倒塌的定义,绘制损伤结构发生竖向连续倒塌的易损性曲线,如图5所示。
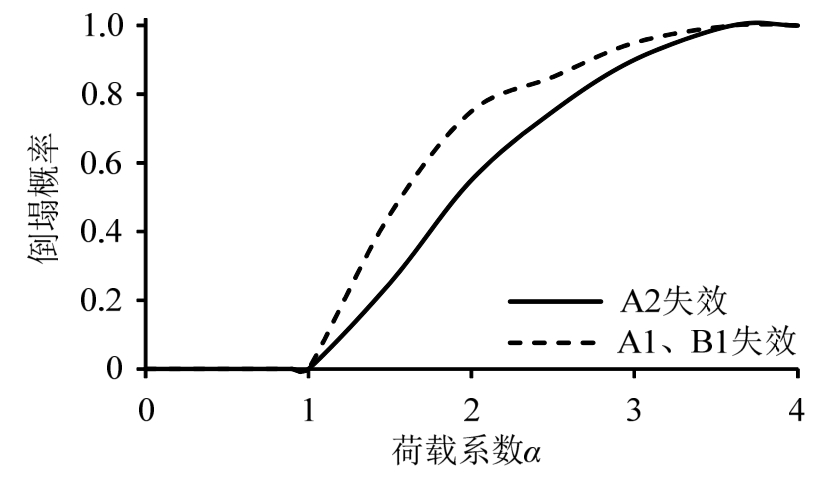
图5 结构竖向连续倒塌易损性曲线
Fig.5 Vulnerability curves of structural vertical progressive collapse
3.4 结构的整体连续倒塌极限状态可靠度分析
根据2.3节结构可靠度分析的二次四阶矩法计算损伤结构功能函数的前四阶矩、失效概率和可靠度指标如表4所示。
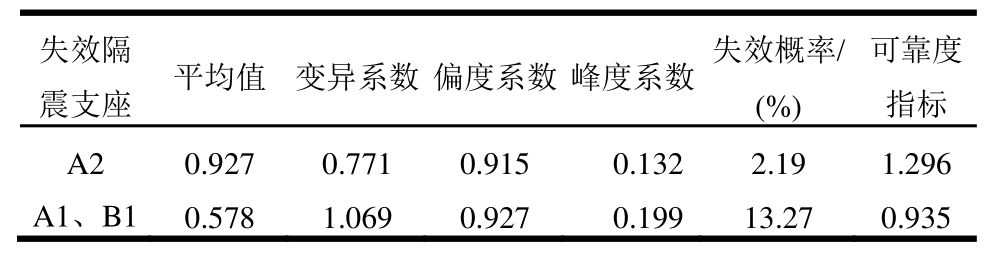
表4 功能函数的统计矩、失效概率及可靠度指标
Table 4 Statistical moments of performance function, failure probability and reliability indices
失效隔震支座 平均值 变异系数 偏度系数 峰度系数 失效概率/(%)可靠度指标A2 0.927 0.771 0.915 0.132 2.19 1.296 A1、B1 0.578 1.069 0.927 0.199 13.27 0.935
从表4可以直观的看出损伤结构发生竖向连续倒塌的失效概率及可靠度指标。如当框架柱下隔震支座A2失效后,损伤结构发生竖向连续倒塌的概率为2.19%,其可靠度指标为1.296。对比两种失效状况的失效概率及可靠度指标可以看出,相比于A2框架柱下隔震支座失效,A1、B1剪力墙下隔震支座失效,损伤结构更容易发生竖向连续倒塌,这与易损性分析得到的结论相同。
4 结论
(1)运用整体可靠度理论对基础隔震框剪结构进行竖向连续倒塌可靠度分析,可直观地得到地震作用下,损伤基础隔震结构发生竖向连续倒塌的概率,为结构的设计及震后加固提供可靠的依据。
(2)由于地震作用下,尤其是强震作用下,剪力墙下隔震支座更容易发生受拉破坏,其损伤指数普遍大于框架柱下隔震支座的损伤指数。因此,在隔震设计时,应对剪力墙下隔震支座进行进一步特殊处理。
(3)从结构发生竖向连续倒塌的失效概率来看,工程人员应在设计中注意且尽量避免地震作用下,结构由于损伤发生竖向连续倒塌的可能性。
[1]Jack W Baker.Efficient analytical fragility function fitting using dynamic structural analysis [J].Earthquake Spectra, 2015, 31(1): 579―599.
[2]尹犟, 易伟建, 胡其高.结构整体抗震性能评估新方法[J].工程力学, 2010, 27(3): 123―131.Yin Jiang, Yi Weijian, Hu Qigao.The new method for estimating seismic performance of structures [J].Engineering Mechanics, 2010, 27(3): 123―131.(in Chinese)
[3]Liu P L, Der Kiureghian A.Finite element reliability of geometrically nonlinear uncertain structures [J].Journal of Engineering Mechanics, 1991, 117(8): 1806―1825.
[4]Au S K, Beck J L.First excursion probabilities for linear systems by very efficient importance sampling [J].Probabilistic Engineering Mechanics, 2001, 16(3): 193―207.
[5]宋鹏彦.结构整体可靠度方法及RC框架非线性整体抗震可靠度分析[D].哈尔滨: 哈尔滨工业大学,2012:74―77.Song Pengyan.Structural globalreliability methods and nonlinear global seismicreliability analysis of RC frames[D].Harbin: HarbinInstitute of Technology, 2012: 74―77.(in Chinese)
[6]杜东升, 王曙光, 刘伟庆, 等.隔震结构损伤性能与可靠度研究[J].振动与冲击, 2016, 35(1): 222―227.Du Dongsheng, Wang Shuguang, Liu Weiqing, et al.Reliability-based damage performance of base-isolated structures [J].Journal of Structural Engineering, 2016,35(1): 222―227.(in Chinese)
[7]GB 50011―2010, 建筑结构抗震设计规范[S].北京:中国建筑工业出版社, 2010.GB50011―2010, Code for seismic design of buildings[S].Beijing: China Architecture Industry Press, 2010.(in Chinese)
[8]陆新征, 李易, 叶列平.混凝土结构防连续倒塌理论与设计方法研究[M].北京: 中国建筑工业出版社,2011: 40―54.Lu Xinzheng, Li Yi, Ye Lieping.Theory and design method for progressive collapseprevention of concrete structures [M].Beijing: China Architecture & Building Press, 2011: 40―54.(in Chinese)
[9]包超.竖向不规则基础隔震结构连续倒塌机制及抗倒塌性能研究[D].兰州: 兰州理工大学, 2015: 26―54.Bao Chao.Research on progressive mechanism and resistance performance of vertically irregular base-isolated structure [D].Lanzhou: Lanzhou University of Technology, 2015: 26―54.(in Chinese)
[10]Park Y J, Ang A H S.Mechanistic seismic damage model for reinforced concrete [J].Journal of Structural Engineering,1985, 111(4): 722―739.
[11]高佳明, 刘伯权, 黄华, 等.带板钢筋混凝土框架连续倒塌理论分析[J].工程力学, 2018, 35(7): 117―126.Gao Jiaming, Liu Boquan, Huang Hua, et al.Theoretical analysis on the progressive collapse of RC frame structures with slabs [J].Engineering Mechanics, 2018,35(7): 117―126.(in Chinese)
[12]Chang Hongche, Yan Feizhu, Yao Yao, et al.An evaluation method to predict progressive collapse resistance of steel frame structures [J].Constructional Steel Research, 2016, 122(1): 238―250.
[13]GSA2003, Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects [S].Washington D.C.: General Service Administration, 2003.
[14]DoD2010, Design of structures to resist progressive collapse [S].Washington, D.C: Department of Defense,2010.
[15]赵国藩.工程结构可靠性理论与应用[M].大连: 大连理工大学出版社, 1996.Zhao Guofan.Reliability theory and its application for engineering structure [M].Dalian: Dalian University of Technology Press, 1996.( in Chinese)
[16]张明.结构可靠度分析-方法与程序[M].北京: 科学出版社, 2009.Zhang Ming.Structural reliability analysis: method and procedure [M].Beijing: Science Press, 2009.(in Chinese)
[17]杨绿峰, 袁彦华, 余波.基于等概率近似变换的向量型层递响应面法分析结构可靠度[J].工程力学, 2014,31(7): 185―191.Yang Lvfeng, Yuan Yanhua, Yu Bo.Vector cooperative response surface method for structural reliability analysis based on approximately equivalent probability transformations [J].Engineering Mechanics, 2014, 31(7):185―191.(in Chinese)
[18]杜永峰, 黄小宁, 李慧.基于性能的基础隔震钢筋混凝土框剪结构的倒塌可靠度分析[J].地震工程学报,2018, 40(5): 879―882, 896.Du Yongfeng, Huang Xiaoning, Li Hui.The performance based collapse reliability analysis of base-isolated framewall structure [J].Journal of Earthquake Engineering,2018, 40(5): 879―882, 896.(in Chinese)
[19]樊剑, 龙晓鸿, 赵军.计算近场地震作用下隔震结构支座破坏易损性曲线的概率凸集混合模型[J].计算力学学报, 2014, 31(4): 199―204.Fan Jian, Long Xiaohong, Zhao Jun.A hybrid probabilistic and convex model for calculating the vulnerability curve of the failure of isolation bearing under near-fault earthquake ground motion [J].Chinese Journal of Computational Mechanics, 2014, 31(4): 199―204.(in Chinese)
[20]易伟建, 水淼.基于节点冲切破坏的板柱结构连续倒塌可靠性分析[J].工程力学, 2015, 32(7): 149―155,175.Yi Weijian, Shui Miao.Reliblty analyasis for progrssive collapse of slab-column structure based on the punching failure of the connection [J].Engineering Mechanics,2015, 32(7): 149―155, 175.(in Chinese)
[21]黄小宁.框—剪隔震结构抗扭设计及双随机地震倒塌可靠度研究[D].兰州: 兰州理工大学, 2017.Huang Xiaoning.Torsional-Resistance Design and Study on Collapse Reliability Based on Double Random of Frame-Shear-Wall Isolated Structure [D].Lanzhou:Lanzhou University of Technology, 2017.( in Chinese)