固结理论包括固结方程、初始条件和边界条件三个方面。自Terzaghi提出固结理论后，土体固结问题的研究主要集中在固结方程和初始条件的优化上，有关边界条件的研究相对较少。Terzaghi边界已广泛用于求解固结问题，其形式简单，但只能表示为完全透水和完全不透水；也有一些关于半透水边界条件的报道，Gray[1]、Schiffman和Stein[2]先后对半透水边界进行了研究，然而其边界条件是孔压的函数，致使求解结果较复杂。基于此，梅国雄等[3]提出了形式简单且能反映排水边界孔压随时间变化的连续排水边界，并获得了该边界条件下瞬时加载的单层土体一维固结问题的解析解；随后，Liu和Lei[4]、何利军等[5]、吴文兵等[6-7]及李勇义等[8]对基于连续排水边界的土体固结问题进行了跟踪研究。但以上基于连续排水边界的固结研究均未考虑土体的流变特性，而土体的流变特性对一些软黏土固结性状的影响不容忽视。
初始条件(加载形式)对土体固结过程有很大影响。Schiffman[9]首先研究了单级加载的一维固结问题。随后众多的学者对矩形荷载[10]、随机荷载[11]、循环荷载[12]、低频荷载[13]下土体的固结进行了研究，极大地丰富了土体固结理论。
土的黏弹性即流变特性是软土的一个重要工程性质，Taylor和Merchant[14]利用Kelvin模型最先研究了软土流变固结问题；Lo[15]基于Merchant模型推导出瞬时荷载下的流变固结解析解；陈宗基[16]采用胡克弹簧与Maxwell体并联的模型研究了流变固结问题；赵维炳[17]基于广义Voigt模型研究了软土流变固结特性，随后众多的学者根据不同的流变模型在考虑半透水边界[18]、变荷载[19-20]、土体非线性[21]及起始水力坡降[22]方面对流变固结进行了深入的研究。以上流变固结的研究往往是考虑加载条件、土体非线性和流变模型对土体流变固结的影响，而对土体排水边界随时间发展过程的研究还不够深入。
本文基于连续排水边界推导出单级加载下单层土体一维流变固结解析解，基于所得解详细讨论了连续排水边界条件界面参数、加载速率及流变参数对土体固结的影响，并与现有其他解答进行对比，验证解答的合理性。
1 基本方程
假定土的本构关系为Schiffman模型，由Maxwell体和Kelvin体串联而成，如图1所示；土体边界孔压消散规律服从梅国雄等[3]提出的连续排水边界形式；其他基本假定均与Terzaghi一维固结理论相同。图1中 E0为独立弹簧的弹性模量；η0为独立黏壶的黏滞系数；E1和η1分别为Kelvin体中弹簧的弹性模量和黏壶的黏滞系数。
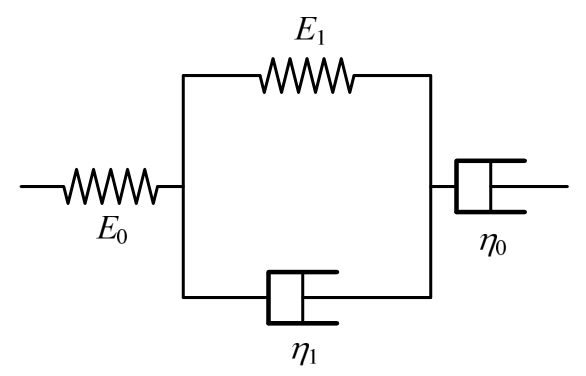
图1 四元件流变模型
Fig.1 Four-element rheological model
四元件流变模型对应的应力-应变关系为：
式中：εz为竖向应变；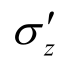
为竖向有效应力；t为时间；E0、E1、η0和 η1分别为图1所示流变模型的参数。
土体一维固结微分方程为：
式中：u为超静孔隙水压力；kv为竖向渗透系数；γw为水的重度；z为竖直方向，向下为正。
对于瞬时荷载q0，由有效应力原理可得：
结合式(1)～式(3)，得瞬时荷载作用下四元件流变固结微分方程：
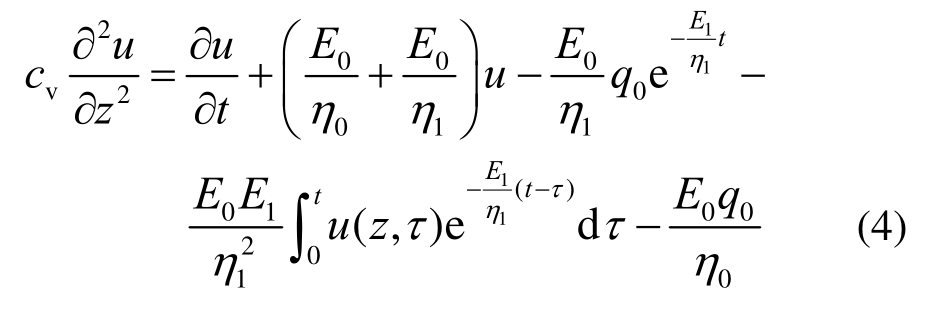
式中，cv为固结系数，其表达式为：
连续排水边界条件下，固结方程式(4)的边界条件表达式为[3]：
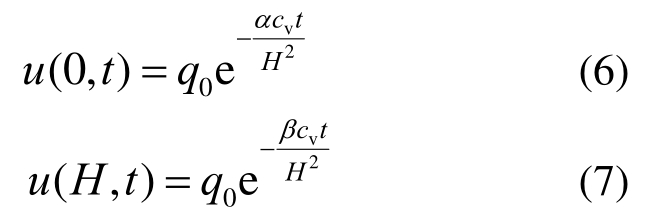
式中：H为土层厚度；α和β为反映土体顶面和底面排水性状的界面参数，其值可以通过试验模拟或工程实测反演得出。
方程初始条件为：
2 瞬时加载下土体一维流变固结解答
2.1 超静孔隙水压力求解
定义无量纲参数
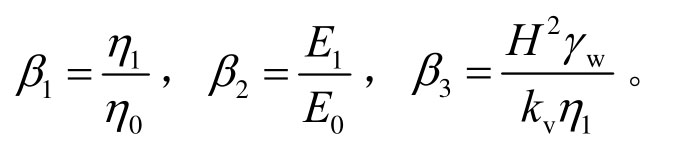其中，
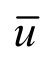为无量纲孔压值；Tv为反映时间变量的时间因数；Z为反映土体竖向位置的无量纲参数；β1为反映粘滞系数；η0为对土体固结影响的无量纲参数；β2为反映流变参数E1对固结影响的无量纲参数；β3为反映流变参数η1对土体固结影响的无量纲参数。
将无量纲参数代入固结方程式(4)，则流变固结方程式(4)变为：
为了进一步将边界条件齐次化，令：
其中：
将式(11)代入式(9)，则无量纲化后的流变固结方程进一步改写为：
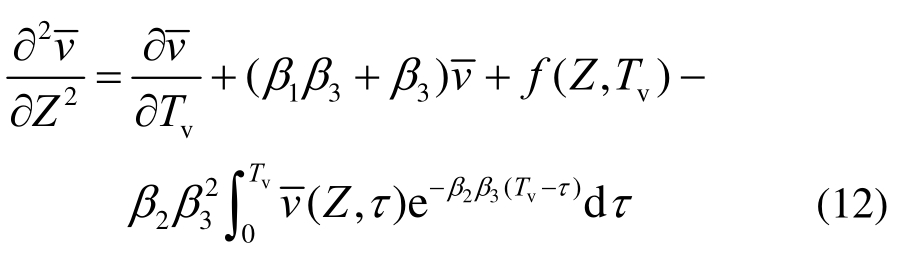
其中：
相应的求解条件变为：
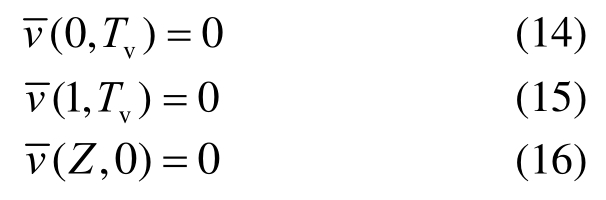
由特征函数法，设方程解的形式为：
将式(17)代入式(12)，可得：
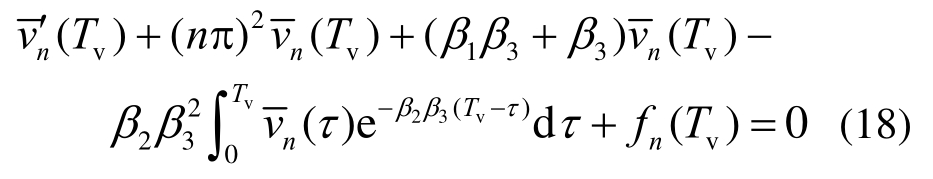
式中，由傅里叶级数可求得fn(Tv)表达式为：
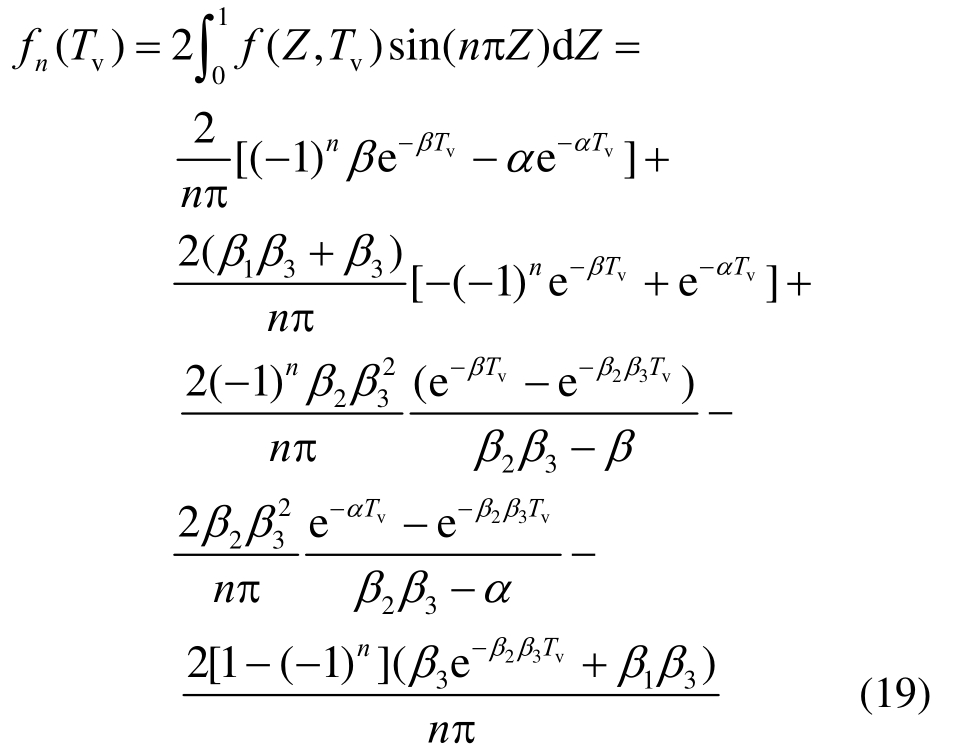
式(18)中对Tv取Laplace变换，且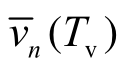
对应的Laplace变换为Vn(s)，s为Laplace变换参数。由于
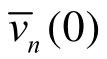=0，则式(18)变换为：
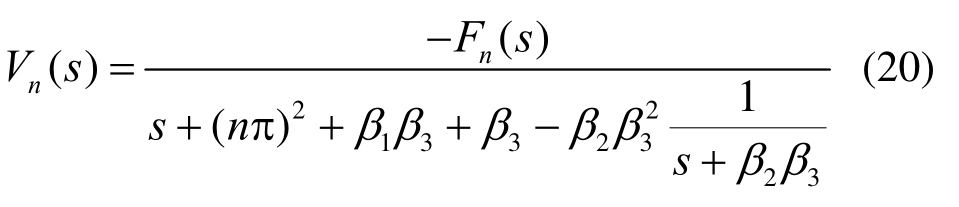
式中，Fn(s)为fn(Tv)的Laplace变换，其表达式为：
对式(20)取Laplace逆变换可得：
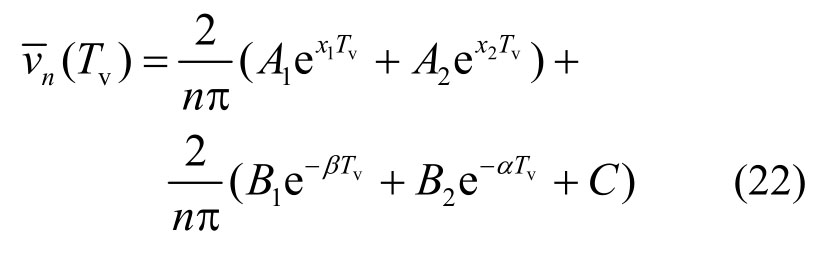
其中，系数x1,2、A1、A2、B1、B2、C的表达式如下：
结合式(10)、式(11)、式(17)和式(22)可求得：
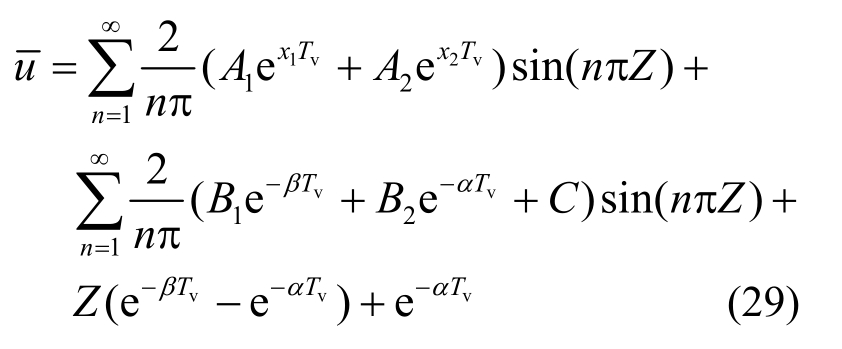
2.2 瞬时荷载下的固结度
按孔压定义的平均固结度Up表达式为：
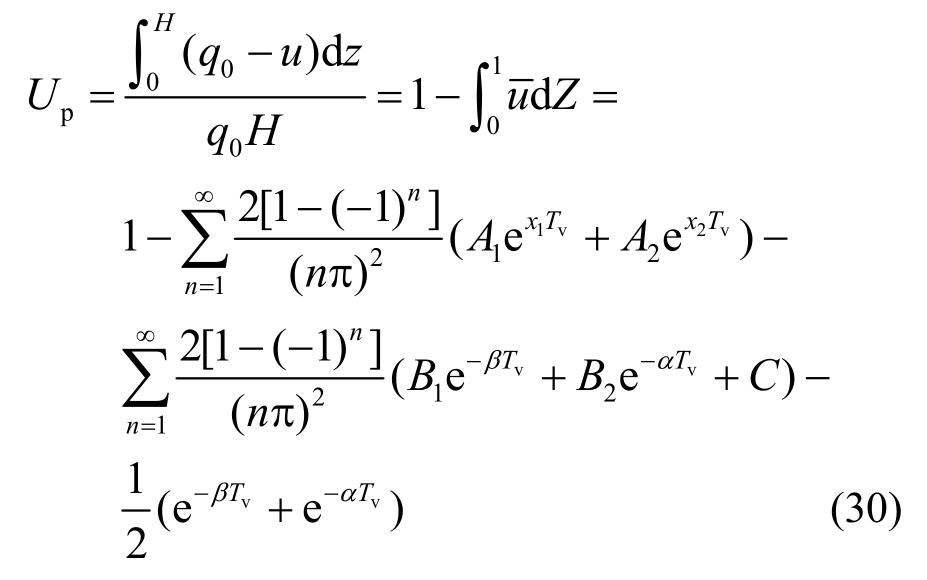
式(29)和式(30)中的系数x1,2、A1、A2、B1、B2、C分别为式(23)～式(28)。
3 单级加载固结解答
利用瞬时加载条件下的孔压解，根据孔压叠加原理，可以利用积分的方法得到单级加载情况下的孔压解答如下所示[19-20]：
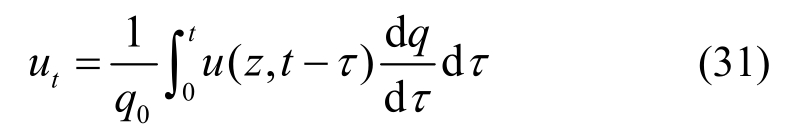
式中：ut为单级加载下的超静孔隙水压力；q0为单级加载最终加载量；u(z,t)为瞬时荷载q0作用时的超静孔隙水压力；q为外荷载，表达式如下：
单级荷载随时间变化关系如图2所示，图中q0表示最终加载量，对应的加载时间为t0，m表示加载速率。为便于无量纲化，式(32)中q(t)可以改写为：
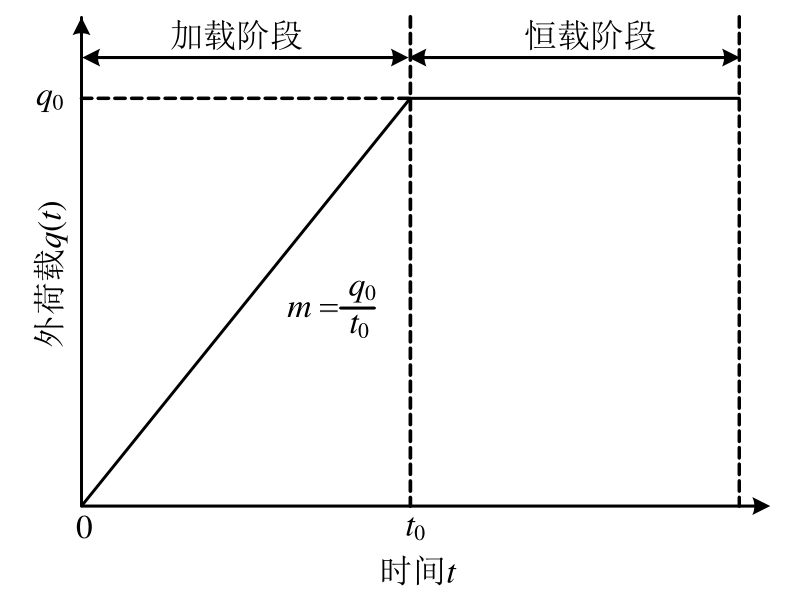
图2 荷载-时间关系
Fig.2 Relation between loading and time
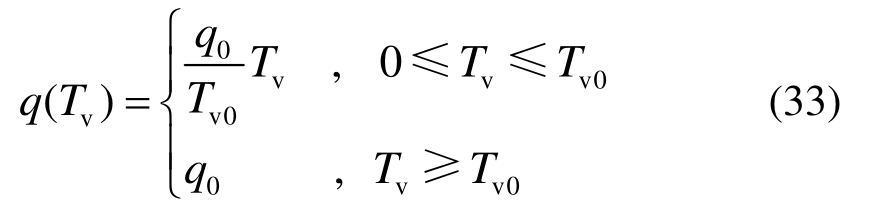
式中：
反映加载速率对固结的影响，t0值越小则加载速率越快。
结合式(31)和式(33)可求得无量纲化后的孔压表达式如下：
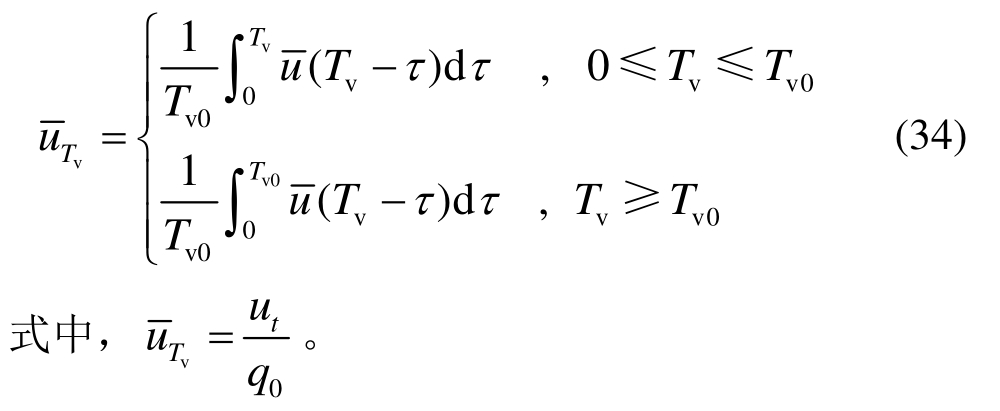
对于加载阶段(0≤Tv≤Tv0)，根据式(34)，积分可得无量纲化后的孔压及平均固结度为：
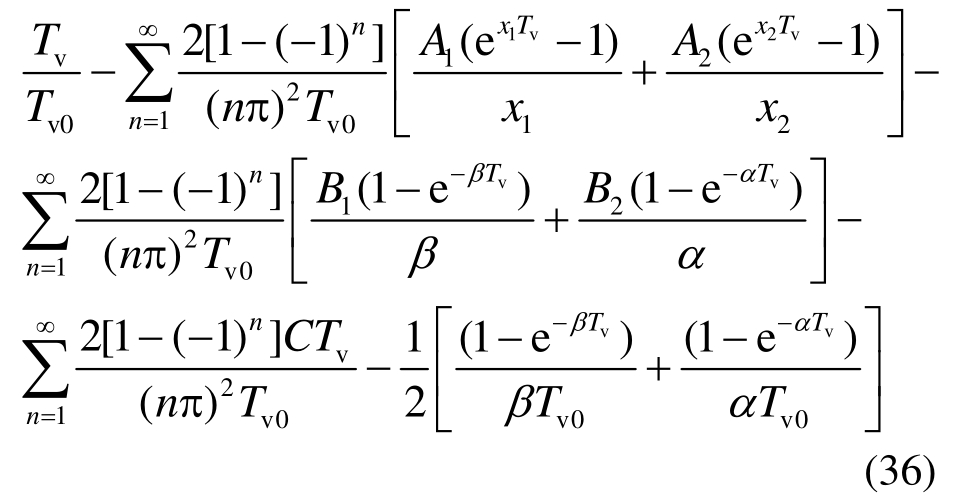
对于恒载阶段(Tv≥Tv0)，根据式(34)，积分可得无量纲化后的孔压及平均固结度为：
式(35)～式(38)中的系数x1,2、A1、A2、B1、B2、C分别为式(23)～式(28)。
4 流变固结解答的退化与验证
4.1 退化为Terzaghi边界
当α→∞且β→∞时，连续排水边界将退化为Terzaghi双面排水边界。此时
因此
这两项为0。此时退化后的系数x1,2、A1、A2、C分别为：
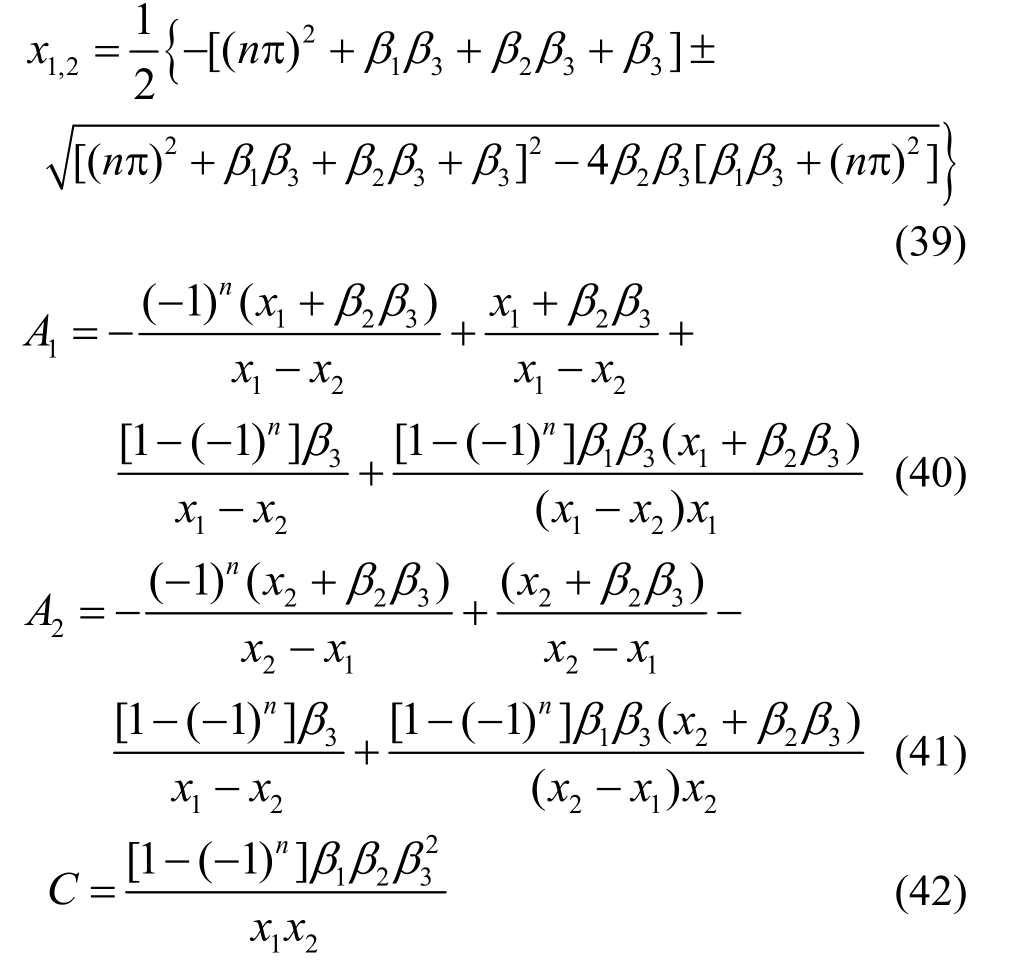
将退化后的系数代入式(29)和式(30)，可得Terzaghi边界条件下瞬时加载的四元件模型孔压及平均固结度如下：
式中，系数x1,2、A1、A2、C分别为式(39)～式(42)。
与瞬时荷载解答类似，分别将退化后的系数x1,2、A1、A2、C代入式(35)～式(38)，可得Terzaghi边界下单级加载四元件流变固结无量纲化的孔压和平均固结度。
4.2 退化为三元件流变模型
当η0→∞时(即β1→0)，四元件流变模型退化为如图3所示的三元件流变模型(即Merchant模型)，四元件流变模型固结解解答中相应的系数x1,2、A1、A2、B1、B2、C分别变为：
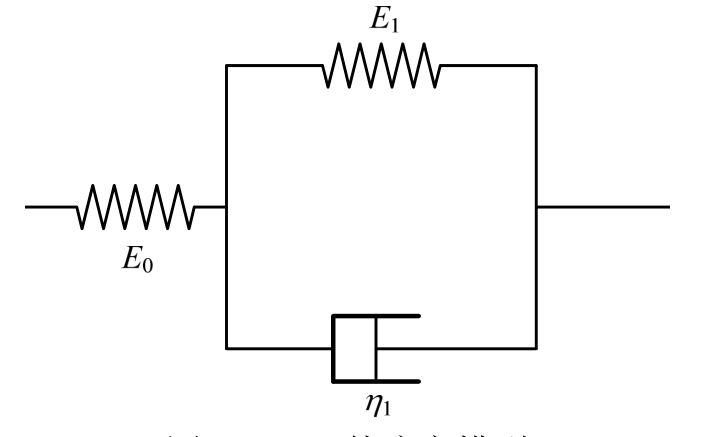
图3 三元件流变模型
Fig.3 Three-element rheological model
将系数式(45)～式(50)代入式(29)和式(30)，可得连续排水边界条件下瞬时加载的三元件流变模型无量纲化孔压解答和按孔压定义的平均固结度如下：
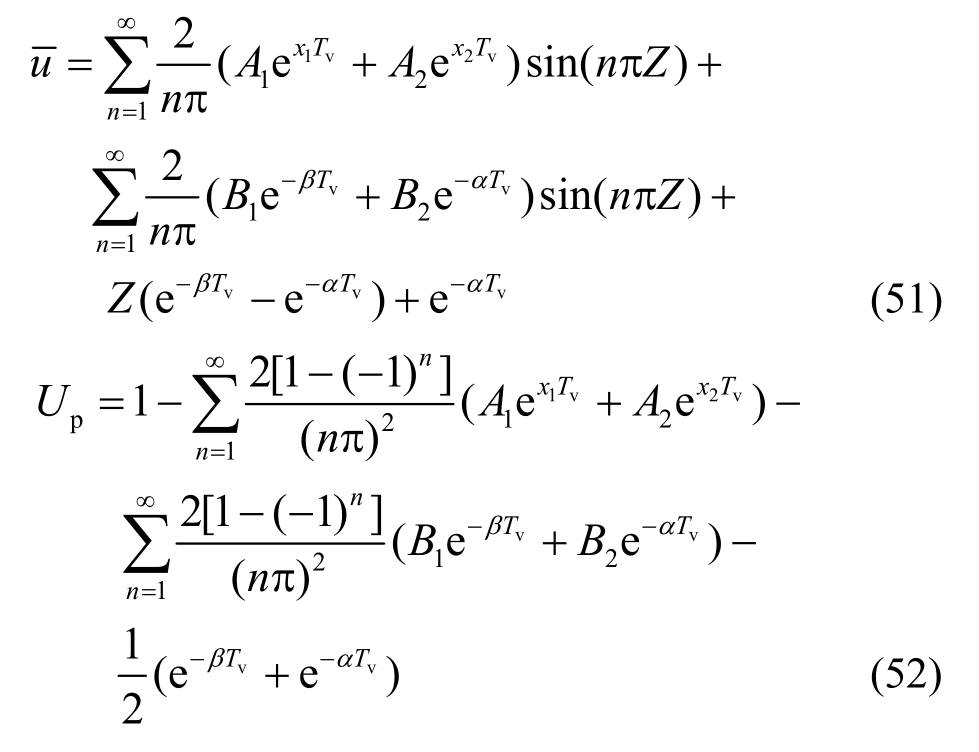
与瞬时荷载解答类似，分别将退化后的系数x1,2、A1、A2、B1、B2 代入式(35)～式(38)，可得连续排水边界条件下单级加载三元件流变固结无量纲化的孔压和平均固结度。
4.3 流变固结解答的验证
当η0→∞且E1→∞时，四元件流变模型将退化为线弹性模型，此时无量纲参数β1→0，2β→∞。图4中，β1和β2的取值分别为0和1000000，利用本文流变解答与梅国雄等[3]进行对比。
图4 瞬时荷载下流变模型退化后的固结度曲线
Fig.4 Consolidation degree curve after degeneration of rheological model under constant loading
梅国雄等[3]基于连续排水边界得到了瞬时荷载的一维固结解答，从图4可以看出，根据式(30)得到的瞬时荷载下的一维流变固结解答与梅国雄解答一致，说明β1=0且β2=1000000时四元件流变模型能够退化为线弹性模型。图4分析了界面参数对固结度的影响，从图中可以看出界面参数取值越大则土体固结越快。此外，图4中流变模型退化后得到的固结度曲线与梅国雄解答一致，一定程度上验证了本文解答的正确性。
5 土体一维流变固结分析
由瞬时加载固结度表达式(30)和单级加载固结度表达式(36)、式(38)可知，对固结度有影响的参数有：α、β、β1、β2、β3及Tv0。这些参数对土体一维流变固结特性的影响在下文中分别进行讨论。
图5反映了瞬时荷载作用下界面参数α、β值对固结度的影响。图中Terzaghi表示根据式(44)得到的Terzaghi双面排水边界下流变固结曲线。连续排水边界下瞬时加载的固结曲线由式(30)获得。对比连续排水边界条件得到的固结度与Terzaghi双面排水边界得到的固结度可以看出：当界面参数α、β取值越大时，透水性越大，孔压消散越快，其结果接近于经典Terzaghi排水边界的固结度。从图5还可以看出，Terzaghi排水边界的固结初期较快，而连续排水边界固结中期更快，当界面参数 α、β取大值时，固结后期与Terzaghi排水边界得到的固结曲线基本重合。这表明基于连续排水边界得出的固结解答与基于Terzaghi双面排水得出的固结解答的差异主要在固结前期，且两者的差异随界面参数α、β取值变大而减小。
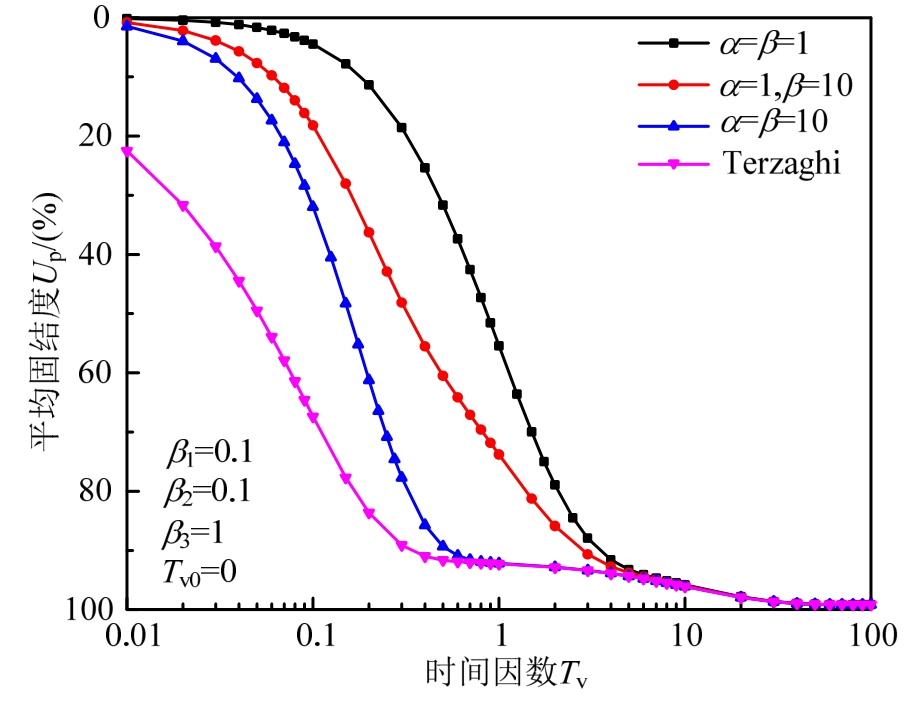
图5 α、β对固结度的影响
Fig.5 Influence of α、β value on consolidation degree
表1 四元件流变模型参数
Table 1 The parameters of the four units rheological model
式样编号 固结压力/kPa 0/(kPas)η · 1/(kPas)η ·0/1 ηη 200 8.50942×108 2.79597×1073.29×10-2 1-1400 3.17099×109 6.36684×1072.01×10-2 800 8.34131×109 1.7304×1082.07×10-2 1600 1.33786×1010 3.51689×1082.63×10-2 2-1 200 7.07422×108 6.90777×1069.76×10-3 400 1.3108×109 9.92537×1067.57×10-3 800 2.97008×109 1.83772×1076.19×10-3 1600 5.16912×1010 4.7667×1079.22×10-4
图6反映了 β1(η1/η0)对固结度的影响，反映了流变参数η0对土体固结过程的影响。从图中可以看出土体固结速率整体是先快后慢。固结初期固结曲线较陡，β1的改变对固结曲线无影响；固结后期固结曲线平缓，土体固结速率随β1值的增大而减小，即 η0变小则土体固结速率变慢。当流变参数 η0变小时(如本例中的β1＞0.1时)，土体在固结后期不能完全固结，这表明即使时间增长，最终孔压也不会完全消散。这一现象对流变参数η0的反演提供了明确范围。李西斌在文献[23]中，通过实验反演得出四元件流变模型的参数取值，如表1所示。从表中可以看出 β1的变化范围为0.00048～0.033。从图6可以看出当β1值为0.1时土体已基本固结完成，由于实际中β1取值很小(一般小于0.1)，因此不会出现图6中土体不能完全固结的现象。
图6 β1对固结度的影响
Fig.6 Influence of β1 value on consolidation degree
图7显示了 β2(E1/E0)对固结度的影响，反映了Kelvin体中E1对固结曲线的影响。β1=0时，η0→∞，此时四元件流变模型退化为三元件流变模型(即Merchant模型)。图中，“线弹性”表示基于土体线弹性应力-应变关系得到的固结曲线。从图中可以看出固结初期固结曲线基本重合，β2的变化对土体固结初期基本无影响；固结后期，固结度随着β2值的增加而增大，当β2增大到10时，所得固结曲线与基于线弹性假定得到的固结曲线一致，表明随着β2的增大流变固结逐渐转变为线弹性固结。
图7 β2对固结度的影响
Fig.7 Influence of β2 value on consolidation degree
图8显示了 β3(H2γw/kvη1)对固结度的影响，反映了Kelvin体中η1对固结曲线的影响。图中，β3的变化范围是0.01～100。从图中可以看出β3对固结曲线的影响较复杂，固结前期土体固结速度随着β3的减小而加快；而固结后期土体固结速度随着 β3的减小而变慢。当β3小到一定程度时，所得固结曲线与基于线弹性假定得到的固结曲线一致，这是由于β3变小时，Kelvin体中η1逐渐变大，而η1足够大时三元件流变模型将退化为线弹性模型。
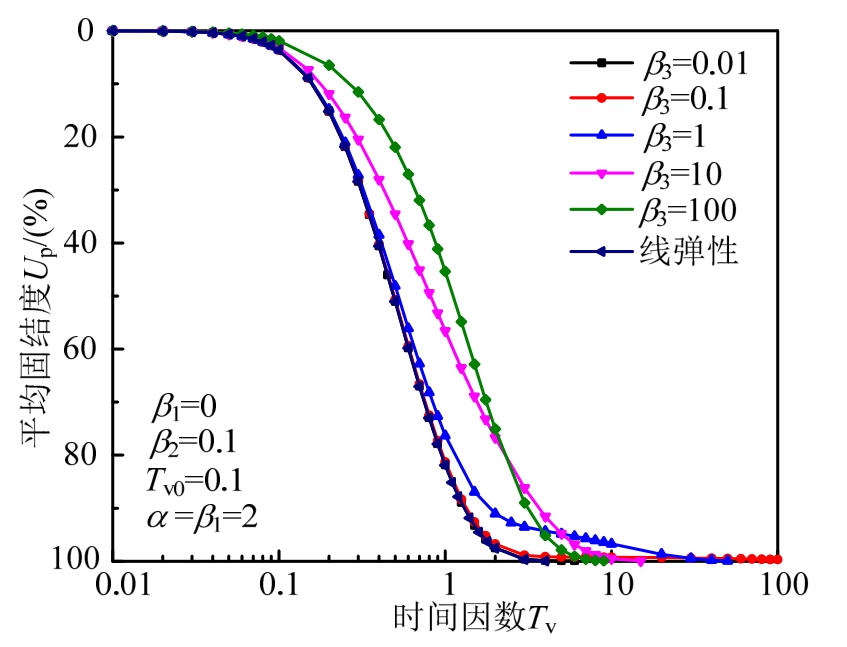
图8 β3对固结度的影响
Fig.8 Influence of β3 value on consolidation degree
如图9所示，在控制其他土体参数不变的情况下，分析了加载速率对流变固结及对线弹性固结的影响。Tv0越小，表示加载速率越快，Tv0=0时表示瞬时加载。从图9可以看出，加载速率越快对应的土体固结也更快。随着加载速率增大，土体固结速率在固结前期更快，而固结后期变慢；相反地，随着加载速率减小，土体固结速率在固结前期更慢，而固结后期变快。此外，随着加载速率变慢，流变固结与线弹性固结的差异逐渐变小。固结前期流变固结曲线与线弹性固结曲线差异非常小，从图中可以看出几乎重合；流变固结与线弹性固结的差别主要是在固结后期，在固结后期流变固结需要经历比较长的时间土体才能完全固结。
图9 不同模型下Tv0对固结度的影响
Fig.9 Influence of Tv0 on consolidation degree under different models
图10对比了基于连续排水条件和基于Terzaghi双面排水条件所得土体一维流变固结解答。从图中可以看出在固结前期基于连续排水边界得出的固结曲线与基于Terzaghi双面排水得出的固结曲线差异较大，其差异随加载速率变慢而减小，当Tv0=10时两者差别已非常小。在固结后期基于连续排水边界得出的固结曲线与基于Terzaghi双面排水得出的固结曲线基本重合，即基于两种边界条件所得固结解答的差异主要在固结前期，且两者的差异随加载速率变慢而减小。
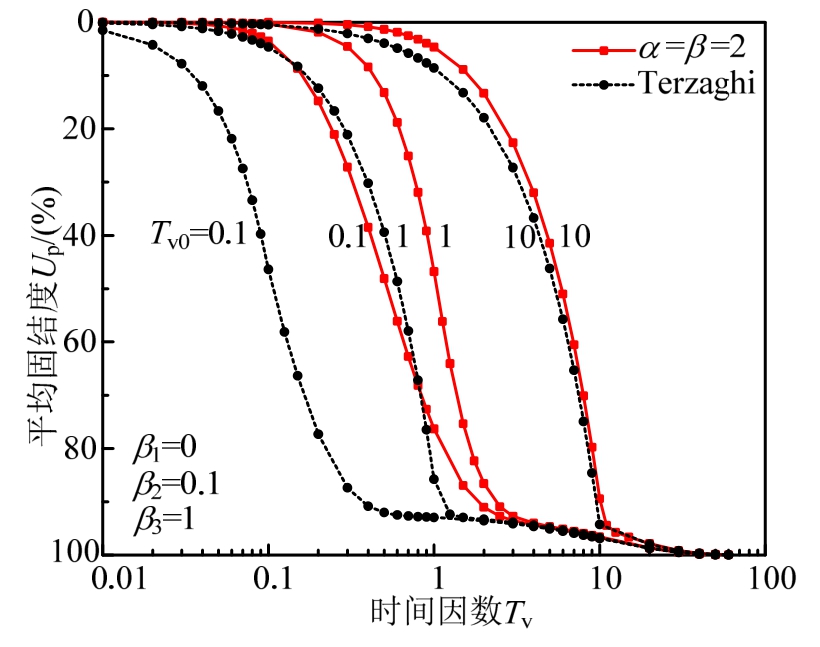
图10 不同边界下Tv0对固结度的影响
Fig.10 Influence of Tv0 on consolidation degree under different boundaries
6 结论
(1)考虑流变特性后，连续排水边界条件下和Terzaghi边界条件下土体完全固结所需时间大致相等；基于连续排水边界得出的固结解答与基于Terzaghi双面排水所得固结解答的差异主要在固结前期，且两者的差异随土层界面参数 α、β取值变大或加载速率变慢而减小。
(2)流变固结与线弹性固结差异主要在固结后期，土体流变固结在固结后期需要更长时间才能完全固结，且流变固结与线弹性固结的差异随加载速率增大而变大。
(3)随着流变参数η0取值变小或E1取值变大，土体固结速率将变慢；流变参数1η对土体固结的影响较复杂，固结前期随着1η增大土体固结速率将加快，而固结后期随着1η增大土体固结速率将变慢。
[1]Gray H.Simultaneous consolidation of contiguous layers of unlike compressible soils [J].Transactions of the American Society of Civil Engineering, 1945, 110:1327―1356.
[2]Schiffman R L, STEIN J R.One-dimensional consolidation of layered systems [J].Journal of Soil Mechanics and Foundations Division, ASCE, 1970, 96(4):1499―1504.
[3]梅国雄, 夏君, 梅岭.基于不对称连续排水边界的太沙基一维固结方程及其解答[J].岩土工程学报, 2011,33(1): 28―31.Mei Guoxiong, Xia Jun, Mei Ling.Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary [J].Chinese Journal of Geotechnical Engineering, 2011, 33(1):28―31.(in Chinese)
[4]Liu J C, Lei G H.One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries [J].Computers and Geotechnics, 2013, 54(10):202―209.
[5]何利军, 吴立松, 张涛, 等.基于连续边界条件的土层厚度随时间变化的平均固结度研究[J].工程力学, 2016,33(增刊1): 11―17.He Lijun, Wu Lisong, Zhang Tao, et al.The average degree of consolidation about soil layer thickness changing with time based on continuous drainage boundary [J].Engineering Mechanics, 2016, 33(Suppl 1):11―17.(in Chinese)
[6]Wu W B, Zong M F, El Naggar M H, et al.Analytical solution for one-dimensional consolidation of double-layered soil with exponentially time-growing drainage boundary [J].International Journal of Distributed Sensor Networks, 2018, 14(10): 1―11.
[7]宗梦繁, 吴文兵, 梅国雄, 等.连续排水边界条件下土体一维非线性固结解析解[J].岩石力学与工程学报,2018, 37(12): 2829―2838.Zong Mengfan, Wu Wenbing, Mei Guoxiong, et al.An analytical solution for one-dimensional nonlinear consolidation of soils with continuous drainage boundary[J].Chinese Journal of Rock Mechanics and Engineering,2018, 37(12): 2829―2838.(in Chinese)
[8]李勇义, 冯健雪, 梅国雄.连续排水边界下梯形循环荷载作用的一维固结解析解[J].工程力学, 2019, 36(2):134―140.Li Yongyi, Feng Jianxue, Mei Guoxiong.One-dimensional consolidation analysis of the trapezoidal cyclic loading under continuous drainage boundary [J].Engineering Mechanics, 2019, 36(2): 134―140.(in Chinese)
[9]Schiffman R L.Consolidation of soil under timedependent loading and varying permeability [J].Proceedings Highway Research Board, 1958, 37: 584―617.
[10]Wilson N E, Elgohary M M.Consolidation of soils under cyclic loading [J].Canadian Geotechnical Journal, 1974,11(3): 420―423.
[11]Alonso E E, Krizek R J.Randomness of settlement rate under stochastic load [J].Journal of the Geotechnical Engineering Division, ASCE, 1974, 100(6): 1211―1226.
[12]Favaretti M, Soranzo M.A simplified consolidation theory in cyclic loading conditions [C].Proceedings of International Symposium on Compression and Consolidation of Clayey Soils.Japan: Hiroshima, 1995,1: 405―409.
[13]关山海, 谢康和, 胡安峰.低频循环荷载下地基一维固结性状分析[J].岩土力学, 2003, 24(5): 849―853.Guan Shanhai, Xie Kanghe, Hu Anfeng.Analysis of one-dimensional consolidation behavior of soil under low-frequency cyclic loading [J].Rock and Soil Mechanics, 2003, 24(5): 849―853.(in Chinese)
[14]Taylor D W, Merchant W.A theory of clay consolidation accounting for secondary compression [J].Journal of Mathematics and Physics, 1940, 19(3): 167―185.
[15]Lo K Y.Secondary compression of clays [J].Journal of Soil Mechanics and Foundation Engineering Division,ASCE, 1961, 87(4): 61―87.
[16]陈宗基.固结及次时间效应的单向问题[J].土木工程学报, 1958, 5(1): 1―10.Tan T K .One dimensional problems of consolidation and secondary time effects [J].China Civil Engineering Journal, 1958, 5(1): 1―10.(in Chinese)
[17]赵维炳.广义Voigt模型模拟的饱水土体一维固结理论及其应用[J].岩土工程学报, 1989, 11(5): 78―85.Zhao Weibing.Theory of 1-D consolidation of saturated clay modeled with the generalized Voigt model and its application [J].Chinese Journal of Geotechnical Engineering, 1989, 11(5): 78―85.(in Chinese)
[18]王奎华, 谢康和, 曾国熙.双面半透水边界的一维粘弹性固结理论[J].岩土工程学报, 1998, 20(2): 34―36.Wang Kuihua, Xie Kanghe, Zeng Guoxi.A study on 1-D consolidation of soils exhibiting rheological characteristics with impeded boundaries [J].Chinese Journal of Geotechnical Engineering, 1998, 20(2): 34―36.(in Chinese)
[19]Xie K H, Xie X Y, Li X B.Analytical theory for onedimensional consolidation of clayey soils exhibiting rheological characteristics under time-dependent loading[J].International Journal for Numerical & Analytical Methods in Geomechanics, 2008, 32(14): 1833―1855.
[20]李西斌, 谢康和, 王奎华, 等.双面半透水边界饱和土层在循环荷载作用下一维粘弹性固结解析解[J].工程力学, 2004, 21(5): 103―108.Li Xibin, Xie Kanghe, Wang Kuihua, et al.Analytical solution of 1-D visco-elastic consolidation of soils with impeded boundaries under cyclic loadings [J].Engineering Mechanics, 2004, 21(5): 103―108.(in Chinese)
[21]高彦斌.饱和软粘土一维非线性流变——固结耦合分析[J].工程力学, 2006, 23(8): 116―121.Gao Yanbin.One-dimensional nonlinear creep-Consolidation analysis of saturated clay [J].Engineering Mechanics, 2006, 23(8): 116―121.(in Chinese)
[22]李传勋, 马浩天, 金丹丹.考虑起始水力坡降的软黏土流变固结解析解[J].工程科学与技术, 2019, 51(2): 53―60.Li Chuanxun, Ma Haotian, Jin Dandan.Analytical solution for rheological consolidation of soft clay with threshold hydraulic gradient [J].Advanced Engineering Sciences, 2019, 51(2): 53―60.(in Chinese)
[23]李西斌.软土流变固结理论与试验研究[D].杭州: 浙江大学, 2005: 126―130.Li Xibin.Theoretical and experimental studies on rheological consolidation of soft soil [D].Hangzhou:Zhejiang University, 2005: 126―130.(in Chinese)