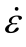分段函数式；同时，通过对比钢纤维增强水泥基材料(SFRCC)和普通混凝土材料，发现PVA-UHTCC材料的DIF应变率敏感性较低。最后，通过LS-DYNA软件模拟试件裂缝扩展和压碎破坏过程，更好地理解了PVA-UHTCC材料动态压缩破坏行为。摘 要：该文基于HJC本构模型，采用分离式霍普金森杆(SHPB)压杆系统，对掺有聚乙烯醇(PVA)纤维的超高韧性水泥基复合材料(PVA-UHTCC)的动态压缩力学性能进行了数值模拟研究。首先，通过系统分析确定了21项HJC本构参数，并验证了模拟的正确性。基于此，通过分析5组应变率下材料的动态压缩应力-应变曲线讨论了峰值应力动态增强因子DIF的应变率效应，并通过LS-DYNA软件探讨了破坏过程、破坏形态与应变率的关系。模拟结果表明：随着应变率的增加，PVA-UHTCC材料的动态压缩应力-应变曲线呈现由应变硬化主导向着损伤软化主导的转变趋势；此外，PVA-UHTCC峰值应力动态增强因子DIF具有明显的应变率效应，其值随着应变率增加而增加，且在不同应变率区间呈现不同敏感性；通过量化DIF这种分区敏感性，提出了适用于PVA-UHTCC材料的DIF 与应变率对数lg分段函数式；同时，通过对比钢纤维增强水泥基材料(SFRCC)和普通混凝土材料，发现PVA-UHTCC材料的DIF应变率敏感性较低。最后，通过LS-DYNA软件模拟试件裂缝扩展和压碎破坏过程，更好地理解了PVA-UHTCC材料动态压缩破坏行为。
基于断裂力学和微观力学原理设计的短纤维增强水泥基复合材料(Engineered Cementitious Composites, ECC)自1992年Li和Leung[1]提出以来，引起了世界范围的关注。此后，国内徐世烺团队[2]通过大量试验研究成功配制出了添加PVA纤维的超高韧性水泥基复合材料(PVA-UHTCC)，并对其力学性能和材料特性(直接拉伸性能、压缩性能、抗冲击性能等)开展了大量研究工作[3-7]。
UHTCC相比普通混凝土存在许多重大突破，具有拉伸韧性高、裂缝控制能力强、损伤容限高等特点[4]。该材料已经成功应用于我国水利、桥梁、隧道和公路工程的建设和维修加固中，在使用过程中会受到爆炸、冲击、地震、风等动力荷载作用。随着对建筑结构可靠性要求的不断提高，动力荷载对建筑结构的影响越来越受关注，研究UHTCC材料动态力学性能的重要性日益凸显。
为了更好地理解UHTCC动态力学性能，学者对其动态拉伸性能[2]、冲击与弯曲疲劳性能、疲劳裂纹扩展规律[5]、冲击压缩性能[6,8]进行了试验研究。文献[6]通过分离式霍普金森杆(Split Hopkinson Pressure Bar, 简称SHPB)压杆装置研究了高应变率下UHTCC的冲击压缩力学响应。但由于试验仪器和技术的限制，数据测量与计算的难度，动态试验研究存在试验成本高、数据局限性大、结果离散性大的缺点。近年来，随着有限元技术的发展，LS-DYNA软件被证明能够有效地模拟混凝土材料在SHPB系统下的动态冲击压缩过程，从而能够更好地理解材料动态压缩力学行为[9-12]；同时借助有限元软件的优势，能够有效降低试验研究成本并提升效率。但目前，针对PVA-UHTCC材料的SHPB系统数值模拟研究尚存空白。因此，通过SHPB压杆数值模拟重现PVA-UHTCC材料动态冲击压缩过程具有必要性和创新性。
在以往对混凝土材料进行动态力学性能研究的数值模拟中，Holmquist-Johnson-Cook(简称HJC)模型是一种运用较多且较为成熟的动态本构模型[13-16]。该模型是一种综合考虑了应变率效应、损伤效应、围压效应和压实效应的本构模型，能够很好地解释混凝土材料在大变形、高应变率和高静水压力下的力学行为。
因此，本文基于HJC本构模型，通过模拟SHPB压杆系统，对PVA-UHTCC材料的动态压缩性能进行研究。本文首先确定了21项HJC本构参数，再通过对比模拟与试验所得波形时程曲线和应力-应变曲线，验证了模拟的正确性。通过分析5种不同应变率下的试件压缩应力-应变曲线，讨论了峰值应力动态增强因子DIF的应变率效应。最终，通过LS-DYNA有限元软件分析了PVA-UHTCC材料压缩破坏过程、破坏形态与应变率的关系。该研究旨在通过数值模拟理解PVA-UHTCC材料的冲击压缩行为，为其更好应用于新材料结构提供重要科学依据。
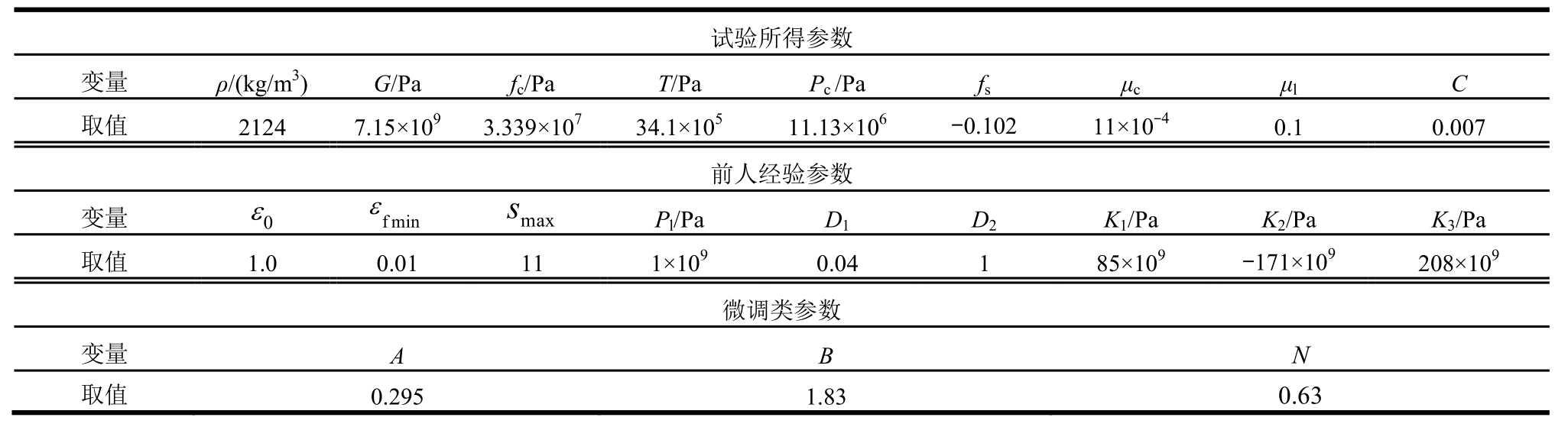
本研究采用的HJC本构模型共有21项参数，主要包括屈服面方程参数、损伤演化方程参数和状态方程参数[13]。根据模型参数的来源，本文将其分为三类：试验所得参数、前人经验参数以及微调类参数，如表1所示。
表1 PVA-UHTCC 的HJC本构参数
Table 1 Parameters of HJC constitutive model
试验所得参数变量 ρ/(kg/m3)G/Pa fc/Pa T/Pa Pc/Pa fs μc μl C取值 2124 7.15×109 3.339×107 34.1×105 11.13×106 -0.102 11×10-4 0.1 0.007前人经验参数变量 0ε fmin ε smax Pl/Pa D1 D2 K1/Pa K2/Pa K3/Pa取值 1.0 0.01 11 1×109 0.04 1 85×109 -171×109 208×109微调类参数变量 A B N取值 0.295 1.83 0.63
结合文献中[4,6,17]对于PVA-UHTCC材料的试验结果，可得试验所得类9项参数，即PVA-UHTCC材料的密度ρ0，剪切模量G，静态抗压强度fc，最大静水拉伸强度T，压碎压力Pc，失效类型fs，压碎体积应变μc，压碎压力体积应变μl和应变率系数C。对于应变率系数C，首先通过试验[6]得到PVA-UHTCC动态抗压强度与应变率的关系，再通过去除静水压力影响的方法[13]，拟合得到C=0.007。
对于前人经验类参数，由于试验数据的匮乏，统计多位学者[16,18-19]采用的HJC参数，确定以下9项参数：参考应变率0ε，破碎前塑性应变εfmin，标准化最大强度Smax，密实压力Pl，损伤常数D1，损伤常数D2，压力常数K1，压力常数K2，压力常数K3。陈星明等[20]通过参数敏感性测试发现这些参数(除了Pl)对模拟结果影响较小。对于参数Pl，由于SHPB试验应变率范围内水泥基材料仅能达到状态方程的平缓地过渡段[21]，其取值对模拟结果影响较小。因此上述参数采用数据统计值具有合理性。
剩余的3项微调类参数，即标准化粘聚力强度A，标准化压力硬化系数B，压力硬化指数N，是先基于试验数据初步确定，再根据模拟环境进行微调。这3项参数被证明对试验结果(应力-应变曲线整体形态，峰值应力，峰值应变等性能)具有较大的影响[20,22]，因此基于模拟环境进行微调能够更好地模拟PVA-UHTCC材料。以往文献中多数学者采用1993年[12]基于假设提出的A、B、N取值，但Polanco-Loria等[14]曾证明这些取值与实测数据符合度并不高。因此，依据塑性屈服面理论中π平面上Mises准则与Mohr-Coulomb 准则的相互关系，熊益波等[19]推导出了标准化粘聚力强度推导公式：
其中K为三轴试验中轴压与围压关系的斜率。通过拟合PVA-UHTCC的轴压-围压试验结果[23]，再按照不考虑损伤与应变率的屈服面方程
进行拟合(σ*和P*分别为无量纲等效应力和静水压力)，初步得到A=0.295，B=1.83，N=0.865。再根据实际模拟环境与试验结果微调N值，最终确定A=0.295，B=1.83，N=0.63。
本次数值模拟采用分离式霍普金森杆(Split Hopkinson Pressure Bar，简称SHPB)压杆系统，是研究高应变率下材料力学性能的最主要实验办法。SHPB压杆装置简图如图1所示，其主要实验原理是通过应变片对入射杆中的入射波、反射波以及透射杆中透射波进行采集，然后根据一维应力波理论得到试样应力-应变关系。
图1 SHPB压杆装置简图
Fig.1 SHPB test set-up
图2 模拟模型示意图
Fig.2 Simulation model sketch
本文根据文献[6]中提到的φ80 mm的SHPB压杆装置进行LS-DYNA有限元建模。与实际试验装置不同的是，为了减少计算量，提高计算效率，模型省略吸收杆，仅保留撞击杆(子弹)、入射杆、试件和透射杆(图2)。模型采用1/4圆建模，在LS-DYNA后处理程序中进行模型镜像复原。同时，模型单元采用Solid164三维实体单元，网格划分采用映射网格划分，具体模型尺寸及网格划分如表2所示。试件与杆之间接触面定义为自动面面接触(ASTS)。
表2 模型尺寸及网格划分
Table 2 Model size and mesh data
参数 子弹 入射杆 试件 透射杆径向直径/mm 80 80 70 80径向每边划分数目 6 6 15 6单元大小/mm 6.7 6.7 2.3 6.7纵向长度/mm 800 4000 35 2500纵向划分数目 80 400 15 250单元大小/mm 10 10 2.3 10
在所建模型中，子弹、入射杆和透射杆为钢材，材料模型选用线弹性模型，主要参数为：密度7850 kg/m3，弹性模量210 GPa，泊松比0.25；试件材料模型采用表1所示HJC本构模型。建模完成后，运用LS-DYNA有限元软件对模拟数据(入射波、反射波、透射波)采用二波法进行处理，得到不同应变率下PVA-UHTCC材料的压缩应力-应变曲线。
通过SHPB压杆试验[6]以及本文数值模拟，分别读取了入射杆中入射波、反射波以及透射杆中透射波的时程曲线数据，得到图3所示试验电压时程曲线与模拟所得应变时程曲线。可以发现，试验实测电压时程曲线和模拟所得应变时程曲线两者吻合度非常高，三波(入射波、反射波、透射波)形状、三波比例和脉冲宽度都具有非常高的一致性，模型初步判断具有可靠性。
图3 试验电压时程曲线与模拟所得应变时程曲线
Fig.3 Voltage-time curves of test and strain-time curves of simulation
利用二波法计算应力、应变和应变率，得到压缩应力-应变曲线(图4)，具体公式如下所示：
式中：
分别为试件应力、应变和应变率；A、E、c分别为杆的横截面积、弹性模量和杆中弹性波波速；A0、l0分别为试样初始横截面积和长度；εt、εr分别为透射波和反射波脉冲。
通过对比，发现在6.3 m/s、7.6 m/s、9.4 m/s三种子弹速度下，无论是应力-应变曲线整体趋势，还是峰值应力、峰值应变等力学参数，模拟结果都与试验符合地非常好。因此，可以认为本次数值模拟在模型建模、网格划分、接触设置以及HJC本构模型参数取值等方面都是合理的，能够真实有效地反应出PVA-UHTCC材料的动态压缩力学行为。
图4 不同子弹速度下材料应力-应变曲线
Fig.4 Stress-strain curves under 3 different projectile velocities
为了使模拟结果更具信服力和普适性，在3组子弹速度(6.3 m/s、7.6 m/s和9.4 m/s)数据基础上，新增2组子弹速度(2.0 m/s和4.5 m/s)模拟数据，由此得到5组子弹速度(5种应变率)下的应力-应变曲线，并利用MATLAB软件对模拟结果进行拟合，得到图5所示结果。
图5 5种应变率下应力-应变曲线
Fig.5 Stress-strain curves under 5 different strain rates
分析上述冲击压缩应力-应变曲线，可以发现PVA-UHTCC材料经历了线弹性变形阶段、非线性强化阶段、应变软化阶段直至完全破坏，是应变硬化和损伤软化效应共同作用的结果。根据应变率的大小，可以归纳为三种特点的破坏过程(图6)，这与学者[10-11]通过大量试验得到现象具有一致性。
应变硬化主导型破坏过程(图6(a))：在较低的应变率下(9.4 s-1)，试件破坏呈现明显的应变硬化特点。在上升段初期，材料受压处于弹性阶段，应力-应变呈线性关系；而后随着压力的增长，PVAUHTCC试件内部的微孔隙和微裂纹开始稳定扩展，出现明显的应变硬化阶段。随着压力的进一步增长，裂缝等损伤进一步加剧，直至达到极限后发生突然性脆性破坏。
应变硬化和损伤软化协同型破坏过程(图6(b))：在较高的应变率下(78.4 s-1)，PVA-UHTCC试件初始处于应力-应变线性阶段，之后出现较为明显的应变硬化阶段，这两阶段与较低应变率(9.4 s-1)时相似。到达极限应力之后，随着荷载继续增加，出现较为明显的应变软化阶段，应力随应变增加而下降。这个应变率下，PVA-UHTCC材料同样首先经历一个微孔洞和微裂缝稳定扩展的应变硬化过程；随即内部孔隙和裂缝等损伤加剧，开始出现较为明显的应变软化现象，直到发生破坏。
损伤软化主导型破坏过程(图6(c))：在高应变率下(以201.5 s-1为例)，应力-应变曲线表现出明显的损伤软化特征。随着压力增长，试件应力-应变呈线性关系，在短时间内达到应力峰值。之后材料呈现明显的应变软化的特征，即在试验达到峰值应力后，微裂纹的二次失稳扩展导致损伤局部化和应变局部化，应力值迅速下降。随后残余一定的应力，直至完全破坏。
图6 3种类型应变率下应力-应变曲线
Fig.6 Typical stress-strain curves under 3 types of strain rates
因此，可以认为，随着应变率的增加，PVAUHTCC材料的应力-应变曲线呈现由应变硬化主导向损伤软化主导的转变趋势。本质上可以认为随着应变率的增加，二次失稳扩展导致的损伤局部化和应变局部化加剧，损伤软化逐渐主导破坏过程。
通过模拟5种应变率下的SHPB系统冲击压缩试验，得到表3所示结果。可以看到PVA-UHTCC材料具有明显的应变率效应，即随着应变率的提高，材料动态应力峰值增加。
表3 SHPB系统模拟结果
Table 3 Simulation results of SHPB test
子弹速度/(m/s)应变率/s-1 应力峰值/MPa DIF 2.0 9.4 46.11 1.38 4.5 78.4 50.72 1.52 6.3 124.4 53.32 1.60 7.6 158.5 56.48 1.69 9.4 201.5 64.55 1.93
通过绘制峰值应力动态增强因子(DIF，Dynamic Increase Factor=动态抗压强度/静态抗压强度)与应变率关系图(图7)，可以发现随着应变率的增加，DIF近似线性增加，应变率效应明显。产生这种现象的原因主要是由于不同应变率下材料的破坏方式以及加载时间不同[24]，静态压缩破坏是薄弱层微裂缝贯通成一条或几条主裂缝，动态压缩破坏则是非薄弱层同时产生大量微裂缝，其裂缝产生需要更多能量；同时撞击速度越高，产生的微裂缝数量更多，因此会消耗更多能量。此外，在冲击压缩破坏过程中，裂缝的形成和扩展需要很高的能量。加载速率越高，留给裂缝产生和发展或者试件变形的时间就越少，材料没有足够的时间用于能量的积累，只有通过增加应力的办法来达到提供能量的目的，从而体现出明显的应变率效应。
图7 DIF与应变率关系曲线
Fig.7 DIF-lg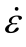curve
进一步量化PVA-UHTCC材料动态增强因子DIF的应变率效应(应变率敏感性)，做出DIF与对数应变率lg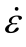的关系曲线(图8)。可以发现，PVA-UHTCC的应变率敏感性存在应变率分界值。当lg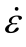低于分界值时，材料应变敏感性较低，DIF随lg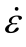增加缓慢线性增长；当lg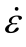高于该值时，材料应变率敏感性提升，DIF出现显著增长。因此，量化DIF的应变率敏感性需要分段推导公式。本研究利用数值模拟的优点，在应变率对数lg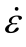值0.97～1.98之间进一步取值模拟，最终确定应变率分界点为
并得到新的DIF与
关系图(图9)。
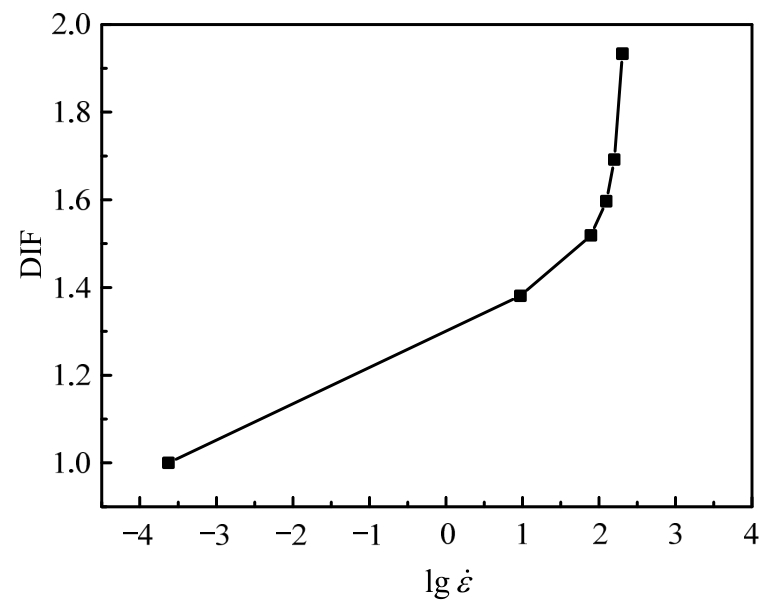
图8 DIF与lg
关系曲线
Fig.8 DIF-lg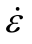curve
图9 新增点后DIF与lg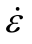关系曲线
Fig.9 Updated DIF-lg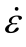curve
通过分段拟合，可以得到以下DIF与lg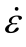函数关系式：
为了进一步了解PVA-UHTCC材料的应变率敏感性特性，本文整理多位学者[25-30]关于PVA纤维增强水泥基材料(Polyvinyl Alcohol Fiber Reinforced Cementitious Composites，简称PVAFRCC)，钢纤维增强水泥基材料(Steel Fiber Reinforced Cementitious Composites，简称SFRCC)和普通混凝土(以下简称NC)动态增强因子DIF在不同应变率下的结果，得到图10所示DIF与应变率对数lg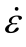关系。
文献中PVAFRCC和SFRCC材料的纤维体积分数含量都为2%，一方面控制纤维含量能够更好地对比三类材料之间DIF应变率敏感性，另一方面该体积含量下材料的拉伸应变硬化性能、制作工艺等方面能够得到有效平衡[1-2]。需要指出，本文中的PVA-UHTCC归属于PVAFRCC类材料。
图10 三种材料DIF与应变率对数关系
Fig.10 DIF-lg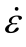curves of PVAFRCC, SFRCC and NC
通过对比三类材料动态增强因子DIF和lg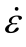的关系曲线，发现在相同应变率下，普通混凝土动态增强因子DIF值最大，其次是SFRCC，而PVAFRCC DIF值最小。添加纤维材料会降低水泥基材料的DIF值，且PVA纤维相较于钢纤维使DIF值降低更明显。这种现象与纤维材料和水泥基材料两者性质有关。从纤维角度来说，这两种纤维相对于水泥基材料基体来说是一种应变率不敏感材料，所以当水泥基材料中加入钢纤维和PVA纤维后会降低DIF应变率敏感性；从水泥基材料角度来说，相较于普通混凝土，PVAFRCC和SFRCC材料不含粗骨料，材料细观结构更致密。因此，纤维增强水泥基材料中的微裂缝等初始缺陷相较于普通混凝土会更少，使得PVAFRCC和SFRCC材料的DIF应变率效应减小。
对于PVAFRCC材料应变率敏感性低于SFRCC材料，可以从两种纤维的特性(强度和粘结力)角度进行解释。钢纤维(抗拉强度为2700 MPa，弹性模量为200 GPa)相对PVA纤维(抗拉强度为1600 MPa，弹性模量为40 GPa)来说抗拉强度更高，但与基体的粘结力较小，因此在低应变率下SFRCC材料多数是拔出破坏而非拉断破坏，是一种薄弱层粘结失效引起的破坏。而随着应变率增加，SFRCC材料由于基体、纤维和粘结层同时出现大量微裂缝而破坏。因此，SFRCC材料动态压缩破坏在低应变率下属于薄弱层粘结失效破坏，在高应变率下则逐步转为非薄弱层的基体、纤维和粘结层的同时破坏。而PVA纤维表面由于存在大量亲水基团，水化之后表面形成紧密覆盖的水化产物[2]，显著提升粘结力(化学粘结和摩擦粘结)；同时PVA纤维抗拉强度较低，破坏方式为纤维断裂破坏，使得PVAFRCC材料从低应变率到高应变率都属于非薄弱层基体、纤维和粘结层的同时破坏。因此，相较于SFRCC材料，PVAFRCC材料(包括PVA-UHTCC)应变率效应较不明显。
试验中由于子弹加载速度过快以及高速摄影机拍摄的局限性，无法全过程且全视角捕捉到冲击作用下材料破坏形态的发展规律。为此，利用LS-DYNA软件，加入失效准则对单元的失效与破坏进行定义。当某一单元超过该失效临界值时，单元失效并删除，以此模拟PVA-UHTCC试件在不同应变率下的压缩破坏失效过程。5种应变率下(9.4 s-1，78.4 s-1，124.4 s-1，158.5 s-1，201.5 s-1)试件的破坏过程及破坏形态如图11所示。
可以看到，不同应变率下PVA-UHTCC出现了不同的破坏形态。当应变率为9.4 s-1时，试样无破坏现象；当应变率从78.4 s-1增至201.5 s-1时，试件出现了明显的破坏现象，大量单元失效删除，试件最终被完全压碎。通过试验，学者[31-32]也观察到应变率低于25 s-1时，纤维增强水泥基试件依旧保持完整性，无破坏现象；随着应变率上升，材料才出现破坏形态。
图11 5种应变率下动态压缩破坏过程
Fig.11 Compressive failure modes under 5 strain rates
进一步分析，可以将这些应变率下PVAUHTCC的破坏过程分为2个阶段，即裂缝扩展阶段和压碎破坏阶段。在裂缝扩展段内，以158.5 s-1应变率为例，可以看到试件初试破坏时裂缝扩展的规律(图12所示)。图中，试件上方为入射杆接触面，下方为透射杆接触面。首先，PVA-UHTCC试件横截面外围开始出现剥落现象，芯部完好(图12(a)和图12(b))，然后破坏逐渐向着横截面芯部扩展，并伴随着纵向裂缝开始出现并快速扩展(图12(c)和图12(d))，最终出现多条较粗的贯穿试件横截面的裂缝(图12(e))，此阶段结束时试件依旧保持着较好的整体性。
图12 裂缝扩展机理
Fig.12 Crack propagation mechanism
在裂缝扩展阶段之后，可以看到材料会经历碎裂成块直至完全压碎的阶段(压碎破坏阶段)。在应变率相对较低(78.4 s-1，124.4 s-1)时，试件首先会明显碎裂成大块，再逐步破碎成小块直至完全被压碎。但随着应变率提高(158.5 s-1，201.5 s-1)，当经历裂缝扩展段之后，试件会直接被压碎成小块，然后被完全压碎。因此，随着应变率增加，PVAUHTCC材料压缩破坏更剧烈，趋向于直接碎裂成小块或者完全碎裂。
本文通过对PVA-UHTCC材料进行数值模拟研究，可以得到以下结论：
(1)针对三类HJC本构模型参数(试验所得参数、前人经验参数以及微调类参数)，通过系统地分析方法能够得到适用于PVA-UHTCC材料的HJC本构模型。
(2)PVA-UHTCC材料冲击压缩破坏过程是应变硬化和损伤软化效应共同作用的结果，在不同应变率下表现出不同的破坏特点。随着应变率增加，PVA-UHTCC试件应力-应变曲线呈现由应变硬化主导向损伤软化主导的转变趋势，本质上是因为随着应变率的增加，二次失稳扩展导致的损伤局部化和应变局部化加剧。
(3)材料峰值应力动态增强因子DIF存在明显的应变率效应，且在不同应变率区间呈现不同敏感性。当应变率小于53.5 s-1时，DIF随lg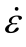增加缓慢线性增加；当应变率大于53.5 s-1时，DIF随lg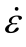增加而显著增加。基于这种应变率分段敏感性，本文提出了适用于PVA-UHTCC材料的DIF与lg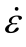函数关系式。
(4)PVA-UHTCC材料应变率敏感性相较于SFRCC和普通混凝土较低，是因为PVAFRCC类材料从低应变率到高应变率都属于非薄弱层基体、纤维和粘结层的同时破坏。
(5)不同应变率下PVA-UHTCC材料会出现不同的破坏形态。当应变率为9.4 s-1时，试样无破坏现象；当应变率从78.4 s-1增至201.5 s-1时，试件出现了明显的破坏现象，最终被完全压碎。
(6)在压缩破坏的裂缝扩展阶段，试件横截面外围首先出现剥落现象并逐渐向着芯部扩展，同时纵向裂缝开始出现并快速扩展，最终出现贯穿试件的纵向裂缝；在压碎破坏阶段，随着应变率增加，碎裂成大块阶段逐渐消失，试件更趋向于直接碎裂成小块或者完全碎裂。
[1]Li V C, Leung C Y.Theory of steady state and multiple cracking of random discontinuous fiber reinforced brittle matrix composites [J].ASCE Journal of Engineering Mechanics, 1992, 188(11): 2246―2264.
[2]徐世烺, 李贺东.超高韧性水泥基复合材料研究进展及其工程应用[J].土木工程学报, 2008, 41(6): 45―60.Xu Shilang, Li Hedong.A review on the development of research and application of ultra high toughness cementitious composites [J].China Civil Engineering Journal, 2008, 41(6): 45―60.(in Chinese)
[3]徐世烺, 蔡向荣.超高韧性纤维增强水泥基复合材料基本力学性能[J].水利学报, 2009, 40(9): 1055―1063.Xu Shilang, Cai Xiangrong.Basic mechanical performance of ultra high toughness cementitious composites [J].Journal of Hydraulic Engineering, 2009,40(9): 1055―1063.(in Chinese)
[4]李庆华, 徐世烺.超高韧性水泥基复合材料基本性能和结构应用研究进展[J].工程力学, 2009, 26(增刊2):23―67.Li Qinghua, Xu Shilang.Performance and application of ultra high toughness cementitious composite: a review[J].Engineering Mechanics, 2009, 26(Suppl 2): 23―67.(in Chinese)
[5]刘问.超高韧性水泥基复合材料动态力学性能的试验研究[D].大连: 大连理工大学, 2012: 95―112.Liu Wen.Experimental study on dynamic mechanical properties of ultra-high toughness cementitious composites [D].Dalian: Dalian University of Technology, 2012: 95―112.(in Chinese)
[6]李庆华, 赵昕, 徐世烺.纳米二氧化硅改性超高韧性水泥基复合材料冲击压缩试验研究[J].工程力学,2017, 34(2): 85―93.Li Qinghua, Zhao Xin, Xu Shilang.Impact compression properties of nano-SiO2 modified ultra high toughness cementitious composites using a split Hopkinson pressure bar [J].Engineering Mechanics, 2017, 34(2):85―93.(in Chinese)
[7]蔡向荣, 徐世烺.UHTCC薄板弯曲荷载-变形硬化曲线与单轴拉伸应力-应变硬化曲线对应关系研究[J].工程力学, 2010, 27(1): 8―16.Cai Xiangrong, Xu Shilang.Study on corresponding relationships between flexural load-deformation hardening curves and tensile stress-strain hardening curves of UHTCC [J].Engineering Mechanics, 2010,27(1): 8―16.(in Chinese)
[8]杜修力, 窦国钦, 李亮, 等.纤维高强混凝土的动态力学性能试验研究[J].工程力学, 2011, 28(4): 138―144.Du Xiuli, Dou Guoqin, Li Liang, et al.Experimental study on dynamic mechanical properties of fiber reinforced high strength concrete [J].Engineering Mechanics, 2011, 28(4): 138―144.(in Chinese)
[9]焦楚杰, 李祯, 高乐.混凝土SHPB试验的数值模拟[J].工程力学, 2010, 27(增刊2): 196―200.Jiao Chujie, Li Zhen, Gao Le.Numerical simulation of SHPB test of concrete [J].Engineering Mechanics, 2010,27(Suppl 2): 196―200.(in Chinese)
[10]陈猛, 李艺, 卢哲安, 等.混杂纤维混凝土动态压缩性能试验及数值模拟研究[J].混凝土, 2015(8): 91―94.Chen Meng, Li Yi, Lu Zhean, et al.Study on dynamic compression properties and numerical simulation of hybrid fiber reinforced concrete [J].Concrete, 2015(8):91―94.(in Chinese)
[11]张文华, 张云升.超高性能水泥基复合材料动态冲击性能及数值模拟[J].混凝土, 2015(10): 60―63.Zhang Wenhua, Zhang Yunsheng.Dynamic impact properties and simulation of ultra-high performance of cementitious composites [J].Concrete, 2015(10): 60―63.(in Chinese)
[12]Lv T H, Chen X W, Chen G.The 3D meso-scale model and numerical tests of split Hopkinson pressure bar of concrete specimen [J].Construction and Building Materials, 2018, 160: 744―764.
[13]Holmquist T J, Johnson G R, Cook W H.A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures [C]//Michael J M.Proceedings of the 14th International Symposium on Ballistics.Sundbyberg: National Defence Research Establishment, 1993.
[14]Polanco-Loria M, Hopperstad O S, Børvik T, et al.Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model [J].International Journal of Impact Engineering,2008, 35(5): 290―303.
[15]Rong Zhidan, Sun Wei.Experimental and numerical investigation on the dynamic tensile behavior of ultra-high performance cement based composites [J].Construction and Building Materials, 2012, 31: 168―173.
[16]Kong Xiangzhen, Fang Qin, Wu Hao, et al.Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J].International Journal of Impact Engineering, 2016, 95: 61―71.
[17]高翔.纳米SiO2改性超高韧性水泥基复合材料试验研究[D].杭州: 浙江大学, 2016: 108―129.Gao Xiang.Experimental study on ultra-high toughness cementitious-composites with nano-SiO2 [D].Hangzhou:Zhejiang University, 2016: 108―129.(in Chinese)
[18]任根茂, 吴昊, 方秦, 等.普通混凝土HJC本构模型参数确定[J].振动与冲击, 2016, 35(18): 9―16.Ren Genmao, Wu Hao, Fang Qin, et al.Determinations of HJC constitutive model parameters for normal strength concrete [J].Journal of Vibration and Shock,2016, 35(18): 9―16.(in Chinese)
[19]熊益波, 陈剑杰, 胡永乐, 等.混凝土Johnson-Holmquist本构模型关键参数研究[J].工程力学, 2012,29(1): 121―127.Xiong Yibo , Chen Jianjie , Hu Yongle, et al.Study on the key parameters of the Johnson-Holmquist constitutive model for concrete [J].Engineering Mechanics, 2012, 29(1): 121―127.(in Chinese)
[20]陈星明, 刘彤, 肖正学.混凝土HJC模型抗侵彻参数敏感性数值模拟研究[J].高压物理学报, 2012, 26(3):313―318.Chen Xingming, Liu Tong, Xiao Zhengxue.Numerical simulation research on HJC constitutive model sensitivity of penetration resistance of concrete [J].Chinese Journal of High Pressure Physics, 2012, 26(3):313―318.(in Chinese)
[21]巫绪涛, 李耀, 李和平.混凝土HJC本构模型参数的研究[J].应用力学学报, 2010, 27(2): 340―344.Wu Xutao, Li Yao, Li Heping.Investigation on HJC constitutive model of concrete [J].Chinese Journal of Applied Mechanics, 2010, 27(2): 340―344.(in Chinese)
[22]吴赛, 赵均海, 王娟, 等.基于砼SHPB试验数值分析的HJC模型参数研究[J].计算力学学报, 2015, 32(6):789―795.Wu Sai, Zhao Junhai, Wang Juan, et al.Numerical analysis on HJC parameters of concrete using SHPB test[J].Chinese Journal of Computational Mechanics, 2015,32(6): 789―795.(in Chinese)
[23]李艳, 王伟伟, 温从格.ECC常规三轴受压力学性能试验研究[J].混凝土, 2016(1): 59―63.Li Yan, Wang Weiwei, Wen Congge.Experiment study on mechanical performance of ECC under conventional triaxial compression [J].Concrete, 2016(1): 59―63.(in Chinese)
[24]Wu Zemei, Shi Caijun, He Wen, et al.Static and dynamic compressive properties of ultra-high performance concrete(UHPC)with hybrid steel fiber reinforcements[J].Cement and Concrete Composites, 2017, 79:148―157.
[25]曹吉星.钢纤维混凝土的动态本构模型及其有限元方法[D].成都: 西南交通大学, 2011: 49―53.Cao Jixing.Dynamic constitutive model of steel fiber reinforced concrete and its finite element method [D].Chengdu: Southwest Jiaotong University, 2011: 49―53.(in Chinese)
[26]崔昭.钢-PVA混杂纤维混凝土动态本构模型及其有限元分析[D].广州: 华南理工大学, 2016: 38―42.Cui Zhao.Dynamic constitutive model and finite element analysis of steel-PVA hybrid fiber concrete [D].Guangzhou: South China University of Technology,2016: 38―42.(in Chinese)
[27]Li Qinghua, Zhao Xin, Xu Shilang, et al.Influence of steel fiber on dynamic compressive behavior of hybrid fiber ultra high toughness cementitious composites at different strain rates [J].Construction and Building Materials, 2016, 125: 490―500.
[28]Wang Shasha, Le H T N, Poh L H, et al.Effect of high strain rate on compressive behavior of strain-hardening cement composite in comparison to that of ordinary fiber-reinforced concrete [J].Construction and Building Materials, 2017, 136: 31―43.
[29]万世强.钢-PVA混杂纤维增强水泥基复合材料冲击特性研究[D].哈尔滨: 哈尔滨工业大学, 2016: 72―73.Wan Shiqiang.The impact performance experimental study of steel and PVA hybrid fiber reinforced cementitious composites [D].Harbin: Harbin Institute of Technology, 2016: 72―73.(in Chinese)
[30]丁彦江.钢-PVA混杂纤维增强水泥基复合材料冲击压缩动力性能试验研究[D].广州: 华南理工大学, 2014:40―44.Ding Yanjiang.The shock compression dynamic performance experimental study of Steel and PVA hybrid fiber reinforced cement matrix composites [D].Guangzhou: South China University of Technology,2014: 40―44.(in Chinese)
[31]Su Haoyang, Xu Jinyu.Dynamic compressive behavior of ceramic fiber reinforced concrete under impact load[J].Construction and Building Materials, 2013, 45:306―313.
[32]Rong Zhidan, Sun Wei, Zhang Yunsheng.Dynamic compression behavior of ultra-high performance cement based composites [J].International Journal of Impact Engineering, 2010, 31: 515―520.
NUMERICAL SIMULATION ON DYNAMIC COMPRESSIVE BEHAVIOR OF ULTRA-HIGH TOUGHNESS CEMENTITIOUS-COMPOSITES
Abstract: Investigates the dynamic compressive behavior of PVA fiber reinforced ultra-high toughness cementitious-composites(PVA-UHTCC)using Split Hopkinson Pressure Bar(SHPB)test based on HJC constitutive model.Firstly, 21 parameters of HJC model are determined and the numerical simulation is verified.Then dynamic compressive stress-strain curves under 5 different strain rates are obtained for analyzing the strain-rate effects on Dynamic Increase Factor(DIF).The failure modes of specimens under different strain rates are also researched.The results show that with the increase of strain rate, DIF increases and the strain-hardening dominated behavior will transform into a strain-softening dominated behavior.Besides, PVA-UHTCC shows an obvious different strain-rate sensitivity in the different range of strain rates.Thusly, a functional expression between DIF and lg is proposed.Compared with Steel Fiber Reinforced Cementitious Composites(SFRCC)and normal concrete, PVA-UHTCC has a lower strain-rate sensitivity.Finally, the crack propagation mechanism and failure modes are observed at LS-DYNA software to furtherly understand the dynamic compressive behavior of PVA-UHTCC.
徐世烺(1953―)，男，湖北人，教授，博士，博导，从事混凝土断裂力学、新型材料与新型结构研究(E-mail: slxu@zju.edu.cn);
陈 超(1993―)，男，浙江人，硕士生，从事新型材料数值模拟研究(E-mail: ChaoChen.Daniel@outlook.com);
赵 昕(1989―)，女，浙江人，博士生，从事新型材料防护冲击方面研究(E-mail: 11212049@zju.edu.cn).