功能梯度材料(FGM)结构因其可设计性、耐高温、耐磨损、抗腐蚀等方面的优良特性，在航空航天、机械、电子信息、生物医疗、核能等诸多工程领域具有广阔的应用前景。因此，FGM梁的稳定性与振动特性一直是近些年学者们研究的热点和前沿课题。
例如，在机械静载荷作用方面：Huang和Li[1]导出了FGM圆形截面简支梁临界载荷和临界应力的精确解。魏东和刘应华[2]数值求解了含裂纹FGM欧拉梁(CBT)与Timoshenko(FSBT)梁的临界失稳问题。Simsek[3]建立了6种剪切变形理论下FGM梁自振的Lagrange频率方程。赵凤群和王忠民[4]探讨了不同剪切理论下FGM简支梁的弯曲问题。Li等[5-6]根据微分方程解的相似性导出了FGM欧拉梁与FSBT梁频率及临界载荷的精确解。Pradhan和Chakraverty[7]采用Ritz法讨论了不同梁理论对FGM梁频率的影响。蒲育和滕兆春[8]采用二维DQM数值研究了弹性地基FGM梁的振动特性。最近，他们基于一种改进型GDQ法，数值求解了功能梯度FSBT梁的自由振动问题[9]。Kahya和Turan[10]则采用FEM分析了功能梯度FSBT梁的屈曲及振动特性。然而，以上相关研究均未考虑温度的影响。
考虑到温度或其他因素(例如湿度)的变化会使FGM梁产生初始轴力而改变其振动特性。因此，在热-机载荷作用方面：牛牧华和马连生[11]采用打靶法研究了热载荷作用下FGM梁的非线性力学行为。赵凤群和王忠民[12]采用WDQ法分析了切向随从力和热载荷共同作用下FGM欧拉梁的稳定性及振动特性。毛丽娟和马连生[13]基于精确解研究了非均匀热载荷作用下FGM梁的非线性静态响应。Pradhan和Murmu[14]应用DQM研究了变弹性地基FGM夹层梁的热-机振动问题。针对材料关于FGM梁的几何中面对称分布，Mahi等[15]考虑了材料物性随温度变化并得出了非均匀升温FGM梁自由振动响应的精确解。文献[16]应用Ritz法分析了均匀升温FGM高阶剪切梁的振动与屈曲特性。最近，Trinh等[17]采用SSM获得了热-机载荷作用下FGM梁振动和屈曲问题的精确解。张靖华等[18]则应用辛方法研究了FGM梁热冲击下的动力屈曲特性。钮鹏等[19]采用打靶法数值研究了夹层梁在均匀升温下的热过屈曲及热弯曲变形。何昊南和于开平[20]考虑了热对材料属性参数的影响，探讨了非均匀升温下FGM梁的热后屈曲及过屈曲振动特性。综上所述，文献调研表明：目前针对湿-热-机-弹耦合FGM梁稳定性与振动特性的研究极为少见。
本文将一种n阶剪切板理论[21]发展为一种广义梁理论(GBT)，基于该广义梁理论，应用Hamilton原理，统一建立了湿-热-机-弹耦合FGM梁屈曲及自由振动方程。采用Navier法求解FGM简支梁屈曲及自由振动响应。通过算例，着重揭示了FGM梁临界屈曲载荷与振动频率这两种静动态响应之间的关联。重点讨论并分析了诸多参数对FGM梁稳定性及振动特性的影响，由此得出一些有益的结论。
1 控制微分方程
1.1 材料属性
考虑一长、宽、高分别为L×b×h的FGM弹性地基梁，上表面为陶瓷，下表面为金属。x轴沿轴线方向，y轴和z轴分别沿梁的宽度和厚度方向，xoy面为梁的几何中面。假设Winkler-Pasternak弹性地基刚度系数分别为kw和kp，梁两端受初始轴向机械压力为P，湿度C和温度T沿梁厚度方向稳态分布，材料性质依赖于温度变化且按Voigt混合幂律模型沿梁厚呈梯度连续分布。物性参数(如弹性模量E，泊松比v，热膨胀系数α，热传导率κ)与坐标z和温度T满足[17,22]：
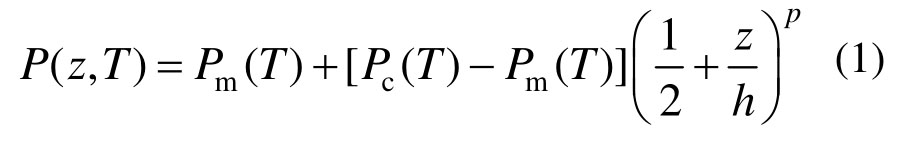
式中：p为FGM梁组分的梯度指标；下标m和c分别表示金属和陶瓷对应的相关物性参数。金属-陶瓷材料的某一物性参数P随温度T的变化可统一表示为[17,22]：
式中，Pi(i=-1,0,1,2,3)表示随温度变化的材料系数。表1给出了金属(SUS 304)和陶瓷(Si3N4)的材料系数[17,22]，其中这两种材料的湿膨胀系数β与密度ρ不随温度变化。
1.2 湿-热分布类型
本文考虑以下三种温度-湿度分布类型：
类型1 均匀分布(UTR)
式中，T0、C0分别为无应力状态时的参考温度和湿度，本文取T0=300 K，C0=0wt%，ΔT和ΔC分别表示温度和湿度的增加。
类型2 线性分布(LTR)
表1 金属(SUS 304)和陶瓷(Si3N4)两种材料随温度变化的物性系数
Table 1 Temperature-dependent coefficients for metal(SUS 304)and ceramic(Si3N4)
材料 物性参数 P0 P-1P1P2 P3 E/Pa 201.04×109 0 3.079×10-4 -6.534×10-7 0金属(SUS 304)α/(1/K)12.33×10-6 0 8.086×10-4 0 0 β 5×10-4 0 0 0 0 κ/(W/mK)15.379 0 -1.264×10-3 2.092×10-7 -7.223×10-10 υ 0.3262 0 -2.002×10-4 3.797×10-7 0 ρ/(kg/m3)8166 0 0 0 0陶瓷(Si3N4)E/Pa 348.43×109 0 -3.070×10-4 2.160×10-7 -8.946×10-11 α/(1/K)5.8723×10-6 0 9.095×10-4 0 0 β 0 0 0 0 0 κ/(W/mK)13.723 0 -1.032×10-3 0 0 υ 0.24 0 0 0 0 ρ/(kg/m3)2370 0 0 0 0
式中，ΔT=Tc-Tm ，ΔC=Cc-Cm。
类型3 非线性分布(NLTR)
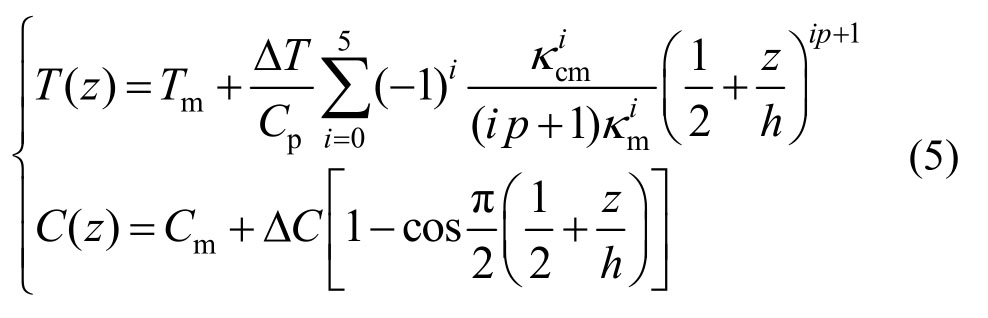
式中，系数
这里温度分布T(z)可由一维稳态热传导方程边值问题的解给出，湿度C(z)分布则均为假定。
1.3 FGM梁振动及屈曲的控制微分方程
位移场可描述为：
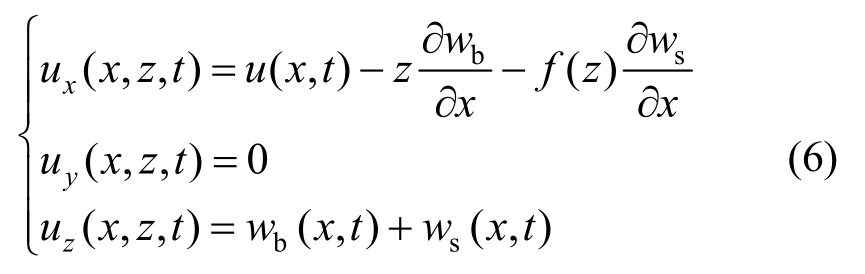
式中，u(x,t)、wb(x,t)、ws(x,t)分别表示轴线上t时刻点的轴向位移、弯曲变形及剪切变形引起的挠度，f(z)=h(2z/h)n/(2n)表示横向切应力形函数。这里将Xiang和Kang[21]提出的n阶剪切变形板理论扩展为一种广义剪切梁理论(GBT)。n=1，退化为CBT；n=3，退化为Reddy三阶剪切理论(TBT)；n=∞，退化为FSBT。
由小变形的几何方程可得非零应变分量：
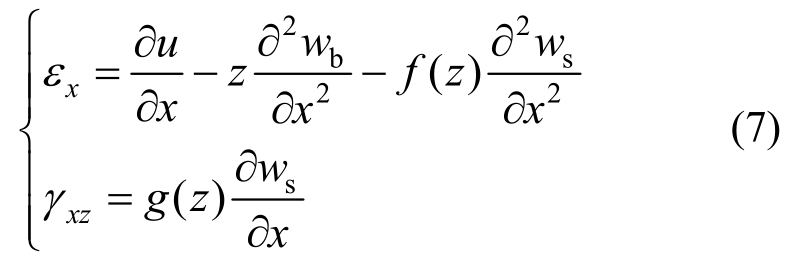
g(z)=1-f′为横向切应变形函数。
本构方程：
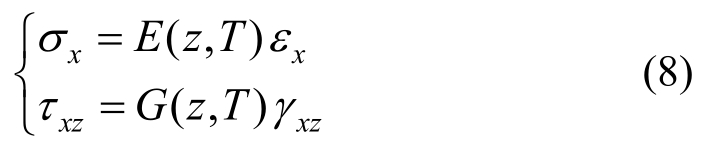
式中，G(z,T)=E(z,T)/2[1+υ(z,T )]为剪切模量。
动能的变分：
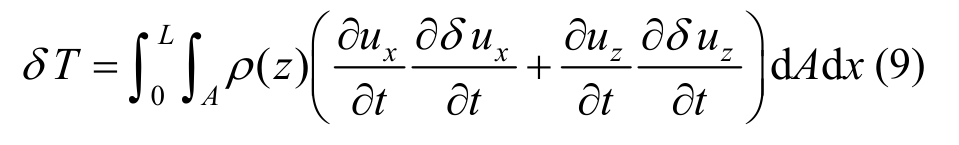
应变能的变分：
湿-热-机-弹载荷做功的变分：
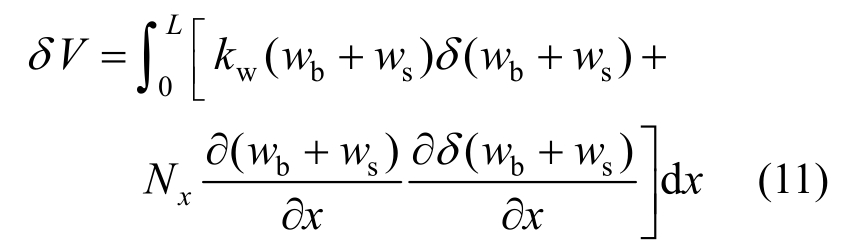
初始总轴力Nx=kp-P-NC-NT ，湿度和温度增加引起的湿轴力和热轴力分别定义为：
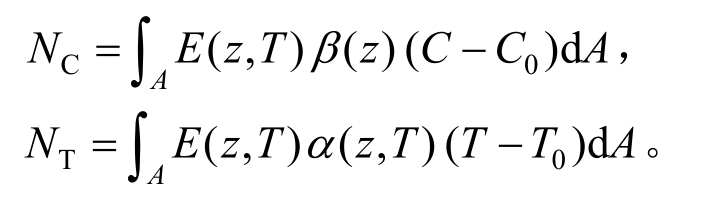
对系统应用Hamilton原理：
将式(7)～式(11)代入式(12)并做一些变分和积分运算后可得FGM梁自由振动的控制微分方程：
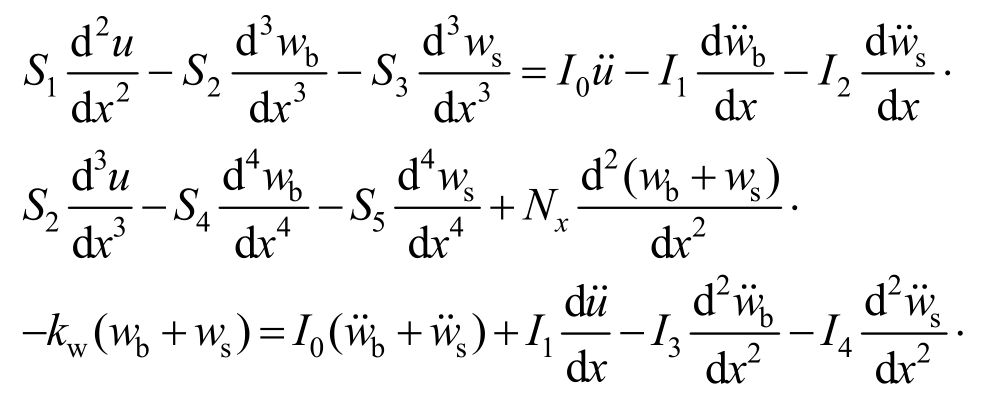
弹性系数定义为
惯性系数定义为
(i=0,1,…,5)。显然，控制方程式(13)中Nx=kp -PNC-NT项为湿-热-机-弹耦合下的初始轴力，而弹性系数与惯性系数项中存在拉压、剪切与弯曲的耦合。此外，式(13)中与时间t无关时，则退化为湿-热-机-弹耦合作用下FGM梁屈曲问题的控制方程。
2 特征值问题
由Navier法，FGM简支梁轴线上一点的位移分量可设为：
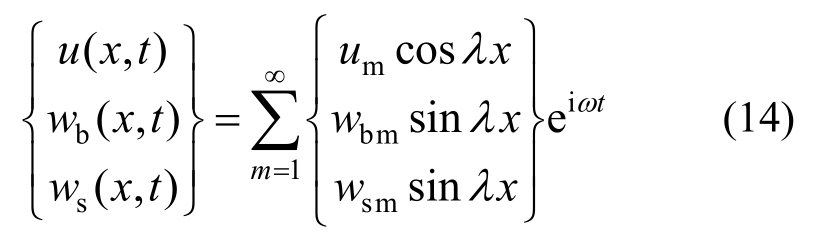
式中：i为虚数单位；λ=mπ/L ；ω为自振频率。将式(14)代入控制方程式(13)可得湿-热-机-弹耦合下FGM简支梁屈曲和自由振动的特征值问题：
其中，刚度矩阵K和质量矩阵M均为3阶对称阵，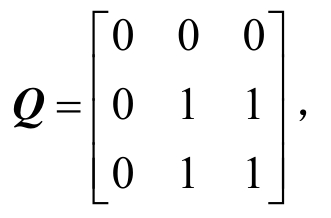
位移向量
刚度矩阵元素
上式刚度元素中
质量矩阵元素
不失一般性，各参数无量纲化如下：
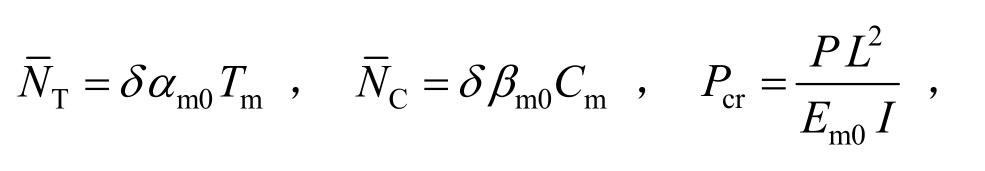
其中Pcr与Ω分别为无量纲临界载荷及无量纲频率，I为惯性矩。Em0、ρm0、αm0、βm0分别表示温度Tm=300 K 时金属材料的弹性模量、密度、热膨胀系数及湿膨胀系数。
求解特征值方程式(15)可得FGM简支梁的临界载荷与屈曲模态、频率与振型。
3 算例与讨论
3.1 探讨GBT阶数n的理想取值
首先，将问题退化，图1～图5刻画了不考虑湿热载荷和弹性地基作用FGM简支梁的振动及屈曲特性。考虑由Al与Al2O3两种材料组成的FGM梁，物性系数[3]分别为Em=70 GPa，ρm=2702 kg/m3，Ec=380 GPa，ρc=3960 kg/m3，绘制图1与图2，υm=υc=0.3[3]，绘制图3～图5，υm=υc=0.23[6]。
图1给出了FGM梁(p=1, δ=5)的无量纲基频Ω1与GBT阶数n之间的关系曲线。总的来看，Ω1随n的变化波动很小，取n=2,4,6…偶数时预测的频率略微高于n=3,5,7…奇数预测的频率。取n=2，Ω1=4.02847为最大，取n=3(TBT)，Ω1=3.99041为最小，极差为0.03806，相对TBT的最大误差为0.9538%。特别指出：取n=1，退化为Euler梁(CBT)，但计算结果显示刚度和质量矩阵奇异。这是由于CBT忽略了剪切作用的影响，特征值方程中计及剪切影响的元素为0，进而刚度和质量矩阵奇异。这时应取n≈1(本文取n=0.998)，Ω1=4.01477。这与Simsek[3]采用CBT与TBT预测的基频结果Ω1=4.14835，3.99042十分吻合。因此需考虑剪切变形作用且在高精度计算中，宜取n≥3的奇数。
图1 无量纲基频Ω1与GBT阶数n之间的关系曲线
Fig.1 Dimensionless fundamental frequency Ω1 versus order n of GBT
图2刻画了FGM梁(p=1)基频Ω1随无量纲轴向载荷P的变化：Ω1随轴向压力(正半轴)的增大而单调减小，直至达到临界载荷时Ω1=0而发生失稳；Ω1随轴向拉力(负半轴)的增大而单调增加，这是轴拉力减小了弯曲变形而增大了梁的整体刚度的缘故。此外，跨厚比δ越大，Ω1也越大。但从Ω1-P曲线的疏密程度来看，δ对Ω1的影响并不显著。
图2 不同跨厚比下无量纲基频Ω1与无量纲轴向载荷P之间的关系曲线
Fig.2 Dimensionless fundamental frequency Ω1 versus dimensionless axial load P for different δ
图3探讨了FGM梁(p=1, δ=5)的屈曲临界载荷Pcr随GBT阶数n的变化：Pcr随阶数n的变化波动也很小。取n≈1，Pcr=24.968 72；取n=3，Pcr=24.68925，这与Li等[6]采用CBT及Levinson梁理论预测的Pcr=26.705，24.671比较吻合，本文CBT预测值Pcr略偏低，且更为接近TBT预测值。
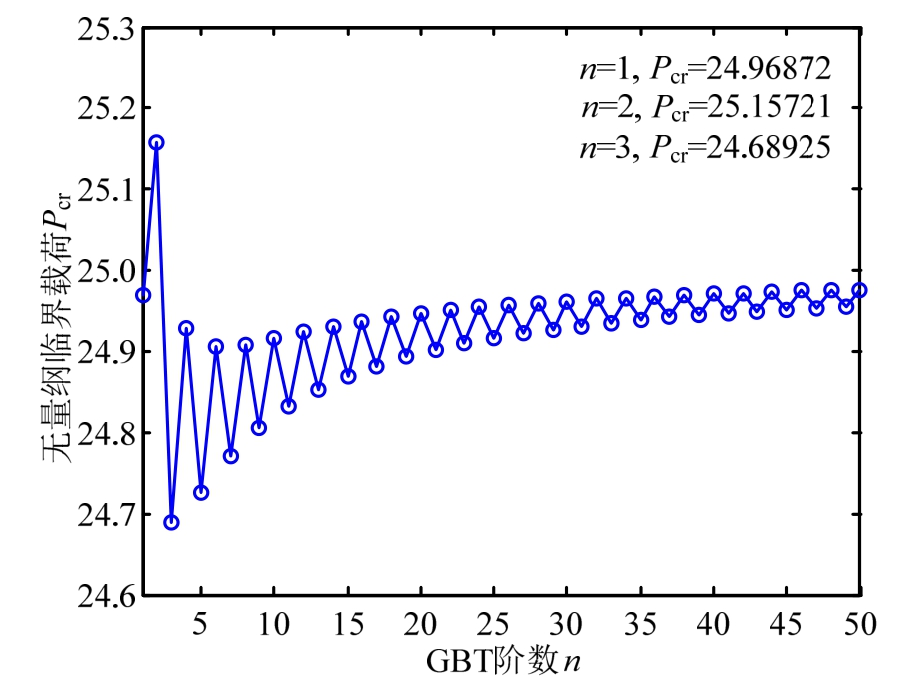
图3 无量纲临界载荷Pcr与GBT阶数n的关系曲线
Fig.3 Dimensionless critical buckling load Pcr versus order n of GBT
图4则采用TBT给出了FGM简支梁(p=1, δ=5)的屈曲模态：弯曲与剪切变形项挠度Wb和Ws曲线都关于ξ=0.5成轴对称，跨中挠度最大，此时Ws约为Wb的11%，剪切影响显著；而轴向位移曲线U关于点(0.5，0)成中心对称，轴线上各点的U值虽较小，但不恒为0，这是由于FGM梁的几何中面和物理中面并不重合，因此FGM梁的屈曲表现为拉压-剪切-弯曲的三重耦合。
图5给出了6种梯度指标p的Ω1-P曲线：由各曲线与横轴的交点不难看出，p越大，Pcr越小，梁越容易失稳；各参数取相同值，p越大，Ω1也越小，即Pcr与Ω1都随p的增大而减小。这是因为随着p的增大，陶瓷的成分减小了，梁的整体刚度降低了。
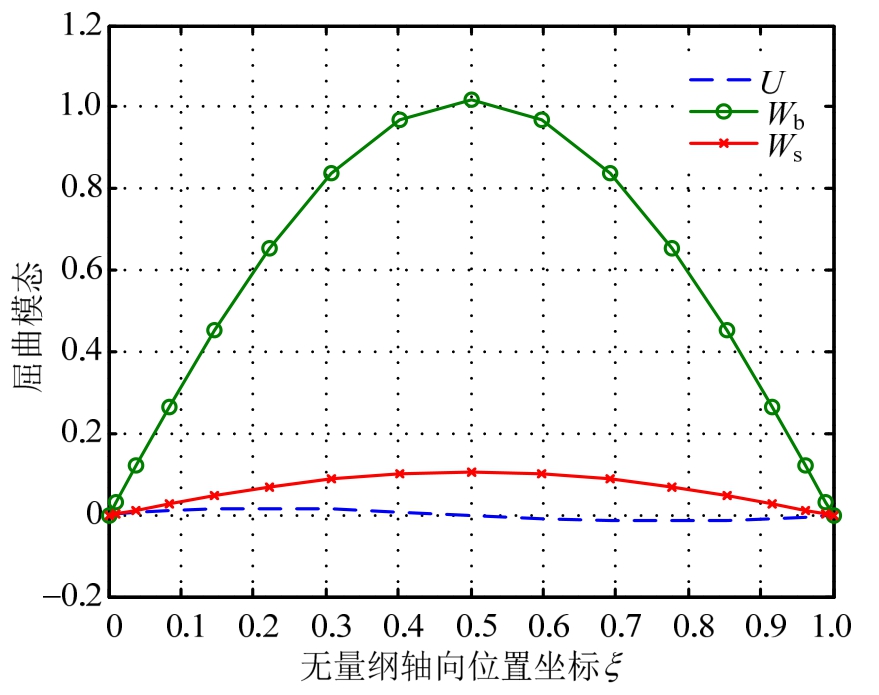
图4 FGM简支梁的屈曲模态
Fig.4 Buckling mode shapes of an FGM simply supported beam
图5 不同梯度指标下无量纲基频Ω1与无量纲轴向压力P之间的关系曲线
Fig.5 Dimensionless fundamental frequency Ω1 versus dimensionless axial load P for different p
3.2 FGM简支梁的耦合屈曲及耦合振动特性
本节用于探讨湿-热-机-弹耦合作用下FGM简支梁的稳定性与振动特性。本节GBT阶数取n=3，这里考虑由SUS 304与Si3N4两种材料组成的FGM梁，物性参数由表1给出[17,22]。
图6反映了均匀升温(UTR)、线性升温(LTR)与非线性升温(NLTR)FGM梁(p=1, δ=20, ΔC=0)的Ω1-ΔT及Pcr-ΔT曲线：对这3种升温类型来说，Ω1和Pcr都随升温ΔT的增加而单调减小，直至达到各自临界升温值ΔTcr而发生屈曲，此时Ω1和Pcr均为0。这是由于升温ΔT的增加使得热轴压力增大。并且各升温类型的Ω1-ΔT与Pcr-ΔT两曲线与横轴交于同一点，该点的横坐标为各自的临界ΔTcr值。UTR对应的ΔTcr=162.9 K，LTR对应的ΔTcr= 332.4 K，NLTR对应的ΔTcr=392.8 K，此时由热变形使梁达到临界平衡。即UTR最易使梁发生热屈曲，LTR次之，NLTR最不易。这是因为温度分布的不同引起各弹性系数不同，进而梁的整体刚度有所不同。
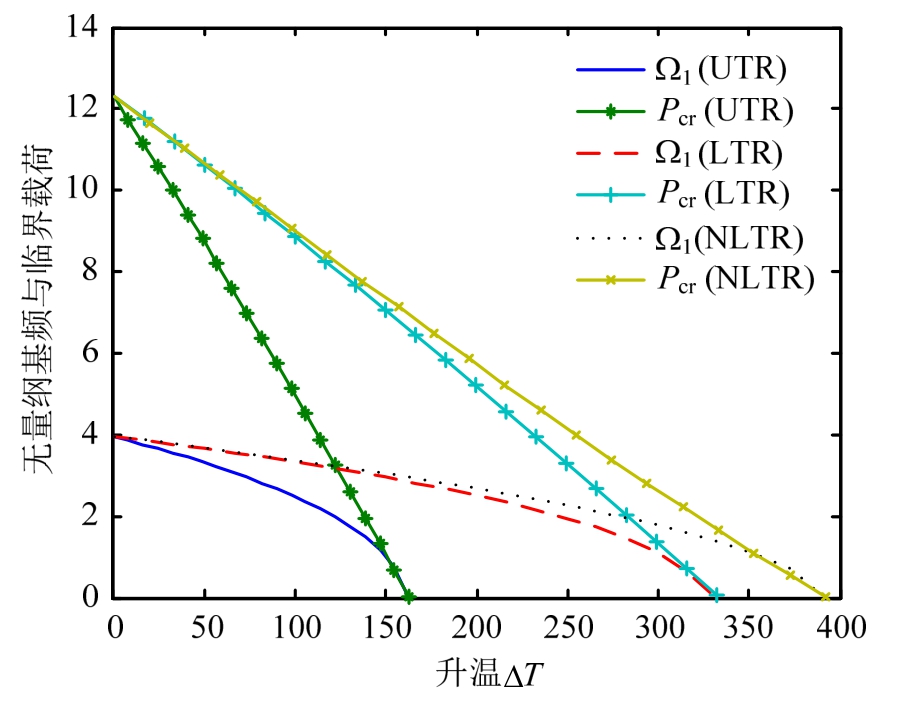
图6 升温对无量纲基频Ω1及临界载荷Pcr的关系曲线
Fig.6 Curves of temperature rise versus Ω1 and Pcr
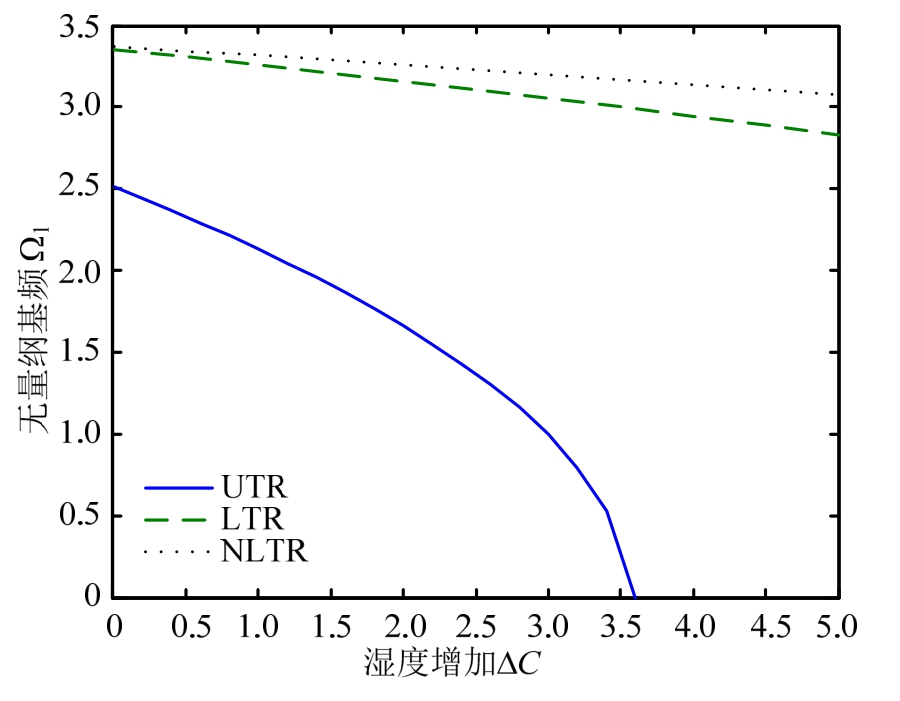
图7 无量纲基频Ω1与湿度增加ΔC的关系曲线
Fig.7 Curves of Ω1 versus moisture rise
图7则探讨了湿-热均为UTR、LTR及NLTR这3种分布类型，给出了FGM梁(p=1, δ=20,ΔT=100 K)的 Ω1-ΔC曲线：Ω1都随ΔC的增加而减小；湿度UTR分布使得Ω1减小最快，LTR分布次之，而湿度NLTR分布影响则最不明显；特别地，湿-热UTR分布，ΔC=3.6wt%，ΔT=100 K时，Ω1=0，此时湿-热载荷使FGM梁屈曲。而这明显低于图6不考虑湿度影响下温度UTR分布的ΔTcr=162.9 K，说明该情况下湿度对FGM梁的稳定性及振动特性影响显著。
图8刻画了湿-热均为LTR分布FGM梁(ΔC=1wt%，δ=20)取6种梯度指标p值时的 Ω1-ΔT曲线：Ω1都随ΔT的增加而单调减小；取相同参数值时，p越大，Ω1越小，ΔTcr也越小，梁越容易失稳。
图8 不同梯度指标下无量纲基频Ω1与线性升温ΔT的关系曲线
Fig.8 Curves of Ω1 versus linear temperature rises ΔT for different material graded indexes
图9反映了湿-热均为LTR分布FGM梁(p=1,δ=20)在5种ΔC取值时的Ω1-ΔT曲线：取相同参数值时，ΔC越大，Ω1则越小。且由各曲线的疏密程度可见，ΔC对Ω1影响较为明显。
图9 不同线性湿度增加下无量纲基频Ω1与线性升温ΔT的关系曲线
Fig.9 Curves of Ω1 versus linear temperature rises ΔT for different linear moisture rises ΔC
图10给出了湿-热均为NLTR分布FGM梁(p=1,ΔT=200 K)5种ΔC取值时的Ω1-δ曲线：由计算结果与各曲线疏密程度来看，Ω1都先随δ的增加而略微增大，当δ＞7以后，Ω1则都随δ的增加而略微减小，当 δ＞15以后，减小变得明显。换言之，湿度增加对FGM长梁的频率影响显著，而对短梁影响较小。
图10 无量纲基频Ω1与跨厚比δ的关系曲线
Fig.10 Curves of Ω1 versus δ under moisture and temperature nonlinear rise
图11反映了湿-热均为LTR分布FGM梁(p=0.2,δ=10, ΔT=200 K, ΔC=1wt%)取6种Pasternak地基刚度值Kp值时的Ω1-Kw曲线：Ω1都随Winkler地基刚度Kw的增加而增大。取相同的Kw值，Kp越大，Ω1也越大。即增大地基刚度提高了梁的抗弯性能，因此频率增大，梁抵抗失稳的能力将提高。
图11 无量纲基频Ω1与地基刚度Kw的关系曲线
Fig.11 Curves of Ω1 versus Kw under moisture and temperature linear rise
图12给出了湿-热均为LTR分布下弹性地基FGM简支梁(δ=10, ΔT=300 K, ΔC=1wt%, Kw=100,Kp=10)的前三阶无量纲频率Ω随p的变化曲线：前三阶频率Ω都随p的增加而减小。当0≤p≤2，Ω随p的增加而快速减小。这是因为此范围内陶瓷的成分将迅速减少而降低了FGM梁的整体刚度。当p＞2以后，Ω随p的增加而减小变得趋于缓慢，直至趋于纯金属(SUS 304)梁的频率。
图12 前三阶无量纲频率Ω与梯度指标p的关系曲线
Fig.12 Curves of the first three dimensionless frequencies Ω versus p under moisture and temperature linear rise
4 结论
基于n阶GBT，建立了湿-热-机-弹耦合FGM梁的屈曲及自由振动方程，采用Navier解法得出FGM简支梁屈曲及自由振动响应的精确解。着重讨论并分析了诸多参数对FGM梁稳定性和振动特性的影响。研究结果表明：
(1)GBT的阶数宜取n≥3的奇数，能取得十分满意的计算结果，且该理论适用范围广，具有重要的理论和工程应用价值。
(2)初始轴向机械压力、热轴力与湿轴力作用影响机理类似，均使FGM梁的频率减小、稳定性减弱，但以热-机载荷影响为主。
(3)临界载荷及频率都随温度、湿度、材料梯度指标的增加而减小，但随地基刚度的增加而增大，湿度和温度分布不同，对其影响有显著差异。特别地，湿度增加对FGM长梁的稳定性和振动特性影响显著，但对短梁影响并不明显。
(4)该分析方法可为FGM梁在复杂工况中工作时的安全设计和功能设计提供必要的理论依据及应用参考。
[1]Huang Y, Li X F.Buckling of functionally graded circular columns including shear deformation [J].Materials and Design, 2010, 31(7): 3159―3166.
[2]魏东, 刘应华.含裂纹功能梯度Euler-Bernoulli梁和Timoshenko梁的屈曲载荷计算与分析[J].复合材料学报, 2010, 27(4): 124―130.Wei Dong, Liu Yinghua.Buckling of functionally graded Euler-Bernoulli and Timoshenko beams with edge cracks[J].Acta Materiae Compositae Sinica, 2010, 27(4):124―130.(in Chinese)
[3]Simsek M.Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories [J].Nuclear Engineering and Design, 2010, 240(4): 697―705.
[4]赵凤群, 王忠民.计及不同剪切变形的功能梯度材料梁的弯曲分析[J].机械工程学报, 2014, 50(1): 104―110.Zhao Fengqun, Wang Zhongmin.Bending analysis of functionally graded materials beam considering different shear deformation theory [J].Journal of Mechanical Engineering, 2014, 50(1): 104―110.(in Chinese)
[5]Li S R, Wan Z Q, Zhang J H.Free vibration of functionally graded beams based on both classical and first-order shear deformation beam theories [J].Applied Mathematics and Mechanics, 2014, 35(5): 591―606.
[6]Li S R, Wang X, Wan Z Q.Classical and homogenized expressions for buckling solutions of functionally graded material Levinson beams [J].Acta Mechanica Solida Sinica, 2015, 28(5): 592―604.
[7]Pradhan K K, Chakraverty S.Effects of different shear deformation theories on free vibration of functionally graded beams [J].International Journal of Mechanical Sciences, 2014, 82(5): 149―160.
[8]蒲育, 滕兆春.Winkler-Pasternak弹性地基FGM梁自由振动二维弹性解[J].振动与冲击, 2015, 34(20): 74―79.Pu Yu, Teng Zhaochun.Two-dimensional elasticity solutions for free vibration of FGM beams resting on Winkler-Pasternak elastic foundation [J].Journal of Vibration and Shock, 2015, 34(20): 74―79.(in Chinese)
[9]蒲育, 滕兆春.基于一阶剪切变形理论FGM梁自由振动的改进型GDQ法求解[J].振动与冲击, 2018,37(16): 212―218.Pu Yu, Teng Zhaochun.Free vibration of FGM beams based on the first-order shear deformation theory by a modified generalized differential quadrature method [J].Journal of Vibration and Shock, 2018, 37(16): 212―218.(in Chinese)
[10]Kahya V, Turan M.Finite element model for vibration and buckling of functionally graded beams based on the first-order shear deformation theory [J].Composites: Part B, 2017, 109: 108―115.
[11]牛牧华, 马连生.基于物理中面FGM梁的非线性力学行为[J].工程力学, 2011, 28(6): 219―225.Niu Muhua, Ma Liansheng.Nonlinear mechanical behaviors of FGM beams on the physical neutral surface[J].Engineering Mechanics, 2011, 28(6): 219―225.(in Chinese)
[12]赵凤群, 王忠民.非保守力和热载荷作用下FGM梁的稳定性[J].工程力学, 2012, 29(10): 40―45.Zhao Fengqun, Wang Zhongmin.Stability of FGM beam under action of non-conservative force and thermal loads[J].Engineering Mechanics, 2012, 29(10): 40―45.(in Chinese)
[13]毛丽娟, 马连生.非均匀热载荷作用下功能梯度梁的非线性静态响应[J].工程力学, 2017, 34(6): 1―8.Mao Lijuan, Ma Liansheng.Nonlinear static responses of FGM beams under non-uniform thermal loading [J].Engineering Mechanics, 2017, 34(6): 1―8.(in Chinese)
[14]Pradhan S C, Murmu T.Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundations using differential quadrature method [J].Journal of Sound and Vibration, 2009, 321: 342―362.
[15]Mahi A, Adda Bedia E A, Tounsi A, et al.An analytical method for temperature-dependent free vibration analysis of functionally graded beams with general boundary conditions [J].Composite Structures, 2010, 92: 1877―1887.
[16]Wattanasakulpong N, Gangadhara P B, Kelly D W.Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams [J].International Journal of Mechanical Sciences, 2011,53(9): 734―743.
[17]Trinh L C, Vo T P, Thai H T, et al.An analytical method for the vibration and buckling of functionally graded beams under mechanical and thermal loads [J].Composites: Part B, 2016, 100: 152―163.
[18]张靖华, 赵幸幸, 李世荣.Hamilton体系下功能梯度梁的热冲击动力屈曲分析[J].爆炸与冲击, 2017, 37(3):431―438.Zhang Jinghua, Zhao Xingxing, Li Shirong.Dynamic buckling analysis of functionally graded beam under thermal shock in Hamilton system [J].Explosion and Shock Waves, 2017, 37(3): 431―438.(in Chinese)
[19]钮鹏, 李旭, 李世荣, 等.弹性地基上复合材料夹层梁的热过屈曲[J].工程力学, 2017, 34(增刊): 26―30.Niu Peng, Li Xu, Li Shirong, et al.The thermal buckling of composite sandwich beams on elastic foundation [J].Engineering Mechanics, 2017, 34(Suppl): 26―30.(in Chinese)
[20]何昊南，于开平.考虑热对材料参数影响的FGM梁热后屈曲特性研究[J].工程力学, 2019, 36(4): 52—61.He Haonan, Yu Kaiping.Thermal post-buckling analysis of FGM beams considering the heat effect on materials[J].Engineering Mechanics, 2019, 36(4): 52―61.(in Chinese)
[21]Xiang S, Kang G W.A nth-order shear deformation for the bending analysis on the functionally graded plates [J].European Journal of Mechanics A/Solids, 2013, 37:336―343.
[22]Farzad E, Mohammad R B.Small-scale effects on hygro-thermomechanical vibration of temperaturedependent nonhomogeneous nanoscale beams [J].Mechanics of Advanced Materials and Structures, 2017,24(11): 924―936.