扩展有限元法[1-3](extended finite element methods, XFEM)是基于单位分解理论对传统有限元(Finite Element Methods, FEM)的扩展，在构建位移场时需要就具体问题来选择相应的富集函数，并用水平集函数表征不连续界面，为含夹杂(孔洞)结构的数值计算提供了新的有效途径[4]，同时极大地避免了在反演分析过程中的网格重剖分。
反分析法是一种缺陷量化法[5]，它是基于结构表面一些关键点的实际响应值，通过建立有效的反演分析模型，在不破坏结构本身的前提下确定其内部缺陷的大小、形状和方向角。至今为止，有各种反分析技术和方法被提出，文献[6]提供了一种可仅在单面检测结构损伤并能够检测倾斜缺陷的方法，采用叠前偏移算法对在混凝土结构表面各检测点多次激励并采集的反射应力波进行处理，显示结构内部缺陷影像。文献[7]提出Lamb波技术进行板类结构的各种缺陷检测。文献[8]提出超声导波技术检测钢杆中的缺陷。除此而外，将智能算法与XFEM相结合进行结构缺陷反分析也日益引起重视。智能优化算法包括遗传算法(Genetic Algorithm, GA)[9]、人工蜂群(Artificial Bee Colony，ABC)算法[5,10]、粒子群算法、多级坐标搜索[11]等。GA借鉴了生物界中的进化规律，由美国Michigan大学的Holland教授于1975年在其论文“自然系统和人工系统的适配”中首次提出。交叉和突变是GA流程中必不可少的一部分，这种方法有助于生成数量最多的后代，再通过适应度值评估使得最优个体拥有更大的生存机会。
在国外，已有相关研究基于XFEM和GA提出了一种反演识别线弹性结构内各种类型的缺陷，包括直裂纹、圆形孔洞及不规则形孔洞等[12]。GA中的锯齿型种群数变化方案和加权平均数突变的结合可以更有效地反演出结构内部缺陷信息，且加权平均数突变能较易嵌入其他程序代码[13-14]。在国内的相关研究中[15]，也有人利用XFEM和ABC算法反演识别出线弹性结构内各种类型的单缺陷，最近文献[16]还基于XFEM和ABC算法对结构内部的多缺陷进行了反演分析。但是考虑到传统ABC算法的标准实施方案通常朝着任意的方向，而与加权平均数突变法的结合使得这种算法同时具备了指向性和任意性，可以很好地规避搜索过程中出现的局部最优现象。
本文提出了一种在传统ABC算法中嵌入加权平均数突变和交叉算子的改进ABC算法，将这种改进算法用于单个圆形、椭圆形缺陷和两个不规则缺陷的反演分析，并研究了该算法在传感器测得值有误差情况下的适应性。算例分析表明，改进的ABC算法相比于传统的ABC算法收敛速度更快且不易出现局部最优，且定位准确，鲁棒性较强。
1 反分析问题
本文提出的算法为缺陷量化反演提供了一种数值方法，即基于结构表面一些关键点的实际响应值确定其内部缺陷的大小、形状和方向角。如图1所示，文中将用cΓ和hΓ分别表示夹杂和孔洞的边界。将XFEM与改进ABC算法相结合寻找合适的参数模型估计结构关键点的响应，并与实际响应值进行比较，使得二者之间误差最小。
图1 含夹杂(孔洞)的结构体及其响应测试示意图
Fig.1 Schematic diagram of the structure with inclusion(void)and its response testing
参数模型通过一组向量表示如下：
式中，n表示待反演的参数个数。
单个圆形夹杂(孔洞)的反演参数如下：
式中：rc是圆的半径；(xc,yc)是圆心坐标。
单个椭圆形夹杂(孔洞)的反演参数如下：
式中：a是椭圆半长轴；b是椭圆半短轴；(xc,yc)是椭圆中心点坐标；β是方位角。
反演分析的目标函数定义如下：
式中：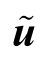
为数值模拟得到的响应测点位移，是一个定值；
为相应参数模型通过反分析法迭代得到的位移值，是参数θi的函数。
因此，反分析问题具体可构建如下：寻到θi∈Γc(或θi∈Γh )使得：
这里n是与缺陷对应的参数个数。
2 孔洞(夹杂)的水平集法表征
XFEM将非连续位移模式与水平集法相结合，使得不连续位移场的描述可以独立于网格的划分。XFEM的位移模式可以表示如下：
式中：ui为常规有限元法结点i处的位移未知量；ai为结点i的改进位移未知量；ψi(x)为扩展有限元法的改进函数，它的具体形式视情况而定；Ni(x)为结点i对应的常规有限元法的插值形函数；
为单位分解函数，其形式可以和Ni(x)相同，也可以不同，文中取两者相同。
圆形夹杂(孔洞)的水平集函数可以表示如下[11]：
式中：xc为圆形界面的圆心坐标；rc为圆形界面的半径。
椭圆形孔洞(夹杂)的水平集函数可以表示如下[3]：
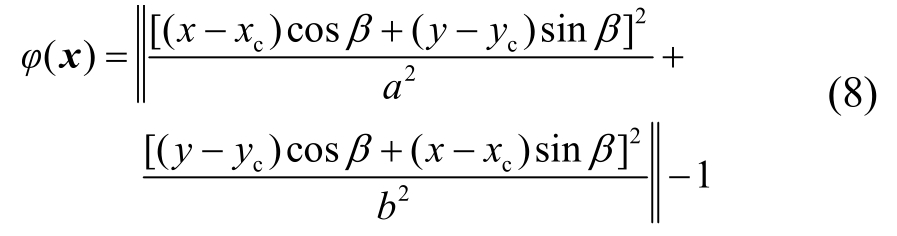
式中：(xc,yc)表示椭圆的中心坐标；a表示椭圆的长半轴；b表示椭圆的短半轴；β表示椭圆的方向角，以逆时针为正，β∈[-π,π]。
3 改进型人工蜂群算法
传统ABC算法在一定程度上朝着任意的方向搜索，在其中嵌入加权平均数突变和交叉算子避免了搜索的局部最优现象。
3.1 加权平均数突变
Liu和Chen[13]首先提出了加权平均数突变，它利用每个个体对应的适应度值，从而提供一种伪概率密度函数，是一种有指向性的突变方案，使得当前种群的参数值朝着适应度值增加的方向。
适应度函数表示如下：
式中：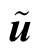
为数值模拟得到的响应测点位移，是一个定值；
为相应参数模型通过反分析法迭代得到的位移值，是参数θi的函数。
加权平均数的计算表示如下：
式中：i对应每个当前个体；ε是为了避免分母为0时加入的一个足够小的数；wi是一个中间变量；fitness(i)表示第i个个体对应的适应度值；child(k,i)表示第i个参数模型的第k个参数值；xm(k)表示到上一代结束为止获得的第k个参数的加权平均数。这个公式可以适当修改，从而使其能够应用于不同类型的问题。
3.2 交叉算子
交叉算子可以有助于将优良个体片段遗传给后代，同时又能起到全局搜索的作用，利于开采未知的空间。
随机交换两个参数模型之间的片段，表示如下：
产生的后代分别是11010xyyxyyxxy和yyxyx011011001。
3.3 主要计算步骤
1)种群数变化方案N(t)
这里利用了GA中迭代效果最好的锯齿型种群数变化方案，种群数在一个恒定的范围内波动，每经过T次迭代，种群数重新回到初始状态，见图2所示。
图2 种群数与迭代次数的关系
Fig.2 Relations between the number of population and the number of iterations
2)初始化求解参数，某个随机可行解参数child(k,j)表示如下：
式中：k取值于(1，n)之间的任意数，为n维解向量的某个分量；j取值于(1，N)；rand1为(0,1)之间的随机数；child(kmin,j)和child(kmax,j)为随机可行解child(k,j)的下、上限值。
3)邻域搜索得到优化解向量parent(k,j)，搜索公式如下：
式中：m取值于(1，N)，且m≠j，m和j均随机生成；rand2为(-1,1)之间的随机数，最后将适应度值较大的参数模型保存下来。
4)交叉算子和加权平均数突变，突变公式如下：
child(k,j)=child(k,j)+rand3×[xm(k)-child(k,j)](13)式中：xm(k)是上节内容里提到的第k个参数的加权平均数；rand3为(-1,1)之间的随机数。
4 数值算例
4.1 算例1：单个圆形夹杂的反演分析
本算例研究了在XFEM数值计算下被离散成19×39均匀网格的长方形板内单个圆形夹杂的反演分析，比较传统ABC算法和改进ABC算法的优劣。长方形(1 m×2 m)板一边受约束，一边受竖向拉伸荷载P=1.0 MPa的作用，计算简图如图3所示。本例是弹性体薄板，假设板处于平面应力状态。材料类型有2种，基体和夹杂。基体的弹性模量为E=22 GPa，泊松比v=0.167；夹杂的弹性模量为E=55 GPa，泊松比v=0.3。反演分析时，平均种群数N=3，种群数变化周期T=5，最大搜索限定次数Nlimit=20，最大迭代次数Niter=300。
图3 单侧受拉板的计算简图 /m
Fig.3 Geometry of tension plate and XFEM mesh
圆形夹杂有3个待反演的参数，分别是圆的半径rc=0.1 m和圆心坐标(xc,yc)=(0.5 m,1 m)。待反演参数的限值为xc∈[0.2,0.8]，yc∈[0.2,1.8]，rc∈[0.05,0.4]。鉴于算例中夹杂的尺寸较小，传感器布置的数量不能太少，在这里除约束边以外，每条边3个传感器，如图2所示，共7个。图4分别比较了在这两种算法下得到的圆心坐标(xc,yc)、半径rc和适应度值f的收敛过程。结果表明，改进ABC算法迭代效果更稳定，收敛速度更快而且能有效地避免局部最优。图5中给出了单个圆形夹杂的反演过程。
图4 传统ABC算法和改进ABC算法对待反演夹杂参数收敛过程的影响
Fig.4 Influence of standard ABC algorithm and improved ABC algorithm on the convergence process for the inversion of inclusion parameter
图5 夹杂的反演过程 /m
Fig.5 Inversion process of the inclusion
反演分析中结构的实际响应值在文中均通过实际结构的FEM数值解得到，FEM数值解通过商业有限元软件ABAQUS计算获取。
4.2 算例2：单个圆形孔洞的反演分析
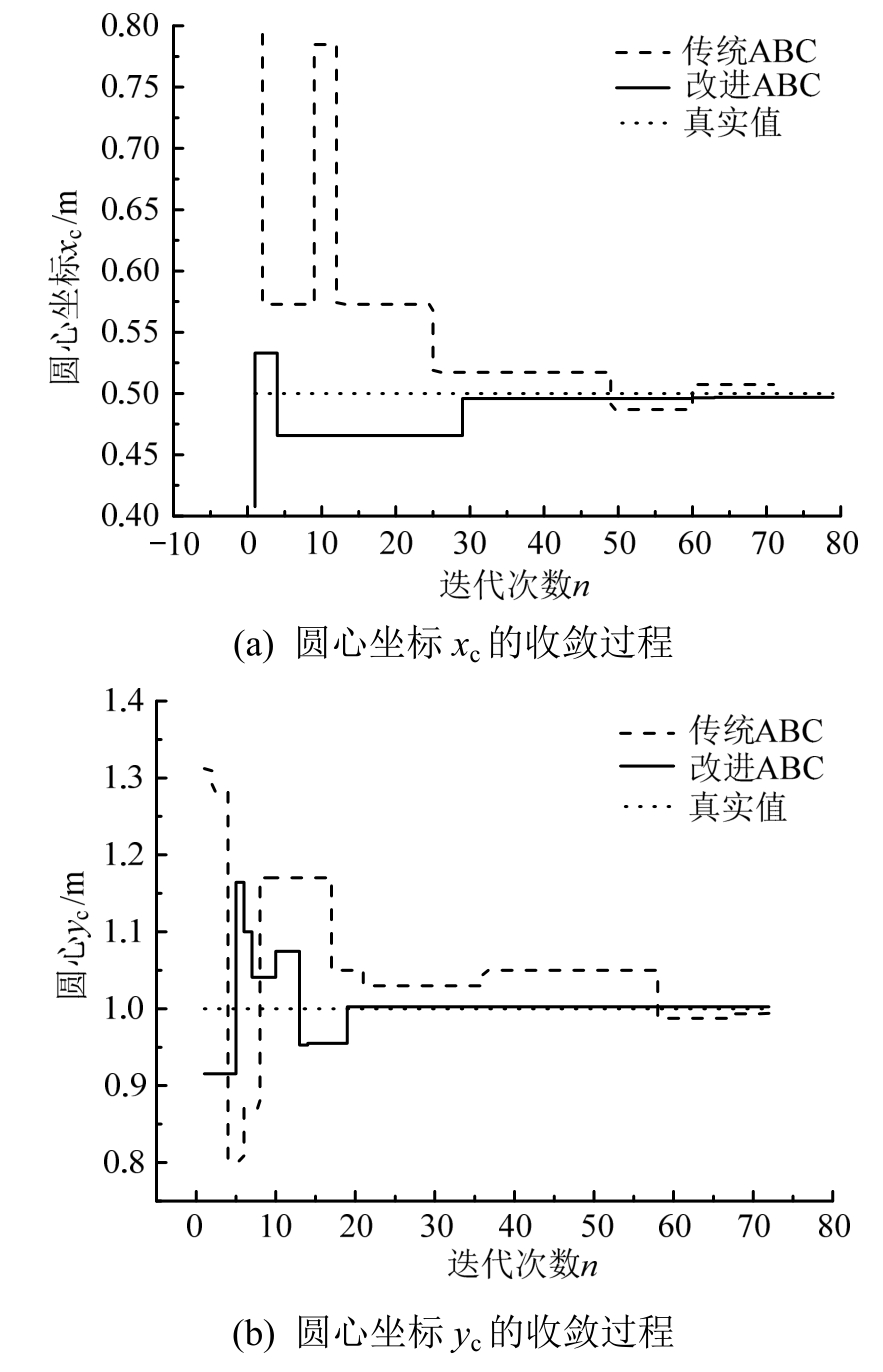
图6 传统ABC算法和改进ABC算法对待反演孔洞参数收敛过程的影响
Fig.6 Influence of standard ABC algorithm and improved ABC algorithm on the convergence process for the inversion of void parameter
本算例同算例1，唯一不同的地方是将圆形夹杂换成了圆形孔洞，这两种算法的反演效果如图6所示，从图中可以得出和算例1相同的结论，所以改进ABC算法同时适用于含孔洞和夹杂结构。图7给出了孔洞的反演过程。
图7 孔洞的反演过程 /m
Fig.7 Inversion process of the void
4.3 算例3：单个椭圆形夹杂(孔洞)的反演分析
这里研究了用改进ABC算法反演椭圆形夹杂(孔洞)边界的有效性问题，这个例子给出了一个更加真实的情况，因为结构内的夹杂(孔洞)几乎不可能是规则的圆形。
在XFEM数值计算下正方形板被离散成20×20均匀网格，板内含单个椭圆形夹杂(孔洞)。方形(2 m×2 m)板下边界受约束，上边界受竖向拉伸荷载P=1.0 MPa的作用。椭圆形夹杂(孔洞)有5个待反演参数，分别是椭圆中心点坐标(xc,yc)=(1 m,1 m)，半长轴a=0.15 m，半短轴b=0.1 m，方位角β=60。反演分析时，待反演参数的限值为xc∈[0.2，1.8]，yc∈[0.2，1.8]，a∈[0.05，0.4]，b∈[0.05，0.4]，β∈[0，90]。迭代最终收敛于最优解附近。可以得出结论：改进ABC算法同样适用于不规则的椭圆形夹杂(孔洞)边界，图8给出了椭圆形孔洞的反演过程；图9给出了椭圆形夹杂的反演过程。
图8 椭圆形孔洞的反演过程 /m
Fig.8 Inversion process of the elliptical void
图9 椭圆形夹杂的反演过程 /m
Fig.9 Inversion process of the elliptical inclusion
4.4 算例4：两个不规则孔洞的反演分析
真实结构内往往不止存在一个缺陷，缺陷的几何形状也会比较复杂，本算例研究了用改进ABC算法反演多个不规则孔洞边界的有效性问题。
本算例中方板的几何尺寸、材料参数、边界条件和荷载条件同算例3，唯一不同的地方是将椭圆形夹杂(孔洞)换成了两个不规则孔洞。在反演前期，考虑到反演效率问题，采用两个圆形孔洞作为真实缺陷的近似，共有6个反演参数，分别为两个圆的圆心坐标和半径。待前期反演结束，缺陷的大致位置和尺寸已经确定，再采用两个椭圆形缺陷作为真实缺陷的近似，这时共有10个反演参数，分别为两个椭圆的中心点坐标，长短半轴和方位角。反演过程如图10所示，从图中可以得出，改进ABC算法同样适用于多个不规则缺陷的反演。
图10 两个不规则孔洞的反演过程 /m
Fig.10 Inversion process of two irregular voids
4.5 算例5：改进ABC算法的鲁棒性分析
在实际测试中受制于仪器的性能和外界环境影响等原因，所测得的信号与真实值相比通常存在一定误差，本算例研究了改进ABC算法在传感器测得值有一定误差情况下的有效性问题。
本算例同算例2，只是在通过FEM数值解得到的结构实际位移值的基础上分别引入5%、10%、15%和20%的误差，以探讨位移误差对反演结果的影响，验证本文提出的改进ABC算法的鲁棒性。不同程度位移误差下的反演结果如图11所示，从图中可以得出，改进ABC算法的鲁棒性较好，但是当误差过大(本算例中为20%)时，反演得到的缺陷位置将出现偏差。
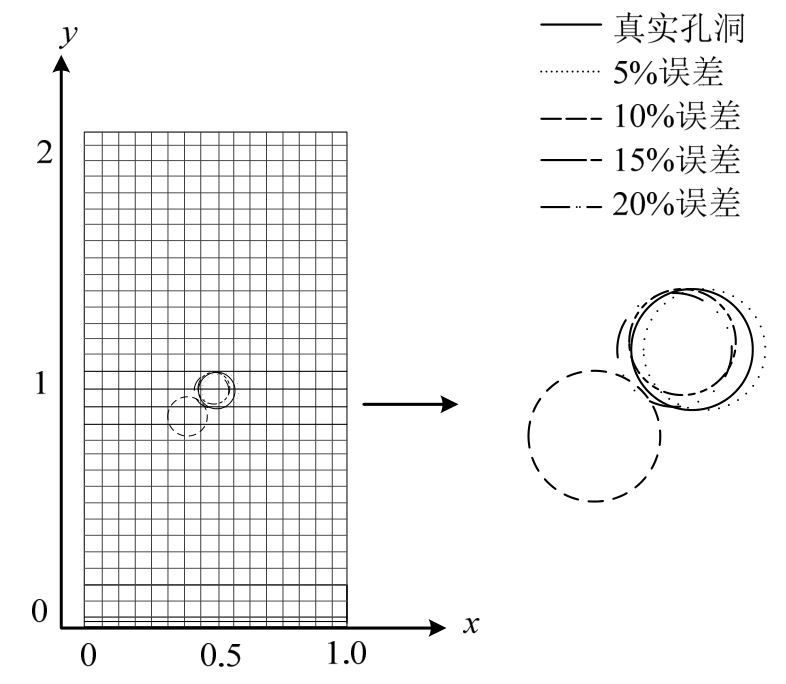
图11 不同程度位移误差下的反演结果 /m
Fig.11 Inversion results under different degrees of displacement error
5 结论
本文结合了加权平均数突变和传统ABC算法的优点，并与XFEM有效地结合在一起。改进ABC算法同时具备了搜索的指向性和任意性，有效地避免了搜索的局部最优现象。算例计算表明：这种改进ABC算法能准确反演出结构的真实缺陷信息；改进ABC算法相比于传统ABC算法收敛速度更快且不易出现局部最优，且定位准确，鲁棒性较强。
文中建立的反演分析模型能够较易拓展到动响应反演和分区域搜索，这是本文后续的研究重点。
[1]Moës N, Dolbow J, Belytschko T.A finite element method for crack growth without remeshing [J].International Journal for Numerical Methods in Engineering, 1999, 46: 131―150.
[2]Daux C, Moës N, Dolbow J, et al.Arbitrary branched and intersecting cracks with the extended finite element method [J].International Journal for Numerical Methods in Engineering, 2000, 48: 1741―1760.
[3]金峰, 方修君.扩展有限元及与其它数值方法的联系[J].工程力学, 2008, 25(1): 1―17.Jin Feng, Fang Xiujun.Extended finite element method and its relationship with other numerical methods [J].Engineering Mechanics, 2008, 25(1): 1―17.(in Chinese)
[4]Jiang S Y, Du C B, Gu C S, et al.XFEM analysis of the effects of voids, inclusions, and other cracks on the dynamic stress intensity factor of a major crack [J].Fatigue & Fracture of Engineering Materials &Structures, 2014, 37: 866―882.
[5]Sun H, Waisman H, Betti R.Nondestructive identification of multiple flaws using XFEM and a topologically adapting artificial bee colony algorithm [J].International Journal for Numerical Methods in Engineering, 2013, 95: 871―900.
[6]骆英, 李忠芳.混凝土结构缺陷检测中的叠前偏移理论及应用[J].工程力学, 2009, 26(2): 182―187.Luo Ying, Li Zhongfang.Theory and application of prestack migration in flaw detection of concrete structure[J].Engineering Mechanics, 2009, 26(2): 182―187.(in Chinese)
[7]刘增华, 徐营赞, 何存富, 等.板状结构中基于Lamb波单模态的缺陷成像试验研究[J].工程力学, 2014,31(4): 232―238.Liu Zenghua, Xu Yingzan, He Cunfu, et al.Experimental study on defect imaging based on single Lamb wave mode in plate-like structures [J].Engineering Mechanics,2014, 31(4): 232―238.(in Chinese)
[8]吴斌, 李隆涛, 王秀彦, 等.基于超声导波技术对钢杆表面缺陷的无损检测[J].工程力学, 2003, 20(5):149―154.Wu Bin, Li Longtao, Wang Xiuyan, et al.Study on nondestructive testing of steel bar surface defects based on ultrasonic guided wave technology [J].Engineering Mechanics, 2003, 20(5): 149―154.(in Chinese)
[9]Rabinovich D, Givoli D, Vigdergauz S.XFEM-based crack detection scheme using a genetic algorithm [J].International Journal for Numerical Methods in Engineering, 2007, 71(9): 1051―1080.
[10]Ma C, Yu T, Le V L, et al.An effective computational approach based on XFEM and a novel three-step detection algorithm for multiple complex flaw clusters[J].Computers & Structures, 2017, 193: 207―225.
[11]Zhang C, Nanthakumar S S, Lahmer T, et al.Multiple cracks identification for piezoelectric structures [J].International Journal of Fracture, 2017, 206(2): 151―169.
[12]Waisman H, Chatzi E, Smyth A W.Detection and quantification of flaws in structures by the extended finite element method and genetic algorithms [J].International Journal for Numerical Methods in Engineering, 2010, 82(3): 303―328.
[13]Liu J L, Chen C M.Improved intelligent genetic algorithm applied to long-endurance airfoil optimization design [J].Engineering Optimization, 2009, 41(2): 137―154.
[14]Chatzi E N, Hiriyur B, Waisman H, et al.Experimental application and enhancement of the XFEM-GA algorithm for the detection of flaws in structures [J].Computers & Structures, 2011, 89(7/8): 556―570
[15]江守燕, 杜成斌.基于扩展有限元的结构内部缺陷(夹杂)的反演分析模型[J].力学学报, 2015, 47(6): 1037―1045.Jiang Shouyan, Du Chengbin.Numerical model for identification of internal defect or inclusion based on extended finite element method [J].Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 1037―1045.(in Chinese)
[16]王珍兰, 赵文虎, 杜成斌, 等.基于扩展有限元法的结构内部多缺陷的反演分析[J].水运工程, 2017(12):57―63.Wang Zhenlan, Zhao Wenhu, Du Chengbin, et al.Inverse analysis for identification of multiple internal flaws using XFEM [J].Port & Waterway Engineering, 2017(12):57―63.(in Chinese)