船体在水下爆炸载荷作用下的响应和毁伤是涉及舰船安全性的重要问题之一[1-2]。针对可能受到的水下爆炸威胁,海洋平台等民用设施针对水下爆炸冲击破坏进行防护设计多采用多层片组防护结构。固支多层片组结构在水下爆炸冲击载荷作用下的毁伤行为研究,对于海上平台的抗冲击防护设计具有重要意义。由于该问题不仅涉及了结构大变形时的各种非线性因素,还必须考虑水下爆炸时的流固耦合作用,因此极大地提高了分析难度。Taylor[3]最早给出了用来考虑水下爆炸时结构同流体耦合的无限大平板理论;Cole[4]进一步推导了考虑入射波衍射时的有限平板压力表达式,并通过假设变形模式,推导了圆膜的变形。但这些方法假设的变形模式只适用于大变形的情况。针对单层固支平板结构在水下爆炸载荷作用产生的塑性大变形或整体断裂破坏模式,Ramajeyathilagam等[5]进行了一系列水下爆炸作用下的固支平板动态响应试验,研究了固支平板在不同冲击因子作用下的失效模式;Rajendran等[6]则从能量的观点对爆炸载荷作用固支板的变形进行了讨论,利用冲击因子对变形模式进行划分;国内方面,吴有生等[7]用能量法推导出计算舰船板架塑性变形与破损的公式;吴成等[8]应用能量原理,推导出反映固支方板在冲击载荷作用下变形的最终挠度的解析解。目前针对多层防护结构的研究还相对较少,胡小利等[9]研究了多层片组模型在射弹侵彻下的毁伤情况,张振华等[10]对多层板架结构在水下接触爆炸作用下的破坏机理开展了试验研究。
本文对固支条件下的多层片组结构在非接触水下爆炸冲击载荷迎面作用下的塑性毁伤机理进行了理论分析,建立了相应的计算模型。通过理论模型的计算预测出多层片组结构的毁伤破坏情况,包括其塑性变形层数、剪切破坏层数和最大破坏深度。利用AUTODYN仿真软件,对不同药量下多层片组结构的毁伤进行了数值模拟,与理论结果进行了比较,其结果具有较好的一致性。通过试验对水下爆炸冲击波强度以及多层片组结构的毁伤程度进行了验证,并分析了试验误差产生原因,试验结果与理论模型比较吻合。
1 理论模型
水下爆炸冲击波冲击多层片组结构示意图如图1,结构由6层圆板构成,其边界固支,层片半径R,厚度h,层片间距为w0;爆源半径R0,中心与多层片组结构距离为d。
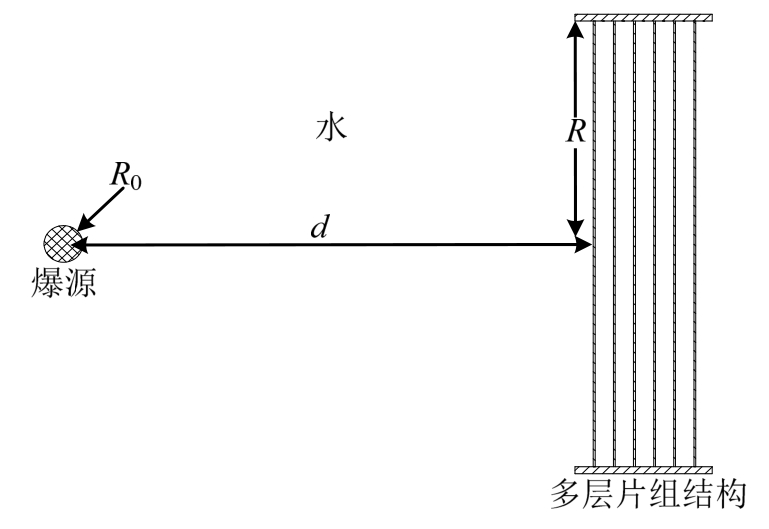
图1 炸药冲击多层片组结构示意图
Fig.1 Schematic diagram of explosive impact multi-layer sheet
对于多层片组结构破坏问题进行直接理论求解存在诸多困难,而结构遭到冲击载荷作用后的大变形和剪切断裂程度才是所关心的重点。能量法不需要考虑复杂的中间过程,只需给出问题的初值,利用近似的能量公式,即可得到与所采用的模型近似适应的解,从而达到实用的目的,因此本文利用能量守恒原理,从能量的角度对固支多层片组结构的损伤破坏进行讨论,建立理论毁伤模型。为简化分析,作如下假定:
1)多层片组材料为理想刚塑性材料,忽略结构的应变率效应。
2)忽略层片变形引起的所受冲击波动能的变化。
3)忽略层片间作用引起的能量损耗。
4)假定水下爆炸冲击波作用过程以及层片在冲击波方向受力是轴对称的。
5)层片受冲击波毁伤后产生的变形挠度符合正弦函数规律。
多层片组结构在受到水下爆炸冲击波作用后,圆形层片结构发生塑性剪切破坏。爆炸冲击波能量首先转变为第一层圆形板的塑性变形能、剪切破坏能以及板的动能,其中层片塑性变形能Up包括相应于弯曲变形的势能U1和相应于中面应变的势能U2。
1.1 层片塑性变形能
层片单位体积的变形能[7]可以写为:
变形能Up包括相应于弯曲变形的势能U1和相应于中面应变的势能U2:
对于U1,仍按照弯曲变形关系处理,即应变满足:
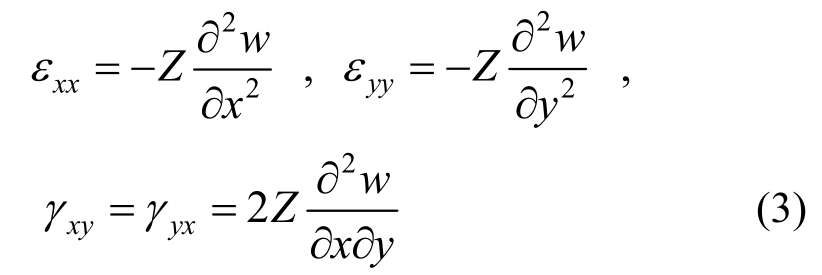

图2 圆形层片坐标系
Fig.2 Circular plate coordinate system
刚塑性材料在屈服时有σxx =σs,σyy=σs,按照Von Mises屈服准则有:
因此,按图2的坐标系,弯曲变形的势能为:
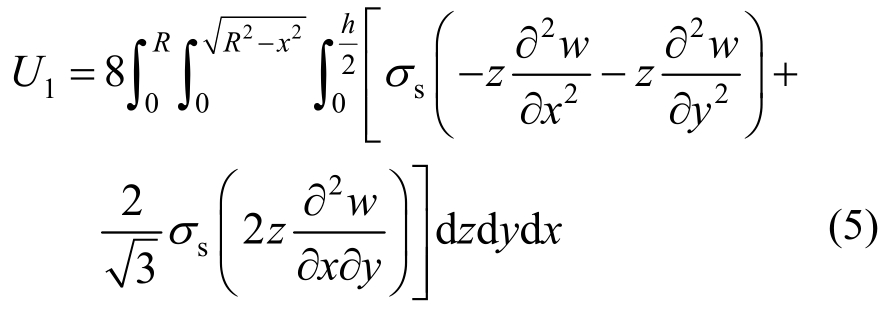
由于位移引起的中面应变为:
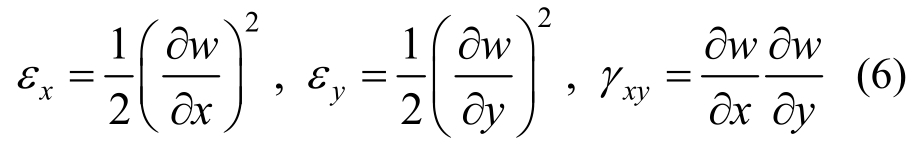
相应于中面应变的势能U2可以表示为:
式中,Nx、Ny、Nxy为中面膜力。Nx=hσx,Ny=hσy,Nxy=hτxy。因而:

假设层片的变形挠度为:
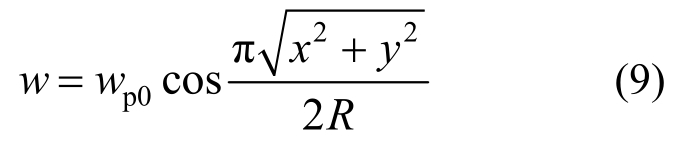
式中,wp0为板中心的变形挠度。
将式(9)代入U1和U2,可得圆形层片的变形能:
式中:
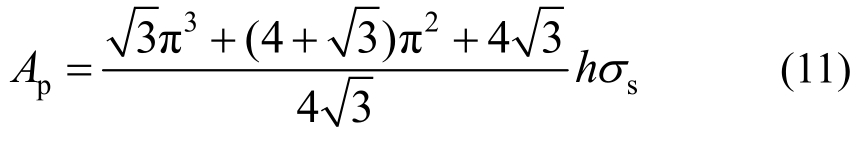
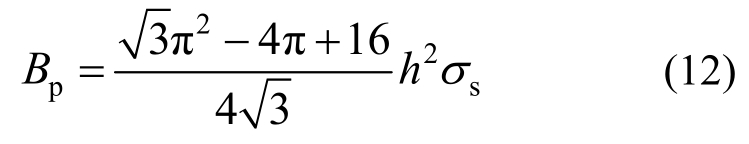
1.2 剪切破坏能
由于层片的边界为固定支撑,当层片的变形相对较小时,层片的变形在边界处呈现出固支边界条件特性,即边界处变形曲线曲率趋近于0。当水下爆炸冲击波爆炸载荷相对层片达到一定强度时,层片的边界变形曲率便达到一定值,边界处产生剪切应力集中区域,出现剪切破坏,此时层片塑性变形挠度为ws,可根据层片弯曲变形达到多大时层片边界处剪切应力达到剪切屈服极限来得出。剪切所消耗的能量Us即为剪切力在此过程中所做功[11]:
式中:z为剪切层片迎爆面距层片背部的距离;R为层片半径;h为层片厚度;τz为层片材料剪切屈服极限,在层片边界部分建立坐标系,如图3所示。
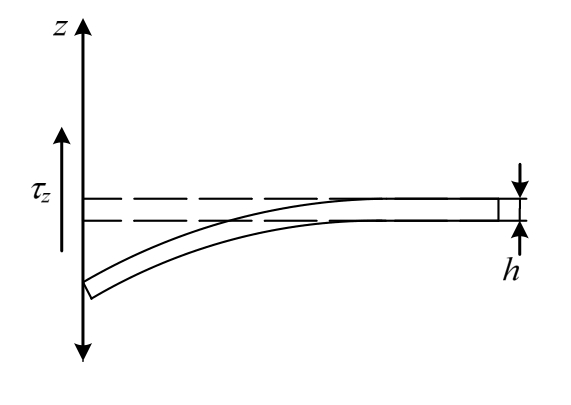
图3 剪切破坏示意图
Fig.3 Schematic diagram of shear failure
1.3 层片的动能
根据圆板在爆炸冲击载荷作用下的实际变形形状,给出其数学描述为[8]:
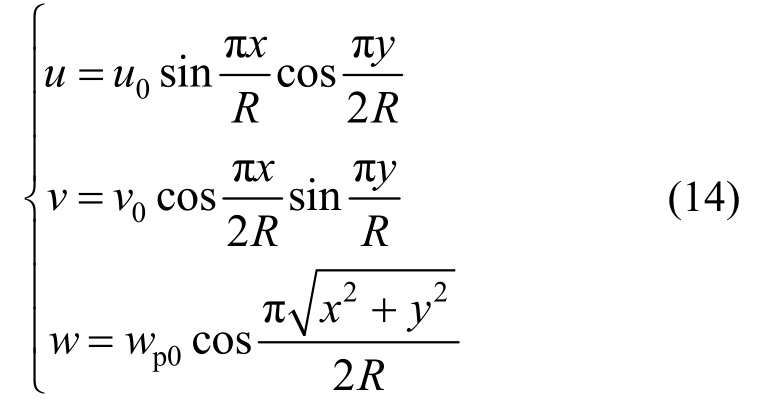
式中:u、v和w分别为x、y和z方向上的位移;u0、v0分别为x、y方向上的最大位移;wp0为板中心点在z方向上的挠度。
层片的动能Uk由式(15)给出:
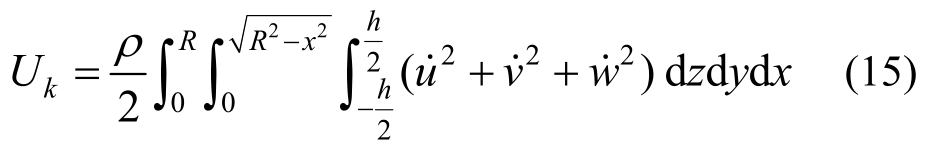
式中:ρ为层片材料的密度,由于层片在x、y方向上的位移u、v与w相比非常小,可忽略不计,因此式(15)可写为:
1.4 水下爆炸冲击波动能
水下爆炸时,单位面积的冲击波动能[12]为:

式中:Q为药包质量;d为计算点到药包中心的距离。对于TNT炸药,系数K=8.14×105,α=2.05,λ为能量修正系数。由于考虑非接触爆炸,冲击波可近似视为平面波形式传播。
1.5 水下冲击波作用下层片毁伤计算
水下爆炸冲击波能量作用在层片上后,其将首先转化为板架初始动能Ke。由能量守恒原理,冲击波初始动能将转化为层片塑性变形能、剪切破坏能以及圆形层片的动能。则可得:
式中,A/m2为层片作用面积。
水下爆炸冲击波首先对多层片组结构的第一层层片进行冲击破坏,第一层层片经过塑性变形和剪切破坏后,利用剩余动能冲击第二层层片,以此类推,直至层片动能全部转化为塑性变形能和剪切破坏能。以第一层层片的外表面作为起始位置,假设多层片组结构冲击破坏的最大深度为L,当塑性变形挠度大于剪切临界挠度ws时即发生剪切破坏。因此,根据L的大小即可得出剪切破坏层数n以及塑性变形层数m,式(18)可写为:
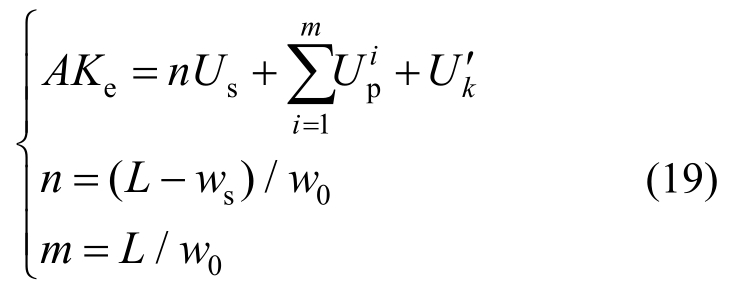
式中:n为多层片组结构剪切破坏层数;m为塑性变形层数;w0为两层层片之间的距离。其中剪切层片的塑性变形挠度为ws,第i层未剪切层片的塑性变形挠度wi =L-(i-1)w0。根据式(19)即可求出多层片组冲击破坏最大深度L,以及塑性变形层数m和剪切破坏层数n。
2 数值计算
2.1 数值仿真模型
利用AUTODYN软件建立如图4的数值仿真模型,由于模型为轴对称结构,因此采用2D建模。模型采用流固耦合算法,水、空气以及炸药为Euler算法,多层片组结构为Lagrange算法。水域长1150 mm,宽1000 mm,周围施加透射边界条件;多层片组结构共6层,半径267 mm,每层间隔20 mm,采用2024t351铝合金材料,6层铝合金圆板边界固支在8 mm厚的壳体上,壳体材料为4340不锈钢。整个片组结构长150 mm,并处于空气域中,炸药距片组结构的迎爆面1000 mm。Euler域以2 mm划分一个网格,共171900个网格单元,为提高计算效率,在远离爆炸区域的边界处采用渐变加宽网格。

图4 仿真计算模型及局部放大图
Fig.4 Simulation calculation model and partial enlargement
2.2 材料模型及参数
上述仿真模型中有水、炸药、空气、铝合金圆板和不锈钢壳体五种材料,仿真计算时利用不同状态方程定义各种材料。其中壳体采用Johnson-Cook状态方程,空气为理想气体状态方程材料参数取自AUTODYN标准数据库[13]。采用SHOCK状态方程[14]模拟水的状态,其方程为:
其中:
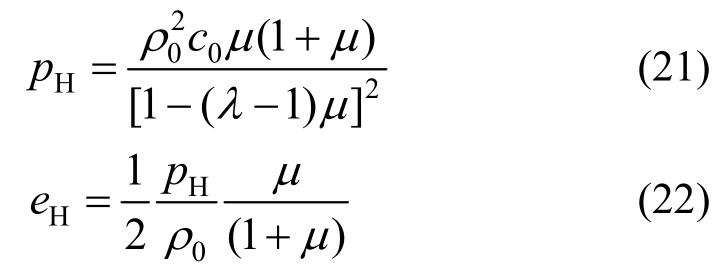
为冲击波关系式,式中λ和c0为常数,由以下冲击波实验关系式确定:
式中:D为冲击波速度;u为波后质点速度。取ρ0=0.998g/cm3,c0=1.647×103m/s,λ=1.921。
炸药采用JWL状态方程,JWL状态方程定义压力为相对体积V和单位初始构形体积内能E的函数:
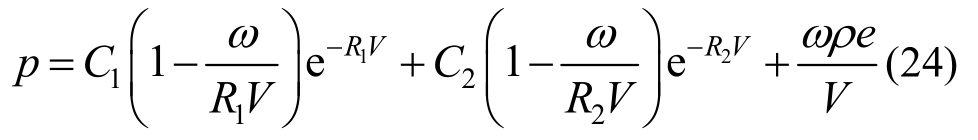
式中:p为压力;V为相对体积;ρ为炸药初始密度;e为单位质量比内能;ω、C1、C2、R1、R2为表征炸药特性的常数。对于TNT炸药,ρ=1.63 g/cm3,e=4.19 MJ/kg,C1=371.2 GPa,C2=3.231 GPa,R1=4.15,R2=0.95,ω=0.30。
由于铝合金圆板在水下爆炸冲击波作用下的动态响应具有应变速率大的特点,因此采用Cowper-Symond本构模型计算应变率的影响[15]。Cowper-Symond本构模型中动态屈服应力与应变率的关系如下:

式中:σy表示动态下的应力;A为材料初始静态屈服应力;B代表幂指数前的系数;n是加工硬化系数;ε为真实应变; 为应变率;D和q为应变率强化效应的系数。对于2024t35铝合金材料,Cowper-Symonds方程中A=180 MPa,B=210 MPa,n=0.20,D=7000 s,q=20[16]。
为应变率;D和q为应变率强化效应的系数。对于2024t35铝合金材料,Cowper-Symonds方程中A=180 MPa,B=210 MPa,n=0.20,D=7000 s,q=20[16]。
2.3 计算结果分析
以北约各成员国普遍采用的冲击因子f*[17]作为评判水下爆炸冲击波作用下多层片组结构失效毁伤评判的标准:
式中:W/kg为炸药质量;d/m为层片和爆炸中心之间的距离。分别对25 g~150 g不同药量下的六种工况进行讨论,验证数值仿真结果与理论模型计算结果的一致性。
1)水下爆炸冲击波压力计算结果分析
在第一层层片中心法线方向距离药包中心1 m处设置高斯点,考察该处的冲击波峰值压力及随时间的变化规律。对于自由场中水下爆炸冲击波的传递,Cole在早期通过对大量实验数据的整理,总结了水下爆炸冲击波经验公式,并得到广泛认可,Zamyshlyayev[18]在其基础上改进为:
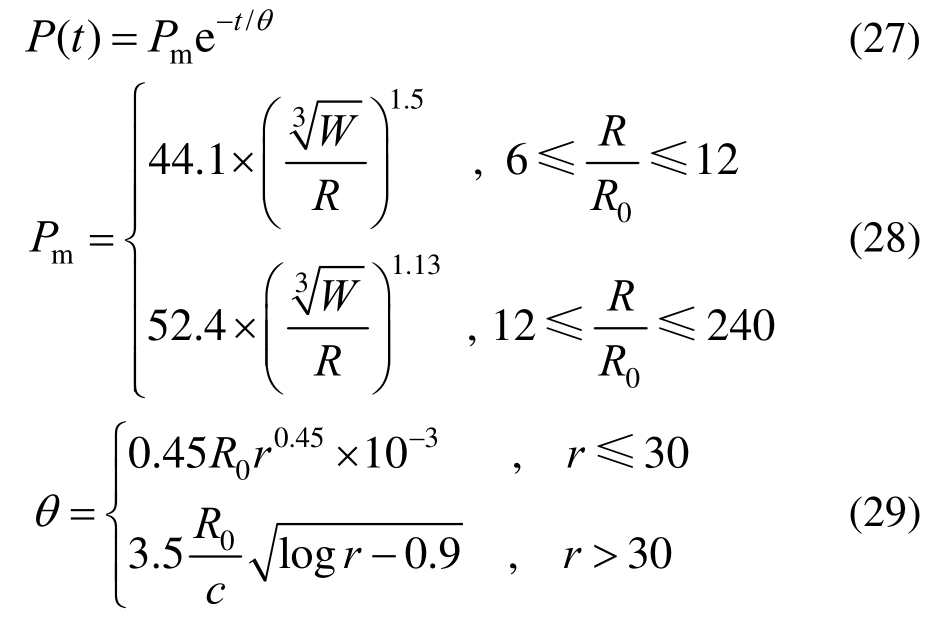
式中:Pm/MPa为冲击波峰值压力;P(t)/MPa为冲击波压力;θ为冲击波的指数衰减时间常数,指冲击波压力峰值Pm/s衰减到Pm/e所需的时间;W/kg为TNT炸药质量;R/m为测点到爆心的距离;R0/m为炸药初始半径;c/(m/s)为水中声速;r为R/R0。
仿真计算得到的距药包中心1 m处爆炸冲击波峰值与理论值对比见表1。100 g炸药在1 m处冲击波压力衰减曲线和其经验公式对比结果见图5。数值计算得到的冲击波压力与经验值误差在13.3%内,仿真结果与理论计算吻合较好。
2)结构毁伤分析
固支平板在水下爆炸冲击波作用下有3种失效模式[19],即模式Ⅰ:塑性大变形;Ⅱ:平板拉伸撕图6是100 g炸药在1 m处爆炸时,水下爆炸冲击波传播过程。在0.56 ms时,冲击波作用到多层片组结构上。图7为结构毁伤变形过程,从毁伤过程可以看出,爆炸冲击波作用到多层片组结构后,多层片组结构首先产生了塑性大变形,进一步出现边界剪切破坏,层片中心处同时有一定的破损。对上述有限元模型计算得到的6种工况下的多层片组破坏结果与理论计算结果进行对比分析(其中λ=4[7]),如表2所示。
表1 冲击波压力峰值仿真与理论对比
Table 1 Comparison of Simulation and Theory of Peak Shock Pressure

工况药量W/g炸药半径R0 /m距离R/m冲击因子1 250.015510.07 2 500.019510.10 3 750.022310.12 41000.024510.14 5 1250.026410.16 6 1500.028110.17 f *冲击波压力理论值/MPa冲击波压力仿真值/MPa误差/(%)13.05811.7759.8 16.95414.68913.3 19.75217.70010.4 22.01220.0608.9 23.94221.33110.9 25.64422.60811.8
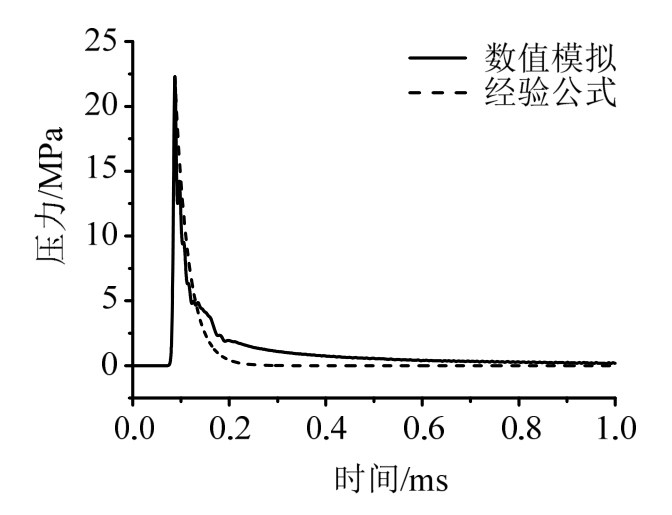
图5 冲击波仿真值与经验公式的对比
Fig.5 Comparison between shock wave simulation values and empirical formulas

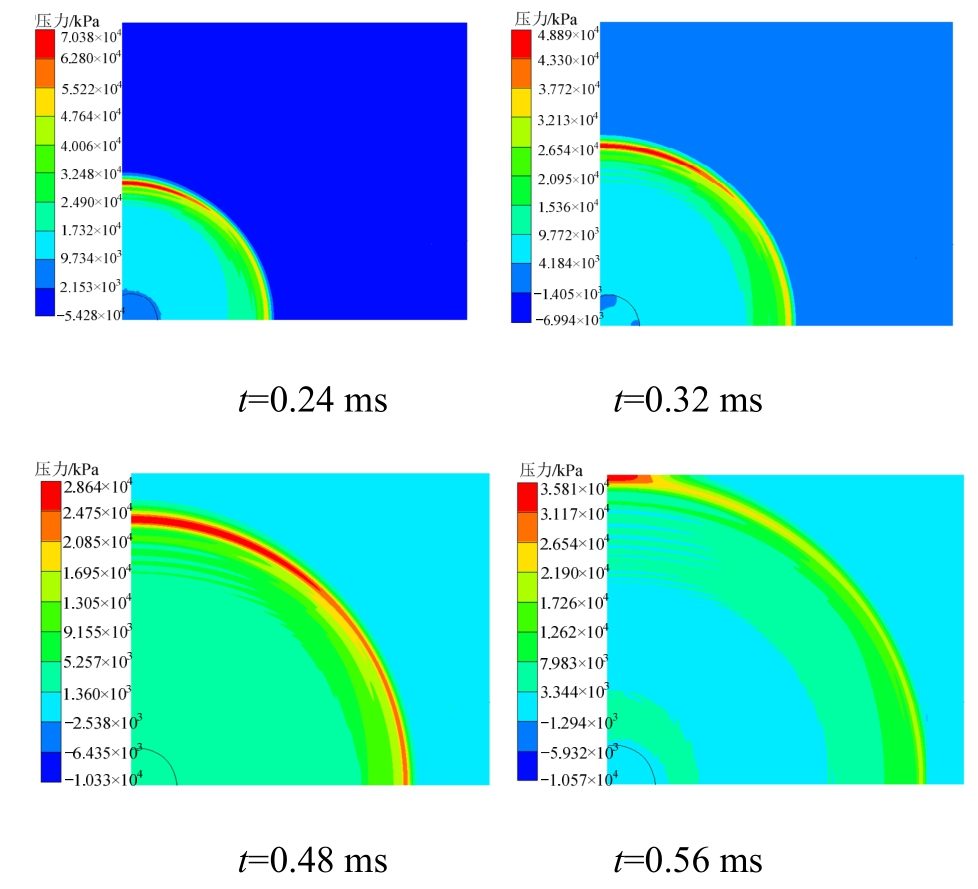
图6 水下爆炸冲击波传播过程
Fig.6 Underwater explosion shock wave propagation
表2 数值仿真破坏结果与理论计算对比
Table 2 Comparison of numerical simulation damage results with theoretical calculations

工况仿真变形仿真剪切仿真最大破坏理论变形理论剪切理论最大破坏最大破坏深度破坏层数m层数n深度L/mm层数m层数n深度L/mm误差值/(%)模式12052.52059.413.1Ⅰ23278.83285.38.2Ⅰ、Ⅱ343101.343109.88.4Ⅰ、Ⅱ、Ⅲ454112.954125.611.2Ⅰ、Ⅱ、Ⅲ565136.665140.87.5Ⅰ、Ⅲ666 —66 — —Ⅰ、Ⅲ
工况6情况下,片组结构产生塑性破坏后,6层层片已经全部剪切并有剩余动能。通过表2可以看出,数值仿真计算结果与理论计算结果基本一致,最大破坏深度误差值在15%以内。随着爆源药量的增多,片组结构破坏层数与最大破坏深度逐渐增加。多层片组结构首先产生塑性大变形,随着药量的增大,出现拉伸断裂破坏。当药量达到一定程度后,边界处将直接产生剪切破坏。
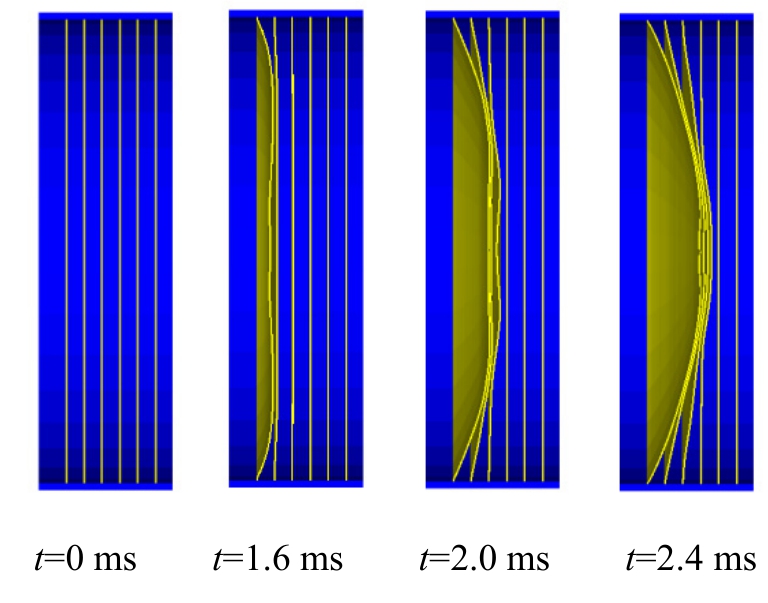

图7 100 g炸药在1 m处毁伤多层片组结构仿真过程
Fig.7 Simulation of the damage of multi-layer sheet structure at 1 m with 100 g explosive
3 试验验证
为了对理论模型进行验证,采用921A钢焊接成的类圆柱结构和测量装置进行水下爆炸毁伤试验。结构总长1100 mm,直径534 mm,壳厚8 mm,总重154 kg,主要分为头罩、毁伤功能模拟舱段、测试舱段三部分。头罩为带有弧度的圆台结构,在其顶部平台和圆弧侧面设置四个测点,用来测试水下压力脉冲强度;毁伤功能模拟舱段即为6层片组结构,每层厚度2 mm,间隔20 mm,采用2024铝合金材料;测试舱段内部采用3个环形加强筋进行加固,外壁设置6个吊环用来在水下固定整体结构,舱段中部开孔便于测量电缆从壳体内引出。三个部分以多个螺栓进行连接,其整体结构及剖视图如图8所示。

图8 整体结构模型
Fig.8 Overall structure model
3.1 试验过程
在头罩顶部与侧面共设置4枚压力传感器,分布位置如图9。爆源中心距头罩顶部1.5 m且在同一水平面上,整个结构布置于水下5 m。实验爆源采用57.5g8701炸药,电雷管起爆。由于模型与爆源的距离远大于气泡半径且位于爆源侧面,气泡产生后由于水压作用向上迁移运动,气泡脉动压力峰值远小于冲击波,因此忽略气泡脉动对圆柱模型的破坏作用。试验采集设备采用NI PXI数据采集仪,PCB113 B22压力传感器,采样率为1 m/s,试验实施示意图如图10所示。
3.2 压力测试结果分析
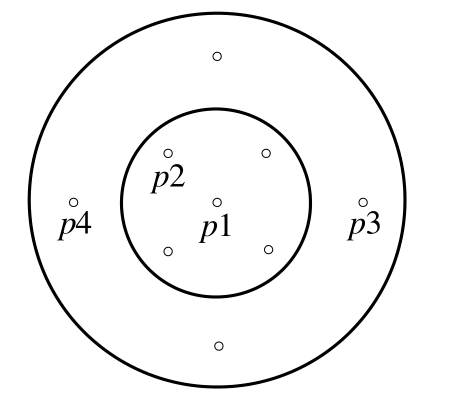
图9 压力传感器布置点
Fig.9 Pressure Sensor Placement

图10 试验实施示意图
Fig.10 Test Implementation Schematic
炸药爆炸产生的冲击波作用到模型头罩后,p1~p4四个压力传感器采集到的压力数据如图11所示,最大压力25.301 MPa出现在初始冲击波过后11.229 ms时,此时的冲击波为经过水面反射后产生的,分析初始冲击波形如图12所示,p1~p4四点峰值压力分别为14.104 MPa、14.848 MPa、13.367 MPa、10.289 MPa,根据式(28)计算得到的理论峰值压力为13.267 MPa,平均误差为0.87%,说明脉冲压力与理论值符合较好。
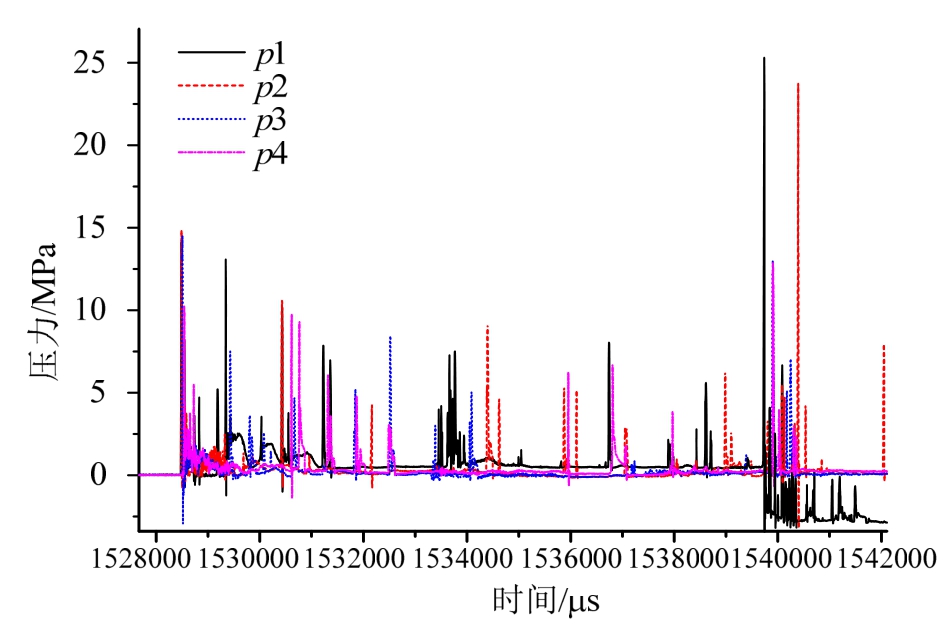
图11 冲击波作用下模型头部测点p-t曲线
Fig.11 p-t curves of the model head atthe shock wave
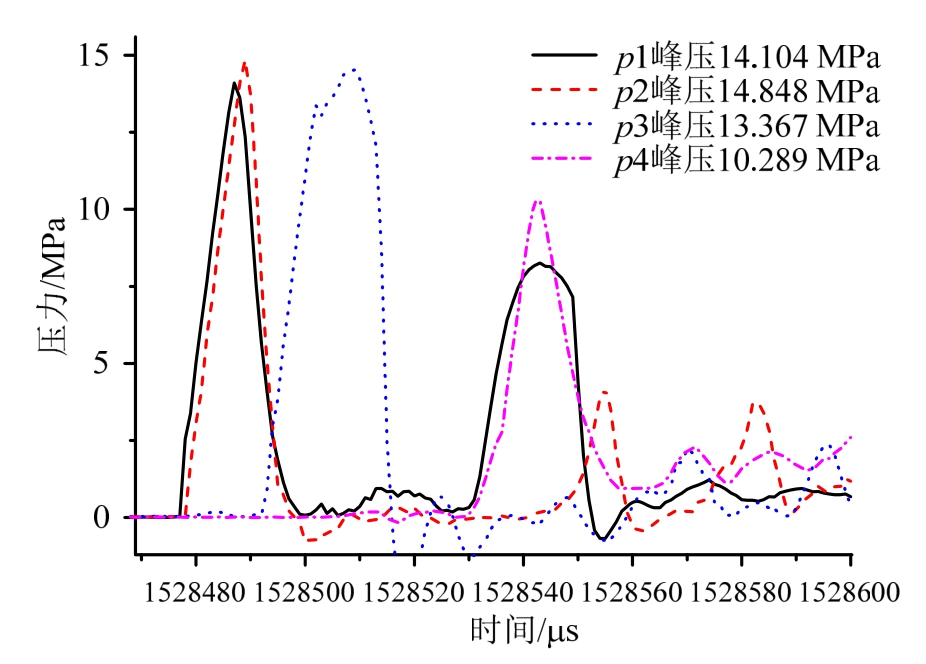
图12 冲击波作用下模型头部测点初始p-t曲线
Fig.12 Initial p-t curves of the model head at the shock wave
由于头罩为921A钢,强度较大,第一次试验过后观察毁伤模拟舱段并未造成破坏。将头罩取下进行第二次试验,使多层片组结构直接暴露在爆炸冲击波作用下,起爆相同的药量,观测其破坏结果如图13所示。
试验结果与理论模型计算结果对比如表3所示,多层片组结构均产生塑性变形,其中剪切破坏层数为5层,最大破坏深度为125.4 mm。由于片组结构上导线孔的存在,使得试验时片组结构夹层有部分进水,并且试验并非理想轴对称情况,因此片组结构下部未完全撕裂,试验结果与理论模型计算结果有一定出入,最大破坏深度误差为15.7%,误差在允许范围内,因此试验结果可以对理论模型提供相对支撑。

图13 毁伤功能模拟舱段破坏结果
Fig.13 Damage function Simulated cabin damage results
表3 试验结果与理论计算结果对比
Table 3 Comparison between test results and theoretical calculations

变形剪切最大破坏深度破坏方法 层数m层数n误差模式L /mm理论模型 6 4 145.2 15.7Ⅰ、Ⅲ试验结果 6 5 125.4
4 结论
本文基于能量法,建立了固支条件下多层片组结构在非接触水下爆炸冲击载荷作用下的塑性毁伤理论模型。利用AUTODYN软件对不同药量下爆炸冲击波冲击固支多层片组结构进行了数值模拟,并与理论结果进行对比,通过试验对水下爆炸冲击波强度以及多层片组结构的毁伤程度进行了比较。结合仿真计算与试验结果可以看出,多层片组结构在水下爆炸冲击波作用下的毁伤破坏情况与理论模型计算结果基本一致,说明所建立的理论计算模型是有效的;通过理论模型的计算可以很好的预测多层片组结构的毁伤破坏情况,包括其塑性变形层数、剪切破坏层数和最大破坏深度;对于2024t351铝合金片组结构,当冲击因子达到0.17,即可将6层固支层片全部剪切。该理论模型为多层防护及后续的可靠性研究提供了一定的理论参考。
[1]Zhang Aman, Zeng Lingyu, Cheng Xiaoda, et al.The evaluation method of total damage to ship in underwater explosion [J].Applied Ocean Research, 2011, 33(4):240-251.
[2]李海涛, 张振华, 牟金磊, 等.水下爆炸作用下弹塑性船体梁整体运动模型及损伤特性[J].工程力学, 2019,36(1): 238-256.Li Haitao, Zhang Zhenhua, Mou Jinlei, et al.Hydro-elastic-plastic dynamic response of a ship hull girder subjected to underwater explosion: a simplified theoretical model [J].Engineering Mechanics, 2019,36(1): 238-256.(in Chinese)
[3]Taylor G I.The pressure and impulse of submarine explosion waves on plates [M].Cambridge: Cambridge University Press, 1963.
[4]Cole R H.Underwater explosions [M].Princeton:Princeton University Press, 1948.
[5]Ramajeyathilagam K, Vendhan C P.Deformation and rupture of thin rectangular plates subjected to underwater shock [J].International Journal of Impact Engineering,2004, 30(6): 699-719.
[6]Rajendran R, Narasimhan K.Damage prediction of clamped circular plates subjected to contact underwater explosion [J].International Journal of Impact Engineering, 2001, 25(4): 373-386.
[7]吴有生, 彭兴宁, 赵本立.爆炸载荷作用下舰船板架的变形与破损[J].中国造船, 1995, 4(131): 55-61.Wu Yousheng, Peng Xingning, Zhao Benli.Deformation and damage of ship plate under blast loading [J].Shipbuilding of China, 1995, 4(131): 55-61.(in Chinese)
[8]吴成, 金俨, 李华新.固支方板对水中爆炸作用的动态响应研究[J].高压物理学报, 2003, 17(4): 275-282.Wu Cheng, Jin Ye, Li Huaxin.Dynamic response of solid supported slabs to underwater explosion [J].Chinese Journal of High Pressure Physics, 2003, 17(4): 275-282.(in Chinese)
[9]胡小利, 王炳, 朱惠民.射弹引起的鱼雷自导系统毁伤仿真[J].兵工自动化, 2015, 34(5): 11-13.Hu Xiaoli, Wang Bing, Zhu Huimin.Damage simulation of torpedo homing system caused by projectiles [J].Ordnance Industry Automation, 2015, 34(5): 11-13.(in Chinese)
[10]张振华, 朱锡, 刘润泉.多层板架结构在水下接触爆炸作用下的毁伤理论分析方法[C].北京: 中国力学学会学术大会, 2005.Zhang Zhenhua, Zhu Xi, Li Runquan.Theory analysis method of multi-layer board structure under underwatercontact explosion [C].Beijing: Chinese Conference of Theoretical and Applied Mechanics, 2005.(in Chinese)
[11]周楠, 王金相, 谢君, 等.球形弹丸作用下钢/铝爆炸复合靶的抗侵彻性能计算与分析[J].高压物理学报,2013, 27(6): 839-846.Zhou Nan, Wang Jinxiang, Xie Jun, et al.Calculation and analysis of anti-penetration performance of Steel/Aluminum explosive composite target under ball projectile [J].Chinese Journal of High Pressure Physics,2013, 27(6): 839-846.(in Chinese)
[12]方斌, 朱锡, 张振华.水下爆炸冲击波载荷作用下船底板架的塑性动力响应[J].哈尔滨工程大学学报,2008, 29(4): 326-331.Fang Bin, Zhu Xi, Zhang Zhenhua.Plastic dynamic response of ship's deck frame under underwater blast shock loading [J].Journal of Harbin Engineering University, 2008, 29(4): 326-331.(in Chinese)
[13]AUTODYN.AUTODYN users manual revision 4.3 [M].California: Century Dynamics Incorporated, 2003.
[14]肖秋平, 陈网桦, 贾宪振, 等.基于AUTODYN的水下爆炸冲击波模拟研究[J].舰船科学技术, 2009,31(2): 38-43.Xiao Qiuping, Chen Wanghua, Jia Xianzhen, et al.Simulation study of underwater explosion shock wave based on AUTODYN [J].Naval Science and Technology,2009, 31(2): 38-43.(in Chinese)
[15]Cowper G R, Symonds P S.Strain hardening and strain rate effects in the impact loading of cantilever beams [R].Providence: Brown University, 1957.
[16]王雷, 李玉龙, 索涛, 等.航空常用铝合金动态拉伸力学性能探究[J].航空材料学报, 2013, 33(4): 71-77.Wang Lei, Li Yulong, Suo Tao, et al.Dynamic tensile mechanical properties of Aluminum alloys used in aviation [J].Journal of Aeronautical Materials, 2013,33(4): 71-77.(in Chinese)
[17]任鹏, 田阿利, 张伟, 等.水下冲击波载荷作用下气背固支圆板动态毁伤实验[J].爆炸与冲击, 2016, 36(5):617-624.Ren Peng, Tian Ali, Zhang Wei, et al.Experiment on dynamic damage of air-backed circular plates under underwater shock wave loading [J].Explosion and Shock Waves, 2016, 36(5): 617-624.(in Chinese)
[18]Zamyshlyayev B V.Dynamic loads in underwater explosion [R].Washington D C: Naval Intelligence Support Center, 1973.
[19]吴国民, 周心桃, 李俊.水下爆炸作用下固支平板动态响应分析[J].舰船科学技术, 2013, 35(4): 25-28.Wu Guomin, Zhou Xintao, Li Jun.Dynamic response analysis of clamped plate under underwater explosion[J].Journal of Ship Science and Technology, 2013, 35(4):25-28.(in Chinese)