模板工程直接影响到整个混凝土工程的造价、工期和质量。我国混凝土模板工程经历了从木模板、组合钢模板、大型模板到工具模板的发展历程,目前对模板工程的质量要求越来越高[1-2],一方面模板的设计也越来越重,越来越保守,造成不必要的浪费;另一方混凝土浇筑施工过程中胀模、爆模等事故仍时有发生。这不仅与施工操作不当有关,而且与目前相关模板设计规范不合理有一定的关系。在20世纪60年代清华、同济等大学和相关企业等对混凝土模板侧压力进行了系统的研究,在此基础上制定了《钢筋混凝土工程施工及验收规范》(GBJ 10―65),以表格形式给出了混凝土模板侧压力的计算公式[3]。之后经历了(GBJ 204―83)和(GB50204―92)等更新[4-5],但在(GB 50204―2002)[6]中没有给出模板侧压力的计算公式。目前关于混凝土模板设计的在行国标规范有《混凝土结构工程施工规范》(GB 50666―2011)[7]和《钢筋混凝土工程施工及验收规范》(GB 50204―2002),行业规范有《建筑施工模板安全技术规范》(JGJ 162―2008)[8]《公路桥涵施工技术规范》(JTG/T F50―2011)[9]和《铁路混凝土工程施工技术指南》(TZ210―2005)[10]、《客货共线铁路桥涵工程施工技术指南》(TZ203―2008)。其中(TZ203―2008)沿用了《公路桥涵施工技术规范》(JTJ 041―89)中关于模板侧压力的计算公式[11],而(JTG/T F50―2011)却直接删除了关于模板侧压力计算部分。从国内外相关模板侧压力计算公式的对比结果中发现,在条件相同的情况下不同规范公式的计算结果之间存在较大差异,有的甚至相差几倍之多[12]。近些年虽然关于新浇筑混凝土模板侧压力计算问题又重新引起了工程界的重视[13],但关于模板侧压力的系统实验研究还相对较少。在国内有限的模板侧压力研究文献中大多数为根据实测数据与规范进行对比分析,王德利和Vanhove等[14-16]对利用雅申理论计算模板侧压力进行了部分研究工作,但并没有考虑混凝土浇筑过程的时变特性。为此本文做了14个不同截面尺寸新浇筑混凝土模板侧压力实验,并根据雅申理论提出了新浇筑混凝土模板侧压力力学模型,推导了侧压力计算公式,并与实测值进行了对比验证。
1 实验概况
本实验共设计14个试件,其中截面尺寸为60 cm×120 cm的试件10个,截面尺寸为30 cm×120 cm的试件2个,1个截面尺寸为15 cm×120 cm的试件,1个截面尺寸为60 cm×60 cm的试件,各试件高度均为300 cm。实验用混凝土标号为C30,主料为金隅牌普通硅酸盐水泥、河沙和机制级配碎石,实验用混凝土的平均密度ρ=2400 kg/m3。
1.1 模板设计及测点布置
由模板最底部至200 cm高位置每隔50 cm布置压力测试点,其中120 cm边每个高度位置设2个测点,60 cm和30 cm边每个高度位置设1个测点,15 cm边上不布置压力测点,典型压力测点布置如图1所示。

图1 压力测点布置 /cm
Fig.1 Pressure test point arrangement
1.2 数据采集系统
为保证测试数据的可靠性,本次试验压力测试仪器采用丹东测试仪器厂和长沙金码公司两个厂家生产的压力测试盒及相应的数据采集系统:1)金码JMZX-5006X智能弦式数码压力盒,量程为0.6 MPa,非线性误差≤1.2% F.S,重复性误差≤1%F.S,迟滞误差≤1% F.S。2)丹东DY-110型单膜压力盒,量程为0.4 MPa,温度范围-20℃~80℃。
1.3 实验过程
每个试件在浇筑之前要进行坍落度实验,详细记录混凝土坍落度;浇筑混凝土时,高度每增加0.5 m且振捣结束后记录一次侧压力,并记录此时的环境温度、浇筑时间等数据,并留取实验混凝土进行初凝时间测试。本试验由试验现场仪器、材料准备到试验完成后对现场的清理,共历时36日,试验所用混凝土方量近35 m3,部分实验过程如图2所示。

图2 部分实验过程图
Fig.2 The figure of part test process
1.4 模板侧压力实测值
对实验数据作如下处理:1)截面尺寸60 cm×60 cm×300 cm的试件每个高度上测点测出的模板侧压力取平均值;2)截面尺寸60 cm×120 cm×300 cm和30 cm×120 cm×300 cm的试件长边与短边测出的结果分别取均值;3)截面尺寸15 cm×120 cm×300 cm的试件长边测出的结果取均值,然后找出试件在整个浇筑过程中出现的最大模板侧压力。典型模板侧压力随浇筑高度变化情况如图3所示,14个试件模板侧压力最大。

图3 典型试件侧压力随浇筑高度变化曲线
Fig.3 The lateral pressure curves of typical specimens
值实测结果见表1,由此可知:
1)模板侧压力最大值不一定发生在模板的最下端,而是出现在距离最下端一定高度位置。这主要是由于随着混凝土浇筑高度的增加,浇筑时间的增长,最先浇筑的混凝土因振捣密实后失去流动性具有一定的自持能力,模板受到侧压力作用越来越大,使得模板发生向外变位,造成最大模板侧压力并不一定发生在最底部。
表1 试件参数及侧压力最大值
Table 1 Specimen parameters and maximum lateral pressure

试件编号尺寸(长×宽×高)/m坍落度/mm初凝时间/h环境温度/(℃)浇筑速度/(m/h)浇筑完成振捣方式时间/h长边 短边实测值/kPa出现位置(浇筑高度)/m实测值/kPa出现位置(浇筑高度)/m 1 0.6×1.2×3 155 7.14 13 1.29 2.32 每0.5m一振27.0 0.5(2.5)25.0 0.5(2.5)2 0.6×1.2×3 203 4.88 24 1.29 2.32 每0.5m一振26.0 1.0(3.0)32.0 1.0(3.0)3 0.6×1.2×3 240 6.25 17 1.33 2.26 每0.5m一振37.5 0.5(3.0)42.1 0.5(3.0)4 0.6×1.2×3 210 5.71 19 0.93 3.23 每0.5m一振41.5 0.5(3.0)37.0 0.5(2.5)5 0.6×1.2×3 154 5.13 24 1.16 2.59 每0.5m一振30.5 0.5(3.0)32.0 0.5(3.0)6 0.6×1.2×3 154 6.45 16 1.16 2.59 每0.5m一振21.5 1.0(2.5)24.0 0.5(2.0)7 0.6×1.2×3 155 5.56 21 0.45 6.67 每0.5m一振27.5 0.5(2.0)26.0 0.5(2.0)8 0.6×1.2×3 86 5.71 20 0.80 3.75 每0.5m一振28.5 0.5(2.0)30.0 0.5(2.5)9 0.6×1.2×3 157 5.41 22 1.45 2.07 每0.5m一振38.2 0.5(2.5)39.0 0.5(2.0)10 0.6×1.2×3 150 6.45 16 1.16 2.59 每0.5m一振27.2 0.5(2.0)28.1 0.5(2.0)11 0.3×1.2×3 157 6.06 18 1.97 1.51 每0.5m一振24.8 1.0(3.0)24.1 0.5(2.0)12 0.3×1.2×3 159 8.70 8 3.30 0.91 每0.5m一振31.3 0(1.5)34.0 0.5(1.5)13 0.15×1.2×3 160 5.71 20 6.38 0.47 每0.5m一振33.0 0(3.0)— —14 0.6×0.6×3 159 6.25 17 1.5 2.00 每0.5m一振36.2 0.5(2.5)
2)不同测点的模板侧压力随混凝土浇筑高度的增加而增大,但当测点以上混凝土的浇筑高度达到某一量值后,该点的侧压力不再随混凝土浇筑高度的增加而增加,随着下部先浇筑混凝土流动性的降低和自持能力的增加,甚至有出现此后该测点侧压力随混凝土浇筑高度增加而有所降低的现象。
3)前12个不等边试件测得短边侧压力最大值的平均值为31.1 kPa,而长边侧压力最大值的平均值为30.1 kPa,因此可忽略长短边对侧压力的影响。
4)从表1数据可得混凝土坍落度和浇筑速度对模板侧压力有较大的影响,而环境温度对模板侧压力的影响不具有明显的规律性。
2 实测值与规范计算值对比分析
由于《公路桥涵施工技术规范》(JTG/T F50―2011)[9]删除了关于模板侧压力计算部分。所以国内规范对比只选择了《混凝土结构工程施工规范》(GB 50666―2011)[7]和《铁路混凝土工程施工技术指南》(TZ210―2005)[10]。国外典型规范主要包括ACI347―14《混凝土模板设计指南》(简称ACI347)和CIRIA Report NO.108(简称CIRIA.108)。受篇幅所限,文中不对国内规范模板侧压力计算公式做介绍。
2.1 国外代表性规范简介
1)ACI347[17]:对于塌落度小于175 mm的混凝土,正常振捣深度不超过120 cm,柱体构件的模板侧压力按式(1)计算,其最小值不低于30Cw kPa,最大值不超过ρgh。
对于浇筑速度不超过2.1 m/h,一次浇筑高度不超过4.2 m的墙体构件,可按式(1)进行模板侧压力计算。对于浇筑速度不超过2.1 m/h,但一次浇筑高度超过4.2 m,或者浇筑速度在2.1 m/h~4.5 m/h的墙体构件,其模板侧压力按式(2)进行计算,其最小值不低于30 Cw kPa,最大值不超过ρgh。
式中:Pmax/kPa为设计模板侧压力;R/(m/h)为混凝土浇筑速度;T/(℃)为混凝土温度;Cw为混凝土重度调整系数;Cc为外加剂调整系数。
2)CIRIA.108[18]:混凝土模板侧压力应按式(3)计算,但不应大于DcH。
当![]() 取DcH为模板侧压力设计值。式中:C1为模板形状调整系数,墙体构件取1,柱体构件取1.5;C2为混凝土外加剂调整系数,不参加缓凝剂混凝土取0.3,参加缓凝剂混凝土取0.45;H/m为模板高度;K为温度调整系数,按式(4)计算。其余同式(1)。
取DcH为模板侧压力设计值。式中:C1为模板形状调整系数,墙体构件取1,柱体构件取1.5;C2为混凝土外加剂调整系数,不参加缓凝剂混凝土取0.3,参加缓凝剂混凝土取0.45;H/m为模板高度;K为温度调整系数,按式(4)计算。其余同式(1)。

2.2 实测值与规范计算值对比
以上4个规范模板侧压力计算值与实测值对比情况如图4所示,其相对误差如图5所示,在图5中相对误差![]()

图4 规范计算值与实测值对比
Fig.4 Comparison of test values with those calculated by codes

图5 规范计算值相对误差对比
Fig.5 Relative error comparison of different codes
由此可知:
1)规范GB50666模板侧压力计算值中有2个试件小于实测值,占总数的14.3%;计算值与实测值的相对误差在-10.8%~+130.5%之间,相对误差的标准差为52.4%。TZ210-2005模板侧压力计算值中有7个试件小于实测值,占总数的50.0%;计算值与实测值的相对误差在-36.7%~+74.4%之间,相对误差的标准差为36.1%。ACI347模板侧压力计算值中有2个试件小于实测值,占总数的14.3%;计算值与实测值的相对误差在-9.8%~+125.4%之间,相对误差的标准差为49.1%。CIRIA.108模板侧压力计算值均大于实测值;计算值与实测值的相对误差在+5.3%~+106.2%之间,相对误差的标准差为33.7%。
2)在浇筑速度低于1.0 m/h的情况下,按规范GB50666计算的模板侧压力有低于实际值的可能,如试件4和试件7的计算值均低于实测值。采用ACI347规范进行模板侧压力计算时,当环境温度较高时计算值可能偏低,如试件5、试件8和试件9均低于或接近低于实测值;而当混凝土塌落度超过180 mm时,规范取值过于保守。当温度较低时采用CIRIA.108规范进行模板侧压力计算可能会因过于保守而造成不必要的浪费,如试件1、试件6、试件10、试件11和试件12的计算值均大幅高于实测值。
3 模板侧压力计算模型
3.1 雅申模型
根据雅申理论,散体在筒仓内对仓壁的侧向压应力P′与竖向压应力P成线性比例关系[16,19]:
式中,K为侧压力折减系数,与散体材料性质和仓壁性质有关。
仓壁对仓内散体材料向上的侧向摩擦应力为:
式中,μ为散体材料与仓壁之间的摩擦系数[16]。
模板内的新浇筑混凝土的受力情况如图6所示,根据力学平衡方程可得:

图6 模板内混凝土受力简图
Fig.6 Force diagram of the concrete in formwork
将边界条件:当h=0时,P=0,代入得到方程的解为:
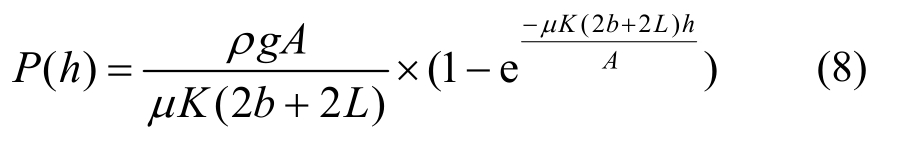
式中:P/kPa为计算点h位置现浇混凝土的侧压力;b/m为模板的宽度;L/m为模板的长度;h/m为混凝土浇筑高度;K为侧压力折减系数;μ为混凝土与模板的摩擦系数。
3.2 折减系数K和摩擦系数μ
侧压力折减系数K和混凝土与模板之间的摩擦系数μ是按式(8)计算模板侧压力的基础,根据以往研究可知混凝土的坍落度对侧压力折减系数K及混凝土与模板之间的摩擦系数μ有直接关系。以文献[15]中5个试件的实测数据为基点,根据雅申理论对参数K和μ进行混凝土坍落度修正,文献[15]中5个试件所用混凝土的坍落度均约等于160 mm。根据雅申理论可知,仓内散体对仓壁的侧压力为:
式中:σv/kPa为计算点散体的竖向压应力;φ/rad为仓内散体的内摩擦角。
常规混凝土其内摩擦角可近似等于坍落度为S的混凝土的自然安息角,假设进行坍落度测试后混凝土坍落成圆锥形,则有:
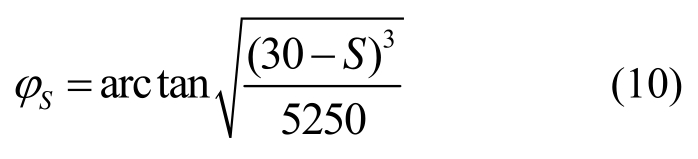
根据相关参考文献,混凝土与模板之间的外摩擦角δ不仅与混凝土坍落度、骨料粒径和胶凝材料用量等自身性质有关,而且与模板类型有关[15,20-22],对于常规混凝土和钢模板可取外摩擦角![]() 考虑到钢模板表面脱模剂的润滑作用和振捣效应对混凝土与模板之间摩擦力的降低作用,取
考虑到钢模板表面脱模剂的润滑作用和振捣效应对混凝土与模板之间摩擦力的降低作用,取![]() 混凝土与模板之间的摩擦系数μ与摩擦角δS近似成正比关系。进而得不同坍落度混凝土的侧压力折减系数K和摩擦系数μ计算公式如下:
混凝土与模板之间的摩擦系数μ与摩擦角δS近似成正比关系。进而得不同坍落度混凝土的侧压力折减系数K和摩擦系数μ计算公式如下:
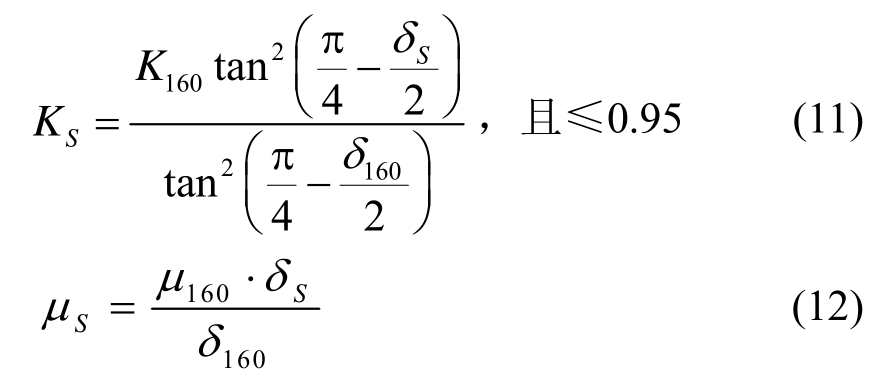
根据文献[15]实验结果,取K160=0.8,μ160=0.045。
以上给出了侧压力折减系数K和摩阻系数的初始值μ,根据相关研究结论K和μ是随混凝土浇筑时间的增长而变化的[23]。根据文献[24]的实测数据,通过拟合发现在混凝土发生初凝之前,新浇筑混凝土的侧应力折减系数随时间成指数关系递减,任意时刻t的侧压力折减系数可按式(13)计算:
根据Vanhove等[16]的研究表明混凝土与钢模板的静摩擦系数随时间的增长关系符合线性关系,其增长速率约为0.02 μS/min,因此任意时刻t的静摩擦系数可按式(14)计算:
考虑折减系数K和摩擦系数μ与时间关系,并引入安全系数k后,现浇混凝土侧压力计算式(8)改为如下所示:
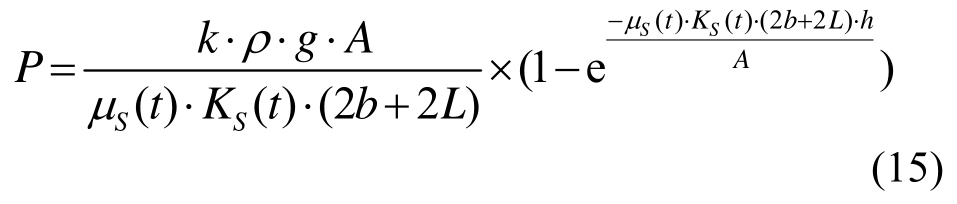
取k=1.0,按式(15)计算出坍落度S=160 mm和S=240 mm,浇筑速度R=0.5 m/h~5.0 m/h情况下的侧压力值如图7所示,由图7可知:按式(15)计算出不同坍落度、不同浇筑速度下现浇混凝土侧压力的变化规律复合实测混凝土模板侧压力分布规律,能够体现出混凝土坍落度和浇筑速度两个主要影响因素对模板侧压力的影响。

图7 模板侧压力随浇筑高度变化图
Fig.7 Pressure variation with casting height
3.3 实验验证
为验证以上基于雅申理论建立的新浇混凝土模板侧压力计算公式的可靠性,采用式(15)对实验中14个试件的侧压力进行了计算,计算值与实测值对比情况如图8所示,典型试件侧压力分布规律实测值与计算值对比如图9所示,计算值与实测值之间的误差统计如表2所示,由此可知:
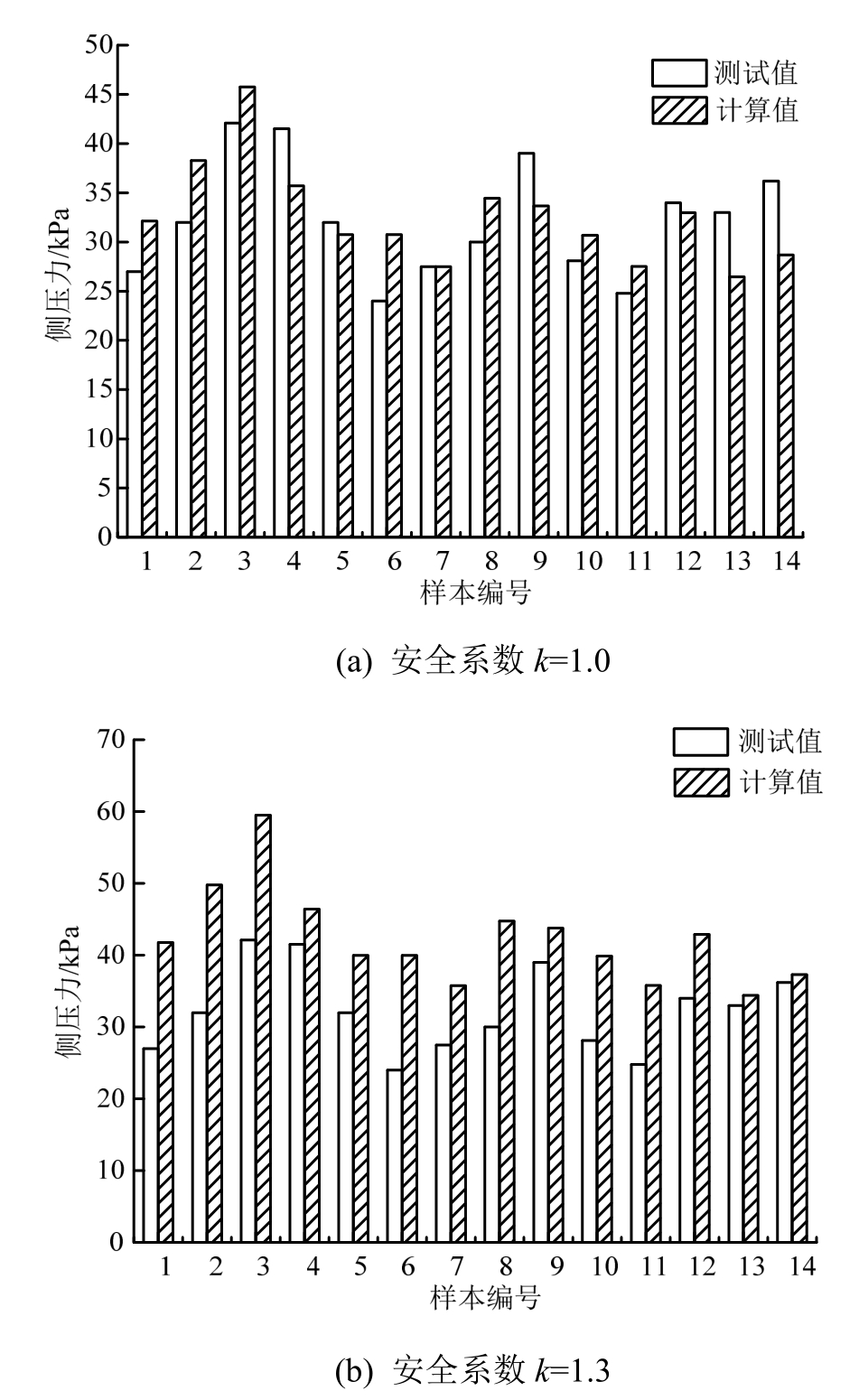
图8 计算值与实测值对比图
Fig.8 The comparison of calculated value with test value

图9 典型试件侧压力实测值与计算值分布规律
Fig.9 Pressure distribution of test value and calculated value of typical specimens
表2 计算值与实测值对比
Table 2 Comparison of the calculated value with test value

试件编号实测值Pt/kPa 计算值Pc/kPa k=1.0绝对误差(Pc-Pt)/kPa k=1.3计算值/kPa 绝对误差(Pc-Pt)/Pt(%)(Pc-Pt)/kPa相对误差相对误差(Pc-Pt)/Pt(%)1 27.0 32.1 5.1 19.0 41.8 14.8 54.7 2 32.0 38.3 6.3 19.7 49.8 17.8 55.6 3 42.1 45.8 3.7 8.7 59.5 17.4 41.3 4 41.5 35.7 -5.8 -14.0 46.4 4.9 11.8 5 32.0 30.8 -1.2 -3.9 40.0 8.0 25.0 6 24.0 30.8 6.8 28.2 40.0 16.0 66.6 7 27.5 27.5 0.0 0.0 35.7 8.2 30.0 8 30.0 34.4 4.4 14.8 44.8 14.8 49.2 9 39.0 33.7 -5.3 -13.7 43.8 4.8 12.2 10 28.1 30.7 2.6 9.2 39.9 11.8 41.9 11 24.8 27.5 2.7 11.0 35.8 11.0 44.3 12 34.0 33.0 -1.0 -3.0 42.9 8.9 26.1 13 33.0 26.5 -6.5 -19.8 34.4 1.4 4.3 14 36.2 28.7 -7.5 -20.8 37.3 1.1 3.0相对误差的标准差 15.6 ― 20.3
1)采用本文提出的侧压力计算公式可以很好的预测现浇混凝土的模板侧压力,在不考虑安全修正系数的情况下,虽然有50%的计算值低于实测值,但计算值与实测值相对误差的平均值仅为2.5%,相对误差的标准差只有15.6%,远低于现行规范。
2)引入安全修正系数k=1.3后,不仅能保证所有的计算值均大于等于实测值,而且计算值与实测值相对误差的平均值为33.3%,远低于规范GB50666的53.0%、规范ACI347的50.3%和规范CIRIA.108的57.5%。相对误差的标准差只有20.3%,均大幅低于规范GB50666的52.4%、规范ACI347的49.1%和规范CIRIA.108的33.7%。单个试件的最大相对误差为66.6%,小于规范GB50666的130.5%、规范ACI347的125.4%和规范CIRIA.108的106.2%。
3)通过表2和图9可知,基于雅申理论推导的模板侧压力计算公式不仅能够反映影响新浇混凝土侧压力的主要因素和发展规律,而且计算结果具有较高的可靠性。
4 结论
为提高新浇混凝土模板侧压力计算的可靠性,进行了14个大尺寸试件的实验,并将实测模板侧压力与典型国内外规范计算值进行了对比,同时基于雅申理论推导了新浇混凝土模板侧压力计算公式,得到以下结论:
(1)现行规范模板侧压力的计算值与实测值之间不仅存在较大偏差,且离散性较大,按规范GB50666、TZ210和ACI347计算出的侧压力值有小于实测值的情况。虽然按规范CIRIA.108计算出的侧压力均大于实测值,但过于保守,存在较为严重的浪费现象。
(2)基于雅申理论建立的模板侧压力计算公式不仅具有较高的可靠性,而且能够反应影响侧压力的主要因素和发展规律,计算值与实测值误差的离散性均小于现行规范。
(3)为更好利用本文提出公式进行模板侧压力计算,建议对侧压力折减系数、混凝土与模板之间的摩擦系数等做进一步深入研究。
[1]安宇骢, 谢楠, 贾影.防连续倒塌高大模板支撑体系的两阶段设计研究[J].工程力学, 2017, 34(增刊): 289―294.An Yucong, Xie Nan, Jia Ying.Research on two-stage design of high falsework system against progressive collapse [J].Engineering Mechanics, 2017, 34(Suppl):289―294.(in Chinese)
[2]肖潭, 胡森, 吴伟, 等.蜂窝夹层铝建筑模板的几何优化与试验研究[J].工程力学, 2019, 36(2): 195―204.Xiao Tan, Hu Sen, Wu Wei, et al, Geometrical optimization and experimental study of aluminum honeycomb sandwich construction formworks [J].Engineering Mechanics, 2019, 36(2): 195―204.(in Chinese)
[3]GBJ 10―65, 钢筋混凝土工程施工及验收规范[S].北京: 中国建筑工业出版社, 1966.GBJ 10―65, Code for construction and acceptance of concrete structures [S].Beijing: China Architecture &Building Press, 1966.(in Chinese)
[4]GBJ 204―83, 钢筋混凝土结构工程施工及验收规范[S].北京: 中国建筑工业出版社, 1984.GBJ 204―83, Code for construction and acceptance of concrete structures [S].Beijing: China Architecture &Building Press, 1984.(in Chinese)
[5]GB 50204―92, 混凝土结构工程施工及验收规范[S].北京: 中国建筑工业出版社, 1993.GB 50204―92, Code for construction and acceptance of concrete structures [S].Beijing: China Architecture &Building Press, 1993.(in Chinese)
[6]GB 50204―2011, 混凝土结构工程施工质量验收规范[S].北京: 中国建筑工业出版社, 2002.GB 50204―2011, Code for acceptance of constructional quality of concrete structures [S].Beijing: China Architecture & Building Press, 2002.(in Chinese)
[7]GB 50666―2011, 混凝土结构工程施工规范[S].北京:中国建筑工业出版社, 2012.GB 50666―2011, Code for construction of concrete structures [S].Beijing: China Architecture & Building Press,2012.(in Chinese)
[8]JGJ162―2008, 建筑施工模板安全技术规范[S].北京:中国建筑工业出版社, 2008.JGJ162―2008, Technical code for safety of forms in construction [S].Beijing: China Architecture & Building Press, 2008.(in Chinese)
[9]JTG/T F50―2011, 公路桥涵施工技术规范[S].北京:人民交通出版社, 2011.JTG/T F50―2011, Technical specifications for construction of highway bridge and culverts [S].Beijing: China Communications Press, 2011.(in Chinese)
[10]TZ210―2005, 铁路混凝土工程施工技术指南[S].北京: 中国铁道出版社, 2005.TZ210―2005, Technical guide for constructional of railway concrete engineering [S].Beijing: China Railway Publishing House, 2005.(in Chinese)
[11]JTJ041―89, 公路桥涵施工技术规范[S].北京: 人民交通出版社, 1990.JTJ041―89, Technical specification for construction of highway bridges and culverts [S].Beijing: China Communications Press, 1990.(in Chinese)
[12]张文学, 李增银, 刘龙.混凝土模板侧压力公式对比分析[J].工业建筑, 2014, 44(7): 132―136.Zhang Wenxue, Li Zengyin and Liu Long.Comparison and analysis on lateral pressure of concrete formwork from different standards [J].Industrial Construction,2014, 44(7): 132―136.(in Chinese)
[13]谢楠.混凝土浇筑期高大模板支架工作状态的试验测试[J].工程力学, 2011, 28(1): 85―89.Xie Nan.In-situ test of working state of high falsework during concrete placement [J].Engineering Mechanics,2011, 28(1): 85―89.(in Chinese)
[14]王德利.“贮仓法”计算混凝土侧压力[J].水利水运,1990(7): 15―17.Wang Deli.Calculation of lateral pressure of fresh concrete by “feed bin” method [J].Port & Waterway Engineering, 1990(7): 15―17.(in Chinese)
[15]Zhang Wenxue, Huang Jian, Li Yunkai and Xie Quanyi,Study of formwork pressure of column under ultra-deep vibration [J].Magzine of Concrete Research, 2016,68(22): 1155―1165.
[16]Vanhove Y, Djelal C and Magnin A, Prediction of the lateral pressure exerted by self-compacting concrete on formwork [J].Magazine of Concrete Research, 2004,56(1): 55―62.
[17]ACI Committee 347, Guide to formwork for concrete [S].FarmingtonHills, MI, USA: ACI Standard, 2004.
[18]CIRIA Report 108.Concrete pressure on formwork [S].London, UK: Construction Industry Research and Information Association, 1985.
[19]Janssen H A.Versuche über Getreidedruck in Silozellen.Zeitschr.d.Vereines deutscher Ingenieure [J].1895,39(35): 1045―1049.
[20]Zhang Wenxue, Chen Ying, Li Yunkai, et al.Study of formwork pressure of wall under ultra-deep vibration [J].Magazine of Concrete Research, 2019, 71(7): 373―384.
[21]Puente I, Santillli A, Lopez A.Lateral pressure over formwork on large dimension concrete blocks [J].Engineering Structures.2010, 32(1): 195―206.
[22]Omran A F, Khayat K H.Choice of thixotropic index to evaluate formwork pressure characteristics of self-consolidating concrete [J].Cement and Concrete Research, 2014, 63: 89―97.
[23]Santilli A, Puente I, Tanco M.A factorial design study to determine the significant parameters of fresh concrete lateral pressure and initial rate of pressure decay [J].Construction Building Materials, 2011, 25(4): 1946―1955.
[24]Omran A F, Elaguab Y M, Khayat K H.Effect of placement characteristics on SCC lateral pressure variations [J].Construction Building Materials, 2014, 66:507―514.