目前对于不等跨框架结构的设计,通常采用截面高度相同的梁贯通整层。该方法虽设计简单但容易造成材料浪费,不利于结构体系抗震性能的提升。外环板式高低梁-方钢管柱节点可以有效的弥补上述不足。采用该种节点可在保证结构体系安全的前提下节约钢材使用量、降低结构自重、节省建设成本,利于提高结构抗震性能。
准确计算节点剪切承载力是进行节点设计的关键。国内外学者采用屈服线理论对钢管柱和钢管混凝土柱节点提出了一系列分析模型及计算公式。立山英二等[1]运用屈服线理论并参考Mansfield方法[2],推导出了单轴对称的H形梁与箱形柱刚性连接时的节点承载力计算公式。森田耕次等[3]、吹田啓一郎等[4]等对立山英二方法进行了简化完善。国内学者也做了大量研究,李成玉等[5],对外环板式钢管混凝土结构节点的力学模型及计算公式进行了研究。同时,牟犇等[6-7]对外环板式不等高钢梁-方钢管混凝土柱节点的抗震性能及节点破坏机制进行了试验研究。
目前,基于屈服线计算模型的钢管柱节点承载力分析方法逐渐成熟,并在钢结构节点分析中广泛应用[8-15]。但外环板式高低梁-方钢管柱节点的屈服机制、破坏形式以及承载力分析模型未见报道,且尚未有研究给出该种节点的承载力计算公式。以上问题都制约了外环板式高低梁-方钢管柱节点在工程建设中的应用。本文在试验研究与有限元模拟基础上分析了外环板式高低梁-方钢管柱节点的破坏机制,提出了节点域整体破坏(SFEPZ)以及节点域部分破坏(SFPPZ)两种破坏形式,以此建立节点弹塑性剪切承载力计算模型并提出相应计算公式。公式计算结果与试验以及有限元软件结果吻合较好,证明该公式有较高的可靠性。可为外环板式高低梁-方钢管柱节点的分析和设计提供参考。
1 试验概况
1.1 节点域的定义
外环板式高低梁节点(unequal depth beams to column connection with external-diaphragm,简称UCE节点)地震作用下的受力状态如图1。本文中将梁1(Beam 1)定义为UCE节点中截面较高的梁;梁2(Beam 2)为截面较低的梁。介于梁1上翼缘至梁2下翼缘中间区域为节点域1(Panel 1);梁1下翼缘与梁2下翼缘中间的区域为节点域2(Panel 2)。
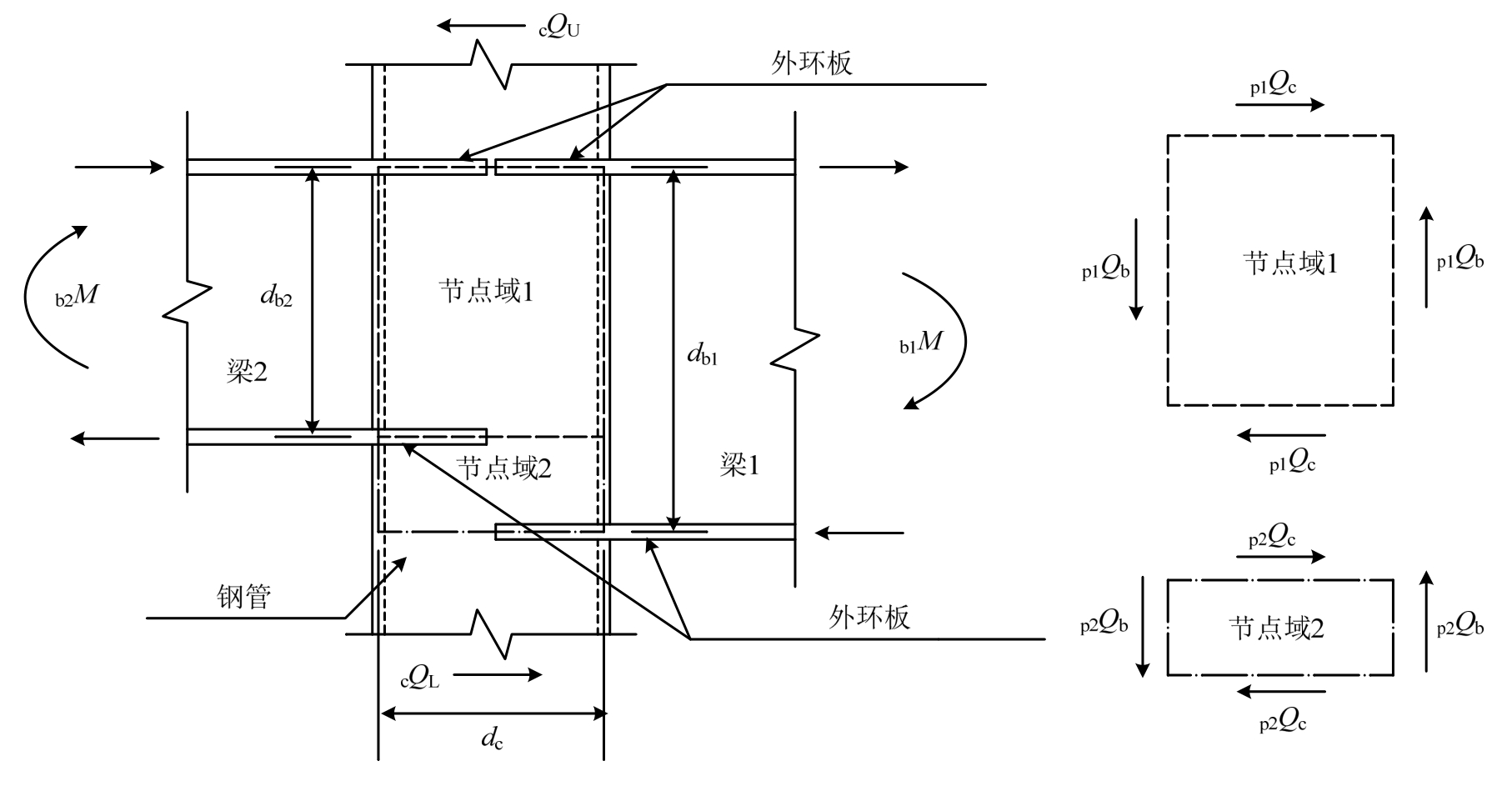
图1 UCE节点域受力状态
Fig.1 Force condition of UCE
注:db1为梁1翼缘板中心线距离;db2为梁2翼缘板中心线距离;dc为节点域翼缘板中心线距离;b1M梁1端弯矩;b2M梁2端弯矩;cQL柱下端剪力;cQU柱上端剪力;p1Qb梁对节点域1的剪力;p2Qb梁对节点域2的剪力;p1Qc柱对节点域1的剪力;p2Qc柱对节点域2的剪力。
1.2 试验过程
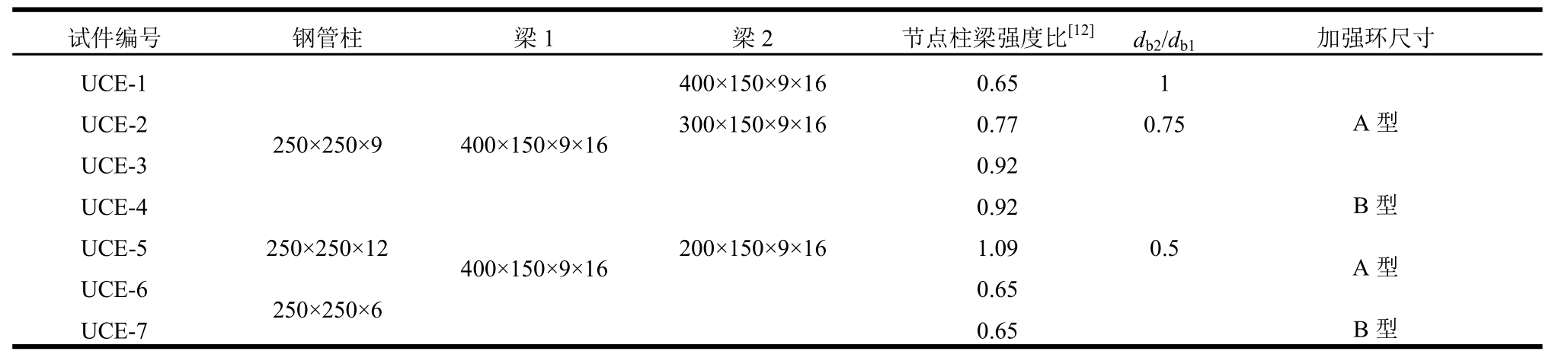
针对7个足尺UCE节点进行了低周循环往复加载试验[16],试验研究了UCE节点的剪切承载力、破坏模式与耗能能力等抗震性能指标。试验所设置的七个试件尺寸见表1。如图2所示,各试件高度为1400 mm,长度为3300 mm。其中试件的主要变量为梁高比(db2/db1=1.0, 0.75, 0.5)、方钢管柱截面宽厚比(D/t=42, 28, 21)和外环板尺寸(如图3所示)。为方便焊接安装,外环板采用日本学者[17]提出的分割式加强环并根据CECS 280―2010《钢管结构技术规程》[18]设计了A、B两种类型外环板。
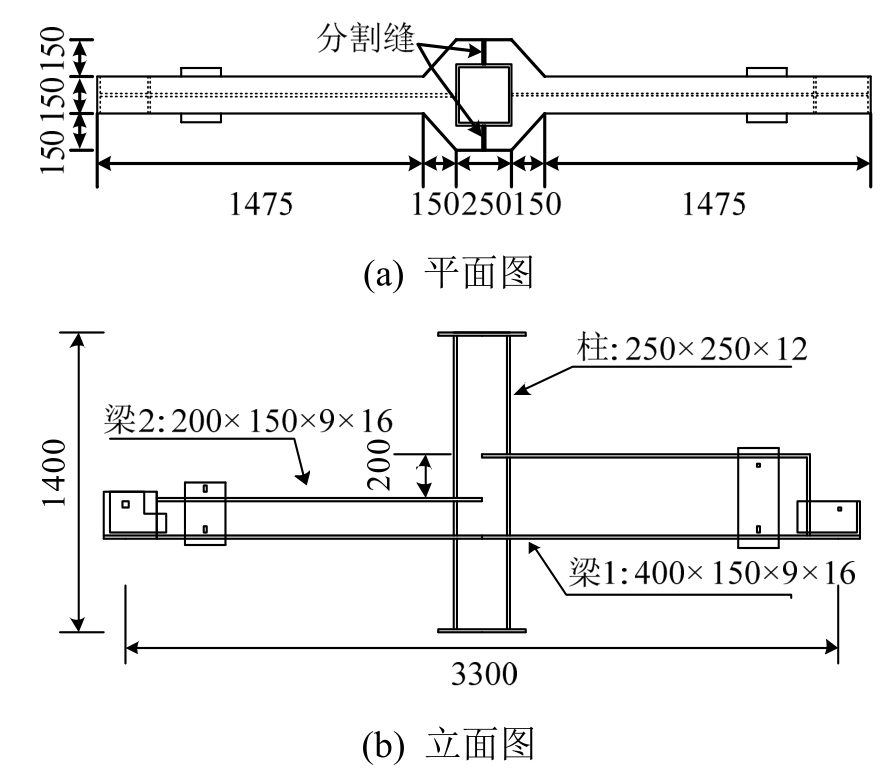
图2 试件详图(UCE-3)
Fig.2 Detail of specimen(UCE-3)
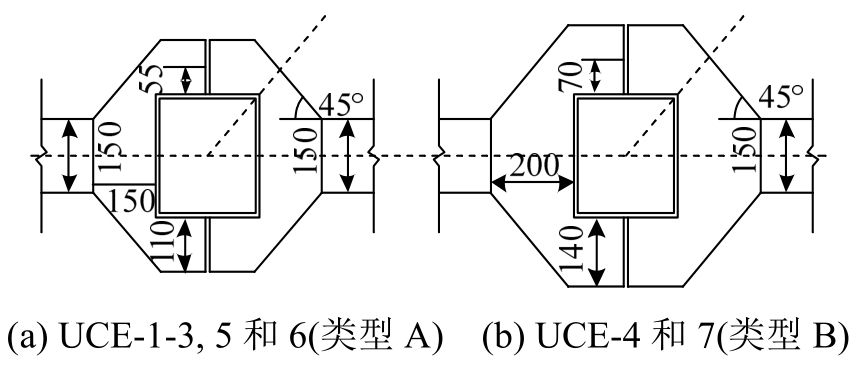
图3 外环板细部尺寸
Fig.3 Details of external diaphragm

图4 加载示意图
Fig.4 Overall view of test setup
表1 试件基本信息
Table 1 Basic information of specimens
试件编号 钢管柱 梁1 梁2 节点柱梁强度比[12] db2/db1 加强环尺寸UCE-1400×150×9×16 0.65 1 UCE-2300×150×9×16 0.77 0.75 UCE-3250×250×9 400×150×9×16 A型0.92 UCE-40.92 B型UCE-5 250×250×12 1.09 A型UCE-6 250×250×6 0.65 UCE-7 0.65 B型400×150×9×16200×150×9×160.5
该试验的加载设备主要由反力架和两个500 kN作动器构成。试件通过铰支座与反力架连接。试件上部通过滑动铰支座与反力架相连,允许试件竖向位移。试件下部通过固定铰支座与反力架相连。作动器提供方向相反、大小相同的荷载,加载设备如图4。
本文规定梁1向上移动,梁2向下移动作为正方向;反之为负方向。试验对所有试件均采用拟静力加载方式。加载全程采用位移控制,位移角按照0.5%、1%、2%、3%、4%、5%逐级加载,每级各循环2次;在完成5%位移角的两次循环后,继续正向加载,直至达到设备最大量程,停止试验。试验过程详述见文献[16]。
试件的初始剪切刚度为θ=5%时对应的的割线刚度[19];按斜率因子法[19]确定试件屈服点;采用0.35%偏移强度法[20]确定试件塑性点。
部分试件的破坏现象如图5所示,通过对试件试验现象的观察。当位移角处于0.005 rad≤R<0.01 rad范围时节点域处于弹性变形阶段,当位移角处于0.01 rad≤R<0.03 rad范围时节点域逐渐进入塑性变形阶段。当位移角R≥0.03 rad时试件破坏。所有试件破坏形式均为节点域剪切破坏,梁端未形成塑性铰。
本文分析典型试件的破坏状态,其他试件的破坏过程分析详见文献[16]。当试件UCE-1加载至R=0.02 rad时外环板表皮掉落,节点域剪切变形不断增大。当R=0.04 rad时达到试件抗剪承载力,该试件最终表现为如图5(a)所示的节点域整体剪切破坏。与UCE-1不同,UCE-2节点域的剪切变形大部分发在Panel 1,而Panel 2的剪切变形不明显;在节点域塑性形变发展过程中,梁1侧外加强环变形与钢管柱壁的面外变形较为明显。当位移角达到R=0.04 rad时试件达到极限承载能力。试件正、负向极限承载力大致相等。UCE-2的最终破坏形态为如图5(b)所示的节点域部分剪切破坏(SFPPZ)。试件UCE-5的破坏形态与试件UCE-2类似表现为节点域部分剪切破坏(SFPPZ)并出现外加强环焊缝撕裂的现象,其最终破坏形态如图5(c)所示。UCE-7与UCE-1破坏现象类似表现为节点域整体剪切破坏(SFEPZ)如图5(d)。

图5 部分试件破坏状态与该状态下应力云图对比
Fig.5 phenomenon of destruction and colored stress patterns
试验结果表明:1试件、6试件和7试件的破坏为节点域整体剪切破坏(SFEPZ),2试件~5试件为节点域部分剪切破坏(SFPPZ)。如图6所示,节点域两侧梁高比(db1/db2)、外环板类型以及宽厚比(D/t)是影响试件节点域承载力和剪切变形的主要因素,不同变量对承载力影响的详细分析见参考文献[16]。
1.3 有限元分析过程
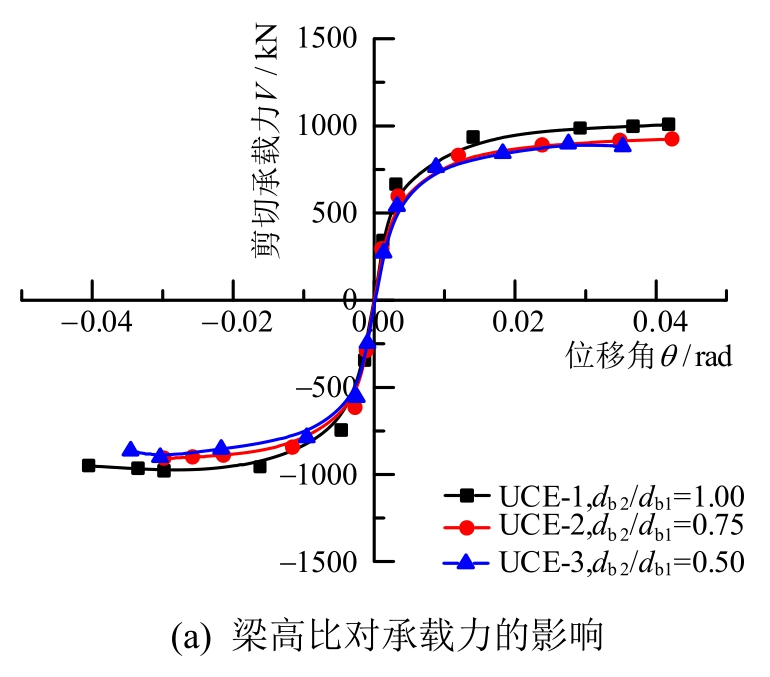
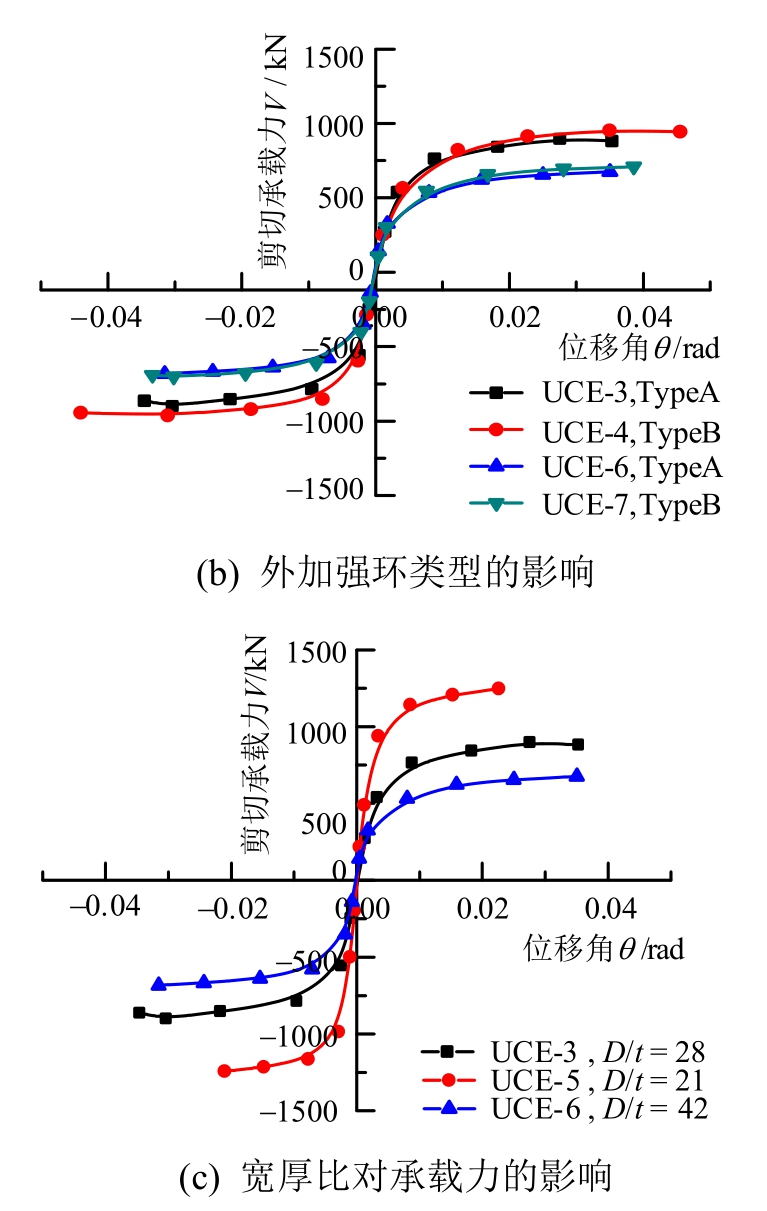
图6 各试件的骨架曲线
Fig.6 Skeleton curves for specimens
作者采用有限元分析方法对20个不同参数UCE节点模型进行了分析[21]。有限元模拟以试验研究作为参照,依据试件的实际尺寸建立精细化实体模型,如图7所示。建模过程中按照试验试件的真实边界条件对构件上下端进行了约束。在加载点施加与试验相同的对称荷载。有限元模拟结果与试验结果吻合较好,分析模型可靠性较高。由模拟结果可知,当试件模型的节点域到达屈服状态时,等高梁节点屈服承载力是由整个节点域共同承担;而不等高梁节点屈服承载力则主要由节点域1(Panel 1)承担。当试件模型的节点域达到塑性变形状态时,出现两类剪切破坏模式:节点域整体剪切破坏和节点域部分剪切破坏,如图5所示。根据有限元分析得知节点域不同破坏模式的重要控制因素是节点单侧最小柱梁强度比,其概念如1.4节所述。


图7 不等高梁节点有限元模型(UCE-6)
Fig.7 Typical 3D finite element analysis model of UCE(UCE-6)
1.4 节点单侧最小柱梁强度比与两种破坏模式
为探究各个模型的破坏形态的变化规律,在节点柱梁强度比[22]的基础上提出节点单侧最小柱梁强度比的概念,如图8所示。节点单侧最小柱梁强度比是指不等高梁节点中柱端极限弯矩之和与单侧梁端极限弯矩最大值的比值,详见式(1):
式中:ROCJB为节点单侧最小柱梁强度比;Mc1+Mc2为节点柱极限弯矩之和;max{Mb1,Mb2}为单侧梁端极限弯矩最大值。
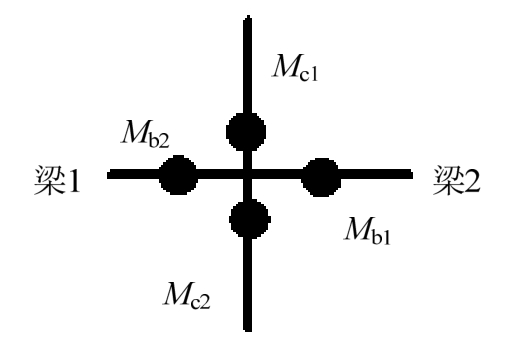
图8 节点单侧最小柱梁强度比
Fig.8 Minimum of one-side column to beam strength ratio
通过有限元分析,本文根据节点单侧最小柱梁强度比,将节点域破坏模式区分如下[21]:节点单侧最小柱梁强度比小于0.92时,试件发生节点域整体剪切破坏(SFEPZ);节点单侧最小柱梁强度比大于0.92时,试件发生节点域部分剪切破坏(SFPPZ)。
总结试验现象及有限元分析结果,两种破坏模式见图9:节点域整体发生塑性剪切变形(SFEPZ),钢管壁面外变形不明显如图9(a);节点域发生部分剪切变形(SFPPZ)时节点域1发生塑性剪切破坏、节点域2的钢管壁发生面外变形,与此同时外环板屈服,如图9(b)。

图9 两种破坏模式
Fig.9 Two failure modes
2 计算分析
2.1 屈服剪切承载力分析
从试验及有限元分析中可以看出,当不存在梁高度差影响时(db2/db1=1),节点屈服承载力由节点域整体共同承担,如图9(a);然而当存在梁高度差影响(0.5<db2/db1<1),节点屈服承载力主要由节点域1承担,节点域2的贡献十分有限,如图9(b)。因此,当节点域1钢材的剪应力到达屈服状态τy时,节点域所受的剪力即可定义为节点域的屈服剪切承载力。节点域的屈服剪切承载力可由以下公式求得:
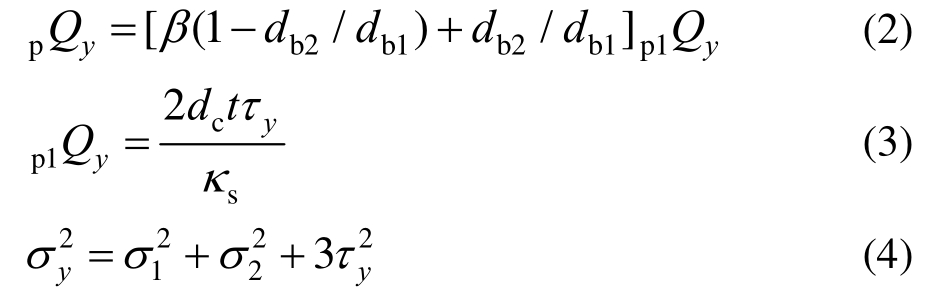
由于节点域只受剪切,σ1=0,σ2=0即:
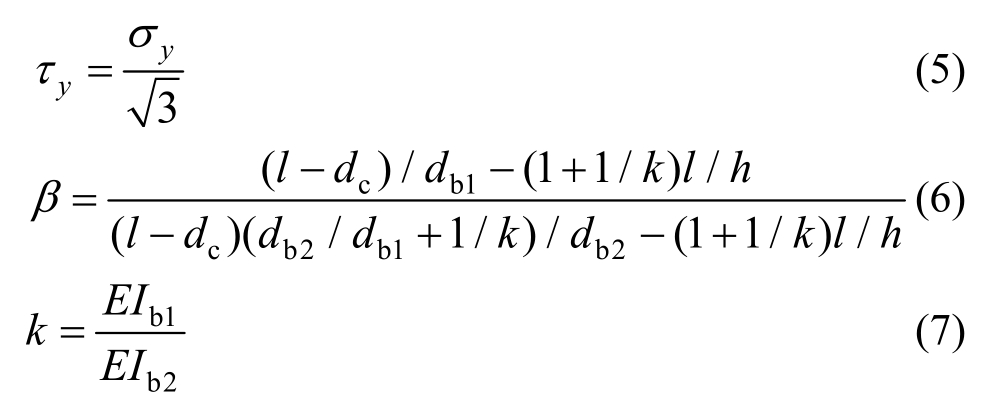
式中:σ1、σ2为梁、柱轴向应力;σy为钢管屈服应力;pQy为整个节点域的屈服剪切承载力;p1Qy为当节点域1的剪切应力到达屈服剪切应力τy时,节点域1的剪切承载力;β为与构件尺寸相关的系数;db1为梁1上下翼缘中心线间的距离;db2为梁2上下翼缘中心线间的距离;dc=D-t,D为柱宽;t为方钢管柱壁厚;κs=9/8;h为上下两支座之间的距离;l为两个加载点之间的距离;k为不等高梁刚度比;E为弹性模量;Ib1为梁1截面转动惯量;Ib2为梁2截面转动惯量。
本文将有限元分析所得屈服剪切承载力与上述公式计算的结果进行对比,见表2。表2中pQyc指文中公式计算的屈服剪切承载力,pQyFEM为20个模型通过有限元模拟得出的屈服剪切承载力。
表2 试件屈服剪切承载力对比
Table 2 Finite element models of UCE

正向荷载 负向荷载试件编号pQyc/kN pQyFEM/kN y y pc pFEM Q QypQyc/kN pQyFEM/kN pc pFEM Q Qy UCE-2 679 602 1.13 679 595 1.14 UCE-3 629 588 1.07 629 593 1.06 UCE-4 629 646 0.97 629 636 0.99 UCE-5 839 813 1.03 839 819 1.02 UCE-6 437 365 1.20 437 335 1.30 UCE-7 437 398 1.10 437 392 1.11 No.8 545 621 0.88 545 626 0.87 No.9 509 546 0.93 509 536 0.95 No.10 508 468 1.09 508 461 1.10 No.11 428 483 0.89 428 493 0.87 No.12 400 424 0.94 400 435 0.92 No.13 399 386 1.03 399 380 1.05 No.14 640 601 1.06 640 607 1.05 No.15 635 600 1.06 635 607 1.05 No.16 641 588 1.09 641 594 1.08 No.17 1047 920 1.14 1047 925 1.13 No.18 895 823 1.09 895 830 1.08 No.19 555 425 1.31 555 428 1.30 No.20 474 367 1.29 474 363 1.31
公式计算所得的屈服剪切承载力是有限元分析所得屈服剪切承载力值的87%~131%。正向荷载作用下公式计算所得屈服剪切承载力与有限元分析所得的屈服剪切承载力比值的平均值为1.074,负向荷载作用下公式计算所得的屈服剪切承载力与有限元分析所得屈服剪切承载力比值的平均值为1.078。正向荷载作用下公式计算所得屈服剪切承载力与有限元分析所得的屈服剪切承载力比值的变异系数为10.9%,负向荷载作用下公式计算所得屈服剪切承载力与有限元分析所得屈服剪切承载力比值的变异系数为11.9%,可见公式计算所得屈服剪切承载力与有限元分析所得屈服剪切承载力比值离散性较小,数据特征稳定。
计算结果pQyc和模拟结果pQyFEM的比较如图10所示,用本文公式计算得到的试件屈服剪切承载力与有限元模型所得的屈服剪切承载力吻合较好,证明了本文所提公式的准确性。
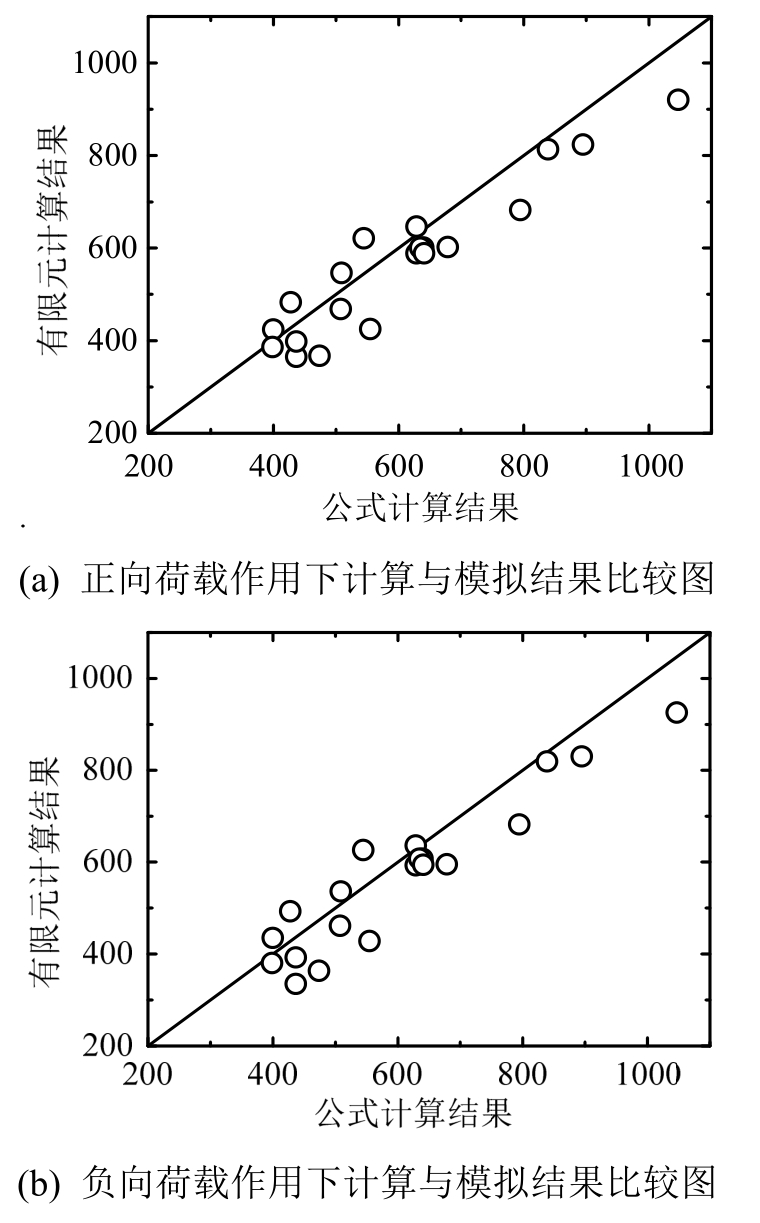
图10 计算结果pQyc和模拟结果pQyFEM的比较图
Fig.10 Comparison of the calculated results(pQyc)and the simulation results(pQyc)
2.2 剪切承载力分析
当节点单侧最小柱梁强度比小于0.92时,节点域发生SFEPZ破坏,整个节点的剪切承载力按下式进行计算:
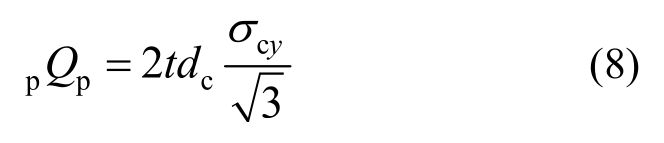
当节点单侧最小柱梁强度比大于0.92时,节点域发生SFPPZ破坏,节点域1产生塑性变形;节点域1的内功为:
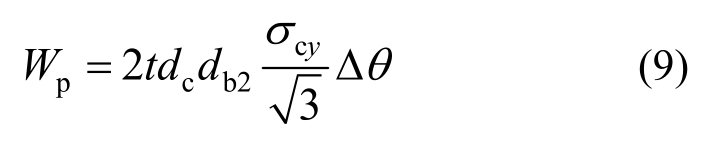
式中,Δθ为虚拟旋转角。
与节点域2相连的外环板产生屈服变形如图11所示,外环板的内功为:
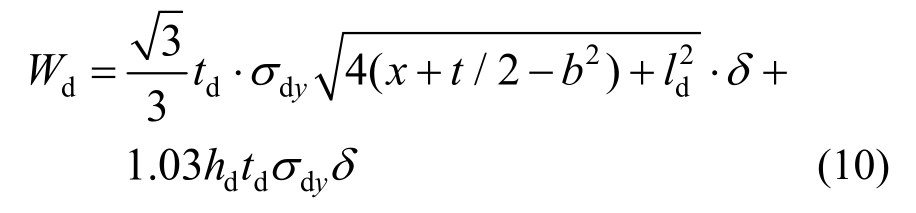
节点域2的钢管壁发生面外变形如图12所示,钢管壁的内功为:

式中:td为外加强环厚度;σdy为加强环屈服强度;x为与梁翼缘连接区域钢管壁面外水平向变形范围;b为环板宽度;ld为钢管外壁与梁端之间距;δ为虚位移;hd为加强环切角至柱腹板的宽度;α为与水平向对应的纵向变形范围系数;s为外环板与方钢管柱角焊缝宽度。
根据虚功原理可得:
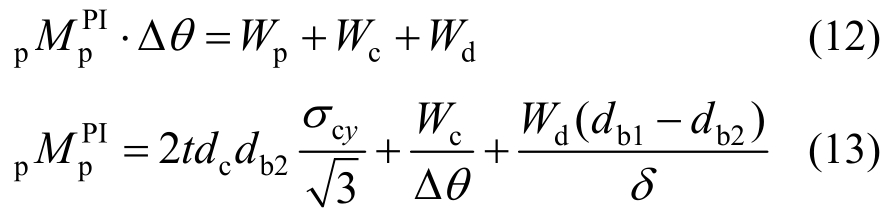
式中,![]() 为节点域1的弯矩值。
为节点域1的弯矩值。
如图1所示,节点域的弯矩值![]() 可由下式求得:
可由下式求得:
式(13)为含有x、α和![]() 的三元函数,由上界定理分别对式(13)中x和α求偏导数可得:
的三元函数,由上界定理分别对式(13)中x和α求偏导数可得:
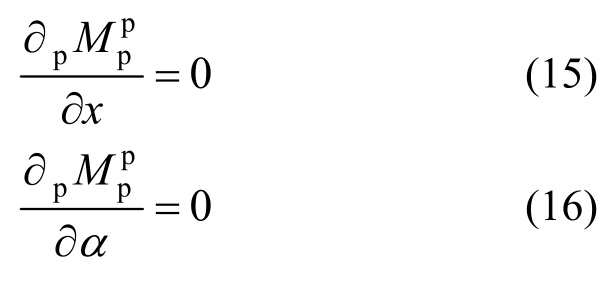
将式(13)和式(14)展开可得:
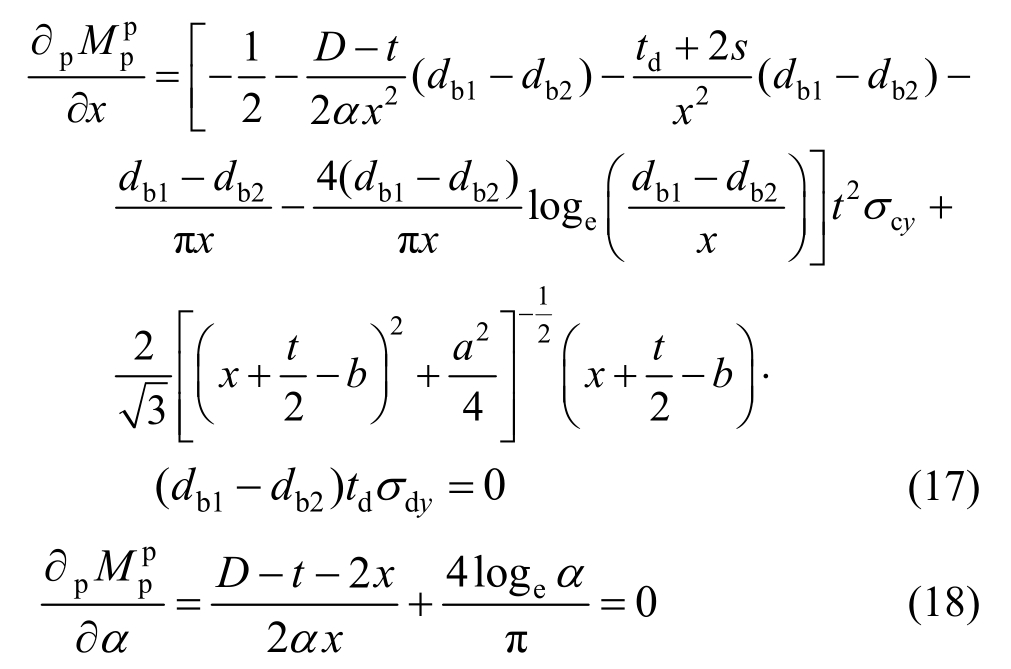
由式(17)和式(18)可以求得数值解。因此节点域剪切承载力为:
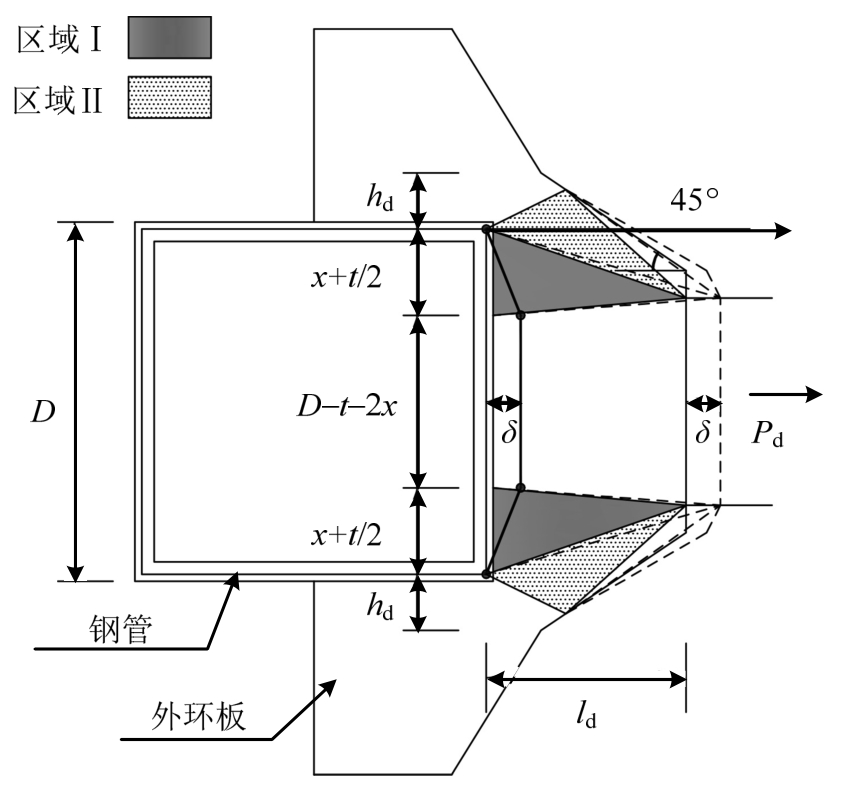
图11 外环板的破坏机构
Fig.11 Collapse mechanism of exterior diaphragm

图12 钢管柱壁的面外破坏机理
Fig.12 Out-of-plane collapse mechanism of column tubular wall
采用有限元模拟所得剪切承载力与本文中的公式计算剪切承载力进行对比。如表3所示。表中pQpc指文中公式计算剪切承载力,pQmax指20个模型通过有限元模拟得出的剪切承载力。
公式计算与有限元分析所得的剪切承载力比较如表3所示。公式计算所得的剪切承载力是有限元分析所得的剪切承载力值的83%~113%。正向荷载作用下公式计算所得的剪切承载力与有限元分析所得的剪切承载力比值的平均值为0.977,负向荷载作用下公式计算所得的剪切承载力与有限元分析所得的剪切承载力比值的平均值为0.976。正向荷载作用下公式计算所得的剪切承载力与有限元分析所得的剪切承载力比值的变异系数为8.6%,负向荷载作用下公式计算所得的剪切承载力与有限元分析所得的剪切承载力比值的变异系数为8.5%,可见公式计算所得的剪切承载力与有限元分析所得的剪切承载力比值离散性较小,数据特征稳定。
表3 试件最大承载力对比
Table 3 Finite element models of UCE

试件编号pQpc/ pQmax/Q正向荷载 负向荷载 单侧柱梁强度比 pQpc/pQmax/Q ppc pmax Q kN kN kN kN ppc pmax Q破坏模式UCE-1 904 966 0.94 904 967 0.93 1.27 整体UCE-2 853 872 0.98 853 871 0.98 1.27 局部UCE-3 820 841 0.98 820 839 0.98 1.27 局部UCE-4 904 891 1.01 904 900 1.00 1.27 局部UCE-5 992 1254 0.79 992 1254 0.79 1.50 局部UCE-6 622 628 0.99 622 630 0.99 0.79 整体UCE-7 622 663 0.94 622 661 0.94 0.79 整体No.8 717 717 1.00 717 719 1.00 1.16 局部No.9 717 657 1.09 717 658 1.09 1.16 局部No.10 717 634 1.13 717 636 1.13 1.16 局部No.11 563 570 0.99 563 570 0.99 0.92 整体No.12 563 540 1.04 563 540 1.04 0.92 整体No.13 563 532 1.06 563 532 1.06 0.92 整体No.14 850 869 0.98 850 871 0.98 1.86 局部No.15 836 846 0.99 836 848 0.99 1.52 局部No.16 804 800 1.01 804 802 1.00 1.09 局部No.17 1171 1413 0.83 11711415 0.83 1.50 局部No.18 1066 1288 0.83 10661278 0.83 1.50 局部No.19 622 652 0.95 622 651 0.96 0.79 整体No.20 622 622 1.00 622 620 1.00 0.79 整体
计算结果pQpc和模拟结果pQmax的比较如图13所示,用本文公式计算得到的试件剪切承载力与有限元模型所得的剪切承载力吻合较好,证明了本文所提公式的准确性。
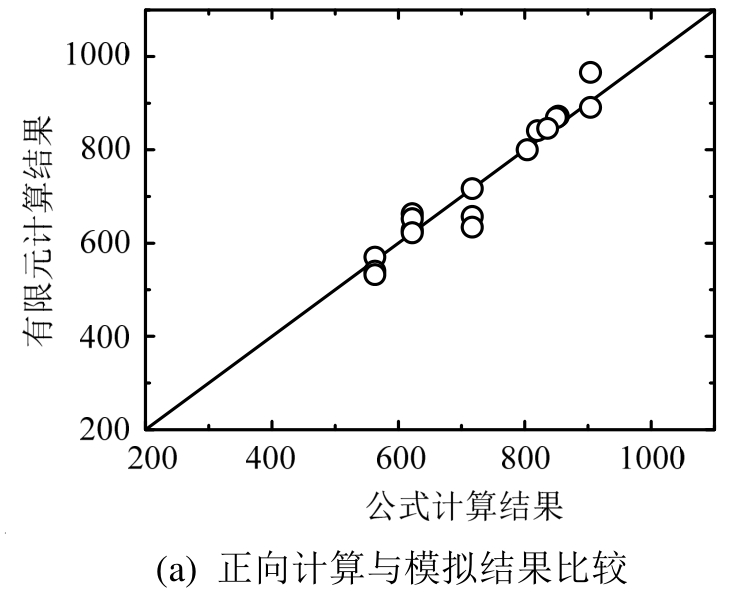
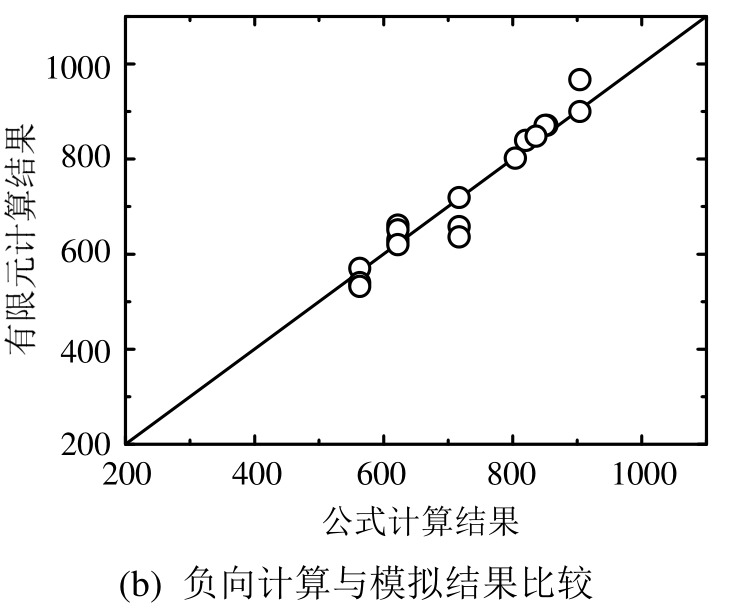
图13 剪切承载力的公式计算结果与有限元分析结果比较
Fig.13 Comparison of the calculated results and the simulation results
3 结论
本文在试验及有限元分析基础上,建立了外环板式高低梁-方钢管柱节点的弹塑性剪切承载力计算模型并提出计算公式,得到以下主要结论:
(1)本文基于屈服线理论结合节点域整体剪切破坏(SFEPZ)以及节点域部分剪切破坏(SFPPZ)两种破坏模式,提出了外环板式不等高H型钢梁-方钢管柱节点的屈服剪切承载力与剪切承载力的计算公式。
(2)对于屈服剪切承载力,公式计算值是有限元分析值的87%~131%;正向荷载作用下公式计算结果与有限元分析结果之比平均值为1.074,变异系数为10.9%;负向荷载作用下公式计算结果与有限元分析结果之比的平均值为1.078,变异系数为11.9%。
(3)对于剪切承载力,公式计算值是有限元分析值的83%~113%;正向荷载作用下公式计算结果与有限元分析结果之比平均值为0.977,变异系数为8.6%;负向荷载作用下公式计算结果与有限元分析结果之比的平均值为0.976,变异系数为8.5%。
(4)外环板式高低梁-方钢管柱节点的屈服剪切承载力及剪切承载力的公式计算结果与有限元分析结果吻合度较高,计算公式简洁明了具有一定实用价值。本文完善了该类型节点的设计理论,可以为外环板式高低梁方钢管柱节点设计分析提供参考。
[1]立山英二, 井上一朗, 杉本正三, 等.通しダイヤフラム形式で角形鋼管柱に接合されるH形断面はりの耐力と変形性能に関する研究[J].日本建築学会構造系論文報告集, 1988, 389: 109-121.Tateyama Eiji, Inoue Kazuo, Sugimoto Shozo, et al.Study on ultimate bending strength and deformation capacity of h-shaped beam connected to RHS column with through diaphragms [J].Journal of Structural and Construction Engineering, 1988, 389: 109-121.(in Japanese)
[2]Mansfield E H.Studies in collapse analysis of rigid-plastic plates with a square yield diagram [J].Proceedings of the Royal Society of London, 1957,241(1226): 311-338.
[3]森田耕次, 江波戸和正, 舟橋明之, 等.箱形断面柱のかど溶接を部分溶込み溶接とした柱はり接合部の力学的挙動に関する研究[J].日本建築学会構造系論文報告集, 1989, 397: 48-59.Morita Koji, Ebato Kazumasa, Funahasi Akiyuki, et al.Study on structural behaviors of beam-to-column connections : in case corner weld of box column is partial penetration weld [J].Journal of Structural and Construction Engineering, 1989, 397: 48-59.(In Japanese)
[4]吹田啓一郎, 田中剛.角形鋼管柱に接合される梁ウェブ接合部の曲げ耐力[J].学術講演梗概集, 2000, C-1:731-732.Keiichiro Suita, Tanaka Tsuyoshi.Flexural strength of beam web to square tube column joints [J].Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan, 2000, C-1: 731-732.(in Japanese)
[5]李成玉, 高原, 周永.基于屈服线理论的钢管混凝土外加强环节点设计公式推导[J].工程建设与设计,2012(2): 44-46.Li Chengyu, Gao Yuan, Zhou Yong.Design formula derivation for exterior stiffener ring connection of concrete fill steel tube based yield-line method [J].Construction and Design for Project, 2012(2): 44-46.(in Chinese)
[6]牟犇, 陈功梅, 张春巍, 等.带外加强环不等高梁-钢管混凝土柱组合节点抗震性能试验研究[J].建筑结构学报, 2017, 38(5): 77-84.Mou Ben, Chen Gongmei, Zhang Chunwei, et al.Experimental investigation on seismic behavior on steel unequal-depth-beams to CFT column connection with external diaphragm [J].Journal of Building Structures,2017, 38(5): 77-84.(In Chinese)
[7]牟犇, 王玲玲, 张春巍, 等.考虑楼板影响的外环板式梁柱节点抗震性能: 试验研究[J].工程力学, 2018,35(2): 160-168, 213.Mou Ben, Wang Lingling, Zhang Chunwei, et al.Aseismic performance of beam-to-column joints with external-diaphragm considering slab effect: experimental investigation [J].Engineering Mechanics, 2018, 35(2):160-168, 213.(in Chinese)
[8]钱炜武, 李威, 韩林海, 等.带楼板钢管混凝土叠合柱-钢梁节点抗震性能数值分析[J].工程力学, 2016,33(增刊): 95-100.Qian Weiwu, Li Wei, Han Linhai, et al.Analytical behaviour of concrete-encased concrete-filled steel tubular column to steel beam joints with RC slabs [J].Engineering Mechanics, 2016, 33(Suppl): 95-100.(in Chinese)
[9]赵毅, 徐礼华, 程康, 等.劲性环梁式钢管混凝土节点受力性能研究[J].工程力学, 2013, 30(增刊): 241-247.Zhao Yi, Xu Lihua, Cheng Kang, et al.A analysis on the mechanical behavior of steel reinforced ring-beam connections of concrete filled steel column and RC beam[J].Engineering Mechanics, 2013, 30(Suppl): 241-247.(in Chinese)
[10]周栋梁, 钱稼茹, 方小丹.RC环梁连接的钢管混凝土柱-RC梁框架计算模型研究[J].工程力学, 2005(6):117-121, 240.Zhou Dongliang, Qian Jiaru, Fang Xiaodan.Analysis model of steel-tube confined concrete column and RC beam frame connected by RC ring beam [J].Engineering Mechanics, 2005(6): 117-121, 240.(in Chinese)
[11]徐礼华, 凡红, 刘胜兵, 等.方钢管混凝土柱-钢梁节点抗震性能试验研究与有限元分析[J].工程力学,2008, 25(2): 122-131.Xu Lihua, Fan Hong, Liu Shengbing, et al.Experimental studies on aseismic behavior of connection between concrete-filled steel square tubular column and steel beam [J].Engineering Mechanics, 2008, 25(2): 122-131.(in Chinese)
[12]薛建阳, 翟磊, 魏志粉, 等.传统风格建筑圆钢管柱-箱形截面双梁节点受力性能试验研究与承载力计算[J].工程力学, 2017, 34(2): 189―196.Xue Jianyang, Zhai Lei, Wei Zhifen, et al.Experimental study on mechanical performance and strength prediction of circle tubular steel column-double box-section beam joints in traditional style building [J].Engineering Mechanics, 2017, 34(2): 189―196.(in Chinese)
[13]胡方鑫, 施刚, 石永久.基于断裂力学的高强度钢材梁柱节点受力性能分析[J].工程力学, 2015, 32(4):41-46.Hu Fangxin, Shi Gang, Shi Yongjiu.Fracture behavior of beam-column connections using high strength steel based on fracture mechanics [J].Engineering Mechanics, 2015,32(4): 41-46.(in Chinese)
[14]Liao F Y, Han L H, Tao Z.Behaviour of composite joints with concrete encased CFST columns under cyclic loading: Experiments [J].Engineering Structures, 2014,59(2): 745-764.
[15]Bai Y, Lin Xuchuan.Numerical simulation on seismic collapse of thin-walled steel moment frames considering post local buckling behavior [J].Thin-Walled Structures,2015, 94: 424-434.
[16]牟犇, 井后凯, 张春巍, 等.外加强环不等高H型钢梁-方钢管柱节点抗震性能试验研究[J].建筑结构学报,2018, 39(8): 80-89.Mou Ben, Jing Houkai, Zhang Chunwei, et al.Experimental investigation on seismic behavior of unequal-depth H-shape steel beam to column connection with external-diaphragm [J].Journal of Building Structures, 2018, 39(8): 80-89.(in Chinese)
[17]Yoshizato J, Nakamura Y, Kuromatsu J, et al.Experimental study on SHS column to H-Beam connections with exterior plate diaphragms [C].Japan:Summaries of technical papers of Annual Meeting Architectural Institute of Japan.Structures II.Architectural Institute of Japan, 1994: 1417-1418.(in Japanese)
[18]CECS 208: 2010, 钢管结构技术规程 [S].北京: 中国计划出版社, 2010.CECS 208: 2010, Technical specification for structures with steel hollow sections [S].Beijing: China Planning Press, 2010.(in Chinese)
[19]Beedle L S, Topractsologlou A A, Johnston B G.Connection for welded continuous portal frames: part III:discussion of test results and conclusions, Progress report No.4 [J].The Welding Journal, 1952, 11 : 543-560.
[20]Kuwahara S, Kumano T, Inoue K.The elasto-plastic behavior of joint panels at the connection of rectangular steel column and two H-shaped beams with different depth [J].Journal of Structural and Construction Engineering, 2000, 65(533): 175-181.
[21]牟犇, 李茜, 王燕, 等.外加强环不等高H型钢梁-方钢管柱节点受力性能有限元分析[J].建筑结构学报,2018, 39(10): 103-111.Mou Ben, Li Xi, Wang Yan, et al.Numerical investigation on unequal-depth-beams-to-column connection panel zone with external-diaphragm [J].Journal of Building Structures, 2018, 39(10): 103-111.(in Chinese)
[22]桑村仁, 佐々木 道夫, 加藤 勉.降伏耐力のばらつきを考慮した全体崩壊メカニズム骨組の設計[J].日本建築学会構造系論文報告集, 1989, 401: 151-162.Kuwamura Hitoshi, Sasaki Michio, Kato Ben.Mechanism-based seismic design considering random yield strength [J].Journal of Structural and Construction Engineering, 1989, 401: 151-162.(in Japanese)