支撑是一种重要的抗侧力构件，但普通支撑受压易屈曲，导致支撑的拉压承载力和刚度相差较大，支撑屈曲后结构的抗震能力下降。为弥补普通支撑受压易屈曲的不足，学者们提出了屈曲约束支撑(Buckling restrained brace，BRB)[1]，BRB的拉压承载力和刚度基本对称，地震作用下具有稳定的承载力和耗能能力，但由于BRB采用自身塑性变形耗散地震能量，且不具备复位能力，导致装配了BRB的结构震后出现较大残余变形，结构震后修复费用大。为了减小支撑结构的震后残余变形，国内外学者提出了自复位耗能支撑的概念[2－4]，自复位耗能支撑同时具备耗能能力和自复位能力，所以其既能控制结构的地震响应，又能降低结构的震后残余位移。
基于性能的抗震设计是结构抗震设计方法发展的新方向，该理念要求确定结构在不同强度地震作用下的损伤或破坏程度[5]。由于结构的破坏状态主要与结构变形相关，而与承载力没有明确的关系，所以与用承载力作为设计变量相比，以变形(位移)作为设计指标能更好地实现基于性能的抗震设计理念[6]。直接基于位移的抗震设计(Direct displacement-based design, DDBD)方法以结构在一定水准地震作用下的预期位移为设计目标对结构、构件的强度和刚度进行设计[7]，与“三水准、两阶段”的设计方法相比，该方法能够避免重复验算而增加的设计计算量[6]。Kowalsky等[8]提出了桥墩的DDBD法，其后Priestley等[9]将DDBD法进一步完善，并且用于多自由度结构的设计。Lin等[10]和李钢等[11]研究了消能减震结构的DDBD法，并且通过数值实例验证了所提方法的实用性和准确性。杨博雅等[12]研究了预应力混凝土结构的DDBD法，表明按照该方法设计的结构能够满足性态目标(目标位移)的要求。
本文基于研发的预压碟簧自复位耗能(Pre-pressed spring self-centering energy dissipation，PS-SCED)支撑，以PS-SCED支撑-钢框架为研究对象，采用DDBD法对支撑参数进行设计。与上述关于DDBD法运用的结构类型相比，自复位支撑-框架结构的等效阻尼比不同，本文首先提出并验证了PS-SCED支撑-钢框架结构的等效阻尼比公式，在此基础上采用DDBD法对支撑参数进行设计，分析了支撑刚度比对结构地震响应的影响，并给出了支撑刚度比的建议取值。
1 PS-SCED支撑
1.1 支撑构造及恢复力模型
PS-SCED支撑的构造如图1所示，其主要由内外管、碟簧和摩擦装置构成，其中摩擦装置决定了支撑的耗能能力，内外管的刚度决定了支撑第一刚度大小，支撑的第二刚度则由碟簧提供，支撑的复位力由碟簧的预压力和碟簧受压变形产生的反力共同提供。支撑的特殊构造使其无论在受拉或受压状态都具有稳定的自复位性能[13]。低周往复荷载作用下，支撑的滞回曲线为旗形，且拉压对称[3]，其恢复力模型如图2所示。
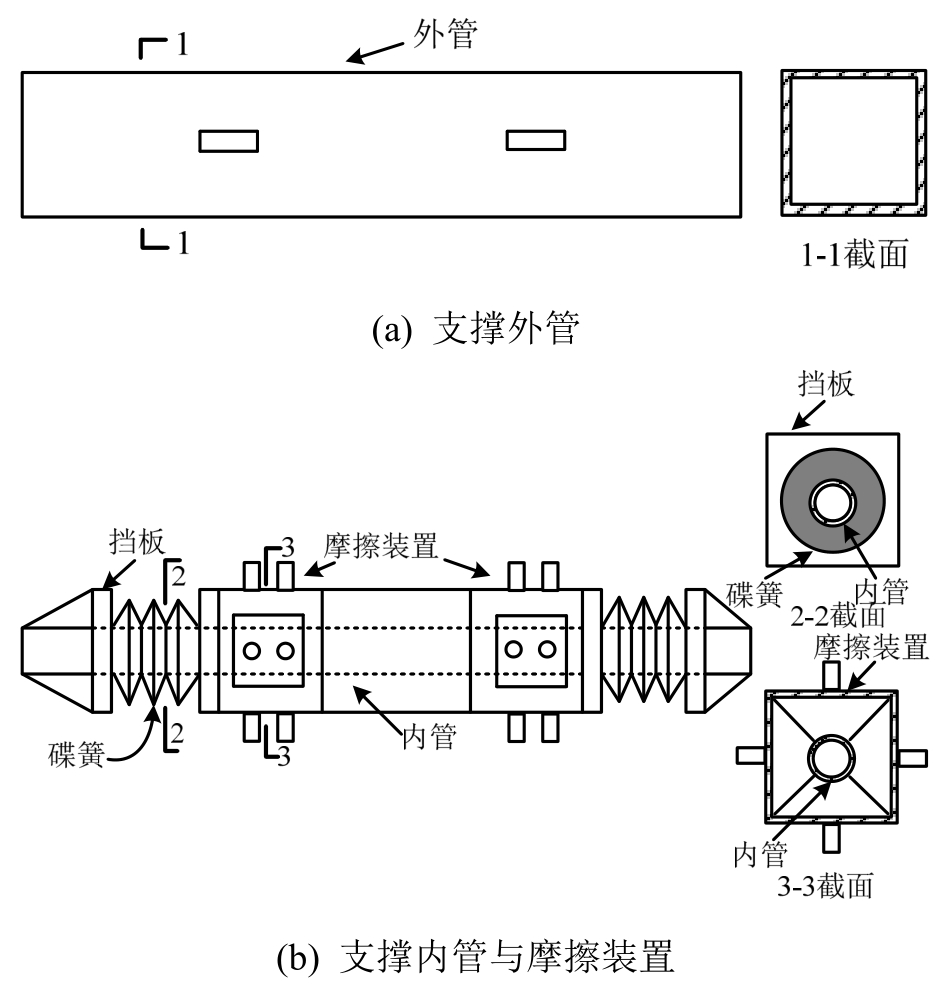
图1 PS-SCED支撑构造
Fig.1 Configuration of PS-SCED brace
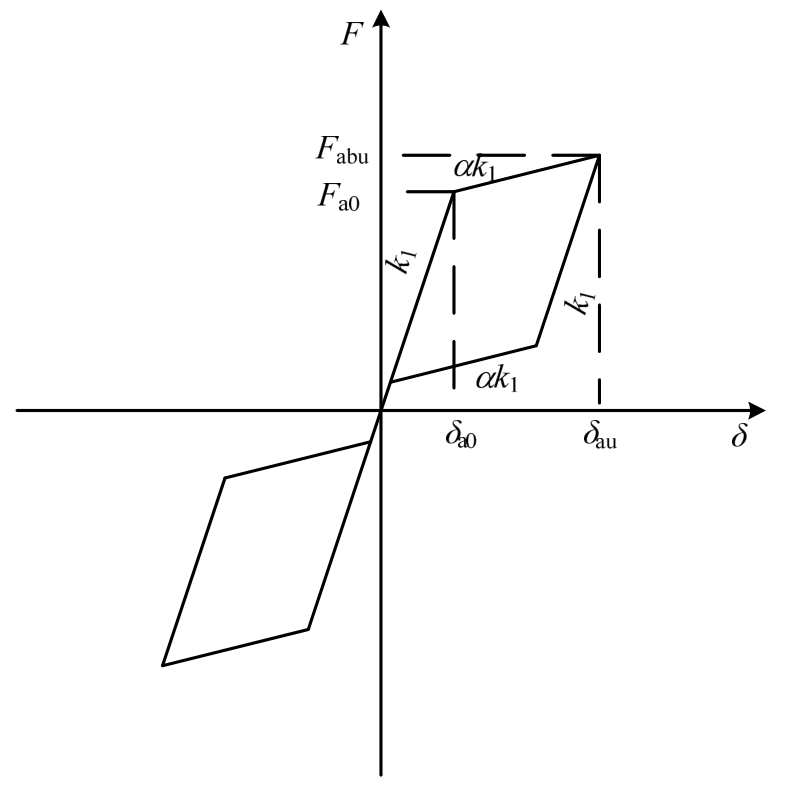
图2 PS-SCED支撑恢复力模型
Fig.2 Restoring force model of PS-SCED brace
影响支撑性能的参数有5个，分别为支撑第一刚度k1，支撑第二刚度与第一刚度之比α，支撑激活力Fa0，支撑极限承载力Fabu，摩擦力与激活力之比β，其表达式为：
式中，Faf为支撑摩擦力。β越大，旗形滞回曲线的面积越大，支撑的耗能能力越强。研究表明[14]，当β大于0.5时，卸载后支撑将出现残余变形，所以为保证支撑的自复位性能，一般要求β不超过0.5。
1.2 支撑刚度比上限
本节从PS-SCED支撑构造出发，推导其刚度比上限。由支撑构造可得k1与内外管刚度的关系为[13]：
式中，ki、ko分别为支撑内管刚度和外管刚度。
为保证支撑的工作性能，要求内外管在整个工作阶段保持弹性，故在Fabu作用下，可得到内外管的最小刚度：
式中：E为钢材弹性模量；fy为钢材屈服强度；l为支撑长度。
将式(3)代入式(2)可得k1下限值为：
由k1与Fa0的关系及式(4)可得Fa0的下限为：
式中，δa0为支撑轴向的激活位移。
Fa0的下限确定之后，可根据下式确定αk1的上限：
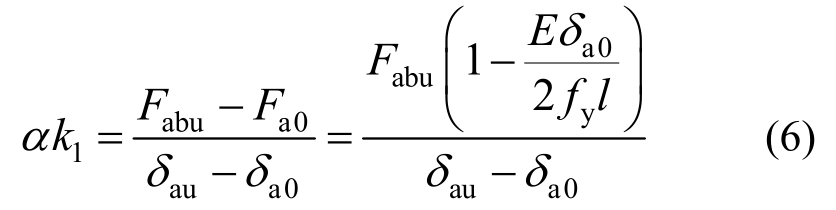
式中，δau为支撑轴向的极限位移。
由式(4)和式(6)可得α的上限为：
因此α的取值范围为[0，αmax]，下文将研究α的变化对结构性能的影响，以验证按照该范围确定的α是否满足性能目标要求。
2 DDBD法基本原理
2.1 DDBD法设计流程
DDBD法以目标位移为设计变量对结构进行承载力和刚度设计，故结构承载力和刚度是目标位移的函数，而目标位移是结构性能目标的函数，所以采用DDBD法得到的结构承载力和刚度与性能目标直接相关，这也是该抗震设计方法相对于传统抗震设计方法的优势。DDBD法的设计流程如图3所示。
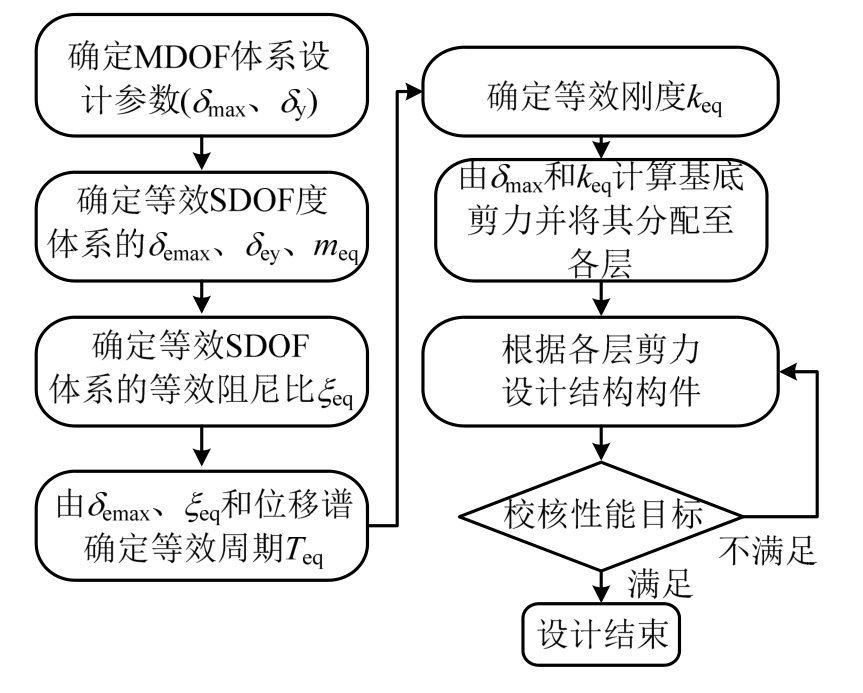
图3 DDBD法设计流程
Fig.3 Design flowchart of DDBD method
采用DDBD时，需将MDOF体系转化为等效SDOF体系，并由结构性能目标确定MDOF体系的顶点位移最大值δmax和结构屈服位移δy，由此得到等效SDOF体系的最大位移δemax和等效质量meq。为确定等效SDOF体系的等效周期Teq，需要计算其等效阻尼比ξeq，而ξeq取决于结构的延性需求和恢复力模型。
2.2 PS-SCED支撑-钢框架结构等效阻尼比
DDBD法将弹塑性结构转化为线弹性的等效SDOF体系，以等效SDOF体系的位移响应估计原弹塑性结构的位移响应，其理论基础是等效线性化原理，即实际弹塑性结构的最大位移响应可用一个低侧向刚度(等效刚度keq)和高阻尼比(等效阻尼比ξeq)的线弹性体系计算[5]。
2.2.1 等效阻尼比计算
确定结构的等效阻尼比ξeq是直接基于位移的抗震设计的关键一环。ξeq由结构初始粘滞阻尼比和结构滞回耗能产生的附加阻尼比构成[15]，附加阻尼比可用结构滞回一周的耗能与结构最大应变能的比值表示[16]，从而可得ξeq的表达式为：
式中：ξv为结构初始粘滞阻尼比，对钢结构取0.02；Eh为结构在预期位移下滞回一周的耗能；Es为结构最大应变能。
对于PS-SCED支撑-钢框架结构，Eh由钢框架塑性变形耗能和支撑摩擦耗能共同组成，Es也需考虑框架和支撑的共同作用。本文取钢框架的滞回本构为双线性模型，则Eh的表达式为：
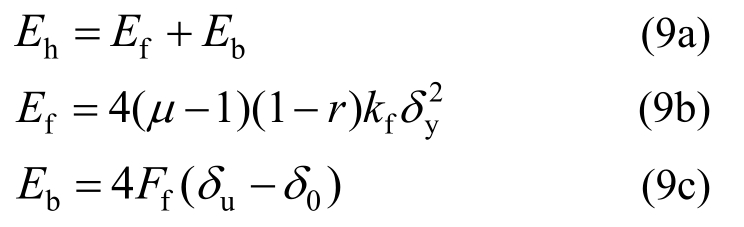
式中：Ef、Eb分别为框架耗能和支撑摩擦耗能；μ为框架的延性系数；kf为框架弹性抗侧刚度；r为框架屈服后刚度与kf之比；Ff为支撑摩擦力水平分量；δu和δ0分别为支撑水平向的最大变形和激活位移。
Es的表达式为：
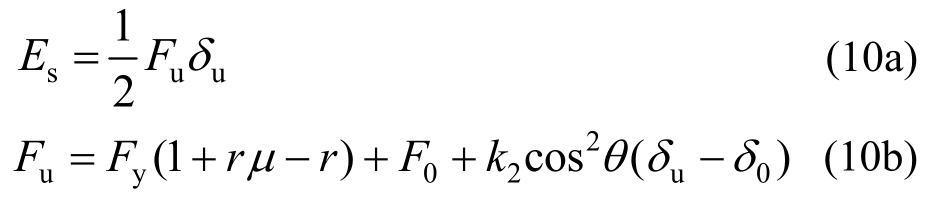
式中：Fy为纯框架的屈服力；Fu为支撑-框架在δu下的承载力；F0为支撑激活力水平分量；θ为支撑与水平向的夹角。
令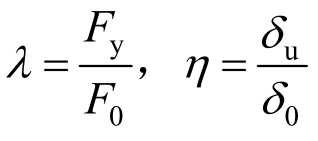
将式(9)、式(10)代入式(8)可得到PS-SCED支撑-钢框架结构的等效阻尼比表达式：
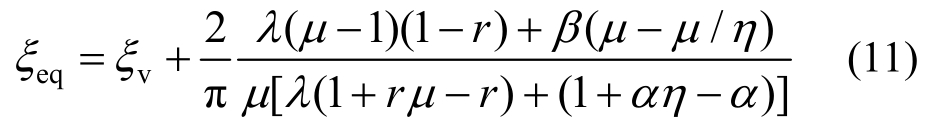
式中：λ为框架的屈服承载力与支撑起滑力之比；η为支撑的延性系数。
影响ξeq的参数中，μ可由结构设计需求决定；结构抗震设计规范规定[17]：支撑-框架中，框架部分按刚度分配计算得到的地震层剪力应不小于结构底部总地震剪力的25%，所以根据λ的定义，在初步设计时λ可取1/3。规范还建议了消能部件在水平方向的起滑位移与层间屈服位移之比不大于2/3，从而可得
对于钢结构，r一般取0.05，所以最终求解等效阻尼比时未知量只有支撑刚度比α。
2.2.2 等效阻尼比验证
由等效线性化法的定义可知，为验证式(11)的合理性，只需采用等效线性化法估计一弹塑性结构的位移响应，若按等效线性化法求解的最大位移响应与弹塑性结构真实最大位移响应相同或接近，则可认为式(11)是合理的。DDBD法采用的等效线性化法为割线刚度法，即等效SDOF体系的keq取弹塑性结构在预定目标位移下的割线刚度，如图4所示。
采用一弹塑性SDOF体系验证等效阻尼比，该SDOF体系同时考虑了框架的双线性滞回模型和支撑的旗形滞回模型，具体步骤如下：
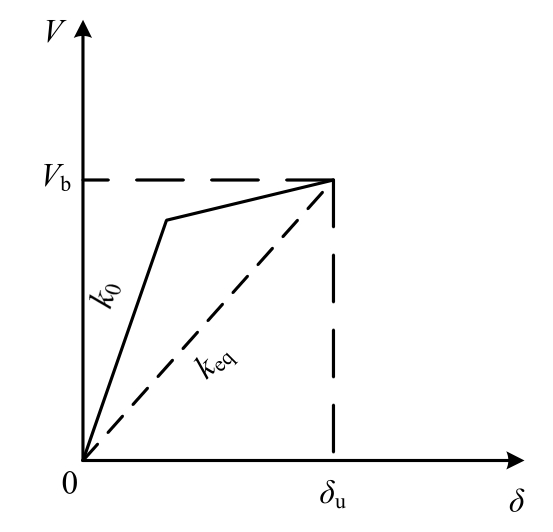
图4 等效SDOF体系的刚度
Fig.4 Stiffness of equivalent SDOF system
1)预设弹塑性SDOF体系的屈服位移δin,y，并计算其在地震波作用下的最大位移响应δin,u和基底剪力Vb；
2)由δin,u和δin,y求得弹塑性SDOF体系的延性系数，根据式(11)求得ξeq，ξeq即为线弹性SDOF体系的阻尼比；
3)计算弹塑性SDOF体系在δin,u下的割线刚度(图4)，将该割线刚度作为线弹性SDOF体系的刚度keq；
4)计算线弹性SDOF体系在同一地震波作用下的最大位移响应δemax；
5)改变支撑k1，重复步骤1)～步骤4)，最后比较不同k1下的δin,u和δemax。
框架周期为2.55s，初始粘滞阻尼比为0.02，支撑刚度比为0.2的弹塑性SDOF体系在大震、不同k1下的δin,u与其相应的弹性SDOF体系的δemax对比如图5所示，δin,u和δemax取3条地震波作用下的最大值。3条地震波由2条天然波(San Fernando和Imperial Valley-02，分别简称为E2和E3)和1条人工波(ren1)组成，均根据8度抗震设防、III类场地的设计反应谱选取，如图6所示。ren1下，各等效SDOF体系的Teq分别为2.48 s、2.27 s、2.10 s、1.96 s、1.86 s、1.76 s，所有等效SDOF体系的meq均为4233 t。图5表明，不同k1下的δemax与δin,u接近，最大误差为7.6%，误差较小，从而验证了等效阻尼比的合理性。
图5 弹塑性SDOF与弹性SDOF最大位移
Fig.5 Maximum displacement of inelastic SDOF system and elastic SDOF system
图6 地震加速度反应谱与设计谱对比
Fig.6 Comparison of acceleration response spectra of earthquake record and design spectra
3 PS-SCED支撑参数设计及分析
在验证等效阻尼比公式后，采用DDBD法对一6层PS-SCED支撑—钢框架的支撑参数进行设计并分析α对结构位移响应的影响。
3.1 结构基本信息及性能水平
选用文献[18]的一榀屈曲约束支撑-框架结构，将屈曲约束支撑替换为PS-SCED支撑，采用DDBD法对支撑参数进行设计。结构立面如图7所示，跨度为8 m，首层层高5 m，其余层高4 m，梁柱刚接；每层质量集中到梁柱节点，边节点和中间节点的质量分别为23.52 t，47.04 t。抗震设防烈度8度，设计基本加速度0.20 g，地震分组第一组，III类场地，场地特征周期0.45 s。梁截面尺寸为H450 mm×250 mm×12 mm×18 mm，柱截面为方管，其尺寸为400 mm×400 mm×20 mm。
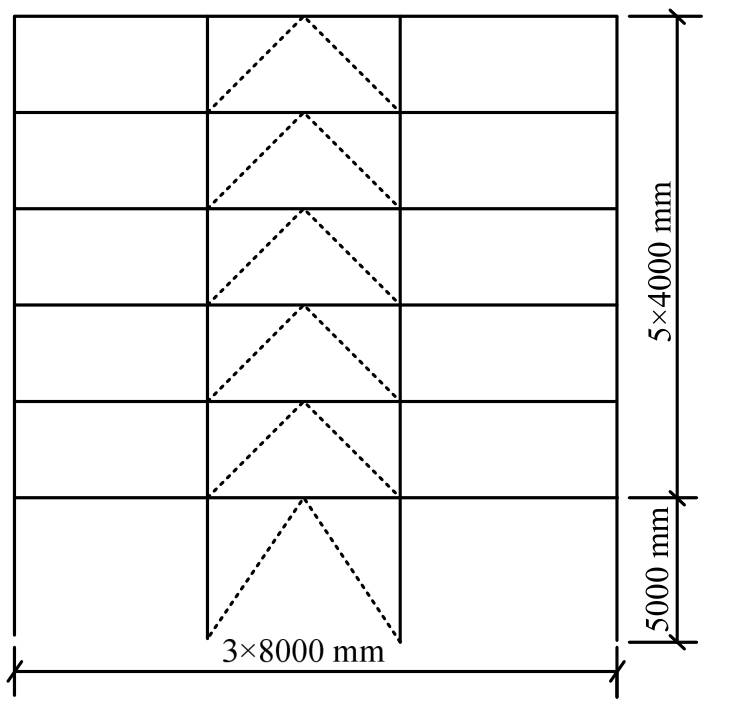
图7 框架立面
Fig.7 Elevation of the frame
本文选取建筑抗震设计规范[17]规定的性能2水平作为性能设计目标，该水平要求结构在罕遇地震作用下只产生轻微至中等破坏，变形参考值为3～4[Δue]，[Δue]为多遇地震下位移角限值，对钢结构[Δue]取0.004，本文选3[Δue]即层间位移角为0.012作为变形限值。根据抗震规范对结构发生轻微损坏的描述和变形参考值取值建议，认为位移角达到2[Δue]即0.008时结构发生屈服。
3.2 结构等效单自由度参数
由一阶振型可知，框架的第二层位移角最大，所以假定该层位移角达到限值，可求出结构顶层侧移为216 mm，再由各楼层的振型值可求出各层的侧移值，这就是满足性能目标要求的结构侧移形状。结构一阶振型和设计侧移曲线如图8所示。
图8 一阶振型及设计侧移曲线
Fig.8 The first mode shape and design displacement profile
同样，令第二层达到屈服位移角限值可求出结构屈服时各层的侧移值。得到各层侧移值后可根据式(13)、式(14)求出等效单自由度体系的等效参数，结果列于表1。
前文α的取值范围是根据支撑构造要求确定的，但为全面分析α对结构位移响应的影响，本文选取范围内的0.05、0.1、0.2和范围外的0.3对支撑参数进行设计并分析。这四个不同α值对应的等效阻尼比列于表1，根据等效阻尼比和等效单自由度位移δemax，通过查图9的位移谱确定结构的等效周期Teq，再根据式(15)求出等效刚度，基底剪力根据式(16)求出。所采用的位移谱由加速度谱转换得到[19]。
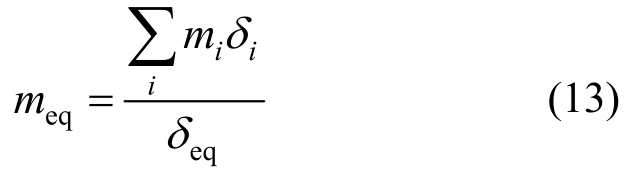
图9 位移反应谱
Fig.9 Displacement response spectra
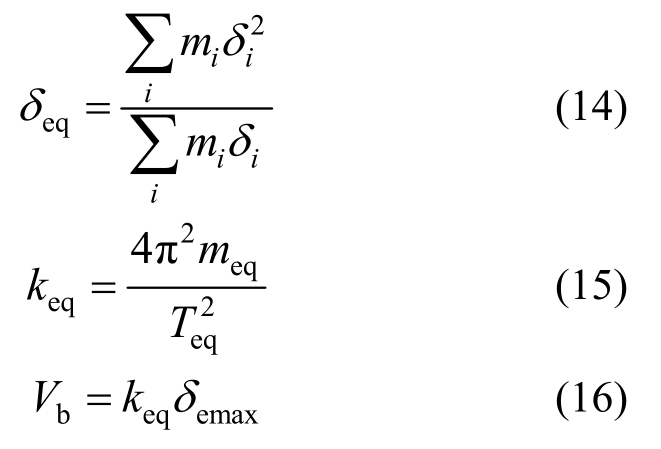
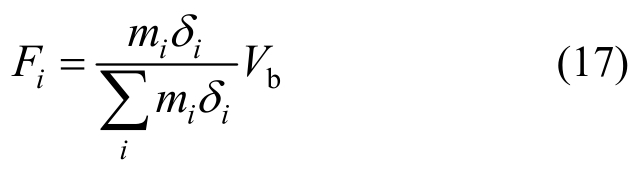
式中：mi、δi、Fi分别为结构第i层质量、侧移值和地震作用力；δeq为等效SDOF体系的位移。
3.3 支撑参数设计
将基底剪力按式(17)分配至结构各层，可得到各层的地震作用和楼层剪力，楼层剪力由框架和支撑共同承担，故设计时应确定框架和支撑的剪力分担率。本文考虑支撑分别承担总剪力的75%、100%两种情况对支撑参数进行设计。式(16)确定的基底剪力是结构相应于设计位移的极限承载力，故按照剪力分担率分配给支撑的力是支撑的极限承载力需求，为确定支撑k1，需按式(18)确定支撑的F0。最终支撑参数设计值如表2所示。
式中，Fbu为支撑的极限承载力需求。
表1 等效单自由度体系等效参数
Table 1 Equivalent parameters of equivalent SDOF system
侧移角限值 危险楼层 δmax/mm δy/mm δemax/mm meq/t 延性μ 刚度比 ξeq Teq/s keq/(kN/mm)Vb/kN 0.05 0.201.96 7.33 1241 0.012 2 216.1 144.1 169.1 716.21.50.1 0.181.93 7.61 1282 0.2 0.161.86 8.14 1376 0.3 0.141.81 8.61 1456
表2 支撑参数设计值 /(kN/mm)
Table 2 Design values of brace parameters
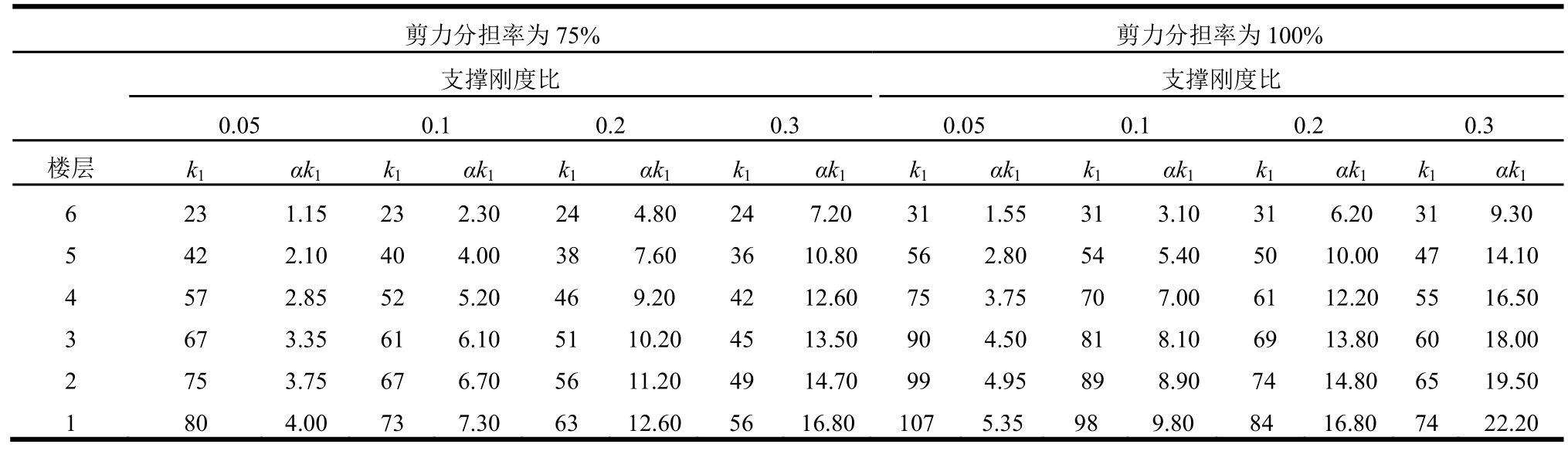
剪力分担率为75%剪力分担率为100%支撑刚度比支撑刚度比0.05 0.1 0.2 0.3 0.05 0.1 0.2 0.3楼层 k1 αk1 k1 αk1 k1 αk1 k1 αk1 k1 αk1 k1 αk1 k1 αk1 k1αk1 6 23 1.15 23 2.30 24 4.8024 7.20 31 1.5531 3.10 31 6.20 319.30 5 42 2.10 40 4.00 38 7.6036 10.8056 2.8054 5.40 50 10.00 4714.10 4 57 2.85 52 5.20 46 9.2042 12.6075 3.7570 7.00 61 12.20 5516.50 3 67 3.35 61 6.10 51 10.2045 13.5090 4.5081 8.10 69 13.80 6018.00 2 75 3.75 67 6.70 56 11.2049 14.7099 4.9589 8.90 74 14.80 6519.50 1 80 4.00 73 7.30 63 12.6056 16.80107 5.3598 9.80 84 16.80 7422.20
3.4 结构位移响应
选取图6的三条地震波作为地震动输入，对结构的位移响应进行分析。小震下，结构在三条地震波下的基底剪力分别为760.0 kN、781.7 kN、777.2 kN，均大于按振型分解反应谱法计算的526.2 kN的基底剪力，满足规范的选波要求。
图10和图11给出了结构在不同剪力分担率下结构侧移的包络值与设计侧移曲线的对比。对于剪力分担率为75%的情况，不同刚度比下的侧移包络值均与设计值吻合较好，可认为按这4种支撑刚度比设计的支撑参数均能使结构满足预定的性能目标。对于剪力分担率为100%的情况，不同支撑刚度比下的侧移包络值均小于设计值，所以也能满足性能目标。
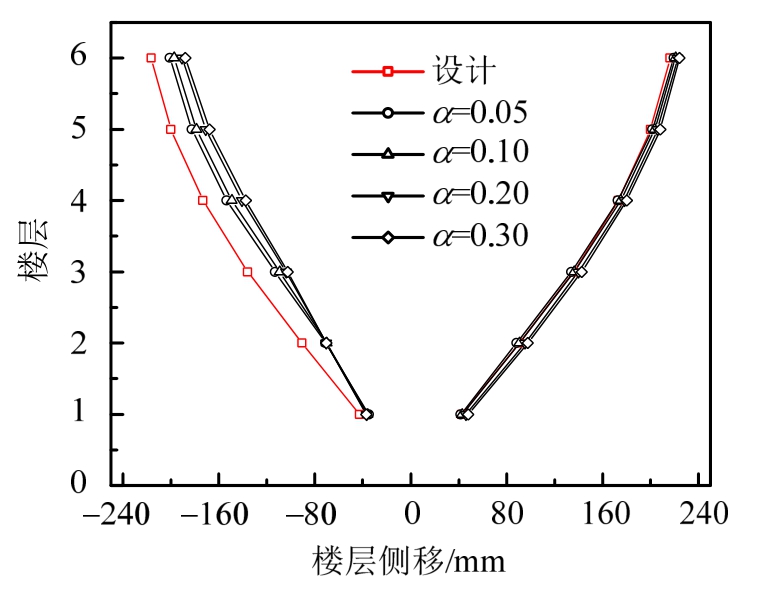
图10 剪力分担率为75%的楼层侧移曲线
Fig.10 Story displacement profiles under 75% shear ratio
图11 剪力分担率为100%的结构侧移曲线
Fig.11 Story displacement profiles under 100% shear ratio
对于图10，α取0.05、0.1、0.2、0.3时，结构第二层位移角分别为0.0133、0.0134、0.0137、0.0139，位移角基本满足0.012的设计目标。α从0.05增加到0.3时，顶点位移值只增加2.2%，增加幅度不大，且基本在设计顶点位移值附近。理论上支撑刚度比的变化不会改变顶点位移值。由表1可以看出，随支撑刚度比的增加，结构的ξeq降低，ξeq小的结构具有更大的keq，而ξeq和keq取决于同一设计目标位移，即由此确定的ξeq和keq能使结构达到相同的顶点位移。以上计算和分析结果表明，当采用DDBD法设计支撑参数时，α的取值对结构的位移响应影响不大，实际设计时，考虑到支撑构造要求，α可在[0，αmax]之间取值。
3.5 支撑刚度变化
图12(a)给出了剪力分担率为75%时，各层支撑第一刚度随α的变化情况。随α的增加，各层支撑第一刚度减小。原因是在支撑极限承载力需求变化不大且起滑位移相同条件下，α越大，则支撑的激活力F0越小，故所需的支撑第一刚度越小。
图12(b)给出了考虑等效阻尼比与不考虑等效阻比时支撑第一刚度的对比(后者按5%的阻尼比设计，剪力分担率为75%)。采用DDBD法时，在相同设计目标位移的条件下，所考虑的阻尼比越小，则由位移反应谱确定的结构等效周期Teq越小，即结构等效刚度keq越大，设计目标位移相同时，keq越大意味着结构承载力需求更大，所以最终设计的支撑参数偏大。图12(b)表明不考虑等效阻尼比时支撑的第一刚度明显增大，增大幅度为50%，这种情况下的结构侧移曲线将明显低于设计侧移曲线，设计过于保守，故按本文所提出的等效阻尼比公式进行支撑参数设计既能使结构满足性能目标，又有利于降低支撑的经济指标。
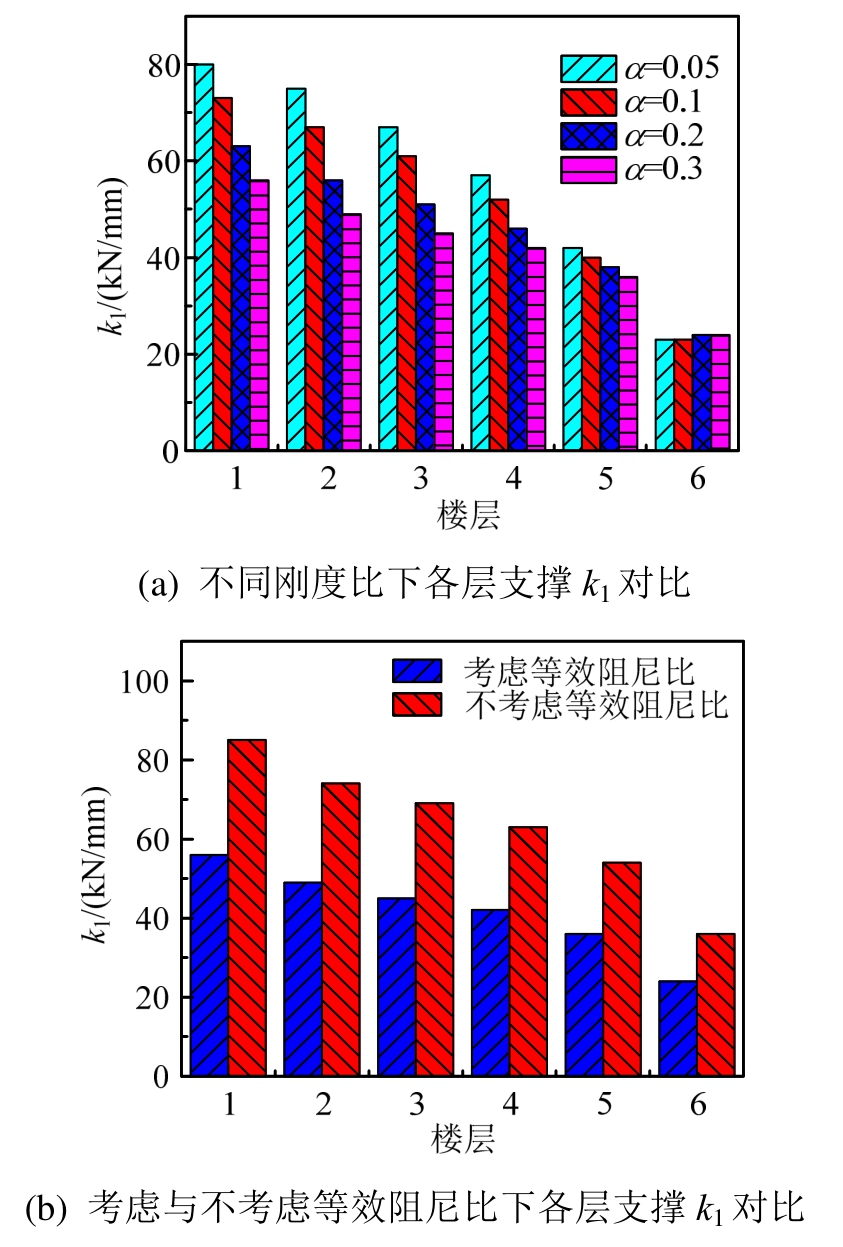
图12 支撑第一刚度k1对比
Fig.12 Comparisons of the first stiffness k1of brace
4 结论
通过本文的研究可得到如下结论：
(1)提出了DDBD法的等效阻尼比公式，其验证表明等效SDOF体系的δemax与相应弹塑性SDOF体系的δin,u接近，说明该公式合理可行，能够用于PS-SCED支撑-钢框架结构直接基于位移的抗震设计。
(2)不考虑等效阻尼比，支撑的承载力需求偏大，设计的支撑刚度偏于保守；考虑等效阻尼比，支撑承载力需求更小，设计的支撑刚度小且能够满足性能目标要求。
(3)在直接基于位移的抗震设计中，支撑刚度比对结构位移响应影响不大，按本文提出的区间确定刚度比对支撑参数进行设计能使结构满足预定的变形限值要求。
[1]郭彦林, 童精中, 周鹏.防屈曲支撑的型式、设计理论与应用研究进展[J].工程力学, 2016, 33(9)： 1－14.Guo Yanlin, Tong Jingzhong, Zhou Peng.Research progress of buckling restrained braces： types, design methods and applications [J].Engineering Mechanics,2016, 33(9)： 1－14.(in Chinese)
[2]Christopoulos C, Tremblay R, Kim H J, et al.Self-centering energy dissipative bracing system for the seismic resistance of structures： development and validation [J].Journal of Structural Engineering, 2008,134(1)： 96－107.
[3]Xu L H, Fan X W, Li Z X.Experimental behavior and analysis of self-centering steel brace with pre-pressed disc springs [J].Journal of Constructional Steel Research, 2017, 139： 363－373.
[4]Xu L H, Xie X S, Li Z X.Development and experimental study of a self-centering variable damping energy dissipation brace [J].Engineering Structures, 2018, 160：270－280.
[5]梁兴文.结构抗震性能设计理论与方法[M].北京： 科学出版社, 2011： 1－15.Liang Xingwen.Theory and approach of structural performance-based seismic design [M].Beijing： Science Press, 2011： 1－15.(in Chinese)
[6]姚谦峰, 常鹏.工程结构抗震分析[M].北京： 清华大学出版社, 2012： 219－220.Yao Qianfeng, Chang Peng.Seismic analysis of engineering structures [M].Beijing： Tsinghua University Press, 2012： 219－220.(in Chinese)
[7]Medhekar M S, Kennedy D J.Displacement-based seismic design of buildings： application [J].Engineering Structures, 2000, 22(3)： 210－221.
[8]Kowalsky M J, Priestley M.Displacement-based design of RC bridge columns in seismic regions [J].Earthquake Engineering and Structural Dynamics, 1995, 24(12)：1623－1643.
[9]Priestley M J N, Calvi G M, Kowalsky M J.Displacement based seismic design of structures [M].Italy： IUSS Press, 2007.
[10]Lin Y Y, Tsai M H, Hwang J S, Chang K C.Direct displacement-based design for building with passive energy dissipation systems [J].Engineering Structures,2003, 25(1)： 25－37
[11]李钢, 李宏男.基于位移的消能减震结构抗震设计方法[J].工程力学, 2007, 24(9)： 88－94.Li Gang, Li Hongnan.Direct displacement-based design for buildings with passive energy dissipation devices [J].Engineering Mechanics, 2007, 24(9)： 88－94.(in Chinese)
[12]杨博雅, 吕西林.预应力预制混凝土剪力墙结构直接基于位移的抗震设计方法及应用[J].工程力学, 2018,35(2)： 59－66, 75.Yang Boya, Lü Xilin.Direct diaplacement-based aseismic design and application for prestressed precast concrete shear-wall structures [J].Engineering Mechanics, 2018, 35(2)： 59－66, 75.(in Chinese)
[13]徐龙河, 樊晓伟, 逯登成, 等.预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J].工程力学, 2016,33(10)： 116－121.Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al.Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation [J].Engineering Mechanics, 2016, 33(10)： 116－121.(in Chinese)
[14]徐龙河, 樊晓伟, 代长顺, 等.预压弹簧自恢复耗能支撑受力性能分析与试验研究[J].建筑结构学报, 2016,37(9)： 142－148.Xu Longhe, Fan Xiaowei, Dai Changshun, et al.Mechanical behavior analysis and experimental study on pre-pressed spring self-centering energy dissipation brace[J].Journal of Building Structures, 2016, 37(9)： 142－148.(in Chinese)
[15]Dwairi H M, Kowalsky M J, Nau J M.Equivalent damping in support of direct displacement-based design[J].Journal of Earthquake Engineering, 2007, 11(4)：512－530.
[16]胡聿贤.地震工程学[M].北京： 地震出版社, 2006：315－318.Hu Yuxian.Earthquake engineering [M].Beijing：Seismological Press, 2006： 315－318.(in Chinese)
[17]GB50011—2010, 建筑抗震设计规范[S].北京： 中国建筑工业出版社, 2010.GB50011—2010, Seismic design code for buildings [S].Beijing： China Architectural Industry Press, 2010.(in Chinese)
[18]冯玉龙.基于损伤控制的屈曲约束支撑框架多指标评价及设计方法研究[D].南京： 东南大学, 2016.Feng Yulong.Research on damage control based mutil-index evaluation and design method of buckling-restrained braced frames [D].Nanjing：Southeast University, 2016.(in Chinese)
[19]吕洋, 熊峰, 葛琪.基于非弹性位移的土-结构相互作用的抗震设计方法[J].工程科学与技术, 2018, 50(3)：142－148.Lü Yang, Xiong Feng, Ge Qi.Inelastic displacementbased seismic design method for soil-structure interaction systems [J].Advanced Engineering Sciences.2018, 50(3)： 142－148.(in Chinese)