高性能轻骨料混凝土(High performance lightweight concrete,HPLWC)是一种使用掺合料、低水胶比具有良好工作性能的混凝土,属于结构轻骨料混凝土中品质等级较高的轻骨料混凝土,与普通混凝土相比,它具有自重轻、保温隔热效果好、极限拉应变较高、抗震和耐久性能优良等性能优势,而且还能满足普通骨料高性能混凝土的性能指标,是高层建筑、大跨结构的理想建筑材料。高性能轻骨料混凝土可分为全轻混凝土和次轻混凝土,全轻混凝土(All-lightweight concrete,ALWC)的粗细骨料分别使用轻粗骨料和轻砂,而次轻混凝土(Semi-lightweight concrete,SLWC)的粗细骨料一般为轻粗骨料和普通砂。大量试验结果[1-2]表明单轴应力条件下,与同强度等级的普通混凝土相比,轻骨料混凝土的拉压强度比、抗弯强度、弹性模量均较低,脆性较大。研究表明[3],各种纤维材料尤其是钢纤维对轻骨料混凝土内部微裂缝有很强的桥接作用,对其抗弯强度、抗拉强度和峰值应变有很大的提升作用,有效改善其韧性和延性,显著地增加其吸能能力,且钢纤维体积掺量在0~2%之间时,钢纤维轻骨料混凝土的密度和弹性模量变化不大;通过掺加硅粉和超细粉煤灰[4-7]等活性掺合料还可以进一步提高纤维轻骨料混凝土的韧性和吸能能力,优化纤维在基体中的分布,提高纤维轻骨料混凝土的抗冲击和抗震性能。研究者[6]还发现各种短切纤维对轻骨料混凝土的改善效果明显强于普通骨料混凝土,尤其是对抗拉强度和韧性的改善作用。
目前,已经有一些研究者对纤维增强普通骨料混凝土在多轴应力条件下的力学行为开展了研究:Saeed等[7]和Ren等[8]等研究者分别对钢纤维高性能混凝土和钢纤维超高性能混凝土进行了常规三轴压试验,发现钢纤维高性能混凝土在三轴压下表现出更好的峰后韧性和吸能能力,其破坏准则可用Mohr-Coulomb二参数、Hsieh-Ting-Chen四参数和William-Warnke五参数强度准则数学模型来表达。王怀亮等[9]建立了钢纤维混凝土破坏包络面方程,并认为钢纤维特征参数对拉子午线形式有较大的影响,忽略对压子午线的影响。Chi等[10]对真三轴压下混杂纤维混凝土的强度和变形性能进行了研究,并建立了考虑混杂纤维影响的五参数强度准则。考虑到建筑结构中高性能轻骨料混凝土处于事实上的二维或三维应力状态,但尚未见到高性能轻骨料混凝土和纤维增强高性能轻骨料混凝土的多轴强度准则和多轴应力-应变本构关系方面的研究。为此,本文通过单双轴、真三轴压强度和变形特性试验,研究了应力比以及钢纤维体积率对高性能全轻混凝土(HPALWC)和高性能次轻混凝土(HPSLWC)强度和变形特性的影响,深入分析钢纤维对高性能轻骨料混凝土多轴力学行为的影响,基于本文和相关文献试验结果,建立钢纤维高性能轻骨料混凝土的多轴强度准则,为轻骨料混凝土结构的设计和有限元分析提供试验依据和设计参考。
1 试验方法
1.1 原材料配合比及试件制作
为了达到高性能轻骨料混凝土的性能指标,通过控制水胶比、减水剂和掺合料用量来实现硬化混凝土的较高强度,而通过调节砂率和轻骨料外裹水玻璃涂层等措施使新拌混凝土具有较好的流动性和抗离析性,并解决了轻骨料上浮问题。本文采用上述方法设计出LC40高性能全轻骨料混凝土基体和次轻骨料混凝土基体,水胶比分别为0.28和0.36,拌合物采用P·O 42.5R普通硅酸盐水泥,减水率为30%的羧酸类高效减水剂和自来水。试验所用原材料如图1所示,其中全轻混凝土细骨料采用细度模数为3.2的连续级配膨胀页岩陶砂,粗骨料采用筒压强度为8.6 MPa碎石型膨胀页岩陶粒;次轻混凝土细骨料采用细度模数2.7的天然河砂,粗骨料采用筒压强度为6.3 MPa的圆球型烧结粉煤灰陶粒;以上粗细骨料的物理性能指标如表1所示。

图1 部分试验原材料
Fig.1 Materials used in the experiment
表1 粗细骨料基本物理性能指标
Table 1 Basic properties of the coarse and fine aggregates used
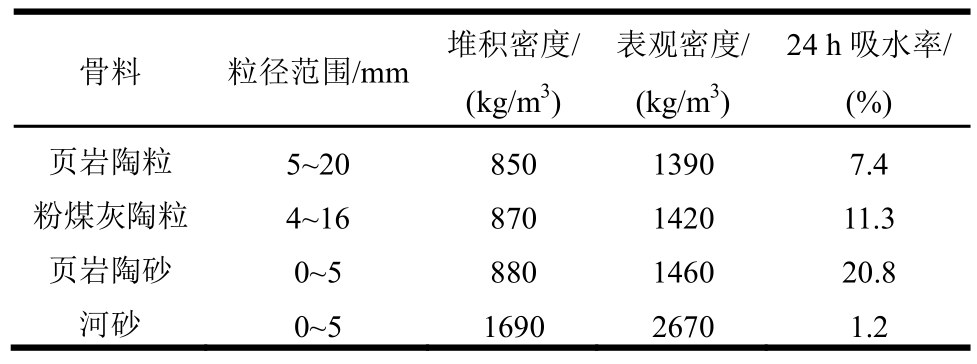
骨料 粒径范围/mm 堆积密度/(kg/m3)表观密度/(kg/m3)24 h吸水率/(%)页岩陶粒 5~20 850 1390 7.4粉煤灰陶粒 4~16 870 1420 11.3页岩陶砂 0~5 880 1460 20.8河砂 0~5 1690 2670 1.2
所用钢纤维为剪切压痕型,长度32 mm,长径比50,密度78 kg/m3,抗拉强度>600 MPa。反复试验发现,钢纤维掺量过高,在搅拌过程中会出现钢纤维聚集成团现象,钢纤维体积掺量不超过1.5%时,新拌高性能轻骨料混凝土坍落扩展度在150 mm~200 mm范围内且无离析和阻塞现象,因此本文确定的钢纤维体积掺量为0~1.5%,以0.5%为级差,全轻混凝土用符号ALF0~ALF15表示,次轻混凝土用符号SLF0~SLF15表示,数字表示钢纤维掺量,如ALF15表示钢纤维体积掺量为1.5%的钢纤维全轻混凝土。多轴试验统一采用100 mm×100 mm×100 mm的立方体试块,共浇筑240块。混凝土试块振捣抹平后在试验室静置2 d后拆模,标准养护室内养护28 d,取出后在自然室温条件下风干1个月准备试验。表2为配合比设计及28 d后试块的自然风干密度、三轴试验机上测得的单轴抗压和单轴抗拉强度。
表2 纤维增强轻骨料混凝土配合比和基本物理力学性能
Table 2 Mixture proportions and strength data of different mixtures

编号 钢纤维掺量/(%)水泥/(kg/m3)硅粉/(kg/m3)水/(kg/m3)粗骨料/(kg/m3)细骨料/(kg/m3)减水剂/(kg/m3)密度/(kg/m3)fc/MPaft/MPa ALF0 0 460 90 154 489 476 8.0 1752 44.822.89 ALF5 0.5 460 90 154 489 476 8.4 1813 47.373.93 ALF10 1.0 460 90 154 489 476 8.7 1859 49.714.36 ALF15 1.5 460 90 154 489 476 9.2 1894 52.885.11 SLF0 0 414 50 167 439 821 5.4 1888 39.581.84 SLF5 0.5 414 50 167 439 821 5.8 1950 43.042.56 SLF10 1.0 414 50 167 439 821 6.1 2007 45.872.91 SLF15 1.5 414 50 167 439 821 7.5 2051 47.353.75
1.2 试验设备和加载程序
加载试验是在TAWZ-5000/3000高压伺服静动真三轴试验机上进行的,如图2所示,该试验机采用整体框架结构,三个相互垂直方向上都具有独立的液压伺服加载作动器,垂直方向(Z),对应的主应力方向为σ3,最大试验力为5000 kN;水平方向(X、Y),分别对应σ1和σ2方向,最大试验力为3000 kN。试验之前对所有试块表面进行处理,用大理石磨面机进行机械磨平,去掉混凝土试件表面强度偏低的水泥砂浆薄弱层,从而保证试件表面与加载板紧密接触。为减少摩擦力,试验时在加载板和试件之间选用塑料薄膜和甘油做减摩,测得减摩后的试件立方体强度和棱柱体强度相似。单轴拉伸试验则采用建筑结构胶(抗拉强度30 MPa)将试件的受拉面与加载钢板进行粘结,经24 h固化后,即可进行受拉试验。混凝土多轴试验更具体的试验方法及其对试验结果的影响讨论可参见作者同一科研团队所发表的论文[11-12]。

图2 真三轴压试验装置
Fig.2 The true triaxial test set-up
规定拉应力和拉应变为正,-σ1≤-σ2≤-σ3,此处σ1、σ2、σ3分别为三向主应力。除了单轴拉压之外,选取其他应力比有σ1/σ2/σ3=0∶1∶1(双轴等压)、0.1∶0.1∶1、0.1∶0.25∶1、0.1∶0.5∶1、…、0.25∶0.25∶1等。为保证单调比例加载全过程中三个方向的应力比恒定,以σ3方向主轴为主动的位移反馈控制,设定加载位移速率为0.004 mm/s,在其他两个压应力方向即σ1和σ2方向则以与σ3方向荷载成一定比例的荷载反馈控制加载。正式加载前先沿试件的两个加载方向进行3次预压,荷载为相应单轴压破坏荷载的40%左右,保证试件物理对中。每个应力比下进行3至5个试块的三轴试验,并剔除异常数据,保证至少3个试件数据有效可靠。变形量测是通过高精度位移传感器(LVDT),在每向加载板两侧通过位移支架布置两套LVDT,如图2(b)~图2(d)所示,将相对两面所测变形值取平均,且扣除事先标定的减摩垫层相应变形值,得到最终的变形量。
2 试验结果分析
2.1 应力-应变曲线对比分析
图3为试验得到的不同钢纤维掺量情形下全轻混凝土和次轻混凝土的单轴压应力-应变曲线,可以看出,两种轻骨料混凝土弹性模量均小于相近强度等级的普通骨料混凝土[1-2],侧向峰值应变远大于普通骨料混凝土,峰值应力后曲线突然下降,脆性大于普通骨料混凝土,而无纤维全轻混凝土峰值应力点处的轴向应变及侧向变形大于次轻混凝土。加入钢纤维后,两种轻骨料混凝土应力-应变曲线上升段无明显变化,峰值变形和峰值强度则随着纤维体积率的增加而增加,软化段下降速度变缓,应力-应变曲线与横轴包围的面积增大,说明高性能轻骨料混凝土延性和韧性随着钢纤维体积率掺量的增加而得到明显的改善,另外还可以看出钢纤维对全轻混凝土延性和韧性的改善效果要好于次轻混凝土,这是由于应力-应变曲线软化段阶段主要为钢纤维拔出破坏阶段,本文的全轻混凝土粗骨料为碎石型页岩陶粒,而次轻混凝土粗骨料为圆球形烧结粉煤灰陶粒,全轻混凝土基体-钢纤维黏结强度大于次轻混凝土。
图4~图7为试验得到的不同钢纤维掺量情形下全轻混凝土和次轻混凝土的真三轴压应力-应变曲线,可以看出,所有试件在三轴压的低应力比(σ1/σ3=0.1)条件下,应力-应变曲线上升段无太大差别,在靠近峰值强度之前,线性段都很显著;无纤维轻骨料混凝土在低压应力比条件下依旧表现出了较大的脆性,下降段比较陡,钢纤维的掺入减缓了曲线的急剧下降趋势,消除了裂缝出现后的损伤局部化现象,其中钢纤维对全轻混凝土延性和韧性的改善效果要好于次轻混凝土。钢纤维对高性能轻骨料混凝土强度和延性的改善作用机理在于,钢纤维通过限制裂缝扩展和减小侧向膨胀变形,为内部混凝土提供了有效的侧向压应力,轻骨料混凝土为压力敏感性材料,侧压可以大大改善轻骨料混凝土材料的强度和延性。在同一应力比条件下,最大主压应力σ3方向对应的峰值应变ε3p随着钢纤维掺量的增加而有明显的增加,中间主应力σ2方向和最小主压应力σ1方向对应的峰值应变ε2p与ε1p均随着钢纤维掺量的增加而略微增加。

图3 单轴压应力-应变全曲线
Fig.3 Uniaxial compressive responses of HPLWC
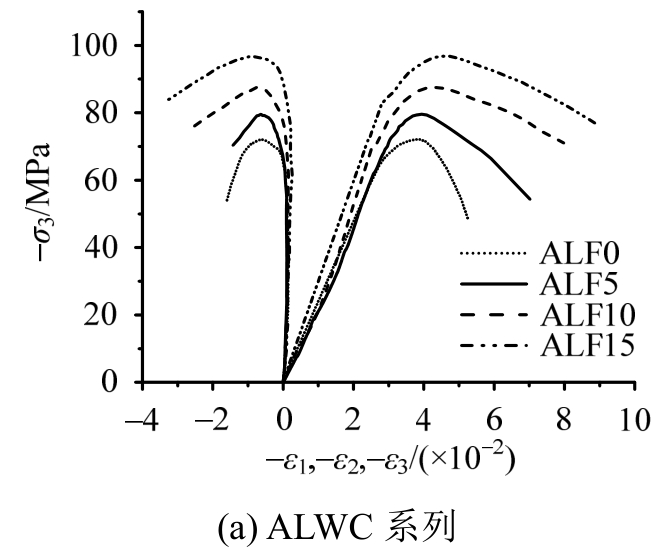
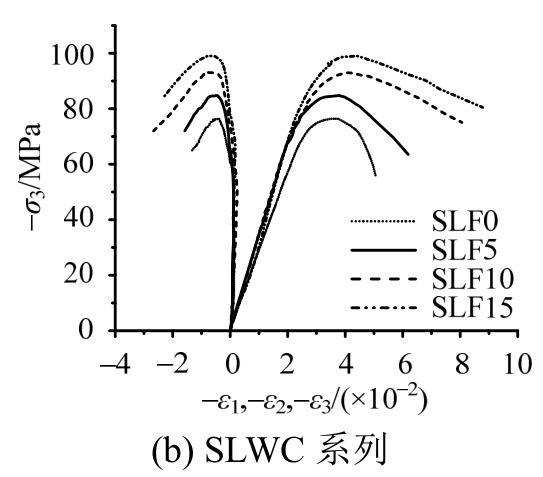
图4 三轴压应力-应变曲线(0.1∶0.1∶1)
Fig.4 Triaxial compressive stress-strain curves(0.1∶0.1∶1)

图5 三轴压应力-应变曲线(0.1∶0.5∶1)
Fig.5 Triaxial compressive stress-strain curves(0.1∶0.5∶1)

图6 三轴压应力-应变曲线(0.1∶1∶1)
Fig.6 Triaxial compressive stress-strain curves(0.1∶1∶1)

图7 三轴压应力-应变曲线(0.25∶0.25∶1)
Fig.7 Triaxial compressive stress-strain curves(0.25∶0.25∶1)
高应力比水平(σ1/σ3=0.25)下,考虑到试验机最大加载能力,只进行了应力比σ1/σ2/σ3=0.25∶0.25∶1的试验,如图7所示,无纤维轻骨料混凝土主压向应力-应变曲线上升段出现了明显的流塑平台,这是由于高性能轻骨料混凝土水泥砂浆品质较高,界面层微观结构比较致密,但内部轻质粗骨料比较软,在高压应力作用下首先被挤压破碎,应力重分布后大部分压应力由水泥砂浆体继续承担,伴随着试块大幅度的压缩变形而出现了应力平台区域,随后试块在“紧密”状态下,继续承受更大的压应力,曲线继续上升,出现强化段;钢纤维的掺入增强了轻骨料混凝土中“砂浆骨架”的延性,使其在应力重分布过程中不会发生突然的变形骤增,从而钢纤维轻骨料混凝土的应力应变曲线上没有出现明显的应力平台区。对于曲线的下降段,无纤维轻骨料混凝土和钢纤维轻骨料混凝土都表现出了明显的受压延性特征,纤维的掺入对应力-应变曲线下降段几乎无影响。峰值应变ε3p随着钢纤维掺量的增加而有明显的增加,而ε1p与钢纤维掺量关系不大,由于全轻混凝土基体和次轻混凝土基体粗骨料颗粒外形的不同,钢纤维全轻混凝土的最大横向变形ε1p大于钢纤维次轻混凝土。
2.2 极限强度和峰值应变
本文试验数据量非常大,每种应力路径下每种混凝土至少3个试件,限于篇幅,表2列出了所有类型混凝土的单轴拉、压强度平均值,表3列出了双轴等压、三轴压应力条件下的极限抗压强度平均值,表4列出了单轴压、双轴等压和三轴压应力条件下的主压向峰值应变平均值。从表2可以看出,加入钢纤维后,两种高性能轻骨料混凝土单轴抗压强度和抗拉强度都得到了提升,钢纤维掺量为1.5%时,全轻混凝土单轴抗压强度和单轴抗拉强度分别提高了18%和76.8%,次轻混凝土单轴抗压强度和抗拉强度分别提高了19.6%和103.8%。普通骨料混凝土掺入钢纤维后[4-5],其单轴抗压强度变化不大,甚至有些是降低的作用,这是由于钢纤维对轻骨料混凝土内部微裂缝面的桥联作用更为显著[9]。
从表3可以看出,无纤维时,全轻和次轻混凝土双轴等压(σ2/σ3=1.0)相对强度分别为1.13和1.21,随着钢纤维掺量的增加,双轴等压强度相对值增大,钢纤维掺量为1.5%时,双轴等压强度增大倍数分别为1.43和1.47。Yin等[13]对钢纤维增强普通骨料混凝土的研究发现普通骨料混凝土双轴等压强度相对值同样随着钢纤维掺量的增加而增加,当钢纤维掺量达到2%时,双轴等压强度相对值为1.7。
从表3还可以看出,对于无纤维混凝土,高性能轻骨料混凝土尤其是全轻混凝土三轴压强度增加幅度要小于普通骨料混凝土[14-15],例如σ1/σ3= 0.1时,普通骨料混凝土[15]三轴压相对强度值为2.25~3.16,低强度轻骨料混凝土[12](fc=16.7 MPa)三轴压相对强度值为1.69~2.08,本文全轻混凝土三轴压相对强度值为1.61~2.51,次轻混凝土三轴压相对强度值为1.93~2.63,这进一步证明了对于塑性变形能力较小的硬脆性材料,其多轴抗压强度比单轴抗压强度提高的幅度要低于普通骨料混凝土。在低静水压力条件(σ1/σ3=0.1)下,同一应力比下两种轻骨料混凝土三轴抗压强度相对值均随着钢纤维掺量的增加而增加,钢纤维体积掺量为1.5%时,高性能全轻混凝土三轴压相对强度值为1.83~2.95,高性能次轻混凝土三轴压相对强度值为2.09~3.16。Chern等[16]开展了钢纤维普通骨料混凝土的多轴压加载试验,钢纤维掺量为0~2.0%,长径比固定为44,以圆柱体抗压强度和劈裂试验结果作为标定的单轴抗压和拉伸强度,发现钢纤维普通骨料混凝土的三轴压相对强度值随着钢纤维掺量的增加而增加,与本文结论相一致。微观试验表明[1-6],高性能轻骨料混凝土内部粗骨料刚度小于水泥砂浆体的刚度,加入刚度较大的钢纤维改变了轻骨料混凝土内各组分的刚度分布,钢纤维对微裂缝面的桥联作用,减小了垂直于最大主压应力方向上的横向膨胀变形,相当于在横向提供了一定的约束压应力,致使钢纤维高性能轻骨料混凝土单轴抗压强度、双轴等压强度提高倍数和低应力比三轴抗压强度相对值均高于对应的无纤维高性能轻骨料混凝土。
表3 混凝土三轴极限抗压强度平均值 /MPa
Table 3 Average of ultimate triaxial strength for different types of concrete

类型σ3设计应力比0∶1∶1 0.1∶0.1∶1 0.1∶0.25∶1 0.1∶0.5∶1 0.1∶1∶1 0.25∶0.25∶1 ALF0 50.65(1.25)72.16(5.65)99.50(8.69)112.50(4.30)106.22(9.55)261.30(10.72)ALF5 57.79(2.03)79.58(4.36)109.90(6.25)125.06(6.32)115.11(4.71)272.85(8.37)ALF10 67.11(2.51)87.49(5.81)121.79(3.43)141.18(2.66)129.74(3.22)294.28(7.41)ALF15 75.62(2.84)96.77(4.29)135.37(5.81)156.00(2.25)139.60(4.05)320.98(9.13)SLF0 47.89(1.73)76.39(3.78)101.32(5.51)104.10(2.43)97.37(3.89)247.38(4.62)SLF5 53.37(1.57)84.79(4.13)112.76(6.03)116.64(5.42)108.46(7.23)265.99(8.01)SLF10 63.76(2.04)93.12(6.04)125.68(7.14)135.78(6.16)121.56(8.52)287.61(7.54)SLF15 69.60(2.15)98.96(5.12)133.05(4.65)149.63(7.51)126.90(5.40)294.83(10.33)
表4 混凝土最大主压力方向峰值应变平均值 /(×10-2)
Table 4 Average of peak compressive strain for different types of concrete

类型ε3设计应力比0∶0∶1 0∶1∶1 0.1∶0.1∶1 0.1∶0.25∶1 0.1∶0.5∶1 0.1∶1∶1 ALF0 0.31(0.013)0.26(0.012)3.86(0.34)4.14(0.42)4.46(0.66)4.41(0.48)ALF5 0.41(0.025)0.46(0.033)3.94(0.27)4.43(0.13)4.76(0.32)4.67(0.73)ALF10 0.47(0.037)0.58(0.016)4.47(0.38)5.67(0.82)5.39(0.29)5.02(0.45)ALF15 0.50(0.026)0.71(0.025)4.93(0.59)6.58(0.28)6.11(0.21)5.42(0.26)SLF0 0.27(0.014)0.32(0.013)3.65(0.35)4.03(0.37)4.07(0.28)3.79(0.17)SLF5 0.30(0.019)0.36(0.018)3.78(0.16)4.26(0.30)4.39(0.38)4.02(0.55)SLF10 0.35(0.038)0.49(0.035)4.14(0.46)4.85(0.84)4.76(0.84)4.33(0.83)SLF15 0.43(0.027)0.67(0.049)4.42(0.33)5.33(0.43)5.01(0.65)4.58(0.54)
在较高静水压力条件(σ1/σ3=0.25)下,两种高性能轻骨料混凝土三轴抗压强度相对值与钢纤维掺量关系无明显的规律,例如无纤维时,全轻和次轻混凝土三轴压相对强度值分别为5.83和6.25,当纤维掺量为1%时,抗压强度相对值分别为5.92和6.27。这是由于在较高静水压力条件下,钢纤维侧向约束所提供的侧向压应力远小于外荷载提供的侧压应力,对提高三轴压强度的贡献可以忽略不计。
从表4可以看出,最大主压应力方向的峰值压应变与应力比、钢纤维掺量关系都比较大,随着侧压应力的增大,峰值压应变成倍的增加,在双轴等压应力状态下,峰值压应变提高了14%~18%,在低侧压应力水平下,三轴压峰值压应变比单轴压提高了11倍~14倍,在高侧压应力水平下,三轴压峰值压应变比单轴压提高了20倍~25倍。同一应力比条件下,钢纤维轻骨料混凝土主压向峰值压应变明显地大于无纤维试件,如钢纤维体积掺量1%时,单轴压下钢纤维全轻混凝土和次轻混凝土峰值压应变分别增加了27%和30%,应力比为0.1∶0.1∶1时钢纤维全轻混凝土和次轻混凝土峰值压应变分别增加了16%和13%。
2.3 中间主应力对极限强度和峰值应变的影响
图8为不同钢纤维体积掺量的情况下,钢纤维全轻和次轻混凝土中间主应力对三轴抗压强度相对值的影响规律。可以看出,随着中间主应力σ2的增加,所有混凝土三轴抗压强度增加幅值均为先增加后减小,呈抛物线变化,在σ2/σ3=0.5附近,增加幅值最高。随着钢纤维掺量的增加,中间主应力对三轴压峰值应力的影响越来越大,这可能是钢纤维的掺入改变了轻骨料混凝土基体的密度,使各向异性特征更加突出的原因。

图8 中间主应力对峰值强度的影响
Fig.8 The influence of the intermediate principal stress on the relative failure stress
图9为钢纤维全轻和次轻混凝土中间主应力对最大主压应力方向峰值压应变的影响规律。可以看出中间主应力对峰值应变ε3p有着显著的影响,并且这种影响程度随着钢纤维含量的增加而明显增大,在同一应力比(σ1/σ3)水平下,随着中间主应力σ2的增长,ε3p绝对值先增大后减小,对无纤维轻骨料混凝土和钢纤维掺量为0.5%时的轻骨料混凝土,最大值大致发生在σ2/σ3=0.5附近,在较高的钢纤维掺量情形下(Vf=1%和1.5%),最大值大致发生在σ2/σ3=0.25附近。
以上说明钢纤维掺量不仅对钢纤维高性能轻骨料混凝土真三轴压极限抗压强度包络线形状有一定的影响,还对峰值压应变的变化规律有一定的影响,而对钢纤维普通骨料混凝土进行的同类真三轴试验[15-16]中,未发现钢纤维掺量和中间主应力对峰值强度和变形影响规律的具体联系。

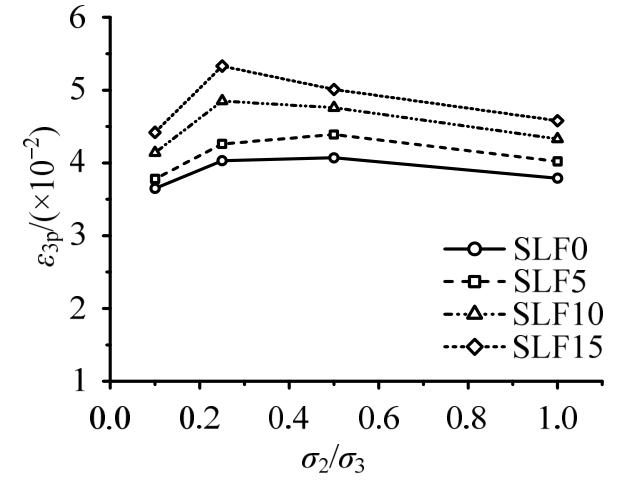
图9 中间主应力对峰值压应变的影响
Fig.9 The influence of the intermediate principal stress on the peak compressive strain
3 破坏形态
图10为高性能轻骨料混凝土单轴拉、压,双轴等压和三轴压时的典型破坏形态。单轴压时为典型的柱状破坏,如图10(a)和图10(b)所示,试块被贯穿裂缝分成若干柱状单元块体,钢纤维轻骨料混凝土则裂而不散,各单元块体间有钢纤维相连;单轴拉为典型的拉断破坏,试块中部形成了一条垂直受力方向的裂缝,轻骨料混凝土水泥砂浆体强度高于粗骨料,裂缝直接贯穿粗骨料,而普通骨料混凝土裂缝一般沿着粗骨料和水泥砂浆之间的界面层扩展[17],钢纤维掺量比较大时,钢纤维轻骨料混凝土拉伸断面上依旧有少数纤维未被完全拔出;双轴等压下,由于泊松比效应在非加载方向上的应变ε1为拉应变,无纤维轻骨料混凝土为典型的片状劈裂破坏,如图10(c)和图10(d)所示,而对钢纤维轻骨料混凝土,钢纤维在裂缝面的桥联作用可以阻滞垂直荷载方向上的裂缝扩展,相当于在未加载方向上施加了一个很小的约束压应力,从而表现为压剪型破坏。在三轴压应力条件下,钢纤维掺量对破坏形态无明显的影响,大多数试块为斜剪破坏。

图10 钢纤维高性能轻骨料混凝土破坏形态
Fig10 Failure modes of steel fiber reinforced HPLWC
4 多轴强度准则
多轴应力状态下混凝土的强度,可以用以三个主应力轴为坐标的空间破坏曲面来表示,又称为破坏包络面,但空间破坏包络面不便绘制也不适用于直接应用,一般用八面体正应力和剪应力作为横纵坐标表示的拉、压子午线以及偏平面上的包络线来表示。首先按照下式将试验得到的混凝土极限破坏时的三个主应力实测值转换为八面体应力空间的正应力、剪应力和相似角:
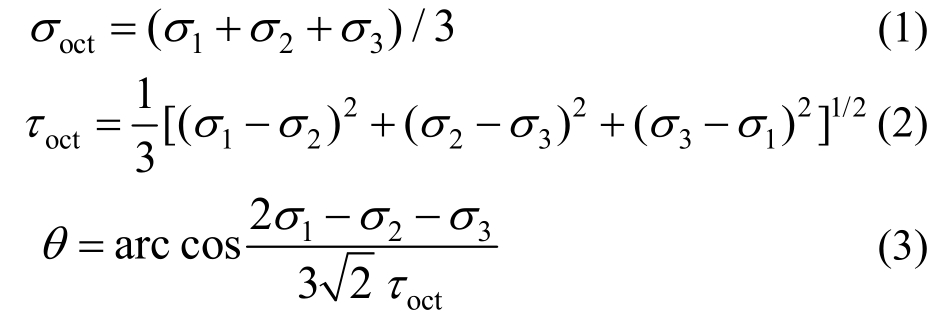
本文强度准则中拉、压子午线方程采用Kotsovos等[18]所建议的幂指数形式:

以上式中σoct和τoct分别为八面体正应力和剪应力;τot和τoc为拉、压子午线上的八面体剪应力;θ为罗德角(相似角);课题组前期研究成员[11-12,14-15]通过开展一系列中低强度混凝土、低强度煤矸石轻骨料混凝土、全轻混凝土、高强混凝土多轴压试验研究,发现子午线方程中待定参数k1=k1(ρ,βp),k2=k2(ρ,βp),k3=k3(ρ,βp),k4=k4(ρ,βp),与混凝土密度等级ρ、混凝土性能等级参数![]() 有关(w/b为水胶比)。基于此,可以确定出文献[15]中无纤维普通骨料混凝土的子午线方程待定参数:
有关(w/b为水胶比)。基于此,可以确定出文献[15]中无纤维普通骨料混凝土的子午线方程待定参数:
对于本文全轻混凝土子午线待定参数取值为:k1=0.614,k2=0.786,k3=0.901,k4=0.743
对于本文次轻混凝土子午线待定参数取值为:
Chi等[10]、宋玉普等[12]、Chern等[16]所进行的一系列钢纤维普通骨料混凝土三轴压试验和本文试验结果均发现钢纤维掺量和长径比是影响各种基体混凝土双轴和三轴强度规律的重要因素,经改造后,钢纤维轻骨料混凝土破坏包络面拉、压子午线方程分别为:
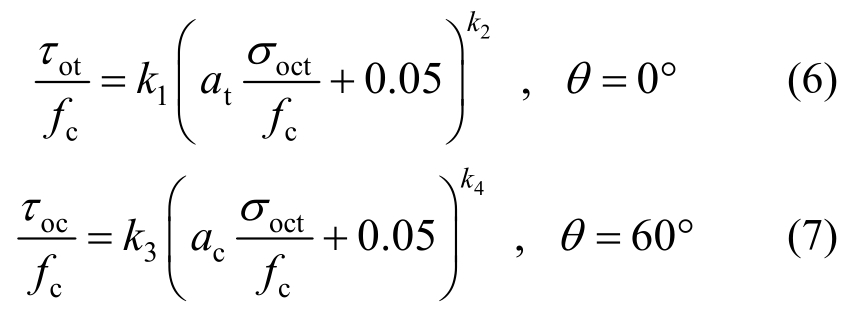
式中:at=1+κtλf 和ac=1+κcλf 为纤维对拉压子午线形状的影响参数[10];![]() 为纤维特征参数,
为纤维特征参数,![]() 分别为纤维体积掺量和长径比;κt和κc为待定参数,共有6个待定参数,可通过拉、压子午线与静水压力轴拉端相交于同一点这一规律减少一个参数,并通过强度试验选取5个特征应力点值来确定5个待定参数。偏平面上的破坏包络线方程(0°≤θ≤60°)采用椭圆曲线方程[18]:
分别为纤维体积掺量和长径比;κt和κc为待定参数,共有6个待定参数,可通过拉、压子午线与静水压力轴拉端相交于同一点这一规律减少一个参数,并通过强度试验选取5个特征应力点值来确定5个待定参数。偏平面上的破坏包络线方程(0°≤θ≤60°)采用椭圆曲线方程[18]:
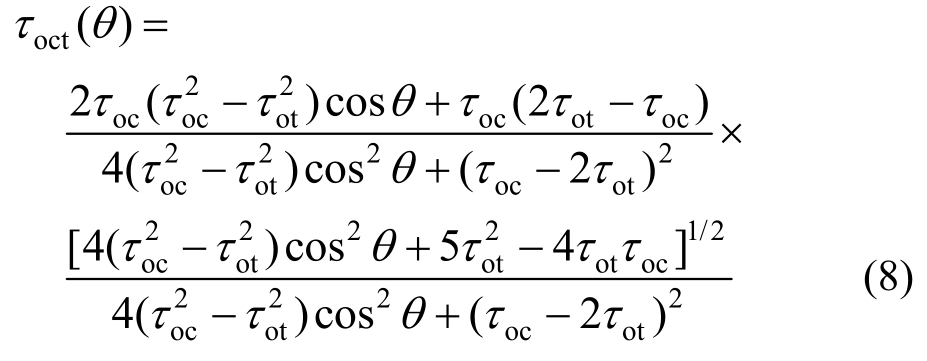
首先将上述强度准则的拉压子午线与文献[15]中的钢纤维普通骨料混凝土拉压子午线上的试验数据进行对比验证,如图11(a)所示,同时,将该强度准则的拉压子午线与本文进行的钢纤维增强全轻混凝土和次轻混凝土试验数据进行对比,如图11(b)和图11(c)所示,可以发现,本文所提出的破坏准则模型基本能预测出钢纤维普通骨料混凝土、钢纤维全轻混凝土和钢纤维次轻混凝土的多轴强度在拉压子午线上的变化规律:随着钢纤维掺量的增加,拉压子午线有向外扩张的趋势,而拉子午线上剪切强度有较为明显的增加,钢纤维在不同材性的混凝土中对拉子午线的增强作用比较显著,这是由于拉子午线上对应的破坏形态一般为拉断破坏(单轴拉)和层状劈裂破坏(双轴等压),而钢纤维对拉伸裂缝有比较强的桥联作用,钢纤维有效地增强了层状块体间的联结,并且钢纤维掺量越大,长径比越大,这种联结越强。无钢纤维和小掺量钢纤维轻骨料混凝土拉压子午线更偏向于横轴,而无钢纤维普通骨料混凝土的拉压子午线开口已经比较大,只有当钢纤维掺量比较大时,钢纤维轻骨料混凝土的开口逐渐扩大,比较接近普通骨料混凝土破坏包络面,换言之,同样钢纤维掺量和类似钢纤维长径比条件下,高性能轻骨料混凝土拉子午线扩张的幅值要高于普通骨料混凝土,这说明钢纤维在多向受力状态下对轻骨料混凝土的增强作用,要强于普通骨料混凝土。

图11 三种钢纤维混凝土的拉压子午线
Fig.11 Comparison of meridians of three types of steel fiber concretes
图12为在偏平面上该强度准则模型与钢纤维增强不同混凝土基体的试验数据对比,可以发现本文模型所导出的强度包络线与不同罗德角加载路径下的试验数据吻合较好,能够反映出不同钢纤维混凝土真三轴压应力状态下中间主应力的影响规律。

图12 三种钢纤维混凝土偏平面上的强度规律
Fig.12 Strength envelopes of three types of steel fiber concretes in deviatoric plane
5 结论
(1)钢纤维轻骨料混凝土和无纤维轻骨料混凝土在单轴压和多轴压下的应力-应变全曲线基本形状一致,无纤维轻骨料混凝土在单轴压、低压应力比条件下表现出了较大的脆性,下降段比较陡,但随着钢纤维掺量的增加,钢纤维能够明显地发挥增强阻裂作用,两种高性能轻骨料混凝土峰值强度和变形有所提高,下降段逐渐变缓,并且钢纤维对全轻混凝土延性和韧性的改善效果要好于次轻混凝土;在较高的应力比条件下,无纤维轻骨料混凝土主压向应力-应变曲线上升段出现了明显的流塑平台,随着钢纤维掺量的增加,特有的应力平台区逐渐消失,而钢纤维掺量对高应力比下高性能轻骨料混凝土峰值强度、峰值变形以及峰后软化段无明显的影响。
(2)双轴压和真三轴压应力状态下钢纤维轻骨料混凝土的极限抗压强度以及峰值应变均显著提高,其提高程度主要与加载应力比以及钢纤维掺量有关;在双轴等压和较低的应力比条件下,钢纤维轻骨料混凝土极限强度提高倍数要高于无纤维轻骨料混凝土,在较高的三轴压应力比条件下,三轴抗压强度提高倍数(三轴抗压强度相对值)与钢纤维体积掺量关系不大。
(3)在真三轴压应力状态下,对无纤维轻骨料混凝土,中间主应力对三轴抗压强度σ3和主压向峰值应变ε3p的影响比较小,随着钢纤维掺量的增加,中间主应力对极限抗压强度和峰值应变的影响越来越大。这说明钢纤维掺量对八面体应力空间偏平面上高性能轻骨料混凝土的强度包络线形状有一定的影响。
(4)与无纤维普通骨料混凝土宏观破坏形态相类似,无纤维轻骨料混凝土在多轴应力状态下的主要破坏形态可分为柱状破坏、拉断破坏、层状劈裂破坏和斜剪破坏形态。钢纤维轻骨料混凝土由于钢纤维对裂缝扩展的限制作用,所有试块都“裂而不碎”,在同一应力比条件下,钢纤维轻骨料混凝土均表现出较大的残余应力和剩余强度,三轴压下破坏形态以剪切和压碎组合的破坏模式为主。
(5)在试验研究的基础上,在八面体应力空间内建立了钢纤维增强轻骨料混凝土的多轴强度准则,发现经过修正后的Kotsovos破坏准则可以较为准确地预测钢纤维掺量和三轴应力比对多轴强度的影响规律,在低应力比条件下和拉子午线附近,多轴强度准则与试验数据吻合很好。
[1]张玉, 陈旭, 魏慧, 等.不同强度等级的高强轻骨料混凝土配合比研究[J].硅酸盐通报, 2016, 35(7):2002―2006.Zhang Yu, Chen Xu, Wei Hui, et al.Mixture of high-strength lightweight aggregate concrete with different strength grades [J].Bulletin of the Chinese Ceramic Society, 2016, 35(7): 2002―2006.(in Chinese)
[2]Cui H Z, Lo T Y, Memon S A, et al.Effect of lightweight aggregates on the mechanical properties and brittleness of lightweight aggregate concrete [J].Construction &Building Materials, 2012, 35(10): 149―158.
[3]Hassanpour M, Shafigh P, Mahmud H B.Lightweight aggregate concrete fiber reinforcement - A review [J].Construction & Building Materials, 2012, 37(37):452―461.
[4]Soonpoh Y, Alengaram U J, Jumaat M Z.Enhancement of mechanical properties in polypropylene- and nylon-fibre reinforced oil palm shell concrete [J].Materials & Design, 2013, 49(8):1034―1041.
[5]Li J J, Niu J G, Wan C J, et al.Investigation on mechanical properties and microstructure of high performance polypropylene fiber reinforced lightweight aggregate concrete [J].Construction & Building Materials, 2016, 118(15): 27―35.
[6]Balendran R V, Zhou F P, Nadeem A, et al.Influence of steel fibres on strength and ductility of normal and lightweight high strength concrete [J].Building &Environment, 2002, 37(12): 1361―1367.
[7]Babanajad S K, Farnam Y, Shekarchi M.Failure criteria and triaxial behaviour of HPFRC containing high reactivity metakaolin and silica fume [J].Construction &Building Materials, 2012, 29(4): 215―229.
[8]Ren G M, Wu H, Fang Q, et al.Triaxial compressive behavior of UHPCC and applications in the projectile impact analyses [J].Construction & Building Materials,2016, 113(6): 1―14.
[9]王怀亮, 王健.钢纤维工业地坪有限元分析方法研究[J].工程力学, 2011, 28(5): 129―134.Wang Huailiang, Wang Jian.Finite element method research in analysis of SFRC industrial ground floors [J].Engineering Mechanics, 28(5): 129―134.(in Chinese)
[10]Chi Y, Xu L, Mei G, et al.A unified failure envelope for hybrid fibre reinforced concrete subjected to true triaxial compression [J].Composite Structures, 2014, 109(6):31―40.
[11]Shen L, Wang L, Song Y, et al.Comparison between dynamic mechanical properties of dam and sieved concrete under biaxial tension-compression [J].Construction & Building Materials, 2017, 132(2):43―50.
[12]Wang L C, Song Y P.Mechanical behavior and failure criterion of the gangue-based haydite concrete under triaxial loading [J].Materials & Structures, 2013, 48(5):1―15.
[13]Yin, W S, Su E C M, Mansur M A, et al.Biaxial tests of plain and fibre concrete [J].ACI Material Journal, 1989,86(3): 236―243.
[14]杨健辉, 张鹏, 王涛, 等.全轻页岩陶粒混凝土三轴受压试验及其破坏准则[J].工程力学, 2015, 32(10):89―98.Yang Jianhui, Zhang Peng, Wang Tao, et al.The tests and failure criteria of full lightweight shale ceramsite concrete under triaxial compression [J].Engineering Mechanics, 2015, 32(10): 89―98.(in Chinese)
[15]宋玉普, 赵国藩.多轴应力下多种混凝土材料的通用破坏准则[J].土木工程学报, 1996, 29(1): 25―32.Song Yupu, Zhao Guofan.General failure criterion for different concrete materials under multiaxial stresses [J].China Civil Engineering Journal, 1996, 29(1): 25―32.(in Chinese)
[16]Chern J C, Yang H J, Chen H W.Behavior of steel fiber reinforced concrete in multiaxial loading [J].ACI Materials Journal, 1993, 89(1): 32―40.
[17]过镇海.混凝土的强度和本构关系: 原理与应用[M].北京: 中国建筑工业出版社, 2004.Guo Zhenhai.The strength and constitutive relationship of concrete—Principal and application [M].Tsinghua University Press, Beijing, 2004.(in Chinese)
[18]Kotsovos M D.A mathematical description of the strength properties of concrete under general stress [J].Magazine of Concrete Research, 1979, 31(108): 151―158.