超高性能混凝土(ultra high performance concrete，UHPC)是高性能纤维增强水泥基复合材料。与传统混凝土材料相比，UHPC具有高强度、高断裂韧性、高延性和高耐久性等优良性能[1－4]。在自然养护条件下，UHPC抗压强度可达120 MPa~150 MPa，抗拉强度约为6 MPa~15 MPa。UHPC可用于建造重载、大跨、抗震[5]、抗爆[6]等结构。对UHPC基本构件力学性能进行研究是UHPC材料结构应用的基础，而UHPC梁正截面受弯承载力是基本构件力学性能评估的一个重要指标，故有必要对UHPC梁正截面受弯承载力进行深入探讨与研究。
普通钢筋混凝土梁受力后，当受拉区混凝土应变超过混凝土极限拉应变时，梁截面受拉区混凝土产生裂缝；在承载能力极限状态时，裂缝截面受拉区混凝土将退出工作，所以正截面受弯承载力计算时，不考虑受拉区混凝土的抗拉作用。与普通混凝土相比，如活性粉末混凝土等UHPC材料，制备时基体中掺入了一定体积分数的钢纤维，当基体受拉开裂后，由于裂缝处钢纤维的桥接作用，裂缝处UHPC仍能承受拉力，所以在进行UHPC梁正截面受弯承载力计算时应考虑UHPC拉区的复杂应力对正截面承载能力的贡献。郑文忠、李莉等[7－8]通过试验研究了活性粉末混凝土梁的受弯承载力计算方法，提出可按拉区应力为0.25倍活性粉末混凝土抗拉强度来等效受拉区复杂拉应力。王文雷[9]通过程序计算分析了活性粉末混凝土梁极限承载力的计算方法，建议按拉区应力为0.40倍活性粉末混凝土抗拉强度来考虑拉应力对正截面受弯承载力的贡献。金凌志等[10]通过5根配置高强钢筋活性粉末混凝土简支梁受弯性能试验，提出了高强配筋活性粉末混凝土梁正截面承载力计算公式，建议受拉区应力按0.30倍活性粉末土抗拉强度计算。由此可见，计算UHPC梁正截面受弯承载力时，UHPC拉区等效拉应力尚无统一的取值，且上述取值多以试验结果反推得到，没有可靠的理论依据。
现阶段，已有的UHPC梁受弯承载力计算模型主要存在两方面的问题：一是上述截面受拉区UHPC应力等效问题；二是对截面受压区复杂应力进行等效时，UHPC受压本构的选取影响等效应力矩形图形参数的取值。为解决这两方面的问题，在进行UHPC梁截面受拉区应力分析时引入了复合材料力学方法。UHPC中由于掺入了钢纤维，可将其看作两相：一相是乱向分布的不连续纤维；一相是UHPC基体。根据复合材料力学，UHPC受拉开裂后，基体退出工作，拉应力由钢纤维承担，这样可简化UHPC梁截面受拉区复杂的应力分布。基于复合材料力学，可从理论角度解决UHPC梁受拉区复杂应力的等效问题。针对不同试验人员给出的不同UHPC受压应力-应变全曲线方程，本文着重研究文献[11]给出的UHPC材料应力-应变全曲线，结合UHPC力学性能参数推导求取UHPC梁受压区等效矩形应力图形参数；建立UHPC梁受弯承载力计算公式，根据28根已有试验梁，代入相关计算参数，验证承载力计算公式的可行性，并给出了UHPC受压区等效矩形应力图形参数的建议取值。
1 UHPC受压力学性能研究
1.1 UHPC受压基本力学性能指标
UHPC受压性能指标有弹性模量Ec、轴心受压强度fc、立方体抗压强度fcu、峰值压应变ε0、极限压应变εcu等。通过对相关文献[8,12－17]研究发现，Ec、fcu、ε0与fc之间存在密切的联系，文献[14]中，通过试验数据拟合了轴心抗压强度与其他性能指标的关系。为了获得较为可靠的拟合结果，本文在文献[14]的试验数据基础上，补充了文献[8,12－17]中相关的试验数据，得到UHPC基本受压力学性能实测值。
按规范方法[18]确定混凝土弹性模量时，需用立方体抗压强度fcu，而有些文献仅提供轴心抗压强度fc，故需建立fcu与fc之间的关系。图1表示fcu与fc之间关系的试验结果，经回归分析可得fcu与fc之间的关系式，即：
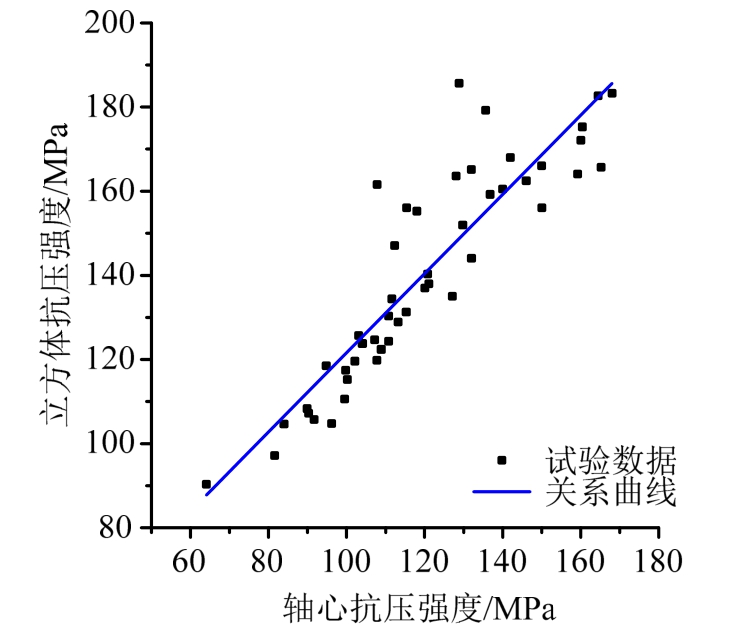
图1 UHPC立方体抗压强度与轴心抗压强度的关系曲线
Fig.1 Relationship curve of the cube and axial compressive strength of UHPC
图2表示UHPC峰值应变ε0与fc之间关系的试验结果，经回归分析可得ε0与fc之间的关系式，即：
规范[18]给出了混凝土弹性模量计算公式：
图2 UHPC峰值应变与轴心抗压强度的关系曲线
Fig.2 Relationship curve of the peak strain and axial compressive strength of UHPC
可参照式(3)对UHPC弹性模量进行拟合，拟合公式采用如下形式：
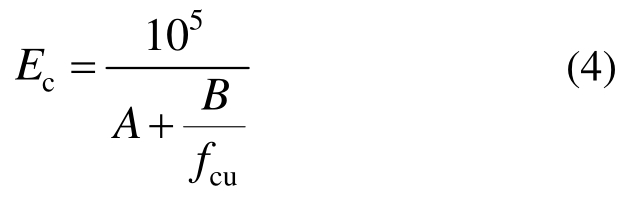
式中，A、B为待定参数。
图3表示UHPC弹性模量Ec与fcu之间关系的试验结果，经拟合可得：
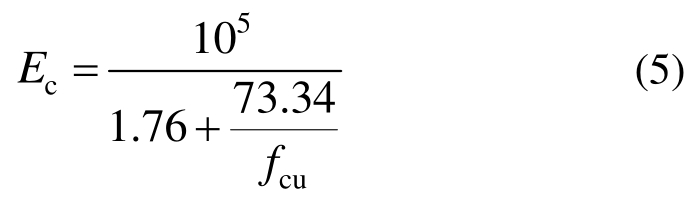
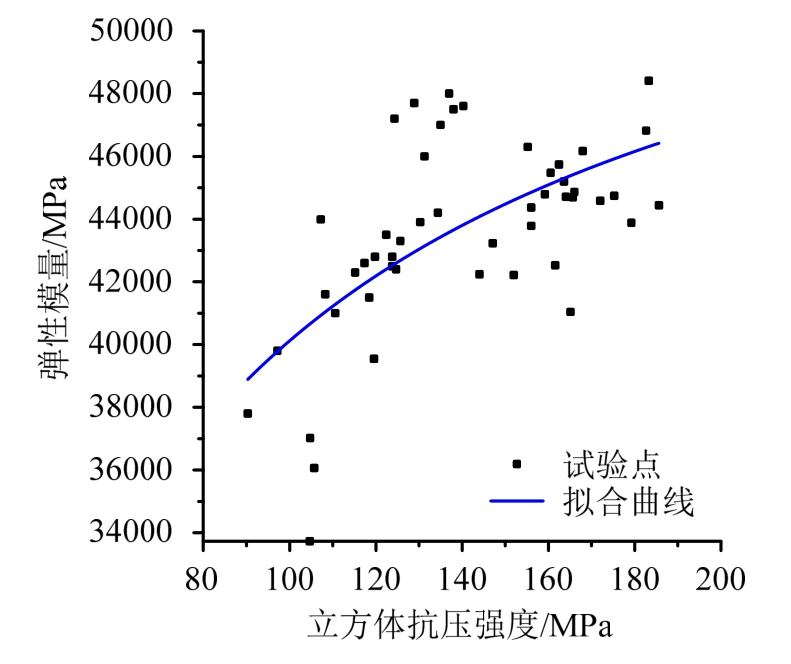
图3 UHPC弹性模量与立方体抗压强度的关系曲线
Fig.3 Relationship curve of the elastic modulus and cube compressive strength of UHPC
UHPC适筋梁达到极限受弯承载力时，受拉纵筋屈服，受压区边缘UHPC达到极限压应变εcu而破坏。对于UHPC极限压应变εcu，鲜有文献给出相应的计算方法，本文参照Hognestad混凝土应力-应变全曲线模型[19](见图4)，取压应力-应变曲线下降段0.85倍峰值应力对应的点为极限点，其对应的应变为极限压应变εcu。
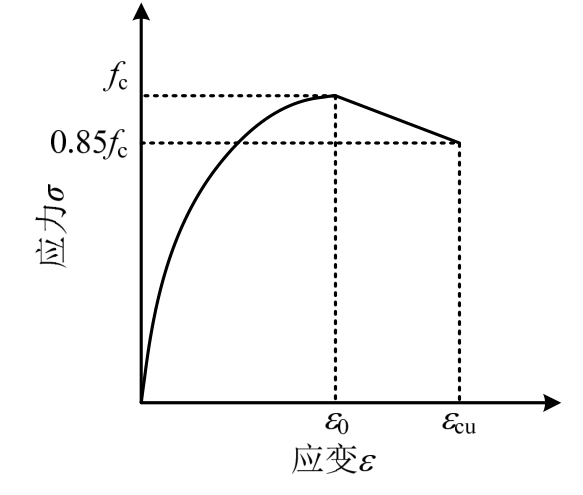
图4 Hognestad应力-应变曲线模型
Fig.4 Stress-strain curve model of Hognestad
1.2 UHPC受压应力-应变全曲线方程
UHPC受压本构方程是UHPC梁受弯承载力计算的基础，通过对几种UHPC受压本构模型的分析研究，发现文献[11]提出的UHPC受压应力-应变全曲线方程具有较强的适用性。将不同强度等级UHPC抗压力学性能指标代入受压本构方程，可得到不同的受压应力-应变全曲线方程。表1中列出了UHPC受压应力-应变全曲线方程的基本形式及各轴心抗压强度对应的计算本构方程，本构方程所需的抗压力学性能指标ε0、Ec分别按式(2)、式(5)计算。
2 基于复合材料力学的UHPC拉应力计算
复合材料力学是运用复合原理计算纤维增强水泥基复合材料的力学性能指标。该理论的基本假定如下：
1)纤维连续均匀地分布在基体中，且纤维的排列方向与受力方向一致；
2)纤维与基体共同受力，无相对滑移；
3)纤维与基体的变形均在弹性范围内；
4)基体开裂后将退出工作，应力仅由纤维承担。
由上述假定可以得纤维增强水泥基复合材料的拉应力计算公式[20]：
式中：σp为复合材料的平均拉应力；σm为基体的平均拉应力；Vf为纤维体积率；σf为纤维顺向拉应力。
极限承载能力状态下，UHPC梁受拉区基体开裂。由基本假定，开裂后复合材料基体退出工作，应力仅由钢纤维承担，即式(6)中σm=0，则式(6)退化为：
由于UHPC材料中钢纤维是不连续、乱向分布的短纤维，直接采用式(7)计算UHPC复合材料开裂后拉应力显然与实际不符。文献[21]在复合材料力学基础上，考虑到纤维在基体中的分布是随意分布的，纤维对基体的增强应该与纤维的长径比、纤维与混凝土的粘结强度、纤维的方向系数、纤维的有效利用系数有关，据此得出基体开裂后纤维增强水泥基复合材料的拉应力计算公式：
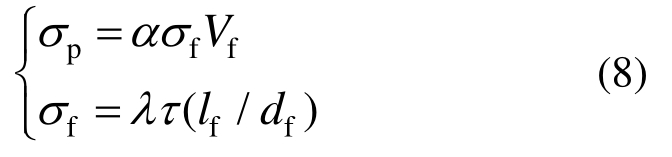
式中：α为钢纤维有效方向系数，为钢纤维方向系数α0与纤维有效利用系数α1的乘积[22]；λ为与纤维受剪长度有关的计算参数，该值一般取为2；τ为钢纤维与UHPC基体间的平均粘结剪应力；lf/df为钢纤维长径比。
文献[22]对UHPC受拉开裂后钢纤维有效方向系数进行了试验研究，结果表明，钢纤维有效方向系数α值在0.35~0.50，且随着纤维掺量的增大，有效方向系数略微减小，故本文建议计算UHPC开裂后拉应力时α可偏于安全地取为0.35。
钢纤维与基体间的平均粘结剪应力τ，文献[23]给出了相应的计算公式：
式中，fc为UHPC的轴心抗压强度。
上述公式中所采用的钢纤维抗拉强度一般在2000 MPa以上，钢纤维在UHPC基体中大多为拔出破坏而非拉断破坏；适用的钢纤维掺量为1%~3%。
3 UHPC梁正截面承载力计算
3.1 基本假定
1)平均应变分布符合平截面假定，即截面平均应变沿高度呈线性分布。
2)截面受拉区的拉力由钢筋和UHPC共同承担，截面受拉区UHPC拉应力按开裂后复合材料拉应力σp计算(式8)。
3)UHPC受压本构可根据UHPC轴心抗压强度采用文献[11]提出的受压本构模型(见表1)。
4)纵向受拉钢筋与UHPC材料间无滑移。
5)纵向钢筋的应力-应变关系采用理想弹塑性模型(见图5)，其表达式为
式中：fy为钢筋的抗拉或抗压屈服强度；σs为对应于钢筋应变为εs时的钢筋应力值；εy为钢筋的屈服应变，即εy=fy/Es ；Es为钢筋的弹性模量；εsu为纵向受拉钢筋极限拉应变，取值0.01。
表1 UHPC受压本构模型
Table 1 Stress-strain models for UHPC
注：ε为压应变；εL为应力-应变全曲线下降段应力为0.8fc对应的压应变；σ为压应力；x=ε/ε0；y=σ/fc 。
编号 应力-应变全曲线方程■■2■■■■σ=εεεε fEE EE csc00 c-■■■+-■＜εεεε0 csc0 σ■■=■+--εεεεεε c f 0≥基本形式[11]■1.5 0 L0 εε■■■■=L0cimages/BZ_78_1861_843_2130_939.png■+■+E■■■■■Esc ■■Efε scc0=(/)(/)(/),1(/2)(/)10.25[(/1)/(/1)],1.254 105/xxx y x x x■■-＜■-1.348 , 01 10.652 1 , 1 11.261(1)2≤本构1=■■■■+-1.5＞f=c100MPa■■-＜■-1.285 , 01 10.715 1 , 1 11.440(1)2≤y本构2=■■xxx x■■+x -1.5x＞f=c110MPa 2≤y =■■■■-＜■-■■+-本构3 1.186 , 01 10.814 1 , 1 11.851(1)xxx x x 1.5x＞f=c130MPa xxx y x x x≤■■-＜■-本构4 2=■■■+-1.111 , 01 10.889 1 , 1 12.357(1)1.5＞f=c150MPa xxx y x x x 2≤■■-＜■-本构5=■■1.051 , 01 10.949 1 , 1 12.992(1)■■+-1.5＞f=c170MPa xxx y x x x 2≤■■-＜■-本构6=■■■■+-1.003 , 01 10.997 1 , 1 13.814(1)1.5＞f=c190MPa
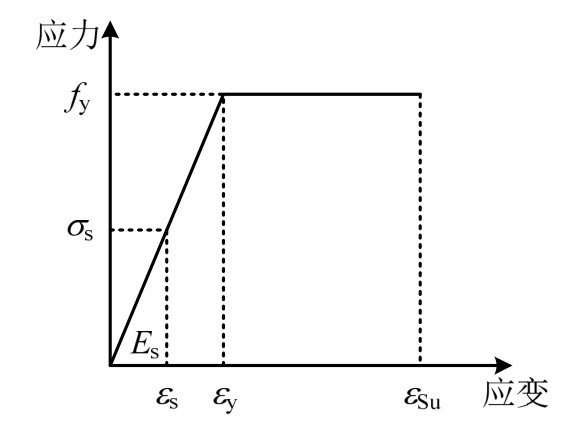
图5 钢筋理想弹塑性模型
Fig.5 Elastic-plastic model of steel bar
3.2 UHPC梁正截面受弯分析
以单筋矩形截面UHPC梁为例，由基本假定，当适筋梁达到极限承载力时，截面应力、应变分布如图6所示，截面受压区边缘UHPC达到极限压应变εcu。假定此时截面受压区高度为xc，则距截面中性轴距离为y的UHPC纤维处的应变可按式(11)计算：
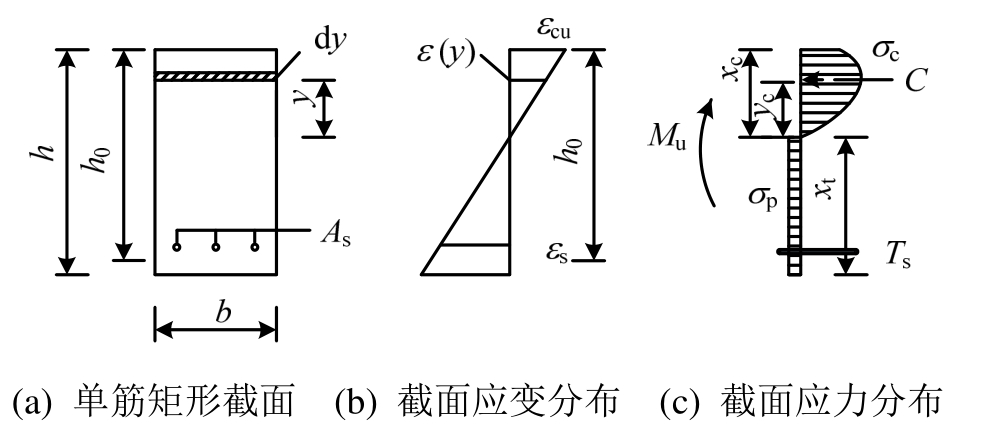
图6 矩形截面受弯分析
Fig.6 Bending analysis of rectangular section
钢筋应变为：
图6(c)所示为截面应力分布图形，压应力的合力C为：
合力作用点到中和轴的距离yc为：
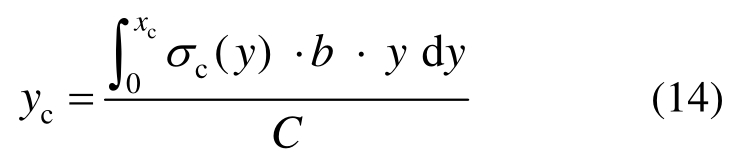
钢筋的拉力Ts及其距中和轴的距离ys可分别按式(15)和式(16)计算：
式中：h0为截面有效高度；As为受拉纵筋面积。
受拉区UHPC的合力Tc可按式(17)计算：
式中：b为截面宽度；xt为截面受拉区高度。
受拉区合力作用点距中和轴的距离可近似按xt/2计算。
根据截面的平衡条件，可写出以下两个平衡方程：
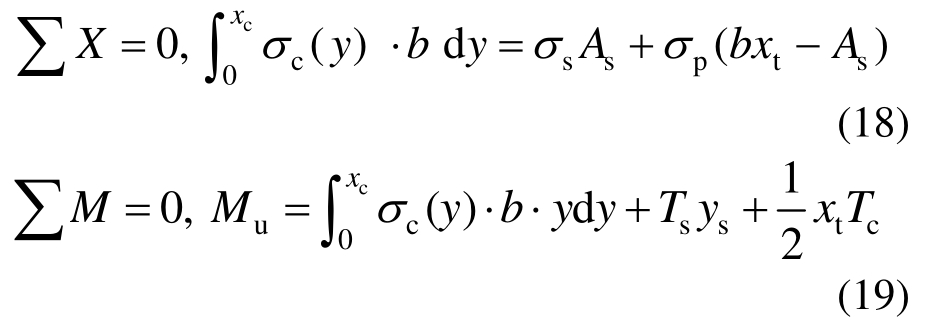
3.3 正截面受压区UHPC应力图形的等效
将UHPC受压本构代入式(18)、式(19)，可求解截面承载力，然而由于受压区应力图形为曲线，计算相对较为复杂。为了简化计算，可对受压区UHPC应力图形进行等效，通常将其等效成矩形应力图形(见图7(c))。等效的基本原则为：
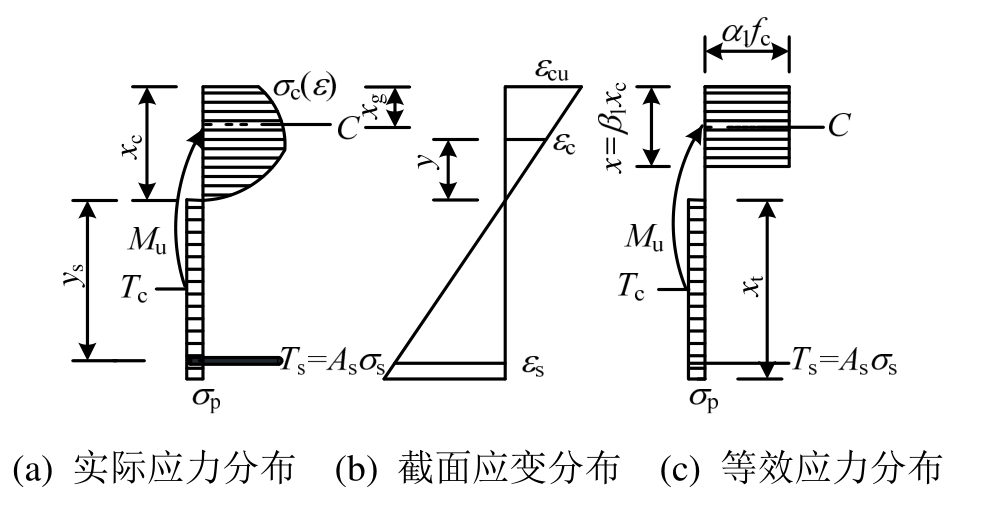
图7 UHPC梁正截面应力、应变分布
Fig.7 Normal section stress and strain distribution of UHPC beam
1)等效矩形应力图形的面积应等于曲线应力图形的面积，即UHPC压应力合力C的大小相等；
2)等效矩形应力图形的形心位置应与曲线应力图形的形心位置相同，即压应力合力C的作用点位置yc不变。
取受压区等效矩形应力图形的高度为x=β1xc，等效应力为α1fc，如图7(c)所示。假定受压区曲线应力图形的面积为Ac，形心位置为xg，如图7(a)所示，则有等效条件如下：
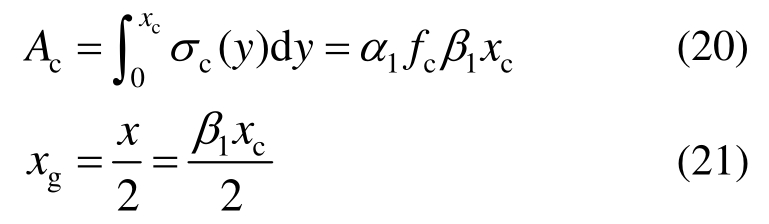
由图7(a)，形心位置xg可按式(22)计算：
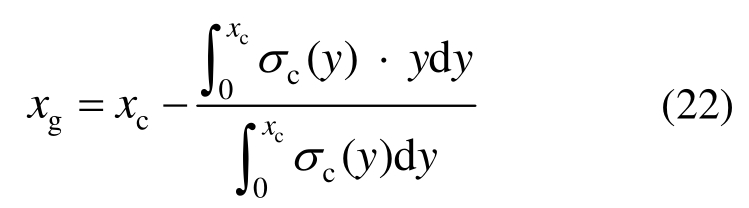
将式(22)代入式(21)可得：
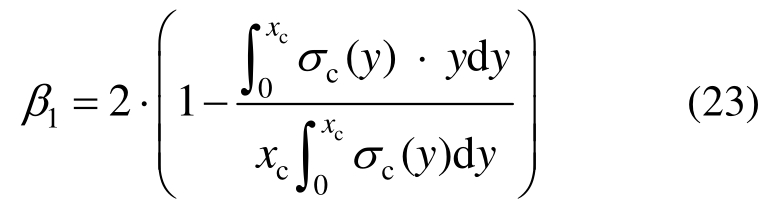
利用式(11)对式(23)进行换元得：
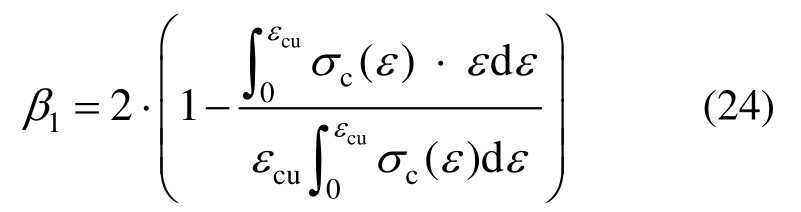
同理，利用式(11)对式(20)进行换元可得：
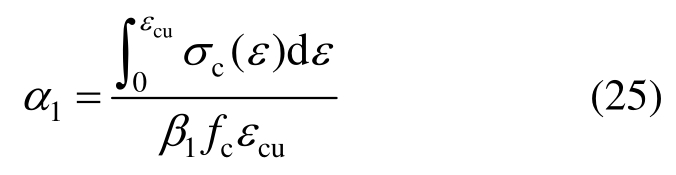
由式(24)、式(25)可以看出，等效矩形应力图形系数β1、α1的值仅与UHPC自身材料属性有关，故只要确定出UHPC受压本构关系及极限压应变值就可求得系数β1、α1的值。
根据图7(c)可得平衡方程：
式中：as为受拉纵筋合力点至受拉区底部边缘的距离，as=h-h0；h为截面高度。
3.4 等效矩形应力图形参数α1、β1取值
由式(26)、式(27)可知，计算正截面受弯承载力Mu需要确定等效矩形应力图形参数α1、β1。已知β1、α1的值仅与UHPC自身材料属性有关，只要确定出UHPC受压本构关系及极限压应变εcu，就可求得系数β1、α1的值。
表1中给出了6种不同轴心抗压强度UHPC对应的受压本构方程。将表1中的本构1~本构6分别代入式(24)、式(25)，可得各轴心抗压强度对应的α1、β1值，如表2所示。
表2 等效矩形应力图形参数α1、β1取值
Table 2 Parameter values(α1,β1)of equivalent rectangular strength block
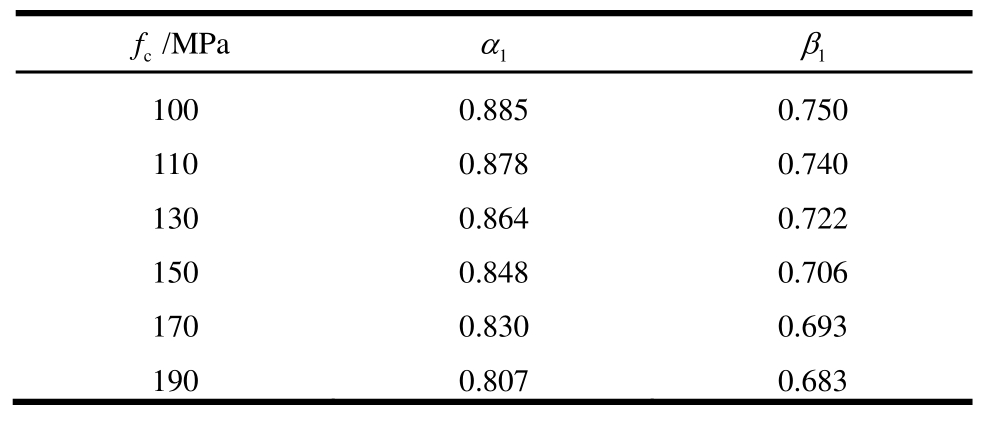
f/MPa α1 β1 c 100 0.885 0.750 110 0.878 0.740 130 0.864 0.722 150 0.848 0.706 170 0.830 0.693 190 0.807 0.683
3.5 相对界限受压区高度ξb及最大配筋率ρmax
当纵向受拉钢筋应力到达其屈服强度的同时，受压区边缘UHPC应变恰好达到其极限压应变εcu，该种破坏被称为“界限破坏”，这是适筋梁与超筋梁的界限状态。此时的钢筋配筋率是适筋梁所能达到的最大配筋率，也称之为“界限配筋率”。
由平截面假定，当梁发生界限破坏时其截面应变沿截面高度分布如图8所示。令界限状态受压区计算高度为xb，则xb与截面有效高度h0的比值称为相对界限受压区高度，用ξb来表示。
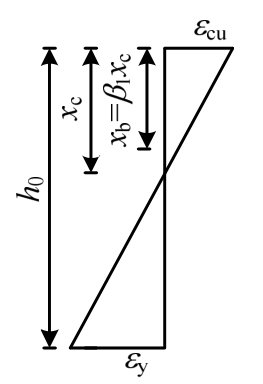
图8 界限破坏时梁正截面应变图
Fig.8 Strain profiles at balanced failure
由几何关系可得：
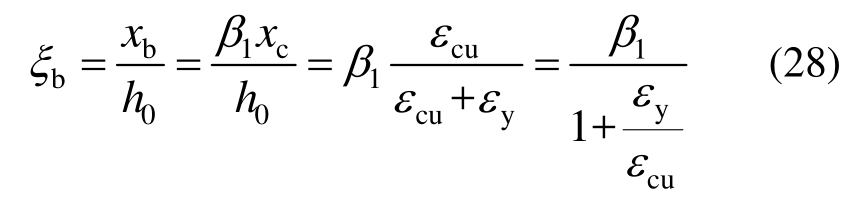
将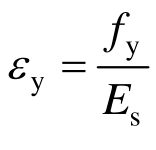
代入式(28)可得：
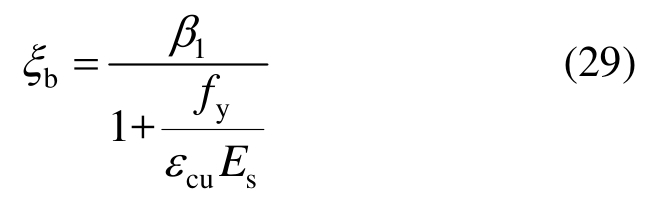
界限破坏时，受弯构件相应的配筋率为最大配筋率ρmax，受拉纵筋应力σs=fy，根据式(26)可得：
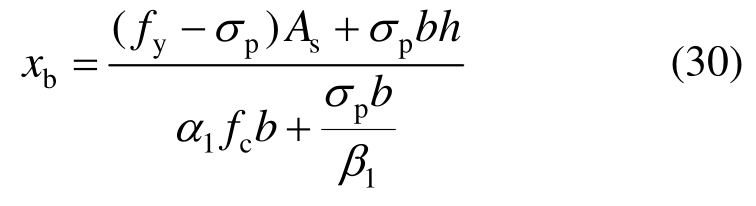
相对界限受压区高度为：
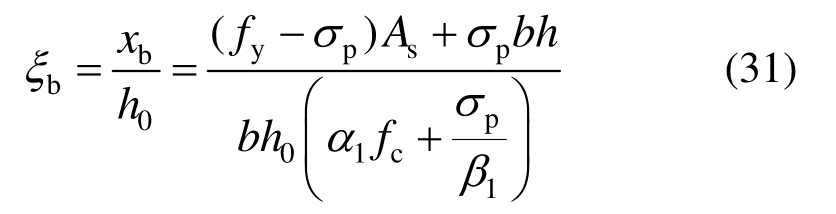
由式(31)可得：
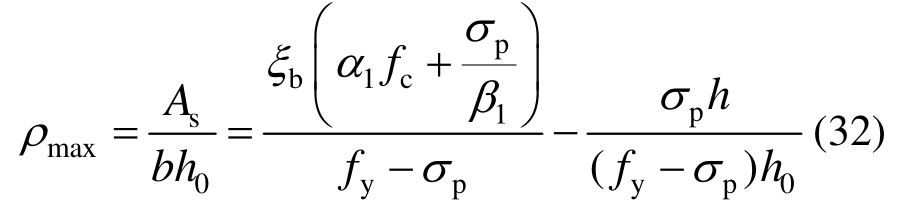
将相关参数代入式(29)、式(32)，可求得相对界限受压区高度ξb及最大配筋率ρmax的值。
根据式(27)可得适筋梁的最大受弯承载力Mumax为：
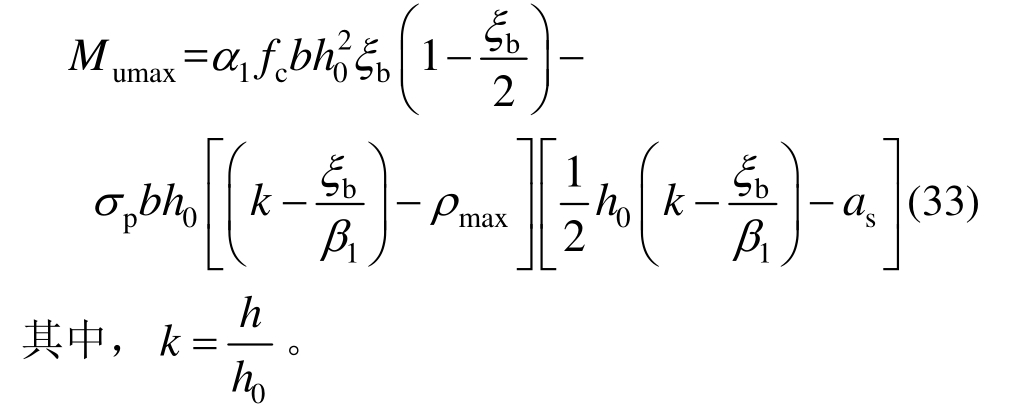
4 试验结果验证
通过文献[8,10,24－26]选取了28根UHPC梁试验数据(见表3)，用以验证承载力计算公式。UHPC梁极限弯矩试验值
与理论计算值
对比见表3所示。由表3可算得UHPC梁极限弯矩试验值
与理论计算值
比值的均值为1.094，标准差为0.093，变异系数为0.085。可见计算值与试验值吻合良好，计算值具有较高的精度和可靠性；等效矩形应力图形参数α1、β1的取值较为合理。
表3 极限弯矩计算值与试验值比较
Table 3 Comparison of ultimate moment calculated and experimental values
注：ρ为受拉纵筋配筋率；材料强度相关取值为试验平均值。
梁编号 Vf/(%)f/f ld ρ b/ mm h/ mm h0/ mmfc/ MPafy/ MPaMut/(kN·m)Muc/(kN·m)Mut/Muc数据来源L1 2.0 59 0.0122 150 200 168110.20476.538.2537.06 1.032 L2 2.0 59 0.0309 150 200 16498.60478.363.564.56 0.984 L3 2.0 59 0.0307 150 200 166105.00467.664.565.29 0.988 L4 2.0 59 0.0590 150 200 15499.30465.28789.83 0.969 L5 2.0 59 0.0967 150 200 13997.80465101101.20 0.998 L6 2.0 65 0.0819 125 140 97.583.1157047.839.63 1.206文献[8]L7 2.0 65 0.0819 125 140 97.599.557051.342.89 1.196 L8 2.0 65 0.0819 125 140 97.5102.257052.543.39 1.210 L9 2.0 65 0.0819 125 140 97.5109.6557054.844.52 1.231 L10 2.0 65 0.0819 125 140 97.594.4157045.541.88 1.086 L11 2.0 65 0.0060 180 270 235190.942083.370.41 1.183 L12 2.0 65 0.0090 180 270 235192.242092.282.07 1.123 L13 2.0 65 0.0120 180 270 235196.1420116.593.99 1.240 L14 2.0 65 0.0131 180 270 215190.9420105.788.95 1.188 L15 2.0 65 0.0196 180 270 215196.1420131.6109.87 1.198 L16 1.5 60 0.0147 150 200 182115.1518.348.146.40 1.037文献[24]L17 1.5 60 0.0221 150 200 182115.1518.362.862.83 1.000 L18 1.5 60 0.0414 150 200 162115.1518.392.883.07 1.117 L19 1.5 60 0.0496 150 200 162115.1518.3101.695.15 1.068 L20 1.0 65 0.0287 150 250 228116.7534124.3120.18 1.034文献[25]L21 1.0 65 0.0489 150 250 201116.7534157.5145.95 1.079 L22 1.0 65 0.0678 150 250 193116.7534180.6172.79 1.045 L23 1.0 65 0.0287 150 250 228116.7432128.65101.07 1.273 L24 1.0 59 0.0300 150 250 218116.7529.2120.3113.18 1.063文献[26]L25 1.0 59 0.0490 150 250 200116.7529.2144.5143.10 1.010 L26 1.0 59 0.0670 150 250 195116.7529.2171.6172.97 0.992 L27 1.0 59 0.0300 150 250 218116.7418.693.6593.44 1.002 L28 1.0 59 0.0300 150 250 202116.7435.090.684.30 1.075文献[10]
5 结论
(1)将复合材料力学引入UHPC受弯承载力计算模型中，简化了截面受拉区复杂应力计算方法，从理论角度解决了截面受拉区UHPC拉应力等效问题。
(2)基于已有的UHPC材料性能试验数据，确定了UHPC受压性能指标，为UHPC受压本构相关参数的确定提供依据。
(3)建立了等效矩形应力图形参数α1、β1的计算公式，结合不同适用强度对应的UHPC受压本构关系，计算得到相应的α1、β1建议取值，其值符合一般规律，可用于计算UHPC梁受弯承载力。
(4)基于平截面假定，建立了UHPC梁受弯承载力计算模型，提出了相对界限受压区高度、最大配筋率的计算方法。
(5)通过28根UHPC试验梁极限弯矩试验值与理论计算值的对比分析可知，本文提出的UHPC梁受弯承载力计算方法能有效、安全地计算其受弯承载力，且计算结果具有良好的精度。
[1]Rossi P.Ultra high performance fiber reinforced concretes [J].Concrete International, 2001, 23(6):1216－1221.
[2]Voo Y L, Foster S J.Characteristics of ultra high performance “ductile” concrete and its impact on sustainable construction [J].Ies Journal Part A Civil &Structural Engineering, 2010, 3(3): 168－187.
[3]Makita T, Brühwiler E.Tensile fatigue behaviour of ultra-high performance fibre reinforced concrete(UHPFRC)[J].Materials & Structures, 2014, 47(3):475－491.
[4]Yi N H, Kim J H J, Han T S, et al.Blast-resistant characteristics of ultra-high strength concrete and reactive powder concrete [J].Construction & Building Materials, 2012, 28(1): 694－707.
[5]邓明科, 卜新星, 潘姣姣, 等.型钢高延性混凝土短柱抗震性能试验研究[J].工程力学, 2017, 34(1): 163－170.Deng Mingke, Bu Xinxing, Pan Jiaojiao, et al.Experimental study on seismic behavior of steel reinforced high ductile concrete short columns [J].Engineering Mechanics, 2017, 34(1): 163－170.(in Chinese)
[6]赖建中, 朱耀勇, 谭剑敏.超高性能混凝土在埋置炸药下的抗爆试验及数值模拟[J].工程力学, 2016,33(5): 193－199.Lai Jianzhong, Zhu Yaoyong, Tan Jianmin.Experimental and simulation of ultra-high performance concrete subjected to blast by embedded explosive [J].Engineering Mechanics, 2016, 33(5): 193－199.(in Chinese)
[7]郑文忠, 卢姗姗, 李莉.GFRP筋活性粉末混凝土梁受力性能试验研究[J].建筑结构学报, 2011, 32(6): 115－124.Zheng Wenzhong, Lu Shanshan, Li Li.Experimental research on mechanical performance of reactive powder concrete beams reinforced with GFRP bars [J].Journal of Building Structures, 2011, 32(6): 115－124.(in Chinese)
[8]李莉.活性粉末混凝土梁受力性能及设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2010.Li Li.Mechanical behavior and design method for reactive powder concrete beams [D].Harbin: Harbin Institute of Technology, 2010.(in Chinese)
[9]王文雷.RPC预应力梁相关设计参数研究[D].北京:北京交通大学, 2006.Wang Wenlei.Investigation on design parameters of RPC prestressed beam [D].Beijing: Beijing Jiaotong University, 2006.(in Chinese)
[10]金凌志, 何来, 吴欣珂.HRB500级钢筋活性粉末混凝土梁受弯性能试验研究[J].建筑结构, 2015, 45(15):87－92.Jin Lingzhi, He Lai, Wu Xinke.Experimental study on flexural property of reactive powder concrete beams with HRB500 steel [J].Building Structure, 2015, 45(15): 87－92.(in Chinese)
[11]Singh M, Sheikh A H, Ali M S M, et al.Experimental and numerical study of the flexural behaviour of ultra-high performance fibre reinforced concrete beams[J].Construction & Building Materials, 2017,138(Complete): 12－25.
[12]杨志慧.不同钢纤维掺量活性粉末混凝土的抗拉力学特性研究[D].北京: 北京交通大学, 2006.Yang Zhihui.Investigation on tensile properties of reactive powder concrete with different content of steel fiber [D].Beijing: Beijing Jiaotong University, 2006.(in Chinese)
[13]金凌志, 李月霞, 付强.不同掺合料掺量的活性粉末混凝土抗压强度试验[J].河南科技大学学报(自然科学版), 2014(5): 55－62.Jin Lingzhi, Li Yuexia, Fu Qiang.Experimental study on compressive strength of Reactive Powder Concrete with different additives [J].Journal of Henan University of Science and Technology(Natural Science), 2014(5):55－62.(in Chinese)
[14]曾建仙, 吴炎海, 林清.掺钢纤维活性粉末混凝土的受压力学性能研究[J].福州大学学报(自然科学版),2005, 33(增刊1): 132－137.Zeng Jianxian, Wu Yanhai, Lin Qing.Researches on the compressive mechanics properties of steel fiber RPC [J].Journal of Fuzhou University(Natural Science), 2005,33(suppl 1): 132－137.(in Chinese)
[15]焦楚杰, 孙伟, 秦鸿根, 等.钢纤维高强混凝土单轴受压本构方程[J].东南大学学报(自然科学版), 2004,34(3): 366－369.Jiao Chujie, Sun Wei, Qin Honggen, et al.Constitutive equation of SFRHSC under uniaxial compression [J].Journal of Southeast University(Natural Science Edition), 2004, 34(3): 366－369.(in Chinese)
[16]吴炎海, 何雁斌, 杨幼华.活性粉末混凝土(RPC200)的力学性能[J].福州大学学报(自然科学版), 2003,31(5): 598－602.Wu Yanhai, He Yanbin, Yang Youhua.Investigation on RPC200 mechanical performance [J].Journal of Fuzhou University(Natural Science), 2003, 31(5): 598－602.(in Chinese)
[17]徐朦.多种钢纤维对超高性能混凝土力学性能影响的比较研究[D].北京: 北京交通大学, 2014.Xu Meng.Comparative study on influences of various steel fibers on mechanical properties of ultra-high performance concrete(UHPC)[D].Beijing: Beijing Jiaotong University, 2014.(in Chinese)
[18]GB 50010－2010，混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010－2010, Code for design of concrete structures[S].Beijing: China Architecture Industry Press, 2010.(in Chinese)
[19]Hognestad E.Concrete stress distribution in ultimate strength design [J].Journal of the American Concrete Institute, 1955, 52(6): 455－479.
[20]Jones R M, Bert C W.Mechanics of composite materials[M].Blacksburg: Scripta Book Co, 1975.
[21]李志武, 许金余, 张国喜, 等.利用纤维增强机理对纤维临界体积率的理论推导[C]// 海峡两岸三地混凝土技术研讨会.南京: 东南大学出版社, 2010.Li Zhiwu, Xu Jinyu, Zhang Guoxi, et al.The theoretical deduction of critical fiber volume quantity using the mechanism of fiber reinforced concrete [C]// Seminar on Concrete Technology in Three Places Across the Taiwan Straits.NanJing: Southeast University Press, 2010.(in Chinese)
[22]Abrishambaf A, Pimentel M, Nunes S.Influence of fibre orientation on the tensile behaviour of ultra-high performance fibre reinforced cementitious composites[J].Cement & Concrete Research, 2017, 97: 28－40.
[23]Ali H M, Hamad L N T.First diagonal cracking and ultimate shear of reactive powder concrete T-beams without stirrups [J].Journal of Engineering and Development, 2014, 18(5): 149－164.
[24]Al-Hassani H M, Khalil W I, Danha L S.Prediction of the nominal bending moment capacity for plain and singly reinforced rectangular RPC beam sections [J].Engineering and Technology Journal, 2015, 33(5):1113－1130.
[25]邓宗才, 王义超, 肖锐, 等.高强钢筋UHPC梁抗弯性能试验研究与理论分析[J].应用基础与工程科学学报,2015, 23(1): 68－78.Deng Zongcai, Wang Yichao, Xiao Rui, et al.Flexural test and theoretical analysis of UHPC beams with high strength rebars [J].Journal of Basic Science and Engineering, 2015, 23(1): 68－78.(in Chinese)
[26]曹霞, 常婧, 王艳俊.高强钢筋RPC梁受弯构件正截面承载力试验研究[J].河南理工大学学报(自然科学版), 2015, 34(1): 109－115.Cao Xia, Chang Jing, Wang Yanjun.Experimental study on flexural capacity of normal section of high strength reinforced reactive powder concrete beam [J].Journal of Henan Polytechnic University(Natural Science), 2015,34(1): 109－115.(in Chinese)