耗能减震技术因其减震机理明确、减震效果显著、构造简单、适用范围广、维护方便等优点，受到众多国内外研究者的重视[1]。由于耗能减震技术研究和应用的历史较短，目前仍存在很多有意义的研究课题值得进一步探索。黏滞阻尼墙就是一种耗能减震装置，它主要由内部钢板、外部钢板及处于内、外钢板之间的黏滞液体三部分构成，内部钢板固定于上层楼面，外部钢板固定于下层楼面，内部钢板能在其中沿平面运动。在地震作用下，楼层间的相对运动使内外钢板间产生速度差，高浓度黏滞材料产生剪切变形形成黏滞阻尼力，从而达到消耗地震能量的目的[2－3]。
黏滞阻尼墙作为一种被动耗能装置，一般布置在结构相对变形比较大的楼层或部位，从而提高耗能能力、达到较为理想的减震效果。但由于结构自身的特点限制，如框架-剪力墙结构或框架-筒体结构本身层间变形相对较小，或特定条件限制如可选的阻尼器布置位置受限等，黏滞阻尼墙可能会因所在位置相对变形较小从而使得黏滞阻尼墙性能的发挥受到影响[4－6]。将位移放大装置应用于黏滞阻尼墙中，不仅能通过放大相对位移和相对速度来增加阻尼墙的耗能，而且能降低阻尼墙在最大位移处的阻尼力[7]。
国内外学者针对位移放大装置展开了一系列研究。哈尔滨建筑大学的陈月明和刘季[8]提出一种带有梯形杠杆摆的黏弹性阻尼墙，在框架中设置人字形支撑，依据杠杆原理将层间位移放大几倍，该放大量传递给黏弹性阻尼材料进而减少结构的地震与风振反应。美国纽约州立大学教授Constantinou等[9]率先提出了基于连杆机构的位移放大系统，并应用于实际工程。Sigaher和Constantinou[10]进一步提出了阻尼墙的剪刀型布置，并指出该布置方法对位移放大效果显著，且由于其所占空间非常小，所以特别适合安装于空间受到限制的结构。Ribakov和Reinhorn[11]基于杠杆原理提出了一种位移放大系统，并将其与阻尼墙连接在一起，分析了其在建筑结构中的实际应用。Berton和Bolander[12]采用齿条齿轮加速墙来放大结构振动传给阻尼墙的位移，并进行了相关试验研究，结果表明该位移放大系统配合阻尼墙工作切实可行。日本学者Watakabe和Fujita等[13]提出一种新型的管形黏弹性阻尼墙，研究表明带位移放大功能的管形阻尼墙对结构振动响应的控制效果较好。
本文提出一种多杠杆并联的放大型黏滞阻尼墙装置并进行了理论分析，同时设计制作了附加3倍位移放大装置的黏滞阻尼墙和普通阻尼墙试验模型并进行了力学性能试验，通过试验研究这两种不同阻尼墙的力学性能特点，最后建立了三层混凝土框架结构模型进行动力响应分析。
1 放大型黏滞阻尼墙的构造与理论分析
1.1 装置构造
本文介绍了一种放大型黏滞阻尼墙(magnified viscous damping wall，MVDW)，通过在黏滞阻尼墙(viscous damping wall，VDW)上附加位移放大装置，把结构的层间位移放大后再施加到阻尼墙的内钢板上，并放大阻尼墙两端相对速度，从而增大阻尼墙的阻尼力，提高其耗能能力[7]。该装置主要由阻尼墙外钢箱、阻尼墙内钢板、放大杠杆、支点轴及连接构件等组成。图1为MVDW系统工作原理示意图，图中u为结构层间位移，经η倍位移放大装置放大后输入到阻尼墙的相对位移为ηu[14]。
图1 MVDW系统工作原理示意图
Fig.1 Working principle diagram of MVDW
图1中的位移放大机构与结构上部楼层和阻尼器活动钢板连接，位移放大机构近端螺栓孔与上连接板连接，中间螺栓孔作为支点孔与外钢箱通过支点轴连接，远端螺栓孔与阻尼器活动钢板连接。
1.2 MVDW系统的理论分析
黏滞阻尼墙的阻尼力公式可简化为[15-16]：
式中：F表示阻尼力；Cα表示黏滞阻尼墙的阻尼系数；sgn(⋅)表示符号函数；α为阻尼指数。黏滞阻尼墙的耗能为：
式中，u表示阻尼墙两端的相对位移。阻尼墙的位移和速度可分别表示为：
对于黏滞阻尼墙附加放大倍数为η倍的放大装置，阻尼墙的相对位移和相对速度为u′=ηu、
代入式(1)，得放大型黏滞阻尼墙的阻尼力和耗能公式分别为：
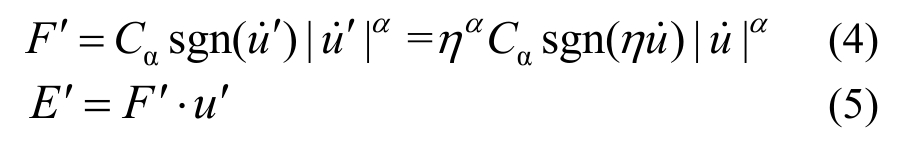
上述黏滞阻尼墙的阻尼力公式只考虑位移放大装置的水平方向运动，而放大型黏滞阻尼墙在实际运动过程中，放大装置会产生竖向提拉。本文在其基础上考虑了放大装置竖向提拉效应(magnified viscous damping wall-vertical，MVDW-V)对阻尼墙耗能的影响，图2为放大装置位移放大示意图。
图2 位移放大示意图
Fig.2 Magnified displacement diagram
图2中uy表示放大装置在运动过程中支点轴产生的竖向位移，当结构水平位移为u时，支点轴圆心竖向位移和速度可分别表示为：
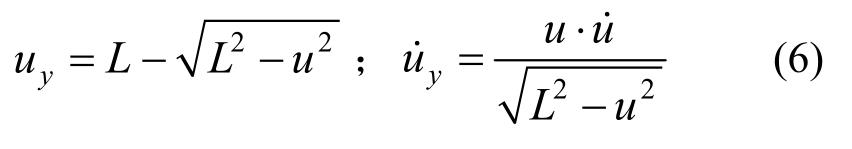
根据黏滞阻尼墙阻尼力公式可得放大型黏滞阻尼墙竖向阻尼力公式：
图3为放大装置考虑竖向提拉效应的简化模型受力分析图，图中m、k、c分别表示结构的质量、刚度、阻尼；Kd为黏滞阻尼墙的内部刚度；L为上连接点到支点轴的圆心距；ηL表示位移放大装置的放大倍数为η倍；θ表示放大装置转动的角度。设上部阻尼力为F′，对O点求矩，即∑Mo =0，则：
放大型黏滞阻尼墙考虑竖向提拉效应的阻尼力及耗能公式可分别表示为：
对于普通黏滞阻尼墙，将其阻尼系数放大ψ倍，此时结构层间位移和相对速度约为u和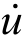
，阻尼墙的阻尼力及耗能分别为：
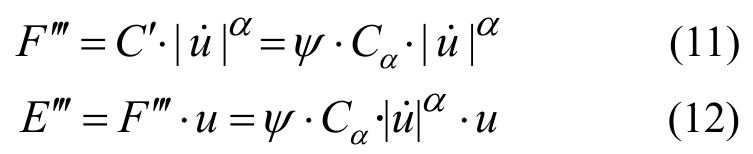
令E′=E′，则可得ψ=η1+α，这说明附加η倍位移放大装置的阻尼墙与阻尼系数放大η1+α的阻尼墙具有相同的耗能效果。再令E′=E′，则可得ψ=η1+α+(1+η)⋅|tanθ|1+α，这说明附加η倍并考虑竖向提拉效应的放大型黏滞阻尼墙的耗能效果会随着放大装置转动角度的变化而变化。
图3 MVDW-V系统简化模型及受力分析示意图
Fig.3 Simplified model and force analysis diagram of MVDW-V
2 MVDW-V的力学性能参数分析
根据上述理论推导，可知MVDW-V的耗能效果与放大装置的转动角度θ有关，并可得出放大装置在考虑竖向提拉效应情况下对阻尼墙耗能的影响。
2.1 力学模型对比
当阻尼系数及阻尼指数一定时，建立圆心距L取50 mm、位移幅值取30 mm时的MVDW、MVDW-V的力学模型进行对比分析，如图4所示。可知，考虑竖向提拉效应情况下的阻尼墙的滞回曲线更加饱满，耗能效果更为显著。
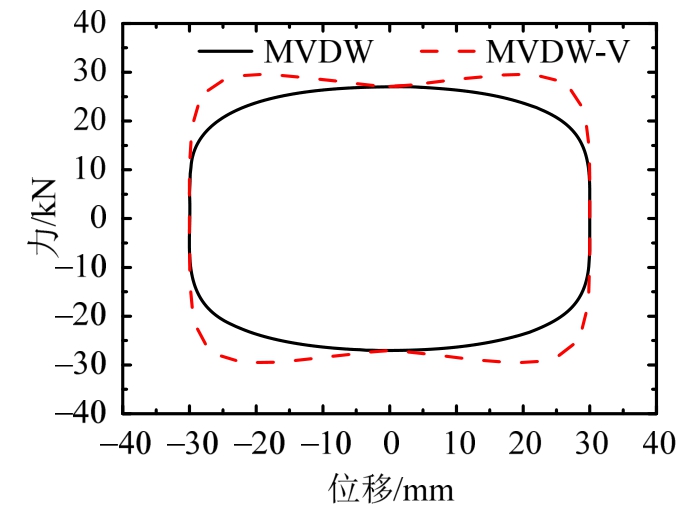
图4 力学模型对比
Fig.4 Comparison of mechanical model
2.2 放大装置的水平及竖向变形
图5为放大装置构造示意图，当杠杆的放大倍率一定时，杠杆的长度由圆心距L决定。由图2可知，放大装置的圆心距L由三部分组成：孔1圆心到连接角钢下边缘的距离d1、连接角钢下边缘到孔2上边缘的距离d2及孔2半径d3。当放大装置转动时，连接角钢水平运动，支点轴产生向上位移，d2不断减小，只有保证d2≥0，才能保证放大装置正常运转[7]。
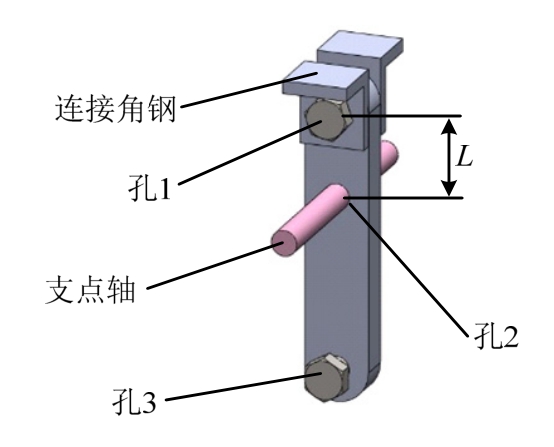
图5 杠杆的组成
Fig.5 The composition of the lever
放大装置孔1圆心至孔2圆心的长度可表示为：
则杠杆转动前：
当结构水平位移为u时，孔2圆心竖向位移为：
则杠杆转动后，由d2′=d2-uy≥0，整理得：
在试验中，d3为8 mm，d1为22 mm，由此可得出在圆心距L分别为50 mm、60 mm、70 mm、80 mm时，所对应放大装置上连接点最大水平位移umax及支点轴最大竖向位移uymax，如表1所示。
表1 水平及竖向变形
Table 1 Horizontal and vertical deformation
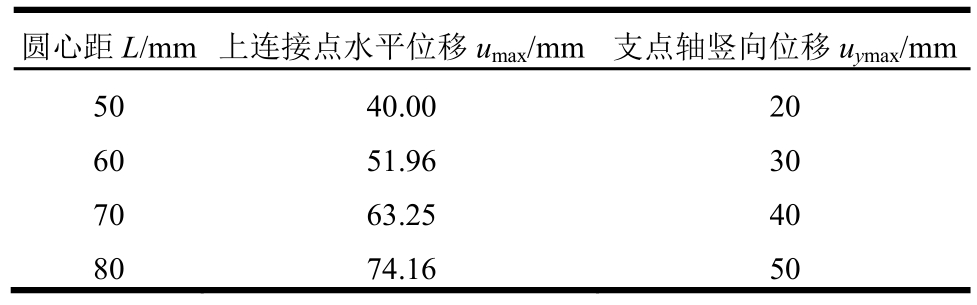
圆心距L/mm 上连接点水平位移umax/mm 支点轴竖向位移uymax/mm 50 40.00 20 60 51.96 30 70 63.25 40 80 74.16 50
2.3 考虑竖向提拉效应对阻尼墙耗能的影响
由于位移放大装置的长度由圆心距L决定，故考虑竖向提拉效应对阻尼墙耗能的提高率受圆心距L的影响，图6给出了附加3倍位移放大装置在不同位移幅值下圆心距L分别为50 mm、60 mm、70 mm、80 mm时竖向提拉效应对阻尼墙耗能的提高率。由图可知，当圆心距L为50 mm、阻尼墙位移幅值为30 mm时，考虑竖向提拉效应的阻尼墙耗能可提高约19.90%；且当圆心距相同时，耗能提高率随着位移幅值的增加而增加。
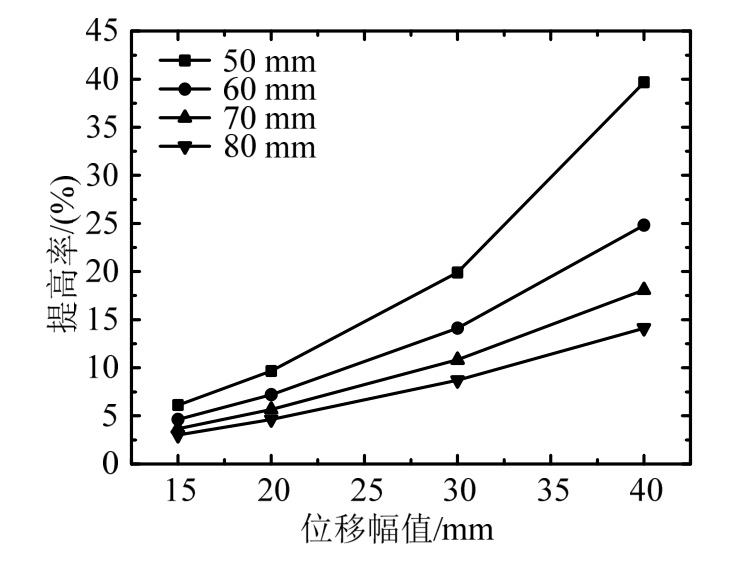
图6 耗能提高率
Fig.6 Increase ratio of energy consumption
3 位移放大装置试验研究
3.1 黏滞阻尼墙模型设计及制作
试验采用的黏滞阻尼墙由内钢板、外钢箱、杠杆、支点轴、连接板和黏滞阻尼材料组成。试验试件均由Q345钢板焊接而成，材料特性为：E=200GPa，ρ=7.85t/m3。试验模型如图7所示。位移放大结构的主要受力包括两方面：用于连接装置元件的螺栓受剪，杠杆及连接构件承压。式(17)、式(18)分别为螺栓受剪承载力及杠杆、连接构件受压承载力计算公式：
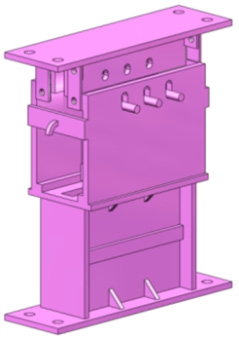
图7 位移放大型阻尼墙试验模型
Fig.7 Test model of displacement MVDW
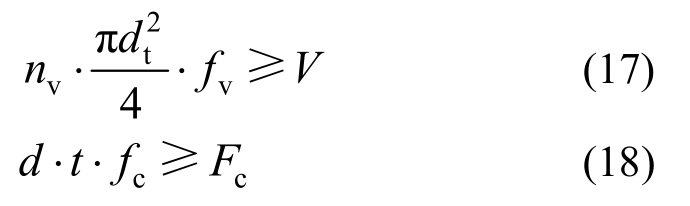
式中：nv为受剪面的个数；dt为受剪螺栓的直径；fv为螺栓抗剪强度设计值；V为螺栓受剪处受到的剪力；d为受压构件的预留螺栓孔直径；t为连接构件的厚度；fc为构件承压强度设计值；Fc为构件承压处受到的压力。
1)内钢板的设计。试验设计缩尺模型，内钢板构造较为简单，是由剪切板及连接孔组成，如图8所示。
图8 黏滞阻尼墙内钢板 /mm
Fig.8 Internal steel plate of fluid viscous damper
2)外钢箱的设计。阻尼器外钢箱由下连接板、侧面钢板和L形钢板焊接而成。在L形钢板上设有形状为U形孔槽的支点孔。如图9所示。
图9 黏滞阻尼墙外钢箱 /mm
Fig.9 External steel plate of fluid viscous damping wall
3)放大装置的设计。试验设计了2种杠杆，一种是放大型黏滞阻尼墙的3倍杠杆，另一种是普通阻尼墙的单倍杠杆。杠杆上有3个螺栓孔，分别通过螺栓固定于上连接梁、外钢箱的支点孔和内钢板，如图10所示。
4)黏滞阻尼材料。采用无锡圣丰减震器有限公司生产的黏滞阻尼液，阻尼指数为0.45。
3.2 试验方案
本试验采用电液伺服作动器进行加载，作动器最大输出力为52 kN，工作行程为400 mm。试验主要测量阻尼墙的变形和阻尼力。将阻尼墙上连接板与作动器固定连接，外钢箱底部与地梁固定连接，如图11所示。
图10 杠杆构造图 /mm
Fig.10 The structure diagram of lever
图11 试验加载装置
Fig.11 Test loading device
试验采用位移控制、动态加载，输入的正弦波时程，见下式：
式中：u为阻尼墙上连接板与外钢箱之间的相对位移；u0为每个工况中相对位移的幅值；f为作动器的加载频率(0.3 Hz)；t为时间，试验在温度20℃±0.5℃范围内进行。为了对比3倍放大型黏滞阻尼墙和普通阻尼墙的力学性能，工况设计保证各种参量等间隔增加，加载位移幅值分别为±5 mm、±7.5 mm、±10 mm，如图12所示。
图12 位移加载曲线
Fig.12 Displacement loading curve
4 试验结果与分析
4.1 MVDW和VDW滞回曲线对比分析
图13为3倍MVDW与VDW在频率f =0.3 Hz，位移幅值分别为±5 mm、±7.5 mm、±10 mm作用下的试验滞回曲线的对比。可知，在相同位移幅值下，3倍放大型黏滞阻尼墙阻尼力峰值远大于普通阻尼墙。当加载频率恒定时，随着位移幅值的增加，放大型黏滞阻尼墙和普通阻尼墙阻尼力峰值随之增加。由于采用了放大杠杆，故内钢板的位移是作动器位移的3倍，且在较大位移作用下3倍放大型黏滞阻尼墙的滞回耗能曲线较饱满，具有良好的耗能效果。
图13 两种阻尼墙滞回曲线对比
Fig.13 Comparison of hysteresis curves of two kinds of damping wall
4.2 阻尼力及耗能对比分析
表2为根据不同工况下试验滞回曲线得出的阻尼力及耗能以及3倍放大型黏滞阻尼墙与普通阻尼墙阻尼力及耗能的对比值。
由表2可知，随着位移幅值的增加，3倍放大型黏滞阻尼墙的阻尼力呈递增趋势，耗能也有明显增加。当位移幅值为5 mm、7.5 mm、10 mm时，MVDW与VDW的阻尼力之比分别为4.48、4.81、4.58，平均放大4.62倍。MVDW与VDW的耗能比分别为3.89、4.24、4.42，平均放大4.19倍。
表2 阻尼力及耗能对比
Table 2 Comparison of damping force and energy consumption
位移幅值/mm 阻尼力F/kN普通阻尼墙 3倍位移放大阻尼墙 阻尼力比耗能比耗能E/(N·m)阻尼力F/kN耗能E/(N·m)5 2.3844.08 10.67 171.54 4.483.89 7.5 2.6976.78 12.95 325.79 4.814.24 10 3.08112.93 14.12 498.96 4.584.42平均值 4.624.19
4.3 MVDW及VDW试验和理论力学模型研究
图14和图15分别为在不同位移幅值下普通阻尼墙和放大型黏滞阻尼墙的试验曲线与理论曲线的对比。由图可知，理论曲线与试验曲线均吻合性较好。图14和图15中的试验曲线在对角线处会产生微小尖角，原因在于活动钢板与外钢箱内壁之间的间隙太小，导致在试验过程中产生挤压回弹力。根据前文MVDW-V的力学性能分析可知，装置的竖向提拉效应仅在位移幅值较大情况有显著的减震效果，由于位移幅值较小，故图15中考虑竖向提拉效应的放大型黏滞阻尼墙减震效果不显著。
图14 普通阻尼墙曲线拟合的对比
Fig.14 Comparison of fitting curve of ordinary VDW
图15 位移放大型黏滞阻尼墙曲线拟合对比
Fig.15 Fitting curve comparison of displacement MVDW
5 工程算例有限元分析
5.1 计算模型
为了进一步研究放大型黏滞阻尼墙的竖向提拉效应对框架结构减震效果的影响，建立结构分析模型为3层钢筋混凝土框架，总质量为14560.2 t，一层、二层、三层质量分别为6295.7 t、4866.0 t、3398.5 t，总高度为22.6 m，层高分别为7.6 m、6 m、9 m。本文采用MATLAB软件建立多质点数值分析模型，并采用本文提出的考虑竖向提拉效应的放大型黏滞阻尼墙力学模型进行纽马克非线性分析计算。简化计算模型如图16所示，图中K表示结构楼层刚度，m表示结构楼层质量，C0表示阻尼系数。
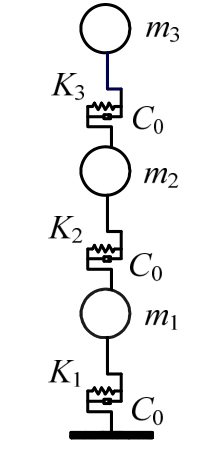
图16 多质点简化模型
Fig.16 Multi-particle model
模型所采用的阻尼墙阻尼系数C0=900 kN·s/m，每层布置2片阻尼墙，考虑竖向提拉效应的单个黏滞性阻尼墙参数设定阻尼系数为
时程分析采用Loma波、Chalfant Valley波和Kocaeli波这3条波，输入峰值为0.3 g。
通过以下四个方案的时程分析结果进行对比分析，方案1：原框架结构(original frame structure，OFS)；方案2：采用普通阻尼墙的减震结构(VDW)；方案3：采用附加3倍位移放大装置的减震结构(MVDW)；方案4：采用考虑竖向提拉效应附加3倍位移放大装置的减震结构(MVDW-V)，分析各方案结构的减震效果。
5.2 减震效应分析
1)层加速度比较。图17为四种方案的结构在Loma波、ChalfantValley波和Kocaeli波作用下，结构各楼层的最大加速度值对比。结果显示，MVDW-V和MVDW的阻尼减震结构的减震效果相比VDW有较大提升，VDW、MVDW和MVDW-V的阻尼减震结构的层加速度值平均减震率分别为13.95%、34.21%、28.06%。虽然MVDW-V的阻尼减震结构的层加速度相对MVDW有所放大，但相对于VDW的减震效果依然显著。
2)层间位移比较。图18为四种方案在Loma波、ChalfantValley波和Kocaeli波作用下，结构各楼层的层间位移值对比。对比结果显示，MVDW-V和MVDW阻尼减震结构的减震效果相比VDW有较大改善，VDW、MVDW和MVDW-V阻尼减震结构的层间位移平均减震率分别为15.46%、43.12%、56.78%。
图17 不同地震波作用下结构层加速度峰值比较
Fig.17 Comparison of peak acceleration of structural layers under different seismic waves
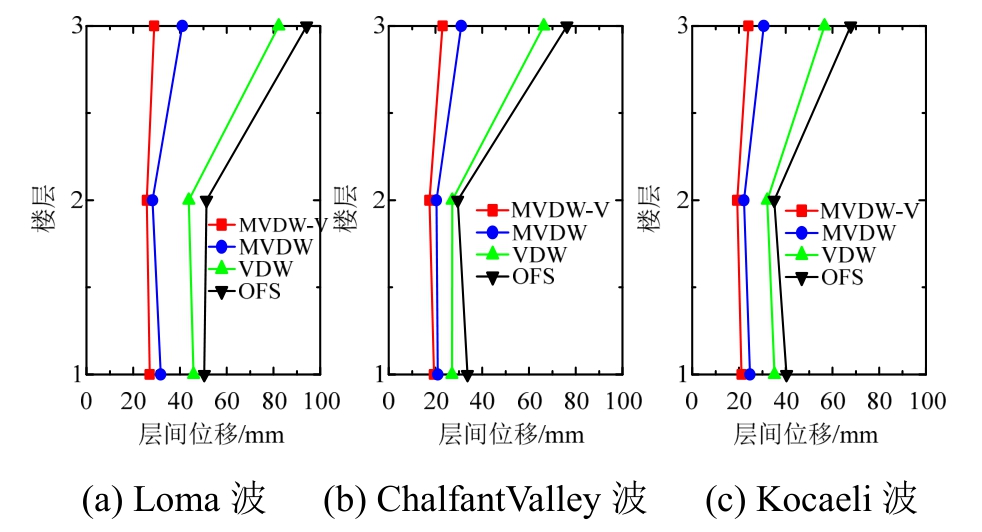
图18 不同地震波作用下结构层间位移峰值比较
Fig.18 Comparison of peak displacement between structures under different seismic waves
5.3 考虑竖向提拉效应的阻尼墙耗能分析
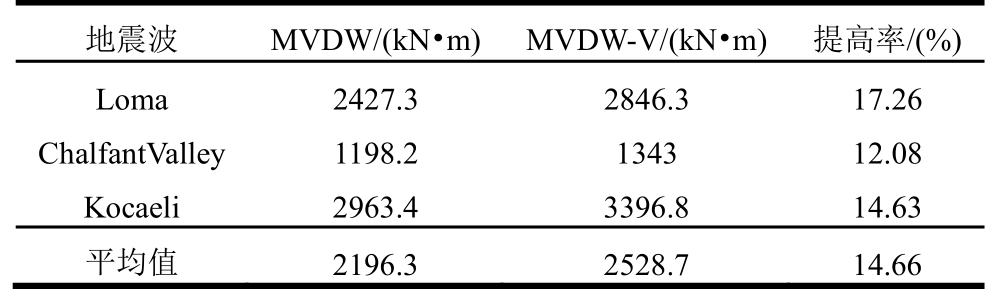
表3为不同地震波作用下，MVDW与MVDW-V阻尼减震结构在Loma波、ChalfantValley波和Kocaeli波作用下阻尼墙耗能的对比，由表中数据可知，MVDW-V比MVDW阻尼减震结构的耗能平均提高14.66%。
表3 不同地震波作用下阻尼墙耗能对比分析
Table 3 Comparison of energy consumption of damping walls under different seismic waves
地震波 MVDW/(kN·m)MVDW-V/(kN·m)提高率/(%)Loma 2427.3 2846.3 17.26 ChalfantValley 1198.2 1343 12.08 Kocaeli 2963.4 3396.8 14.63平均值 2196.3 2528.7 14.66
图19给出了结构底层的阻尼墙在Loma波、ChalfantValley波和Kocaeli波作用下的滞回耗能曲线，可知与MVDW相对比，MVDW-V滞回曲线更加饱满。
图19 不同地震波作用下阻尼墙滞回曲线比较
Fig.19 Comparison of hysteretic curves of damping walls under different seismic waves
6 结论
设计了一种位移放大型的黏滞阻尼墙，并对其进行了理论分析和力学性能试验，对比了两者的耗能效果，最后建立有限元分析模型，并对不同减震结构进行了地震响应分析，主要结论如下：
(1)提出一种放大型黏滞阻尼墙，通过在黏滞阻尼墙上附加位移放大装置，把结构的层间位移放大后再施加到阻尼墙的内钢板上，同时放大阻尼墙两端的相对速度，从而增大阻尼墙的阻尼力，提高其耗能能力。
(2)通过对位移放大装置进行理论分析，提出考虑竖向提拉效应的阻尼力及耗能理论计算公式。分析结果表明，附加η倍位移放大装置的阻尼墙的最大阻尼力与耗能与普通阻尼墙相比可放大接近η1+α倍，而附加η倍位移放大装置并考虑竖向提拉效应的阻尼墙，其等效阻尼系数为ψ=η1+α+(1+η)|tanθ|1+α，耗能效果会随着放大装置转动角度的变化而变化。
(3)以三层框架结构为计算模型，得出附加3倍位移放大装置并考虑竖向提拉效应的减震结构层加速度、层间位移减震效果分别为28.06%、56.78%；附加3倍位移放大装置的减震结构减震效果次之，分别为34.21%、43.12%；普通减震结构的减震效果最差，为13.95%、15.46%。可知附加3倍位移放大装置并考虑竖向提拉响应的减震结构减震效果显著。
[1]周云, 吴从晓, 邓雪松.铅粘弹性阻尼器的开发、研究与应用[J].工程力学, 2009, 26(增刊2): 80－90.Zhou Yun, Wu Congxiao, Deng Xuesong.Development,research and application of lead viscoelastic damper [J].Engineering Mechanics, 2009, 26(Suppl 2): 80－90.(in Chinese)
[2]欧谨.粘滞阻尼墙结构的减振理论分析和试验研究[D].南京: 东南大学, 2006, 25(1): 108－112.Ou Jin.Theoretical and experimental research on structures with viscous damping wall [D].Nanjing:Southeast University, 2006, 25(1): 108－112.(in Chinese)
[3]周云, 粘滞阻尼减震结构设计[M].武汉: 武汉理工大学出版社, 2006.Zhou Yun.Design for energy-dissipated structures with viscous dampers [M].Wuhan: Wuhan University of Technology Press, 2006,(in Chinese)
[4]汪志昊, 陈政清.高层建筑结构中粘滞阻尼器的新型安装方式[J].世界地震工程, 2010, 26(4): 135－140.Wang Zhihao, Chen Zhengqing.New installations of viscous dampers in high rise buildings [J].World Earthquake Engineering, 2010, 26(4): 135－140.(in Chinese)
[5]Julián M Londoño, Simon A Neild, David J Wagg.Using a damper amplification factor to increase energy dissipation in structures [J].Engineering Structures,2015, 84: 162－171.
[6]周云, 汪大洋, 张敏, 等.新型粘滞-弹性阻尼器的力学性能试验与理论研究[J].工程力学, 2013, 30(1):331－338.Zhou Yun, Wang Dayang, Zhang Min, et al.Experimental and theory study on mechanical property of a new viscous-elastic damper [J].Engineering Mechanics, 2013, 30(1): 331－338.(in Chinese)
[7]刘文光, 董秀玲, 何文福, 等.位移放大型阻尼墙减震结构的模型试验与数值分析[J].振动工程学报, 2015,28(4): 601－609.Liu Wenguang, Dong Xiuling, He Wenfu, et al.Dynamic tests and numerical response analysis of energy dissipated structures based on displacement amplification device [J].Journal of Vibration Engineering, 2015, 28(4):601－609.(in Chinese)
[8]陈月明, 刘季.杠杆粘弹性阻尼器及其受控制结构的试验研究[C].第一届全国结构控制会议论文集, 承德,1998.Chen Yueming, Liu Ji.Experimental study on lever viscoelastic damper and controlled structure [C].Proceedings of The First National Conference on Structural Control, Chengde, 1998.(in Chinese)
[9]Constantinou M C, Tsopelas P, Hammel W, et al.Toggle-brace-damper seismic energy dissipation system[J].Journal of Structural Engineering, ASCE, 2001,127(2): 105－112.
[10]Sigaher A N, Constantinou M C.Scissor-jack-damper energy dissipation system [J].Earthquake Spectra, 2003,19(1): 133－158.
[11]Ribakov Y, Reinhorn A M.Design of amplified structural damping using optimal considerations [J].Journal of Structural Engineering, ASCE, 2003, 129(10): 1422－1427.
[12]Berton Stefano, Bolander John E.Amplification system for supplemental damping devices in seismic applications [J].Journal of Structural Engineering,ASCE, 2005, 131(6): 979－983.
[13]Watakabe Tomoyoshi, Fujita Satoshi.Research and development of vibration control device suitable for detached houses by using displacement amplification mechanism [J].Journal of System Design and Dynamics,2009, 3(3): 368－379.
[14]郭彦, 刘文光, 何文福, 等.长周期地震波作用下超高层框架-核心筒减震结构动力响应分析[J].建筑结构学报, 2017, 38(12): 68－77.Guo Yan, Liu Wenguang, He Wenfu, et al.Dynamic response analysis of super high-rise frame-core tube structure under long-period ground motions [J].Journal of Building Structures, 2017, 38(12): 68－77.(in Chinese)
[15]Wen-Hsiung Lin, Anil K Chopra.Earthquake response of elastic SDF systems with non-linear fluid viscous dampers [J].Earthquake Engineering and Structural Dynamics, 2002, 31(9): 1623－1642.
[16]Stefano Berton, John E Bolander.Amplification system for supplemental damping devices in seismic applications [J].Journal of Structural Engineering,ASCE, 2005, 131(6): 979－983.