1968年Ronan Point公寓发生的连续倒塌事故首先引起了工业界及学术界对连续倒塌问题的关注;但由于随后 20余年无重大连续倒塌事故的发生,1978年后连续倒塌问题研究逐渐趋于平淡。随着1995年Alfred P Murrah联邦政府大楼因汽车爆炸引发连续倒塌事故及 2001年世贸大厦由于恐怖袭击的整体倒塌,连续倒塌问题又再次引起了业界的高度重视。提升结构抗连续倒塌性能已然成为结构工程领域的一个重要研究课题[1]。ASCE7―05[2]将连续倒塌定义为局部破坏引发连锁反应,使破坏向结构其他部分扩散,最终导致结构整体坍塌或与初始破坏不成比例的大范围破坏。已有设计指南(GSA2003[3]、DoD2009[4])提出了间接法和直接法两种方法用以设计或者评估建筑结构的连续倒塌能力。间接法主要通过对结构的强度、整体性、冗余度以及延性的最低要求来保证结构的抗倒塌能力。而直接法主要通过具体计算来评估结构的抗倒塌性能,其又可分为局部加强法和替代荷载路径法(ALP)。由于意外事故发生的位置和失效柱个数通常具有不确定性,因此,局部加强法易导致不经济或不安全的设计结果。而 ALP方法独立于初始的局部损伤,主要评估去柱后剩余结构是否依然可以保持整体稳定,所以该方法被广泛用于结构的抗连续倒塌设计。
虽然国外设计指南[3-4]以及国内《建筑结构抗倒塌设计规范》[5]对 RC框架提供了具体的抗倒塌设计方法,但是规范中建议的设计方法和破坏准则多借鉴于抗震设计规范,缺少连续倒塌的相关试验,因此需进一步细化和改进。为此,国内外学者对 RC框架抗连续倒塌性能开展了一系列相关研究:Sasani和 Kropelnicki[6]研究了 RC平面框架的抗连续倒塌性能;Yu等[7-8]研究了中柱缺失后梁柱子结构的抗倒塌性能;Yi等[9-10]通过试验研究了RC多层框架在倒塌过程中的抗力机制。
以上研究极大地提高了人们对RC框架抗倒塌性能及破坏机制的了解,但忽略了楼板对结构抗倒塌的作用。相对于纯框架试验,带板子结构的试验明显偏少:初明进等[11]通过数值模拟对板配筋率、板截面尺寸等关键参数研究了RC单向板在连续倒塌过程中的荷载传递机理;任沛琪[12]通过试验研究了板厚、梁高和抗震设防等级对RC梁-板子结构边柱失效后抗连续倒塌性能影响;Qian和 Li[13-14]研究了角柱及中柱失效工况下楼板对梁-板柱子结构抗连续倒塌的影响。为了研究RC框架在倒数第2边柱失效后的抗倒塌性能,本文设计并试验了1个1/3缩尺的梁-板子结构。为评估楼板对边柱失效工况下RC框架抗倒塌的作用,基于LSDYNA开展了一系列仿真分析。
1 试验概况
1.1 试件设计
原结构根据新加坡设计规范CP65(1999)[15]设计了一栋9层RC框架,并且满足《混凝土结构设计规范》(GB 50010―2010)[16]与 ACI318―08(2008)[17]要求。因为本次研究只考虑在倒数第2个边柱移除后结构的反应,所以子结构只选取靠近失效柱的两跨进行制作。原结构与所选子结构的位置如图1所示。
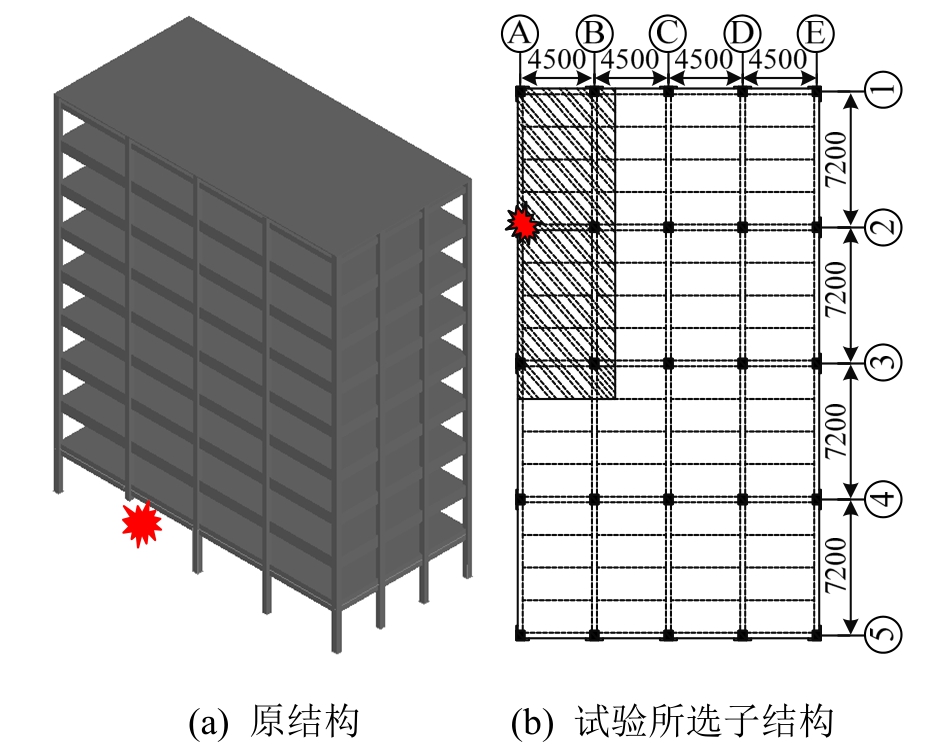
图1 原结构与所选子结构的设计参数
Fig.1 The details of the prototype building and test model
原型结构设计活荷载为2.5 kPa,包含楼板自重的设计恒载为6.0 kPa。考虑到试验场地的限制,依据相似理论进行1/3缩尺后的试件尺寸以及配筋如图2所示。

图2 试件尺寸及配筋
Fig.2 The dimensions and reinforcement details of the specimen
纵梁和横梁的设计跨度分别为2.4 m和1.5 m,纵梁和横梁的截面尺寸分别为 170 mm×100 mm和155 mm×100 mm,现浇板厚为85 mm。因为混凝土保护层厚度为 7 mm,所以采用最大粒径为 10 mm的碎石混凝土。板中纵横向配筋率均为0.2%,图2中R3代表直径为3 mm的光圆钢筋,T10代表直径为10 mm的变形钢筋。
1.2 加载装置及测点布置
如图3所示,试件通过5个钢支撑固定,钢支撑与试验室地面通过预应力螺杆连接。为模拟抽柱前试件受力特性,在A2柱下部安装1个液压千斤顶。楼板上方堆积混凝土块模拟正常工作下的受荷状态,当所有混凝土堆放完成后下部千斤顶行程缓慢地回缩以模拟A2柱缓慢失效。当下部千斤顶与柱底部分离后,如果试件可以达到新的平衡,上部千斤顶对失效柱A2施加外加竖向荷载[18]。
需要说明的是,楼板上堆积的混凝土块设计重量为120 kN。因此,板的等效压力为16.7 kPa,是设计指南 DoD(2009)[3]提出设计工作压力(1.2DL+0.5LL)的两倍。
为了测量试件的各项性能,在试件内部和外部安装了一系列测量装置。通过一系列位移传感器(LVDT)测量与失效柱相连梁的竖向位移及楼板变形;在失效柱上部与下部千斤顶处各安装荷载传感器;A1柱水平安装1个LVDT用于测量A1柱的水平位移;试件梁的纵向钢筋以及板内钢筋上各安装一系列应变片,用于记录钢筋应变的分布与变化。

图3 试验装置
Fig.3 Test setup of test specimen
2 试验结果及分析
2.1 荷载-位移曲线
RC梁-板子结构的荷载-位移曲线如图4所示。ab段为下部千斤顶释放轴力阶段,荷载主要由梁机制的抗弯承载力承担。达到b点时,下部千斤顶与失效柱分离,bc段由上部千斤顶施加附加竖向荷载。达到c点时,梁端形成塑性铰,受拉钢筋屈服。cd段承载力提升主要是由于钢筋强化及板与梁中开始发展压拱机制。此后进入de阶段,承载力主要由板中钢筋发展拉膜作用提高。e点之后结构抗力主要由梁中纵筋发展悬链线机制及板钢筋继续发展拉膜作用共同承担,并且随着位移的增大,悬链线机制的贡献也越大。到达f点时,板钢筋出现断裂,承载能力也出现陡降。继续加载承载能力继续上升,到达g点时梁中钢筋被拉断,承载能力下降明显,试验停止。
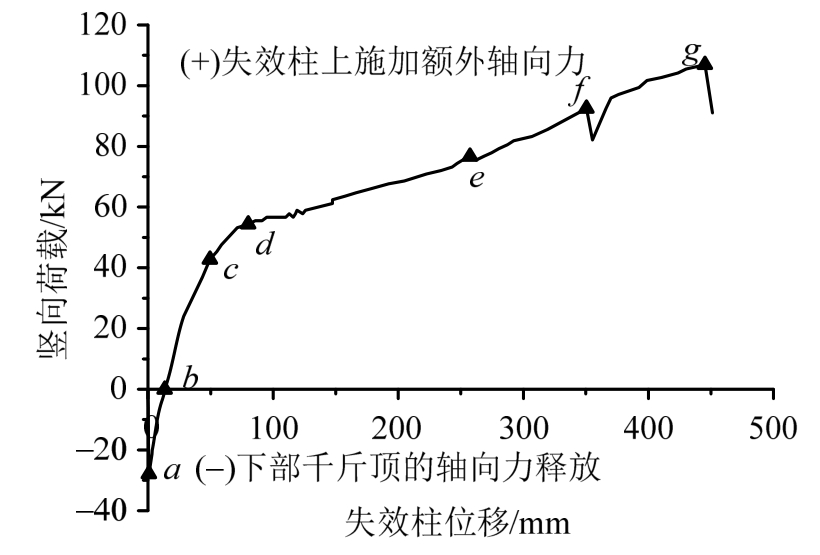
图4 荷载-位移曲线
Fig.4 Load-displacement curve
2.2 试件破坏过程与破坏形态
施加 120 kN的均布荷载后,下部千斤顶测得的轴力为-28 kN。随后,下部千斤顶开始逐渐回缩模拟A2柱的缓慢失效。随着下部轴力的释放,A2柱竖向位移不断增加。当轴力减小到-8 kN时,梁端和板面同时出现裂缝。当 A2柱竖向位移达到13 mm时,下部荷载传感器显示为0 kN,表明A2柱下部千斤顶与A2柱完全分离。图5为释放下部轴力后试件破坏形态,板端和梁端混凝土开裂,但裂缝宽度均小于0.7 mm。
如图5所示,试验中观察到靠近边柱梁端裂缝宽度大于靠近失效柱 A2梁端裂缝宽度。而在文献[19]中试验现象为靠近失效柱梁端裂缝宽度与靠近边柱裂缝宽度相近。这是由于文献[19]试验中仅在失效柱上部施加集中荷载,然而本次试验还考虑了楼板实际工作时的均布荷载,使得荷载传递机理发生了改变,但更加接近实际情况。此外,由于试件在完全释放A2柱轴力后能够重新保持稳定,说明只瞬间去除一个边柱,该子结构不会发生倒塌,因为试验中施加的配重已经考虑了瞬间去除柱产生的动力效应(假设动力放大系数为2.0)。

图5 释放下部轴力后试件开裂形态
Fig.5 Crack pattern of specimen after fully released the axial force
为了进一步研究子结构在倒塌过程中荷载传递机理和破坏模式,在下部千斤顶与A2柱分离后,上部千斤顶开始施加附加竖向荷载(出于安全考虑,使用千斤顶仅在A2柱上部施加外加轴力,而不是在楼板上堆积更多的重物)。上部千斤顶施加外加集中荷载(在图 4中由正值表示)。随着集中荷载的增加,梁和板中形成更多裂缝。当失效柱竖向位移达到50 mm,结构抗力为43 kN,观察到梁纵向钢筋屈服。位移进一步增加到 71 mm时,测得大小为53 kN的第一峰值荷载。随后结构抗力并没有明显减少,承载能力随着失效柱竖向位移的增加而继续增加。当失效柱竖向位移达到451 mm时,测得极限承载力为107 kN,此时,A3柱梁端上部钢筋发生断裂,试件承载能力下降明显而停止试验。图6为移除混凝土块(重物荷载)后试件的破坏形态。
如图6所示,由于在悬链线阶段梁A1-A2中产生较大水平拉力,导致柱A1节点产生严重的剪切破坏。虽然靠近柱A3梁端观察到上部钢筋断裂,但是在靠近柱A1和A2的梁端并没有发生钢筋断裂。由于在大变形阶段,板中钢筋发展拉膜作用导致梁A1-B1承受很大的扭矩而发生扭转破坏,此外沿着梁A1-B1,部分板中钢筋也发生断裂。另外,B2柱附近板面混凝土保护层剥落严重。从底部看,在靠近柱A1和A3的梁端也观察到严重混凝土破碎。


图6 试件的破坏形态
Fig.6 Failure mode of the specimen
2.3 角柱水平位移结果
如上所述,由水平安装的位移传感器监测 A1柱的水平位移,用以间接分析试件主要抗力机制的转换。图7为A1柱的水平位移与A2柱的竖向位移曲线。首先在施加均布荷载完成后观察到曲线由0点下降到a点,表明A1柱由于承受部分弯矩作用而向外移动0.3 mm(负值代表向外移动)。随着下部千斤顶的回缩或者上部千斤施加附加竖向荷载,A1柱继续向外移动。当到达b点时,A1柱测得最大负向移动位移-1.7 mm,此时A2柱的竖向位移为86.8 mm。对比上述裂缝发展及荷载-位移曲线结果,此位移对应于RC梁和楼板发展压拱机制阶段。

图7 A1柱的水平位移
Fig.7 Horizontal movement of column A1
b点之后,向外水平位移开始减小。当到达c点时,A1柱回到平衡位置,此时,柱A2竖向位移为246.5 mm。之后,随着柱A2竖向位移的继续增加,柱A1开始向内移动。最终到达d点时,测得最大向内位移10.1 mm。柱A1向外和向内的转换主要是由RC梁由压拱机制向悬链线机制转换。
2.4 梁与板的变形
试件在不同阶段与失效柱相连梁 A1-A3和B2-A2的变形如图8所示。在图8(a)中观察到在试验期间梁A1-A3中出现双曲率(双线性)现象。在试件的最终破坏形态中,靠近柱A3和A1的梁端的旋转角比DoD (2009)[3]中定义的旋转角小(注:旋转角定义为失效柱的竖向位移与梁净跨之比[3])。然而,靠近中心柱A2的梁端旋转角稍大于规范预测值,这与文献[20]的结果不同。这主要是由于在板上施加了均布荷载,改变了结构的破坏模态,导致在试验中梁的悬链线更接近于曲线型而集中荷载单独作用时梁通常产生直线型悬链线。图8(b)为横梁B2-A2在不同阶段的变形。尽管在加载初期,梁A1-A3可以给梁B2-A2在A2端提供一定的旋转约束,但是随着位移的增加,梁B2-A2的最终变形和破坏模式与悬臂梁类似。

图8 梁A1-A3与B2-A2的变形
Fig.8 Deformation of beams A1-A3 and B2-A2
2.5 应变计结果
梁A1-A3纵向钢筋应变如图9所示,与文献[19]中的试验结果类似。图9(a)为梁上部钢筋应变,由于受梁变形双曲率(双线性)影响,靠近柱A1与A2梁端为拉应变,靠近柱A2梁端为压应变。图9(b)为梁底部钢筋应变,靠近柱A2梁端测量到拉应变,靠近柱A1与A2梁端为压应变。这是由于在移除柱 A2之后,梁端弯矩方向出现反转。图10为梁B2-A2纵向钢筋应变结果。只在靠近柱B2梁端观察到钢筋屈服,所以应变结果也证实了梁B2-A2更接近于悬臂梁工作机理。
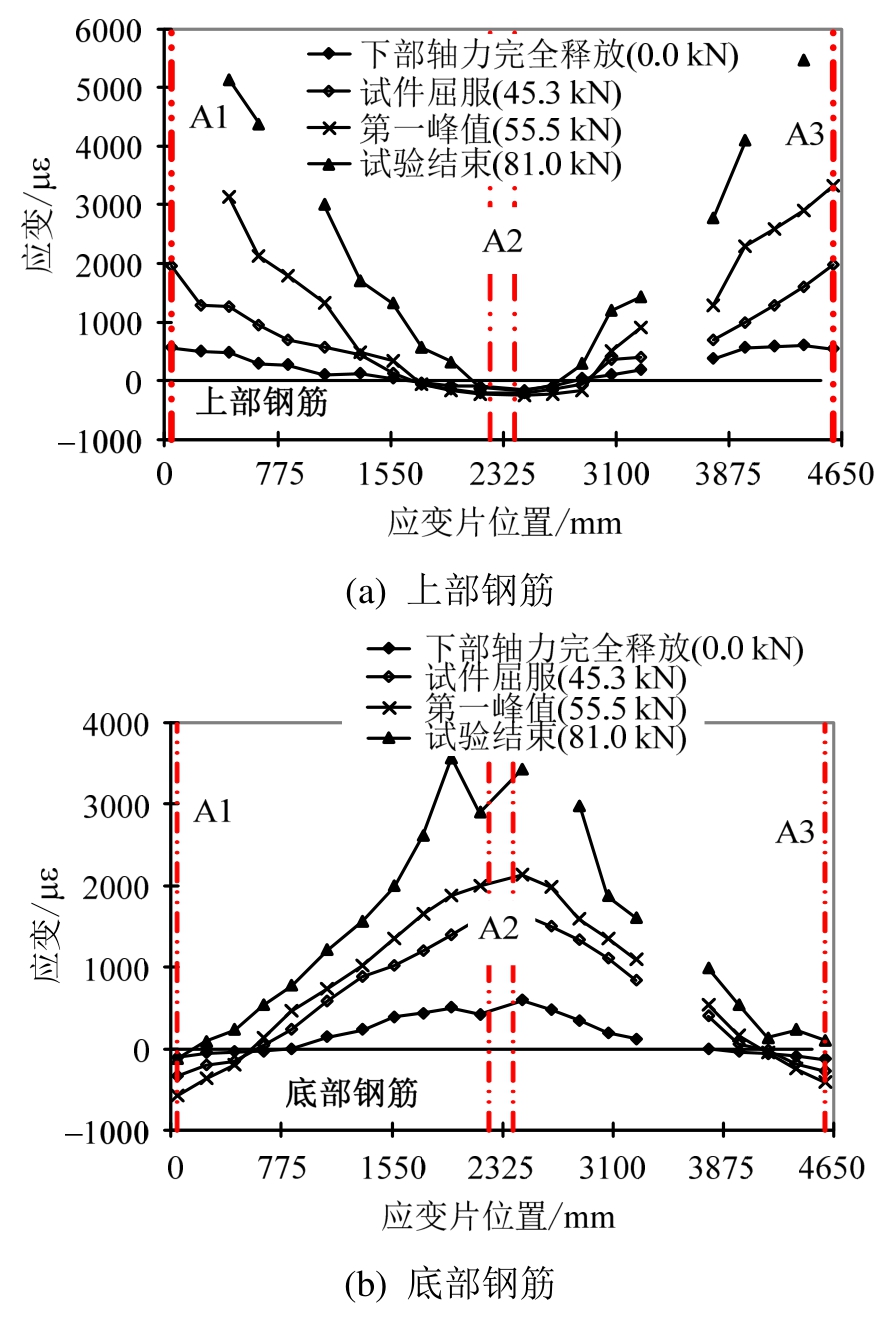
图9 梁A1-A3钢筋应变
Fig.9 Strain varying of longitudinal reinforcement in beam A1-A3

图10 梁B2-A2钢筋应变变化
Fig.10 Strain varying of longitudinal reinforcement in beam B2-A2
图11为RC梁-板子结构破坏时板的变形图,由底部位移计测得结果通过 MATLAB插值后绘制而成。由图11(a)可知,整个板面变形为曲面,竖向位移均匀向四周扩散。由图11(b)可知,左右两块板变形较为对称,靠近失效柱与梁边缘变形梯度较缓,板中部变形梯度较急。由此可知,靠近失效柱与梁边缘板变形曲率较大,板中部变形曲率较小。

图11 试件破坏时板变形 /mm
Fig.11 The deformation shape of specimen at failure stage
图12显示出了在试验结束时板内钢筋应变分布。从图中可知,板内钢筋应变分布并不均匀,靠近柱A1与A3区域板上部拉应变较大(T形梁机制)。应变结果同时也表明,混凝土梁翼缘有效宽度大于2.9ds(ds为板的厚度)。板底部钢筋结果表明板中部钢筋具有较大的拉应变,证明板中拉膜作用主要由底部钢筋提供。

图12 试验结束时板内钢筋应变分布 /με
Fig.12 Strain distribution in the slab reinforcement at final test
3 有限元分析
3.1 建模过程
在本次研究中采用非线性有限元显式动力分析软件LSDYN模拟试件的受力过程[20-21]。混凝土与钢板采用8节点6面体单元(Soild164)建模并选用单点积分;钢筋采用 2节点 Hughes-Liu梁单元(Beam161)建模并选用 2×2高斯正交积分。钢筋与混凝土界面由关键字*CONSTRAINED_BEAM_IN_SOLID建模,该方法优点是可以准确模拟混凝土破坏后释放对钢筋的约束,是一种较为理想模拟钢筋与混凝土协同工作的模型。
在有限元分析中,材料模型的选取对结果的可靠性和精确性非常重要。目前LSDYNA提供了很多混凝土本构模型,例如*MAT_CONCRETE_DAMAGE_REL3、*MAT_JOHNSON_HOLMQUIST、*MAT_WINFRITH_ CONCRETE以及*MAT_CSCM_CONCRETE等。本次研究选用连续面盖帽模型*MAT_CSCM_CONCRETE(MAT159)。MAT159本构模型的特点是结合最大主应变破坏准则的应用,可以有效地模拟准静态和爆炸条件下RC结构的实际反应和损伤模式。同时MAT159可以有效地捕捉材料尖峰软化、剪切膨胀、约束效应和应变率硬化等力学特性。钢筋与钢板使用各向同性的弹塑性本构模型*MAT_PIECEWISE_LINEAR_PLASTICIT(MAT024),该材料本构模型用于假定拉伸和压缩相同应变的材料。通过前期研究表明,虽然通过细化网格可以提高计算精度,但会使计算时间成指数增加[22-25]。经过试算,本次数值模拟所有单元网格均采用尺寸30 mm时收敛和准确性都较好,试件模型如图13所示。

图13 LSDYNA中的几何模型
Fig.13 Geometric model in LSDYNA
3.2 模型验证
采用与试验一致的加载方式对有限元模型进行加载,计算结果如图14所示。由图可知,模拟的荷载-位移曲线与试验结果趋势接近。模拟初始刚度值为1.51 kN/m而试验值为1.15 kN/m,模拟刚度较试验刚度高了31%。这主要是因为数值模拟过程中没有考虑混凝土初始损伤(比如微裂缝)等因素,使得模拟的初始刚度大于试验值。试验模拟所得的屈服荷载分别为43 kN与40 kN,误差为7.5%;试验第一峰值荷载与模拟第一峰值荷载分别为 53 kN与59 kN,误差为10%;试验与模拟的极限荷载分别为107 kN与104 kN,误差为3%。由图14可知,在达到第一峰值荷载前,模拟值和试验值有一定差别,但在第一峰值后模拟荷载-位移曲线与试验荷载-位移曲线吻合的更好。
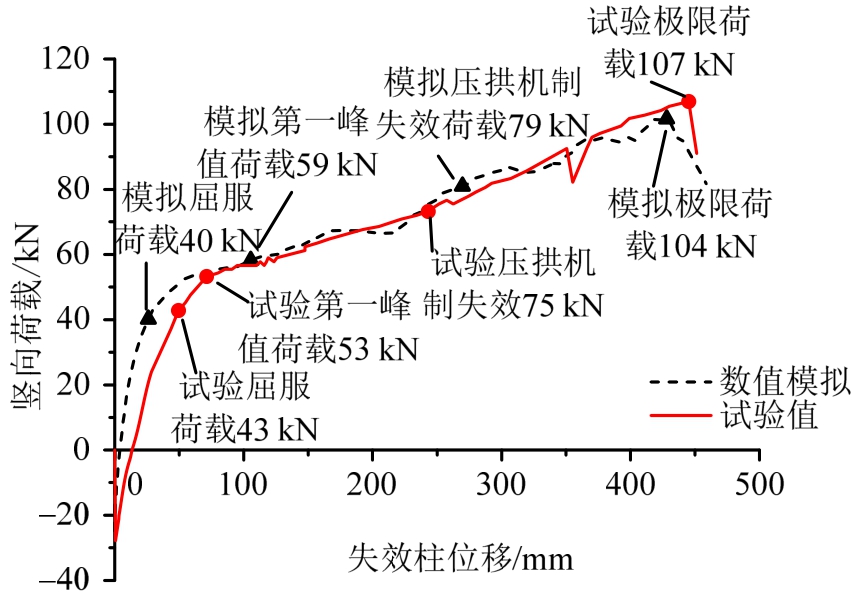
图14 荷载-位移曲线对比
Fig.14 Comparison of the load- displacement curves
图15对比A1柱的试验水平位移曲线与模拟结果。由图可知,从试验向外位移峰值到压拱机制失效点之间的模拟曲线与试验曲线存在一定偏差,但趋势接近。产生原因可能是数值模型在5个钢支撑处与实际试件有一定偏差以及试验中使用的位移计灵敏度等。试验向外峰值位移与模拟向外峰值位移分别为1.8 mm与2.5 mm,误差为29%;试验压拱机制失效竖向位移与模拟压拱机制失效竖向位移分别为246.5 mm与250.2 mm,误差为1.6%;试验向内峰值位移与模拟向内峰值分别为10.1 mm与9.9 mm,误差为0.6%。总体上,该模型在预测水平位移上的精度较好,同时也表明该数值模型的抗力机制与试件各阶段的抗力机制一致。
图16为数值模型的最终破坏形态。对比图16与图6结果表明:总体来说,数值模型可以准确模拟试件的裂缝形式。如图16(c)所示,数值模型准确模拟了柱A1节点剪切破坏及A3柱附近板中钢筋的断裂。因此,该验证后的数值模型可以用来研究边柱失效工况下楼板作用。
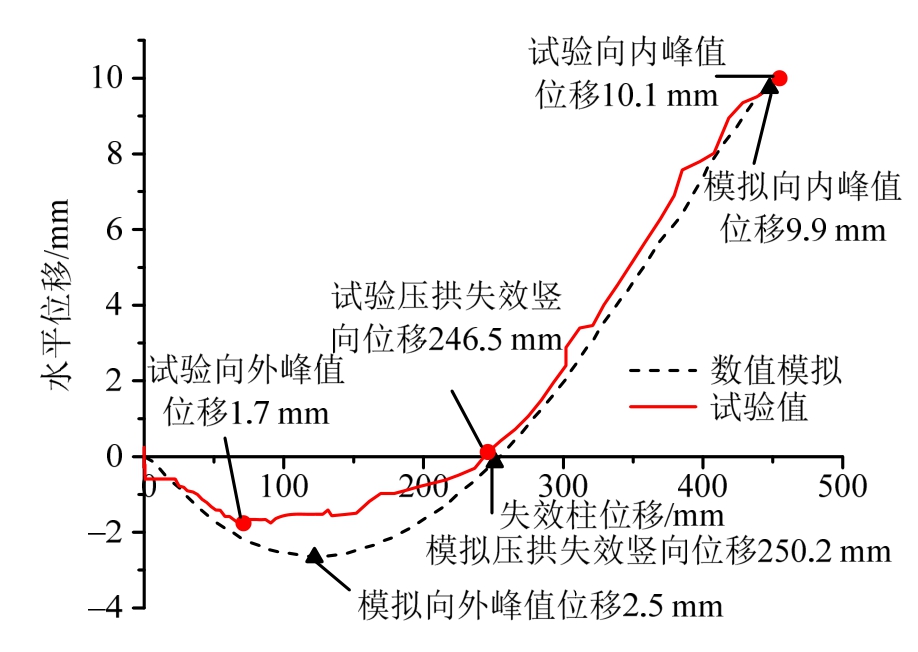
图15 水平位移曲线对比
Fig.15 Comparison of the horizontal displacement curves

图16 试件的数值模型破坏形态
Fig.16 Failure mode of test specimen from numerical models
3.3 拓展参数分析
基于所建立的有限元模型,对试件进行拓展参数分析。为研究楼板对RC框架荷载传递机理以及抗力机制的影响,将原模型中的楼板去除,把均布荷载施加在梁上,模型的破坏形态如图17所示。
由图17可知,梁A在结构最终破坏时发展了较大的拉应变;空框架的破坏主要集中于梁端钢筋受拉断裂,以及边柱发生剪切破坏。图18为有限元模型中带板框架与空框架荷载-位移曲线。由图可知,楼板不但可以提高RC框架的刚度,而且还提高其屈服承载力与极限承载力分别高达 65%和61%。
RC框架抗力分解如图19所示。初始阶段,楼板对抗力的贡献达到71.5%。随着位移的增加,梁中压拱效应的增大,使得梁对抗力贡献增加,最大抗力贡献占比为51.4%。随着梁中受压区混凝土的压碎,梁的抗力开始下降,同时楼板中钢筋开始发展拉膜作用,使得楼板抗力贡献逐渐上升。楼板在这个阶段的最大抗力贡献占比为75.1%。在竖向位移达到400 mm时,板内发生钢筋断裂,梁中发展的悬链线效应使得梁抗力贡献开始增大。结构破坏时,梁与板贡献抗力分别为34.6%与65.4%。在整个RC框架倒塌过程中,板对抗力贡献平均约占65%。

图17 空框架有限元模型破坏形态
Fig.17 Failure mode of bare frame from numerical model
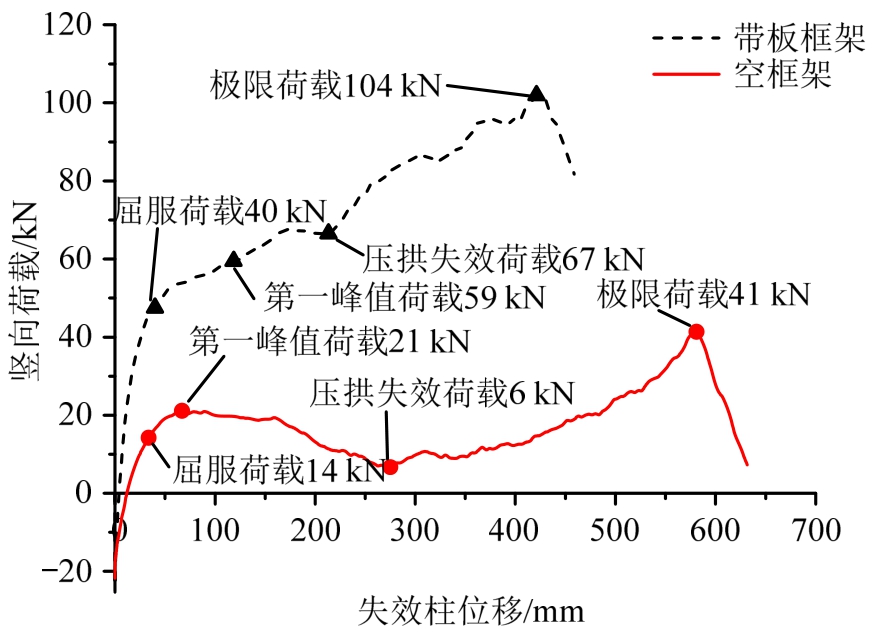
图18 荷载-位移曲线
Fig.18 Load-displacement curves

图19 抗力分解
Fig.19 Resistance capacity decomposition
4 结论
试件完全释放轴力后能够保持稳定,且裂缝较少。说明在柱子突然失效工况下,假设动力放大系数(DIF)为2.0时,结构不会发生倒塌。
由试验结果可知,在RC梁-板子结构倒数第2个边柱失效工况下结构先由梁A1-A3与B2-A2中梁机制提供抗力;再由梁A1-A3及板中形成的压拱机制提供抗力,随后有板中发展拉膜作用提供抗力;最后由梁A1-A3悬链线机制与板拉膜机制共同作用提供抗力。
由于在试件上施加均布荷载,使得梁A1-A3在最终破坏形态中出现曲线性悬链线作用。从而加剧了柱A1与A3区域的破坏,减轻了柱A2区域的破坏,这与先前试验研究结果不一致。表明施加均布荷载会改变试件的荷载传递机理与破坏形态。
基于 LSDYNA建立的数值模型可以很好地预测RC梁-板子结构的屈服荷载、第一峰值荷载、压拱机制、失效位移、极限荷载与极限位移,同时还可以准确预测结构的抗力机制与破坏形态。
通过对有限元模型拓展分析可以得出:楼板提高RC框架屈服承载力与极限承载力分别高达65%和61%,在RC框架倒塌过程中楼板的平均抗力贡献约占65%。
[1]胡晓斌, 钱稼茹.结构连续倒塌分析与设计方法综述[J].建筑结构, 2006, 36(增刊1): 573-577.Hu Xiaobing, Qian Jiaru.Overview of analysis and design approaches for progressive collapse of structural[J].Building Structure,2006, 36(Suppl): 573-577.(in Chinese)
[2]ASCE/SEI.Minimum design loads for buildings and other structures[S].Reston: Structural Engineering Institute- American Society of Civil Engineers, 2010.
[3]DoD.Design of structures to resists progressive collapse[S].Washington DC: Department of Defense, 2009.
[4]GSA.Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects[S].Washington DC: General Service Administration, 2003.
[5]CECS 392—2014, 建筑结构抗倒塌设计规范[S].北京: 中国计划出版社, 2015.CECS 392—2014, Code for design of anti-collapse of building structures[S].Beijing: China Planning Press,2015.(in Chinese)
[6]Sasani M, Kropelnicki J.Progressive collapse analysis of an RC structure[J].The Structural Design of Tall and Special Buildings, 2008, 17(4): 757-771.
[7]Yu J, Tan K.Structural behavior of RC beam-column sub-assemblages under a middle column removal scenario[J].Journal of Structural Engineering, 2013,139(2): 233-250.
[8]郭义庆, 喻君.单柱失效下结构连续倒塌的动力响应分析[J].工程力学, 2017, 34(4): 72-77.Gou Yiqing, Yu Jun.Dynamic structural response of progressive collapse under a single-column-removal scenario[J].Engineering Mechanics, 2017, 34(4): 72-77.(in Chinese)
[9]Yi W J, He Q F, Xiao Y, et al.Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures[J].ACI Structural Journal,2008, 105(4): 433-439.
[10]易伟建, 张凡榛.钢筋混凝土板柱结构抗倒塌性能试验研究[J].建筑结构学报, 2012, 33(6): 35-41.Yi Weijian, Zhang Fangzhen.Experimental study on collapse performance of a RC flat plate frame structure[J].Journal of Building Structures,2012, 33(6): 35-41.(in Chinese)
[11]初明进, 周育泷, 陆新征, 等.钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J].土木工程学报, 2016,49(2): 31-40.Chu Mingjin, Zhou Yulong, Lu Xingzhen, et al.An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse[J].China Civil Engineering Journal, 2016, 49(2): 31-40.(in Chinese)
[12]任沛琪.钢筋混凝土梁-板子结构在边柱失效下的连续倒塌试验研究[D].北京: 清华大学, 2015.Ren Peiqi.Experimental study on the progressive collapse resistance of reinforced concrete beam-slab substructures under an edge-column-removal scenario[D].Beijing: Tsinghua University,2015.(in Chinese)
[13]Qian K, Li B.Slab effects on response of reinforced concrete substructures after loss of corner column[J].ACI Structural Journal, 2012, 109(6): 845-855.
[14]Qian K, Li B.Experimental study of drop-panel effects on response of reinforced concrete flat slabs after loss of corner column[J].ACI Structural Journal, 2013, 110(2):319-329.
[15]CP 65.Structural use of concrete, Part 1.Code of practice for design and construction[S].Singapore Standard, Singapore, 1999.
[16]GB 50010-2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010-2010, Code for design of concrete structures[S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[17]ACI Committee 318.Building code requirements for structural concrete and commentary[S].American Concrete Institute, Farmington Hills, MI, 2008.
[18]钱凯, 罗达, 贺盛, 等.钢筋混凝土框架结构底部相邻两柱失效的抗连续倒塌性能研究[J].建筑结构学报,2018, 39(1): 61-68.Qian Kai, Luo Da, He Sheng, et al.Progressive collapse performance of reinforced concrete frame structures subjected to ground two-column removal scenario[J].Journal of Building Structures,2018, 39(1): 61-68.(in Chinese)
[19]Qian K, Li B, Ma J X.Load-carrying mechanism to resist progressive collapse of RC buildings[J].Journal of Structural Engineering, 2015, 104(2): 04014107.
[20]Anh T P, Namyo S L, Tan K H.Investigations of tensile membrane action in beam-slab systems under progressive collapse subject to different loading configurations and boundary conditions[J].Engineering Structures 2017, 150(1): 520-536.
[21]秦卫红, 冯鹏, 施凯捷, 等.玻璃纤维加固梁柱结构抗连续倒塌性能数值分析[J].同济大学学报(自然科学版), 2014, 42(11): 1647-1653.Qin Weihong, Feng Peng, Shi Kaijie, et al.Numerical analysis of progressive collapse behavior of glass fiber reinforced polymer strengthened beam-column structures[J].Journal of Tongji University (Nature Science), 2014,42(11): 1647-1653.(in Chinese)
[22]高佳明, 刘伯权, 黄华, 等.带板钢筋混凝土框架连续倒塌理论分析[J].工程力学, 2018, 35(7): 117-126.Gao Jiaming, Liu Boquan, Huang Hua, et al.Theoretical analysis on the progressive collapse of RC frame structures with slabs[J].Engineering Mechanics, 2018,35(7): 117-126.(in Chinese)
[23]王景玄, 王文达, 李华伟.钢管混凝土平面框架子结构抗连续倒塌精细有限元分析[J].工程力学, 2018,35(6): 105-114.Wang Jingxuan, Wang Wenda, Li Huawei.Refined finite element analysis of progressive collapse of planar frames with concrete-filled steel tubular columns[J].Engineering Mechanics, 2018, 35(6): 105-114.(in Chinese)
[24]Qian K, Weng Y H, Li B.Impact of two columns missing on dynamic response of RC flat slab structures[J].Engineering Structures, 2018, 177(15): 598-615.
[25]Qian K, Weng Y H, Li B.Improving behavior of reinforced concrete frames to resist progressive collapse through steel bracings[J].Journal of Structural Engineering, 2019, 192(2): 0002263.