预制混凝土构件间连接节点是预制混凝土结构中最易遭受破坏的部位,其连接节点的可靠与否直接影响到整体结构的受力性能和抗震性能[1-2]。近年来,随着预制构件间连接技术的一发展,一种新型的钢-混凝土预制混合梁(简称预制混合梁)受到国内外学者的广泛关注。与组合梁不同,钢-混凝土预制混合梁是由钢梁和混凝土梁通过连接节点组合而成的预制梁,钢梁通常位于预制梁端部。相比传统的预制混凝土梁,预制混合梁充分发挥了端部钢梁适合装配化施工的特点,具有施工便捷、建造周期短和造价低等优势[3-4]。
目前,国内外学者对预制混合梁进行了相关的试验和理论研究。Korkmaz和Tankut[5]提出了预制混凝土梁间采用焊接钢板的混合连接方式并进行了试验研究。结果表明,采用混合连接方式的预制混凝土梁构件具有较好的延性。Yang等[6]提出了一种钢梁和混凝土梁间非螺栓连接形式,并通过试验研究了其受弯性能。试验结果表明,连接节点能满足刚性节点连接要求,连接节点区域未出现剪切裂缝和劈裂裂缝。Guo等[7]对端部内嵌槽钢的混凝土梁进行了试验研究,结果表明,当槽钢埋入长度与槽钢截面高度比值在0.8~1时,该新型梁失效模式表现为梁端混凝土破坏,极限受弯承载力相对较高。刘昌永等[8]完成了两端带钢接头的预制混合梁的受弯试验。研究结果表明,预制混合梁的受弯性能与普通预制混凝土梁类似,节点连接可靠,未出现明显滑移。焦安亮等[9]提出了一种端部带钢接头的预制混合梁形式,并完成了6个足尺节点试件的低周往复加载试验,结果表明,预制混合梁的破坏模式与普通预制混凝土梁相似,钢接头连接可靠,节点具有较好的延性。
综上所述,现有文献主要集中在预制混合梁的静力受弯和受剪性能研究。而有关预制混合梁在静力荷载作用下的变形性能研究则鲜见报道。此外,由于预制混合梁的特殊构造,目前我国规范尚无该类型预制构件的挠度计算公式,而现有文献一般推荐采用差分法、图解法、有限单元法、奇异函数法和分段独立一体化积分法等来求解变截面梁的变形[10-11]。为此,本文对两端固定边界条件下的预制混合梁进行了静力加载试验,分析其受弯性能和变形机理;充分考虑预制混合梁的构造特征,利用奇异函数法建立预制混合梁的挠曲线计算公式,提出该类型预制混合构件挠度计算方法,分析不同参数对预制混合梁变形性能的影响。
1 试验概况
1.1 试件设计
试验设计了4个预制梁试件,包括3个预制混合梁试件PHSC1~PHSC3和1个普通预制混凝土梁试件PC1。各试件几何尺寸及构造见图1。所有试件净跨均为 3600 mm,混凝土梁段截面宽度为300 mm,高度为400 mm,H形钢梁段截面尺寸为H300×150×8×10。各试件箍筋直径为10 mm,间距为 100 mm,加载点及连接节点区域箍筋间距为50 mm。预制混合梁连接节点处端板和连接板厚10 mm,端板中部设有6个直径16 mm的抗剪栓钉,高度 90 mm,间距 100 mm。实测混凝土立方体抗压强度平均值为 38.8 MPa,弹性模量为Ec=31.5 GPa;实测型钢翼缘和腹板屈服强度分别为361 MPa和363 MPa,抗拉强度分别为521 MPa和488 MPa,弹性模量为Es=198 GPa;纵筋和箍筋的屈服强度分别为403 MPa和475 MPa,抗拉强度分别为 527 MPa和 630 MPa。试件 PHSC1、PHSC2和PHSC3的钢梁段长度Ls分别为200 mm、400 mm和600 mm。

图1 试件几何尺寸及构造
Fig.1 Dimensions and details of specimens
试件PHSC1~PHSC3连接节点的详细构造如图2所示。H型钢梁上下翼缘在连接节点处通过端板与上下连接板相连,混凝土梁内纵筋与连接板采用焊接连接;为保证端板与混凝土交界面处的剪力传递,在端板内侧上下连接板高度范围内焊接6个栓钉,同时连接节点处箍筋由穿过连接板内预留孔的2个U形箍筋焊接而成。

图2 连接节点构造
Fig.2 Schematic diagram of connection joint construction
1.2 试验加载与量测
图3为试验加载装置和测点布置。试验前通过地锚螺栓和压梁将试件两端刚性块体与地面固定,使之成为梁端的固定支座。试验中采用 100 t千斤顶对梁跨中进行分级加载,试件开裂前,每级荷载增量为 20 kN;开裂后每级荷载增量为 30 kN;试件屈服后改为位移控制加载,每级位移增量10 mm。当荷载下降至峰值荷载的85%时,停止加载。

图3 试验加载装置和测点布置
Fig.3 Test setup and layout of measurement points
试验量测主要内容有:梁跨中竖向荷载、梁跨中挠度、梁沿跨度方向的竖向变形、支座变形、钢梁及钢筋的应变值。位移计 D1~D7沿预制梁轴线方向依次布置,以量测预制梁沿跨度方向的竖向变形;百分表B1~B6用于测量梁端刚性块体的水平位移和整体转动。试件的主要测点布置见图3。
2 预制混合梁挠曲线计算公式建立
2.1 基本假定
预制混合梁由两端钢梁和中部混凝土梁通过连接节点组合而成。在公式推导中,定义系数μ为单侧钢梁段长度与预制混合梁跨度的比值(简称长跨比),系数α为钢梁截面抗弯刚度与混凝土截面抗弯刚度的比值(简称抗弯刚度比),系数γ为钢梁截面抗剪刚度与混凝土截面抗剪刚度的比值(简称抗剪刚度比)。系数μ、α和γ的计算式分别如式(1)、式(2)和式(3)所示:
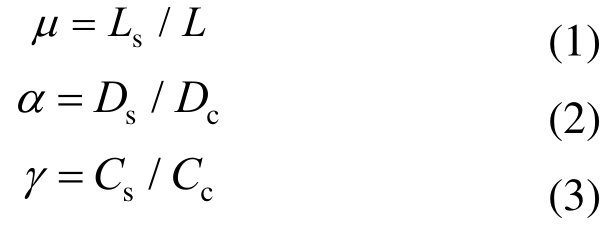
式中:μ的取值范围为 0<μ<0.5;Ls为预制混合梁单侧钢梁段长度;L为预制混合梁跨度;Ds和Dc分别为钢梁和混凝土的截面抗弯刚度;Cs和Cc分别为钢梁和混凝土的截面抗剪刚度。
预制混合梁计算模型如图4(a)所示,挠曲线计算公式推导时采用以下基本假定:
1)预制混合梁在跨中竖向集中荷载作用下变形采用弹性分析方法,混凝土梁段刚度计算时,截面惯性矩按匀质混凝土全截面计算。
2)钢梁和混凝土梁间连接节点假定为刚性节点[12]。

图4 预制混合梁计算模型
Fig.4 Calculation model of precast hybrid beam
2.2 奇异函数的性质
奇异函数又称为麦考利函数,其定义如下[13]:

奇异函数的微积分规律如下:
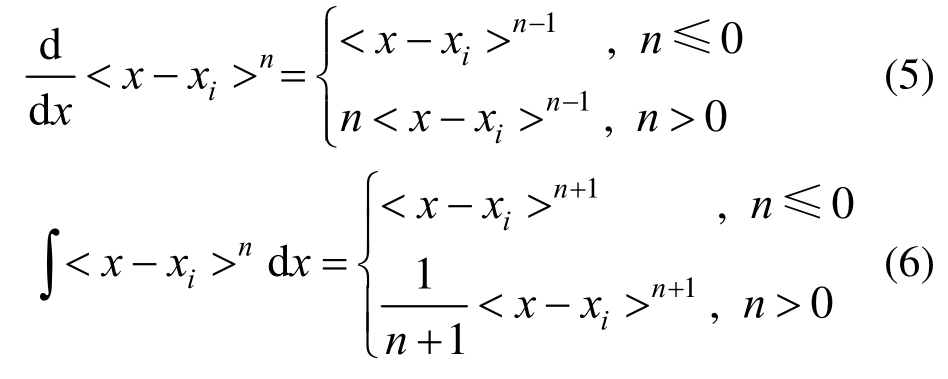
2.3 公式推导
由于预制混合梁几何形状、杆件截面尺寸和弹性模量均对称于跨中截面,故取半结构进行分析,其计算简图如图4(b)所示。
两端固支等截面梁在对称载荷q(x)作用下,其平衡方程及其边界条件为[14]:
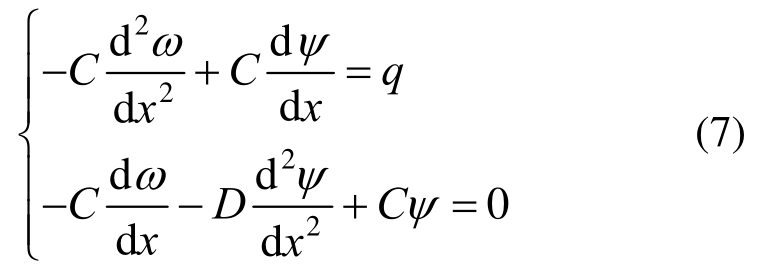
在x=0及x=L处:
式中:ω及ψ为广义挠度与转角;广义载荷q为单位长度内的载荷在y轴上的投影。
令ω0为预制混合梁在忽略剪切变形情况下的挠度,则ω0满足下列方程和边界条件:
当x=0时,ω0=0,ω0′=0;当![]() 时:
时:
若取![]()
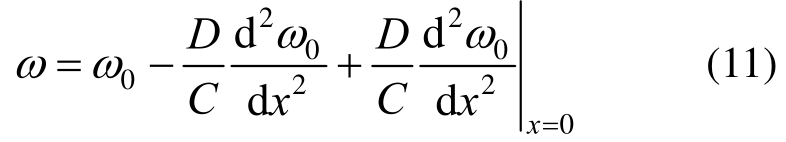
当式(7)和式(10)均满足时,通过式(11)即可求解预制混合梁的挠度。此外,预制混合梁中由剪切变形引起的附加挠度ω1为:
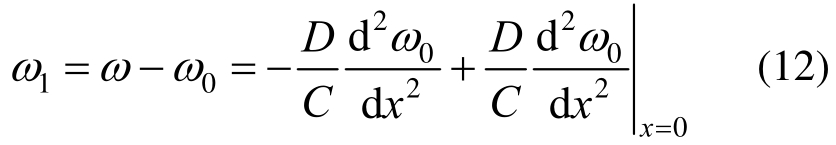
以下通过对式(7)中抗弯刚度和抗剪刚度进行修正,以考虑预制混合梁沿梁长方向截面的变化。
对任意非均质材料变截面梁,其截面抗弯刚度的倒数![]() 可表示为下列奇异函数:
可表示为下列奇异函数:
式中:![]()
截面抗剪刚度的倒数1/C(x)可表示为下列奇异函数:
式中![]()
由式(2)和式(13)可得预制混合梁截面抗弯刚度的倒数表达式,如式(15)所示:
由式(3)和式(14)可得预制混合梁截面抗剪刚度的倒数表达式,如式(16)所示:
根据计算简图,建立梁的外力线分布集度函数如下:
将式(15)和式(17)代入式(9),得:
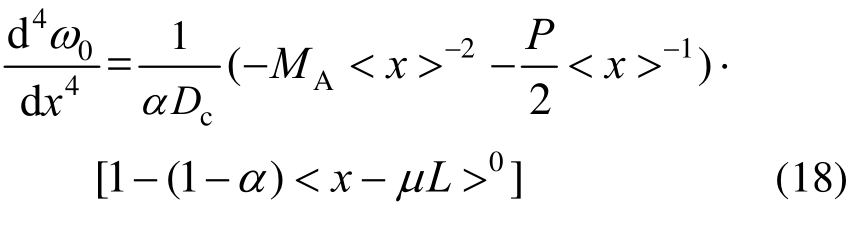
对式(18)积分4次,得挠度公式:
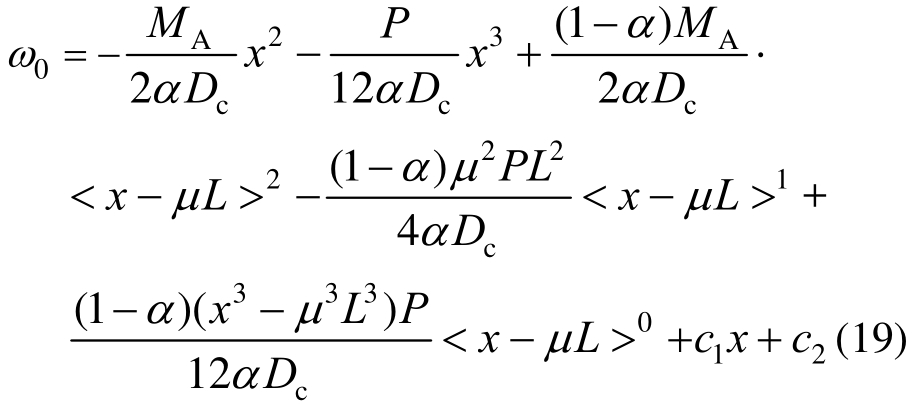
将式(10)代入式(19),得:
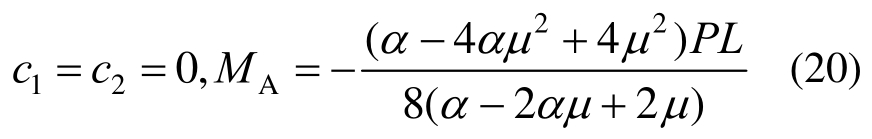
将式(20)代入式(19)可得到预制混合梁在忽略剪切变形情况下的挠曲线计算公式:
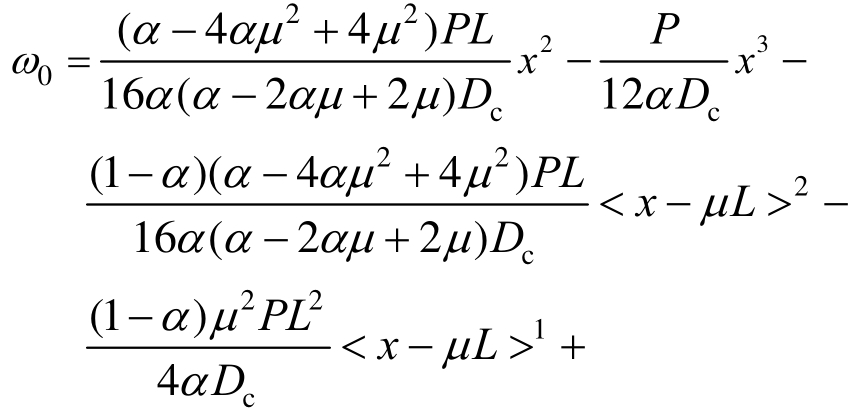
将式(16)和式(21)代入式(12)中,得预制混合梁剪切变形引起的附加挠度如下:
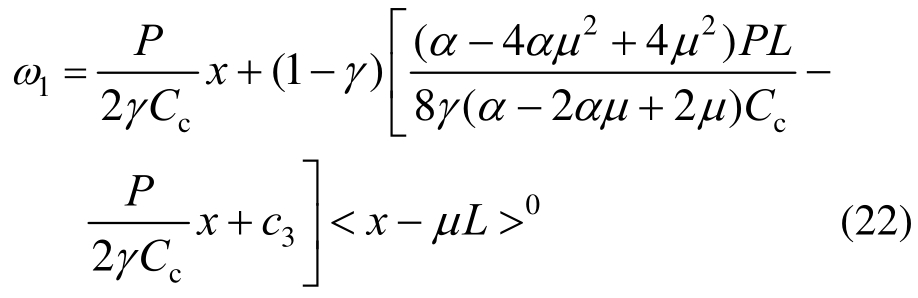
式中,c3为考虑剪切刚度突变而引入的修正常数。
由于剪切变形曲线是连续的,因此应满足:
将式(23)代入式(22),得:
将式(24)代入式(22),得:
将式(21)和式(25)代入式(11),可得预制混合梁考虑剪切变形时的挠曲线计算公式:

由式(26)可知,预制混合梁的挠度可分解为弯曲变形引起的挠度和剪切变形引起的附加挠度两部分。
当取x=L/2时,由式(26)可得预制混合梁跨中挠度计算公式,如式(27)所示:
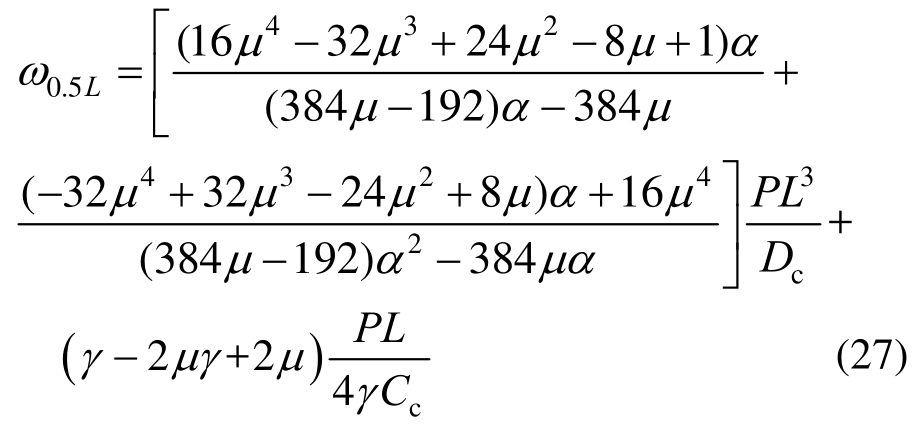
式(21)和式(25)~式(27)中:x的取值范围均为![]()
当取α=1,μ=0,γ=1 时,由式(26)可得预制混凝土梁挠曲线计算公式:
在式(28)基础上取x=L/2时,可得预制混凝土梁跨中挠度计算公式,如式(29)所示:

3 预制混合梁挠曲线计算公式验证及分析
为验证预制混合梁挠曲线计算公式的准确性,取开裂荷载下预制混合梁试验结果与推导公式计算结果进行对比分析,表1为各试件开裂荷载和设计参数。
表1 各试件开裂荷载和设计参数
Table 1 Cracking load and parameters of specimens

注:Pcr为开裂荷载;截面抗剪刚度C=k/GA,k为截面系数,其取值根据文献[15]确定。
?
图5为各试件挠度曲线试验值与挠曲线公式计算值的对比。由图可知,

图5 各试件试验与计算挠度曲线
Fig.5 Test and calculation deflection curves of specimens
1)试件 PC1试验挠曲线与考虑剪切变形的计算挠曲线吻合较好,最大误差仅为4.4%,而与忽略剪切变形的计算挠曲线吻合较差,最大误差为19.4%,说明预制混凝土梁中剪切变形引起的附加挠度不可忽略,其原因在于预制混凝土梁截面高跨比较大,剪切变形的作用随无量纲参数![]() 的增大而增大。
的增大而增大。
2)试件 PHSC1~PHSC3试验挠曲线与考虑剪切变形的计算挠曲线整体吻合较好,最大误差为9.4%(试件PHSC1),与忽略剪切变形的计算挠曲线整体吻合较差,最大误差为33.9%。与预制混凝土梁相比,剪切变形对预制混合梁挠度的影响更大。其原因是梁端钢梁截面抗剪刚度较预制混凝土梁小,剪切变形的影响更显著。
3)利用式(26)可以较好地预测预制混合梁在跨中竖向集中荷载作用下的竖向变形。
图6给出了各试件跨中挠度试验值与计算值的对比图,图7给出了各试件跨中挠度计算值的组成。
由图6和图7可知:

图6 各试件跨中挠度
Fig.6 Mid-span deflection of specimens

图7 各试件跨中挠度组成
Fig.7 Components of mid-span deflection of specimens
1)试件 PC1跨中挠度试验值与计算值相差较小,相对误差为4.4%;跨中挠度值中由剪切变形引起的附加挠度与跨中挠度的比值为12.5%。
2)试件 PHSC1~PHSC3跨中挠度试验值与考虑剪切变形的跨中挠度计算值吻合较好,其相对误差分别为9.4%、4.0%和4.9%;跨中挠度值中由剪切变形引起的附加挠度占比分别为 14.2%、17.8%和21.7%,说明预制混合梁中由剪切变形引起的附加挠度不可忽略,其附加挠度随钢梁长度的增大而逐渐增大。原因在于预制混凝土梁端的混凝土梁段为钢梁段所代替,削弱了梁端截面的抗剪刚度,而钢梁长度的增大导致了剪切变形作用的增大。
3)式(27)可以较好地预测预制混合梁在跨中竖向集中荷载作用下的跨中挠度。
4 预制混合梁竖向变形影响因素分析
为深入研究预制混合梁在跨中竖向集中荷载作用下的变形性能,以试件 PHSC2为基准模型,重点分析开裂荷载作用下抗弯刚度比α、长跨比μ和高跨比h/L等参数对预制混合梁竖向变形性能的影响。
4.1 抗弯刚度比
通过调整钢梁翼缘宽度来改变预制混合梁抗弯刚度比,选取的抗弯刚度比分别为 0.31、0.39、0.47和 0.55(对应钢梁翼缘宽度分别为 150 mm、200 mm、250 mm和300 mm)。采用式(26)和式(27)计算得到预制混合梁计算挠曲线与跨中挠度随抗弯刚度比的变化情况分别如图8和图9所示。

图8 不同抗弯刚度比下预制混合梁挠度曲线
Fig.8 Deflection curves of precast hybrid beams corresponding to different bending stiffness ratios
由图8可知,其他影响参数相同的条件下,抗弯刚度比为0.39、0.47和0.55时的挠度较抗弯刚度比为0.31时分别减少了8.4%、14.9%和20%。可见,预制混合梁挠度随抗弯刚度比的增大而减小,且减小趋势逐渐变缓。其原因在于随着抗弯刚度比的增大,预制混合梁的整体抗弯刚度逐渐增大,从而使构件整体刚度提高,挠度减小。因此,在工程设计中,可适当提高预制混合梁抗弯刚度比,以减小构件的挠度使之满足限值要求。
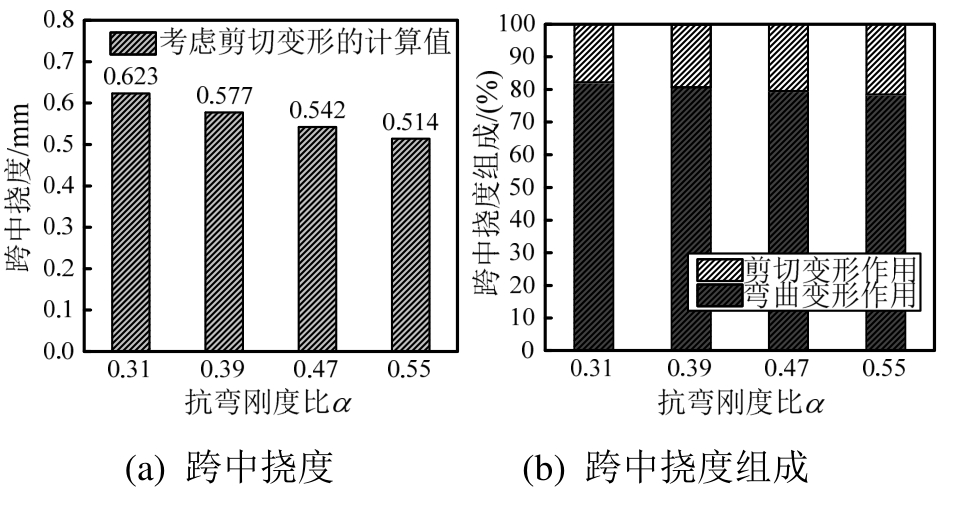
图9 不同抗弯刚度比下跨中挠度及其组成
Fig.9 Mid-span deflection and its components corresponding to different bending stiffness ratios
由图9可知,预制混合梁跨中挠度随抗弯刚度比的增大而减小,当抗弯刚度比从0.31变为0.39、0.47和 0.55时,跨中挠度分别减少了 7.3%、13%和17.6%,说明预制混合梁的整体刚度增大,变形减小。同时,4种抗弯刚度比下由剪切变形引起的附加挠度占比分别为 17.8%、19.2%、20.5%和21.6%,表明剪切变形作用随抗弯刚度比的增大而逐渐增大,原因是变参数时预制混合梁由剪切变形引起的附加挠度并未受到影响,而由弯曲变形引起的挠度随抗弯刚度比的增大而减小,从而导致剪切变形作用影响的增大。
4.2 长跨比
图10给出了不同长跨比下预制混合梁的计算挠曲线。由图可知:
1)长跨比为0和0.03时计算挠曲线差异显著,曲线平均增幅为69.7%,表明钢梁段的存在对预制混合梁变形性能影响较大。
2)其他参数相同的条件下,预制混合梁挠度随长跨比的增大而逐渐增大,当长跨比从0.03增大至0.08时,曲线平均增长幅度最大,为35%;当长跨比大于0.08时,挠度增长缓慢,曲线间平均增幅分别为9.2%、4.8%和5.4%。增幅略有回调的原因是此时钢梁段总长度已达到跨度的 1/2,预制混合梁的变形性能逐渐接近于同跨度的纯钢梁。
3)预制混合梁计算挠曲线沿梁长方向可分为3部分,即两端钢梁段和中间混凝土梁段。在钢梁段内,同位置处的挠度随长跨比变化并不明显;而在混凝土梁段,相应挠度变化有明显差异。其原因在于随着长跨比的增大,预制混合梁截面整体抗弯刚度变化趋势缓慢减小至渐趋稳定,而截面整体抗剪刚度仍呈减小趋势。
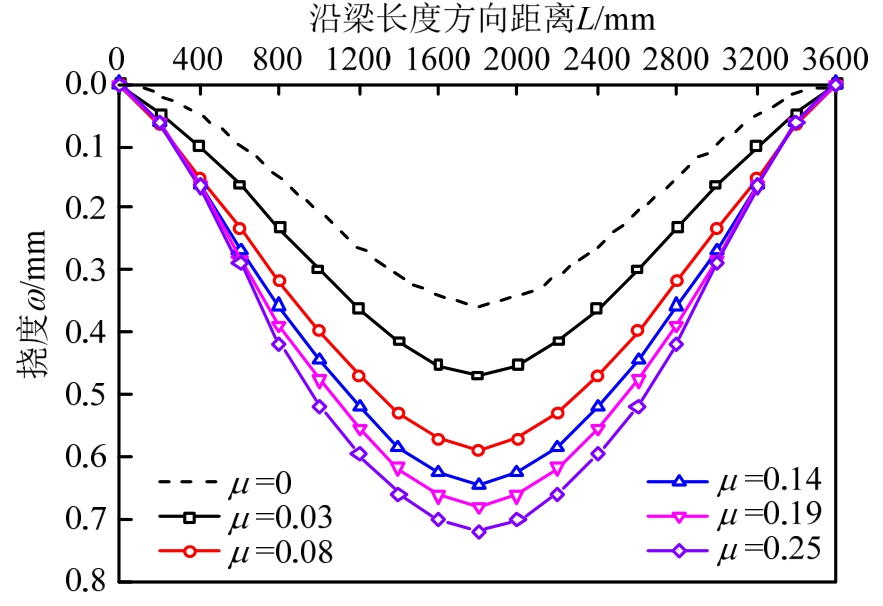
图10 不同长跨比下预制混合梁挠度曲线
Fig.10 Deflection curves of precast hybrid beam corresponding to different length-span ratios
图11为不同长跨比下跨中挠度及其组成。从图中可以看出:
1)对预制混合梁,剪切变形引起的附加挠度对跨中挠度影响较大,其影响程度随长跨比的增大而逐渐增大。当长跨比μ从0增大至0.25时,剪切变形引起的附加挠度占跨中挠度的比重从14.2%增大至36.7%。因此,对预制混合梁,由剪切变形所引起的附加挠度不可忽略。
2)考虑剪切变形影响时,预制混合梁跨中挠度随长跨比的增大而逐渐增大,当长跨比从 0变为0.03、0.08、0.14、0.19和 0.25时,跨中挠度分别增大31%、64.8%、80.4%、90.2和101.4%,表明长跨比对预制混合梁的变形性能影响较大。因此进行此类梁的工程设计时,在钢梁段长度满足装配安装空间的前提下,应尽可能地缩短钢梁段长度,以控制混合梁的挠度和剪切变形。

图11 不同长跨比下跨中挠度及其组成
Fig.11 Mid-span deflection and its components corresponding to different length-span ratios
3)预制混合梁的跨中挠度主要由弯曲变形引起;当长跨比从0增大至0.03时,由剪切变形引起的附加挠度占比基本没有变化;而当长跨比从0.03逐渐增大至 0.25时,附加挠度占比从 13%变为26.9%,比值近似呈线性增长,其原因在于弯曲变形引起的挠度变化随长跨比的增大而渐趋稳定,而剪切变形引起的附加挠度仍呈线性增长。因此,当钢梁与混凝土梁截面抗剪刚度相差较大时可通过减少钢梁段长度来控制预制混合梁的竖向变形。
4.3 高跨比
定义h/L为混凝土梁段截面高度与跨度的比值(简称高跨比)。框架结构中框架梁的高跨比一般为1/10~1/18,以4.2节中计算模型为基准,通过改变预制混合梁跨度得到高跨比为1/10、1/12、1/15和1/18时的跨中挠度组成情况,如图12所示。

图12 不同高跨比下跨中挠度组成
Fig.12 Components of mid-span deflection corresponding to different depth-span ratios
从图12可以看出:
1)长跨比相同时,预制混合梁中由剪切变形引起的附加挠度占比随高跨比的减小而减小。当高跨比分别为1/10、1/12、1/15和1/18时,最大附加挠度占比分别为21.7%、14.5%、8.5%和5.4%;表明对高跨比较大的预制混合梁,剪切变形对跨中挠度的影响更显著。
2)对于高跨比较大的预制混合梁(h/L=1/10),当长跨比从0增大至0.25时,由剪切变形引起的附加挠度占比由10.4%增至21.7%;而对于高跨比较小的预制混合梁(h/L=1/18),相应的附加的挠度占比由3.4%增至5.4%。由此可见,随着高跨比的减小,长跨比对预制混合梁变形性能的影响也在减小。
3)综上所述,当预制混合梁的高跨比大于1/12时,由剪切变形引起的最大附加挠度占比大于10%;当高跨比小于1/15时,由剪切变形引起的最大附加挠度占比小于10%。因此,建议预制混合梁在高跨比大于1/12时考虑剪切变形对挠度的影响。
5 结论
钢-混凝土预制混合梁适合装配化施工,具有施工便捷、受力明确、连接质量可靠等特点。本文基于奇异函数法建立了跨中竖向集中荷载作用下的预制混合梁挠曲线和跨中挠度计算公式,基于试验结果对该公式的准确性进行了验证,并在此基础上进行了变参数分析,得到以下结论:
(1)根据公式计算所得挠曲线和跨中挠度值与试验结果吻合较好,可用于分析弹性状态下预制混合梁的变形性能和预测其跨中挠度。
(2)钢梁长度的改变对试件PHSC1~PHSC3的变形性能有显著影响,钢梁长度越长,试件挠度越大,由剪切变形引起的附加挠度占比呈线性增长。因此在钢梁段长度满足装配安装空间的前提下,应尽可能地缩短钢梁段长度,以控制混合梁的挠度和剪切变形。
(3)随着抗弯刚度比的增大,预制混合梁的挠度减小,由剪切变形引起的附加挠度占比略有增大。
(4)长跨比相同时,预制混合梁中由剪切变形引起的附加挠度占比随高跨比的减小而减小;当高跨比大于1/12时,附加挠度占比大于10%,建议预制混合梁在高跨比大于 1/12时考虑剪切变形对挠度的影响。
[1]侯和涛, 朱文灿, 曲哲, 等.屈曲约束支撑钢筋混凝土框架结构干式柔性梁柱节点的试验研究[J].工程力学,2018, 35(6): 151-161.Hou Hetao, Zhu Wencan, Qu Zhe, at al.Experimental study on dry flexible beam-column joint in buckling restrained braced reinforced concrete frame structures[J].Engineering Mechanics, 2018, 35(6): 151-161.(in Chinese)
[2]张锡治, 马健, 韩鹏, 等.装配式剪力墙齿槽式连接受剪性能研究[J].建筑结构学报, 2017, 38(11): 93-100.Zhang Xizhi, Ma Jian, Han Peng, et al.Shear behavior on prefabricated shear wall alveolar type connection[J].Journal of Building Structures, 2017, 38(11): 93-100.(in Chinese)
[3]Kulkarni S A, Li B, Yip W K.Finite element analysis of precast hybrid-steel concrete connections under cyclic loading[J].Journal of Constructional Steel Research,2008, 64(2): 190-201.
[4]Zhang X, Zhang J, Gong X, et al.Seismic performance of prefabricated high-strength concrete tube column–steel beam joints[J].Advances in Structural Engineering,2017, 21(5): 658-674.
[5]Korkmaz H H, Tankut T.Performance of a precast concrete beam-to-beam connection subject to reversed cyclic loading[J].Engineering Structures, 2005, 27(9):1392-1407.
[6]Yang K H, Seo E A, Hong S H.Cyclic flexural tests of hybrid steel–precast concrete beams with simple connection elements[J].Engineering Structures, 2016,118(2): 344-356.
[7]Guo X, Gao S, Wang L, et al.Bearing capacity of embedded channel-shaped steel connections at precast concrete beam end[J].Engineering Structures, 2018,175: 177-190.
[8]刘昌永, 王庆贺, 王玉银, 等.带钢接头的装配式钢筋混凝土梁受弯性能研究[J].建筑结构学报, 2013,34(增刊 1): 208-214.Liu Changyong, Wang Qinghe, Wang Yuyin, et al.Flexural behavior of precast reinforced concrete beams with steel end connectors[J].Journal of Building Structures, 2013, 34(Suppl 1): 208-214.(in Chinese)
[9]焦安亮, 冯大阔, 张中善, 等.装配式钢管混凝土柱-带钢接头钢筋混凝土梁节点抗震性能试验研究[J].建筑结构, 2017, 47(10): 53-64.Jiao Anliang, Feng Dakuo, Zhang Zhongshan, et al.Experimental study on seismic behavior of nodes fabricated by concrete-filled steel tubular column and reinforced concrete beam with steel joints[J].Building Structure, 2017, 47(10): 53-64.(in Chinese)
[10]姚浩, 程进.基于变分原理的波形钢腹板箱梁挠度计算解析法[J].工程力学, 2016, 33(8): 177-184.Yao Hao, Cheng Jin.Analytical method for calculating defection of corrugated box girders based on variational principle[J].Engineering Mechanics, 2016, 33(8): 177-184.(in Chinese)
[11]李银山, 官云龙, 李彤, 等.求解变截面梁变形的快速解析法[J].工程力学, 2015, 32(增刊 1): 116-121.Li Yinshan, Guan Yunlong, Li Tong, et al.A fast analytical method for the deformation of beams with varying cross-sections[J].Engineering Mechanics, 2015,32(Suppl 1): 116-121.(in Chinese)
[12]牛四欣.钢-混凝土预制混合梁受弯性能试验研究[D].天津: 天津大学, 2017: 62-64.Niu Sixin.Flexural test of precast hybrid steel-concrete beam[D].Tianjin: Tianjin University, 2017: 62-64.(in Chinese)
[13]王燮山.用奇异函数法求解某些变截面梁的变形[J].力学与实践, 1984, 6(4): 53-55.Wang Xieshan.Using singular function method to solve the deformation of some variable cross section beams[J].Mechanics in Engineering, 1984, 6(4): 53-55.(in Chinese)
[14]胡海昌.弹性力学的变分原理及其应用[M].北京: 科学出版社, 1981: 147―149.Hu Haichang.Variational principles in elasticity and their applications[M].Beijing: Science Press, 1981: 147-149 (in Chinese)
[15]朱慈勉, 张伟平.结构力学(上册)[M].北京: 高等教育出版社, 2009: 113-115.Zhu Cimian, Zhang Weiping.Structural mechanics(Volume One)[M].Beijing: Higher Education Press,2009: 113-115.(in Chinese)