近年来,随着建筑物向大跨空间结构方向发展,体型复杂的不等跨结构逐渐增多。当前,随着建筑空间结构和功能的改变,高低梁与柱异型节点在钢结构建筑中广泛出现。高低梁与柱异型节点自身抗震性能,以及它们框架整体性能的影响引起了一些研究人员的关注[1-4]。在Northridge和Kobe地震中[5-6],钢结构建筑由于梁柱节点焊缝开裂而遭受严重破坏,震后研究发现,节点的破坏大多是由于钢柱翼缘与梁下翼缘的连接焊缝的断裂。于是改进钢框架结构的主要思路和设计思想转变为通过优化构造措施实现塑性铰外移从而达到“强节点弱构件”。然而采用等高粱贯穿整个不等跨框架,是国内外最普遍的设计方法[7-8]。采用此类设计的结构体系,不仅会造成钢材浪费,且中柱节点域的承载力往往弱于梁,以致于结构在地震作用下,节点域易发生剪切破坏,而使结构出现局部倒塌。
目前,日本规范[9]设计使用的高低梁与柱异型节点,通常采用图1(a)所示的型式(注:本文称普通高低梁与柱异型节点)。此种连接方式由于梁高度不同,不但增加了施工难度,而且使得正交方向连接构造的相互干扰问题尤为突出[10]。因此,本文提出一种改进型钢管柱与钢梁连接节点,见图1(b)。该种节点形式是将节点域附近的构造采用与等高梁节点构造相同措施,将低梁端部翼缘与T型连接件腹板焊接,梁与外环板的翼缘和腹板通过螺栓连接。不仅有效地解决了构造干扰问题,而且减少了施工工序,提高了施工速度。此连接方式装配程度高,施工更简便,更有利于实际工程的应用和推广。
国内外学者对梁柱节点域进行了一系列理论和试验研究。桑原進等[11]由两种破坏机理推导出内隔板式高低梁节的承载力计算公式,并通过试验验证了公式的准确性。刘洪波等[12]依据有限元和理论分析,研究了钢结构箱形柱与工字梁刚性节点域的受力性能和隔板对节点刚度和强度的影响。曹正罡等[13]提出一种梁高可调节的装配式钢框架节点,并对其抗震性能进行了试验研究。李刚和陈以一[14]推导了左右梁不等高的节点域承载力计算公式。相比于传统的梁柱节点域,高低梁与柱异型节点的相关研究与设计规范有待于进一步深入拓展。
本文参考《钢构造接合部设计指针》[9]和《钢结构设计规范》(GB 50017—2003)[8]中的外加强环梁柱节点形式,设计了三个高低梁异形节点试件,通过低周反复荷载试验,分析节点域的滞回性能,研究其变形能力和破坏机制。在此基础上,采用有限元分析软件MSC.Marc 2012进行一系列数值模拟分析,以深入研究有无T型连接件和梁截面高度比对梁柱节点抗震性能的影响,最后提出了T型连接装置的计算模型和设计方法。

图1 改进型钢管柱与钢梁连接节点
Fig.1 Improved square steel hollow column to steel beam joint
1 试验概况
1.1 材料性能
通过对钢材进行的单向拉伸试验,实测其材料性能:钢板厚度t、弹性模量E、屈服强度fy、抗拉强度fu、屈强比、伸长率δ,见表1。
表1 钢材的材料性能
Table 1 Material properties of steel

截面位置 板厚/mm弹性模量E /MPa屈服强度fy /MPa抗拉强度fu /MPa屈强比/(%)伸长率δ /(%)梁翼缘、外加强环、T型连接件15.9 204000 386 534 72 18.9梁腹板 9.2 203000 397 537 74 20.3方管柱 12.2 206000 393 473 83 20.5
1.2 试件设计
试验中设计了3个试件,试件的几何构造和基本信息如图2和表2所示。试验设定的变化参数为是否设置T型连接件和梁1与梁2的梁截面高度比(hb2/hb1=0.75,0.5)。试件 No.1为普通高低梁与柱异型节点标准试件,方钢管柱口径均为 250 mm,柱壁厚为12.2 mm(实测值)。梁1高度为400 mm,梁2高度为200 mm。试件No.2和No.3为改进型钢管柱与钢梁连接节点,试件No.2与试件No.1的梁柱尺寸完全相同,区别仅在于梁2端部焊接的T型连接件。试件3与试件2均有T型连接件,但梁截面高度比不同,分别为0.75和0.5。
梁柱连接采用了外环板式节点,外环板的细部尺寸如图3所示。外加强环通过角焊与方钢管柱进行连接,焊脚尺寸为13 mm,环板采用的分割式外环板[15]是由两块厚度为12 mm的钢板拼接而成,拼接处预留5 mm安装缝。
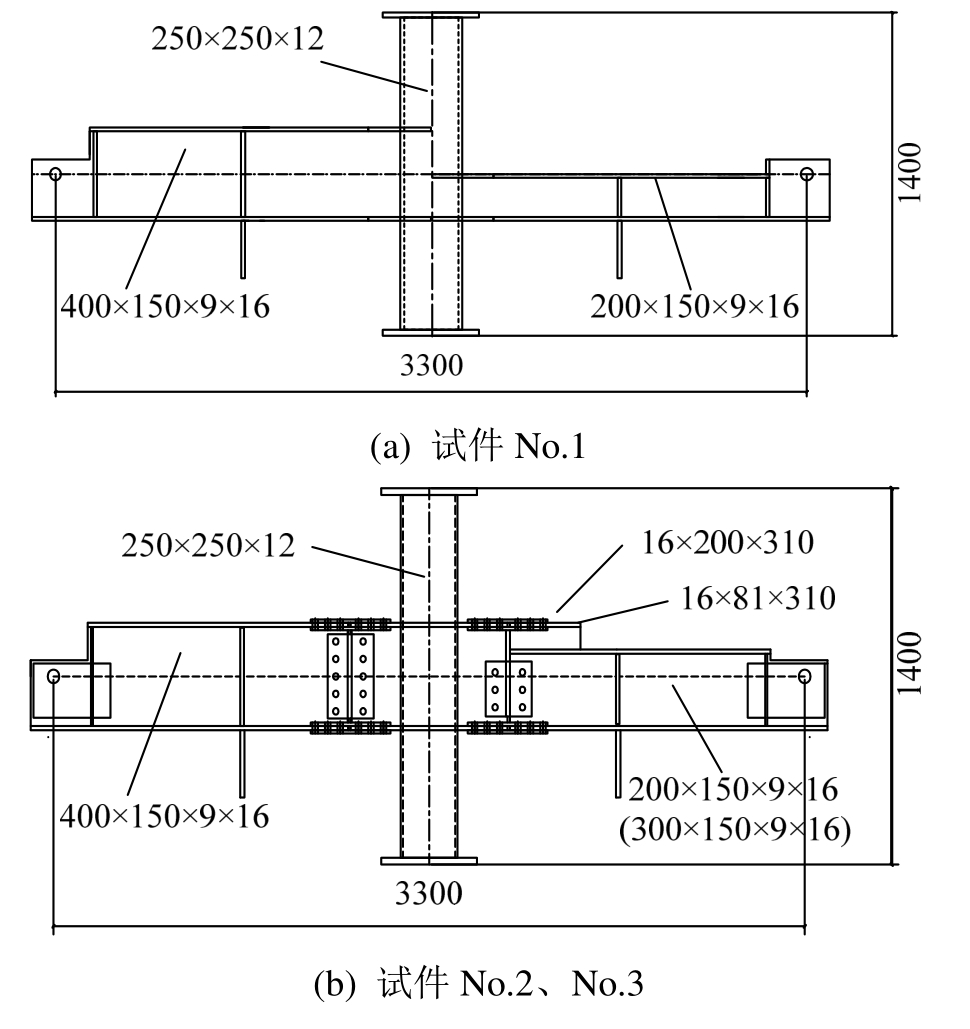
图2 试件详图
Fig.2 Details of specimen

图3 外加强环细部尺寸
Fig.3 Details of external diaphragm
表2 试件基本信息
Table 2 Basic information of specimens

试件编号 方钢管柱 梁1 梁2 T型连接件 梁高比No.1 250×250×12 400×150×9×16 200×150×9×16 无 0.5 No.2 250×250×12 400×150×9×16 200×150×9×16 有 0.5 No.3 250×250×12 400×150×9×16 300×150×9×16 有 0.75
1.3 加载装置
试验加载装置如图4所示,试验采用梁端位移加载方式,两端各连接一个液压加载系统,对其施加作用方向相反的位移荷载,两个加载点间距为3300 mm。柱试件竖直放置,柱上无轴向荷载。柱顶柱脚均为铰接,但柱顶滑动铰支座约束了水平方向位移而允许轴向变形,柱脚约束水平方向以及柱轴向的位移,两支座间距1800 mm。

图4 加载装置图
Fig.4 Overall view of test setup
1.4 加载机制
试验采用拟静力加载方式,位移控制加载历程曲线如图5所示。每个试件全部按照层间位移角的0.5%、1.0%、2.0%、3.0%、4.0%进行位移加载,且每级荷载循环2次,再按层间位移角5%继续循环加载,直至试件出现焊缝开裂,试验停止。

图5 加载历程曲线
Fig.5 Loading protocol
1.5 节点域定义及测量计算
1.5.1 节点域定义
当钢框架结构遭受罕遇地震时,有外加强环的梁柱节点域受力状态如图6所示。由于试件 No.1左、右梁高不同造成节点域受力状态与常规节点不同。将梁高较高的梁称为梁 1,梁高较小的梁称为梁2,节点域分为节点域1和节点域2两个部分。对于 No.2、No.3试件,整个节点域范围是指柱的腹板在梁高范围内的区域。

图6 节点域受力状态
Fig.6 Force condition of beam-to-column connection panel
注:dc为节点域翼缘板中心线距离;db1为梁1翼缘板中心线距离;db2为梁2翼缘板中心线距离;Mb1为梁1端弯矩;Mb2为梁2端弯矩;Qc,U为柱上端剪力;Qc,L为柱下端剪力;Qc,p1为柱对节点域1的剪力;Qc,p2为柱对节点域2的剪力;Qb,p1为梁对节点域1的剪力;Qb,p2为梁对节点域2的剪力。
1.5.2 测量计算
节点域的剪切力通过加载点上的作动器获得,整个节点域的剪切变形如图7(a)所示,节点域的剪切变形角通过设置在节点域对角线上的2个位移传感器测得,见图7(b)。节点域的剪切变形角按式(1)计算:

式中:hp1为整个节点域的测量高度;bp为整个节点域的测量宽度;d1和d2分别为两对角线位移计变形;α为变形前节点域对角线与底边夹角。
节点域1(Qp1)、节点域2(Qp2)和整个节点域(Qp)的剪切力按式(2)~式(4)计算:


图7 节点域测量方法
Fig.7 Measuring method of panel zone

式中:Lb为加载点距离,取3300 mm;Lc为两铰支座距离,取1800 mm;Qb1为梁1的剪力;Qb2为梁2的剪力;dc为节点域翼缘板中心线距离;db1为梁1翼缘板中心线距离;db2为梁2翼缘板中心线距离(见图6)。
通过骨架曲线,可得一系列的主要性能点,如剪切刚度、屈服点、塑性点等(见图 8)。剪切刚度Ke采用了荷载在达到第一个层间位移角 0.005 rad时的割线刚度[16],试件屈服点采用斜率因子法[16]确定,塑性点采用0.35%偏移强度法[17]确定。

图8 主要性能点的定义
Fig.8 Definition of main performance
2 试验结果
2.1 滞回特性及骨架曲线

图9 节点域剪切力和剪切变形角
Fig.9 Relations between shear force and shear deformation angle of entire panel

图10 加载试件的骨架曲线
Fig.10 Skeleton curves of specimens
图9和图10分别给出了试验得到的节点域剪切力和剪切变形角的滞回曲线和骨架曲线。各个试件在加载过程中滞回曲线均呈饱满纺锤形,表现出良好的延性性能和耗能能力。当db2/db1为0.5时,试件No.2比试件No.1节点域的剪切力峰值提高了能力,说明普通高低梁异型节点降低梁高后削弱了23.75%,且其滞回曲线更加饱满,具有更好的耗能节点域的承载力和刚度。No.2和No.3相比,梁高比虽然不同,但No.3比No.2试件节点域的承载力仅提高了1.42%,可见梁高比对整个节点域的剪切承载能力和耗能能力影响较小。
2.2 节点各部分变形
节点的变形主要包括:局部变形角Rl(图11(a))、柱变形角Rc(图11(b))、梁变形角Rb(图11(c))和节点域剪切变形Rp(图11(d))。

图11 节点各部分变形
Fig.11 Deformation of components
为了说明各构件的抵抗变形能力,图12分别描述了各构件在层间位移角为0.5%、1.0%、2.0%、3.0%、4.0%时的旋转角及其百分比。当层间位移角为 0.5%时,梁变形占总变形的比重较大,在32%~44%主要是由滑动铰连接的空隙造成的;当层间位移角大于0.5%时,改进型方钢管柱与钢梁连接节点的局部变形随着层间位移角的增大而略有增加,在20%~24%,然而普通高低梁与柱异形连接节点的局部变形随着层间位移角的增大而明显增加,在28%~44%是由其几何形状不对称造成的。当层间位移角大于 0.5%时,普通高低梁与柱异形连接节点柱变形的比重从20%降至8%,改进型方钢管柱与钢梁连接节点柱变形从28%降至8%;普通高低梁与柱异形连接节点梁变形的比重从 41%降至16%,改进型方钢管柱与钢梁连接节点梁变形从40%降至14%;普通高低梁与柱异形连接节点节点域变形的比重从10%增至38%,改进型方钢管柱与钢梁连接节点节点域变形从12%增至52%。因此,改进型方钢管柱与钢梁连接节点为节点域剪切破坏。


图12 各要素的旋转角百分比
Fig.12 Rotation percentage of each component
3 有限元分析
3.1 模型建立
采用有限元分析软件MSC.Marc 2012按照试验试件尺寸以 1∶1比例建立精细化三维实体有限元模型,分析模型由H型钢梁、方形钢管柱、八边形外环板等部件组成,所有部件均采用三维实体单元,其中试件No.3的有限元模型如图13所示。进行低周反复加载模拟分析,包括设置单元几何属性、材料本构的定义和选取、接触单元的定义与选取、边界条件的施加、设置荷载工况等。

图13 No.3有限元模型
Fig.13 Finite element models of No.3
为了精确模拟试验加载过程,考虑到螺栓中预应力的存在,对全部的螺栓设置初始应力。构件采用尺寸M27的高强螺栓,螺栓杆与螺栓孔之间通过设置touch模拟两者之间的界面行为,其中摩擦系数取为 0.2,将螺栓帽与接触面一端定义为 glue,另一端定义为 touch,本构关系采用前期试验中实测的三折线型应力-应变关系。
在有限元模型柱两端50 mm外定义耦合点,通过耦合点对柱施加边界条件,柱底部模拟加载装置中的固定铰支座,限制ux、uy、uz三个方向的平动位移和θx和θz两个方向的转动,允许柱在θy方向的转动,柱顶耦合点模拟加载装置的滑动铰支座,约束ux、uy两个方向的平动位移和θx、θz两个方向的转动,允许柱在uz方向上发生竖向变形和θy方向的转动,在梁自由端截面50 mm外设置耦合点,模拟梁端位移加载点,在加载点上,采用位移控制,施加与试验相同的荷载历程,定义梁1向上、梁2向下为正方向加载。
3.2 试验验证
3.2.1 滞回曲线
有限元分析模型与试验往复加载所得的节点域剪切力-剪切变形角滞回曲线对比图如图14所示,具有较高的一致性,然而有限元比试验的滞回曲线更为光滑饱满,这主要是由有限元分析模型未考虑构件的初始缺陷、焊接加工过程的应力集中等因素造成的。有限元曲线与试验曲线具有较高的吻合度,有限元模型能够较好地模拟新型高低梁异型节点的受力性能。

图14 有限元分析与试验的滞回曲线对比
Fig.14 Comparisons of hysteretic loops between FEM and test results
3.2.2 骨架曲线
有限元模型与试验的节点域骨架曲线对比图如图15所示,试验和有限元模型之间的差异是由高强度螺栓的应力-应变关系不准确所致,模型采用的先前试验研究的本构,然而这些螺栓的实际强度可能低于有限元法,在这种情况下,试验中的螺栓可以会产生更多的塑性和残余变形,从而导致螺栓和端板之间的间隙比在数值模拟中的大。在螺栓端板连接上的角焊缝的存在也被忽略,对性能有一定的影响。

图15 有限元分析与试验的骨架曲线对比
Fig.15 Comparisons of skeleton curves between FEM and test results
3.3 节点域应力分布
有限元模型的von Mises应力分布以及试验节点域对应的破坏形态如图16所示。破坏模式上,3个试件整个节点域呈剪切变形,试件 No.1到达塑性阶段时,节点域的剪切变形主要在节点域 1,梁1侧的外加强环变形较大,方形钢管也明显内凹,加载到最后方钢管柱与外环板上侧角部出现裂缝并迅速扩展(见图16(b));相比 No.1,No.2试件承载力有较明显的提升,在T型连接件与梁的翼缘焊缝处出现裂纹(见图16(d));No.3试件破坏形态与No.2试件类似,但加载到后期,梁1端的变形更加明显同时在方钢管柱与外加强环下部焊接处产生裂缝(图16(f))。从应力图可以看出,节点域1已进入塑性状态,而节点域2的大部分区域的应力未超过屈服应力,故柱两侧的梁高度不同时,整个梁柱节点域的剪切变形主要都集中在节点域 1,相比之下,节点域2的剪切变形不太明显,与试验结果对应。带有T型连接件的试件,节点域的应力远远低于普通的高低梁异型节点,这也进一步说明T型连接件可以大大提高节点的抗剪承载力。

图16 节点失效模式
Fig.16 Failure mode of panel zone
3.4 主要性能点比较
有限元模型与试验试件在主要性能点的比较见表3,其中有限元所得的剪切刚度是试验值的93%~134%,有限元分析得到的屈服点和塑性点剪切承载力分别为试验值的 94%~119%和 93%~112%。再次说明有限元分析模型模拟的梁柱节点在低周反复荷载作用下的受力特性具有较高的精确度。
3.5 变截面处应变分析
在有限元结果文件中选取截面A、截面B以及截面C上沿高度方向分布的一系列特殊点位如图17所示,得到这些点的应变在正、副向加载至层间位移角的 0.05%、0.5%、1%、2%、3%、4%、5%以及最大值时沿高度方向的分布情况如图18所示,讨论应变的传递过程。

图17 截面选取位置
Fig.17 Section selection position
由图17可以看出,对于截面A而言,在正向荷载作用下,No.2试件的中性轴有向梁几何中心下移的趋势;在负向荷载作用下,No.2的中性轴有向梁几何中心上移的趋势。而对于 No.3试件,在正负荷载作用下,中性轴和几何中心一致。对于截面B而言,在层间位移角到达0.03 rad之后,No.2梁腹板的应变量急剧增加,梁腹板屈服;对于试件No.2和No.3,在正向荷载作用下,应变随T型连接件高度的增加而降低。对于截面C而言,在正负荷载作用下,上、下翼缘承当相同程度的应力。
表3 试验和有限元节点域的剪切刚度、屈服点和塑性点
Table 3 Experimental and numerical shear stiffness, yield point and plastil point of entire panel

注:ke为试验所得剪切刚度;Qpy为试验所得屈服点剪切力;Qp为试验所得塑性点剪切力;KFEM为有限元分析所得剪切刚度;QpyFEM为有限元分析所得的屈服点剪切力;QpFEM为有限元分析所得的塑性点剪切力。
试件编号 加载方向Ke/(kN/rad)KFEM/(kN/rad)KFEM/KeQpy/kNQpyFEM/kNQpyFEM/QpyQp/kNQpFEM/kNQpFEM/Qp No.1 正向 465801 473461 1.01 845 867 1.02 1143 1068 0.93负向 507012 473382 0.93-959-928 0.96 1207-1123 0.93 No.2 正向 275223 335616 1.22 1247 1178 0.94 1457 1349 0.92负向 268856 267567 0.99 1330-1369 1.03 1469-1375 0.93 No.3 正向 259113 348402 1.34 1276 1529 1.19 1464 1647 1.12负向 283889 269640 0.94 1298-1366 1.05 1479-1383 0.93

图18 沿高度方向应变分布
Fig.18 Strain distribution along height
由图18中截面C的应变大小也能解释一定的试验现象,对于No.2应变较大,故T型连接板与梁翼缘连接处焊缝开裂;而相比之下 No.3应变较小,故试件最终在柱环连接处焊缝裂缝。
4 T型连接件设计
T型连接件处的受力弯矩图如图19所示,对T型连接件与梁接缝采用的设计顺序以及计算结果如下:
1)假定梁跨度中心为反弯点,忽略竖向荷载;
2)如图19所示,在T型连接件的端部,假定梁已达到屈服弯矩My,根据力矩斜率可得出梁接缝位置的弯矩Mj。
3)假定梁翼缘接缝只承担弯矩,梁腹板接缝只承担剪力,可得到设计条件:计算得到的梁接缝位置的弯矩Mj小于梁翼缘接缝的抗弯强度,计算得到的剪力值小于梁腹板接缝的抗剪强度。
其中,T型连接件所受的剪切力是由梁翼缘接缝的抗弯强度而求出的力偶,T型连接件的梁翼缘厚度是根据外加强环构造的厚度决定的。

图19 受力弯矩图
Fig.19 Bending moment diaphragm
根据以上设计条件,可列出公式:

从而可以求出T型连接件的允许长度为:

式中:L为反弯点到梁接缝间距离;jMfy为接缝处屈服弯矩;tf为T型连接件翼缘厚度;Bf为T型连接件翼缘宽度;Lw为 T型连接件的允许长度;σy为T型连接件的屈服应力。
腹板剪切计算图如图20所示。由T型连接件与梁腹板焊缝所受剪切力Qwy大于腹板母材的抗剪强度可得公式(8),从而求得T型连接件的腹板厚度:

图20 腹板剪切计算图
Fig.20 Web shear calculation chart

由于焊缝强度应不小于腹板母材的强度,可求出焊缝尺寸:

式中:tw,T为T型连接件腹板厚度;Db为T型连接件的高度;tf为T型连接件翼缘厚度;s为焊脚高度。
5 结论
作为新型装配式钢结构节点研究的一部分,本文作者提出了一类改进型方钢管柱与钢梁连接节点并开展了相关的低周反复加载试验及其有限元分析。分析了T型连接件与梁高比对节点域剪切承载力的影响,根据试验和有限元分析结果,得到下列结论。
(1)相比于普通高低梁与柱异型节点试件,改进型方钢管柱与钢梁连接节点试件的失效模式是在T型连接件与梁2的焊接处发生撕裂,且破坏前能够表现出足够的延性。即通过T型连接件可获得设计所期望的节点失效模式。
(2)采用T型连接件的改进型方钢管柱与钢梁连接节点具有足够的承载力和滞回性能,具有良好的抗震性能。虽然两种节点各部分的变形分担率十分接近,但改进型方钢管柱与钢梁连接节点的剪切承载力和耗能能力提高了20%和200%。
(3)采用T型连接件的改进型方钢管柱与钢梁连接节点试件,左右梁高度不同对其各项力学性能影响不大,有待于进一步深入研究。
(4)采用MSC.Marc 2012有限元软件建立的三维有限元分析模型可以较精确地模拟高低梁异型节点在低周反复荷载作用下的滞回性能和单调加载性能,能较好地模拟高低梁异型节点的受力行为。
(5)在论文的最后,提出了T型连接装置的计算模型和设计方法,对今后实际工程应用中提供理论支持。
[1]牟犇, 王玲玲, 张春巍, 等.考虑楼板影响的外环板式梁柱节点抗震性能:试验研究[J].工程力学, 2018,35(2): 160―168, 213.Mou Ben, Wang Lingling, Zhang Chunwei, et al.Aseismic performance of beam-to-column joints with external-diaphragm considering slab effect: Experimental investigation[J].Engineering Mechanics, 2018, 35(2):160―168, 213.(in Chinese)
[2]牟犇, 井后凯, 张春巍, 等.外加强环不等高 H 型钢梁-方钢管柱节点抗震性能试验研究[J].建筑结构学报, 2018, 39(8): 80―89.Mou Ben, Jing Houkai, Zhang Chunwei, et al.Experimental investigation on seismic behavior of unequal-depth H-shape steel beam to column connection with external-diaphragm[J].Journal of Building Structures, 2018, 39(8): 80―89.(in Chinese)
[3]隋伟宁, 孙希, 王占飞, 等.左右梁高不同异形节点设计方法及力学性能研究[J].工程力学, 2013, 30(S1):83―88.Sui Weining, Sun Xi, Wang Zhanfei, et al.Research on design method and mechanical performance of the irregular joint with different beam depths[J].Engineering Mechanics,2013, 30(S1): 83―88.(in Chinese)
[4]薛建阳, 胡宗波, 彭修宁, 等.钢结构箱形柱与梁异型节点抗剪承载力分析[J].土木工程学报, 2011, 44(8):9―15.Xue Jianyang, Hu Zongbo, Peng Xiuning, et al.Analysis of shear resistance of irregular joint between steel box columns and beams[J].China Civil Engineering Journal,2011, 44(8): 9―15.(in Chinese)
[5]Miller D K.Lessons learned from the Northridge earthquake[J].Engineering Structures, 1998, 20(4-6):249―260.
[6]胡方鑫, 施刚, 石永久.基于断裂力学的高强度钢材梁柱节点受力性能分析[J].工程力学, 2015, 32(4):41―46.Hu Fangxin, Shi Gang, Shi Yongjiu.Fracture behavior of beam-column connections using high strength steel based on fracture mechanics[J].Engineering Mechanics, 2015,32(4): 41―46.(in Chinese)
[7]ANSI/AISC 360―10, Specification for structural steel buildings[S].Chicago: American Institute of Steel Construction, 2010.
[8]GB 50017—2003, 钢结构设计规范[S].北京:中国计划出版社, 2003.GB 50017—2003, Ministry of housing and urban-rural development[S].Beijing: China Planning Press, 2003.(in Chinese)
[9]日本建筑学会.钢构造接合部设计指针[S].东京: 日本建筑学会, 2012.Architectural Institute of Japan.Recommendation for design of connections in steel structures[S].Tokyo:Architectural Institute of Japan, 2012.(in Japanese)
[10]Eslami M, Namba H.Elasto-plastic behavior of composite beam connected to RHS column, experimental test results[J].International Journal of Steel Structures,2016, 16(3): 901―912.
[11]Kuwahara S, Kumano T, Inoue K.The elasto-plastic behaviors of joint panels at the connection of rectangular steel column and two H-shaped beams with different depth[J].Journal of Structure Construction Engineer,2000, AIJ (533): 175―181.
[12]刘洪波, 谢礼立, 邵永松.钢结构箱形柱与工字梁刚性节点有限元分析[J].哈尔滨工业大学学报, 2007(8):1211―1215.Liu Hongbo, Xie Lili, Shao Yongsong.Finite element analyses of the rigid connections with steel box columns and I section beams[J].Journal of Harbin Institute of Technology, 2007(8): 1211―1215.(in Chinese)
[13]曹正罡, 杜鹏, 李江东, 等.低周往复荷载作用下可变梁高装配式钢框架节点力学性能研究[J].建筑结构学报, 2015, 36(4): 1―8.Cao Zhenggang, Du Peng, Li Jiangdong, et al.Research on mechanical performance of bolted height adjustable steel beam-to-column connections under low cycle reversed loading[J].Journal of Building Structures,2015, 36(4): 1―8.(in Chinese)
[14]李刚, 陈以一.钢框架圆管柱梁节点域的抗剪承载力[J].建筑钢结构进展, 2009, 11(6): 33―39.Li Gang, Chen Yiyi.Shear resistance of panel zone of frame joint connecting CHS column and H steel beams.[J].Progress in Steel Building Structures, 2009, 11(6):33―39.(in Chinese)
[15]Kubota J, Taki M, Tsukamoto K, et al.Elasto-plastic behavior of connection between concrete-filled square steel tubular column and steel beam using split external diaphragm[R].Annual Report, Kajima Technical Research Institute, Kajima Corporation, 2007: 65―70.
[16]Imai K, Yoshida Y, Saijo K, et al.An experimental report on elasto-plastics behaviors of beam-to-column connections with an offset in right and left beam positions[J].Journal of Structure Construction Engineer,1991, AIJ(425): 27―35.
[17]Beedle L S, Topractsologlou A A, Johnston B G.Connection for welded continuous portal frames (part III Discussion of test results and conclusions), Progress report NO.4[J].The Welding Journal, 1952, 11(4):543―560.