混凝土作为常见的建筑材料，从最初使用到现在已经进行了一定程度的优化和改善，但在实际应用时仍存在诸多不足。混凝土的缺陷主要在于极端荷载下的脆性破坏，耐久性不足等原因。在这种背景下，高延性纤维增强水泥基复合材料(ECC材料)得到广泛关注。ECC材料是一种具有高延性、高韧性和细密裂缝特征的纤维增强水泥基复合材料。在直接拉伸和弯曲荷载下可呈现出应变硬化特性和多缝开裂的水泥基材料，具备很好的延展性和微裂缝宽度控制能力[1]。为了将ECC材料用于数值模拟，本文将 ECC本构模型通过二次开发嵌入 OpenSees中。在采用ECC材料建立有限元模型时，很多研究者在得到其结构响应的同时，也希望进行高效的敏感性分析，所以本文将 ECC材料的敏感性分析程序也编入 OpenSees中。敏感性分析可以帮助研究者进行结构的不确定性分析，并为研究者进一步了解结构响应提供了一个重要工具。响应的敏感性分析现如今用于结构工程的诸多方面，包括结构优化、结构可靠性分析以及有限元模型修正等[2-3]。目前有限元响应敏感性分析常用的方法包括有限差分法(FDM)、伴随法(AM)、摄动法(PM)和直接微分法(DDM)等。其中，有限差分法是敏感性分析中最简单、常用的一种方法，但此方法计算量大，对有限元响应的计算精度要求很高，易受数值噪声的影响[4－6]。而直接微分法计算高效、准确，可应用于复杂的非线性体系中[6]，是解决这一类问题最合适的方法。本文对 ECC弹塑性本构模型进一步推导和编程实现了基于直接微分法(DDM)的响应敏感分析算法。并通过DDM和FDM的结果对比，验证DDM方法的正确性和高效性。
1 ECC材料
1.1 材料简介
ECC材料是一种具有高延性、高韧性和细密裂缝特征的高性能材料，由于开裂时状态的稳定性，在承受应力作用下，呈现出多重细微裂纹[7]。ECC材料相对于混凝土有着更高的拉伸延展性，拉伸(应变)硬化行为和能量耗散均优于普通混凝土。ECC材料具有3%～7%的高延展性[8]。钢筋混凝土构件的荷载-变形行为受到加筋和水泥基材料的性能及其相互作用的影响，ECC材料的本构包含类似于金属应变硬化的阶段[9―11]。ECC材料和普通混凝土的抗拉特性有很大的区别，ECC材料具有拉伸强化段，普通混凝土没有抗拉强化段而且抗拉能力与 ECC材料相比要低的多。
1.2 基于递归方法的模型优化
ECC的模型最初由Han等提出[8]，该模型非常适合于数值计算。该材料的应力-应变曲线如图1所示，具体的本构关系不再赘述。
图1 ECC材料本构简化说明图
Fig.1 ECC material structure simplified illustration
为了简化说明过程，本文对 ECC材料本构的应力-应变曲线进行如图1的编号，并以受拉区完全卸载为例，说明记录历史应力、应变的重要作用。
当材料从2骨架线上卸载，下一时步会向(εtul,0)点运动，而εtul的计算和εtmax有很大的关系。εtmax的值是由历史时步在 2骨架线上的应变最大值确定。当研究者进行计算时，不仅需要下一时步的应变，还需要当前时步的运动状态，以及某些历史变量。ECC材料在文献中的算法采用传统排列组合的方式，即遍历从上一时步状态通过加载或卸载沿全部应力-应变曲线的可能性。通过对当前时步传来的应变大小，通过不断的筛选，最终选择真实走过的应力-应变曲线进行计算。
在这种情况下，本文算法考虑采用递归的方式，减少判断流程，减少迭代和收敛的次数，简化计算流程，最终达到加快计算的目的。同样以图 2为例，递归法将ECC材料的应力-应变曲线划分为12个模式(mode)，以mode为判断基础，每次计算先通过当前时步传来的应变计算更新的 mode位置，然后在不同的mode下，采用不同的应力-应变关系，计算新一步的应力。
本文通过一个简单的例子来说明自调用的实现。假设上一时步处于5骨架线上，当前时步判断为加载。如图2所示，传统编写会先按照穷举法判断当前应力-应变所处的位置和加卸载情况，然后分部判断加载后最终所处的位置，根据不同的位置和对应的函数计算应力大小。History⑤=1代表经历过⑤骨架线，线路1和2分别代表本构函数历史分别从②和③骨架线上进行过卸载。
图2 传统算法流程图
Fig.2 Flow chart of traditional algorithm
图3 递归算法流程图
Fig.3 Flow chart of recursive algorithm
而本文提出的递归方法，首先会自动识别上一时步所处的位置 mode=5。在这种情况下，加载的条件只会产生mode=5，mode=6，mode=7三种情况。通过应变大小判断哪个 mode。比如当应变超出mode=5而进入mode=6时，模型将执行mode=6这个分区内的判断。History⑦=0表示从未经历过 7骨架线，12个mode的互相调用，不仅记录了上一时步的位置，省去了初始状态的重新确定，而且减少了穷举法多余的判断。无论是从编写上，还是在模拟计算上，递归法都简化了流程，加快了计算的速度和效率。
1.3 数值模拟同实验对比
本文采用编译的 ECC本构，模拟 Fischer和Li[12]所研究的 ECC材料构件在往复循环加载条件下弯曲变形的实验，然后将数值模拟结果同实验结果进行对比。进一步说明二次开发的材料本构模型的正确性和可行性。下面简要阐述实验模型和实验材料参数[13]。
本文采用悬臂梁模型，对ECC材料弯曲构件的结构性能进行数值模拟，并与实验数据进行对比验证。该实验悬臂梁梁高500 mm，采用方形横截面，截面尺寸为100 mm×100 mm。纵向钢筋由4根钢筋(φ10 mm)提供，相对于两根轴线对称布置。截面采用核心区尺寸80 mm×80 mm，附 10 mm保护层，钢筋布置于核心区四角。具体布置方式如图4所示，材料参数如表1所示。
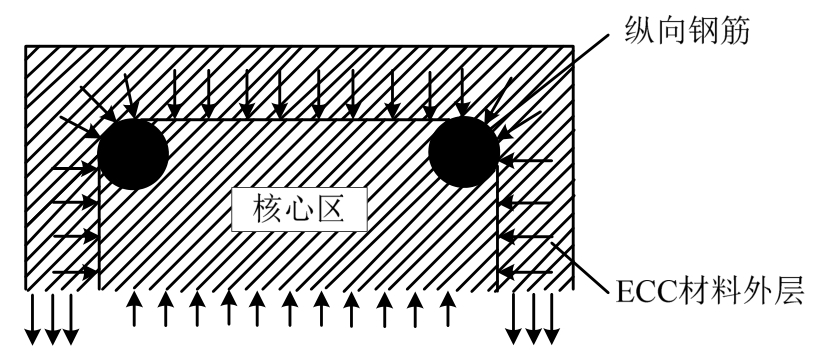
图4 悬臂梁截面示意图
Fig.4 Cross section of cantilever beam
表1 模拟材料的参数设计
Table 1 Parametric design of simulation materials
ECC材料 应变/(%)-2.0-0.5 0 0.01 3.8 6应力/MPa 0.0-80 0 4.5 6.0 0.0钢筋 应变/(%)-14-0.2 0 0.2 14 16应力/MPa-620-410 0 410 620 650
该实验研究的是ECC材料弯曲构件在往复循环加载卸载条件下的变形，即在悬臂梁的顶端加载水平推力，以位移控制的方式对构件进行加载。位移的加载方式如图5所示，采用往复循环加载[14―15]。
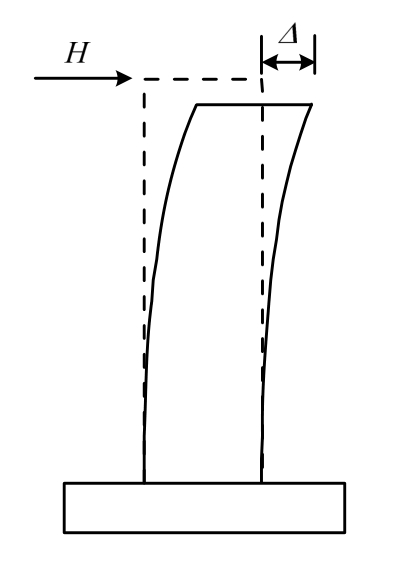
图5 结构和荷载布置示意图
Fig.5 Diagram of structure and load
加载形式如图6所示，该荷载的位移加载幅值不断增大，最大顶部加载位移为75 mm，层间位移角约15%。通过对结构进行分析计算，进一步得到结构的位移和反力，材料的应力和应变。经过数值模拟，本文得到了材料的水平荷载和层间位移角的关系。
图6 水平位移加载示意图
Fig.6 Horizontal displacement loading diagram
图7为实验所做的材料水平力与滑移率的关系曲线，和由 OpenSees模拟的关于相同材料、相同荷载条件下的模拟结果。从曲线上可以看出，实验结果和数值模拟的结果在形状和数值上都比较接近，最大的承载力均出现在层间位移角 3%附近，且承载力大约17 kN。另输出(-0.5，-0.5)这个角点上，关于 ECC材料的应力-应变关系曲线，如图 8所示。通过观察和对比，ECC材料的拉裂强度为4.0×106 Pa，拉裂应变大小为0.0001，抗拉强化强度为6.0×106 Pa，抗拉强化应变为0.038，抗拉破坏应变为 0.056，压裂强度为-0.8×107 Pa，压裂应变为-0.005，压碎应变为-0.012，这些参数均符合本研究所设计的材料参数。由此说明本文在 OpenSees中所研究编译的 ECC材料，可以较好地模拟实验的结果[16―17]。
图7 水平荷载和滑移率示意图
Fig.7 Horizontal load and drift ratiot
图8 ECC材料应力-应变关系曲线图
Fig.8 ECC material stress-strain diagram
2 ECC材料敏感性分析
有限元敏感性分析是计算梯度的一种重要的工具，常常用于基于梯度的优化分析、系统识别、模型更新和参数重要性研究等问题的研究。结构响应的敏感性或者梯度通常定义为
其中r代表结构任何的输出响应，例如全局响应(位移、速度、加速度等)和局部响应(高斯点上的应力、应变等)；θ为敏感性参数，在当前 ECC模型中取为材料参数，也包括荷载等。这里响应敏感性从数学上定义为响应r对θ的偏导数，即在其他参数确定不变的情况下，分析考虑由制定参数θ改变引起的响应r改变，也可以理解为响应的梯度。本文主要研究基于直接微分法(DDM)的 ECC材料敏感性，并同有限差分法(FDM)进行对比，以体现 DDM 的高效性和准确性[18―20]。
2.1 直接微分法框架
此方法是对有限元离散化后的平衡方程直接求导，通过求解此方程，计算材料敏感性。对涉及影响 ECC材料本构的各个参数可进行分别求导。通过直接微分法可以计算响应敏感性的精确值，计算方法可能得到解析解，因而可以弥补FDM算法上的某些缺点[21-22]。
本文采用有限元方法进行空间离散后，对结构系统的材料非线性模型的运动方程采用以下非线性微分方程：
式中：t表示时间；θ表示本研究要考虑的敏感性参数；u(t)表示节点位移矢量；M 表示质量矩阵；C表示阻尼矩阵；R表示历史结构内的非线性抵抗力矢量；F(t)表示施加的动荷载矢量。本文运用时间连续的空间离散运动方程(1)，利用已知的Newmark-β结构动力学时间步长的方法对时间进行数值积分，得到非线性矩阵代数方程(2)：
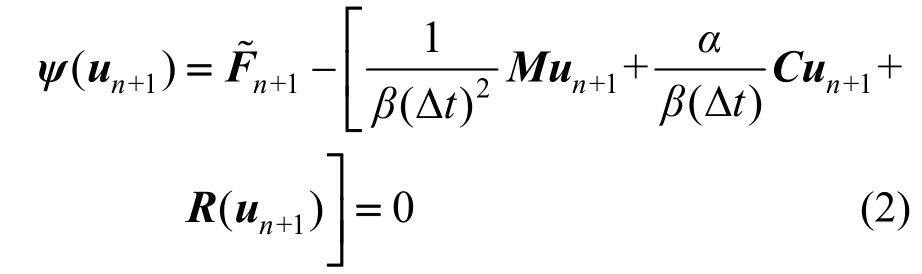
其中：
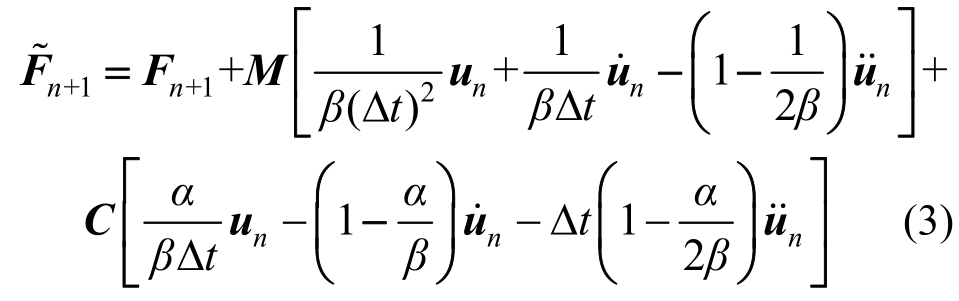
参数α、β控制Newmark-β法的准确性和稳定性；对式(2)进行直接求导：
其中：
式(4)中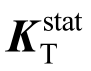
表示一致切线刚度矩阵，其可由
获得。
敏感性分析需对每一个敏感性参数θ都进行式(4)的求解。其中
的计算最为关键。该过程需要分别计算
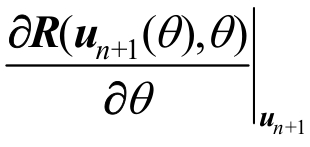和
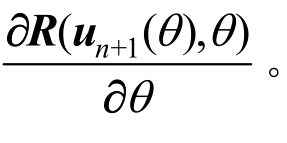求解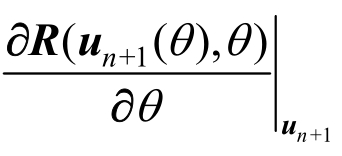
采用式(6)，即在单元的层面上求解，然后进行内力梯度的集成。
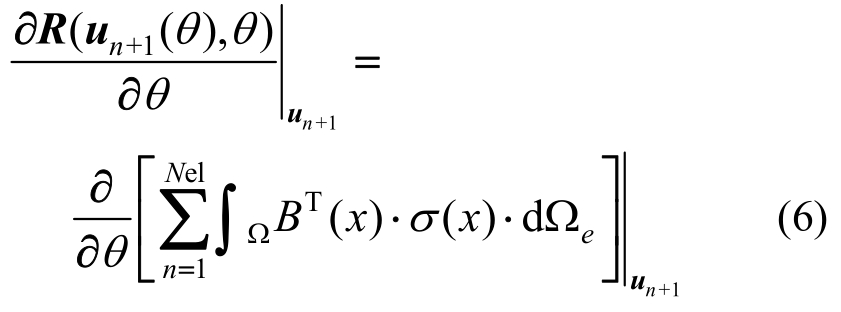
式中：
表示固定位移un+1再对敏感性参数θ求导；B表示应变位移转换矩阵；x表示空间坐标；Ω为单元域。先求解当应变un+1固定时，即
时的值
，求解之后，可以根据式(4)求解
再根据：
求解出无条件下的
然后求解无条件下的
2.2 有限差分法(FDM)简介
有限差分法通过两次扰动计算近似得到位移敏感性。有限差分方法具有简单、灵活以及通用性强的特点，计算过程如下:
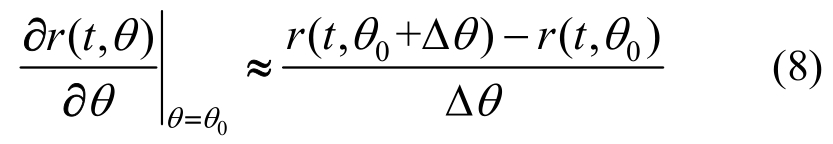
有限差分法的计算方式较为简单，比较适用于计算机计算，但是同时存在着很多缺点，比如计算成本较高，噪声对数值计算的影响较大，对精度要求较高。本文主要研究的是直接微分法，有限差分法作为验证 DDM 结果的一种方式，进一步体现DDM方法的准确性。
2.3 DDM和FEM对比分析
本文对ECC材料进行定义，根据如图2所示的ECC材料模型，需要确定拉裂强度σt0，拉裂应变大小εt0，抗拉强化强度σt1，抗拉强化应变εt1，抗拉破坏应变εt2，压裂强度σc0，压裂应变εc0，压碎应变εc1，以及部分加载卸载过程中需要的tα、cα、tβ、cβ，共12个参数，也就需要研究关于这十二个材料参数的敏感性分析[3,22]。
本研究采用图9的结构，在2节点处添加一个随时间序列的三角函数水平荷载，对2节点处的荷载采用梯段式逐步增大，逐渐的触发关于材料的12个参数，通过DDM和FEM对比，验证DDM敏感性的正确性。
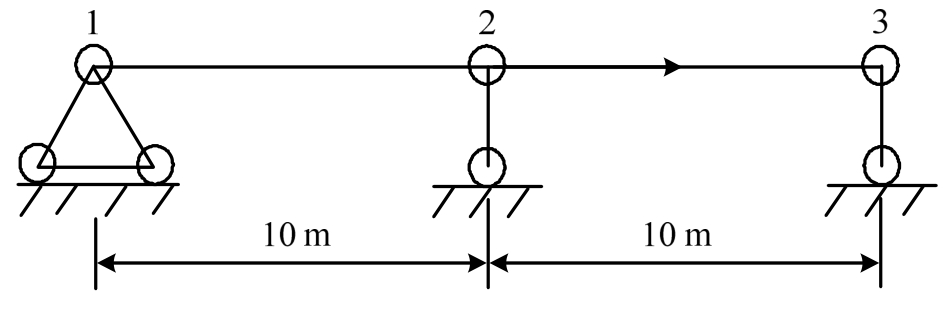
图9 简支梁水平加载示意图
Fig.9 The horizontal load acts on the simple beam
首先在2点作用一个大小为5000 N的水平三角函数荷载，通过600次迭代计算，每次迭代计算改变大小为50 N的荷载，以200次迭代为一个周期，对2点施加往复荷载。本文通过记录直接求导的结果，即直接微分法计算材料的敏感性，并通过扰动敏感性参数，即采用有限差分法，得到敏感性结果。图10为将二者进行比较和对照[23]。
由于有限差分法的局限性，即扰动的最佳幅度不易确定，故本研究分别设计了扰动值大小为1/10、1/100、1/1000等众多对照组，用来同直接微分法进行结果对比。图11是放大后的结果对比。
经过对比，不难发现，随着扰动值的逐渐缩小，即扰动值从1×10-1逐渐缩小直至1×10-5～1×10-7时，有限差分法计算的结果越来越接近直接微分法计算的结果，也就是通常所说的解析解的结果，这一点同本研究设计目的相同，同时也验证了直接微分法的正确性。但是当扰动值从1×10-7再次缩小时，通过图像可以发现，直接微分法计算的结果逐渐远离有限差分法计算的敏感性曲线，分析原因主要是由于精度的局限性等，由于需计算r ( t,θ0+Δθ)-r( t,θ0)，在相减的过程中损失了精度，因此更加说明有限差分法对响应的精度要求很高。本文采用了保留16位有效数字的方式，根据同DDM方法的对比，发现 FEM 计算的结果逐渐收敛于 1.0×10-7附近。
图10 ECC材料关于σt0参数的敏感性曲线
Fig.10 Sensitivity curve of ECC material forσt0
图11 ECC材料关于σt0参数的敏感性曲线(放大图)
Fig.11 Sensitivity curve of ECC material forσt0(enlarged view)
2.4 各参数敏感性分析
因为决定 ECC材料的参数有很多，所以有必要研究所有参数敏感性的相对重要程度[13]。同样以图7为例，本研究将示例从静力荷载更改为动力荷载。对该模型加载地震波，加速度的大小如图12所示。
本文将简支梁在该地震波荷载下各参数的位移敏感性归一化后的结果进行输出，对它们的峰值的绝对值进行比较，图13显示了ECC材料简支梁的 12个材料参数对水平位移响应的相对敏感性。此结构响应的敏感性参数按重要程度排列如下：拉裂强度σt0，抗拉强化强度σt1，参数βt，压裂应变εc0，压裂强度σc0。
图12 tabas地震波地震加速度示意图
Fig.12 Earthquake acceleration diagram
图13 各参数的位移敏感性比较
Fig.13 Comparison of the displacement sensitivity of each parameter
3 结论
本文在研究Tong-Seok Han等[8]提出的ECC本构的基础上，利用 OpenSees平台进行二次开发，实现了 ECC材料在通用有限元软件上的应用，为研究者通过数值模拟的方式研究 ECC材料提供了便利。从方法上，本文采用了递归的方式，对原有的 ECC的本构关系重新分类编号，通过多次自调用，达到减少判断、提高计算效率的目的。随后本文通过数值模拟与Gregor Fischer所研究的ECC材料构件在往复循环加载条件下弯曲变形的实验进行对比，证明了数值模拟结果的正确性和可行性。
随后本文使用直接微分法，研究了 ECC本构关于材料参数的敏感性，并同有限差分法的结果进行对比，不仅说明了DDM在计算精度和效率上的优势，同时对影响结构的材料参数相对敏感性进行了分析对比。本文将敏感性分析的方法应用于具体的连续梁之中，得到了在具体的地震荷载下各个参数相对于该连续梁模型的位移敏感性结果。该结果为基于敏感性响应的，进一步结构优化、结构可靠性分析以及有限元模型修正提供了基础。
[1]LI Victor C.高延性纤维增强水泥基复合材料的研究进展及应用[J].硅酸盐学报, 2007, 35(4): 531―536.LI Victor C.Progress and application of engineered cementitious composites[J].Journal of the Chinese Ceramic Society,2007, 35(4): 531―536.(in Chinese)
[2]Stavroulakis G E.Parameter sensitivity in nonlinear mechanics.Theory and finite element computations: by Kleiber M, Antúney H, Hien T D, Kowalczyck P, (Wiley,Chichester, 1997)[J].European Journal of Mechanics-A/Solids, 1998, 17(4): 702―703.
[3]Conte J P.Finite element response sensitivity analysis in earthquake engineering[J].Earthquake Engineering Frontiers in the New Millennium, 2001: 395―401.
[4]Conte J P, Vijalapura P K, Meghella M.Consistent finite-element response sensitivity analysis[J].Journal of Engineering Mechanics, 2003, 129(12): 1380―1393.
[5]Ditlevsen O, Madsen H O.Structural reliability methods[M].New York: Wiley, 1996.
[6]Zhang Y, Kiureghian A D.Dynamic response sensitivity of inelastic structures[J].Computer Methods in Applied Mechanics & Engineering, 1993, 108(1–2): 23―36.
[7]丁然, 芶双科, 樊健生, 等.后浇 LSECC 装配整体式梁受力性能试验研究[J].工程力学, 2018, 35(10): 56―65, 74.Ding Ran, Gou Shuangke, Fan Jiansheng, et al.Experimental research on mechanical performance of monolithic precast beams using cast-in-place low-shrinkage engineered cementitious composite[J].Engineering Mechanics, 2018, 35(10): 56―65, 74.(in Chinese)
[8]Han T S, Feenstra P H, Billington S L.Simulation of highly ductile fiber-reinforced cement based composite components under cyclic loading[J].ACI Structural Journal, 2003, 100(6): 749―757.
[9]Li V C, Leung C K Y.Steady-state and multiple cracking of short random fiber composites[J].Journal of Engineering Mechanics, 1992, 118(11): 2246―2264.
[10]Li V C, Stang H, Krenchel H.Micromechanics of crack bridging in fibre-reinforced concrete[J].Materials &Structures, 1993, 26(8): 486―494.
[11]Dhawale A W, Joshi V P.Engineered cementitious composites for structural applications[J].Journal of Materials in Civil Engineering, 1998, 10(2): 66―69.
[12]Fischer G, Li V C.Effect of matrix ductility on deformation behavior of steel reinforced ECC flexural members under reversed cyclic loading conditions[J].ACI Structural Journal, 2002, 99(6): 781―790.
[13]Fischer G, Li V C.Deformation behavior of fiber-reinforced polymer reinforced engineered cementitious composite (ECC)flexural members under reversed cyclic loading conditions[J].ACI Structural Journal, 2003, 100(1): 25―35.
[14]司炳君, 孙治国, 艾庆华, 等.钢筋混凝土桥墩滞回性能的有限元参数敏感性分析及模型改进[J].工程力学,2009, 26(1): 174―180.Si Bingjun, Sun Zhiguo, Ai Qinghua, et al.Sensitive analysis and model modification for finite element analysis of R/C bridge piers under cyclic loading[J].Engineering Mechanics, 2009, 26(1): 174―180.(in Chinese)
[15]潘金龙, 何佶轩, 王路平, 等.ECC双轴压力学性能及破坏准则试验研究[J].工程力学, 2016, 33(6): 186―193.Pan Jinlong, He Jixuan, Wang Luping, et al.Experimental study on mechanical behaviors and failure criterion of engineered cementitious composites under biaxial compression[J].Engineering Mechanics, 2016,33(6): 186―193.(in Chinese)
[16]Zheng Y, Dong Y.Performance-based assessment of bridges with steel-SMA reinforced piers in a life-cycle context by numerical approach[J].Bulletin of Earthquake Engineering, 2018: 1―22.
[17]Zheng Y, Dong Y, Li Y.Resilience and life-cycle performance of smart bridges with shape memory alloy(SMA)-cable-based bearings[J].Construction and Building Materials, 2018, 158: 389―400.
[18]Conte J P, Barbato M, Spacone E.Finite element response sensitivity analysis using force-based frame models[J].International Journal for Numerical Methods in Engineering, 2004, 59(13): 1781―1820.
[19]Gu Q, Barbato M, Conte J P.Handling of constraints in finite-element response sensitivity analysis[J].Journal of Engineering Mechanics, 2009, 135(12): 1427―1438.
[20]Fenves G L, Filippou F C, Scott M H, et al.Response sensitivity for nonlinear beam column elements[J].Journal of Structural Engineering, 2004, 130(9): 1281―1288.
[21]Haukaas T, Kiureghian A D.Strategies for finding the design point in non-linear finite element reliability analysis[J].Probabilistic Engineering Mechanics, 2006,21(2): 133―147.
[22]Gu Q, Conte J P, Elgamal A, et al.Finite element response sensitivity analysis of multi-yield-surface J 2, plasticity model by direct differentiation method[J].Computer Methods in Applied Mechanics & Engineering, 2009,198(30–32): 2272―2285.
[23]Barbato M, Gu Q, Conte J P.Probabilistic push over analysis of structural and soil-structure systems[J].Journal of Structural Engineering, 2010, 136(11): 1330―1341.