近年来，巨型混合结构体系(如巨型框架-核心筒-伸臂)[1―3]成为超高层建筑的主要抗侧力体系之一，其中伸臂桁架是连接外围框架和内部核心筒的重要抗侧力构件[4]。众多学者以试验为基本手段，研究了不同构造伸臂桁架及连接节点的抗震工作机理。如赵宪忠等[5]、陈以一等[6―7]以上海中心为工程背景，选取典型单榀伸臂桁架，进行了单调加载和往复加载试验，发现试件的破坏模式均表现为伸臂桁架斜腹杆的受压屈曲，导致承载力出现退化；聂建国等[8―9]以武汉中心超高层建筑为背景，对两个不同构造的伸臂桁架-核心筒剪力墙节点进行拟静力试验研究，也发现了类似的破坏模式，即两个试件的破坏均为伸臂桁架斜腹杆的弹塑性整体屈曲。可见，传统伸臂桁架斜腹杆的受压屈曲是其主要破坏形式，进而会影响其对整体结构响应的控制。
为提高伸臂桁架对结构振动的控制作用，众多学者开展了新型伸臂桁架的研究。如 Smith和Willford[10]提出了阻尼伸臂桁架的概念，在传统伸臂桁架中设置阻尼器，提高耗能能力，进而减小高层建筑在风荷载作用下的振动；周颖等[11―12]、丁洁民等[13]研究了粘滞阻尼伸臂桁架的抗震性能及其对结构抗震性能的影响；杨青顺等[14]研究了端部阻尼器伸臂桁架的抗震性能。另外，杨青顺等[15]、任重翠等[16]提出了用屈曲约束支撑替换传统伸臂桁架斜腹杆的新型伸臂桁架，Lin等[17]提出了利用屈曲约束支撑连接伸臂和外围巨柱的新型阻尼伸臂概念。上述新型伸臂桁架虽然能从一定程度上改善传统伸臂刚度、承载力退化、耗能不足等问题，但仍然存在优化空间。如阻尼伸臂桁架的刚度较小，可能会影响内、外筒之间力的传递效率；而屈曲约束支撑伸臂桁架有较明显残余变形，不利于震后结构的快速修复[18―19]。
为进一步完善上述问题，本文借鉴新型伸臂桁架的优点，提出了一种自复位粘弹性斜腹杆(SC-VEDM)代替传统的型钢腹杆，通过合理的构造措施将具有复位能力的预应力钢筋和具有耗能能力的粘弹性材料相结合，实现伸臂桁架的自复位功能和耗能能力；重点阐释了该斜腹杆的构造形式、工作原理和各阶段受力特性，并提出SC-VEDM的恢复力模型；设计了典型的 SC-VEDM，并建立其相应的精细有限元模型，模拟其滞回性能，验证了恢复力模型的合理性，为后续自复位耗能伸臂桁架的试验及抗震性能研究提供了理论依据。
1 SC-VEDM构造形式与工作原理
1.1 构造形式
SC-VEDM 主要包括传力机构、耗能元件和复位元件，构造形式如图1所示。传力机构包括内、外管件和左、右端板，初始状态下，内、外管件均与左、右端板接触但不固定；耗能元件为粘弹性材料层，通过工业硫化的方法将粘弹性材料层粘贴在内、外管之间；复位元件为预应力筋，通过将预应力筋两端分别锚固于左、右端板，并施加一定的预拉力使得各部分形成整体，使杆件具备较大的初始刚度。当杆件轴力小于预拉力时，杆件作为整体发生变形；当杆件轴力大于激活力时，内、外管发生相对运动，粘弹性层开始剪切耗能，且内、外管推动左、右端板使预应力钢筋受拉伸长，从而提供恢复力保证腹杆的自复位能力。设计时，可根据不同地震水准下结构的性能需求灵活调整预拉力和粘弹性层等参数，使杆件能同时满足不同地震水准下的功能需求，如多遇地震下提供足够的刚度保证结构稳定，设防或罕遇地震下提供足够的耗能能力减轻结构损伤，且震后能复位。
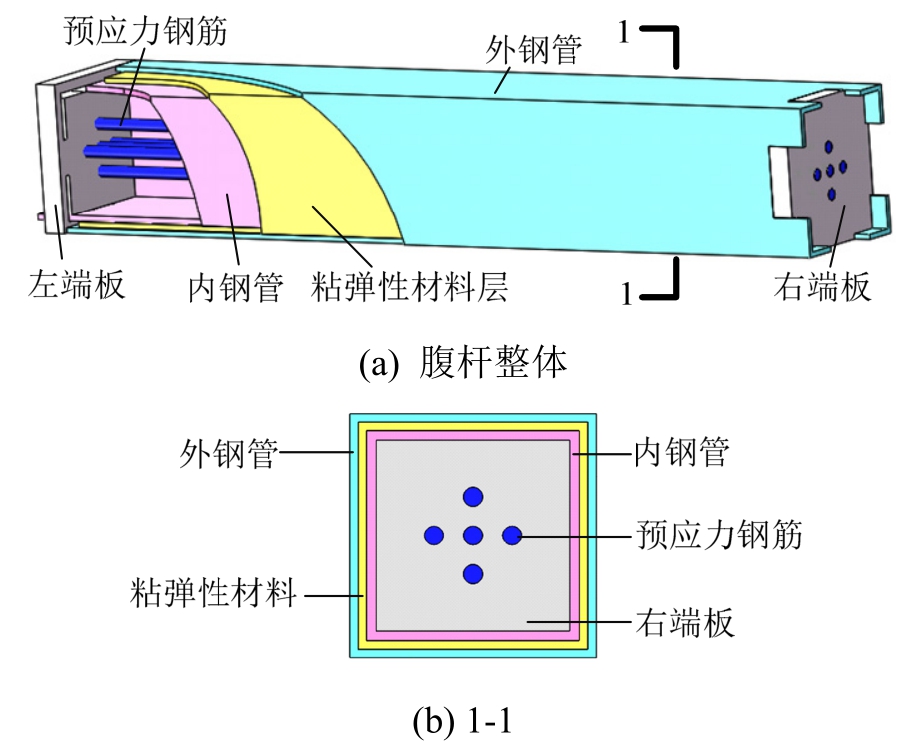
图1 SC-VEDM构造形式
Fig.1 Configuration of SC-VEDM
1.2 工作原理
由构造形式可知，SC-VEDM 的受力特性主要由预应力筋和粘弹性层确定。在预应力筋未屈服前，其力和位移关系为线弹性。当不考虑粘弹性层，杆件中仅包含内、外管件、左右端板和预应力筋时，其恢复力模型体现为典型的双线性弹性，如图2(a)所示，其中K1为腹杆第一刚度，kp为预应力筋刚度；对于粘弹性层，文献研究[20―21]表明其剪力与剪切变形的关系近似为椭圆，如图2(b)所示，可采用经典的弹簧和阻尼单元并联的Kelvin模型描述，可用式(1)表示：
式中：fs=kvδ表示粘弹性材料变形产生的弹性力；fd=(ηkv/ω)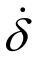
表示粘弹性材料变形产生的阻尼力；kv为粘弹性材料的等效刚度；η为粘弹性材料的耗损因子；ω为外荷载频率。
当上述两个系统组合在一起共同作用时，杆件的恢复力模型可近似由两个系统并联叠加得到，其恢复力模型示意图如图2(c)所示，呈现出典型的旗形特征。当受力较小时，杆件具有较大的初始刚度，发生整体弹性变形；当受力较大超过激活力时，粘弹性层被激活，开始耗能；且整个受力过程中，预应力筋一直处于被拉伸状态，提供复位力使杆件回到初始状态。
腹杆的工作原理如图3所示，杆件各阶段的工作机理与受力特征讨论如下。
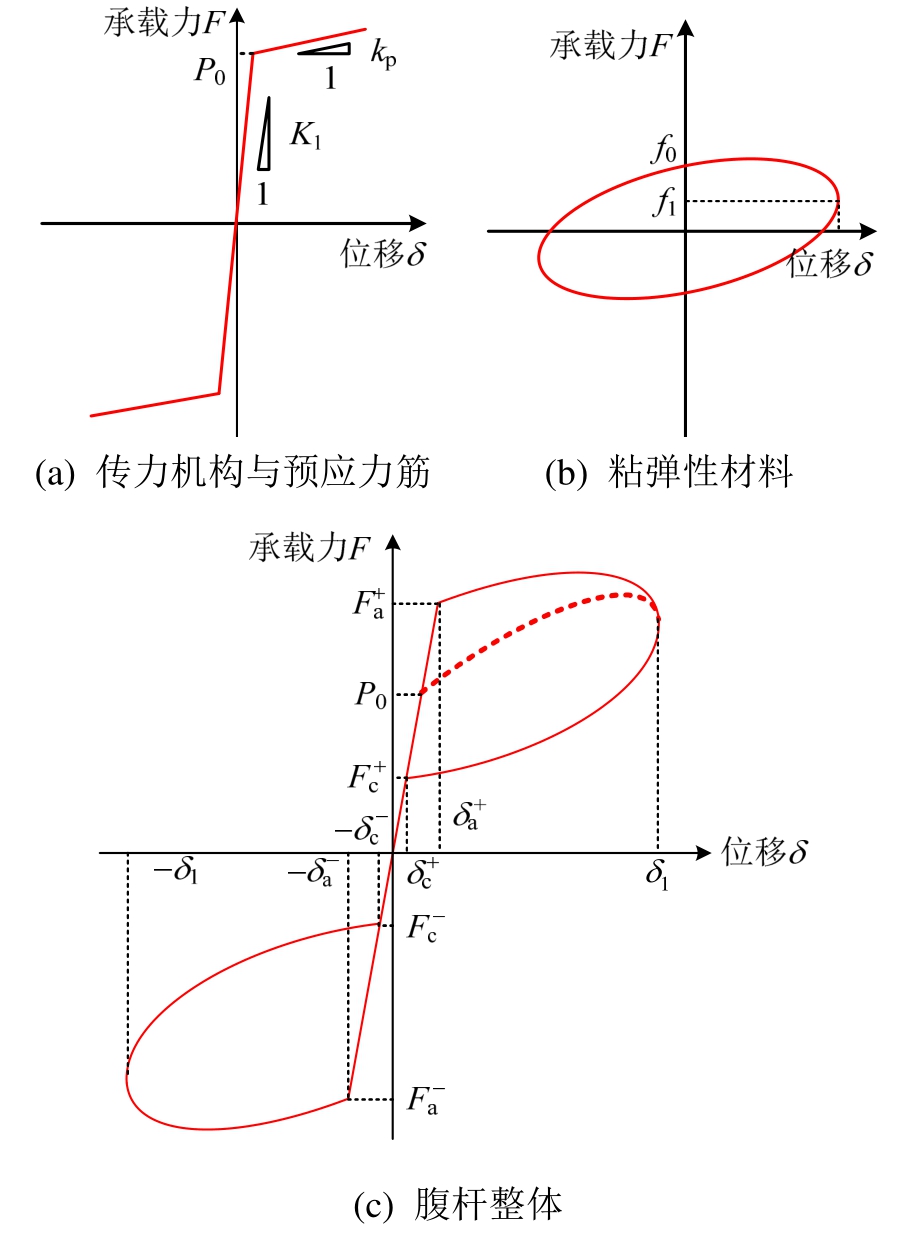
图2 SC-VEDM滞回模型
Fig.2 Hysteretic model of SC-VEDM
图3 SC-VEDM工作原理
Fig.3 Mechanism of SC-VEDM
初始状态下，预应力筋通过初始预拉力P0连接两端端板与内、外管紧密相连形成整体，为自平衡体系。此时，内、外管所受的压力与预应力筋的拉力平衡，内、外管的轴压力大小可按其轴向刚度分配，具体可按式(2)和式(3)计算得到：
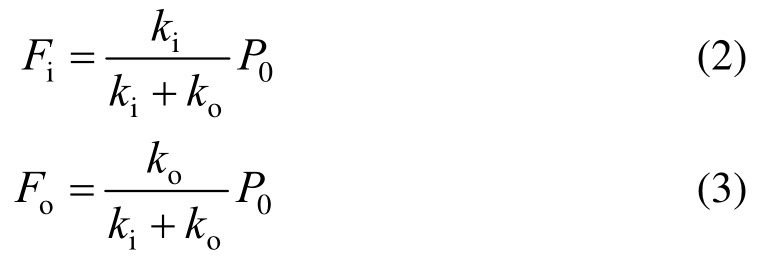
式中：P0为预应力筋初始预拉力；ki和ko分别为腹杆内、外管轴向刚度。
在拉力F作用且端板与内、外管未脱开时，杆件发生整体弹性变形，此时杆件的刚度由内、外管、预应力筋和粘弹性层的轴向刚度并联组成。由于粘弹性层的轴向刚度远小于内、外管和预应力筋的刚度，故杆件的初始刚度K1可按式(4)计算。此时，内、外管的内力分别如式(5)和式(6)所示：
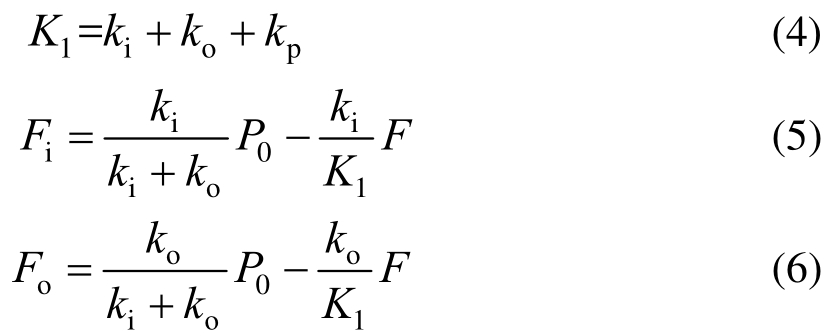
当拉力继续增大，直至等于杆件的激活力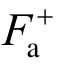
时，两侧端板处于即将与内、外管脱开的临界状态，此时杆件受力为
假设此时杆件受拉的轴向变形为
即可得到杆件受拉的起滑力如式(7)所示。若预应力筋的刚度远小于内、外管轴向刚度，则激活力近似为预拉力与阻尼力之和。在该临界状态下，外力全部由预应力筋承担，内、外管的内力理论上基本为 0。需要特别说明的是，粘弹性材料是一种位移和速度均相关的材料，在首次激活发生剪切变形时，剪切变形和速度均为0，故此时的阻尼力f0为0；但再次被激活发生剪切变形时，虽然剪切变形为 0，但速度却不为0，故f0也不为0。
随着拉力继续增加，超过该临界状态后，内、外管发生相对运动，粘弹性层开始发生剪切变形。此时，杆件的刚度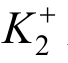
主要由预应力筋的轴向刚度和粘弹性层的剪切刚度并联组成，如式(8)所示。杆件的变形主要体现为粘弹性层的剪切变形和预应力筋轴向变形，此时，内、外管主要受粘弹性材料层的弹性力和阻尼力，可用式(9)表示：
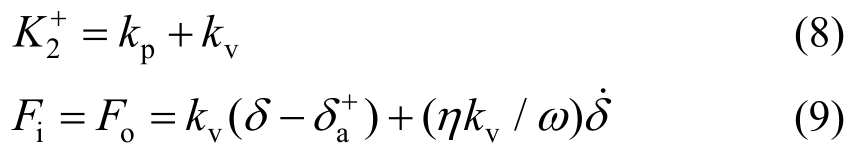
当拉力逐渐卸载至端板与内、外管间隙闭合时，杆件的受力为
假设此时杆件卸载的闭合位移为
即可得到杆件的闭合力如式(10)所示。当拉力继续减小时，杆件再次发生整体变形。
对于杆件受压过程，与受拉基本一致，但存在以下两点差异：
1)杆件受压且端板与内、外管未脱开前，杆件整体被压缩，预应力筋缩短进而引起应力损失。故受压端板与内、外管脱开临界状态时，杆件压力为
假设此时杆件受压的轴向变形
，可得杆件受压的起滑力如式(11)所示。可见，杆件受压的激活力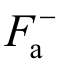
略小于受拉激活力
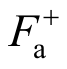，当预应力筋的轴向刚度远小于内、外管轴向刚度时，受拉和受压的激活力近似相等；
2)当压力超过激活力后，内、外管发生相对运动，粘弹性层发生剪切变形，此时杆件的刚度为预应力轴向刚度与粘弹性层等效刚度并联后再与内、外管轴向刚度串联(如图3所示)，如式(12)所示。可见，受压激活后，杆件的轴向刚度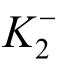
略小于受拉刚度
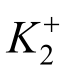，当内、外管刚度远大于预应力筋和粘弹性层刚度时，两者近似相等。
2 SC-VEDM恢复力模型
根据前文所述SC-VEDM各阶段工作原理与滞回曲线示意图，滞回曲线各阶段恢复力F与位移δ对应关系可进行如式(13)归纳：
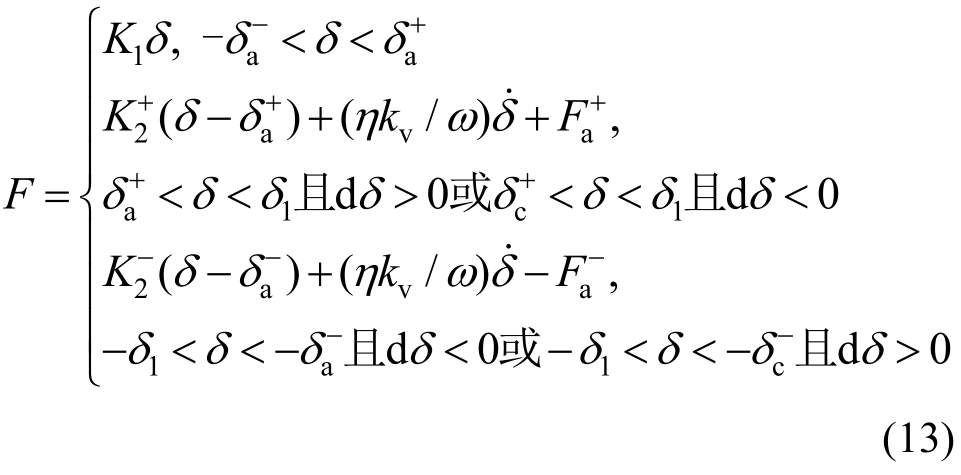
式中：
分别为受拉起滑与闭合时的位移；δ1为腹杆变形最大位移；
分别为受压起滑与闭合时的位移。
3 SC-VEDM滞回特性数值模拟
为进一步研究SC-VEDM的滞回特性，设计了一根典型的SC-VEDM腹杆，利用通用有限元软件MSC.Marc建立了精细有限元模型，对其滞回特性进行模拟，并与理论恢复力模型进行了对比。
3.1 粘弹性材料模拟方法
在最大设计变形范围内，SC-VEDM 中内、外钢管和预应力筋基本保持弹性，故关键在于粘弹性材料的模拟。研究表明[22―23]，Mooney-Rivlin材料本构模型能较好地模拟粘弹性材料的力学特性。Mooney-Rivlin材料模型中的弹性常数可根据材性试验确定，而粘性参数如松弛剪切模量Gi和松弛时间τi等则很难通过试验直接测量。目前大多数粘弹性材料试验均能直接获取不同频率下材料的存储剪切模量和耗损剪切模量(或耗损因子)。研究表明[24―25]，不同频率下的剪切存储模量和耗损剪切模量与粘性参数可通过拉普拉斯变换(如式(14)和式(15)所示)进行相互转换。
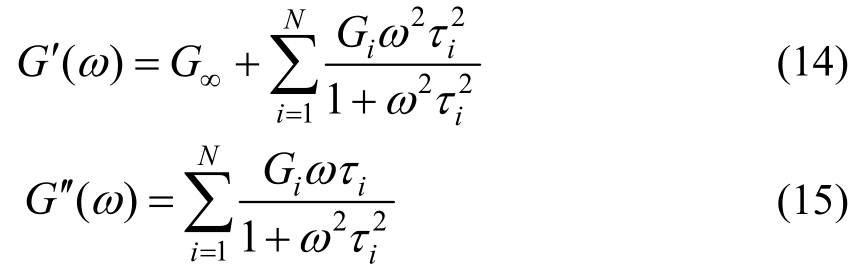
式中：G∞表示长期剪切模量；N表示函数阶数。
为了保证数值模拟的准确性，首先选取Montgomery 和 Christopoulos等[26]、Xu 等[27]开展的粘弹性材性试验对上述模拟方法的准确性进行验证。
Montgomery和Christopoulos等[26]提出了一种新型粘弹性阻尼连梁代替传统的混凝土连梁，来提高超高层建筑的抗风和抗震性能，并开展了相应粘弹性材料的材性试验。材性试验的构件主要尺寸如图4所示，对其在不同频率和不同位移幅值下的滞回特性进行了测试。利用有限元软件MSC.Marc建立了试件的实体单元模型，采用Mooney-Rivlin材料模型模拟粘弹性材料。其粘性参数根据文献试验中获取的不同频率下的存储剪切模量和耗损剪切模量进行拉普拉斯变换后拟合得到。粘弹性材料50%应变下，不同加载频率的模拟与试验滞回曲线对比如图5(a)所示，0.2 Hz加载频率下，不同加载应变的模拟与试验滞回曲线对比如图5(b)所示，可见，模拟结果与试验拟合良好。
图4 Christopoulos等[26]的粘弹性阻尼器尺寸
Fig.4 Details of viscoelastic damper of Christopoulos et al’s[26]
图5 Christopoulos等[26]的试验与有限元分析对比
Fig.5 Comparison of Christopoulos et al’s[26] test with FEM
Xu等[27]为了使粘弹性材料在土木工程中广泛应用，研制了一种高耗能、低频率的粘弹性材料，并制作粘弹性阻尼器(3层7 mm厚钢板夹 2层 10 mm厚粘弹性材料，每层材料面积为3000 mm2)对材料进行试验测试。本文根据其试验数据得到相应材料参数，在 MSC.Marc中建立了试件的实体有限元模型，对其滞回性能的模拟如图6所示。图6(a)为控制加载位移为10 mm时不同频率的滞回曲线对比情况，图6(b)为控制加载频率为0.2 Hz时不同幅值的滞回曲线对比情况，可见，在不同频率和加载位移下，模拟与试验结果均吻合良好。
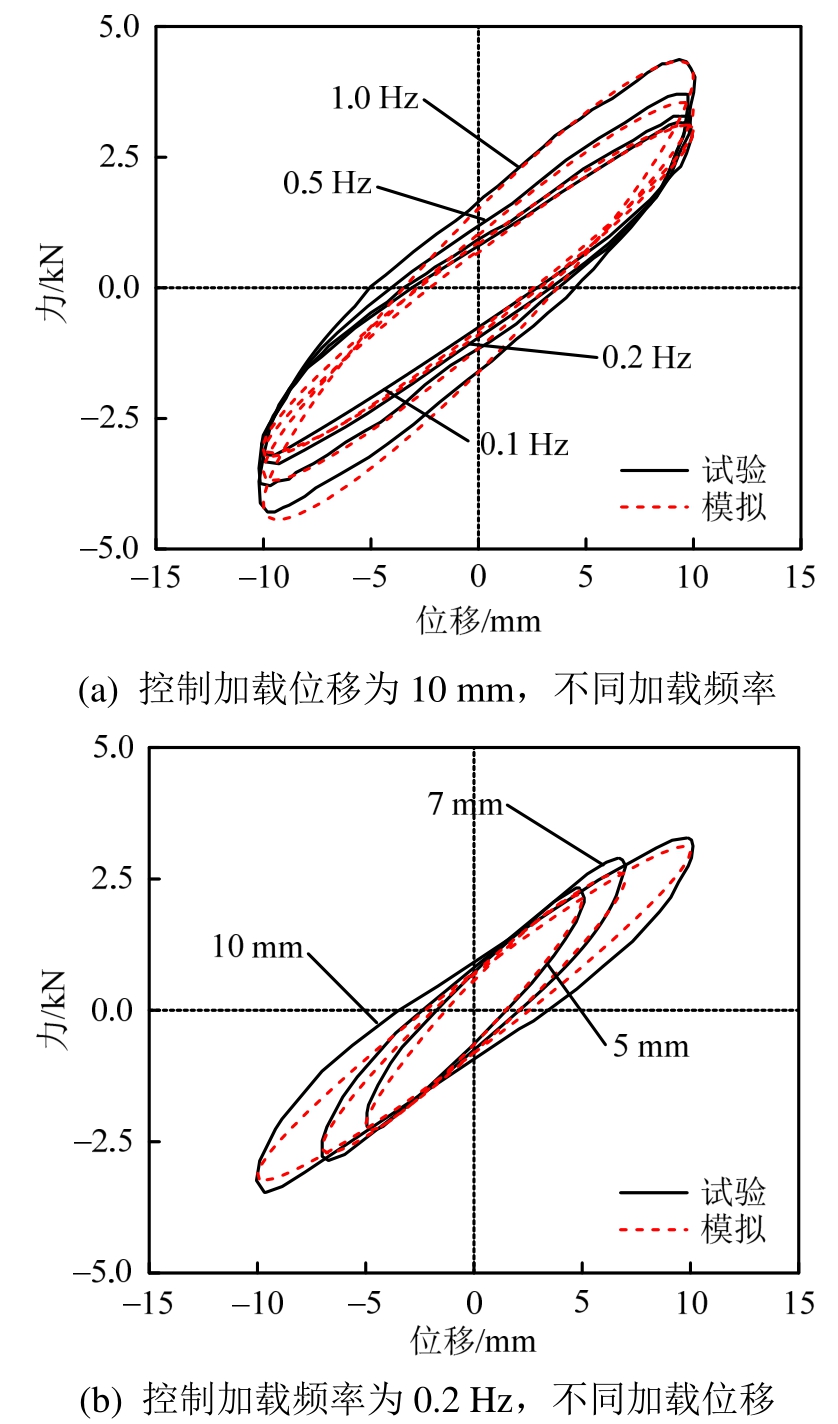
图6 Xu等[27]的试验与有限元分析对比
Fig.6 Comparison of Xu et al’s[27] test with FEM
综上对比，利用Mooney-Rivlin材料模型模拟粘弹性材料，并利用拉普拉斯变换后拟合粘性参数的方法能较好地模拟粘弹性材料不同频率和位移幅值下的滞回特性。
3.2 SC-VEDM滞回特性模拟
首先以文献[15]中的伸臂桁架为原型，设计自复位粘弹性腹杆。设计时，以普通型钢腹杆为参考，并假定 SC-VEDM 的性能目标是多遇地震下不激活，能提供足够刚度，在设防或罕遇地震下被激活，开始耗能。故SC-VEDM的初始刚度K1可近似与普通腹杆相等，激活力大于多遇地震下普通腹杆的轴力。进而可根据第一刚度K1估算内、外管截面尺寸，此外内、外钢管还需满足强度和稳定性需求[28]。
最终设计杆件的主要尺寸如下：腹杆全长1310 mm，外管为205 mm×205 mm×7 mm的箱形截面钢管，内管为 177 mm×177 mm×8 mm 的箱形截面钢管，粘弹性材料厚7 mm，端板为30 mm厚钢板，直径为15.2 mm的预应力筋共5根，总预拉力为450 kN。内、外管采用Q345钢材，端板采用Q420钢材，预应力筋抗拉强度1860 MPa，粘弹性材料参数根据当地某粘弹性材料公司生产的材料取值[29]。采用MSC.Marc有限元软件建立有限元模型如图7所示，其中预应力筋用9号杆单元模拟，内、外管、端板和粘弹性材料用7号实体单元模拟，端板通过设置接触与内、外管连接。
图7 SC-VEDM的有限元模型
Fig.7 Finite element model of SC-VEDM
采用正弦位移激励，对SC-VEDM的滞回特性进行模拟。如图8所示，SC-VEDM的滞回特性与前文描述相符合，起滑之前主要是杆件整体变形，刚度较大；起滑之后预应力筋开始提供复位能力，同时粘弹性材料开始耗能，且耗能随频率、位移增大而增大。图8(a)所示为加载频率0.3 Hz，加载位移分别为3 mm、5 mm、7 mm时模拟结果与理论恢复力模型对比，整体吻合良好，其中第一刚度相对偏差为0.4%，7 mm受压时极限承载力相对偏差最大，相对偏差值为4.64%；图8(b)所示为加载位移5 mm，加载频率分别为0.1 Hz、0.3 Hz、0.5 Hz时模拟结果与理论恢复力模型比较，两者吻合良好，0.5 Hz时受压极限承载力相对偏差最大，相对偏差最大值为3.91%。
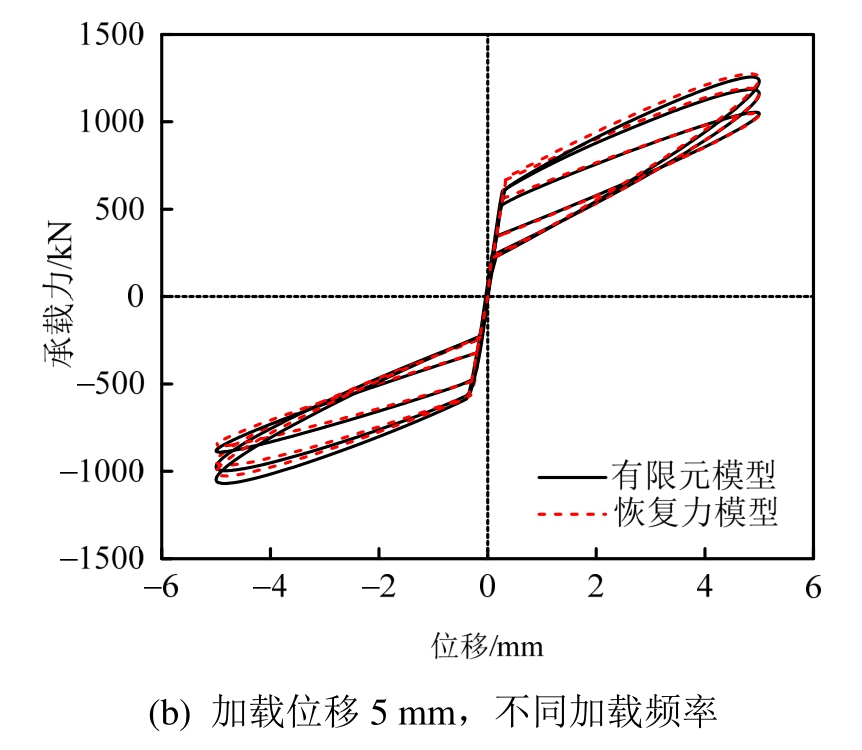
图8 有限元模型与恢复力模型结果对比
Fig.8 Comparison of results between finite element model and restoring force model
图9(a)给出了加载频率0.3 Hz，加载位移分别为3 mm、5 mm、7 mm时有限元模型与恢复力模型的耗能对比情况，可见恢复力模型预测与有限元模拟结果基本一致，且腹杆受拉时耗能大于受压时耗能，在腹杆受压7 mm时，结果相差最大，相对偏差为10.9%；图9(b)为加载位移5 mm时，加载频率分别为 0.1 Hz、0.3 Hz、0.5 Hz时有限元模型与恢复力模型的耗能对比情况，拟合结果吻合良好，在腹杆加载频率为0.5 Hz受压时，对比结果相差最大，相对偏差为7.4%。
图9 有限元模型与恢复力模型耗能对比
Fig.9 Comparison of energy consumption between finite element model and restoring force model
对比分析表明，承载能力和耗能能力的最大相对偏差均出现在腹杆受压过程中。这是由于腹杆中粘弹性材料几乎通长布置，在腹杆受压全过程中，粘弹性材料会影响内、外管整体变形；而恢复力模型为简化计算，忽略受压过程中粘弹性材料对内、外管的影响，导致恢复力模型中第二刚度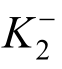
略小于实际刚度，进而引起恢复力模型的承载力和耗能能力略小于有限元模拟结果，但承载力的最大偏差不超过5%，仍在工程可接受的范围内。
在不超过最大容许设计变形时，SC-VEDM 的内、外管和预应力筋始终保持弹性，由粘弹性层剪切变形耗散地震能量，但在极罕遇地震下，容许杆件超出最大变形，预应力筋可能发生屈服，本节进一步考查了SC-VEDM在预应力筋屈服后的滞回性能。图10为加载频率为0.1 Hz，加载位移为11 mm时有限元模型模拟的滞回曲线，此时预应力筋已经进入塑性，在预应力筋第一次受拉进入塑性时，杆件的刚度迅速降低，主要由粘弹性层的剪切刚度提供，承载力不再上升，基本保持稳定。由于预应力筋进入塑性，出现了不可恢复的塑性变形，会导致预应力的损失，因此，杆件再次激活时，激活力从原来的450 kN降为314 kN，但其滞回特性仍与预应力筋未屈服时一致，滞回环形状仍然类似“旗形”，呈现出了较好的耗能能力和复位性能。
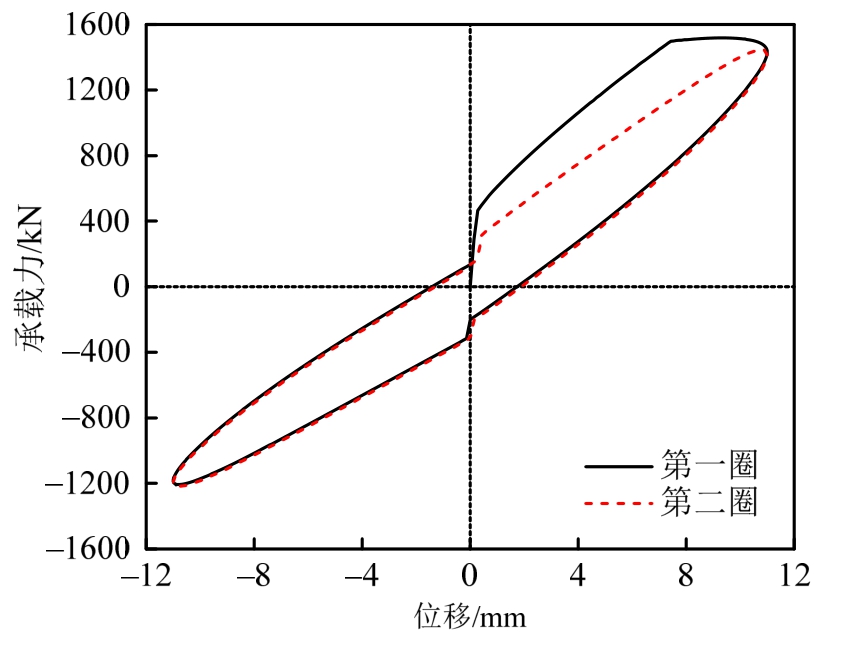
图10 预应力筋屈服后杆件的滞回曲线
Fig.10 Hysteretic curves of SC-VEDM after prestressed tendon yielded
4 结论
本文提出了一种新型自复位粘弹性腹杆(SC-VEDM)，介绍了其构造形式和各阶段的工作原理，建立了描述SC-VEDM 的理论恢复力模型，并对其滞回特性进行了数值模拟，得到如下主要结论：
1)本文提出的构造措施保证伸臂桁架的SC-VEDM 腹杆在多遇地震下具有较大的刚度，在设防或罕遇地震下具有较强的耗能和复位能力，为后续自复位耗能伸臂桁架的抗震性能研究奠定了基础。
2)利用拉普拉斯变换拟合的方法可以从不同频率下存储和耗损剪切模量中识别出粘弹性材料的关键粘性参数Gi和τi，利用试验与模拟结果对比，论证了该方法的准确性与合理性。
3)SC-VEDM的数值模拟与理论恢复力模型吻合良好，两者第一刚度相对偏差为0.4%，在受压最大位移处的承载力相对偏差最大值为4.64%，论证本文建立的理论恢复力模型的正确性。
4)在极罕遇地下，SC-VEDM超出容许变形且预应力筋屈服后，激活力略有降低，耗能能力稳定，残余变形可控，表明SC-VEDM在极罕遇地震下仍具有较好的抗震和复位性能。
[1]徐培福, 王翠坤, 肖从真.中国高层建筑结构发展与展望[J].建筑结构, 2009, 39(9): 28―32.Xu Peifu, Wang Cuikun, Xiao Congzhen.Development and prospect of high-rise building structures in China[J].Building Structure, 2009, 39(9): 28―32.(in Chinese)
[2]王翠坤, 田春雨, 肖从真.高层建筑中钢-混凝土混合结构的研究与应用进展[J].建筑结构, 2011, 41(11):28―33.Wang Cuikun, Tian Chunyu, Xiao Congzhen.Development of research and application of concrete-steel hybrid high-rise building structures[J].Building Structure, 2011, 41(11): 28―33.(in Chinese)
[3]汪大绥, 周建龙.我国高层建筑钢-混凝土混合结构发展与展望[J].建筑结构学报, 2010, 31(6): 62―70.Wang Dasui, Zhou Jianlong.Development and prospsct of hybrid high-rise building structures in China[J].Journal of Building Structures, 2010, 31(6): 62―70.(in Chinese)
[4]徐培福, 黄吉锋, 肖从真, 等.带加强层的框架-核心筒结构抗震设计中的几个问题[J].建筑结构学报,1998, 20(4): 2―10.Xu Peifu, Huang Jifeng, Xiao Congzhen, et al.Some problems in aseismic design of frame-core wall structures with strengthened storeys[J].Journal of Building Structures, 1998, 20(4): 2―10.(in Chinese)
[5]赵宪忠, 王斌, 陈以一, 等.上海中心大厦伸臂桁架与巨柱和核心筒连接的静力性能试验研究[J].建筑结构学报, 2013, 34(2): 20―28.Zhao Xianzhong, Wang Bin, Chen Yiyi, et al.Monotonic static tests on outrigger truss and its connection with mega column and core tube of the Shanghai Tower[J].Journal of Building Structures, 2013, 34(2): 20―28.(in Chinese)
[6]陈以一, 王斌, 赵宪忠, 等.上海中心大厦伸臂桁架与巨柱和核心筒连接的抗震性能试验研究[J].建筑结构学报, 2013, 34(2): 29―36.Chen Yiyi, Wang Bin, Zhao Xianzhong, et al.Hysteretic tests on outrigger truss and its connection with mega column and core tube of the Shanghai Tower[J].Journal of Building Structures, 2013, 34(2): 29―36.(in Chinese)
[7]严鹏, 王伟, 陈以一.钢管混凝土柱与伸臂桁架连接节点试验研究[J].工程力学, 2013, 30(增刊): 78―82.Yan Peng, Wang Wei, Chen Yiyi.Experimental study on concrete filled steel tube column to outrigger truss connection[J].Engineering Mechanics, 2013, 30(Suppl):78―82.(in Chinese)
[8]聂建国, 丁然, 樊健生.超高层建筑伸臂桁架-核心筒剪力墙节点受力性能数值与理论研究[J].工程力学,2014, 31(1): 46―55.Nie Jianguo, Ding Ran, Fan Jiansheng.Numerical and theoretical research on mechanical performance of outrigger truss-wall joint in super high-rise buildings[J].Engineering Mechanics, 2014, 31(1): 46―55.(in Chinese)
[9]Nie J G, Ding R.Experimental research on seismic performance of K-style steel outrigger truss to concrete core tube wall joints[C]//Structures Congress 2013:Bridging Your Passion with Your Profession.Pittsburgh:Structural Engineering Institute of ASCE, 2013: 2802―2813.
[10]Smith R J, Willford M R.The damped outrigger concept for tall buildings[J].The Structural Design of Tall and Special Buildings, 2007, 16(4): 501―517.
[11]李宏描, 周颖.黏滞阻尼器伸臂桁架布置对超高层结构减震性能影响研究[J].结构工程师, 2015, 31(3):63―68.Li Hongmiao, Zhou Ying.The effect of the configurations of viscous damped outriggers on the seismic performance of a super-tall building[J].Structural Engineer, 2015, 31(3): 63―68.(in Chinese)
[12]邢丽丽, 周颖.黏滞阻尼器型伸臂桁架的最优布置形式研究[J].地震工程与工程振动, 2016, 36(1): 68―76.Xing Lili, Zhou Ying.The study of optimal arrangement form of outrigger trusses with viscous dampers[J].Seismic Engineering and Engineering Vibration, 2016,36(1): 68―76.(in Chinese)
[13]丁洁民, 王世玉, 吴宏磊.黏滞阻尼伸臂桁架在超高层结构中的应用研究[J].建筑结构学报, 2016, 37(增刊1): 48―54.Ding Jiemin, Wang Shiyu, Wu Honglei.Application research of viscous damping outrigger truss in super high-rise building[J].Journal of Building Structures,2016, 37(Suppl 1): 48―54.(in Chinese)
[14]杨青顺, 甄伟, 陆新征, 等.带端部阻尼器伸臂桁架的抗震性能试验研究[J].工程力学, 2018, 35(2): 47―58.Yang Qingshun, Zhen Wei, Lu Xinzheng, et al.Experimental study on the seismic performance of damped outriggers[J].Engineering Mechanics, 2018,35(2): 47―58.(in Chinese)
[15]杨青顺, 甄伟, 解琳琳, 等.耗能伸臂桁架抗震性能的试验研究[J].工程力学, 2016, 33(10): 76―85.Yang Qingshun, Zhen Wei, Xie Linlin, et al.Experimental study on the seismic performance of energy dissipation outriggers[J].Engineering Mechanics, 2016, 33(10): 76―85.(in Chinese)
[16]任重翠, 徐自国, 肖从真, 等.防屈曲支撑在超高层建筑结构伸臂桁架中的应用[J].建筑结构, 2013, 43(5):54―59.Ren Chongcui, Xu Ziguo, Xiao Congzhen, et al.Application of unbonded brace in super high-rise structure with cantilever truss[J].Building Structure,2013, 43(5): 54―59.(in Chinese)
[17]Lin P C, Takeuchi T, Matsui R.Seismic performance evaluation of single damped-outrigger system incorporating buckling-restrained braces[J].Earthquake Engineering & Structural Dynamics, 2018, 47(12):2343―2365.
[18]张艳霞, 李振兴, 刘安然, 等.自复位可更换软钢耗能支撑性能研究[J].工程力学, 2017, 34(8): 180―193.Zhang Yanxia, Li Zhenxing, Liu Anran, et al.Research on the behavior of self-centering replaceable mild steel energy-dissipating braces[J].Engineering Mechanics,2017, 34(8): 180―193.(in Chinese)
[19]Kiggins S, Uang C M.Reducing residual drift of buckling-restrained braced frames as a dual system[J].Engineering Structures, 2006, 28(11): 1525―1532.
[20]周云.粘弹性阻尼减震结构设计理论及应用[M].武汉: 武汉理工大学出版社, 2013: 31―34.Zhou Yun.Design theory and application of viscoelastic damping structure[M].Wuhan: Wuhan University of Technology Press, 2013: 31―34.
[21]Drozdov A D.Mechanics of viscoelastic solids[M].New York: John Wiley Sons, 1998: 56―63.
[22]Zhao G F, Ma Y H, Li Y M, et al.Development of a modified Mooney-Rivlin constitutive model for rubber to investigate the effects of aging and marine corrosion on seismic isolated bearings[J].Earthquake Engineering and Engineering Vibration, 2017, 16(4): 815―826.
[23]Yeoh O H.Some forms of the strain energy function for rubber[J].Rubber Chemistry and Technology, 1993,66(5): 754―771.
[24]Tschoegl N W.The phenomenological theory of linear viscoelastic behavior[M].Berlin: Springer, 1989: 396―442.
[25]Park S W.Analytical modeling of viscoelastic dampers for structural and vibration control[J].International Journal of Solids and Structures, 2001, 38(44): 8065―8092.
[26]Montgomery M, Christopoulos C.Experimental validation of viscoelastic coupling dampers for enhanced dynamic performance of high-Rise buildings[J].Journal of Structural Engineering, 2015, 141(5): 04014145.
[27]Xu Z D, Liao Y X, Ge T, et al.Experimental and theoretical study of viscoelastic dampers with different matrix rubbers[J].Journal of Engineering Mechanics,2016, 142(8): 04016051.
[28]GB 50017―2003, 钢结构设计规范[S].北京: 中华人民共和国建设部, 2003.GB 50017―2003, Code for design of steel structures[S].Beijing: Ministry of Construction of the People’s Republic of China, 2003.(in Chinese)
[29]赵刚, 潘鹏, 钱稼茹, 等.黏弹性阻尼器大变形性能试验研究[J].建筑结构学报, 2012, 33(10): 126―133.Zhao Gang, Pan Peng, Qian Jiaru, et al.Experimental study of viscoelastic dampers subjected to large deformation[J].Journal of Building Structures, 2012,33(10): 126―133.(in Chinese)