传统支撑体系增大了结构的抗侧刚度，但普通钢支撑受压易屈曲，耗能能力较差[1]，屈曲约束支撑限制支撑受压时的屈曲行为，滞回曲线饱满，耗能能力较强，但支撑震后具有较大的残余变形，增加结构后续维修难度和成本[2―3]。Christopoulos等[4]提出一种自复位耗能支撑，该支撑利用复合纤维筋的预拉力复位，利用构件间的摩擦力耗能；Chou等[5―6]提出的自复位耗能支撑由预应力玻璃纤维筋提供恢复力，以减少支撑的残余变形；Miller等[7―9]利用形状记忆合金(SMA)材料为支撑提供弹性恢复力并同时耗散能量；刘璐等[10―12]提出一种利用预应力钢绞线提供复位力的自复位防屈曲支撑，并对支撑结构进行分析；徐龙河等[13―15]提出一种新型预压碟簧自复位耗能支撑，并建立该支撑的恢复力模型。以上形式的自复位支撑能够有效消除残余变形并耗散地震能量，但复合纤维筋锚固困难，SMA材料的复位性能需要加温才能实现[16]，预应力钢绞线极限弹性变形小，支撑的变形能力较差，预压碟簧自复位支撑采用焊接工艺较多，具有较大的残余应力，且震后不易更换部件。
本文提出一种利用摩擦装置耗能、碟形弹簧进行复位的装配式自复位耗能(ASCED)支撑，该支撑构造简单，可装配，各部件由工厂预制，加工精度较高，部件易于更换，工作性能稳定。通过对支撑的工作原理和力学特性的分析，基于经典的Bouc-Wen模型建立了装配式自复位耗能支撑的恢复力模型，通过拟静力试验分析支撑的滞回特性、耗能能力与自复位能力，并验证了所建立的装配式自复位耗能支撑恢复力模型的准确性。
1 ASCED支撑工作性能
1.1 工作原理
ASCED支撑主要由耗能系统和复位系统组成，耗能系统由摩擦板、核心杆、外管组成，摩擦片布置在外管与核心杆之间，复位系统由碟形弹簧、碟簧挡板以及核心杆与外管上的挡块组成，核心杆与外管承担并传递外力，支撑构造如图1所示。首先将碟形弹簧分组布置在外管的碟簧挡块之间，将摩擦片置于外管内侧，之后将核心杆穿过碟簧布置于两外管之间，用外管与核心杆固定摩擦片，利用高强螺栓连接核心杆与外管并挤压摩擦板，最后组装碟簧挡块挤压碟簧，完成支撑的组装。支撑初始状态下利用碟簧挡板对碟簧施加预压力，无论支撑处于受拉或受压状态下，核心杆与外管上的挡块使碟簧均处于受压状态，因此碟簧在两种状态下均能提供恢复力使支撑复位，核心杆与外管之间允许发生相对滑动，此时摩擦板耗散能量，同时碟簧进一步被挡块压缩，碟簧提供的复位力逐渐增大，卸载后迫使支撑复位。以碟簧为主的自复位系统和以摩擦板为主的耗能系统共同工作，保证了ASCED支撑的工作性能。
图1 ASCED支撑构造
Fig.1 Configuration of ASCED brace
1.2 力学性能
在摩擦耗能系统与碟簧复位系统的协同工作下，ASCED支撑具有独特的旗形滞回曲线，如图2所示，未加载时支撑的碟簧预压力作用于挡块上，挡块将力传递给支撑的核心杆与外管。
根据刚度和恢复力的变化，支撑在低周往复荷载作用下分为4个工作阶段。当外荷载不超过支撑的摩擦力F0和碟簧预压力P0之和时，支撑的变形主要是核心杆与外管的弹性变形之和，核心杆与外管之间没有相对滑动，摩擦装置与碟簧复位装置均未被激活，两外管内力之和与核心杆内力相等，且等于支撑所受外荷载，两外管并联并同时和核心杆串联，支撑刚度主要由核心杆与外管提供，记此时刚度为K1，由下式确定：
式中：F为支撑此时所受外力；δ为支撑的变形，其数值等于核心杆弹性变形δi和外管弹性变形δo之和，因此式(1)又可写成如下形式：
式中，δi和δo分别由下式计算：
因此，支撑的第一刚度K1由下式确定：
式中：Ki为支撑核心杆刚度；Ko为外管刚度，分别为：
式中：E为支撑核心杆与外管弹性模量；Ai为核心杆等效截面面积，即核心杆扣除螺栓孔槽的截面面积；Ao为外管等效截面面积，即外管扣除螺栓孔的截面面积；Li为核心杆长度；Lo为外管长度。
当外荷载超过摩擦力与碟簧预压力之和时，支撑的核心杆与外管开始发生相对滑动，摩擦装置耗能，支撑进入第II工作阶段，支撑的第二刚度K2主要由碟簧复位系统决定。在加载到最大位移幅值δmax后，支撑进入卸载阶段，摩擦力反向，碟簧提供的恢复力使支撑复位，支撑刚度等于第一刚度。随着卸载继续，支撑进入第IV工作阶段，核心杆与外管重新开始相对滑动，碟簧推动支撑复位，直至恢复到初始状态，该工作阶段类似于第II工作阶段，支撑的刚度等同于碟簧的组合刚度。
支撑受压时的工作情况与受拉时相同，当支撑的碟簧预压力大于摩擦力时，在卸载完成后，支撑能够复位，支撑无残余变形出现，如图2(d)所示，碟簧预压力小于摩擦力时，支撑的复位力小于摩擦力，碟簧无法继续推动外管复位，因此支撑出现一定的残余变形，如图2(e)所示，残余变形的大小与摩擦力、碟簧预压力以及支撑刚度有关[13]。残余变形值δr的理论计算公式如下：
式中：η为第二刚度与第一刚度的比；ΔF为摩擦力F0与碟簧预压力P0的差值。
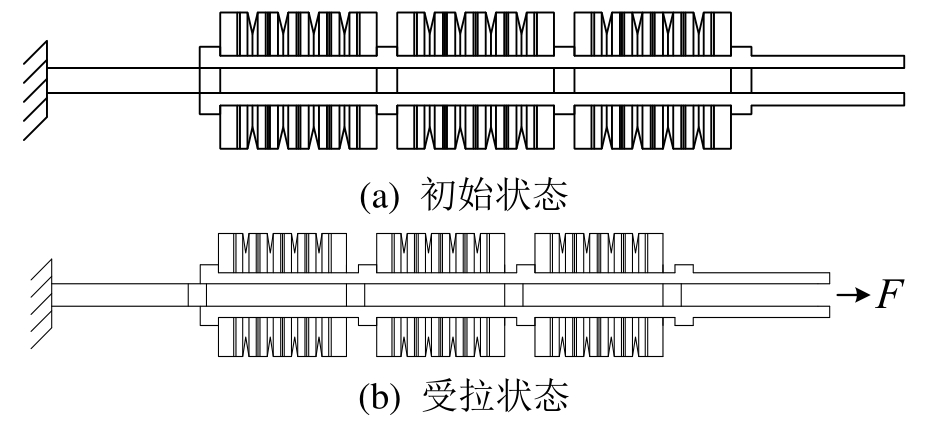
图2 ASCED支撑工作原理
Fig.2 Working principle of ASCED brace
2 ASCED支撑恢复力模型
图3为ASCED支撑在低周往复作用下的旗形滞回曲线，该滞回曲线的旗形特征取决于支撑的碟簧复位系统和摩擦耗能系统的协同工作。有学者[11]利用折线模型模拟旗形滞回曲线，但由于碟簧之间的摩擦以及各部件之间的连接紧密性，复位模型和耗能模型都不是理想的折线，支撑的滞回曲线不会呈现理想的折线模型，利用折线模型模拟这种滞回曲线往往会有较大的耗能近似性，且分段式恢复力模型不够简洁，不利于以后二次开发利用。Bouc-Wen模型利用具有不确定参数的非线性微分方程描述力与位移的关系，易于用数值方法求解，通过改变模型参数，能准确模拟各种不同类型装置的滞回特性，具有良好的鲁棒性、普适性。该模型最早由Bouc于1967年提出[17]，被Wen加以拓展[18]，自提出以来不断被学者加以改进，应用到不同领域中[19―20]。
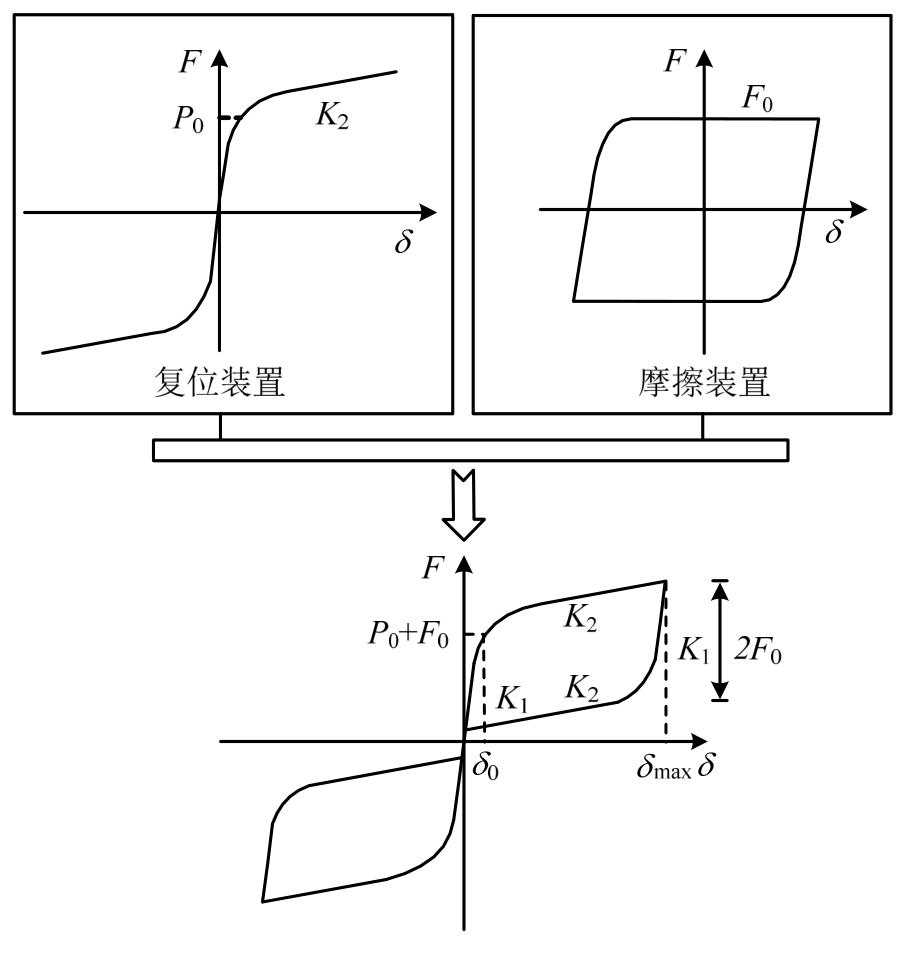
图3 ASCED支撑恢复力模型
Fig.3 Restoring force model of ASCED brace
结合ASCED支撑的工作原理，基于Bouc-Wen模型，利用非线性滞回变量W(t)描述支撑的耗能能力，在非线性滞回变量Z(t)中加入捏缩函数用以描述支撑中复位装置的力学性能，最终提出一种能描述 ASCED支撑旗形滞回特性的非线性恢复力模型，如图3所示，其数学表达如下：
式中：x为支撑的位移；W(t)和Z(t)分别为控制耗能和复位的非线性滞回变量，由下式确定：
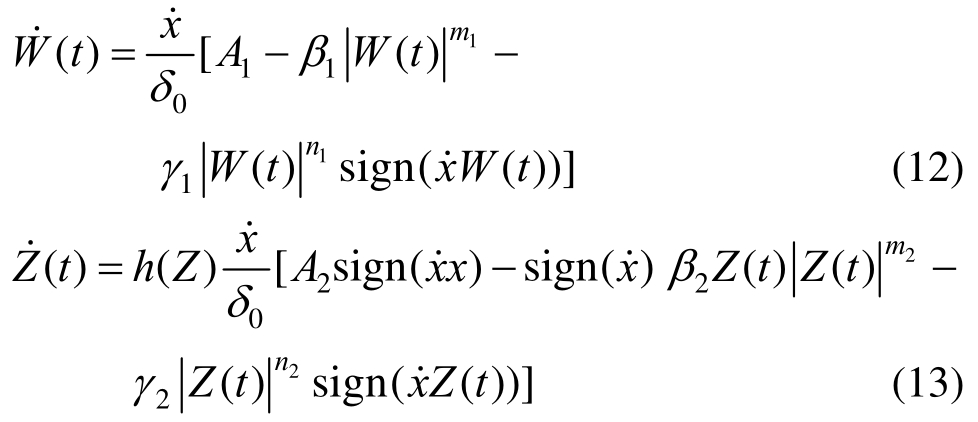
式中：A1、β1、γ1、A2、β2、γ2为 Bouc-Wen 模型滞回环形状的基本控制参数；m1、n1、m2、n2为滞回曲线刚度变化尖锐程度的控制参数，以上 10个参数均无实际物理意义；δ0为起滑位移，由下式决定：
此外，h(Z)为控制“捏缩效应”的捏缩函数，由下式决定：
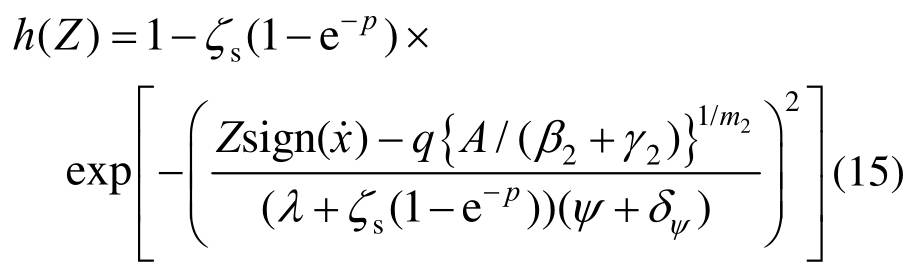
式中，ζs、p、q、ψ、δψ和λ为捏缩效应的控制参数，无实际物理意义。
3 ASCED支撑拟静力试验
3.1 试件设计
设计并加工一个ASCED支撑，对其进行低周往复加载试验。支撑试件的主要尺寸如图4所示，除碟簧外，支撑各部件均由 45号钢制成，支撑核心杆长1032.8 mm，主要截面为矩形，中间开有螺栓孔槽，两个外管长1032.8 mm，矩形截面，中间开有等间距螺栓孔，核心杆与外管沿轴向均设有等间距的碟簧挡块。摩擦片为无石棉有机材料，预留螺栓孔洞，粘贴于核心杆与两个外管的接触面处。碟簧挡板的外径为 200 mm，厚度为 25 mm，上面开有螺栓孔。碟簧的外径为 200 mm，内径为112 mm，厚度 11.25 mm，本次试验共布置 3组碟簧，每组8片。由于支撑的装配式功能要求，以上各构件均由工厂加工完成之后装配组装，各部件之间采用螺栓连接，支撑与支座铰接。
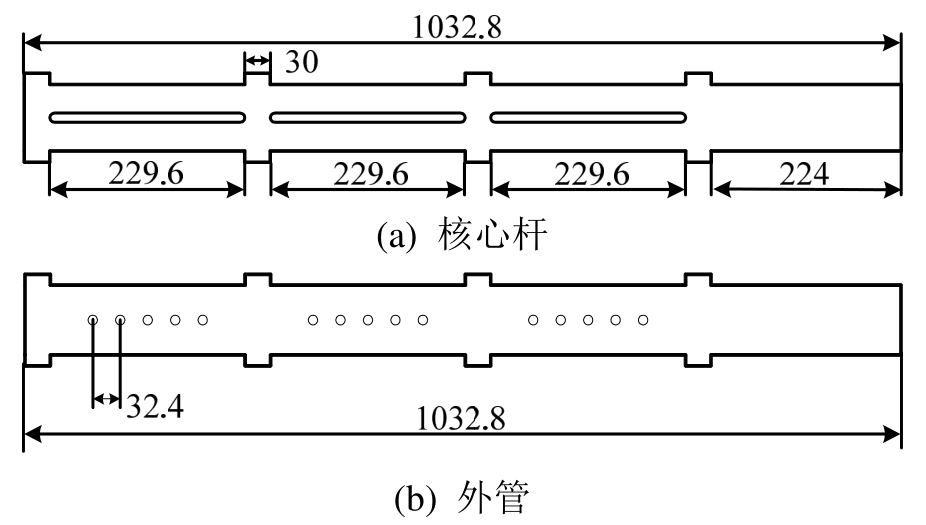
图4 ASCED支撑试件尺寸
Fig.4 Dimensions of ASCED brace specimen
3.2 试验装置与加载制度
对ASCED支撑试件进行拟静力试验，加载装置如图5所示，以位移控制方式进行加载，设定的位移幅值为5 mm、10 mm、15 mm、20 mm，每级位移幅值循环3次，支撑加载制度如图6所示。通过调节螺栓预紧力调整支撑摩擦力为 80 kN，碟簧预压力分别设置为 40 kN、65 kN、90 kN，以下称为工况1、工况2、工况3，由于支撑与支座连接处的缝隙，3个工况下的加载幅值不完全相同，但相同加载循环下的位移相对值接近。对以上3种工况下的支撑进行低周往复加载，以分析ASCED支撑的滞回性能，自复位性能和耗能能力。
图5 试验装置
Fig.5 Test setup
图6 加载制度
Fig.6 Loading scheme
4 试验结果及分析
4.1 滞回性能
试验得到的3个工况下支撑滞回曲线如图7所示，在低周往复荷载作用下，支撑呈现出饱满的旗形滞回曲线，受拉受压状态下均分为4个工作阶段，表明支撑的自复位系统和耗能系统能有效共同工作。在每一个工况下，任意位移幅值3次循环加载下的滞回曲线基本重合，支撑刚度保持较好，没有随加载出现退化，表明支撑的核心杆与外管保持弹性状态，碟簧和摩擦板工作性能没有降低。随着加载幅值增大，支撑的滞回曲线越来越规则，第II工作阶段与第IV工作阶段的滞回曲线有向外扩张的趋势，耗能能力增强，这是由于加载位移越大，碟簧受到的压力越大，碟簧表面的摩擦力越大[21]。在受拉和受压两种工作状态下滞回性能接近，支撑的拉压恢复力的差值随加载幅值增大而减小，最大加载幅值对应的拉压恢复力相差为4.7%，说明支撑具有良好的拉压对称性，优于普通钢支撑利用塑性变形耗能而引起的拉压不对称。
4.2 恢复力模型参数的确定及影响分析
本文所提出恢复力模型共有21个参数，其中5个支撑设计参数，分别为第二刚度K2、第二刚度对第一刚度的比η、摩擦力F0、预压力P0、起滑位移δ0；16个滞回曲线形状控制参数，其中参数A1、A2、β1、γ1、β2、γ2、m1、n1、m2、n2 为滞回曲线的基本形状控制参数，而ζs、p、q、ψ、δψ、λ为捏缩效应控制参数，参考已有研究成果[22―24]，q、ψ、δψ、λ对滞回曲线的影响较小，其取值分别为0.15、0.1、0.005和0.5。根据试验数据，确定支撑3个工况下的碟簧预压力分别为40 kN，65 kN和90 kN，摩擦力为 80 kN，由式(5)计算得到支撑第一刚度为117.07 kN/mm，因此3个工况下支撑的激活位移分别为1.03 mm、1.24 mm和1.45 mm。
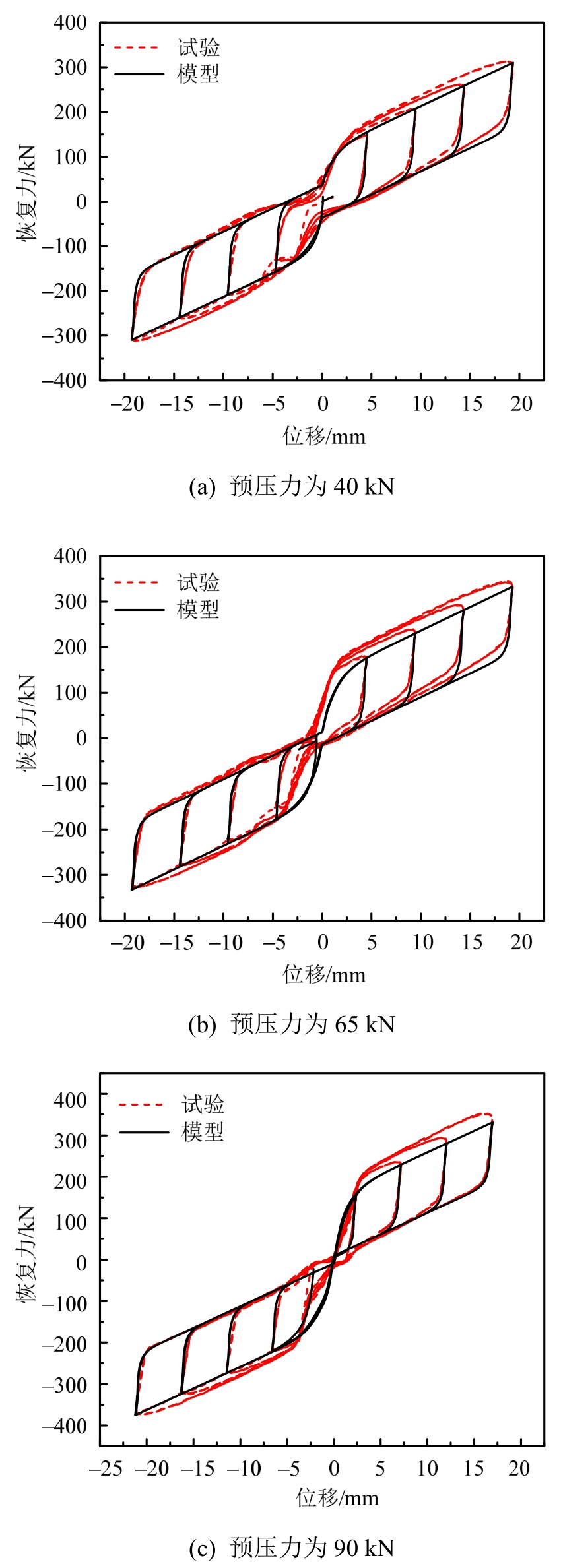
图7 恢复力模型与试验滞回曲线对比
Fig.7 Comparison of hysteretic curves obtained from tests and restoring force model
根据工况1下的试验数据，利用MTALB编写遗传算法程序对无法确定的参数进行识别，采用的适应度函数为：
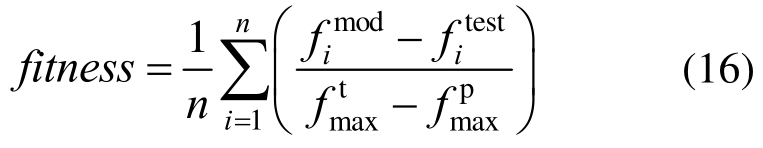
式中：n为数据点的个数；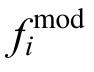
为第i个模拟得到的恢复力数值；
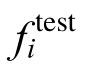为第i个试验得到的恢复力数值；
为试验得到的受拉恢复力最大值；
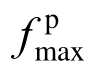为试验得到的受压恢复力最大值，利用摩擦力为 80 kN、预压力为40 kN下的试验位移激励和恢复力数据对未知参数进行识别，设定变异概率为 0.2，交叉概率为 0.8，迭代次数 100次，识别结果为K2=10.38 kN/mm，η=0.089，β1=0.994，γ1=0.006，β2=0.004，γ2=0.996，m1=0.01，n1=0.02，m2=0.0001，n2=0.0002，ζs=0.515，p=0.369。
以试验工况1的位移激励数据为例，分析关键参数K2、η、β1、γ1、β2、γ2、m1、n1、m2、n2、ζs和p对支撑滞回曲线的影响，如图8所示，除图8中特别注明外，参数取值均为识别所得数值。由图8可知，K2越大，支撑的承载力越大，而K2不变，刚度比越大，支撑进入第II工作阶段越晚。对于形状控制参数，β1、γ1与β2和γ2作用类似，因此仅对β1、γ1进行分析，β1和γ1越大，滞回曲线K3到K4过渡的越快，m1、n1与m2和n2作用类似，因此仅对m2和n2进行分析，m1和n1影响支撑刚度过渡的尖锐度，m1和n1越小，支撑滞回曲线就越圆滑，ζs和p控制滞回曲线的捏缩，其值越小，捏缩效应越不明显，当其值为0时，滞回曲线不捏缩。
4.3 自复位性能
ASCED支撑具有良好的自复位能力，从图 7可以看出，支撑的滞回曲线在原点附近出现了明显的“捏缩”，且碟簧预压力越大，捏缩现象越明显，即支撑的残余变形越小，支撑的复位能力越强。3个工况下支撑最大加载幅值对应的残余变形如图9所示，工况1下，支撑的残余变形为4.2 mm，为最大加载幅值的21.7%；工况2下，支撑的残余变形为1.9 mm，为最大加载幅值的9.8%；工况3下，支撑的残余变形为 1.5 mm，为最大加载幅值的8.9%。当支撑的摩擦力一定时，碟簧预压力越高，支撑的残余变形越小。除工况4外，恢复力模型得到的残余变形计算值与式(8)计算值完全一致，工况3下碟簧预压力大于摩擦力，理论上支撑不会出现残余变形，表明残余变形计算公式很好的反映了支撑的残余变形形成机制，对支撑的设计具有一定的指导意义，根据公式计算的残余变形随预压力下降呈非线性降低，因此对于不同的工程需求，在支撑设计中可以通过调节碟簧预压力实现所需要的自复位能力。
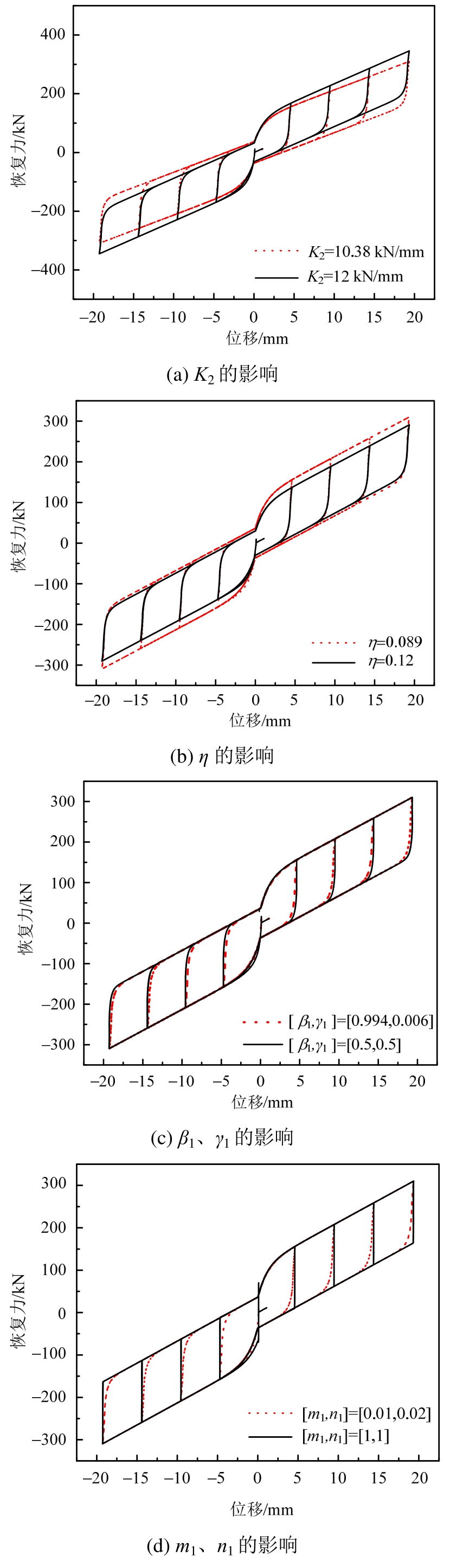
图8 恢复力模型参数对ASCED支撑滞回曲线的影响
Fig.8 Effect of restoring force model parameters on hysteretic curves of ASCED brace
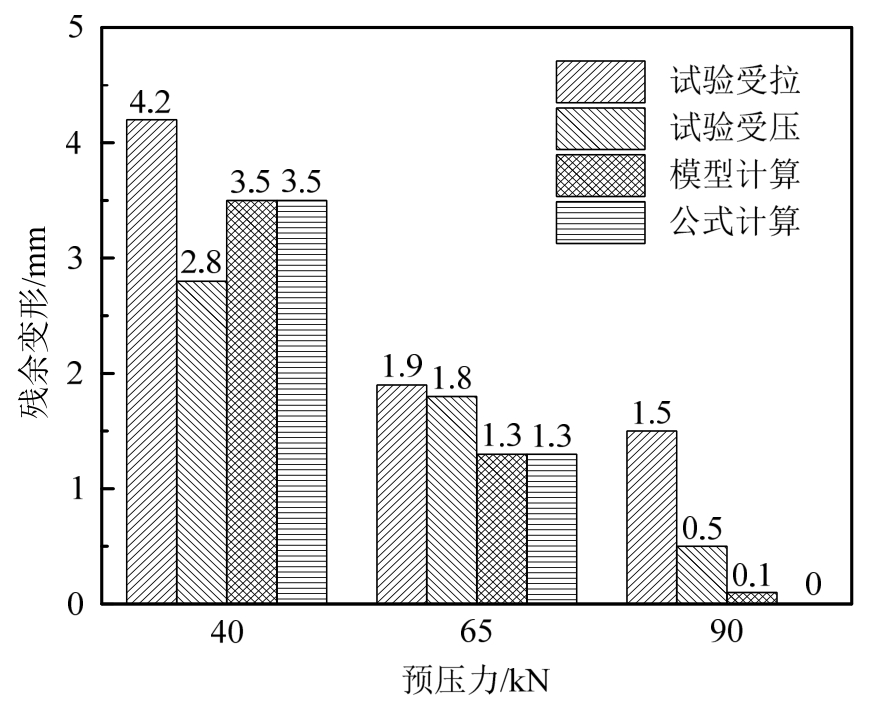
图9 残余变形对比
Fig.9 Comparison of residual deformations
4.4 耗能能力
支撑各个工况下的试验耗能如表1所示，通过计算滞回环面积得到的支撑在3个工况下的总耗能接近，分别为39.43 kJ、38.40 kJ、37.30 kJ，最大相差为 5.7%，表明碟簧预压力对支撑耗能的影响较小，取支撑每次加载循环下的受拉位移与受压位移之和为循环位移，支撑的耗能随循环位移的增加而增加，而耗能的增加值也随循环位移增大而增大。支撑耗能的非线性增长是由于加载幅值增加，碟簧变形增加，碟簧之间的摩擦力增加。根据模拟得到支撑滞回曲线计算支撑在3个工况下的模拟耗能，如表1所示，由于支撑的恢复力模型未能考虑碟簧之间以及碟簧与核心杆和外管之间的摩擦耗能，3个工况下模拟的支撑总耗能均小于支撑在试验中的实际耗能，但3个工况下耗能相差分别为2.2%、3.8%和6.5%，表明所提出的恢复力模型能准确描述支撑的实际耗能能力。
等效粘滞阻尼比是衡量支撑耗能能力的一个重要抗震参数，计算公式如下：
式中：Ec为支撑在一次加载循环下耗散的能量；Es为位移幅值对应的弹性应变能。根据式(17)计算得到的ASCED支撑等效粘滞阻尼比如表1所示。由表1可知，支撑的等效粘滞阻尼比随着碟簧预压力的增加而减小，在工况2和工况3下，支撑在第一个循环位移下的等效粘滞阻尼比小于第二个循环位移下的。总体而言，支撑的阻尼比随循环位移增大变化比较稳定，没有出现突然大幅度减小的情况，表明支撑的耗能能力比较稳定，支撑处于比较稳定的工作状态中。
为综合评价支撑的耗能能力和复位性能，提出支撑的耗能变形比ε，定义如下：
式中：
为支撑各循环位移等效粘滞阻尼比的平均值；μ为拉压残余变形之和与循环位移的比值，在相同的残余变形下，耗能变形比越高，支撑的耗能能力越强；在相同的耗能下，耗能变形比越高，支撑的残余变形越小。利用支撑的试验耗能，根据式(18)计算得到 3个工况下的耗能变形比分别为1.00、1.64、2.56，表明支撑在工况3下能发挥更好的性能。
表1 支撑的耗能
Table 1 Energy dissipation of ASCED brace
预压力/kN 循环位移/mm 耗能/kJ 增长值/kJ 等效阻尼比 总耗能/kJ 总耗能误差/(%)试验 模拟 试验 模拟 试验 模拟 试验 模拟40 9.3 2.40 3.28 — — 0.198 0.239 39.44 38.59 2.2 19.0 7.11 7.50 4.71 4.22 0.196 0.182 28.8 12.23 11.77 5.12 4.27 0.177 0.167 38.6 17.70 16.04 5.47 4.27 0.160 0.144 65 9.2 2.23 2.83 — — 0.160 0.186 38.40 36.93 3.8 19.0 6.74 7.10 4.51 4.37 0.165 0.172 28.8 11.93 11.36 5.19 4.26 0.158 0.149 38.6 17.50 15.64 5.70 4.28 0.146 0.129 90 8.8 1.76 2.27 — — 0.104 0.239 37.33 34.91 6.5 18.7 6.49 6.63 4.73 4.36 0.146 0.182 28.4 11.69 10.87 5.20 4.24 0.145 0.167 38.1 17.39 15.14 5.70 4.27 0.137 0.144
4.5 恢复力模型与试验对比
由双Bouc-Wen恢复力模型计算得到的承载力与试验结果对比如表2所示。由表2和图7可知，随着加载幅值增大，恢复力模型计算值与试验结果越接近。在预压力为 40 kN，加载幅值为-4.6 mm时，计算最大承载力与试验结果最大相差21.7%，在加载幅值为19.3 mm时，模型计算结果与试验的误差仅为 0.3%；在预压力为 65 kN，加载幅值为-4.7 mm时，模型计算最大承载力与试验结果最大相差19.9%，由图7可知，在预压力为40 kN和65 kN时，支撑的滞回环在第一次受压加载幅值处出现了不规则的“内陷”，该现象是由于摩擦板出现不规则运动，摩擦装置提供的摩擦力有所下降，在此加载幅值处模型计算结果与试验结果相差较大，而在预压力为90 kN时，支撑的滞回曲线比较饱满，没有出现内陷的情况，因此模型计算结果与试验结果比较接近，在加载幅值处的最大误差仅为4.5%，且仍然发生于最小加载幅值处，之后随着加载幅值增大，恢复力模型计算结果与试验的误差逐渐缩小，这表明ASCED支撑滞回曲线的旗形特征随加载幅值增大而愈加明显，在允许变形范围内，支撑的工作性能不会随加载幅值的增大而退化。在工况1下，加载幅值处恢复力模型与试验结果的平均误差为4.9%；在工况2下，加载幅值处恢复力模型与试验结果的平均误差为3.7%；在工况3下，加载幅值处恢复力模型与试验结果的平均误差为1.9%，恢复力模型计算值与试验值吻合较好。
表2 试验与恢复力模型计算最大承载力对比
Table 2 Comparison of maximum strength between restoring force model and tests
预压力/kN 加载幅值/mm 承载力/kN 误差/(%)试验 模拟40 4.6 146.6 155.8 6.3-4.7-129.2-157.3 21.7 9.5 200.9 207.9 3.5-9.5-203.7-208.6 2.4 14.4 253.4 259.0 2.2-14.4-255.5-259.0 1.4 19.3 302.0 301.1 0.3-19.3-305.22-309.5 1.4 65 4.5 174.3 173.5 0.1-4.7-147.9-177.3 19.9 9.5 233.2 230.3 1.2-9.5-221.5-231.2 4.4 14.4 282.0 280.7 0.5-14.4-273.1-281.3 3.0 19.3 332.1 332.1 0-19.3-323.1-332.3 0.3 90 2.4 149.5 156.3 4.5-6.6-216.8-222.2 2.5 7.2 227.9 229.0 0.5-11.5-268.0-273.8 2.2 12.1 281.5 280.1 0.5-16.3-316.6-324.4 2.5 16.9 333.9 330.8 0.3-21.2-366.5-375.0 2.3
5 结论
本文提出一种新型装配式自复位耗能支撑构件，基于Bouc-Wen模型建立了描述ASCED支撑滞回特性的的双 Bouc-Wen恢复力模型。对足尺ASCED支撑试件进行拟静力试验，分析支撑的滞回性能，自复位性能以及耗能能力，得到以下结论：
(1)ASCED支撑在三个工况下的总耗能最大相差5.7%，支撑在低周往复加载下的总耗能受碟簧预压力影响较小，碟簧之间的摩擦力使支撑的耗能能力有所增强。恢复力模型模拟的支撑耗能与试验耗能最大仅相差6.5%，表明所提出的恢复力模型能准确描述支撑的耗能能力；
(2)ASCED支撑在低周往复荷载作用下呈现饱满的旗形滞回曲线，没有发生刚度退化，支撑残余变形较小，可通过调整支撑的碟簧预压力与摩擦力的相对大小来消除支撑的残余变形；
(3)提出的双 Bouc-Wen恢复力模型计算结果与拟静力试验结果吻合较好，除个别加载幅值下误差较大，其余情况下误差最大仅为 6.3%，双Bouc-Wen恢复力模型可以准确描述ASCED支撑的滞回特性。
[1]Tremblay R, Robert N.Seismic performance of low- and medium-rise chevron braced steel frame[J].Canadian Journal of Civil Engineering, 2011, 27(6): 1192―1206.
[2]Christopoulos C, Pampanin S, Nigel Priestley M J.Performance-based seismic response of frame structures including residual deformations.Part I: Single-degree of freedom systems[J].Journal of Earthquake Engineering,2003, 7(1): 97―118.
[3]Zhu S, Zhang Y.Seismic behavior of self-centering braced frame buildings with reusable hysteretic damping brace[J].Earthquake engineering & structural dynamics,2007, 36(10): 1329―1346.
[4]Christopoulos C, Tremblay R, Kim H J, et al.Self-centering energy dissipative bracing system for the seismic resistance of structures: development and validation[J].Journal of Structural Engineering, 2008,134(1): 96―107.
[5]Chou C C, Wang Y C, Chen J H.Seismic design and behavior of post-tensioned steel connections including effects of a composite slab[J].Engineering Structures,2008, 30(11): 3014―3023.
[6]Chou C C, Chen J H.Seismic design and shake table tests of a steel post-tensioned self-centering moment frame with a slab accommodating frame expansion[J].Earthquake Engineering & Structural Dynamics, 2011,40(11): 1241―1261.
[7]Miller D J.Development and experimental validation of self-centering buckling-restrained braces with shape memory alloy[D].Urbana，Illinois: University of Illinois at Urbana-Champaign, 2011: 76―129.
[8]Miller D J, Fahnestock L A, Eatherton M R.Self-centering buckling-restrained braces for advanced seismic performance[C]// Proceedings of the 2011 Structures Congress.Las Vegas, USA: Structural Engineering Institute of ASCE, 2011: 960―970.
[9]Miller D J, Fahnestock L A, Eatherton M R.Development and experimental validation of a nickel-titanium shape memory alloy self-centering buckling-restrained brace[J].Engineering Structures,2012, 40: 288―298.
[10]刘璐.自复位防屈曲支撑结构抗震性能及设计方法[D].哈尔滨: 哈尔滨工业大学, 2013.Liu Lu.Seismic behavior and design of structure with self-centering buckling-restrained braces[D].Harbin:Harbin Institute of Technology, 2013.(in Chinese)
[11]刘璐, 吴斌, 李伟, 等.自复位防屈曲支撑结构动力位移反应的关键参数[J].工程力学, 2016, 33(1): 188―194.Liu Lu, Wu Bin, Li Wei, et al.Key parameters of structure with self-centering buckling-restrained braces for seismic analysis[J].Engineering Mechanics, 2016,33(1): 188―194.(in Chinese)
[12]刘璐, 吴斌, 李伟, 等.等效线性化方法在自复位防屈曲支撑结构中的应用[J].工程力学, 2016, 33(3): 204―213.Liu Lu, Wu Bin, Li Wei, et al.The application of the equivalent linearization methodology in self-centering buckling-restrained braced frames[J].Engineering Mechanics, 2016, 33(3): 204―213.(in Chinese)
[13]徐龙河, 樊晓伟, 代长顺, 等.预压弹簧自恢复耗能支撑受力性能分析与试验研究[J].建筑结构学报, 2016,37(9): 142―148.Xu Longhe, Fan Xiaowei, Dai Changshun, et al.Mechanical behavior analysis and experimental study on pre-pressed spring self-centering energy dissipation brace[J].Journal of Building Structures, 2016, 37(9): 142―148.(in Chinese)
[14]徐龙河, 樊晓伟, 逯登成, 等.预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J].工程力学, 2016,33(10): 116―122.Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al.Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace[J].Engineering Mechanics, 2016, 33(10): 116―122.(in Chinese)
[15]Xu Longhe, Fan Xiaowei, Li Zhongxian.Experimental behavior and analysis of self-centering steel brace with pre-pressed disc springs[J].Journal of Constructional Steel Research, 2017, 139: 363―373.
[16]高丛峰.温度和应变率对拉伸载荷下记忆合金本构关系的影响[J].天津大学学报, 2001, 34(3): 372―375.Gao Congfeng.Study on effect of temperature and strain rate on constitutive relation of shape memory alloy under tension[J].Journal of Tianjin University, 2001, 34(3):372―375.(in Chinese).
[17]Ismail M, Ikhouane F, José Rodellar.The hysteresis Bouc-Wen model, a survey[J].Archives of Computational Methods in Engineering, 2009, 16(2):161―188.
[18]Wen Y K.Method for random vibration of hysteretic systems[J].Journal of Engineering Mechanics, 1976,102(2): 249―263.
[19]Rodellar F I J.Systems with hysteresis-analysis,identification and control using the Bouc-Wen model[M].West Sussex, England: John Wiley & Sons Ltd,2007: 14―18.
[20]Triantafyllou S, Koumousis V.An inelastic Timoshenko beam element with axial-shear-flexural interaction[J].Computational Mechanics, 2011, 48(6): 713―727.
[21]Xu Longhe, Fan Xiaowei, Li Zhongxian.Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace[J].Engineering Structures, 2016, 127: 49―61.
[22]Ma F, Zhang H, Bockstedte A, et al.Parameters analysis of the differential model of hysteresis[J].Journal of Applied Mechanics, 2004, 71(3): 342―349.
[23]余波, 洪汉平, 杨绿峰.非弹性体系地震动力响应分析的新型单轴 Bouc-Wen模型[J].工程力学, 2012,29(12): 265―294.Yu Bo, Hong Hanping, Yang Lüfeng.Improved uniaxial Bouc-Wen model for seismic dynamic response analysis of inelastic system[J].Engineering Mechanics, 2012,29(12): 265―294.(in Chinese)
[24]Goda K, Hong H P, Lee C S.Probabilistic characteristics of seismic ductility demand of SDOF systems with Bouc-Wen hysteretic behavior[J].Journal of Earthquake Engineering, 2009, 13(5): 600―622.