型钢混凝土结构(steel reinforced concrete structures,SRC)因其刚度大、承载力高和抗震性能好等优点被广泛应用于大跨重载及超高层结构中,但因其施工工序复杂而较少用于量大面广的公用建筑中[1]。为了进一步推进型钢混凝土结构的应用及建筑工业化的进程,许多学者结合预制装配结构与型钢混凝土结构的优势,提出了预制装配型钢混凝土结构。宋玉普等[2―3]提出了在梁柱节点区采用型钢连接的预制装配部分钢骨混凝土框架体系,张雪松和李忠献[4]提出了梁端采用狗骨式连接的装配整体式钢骨混凝土框架体系,Hong等[5]提出了由部分预制装配型钢混凝土构件组成的 MHS(modularized hybrid system)体系。
上述预制装配型钢混凝土结构多为全预制结构,其连接部整体性相对于现浇SRC结构仍有一定差距,而 Hong提出的部分预制装配型钢混凝土结构在保证新旧混凝土粘结性能的构造措施方面仍需改善。据此本课题组提出了新型预制装配型钢混凝土(PSRC)梁,并较为详尽地分析了其弯剪性能[6―8],但并未提出相应的受剪承载力计算方法。
剪切破坏作为一种脆性破坏形式,在结构设计中应尽量避免[9]。因此,如何准确预测PSRC梁的受剪承载力即为PSRC梁设计方法中的关键科学问题。近年来,许多学者提出了适用于SRC梁的受剪承载力计算方法,郑山锁等[10]基于现行规范提出了型钢高强混凝土梁的受剪承载力计算公式,但是缺少明确的力学模型;吴轶等[11]基于软化拉-压杆模型计算了内置钢构架型钢混凝土深梁受剪承载力,但并未提出配置实腹式型钢混凝土梁的受剪承载力计算公式;邓明科等[12]提出了基于修正拉-压杆模型的型钢混凝土深梁受剪承载力分析方法,但SRC梁中型钢翼缘的存在会扰动混凝土斜压杆的传力机制,使传力机理改变。
本文在PSRC梁受剪性能试验研究的基础上,基于变形协调桁架-拱模型及Nakamura模型建立了一种PSRC梁与普通SRC梁共同适用的受剪承载力计算模型,并提出了PSRC梁及SRC梁的受剪承载力计算方法。最后采用本文建议的计算方法和规范 AISC 360―2010及JGJ 138―2016中建议的计算方法对本文及文献[6,13―17]中75根发生剪切破坏的PSRC及SRC梁进行受剪承载力分析,并与试验结果进行比对。
1 试验概况
1.1 试件设计
本次试验共设计了2个足尺PSRC试件,主要试验参数为剪跨比,试件截面见图1。试件截面宽度均为450 mm,截面高度均为650 mm。各试件中型钢均采用 Q235轧制型钢,型钢规格为HN500×200×9×14。各试件中配置纵筋 10 25,箍筋
25,箍筋 6@80,混凝土保护层厚度为30 mm。为了保证型钢与混凝土的粘结性能,分别在型钢上、下翼缘端部钻孔,并按间距70 mm布置6排10.9级高强螺栓。为了加强预制混凝土与现浇混凝土的共同工作性能,在制作 U形预制外壳时同期浇筑 4道厚度为200 mm的混凝土隔板。各试件的主要设计参数见表1。
6@80,混凝土保护层厚度为30 mm。为了保证型钢与混凝土的粘结性能,分别在型钢上、下翼缘端部钻孔,并按间距70 mm布置6排10.9级高强螺栓。为了加强预制混凝土与现浇混凝土的共同工作性能,在制作 U形预制外壳时同期浇筑 4道厚度为200 mm的混凝土隔板。各试件的主要设计参数见表1。
各试件预制U形外壳均采用C50级混凝土浇筑,实测立方体抗压强度fcu,out=45.0 MPa;梁核心区现浇部分均采用C30级混凝土浇筑,实测立方体抗压强度fcu,in=24.3 MPa。型钢翼缘实测屈服强度为273 MPa,极限强度为 432 MPa;腹板实测屈服强度为317 MPa,极限强度为453 MPa;受力纵筋实测屈服强度为443 MPa,极限强度为598 MPa;箍筋实测屈服强度为387MPa,极限强度为562MPa。

图1 试件截面图
Fig.1 Diagrams of specimens
表1 试件参数
Table 1 Parameters of specimens

试件编号 剪跨比 剪跨段长度/mm截面有效高度/mm预制混凝土立方体强度/MPa现浇混凝土立方体强度/MPa 配钢率(ρss)配筋率(ρs)配箍率(ρv)PSRC-1 1.0 600 600 45.0 24.3 HN500×200×9×14(3.46%)5■25/5■25(1.82%)■6@80(0.16%)PSRC-2 1.5 900 600 45.0 24.3
1.2 加载及量测方案
试验采用四点对称静力加载方式,使用20000 kN油压千斤顶通过液压伺服仪进行位移控制加载,试验时千斤顶将刚性平台上顶,通过刚性顶板产生的反力进行加载,加载装置如图2所示。加载过程中主要监测试件加载点、跨中和支座处的竖向位移,以及型钢与箍筋的应变,位移计布置如图3所示。当竖向荷载下降至峰值荷载的85%以下或试件跨中位移过大时终止试验。
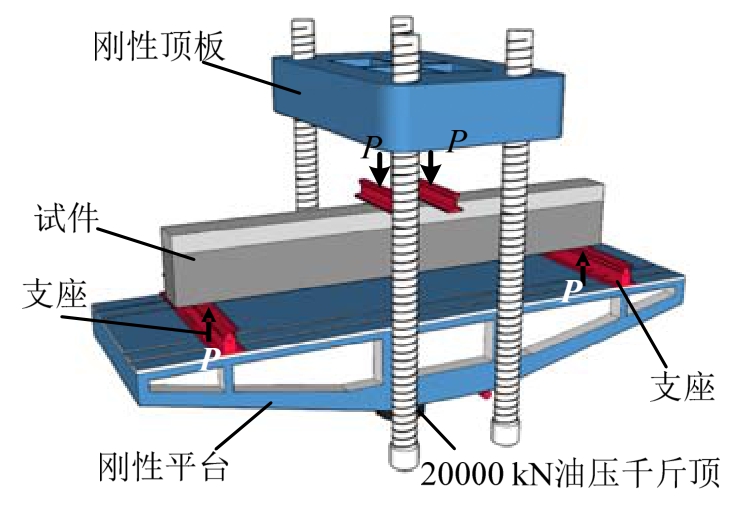
图2 加载装置图
Fig.2 Test device
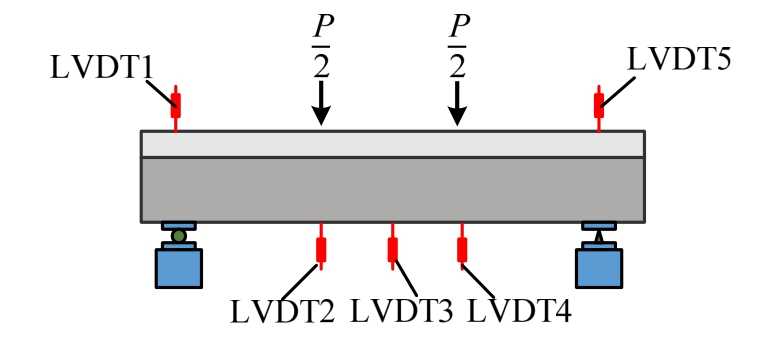
图3 位移计布置图
Fig.3 Layout of LVDTs
2 主要试验结果
2.1 破坏形态
主要试验结果如表2所示,各试件的破坏形态如图4所示。剪跨比为1.0的试件PSRC-1发生斜压破坏,试验后期未发现明显的主斜裂缝,试件腹部斜裂缝间的混凝土形成若干平行的混凝土短柱。试件最终破坏时加载点及支座处混凝土斜压短柱压碎脱落。剪跨比为1.5的试件PSRC-2发生剪压破坏,试验初期试件跨中出现多条弯曲裂缝但并未随荷载的增长而向上延伸,试验后期试件剪跨段形成主斜裂缝,最终破坏时剪压区混凝土压溃失效。
各试件在预制阶段均浇筑制作了混凝土横隔板,如图1(c)所示,混凝土横隔板可起到抗剪连接件的作用,以保证预制与现浇混凝土的共同工作性能。另外预制混凝土U型壳在浇筑后内部未进行人工抹平,以形成天然粗糙面进一步加强新旧混凝土的粘结性能。如图4所示,各试件在加载过程中新旧混凝土界面处均未发现明显的纵向粘结裂缝,故可认为各试件中预制与现浇混凝土粘结良好。
2.2 荷载-位移曲线和荷载-应变曲线
图5为各试件的荷载-跨中位移曲线。由图5可知,因截面内配置了型钢,各试件均拥有较大的初始刚度。剪跨比是影响PSRC梁受剪性能的重要影响因素,试件的受剪承载力随剪跨比的增大而减降低,但变形能力和延性系数随剪跨比的增大而增大。延性系数,即试件屈服位移与极限位移的比值,其中试件的屈服位移由等能量法[18]确定,极限位移即终止试验时的跨中位移。由表2可知,发生剪压破坏的试件PSRC-2的位移延性远大于发生斜压破坏的试件 PSRC-1,因此,在实际设计中应尽量避免构件发生斜压破坏。
图6为各试件的荷载-箍筋应变曲线。由图6可知,各试件中的箍筋在试件最终破坏时均已屈服,说明箍筋在PSRC梁受剪性能中起到重要的作用。
表2 主要试验结果
Table 2 Test results
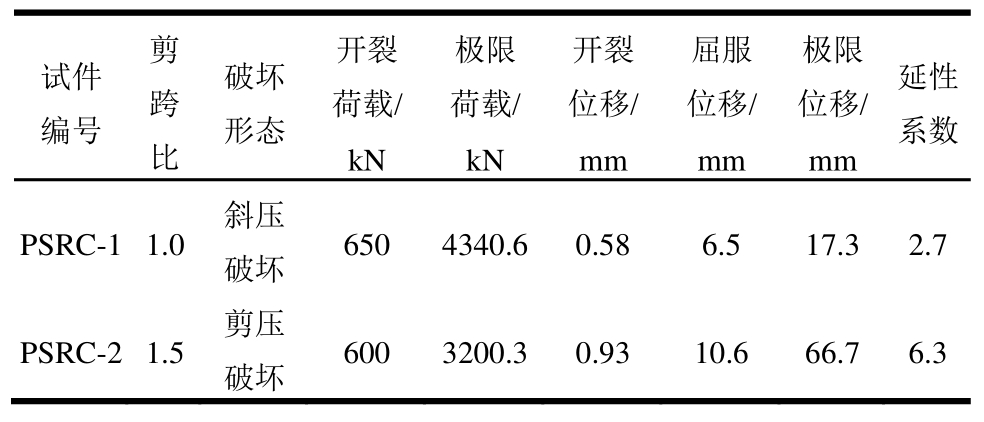
试件编号剪跨比破坏形态开裂荷载/kN极限荷载/kN开裂位移/mm屈服位移/mm极限位移/mm延性系数PSRC-1 1.0 斜压破坏 650 4340.6 0.58 6.5 17.3 2.7 PSRC-2 1.5 剪压破坏 600 3200.3 0.93 10.6 66.7 6.3
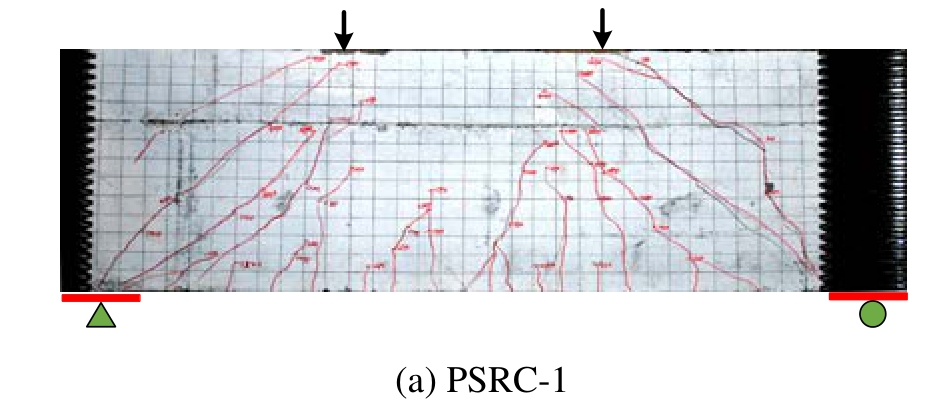

图4 试件破坏形态
Fig.4 Failure modes of specimens
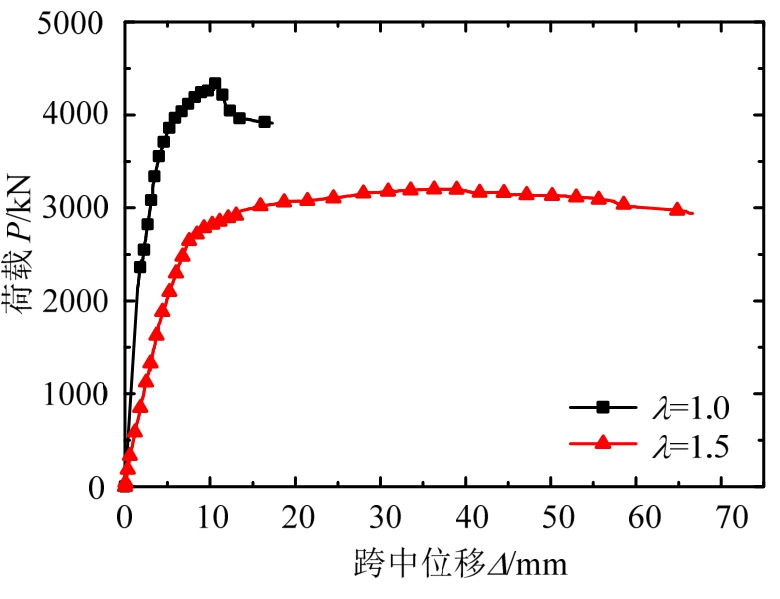
图5 荷载-跨中位移曲线
Fig.5 Load-displacement curves at mid-span
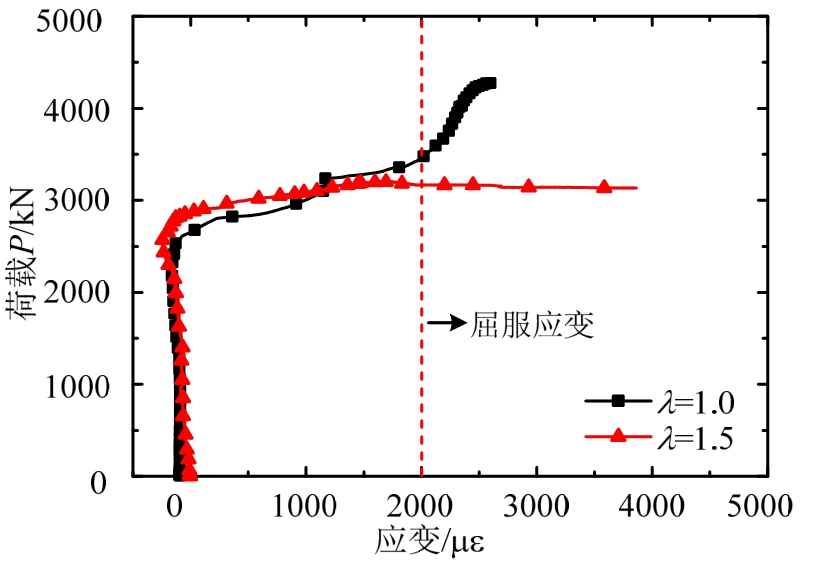
图6 荷载-箍筋应变曲线
Fig.6 Load-strain curves of stirrups
3 受剪承载力计算
近年来,多位学者[11―12]基于拉-压杆模型提出了适用于SRC梁的受剪承载力计算方法,但因SRC梁中型钢翼缘的存在,处在型钢翼缘宽度内的混凝土斜压杆传力机制会因此收到扰动,传力路径会因型钢翼缘的存在而改变。《美国钢结构规范》(AISC 360-2010)[19]及我国组合结构设计规范 JGJ 138-2016[20]也基于叠加法和回归分析提出 SRC梁的半经验-半理论受剪承载力计算公式,但缺少明确的力学模量。对于PSRC梁,因其截面内存在两种强度混凝土,在受剪承载力计算方法中如何合理体现两种混凝土的贡献而不是采用面积加权法定义等效混凝土强度也是亟待解决的问题。
本文提出一种适用于PSRC梁与SRC梁的受剪承载力计算模型,计算简图如图7所示。在该模型中,构件的受剪承载力由型钢及内部混凝土部分和钢筋混凝土部分共同组成。型钢及腹板内部混凝土的受力机理类似于PEC (partially encased concrete,型钢部分包裹混凝土柱)构件,其承载力可采用用于计算PEC梁受剪承载力的Nakamura模型[21]进行修正;而钢筋混凝土(reinforced concrete,RC)部分的受剪承载力可由修正变形协调桁架-拱模型[22]确定,因RC部分的宽度定义为构件整体宽度减去型钢翼缘宽度,故其桁架作用与拱作用均不会因型钢翼缘的存在而扰动。
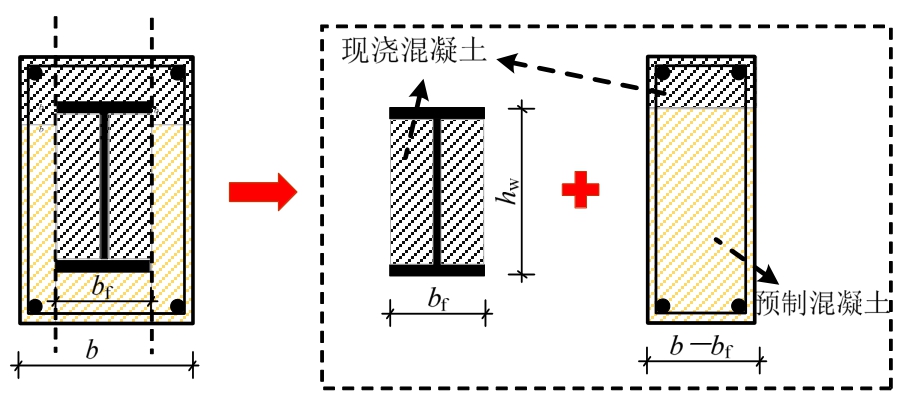
图7 计算简图
Fig.7 Calculation diagram
PSRC构件的受剪承载力可由式(1)确定:
式中:Vct和Vs为桁架作用中混凝土与箍筋的贡献;Va为拱作用的受剪承载力;Vss为型钢及内部混凝土的受剪承载力。因PSRC梁的现浇部分高度较小(一般为楼板的厚度),为了简化计算,可近似取腹板混凝土强度为现浇混凝土强度,剩余部分混凝土强度为预制混凝土强度。
式(1)中RC部分中桁架作用的贡献由简化的修正压力场模型(MCFT)[23]确定:

式中:b为构件宽度;bf为型钢翼缘宽度;h0为截面有效高度,即受拉纵筋形心至受压区混凝土边缘的距离;fc,o为预制混凝土受压强度;Asv为箍筋截面面积;fys为箍筋屈服强度;θ为桁架模型中裂缝与纵轴的倾角。
式(2)中的系数β可由下式确定[18]:
式中:sze为裂缝间距,取sze=300 mm[23];εx为构件截面中心平均纵向应变,由式(5)确定:
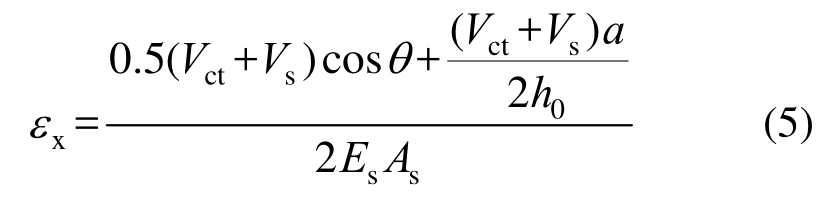
式中:Es为钢筋弹性模量;As为受拉纵筋截面面积。
桁架模型中裂缝与纵轴的倾角θ的确定方法较多,但多基于迭代计算而求解繁琐或基于回归分析而缺少明确的物理含义[23],本文采用 Kim 和Mander[24]基于最小能量原理推导出的θ表达式:
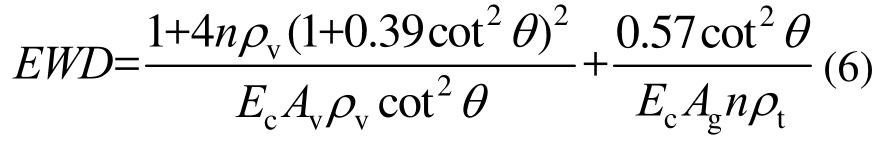
EWD为单位剪力下的总功,故根据最小能量原理,倾角θ可表示为:
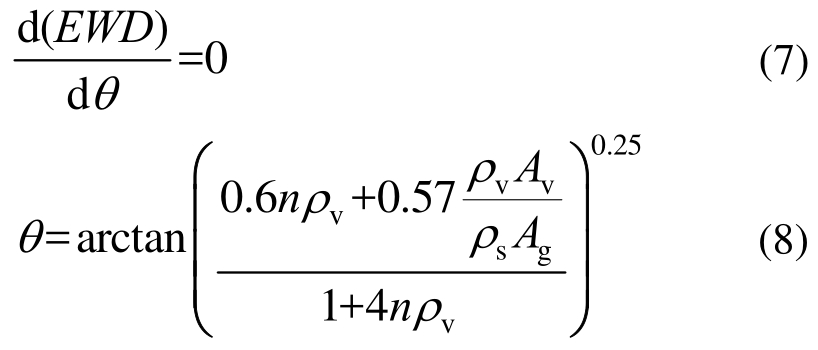
式中:n为钢材与混凝土弹性模量的比值,n=Es/Ec;Ag为RC部分截面面积;ρv为配箍率;ρs为配筋率。
因此,由式(2)~式(8)即可得到RC部分桁架作用受剪承载力。
根据变形协调桁架-拱模型[22],拱作用的贡献可由桁架作用与拱作用的变形协调关系得出:
式中:Kt为桁架作用剪切刚度;Ka为拱作用剪切刚度。
如图8所示,桁架作用的剪切刚度为:
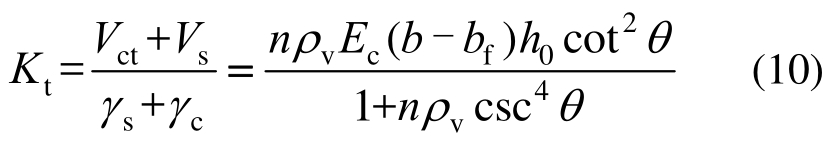

图8 桁架作用剪切变形图
Fig.8 Shear deformation of truss action
如图9所示,拱作用的剪切刚度为:
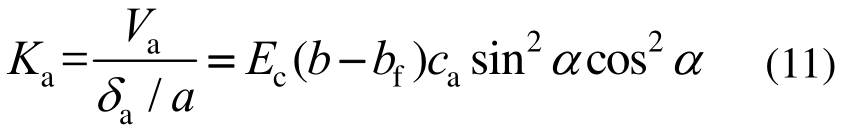
式中:ca为剪压区混凝土高度,即拱作用宽度;α为拱作用与纵轴的夹角。
Ichinose提出的传统桁架-拱模型将拱作用宽度定义为构件高度的 1/2[25],但其与试验值吻合度不高[17],本文采用Choi和Park[26]基于截面分析与回归分析推导出的表达式:
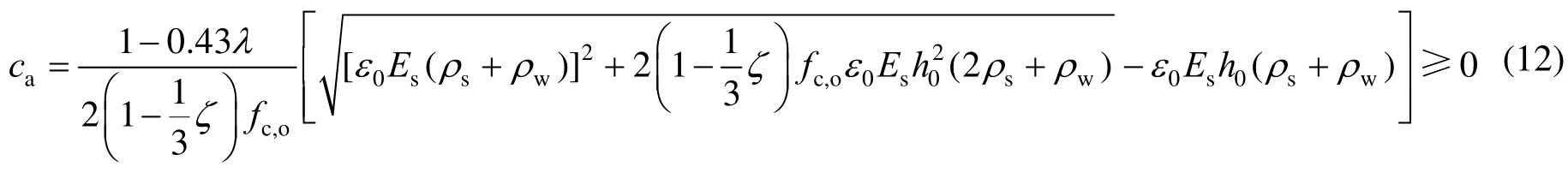
式中:λ为剪跨比;ρw为型钢腹板配钢率;系数ζ由式(13)确定:
因此,RC部分的受剪承载力为:


图9 拱作用剪切变形图
Fig.9 Shear deformation of arch model
型钢及内部混凝土的受剪承载力由修正的Nakamura模型确定。如图10所示,型钢及内部混凝土在剪切荷载作用下,混凝土压杆与型钢拉杆可构成X构架[21]。在Nakamura模型中,压杆和拉杆的有效宽度be在 0.3hw~0.4hw,hw为型钢高度。在PSRC梁中,外部混凝土可有效约束型钢上下翼缘,故在本文中取be=0.4hw。故型钢及内部混凝土的受剪承载力为:
式中:fy为型钢腹板屈服强度;tw为型钢腹板厚度;fc,in为现浇混凝土强度;αs为压杆与纵轴的夹角。
通过式(1)~式(15)即可求得 PSRC梁受剪承载力,若令fc,i=fc,o,则利用该设计方法即可计算普通现浇SRC梁的受剪承载力。
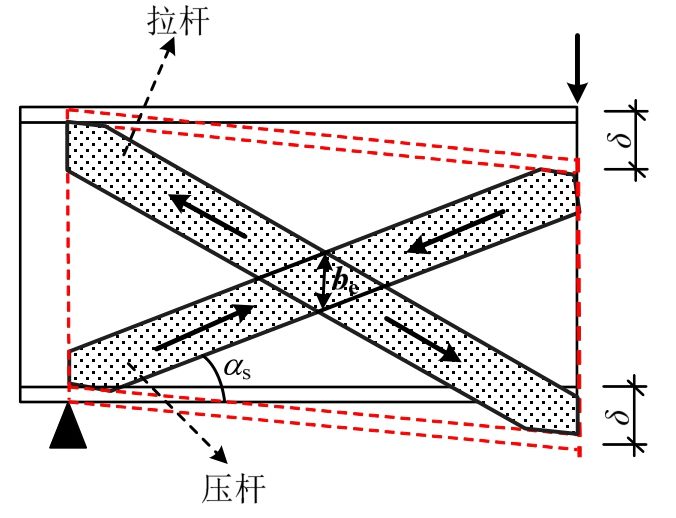
图10 型钢变形图
Fig.10 Shear deformation of encased steel shape
4 模型验证
为了验证上述计算方法的有效性,本文根据上述方法计算了本文和文献[6]、文献[13―17]共 75根发生剪切破坏的PSRC或SRC梁的受剪承载力。其中试件的宽度从 160 mm到 450 mm,高度从240 mm到650 mm。试件的加载方式包括三点加载及四点加载,试件混凝土棱柱体抗压强度15.7 MPa~82.9 MPa,混凝土种类包括普通混凝土、轻骨料混凝土、再生骨料混凝土及超高强混凝土,试件配钢率2.70%~7.50%。
同时采用规范AISC 360―2010和JGJ 138―2016中建议的方法对上述文献中的试件的受剪承载力进行计算,计算结果见图11及表3。
由图11和表3可以看出,本文提出的方法可有效预测SRC梁及PSRC梁的受剪承载力,计算值与试验值比值均值为0.92,变异系数为0.18。规范JGJ 138-2016与AISC 360-2010建议的方法均较为保守,其中使用AISC 360-2010建议方法计算的结果与试验结果相比离散度较大。
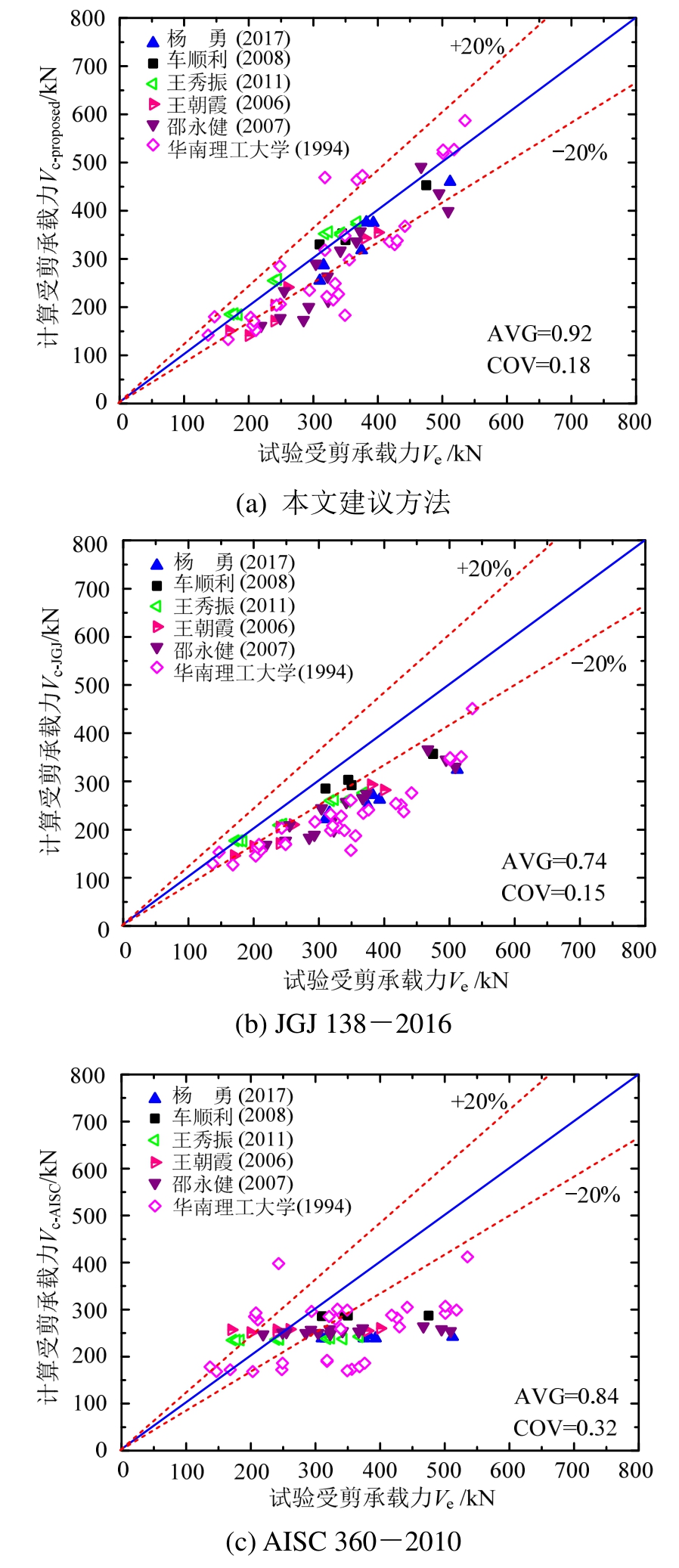
图11 试验值与理论值的对比
Fig.11 Comparison of calculated and experimental results
表3 75个剪切破坏SRC梁的主要参数
Table 3 Details of 75 shear-critical SRC beams

参考文献 试件编号 剪跨比 混预凝制土 抗压强度现/浇M Pa 配(钢%率)/Ve/kNVc-p kroNposed/Ve/Vc-proposedVc-JGJ/kN Ve/Vc-JGJ Vc k-ANIS C /Ve/Vc-AISC本文 PSRC-1 1.0 36.0 19.4 3.46 2170 2311 1.07 1749 0.81 1321 0.61 PSRC-2 1.5 36.0 19.4 3.46 1600 1605 1.00 1321 0.83 1307 0.82 PSRC-2-1 1.0 43.2 30.5 4.29 512 460 0.90 324 0.63 242 0.47 PSRC-2-2 1.5 43.2 30.5 4.29 375 318 0.85 249 0.67 239 0.64杨勇PSRC-2-3 1.8 43.2 30.5 4.29 310 255 0.82 222 0.72 239 0.77(2017)PSRC-2-4 1.5 43.2 17.4 4.29 316 287 0.91 235 0.74 239 0.76 PSRC-2-5 1.5 43.2 54.4 4.29 393 375 0.95 262 0.67 239 0.61 SRC-2-6 1.5 54.4 54.4 4.29 382 376 0.99 272 0.71 246 0.65 SRC-18 1.0 69.1 5.61 475 453 0.95 357 0.75 287 0.60车顺利SRC-19 1.5 69.1 5.61 310 330 1.07 285 0.92 286 0.92(2008)SRC-24 1.5 73.2 5.61 350 339 0.97 292 0.83 287 0.82 SRC-25 1.5 82.9 5.61 345 353 1.02 303 0.88 291 0.84 SRRC-1 1.2 31.92 6.03 318 352 1.11 260 0.82 238 0.75 SRRC-2 1.6 31.92 6.03 239 255 1.07 209 0.87 236 0.99 SRRC-3 2.1 31.92 6.03 184 184 1.00 176 0.95 235 1.27 SRRC-4 1.2 32.80 6.03 343 354 1.03 261 0.76 238 0.69 SRRC-5 1.6 32.80 6.03 245 257 1.05 210 0.86 236 0.96王秀振SRRC-6 2.1 32.80 6.03 172 185 1.08 177 1.03 235 1.37(2011)SRRC-7 1.2 33.52 6.03 324 356 1.10 262 0.81 239 0.74 SRRC-8 1.6 33.52 6.03 245 258 1.05 211 0.86 237 0.97 SRRC-9 2.1 33.52 6.03 178 186 1.05 177 1.00 235 1.32 SRRC-10 1.2 41.12 6.03 368 372 1.01 273 0.74 242 0.66 SRRC-11 1.2 43.36 6.03 368 377 1.02 276 0.75 243 0.66 SRRC-12 1.2 30.88 6.03 343 350 1.02 258 0.75 237 0.69 SBⅠ-1 1.2 36.00 7.32 400 355 0.89 282 0.70 260 0.65 SBⅠ-2 1.8 36.00 7.32 260 241 0.93 210 0.81 258 0.99王朝霞SBⅠ-3 2.3 36.00 7.32 240 171 0.71 171 0.71 257 1.07(2006)SBⅠ-4 2.9 36.00 7.32 170 151 0.89 146 0.86 257 1.51 SBⅠ-5 1.1 36.00 6.13 380 343 0.90 293 0.77 255 0.67 SBⅠ-6 1.8 36.00 6.13 240 204 0.85 205 0.85 252 1.05 SBⅠ-7 2.4 36.00 6.13 200 141 0.71 165 0.82 251 1.26 B1-1.0 0.9 31.50 5.75 509 399 0.78 330 0.65 254 0.50 B1-1.5 1.4 31.50 5.75 304 290 0.95 244 0.80 250 0.82 B1-2.0 1.8 31.50 5.75 323 213 0.65 198 0.60 248 0.75 B1-2.5 2.3 31.50 5.75 219 161 0.74 168 0.77 247 1.13 B1-1.5p 1.4 36.72 5.75 367 336 0.92 265 0.72 253 0.69 B1-2.5p 2.3 36.72 5.75 285 173 0.61 183 0.64 250 0.88邵永健B2-1.0 0.9 39.80 5.75 495 436 0.88 345 0.70 258 0.52(2007)B2-1.5 1.4 39.80 5.75 342 317 0.93 257 0.75 254 0.74 B2-2.0 1.8 39.80 5.75 255 233 0.92 209 0.82 252 0.99 B2-2.5 2.3 39.80 5.75 249 177 0.71 177 0.71 251 1.01 B3-1.0 0.9 52.30 5.75 467 491 1.05 366 0.78 264 0.57 B3-1.5 1.4 52.30 5.75 373 357 0.96 274 0.73 260 0.70 B3-2.0 1.8 52.30 5.75 322 263 0.82 223 0.69 258 0.80 B3-2.5 2.3 52.30 5.75 293 200 0.68 189 0.65 257 0.88
续表

参考文献 试件编号 剪跨比 混凝土抗压强度/MPa 配钢率/V/kNVc-proposed/V/VV/kN V/V Vc-AISC/V/V预制 现浇(%)ekNec-proposedc-JGJec-JGJkN ec-AISC B1-1a 1.5 25.45 2.70 356 298 0.84 187 0.53 173 0.49 B1-1b 2.0 25.45 2.70 349 183 0.52 157 0.45 170 0.49 B1-2a 1.0 23.39 2.70 368 464 1.26 234 0.64 178 0.48 B1-2b 2.0 23.39 2.70 147 132 1.22 153 1.04 168 1.14 B2-1a 1.5 15.72 2.70 248 285 1.15 171 0.69 172 0.69 B2-1b 2.0 15.72 2.70 203 179 0.88 145 0.71 168 0.83 B2-2a 1.0 23.11 2.70 376 473 1.26 241 0.64 186 0.49 B2-2b 3.0 23.11 2.70 168 133 0.79 127 0.75 172 1.02 B3-1a 1.5 20.94 2.70 318 318 1.00 198 0.62 190 0.60 B3-1b 2.0 20.94 2.70 249 206 0.83 169 0.68 186 0.75 B3-2a 1.0 16.17 2.70 318 469 1.48 232 0.73 192 0.60 B3-2b 3.0 16.17 2.70 137 142 1.04 129 0.94 178 1.30 B6-1a 1.5 21.51 4.91 426 330 0.78 251 0.59 282 0.66华南理工B6-1b 2.0 21.51 4.91 331 215 0.65 204 0.62 279 0.84大学B6-2a 1.0 24.23 4.91 501 519 1.04 345 0.69 292 0.58(1994)B6-2b 3.0 24.23 4.91 211 152 0.72 157 0.74 278 1.32 B7-1a 1.5 19.73 4.91 418 336 0.80 254 0.61 288 0.69 B7-1b 2.0 19.73 4.91 321 222 0.69 208 0.65 285 0.89 B7-2a 1.0 23.46 4.91 518 527 1.02 351 0.68 299 0.58 B7-2b 3.0 23.46 4.91 206 162 0.79 163 0.79 285 1.38 B8-1a 1.5 23.27 4.91 442 368 0.83 276 0.62 305 0.69 B8-1b 2.0 23.27 4.91 334 249 0.75 228 0.68 301 0.90 B8-1a' 1.5 17.31 4.91 349 348 1.00 261 0.75 299 0.86 B8-1b' 2.0 17.31 4.91 294 235 0.80 216 0.73 296 1.01 B8-2a 1.0 18.66 4.91 501 526 1.05 349 0.70 307 0.61 B8-2b 3.0 18.66 4.91 208 171 0.82 169 0.81 293 1.41 B9-1a 1.5 17.02 4.91 430 338 0.79 237 0.55 263 0.61 B9-1b 2.0 17.02 4.91 339 227 0.67 198 0.58 259 0.76 B9-2a 1.0 19.09 7.50 535 587 1.10 451 0.84 412 0.77 B9-2b 3.0 19.09 7.50 243 204 0.84 203 0.84 398 1.64平均值 0.92 0.74 0.84变异系数0.18 0.15 0.32
图12为式(12)计算出的剪压区高度与试件高度的比值和剪跨比之间的关系图。从图中可以看出,加载点处混凝土剪压区高度随剪跨比的增大而减小,即拱作用随剪跨比的增大而减弱。由传统桁架-拱模型(ca=0.5h0)预测出的抗剪承载力偏于不安全。
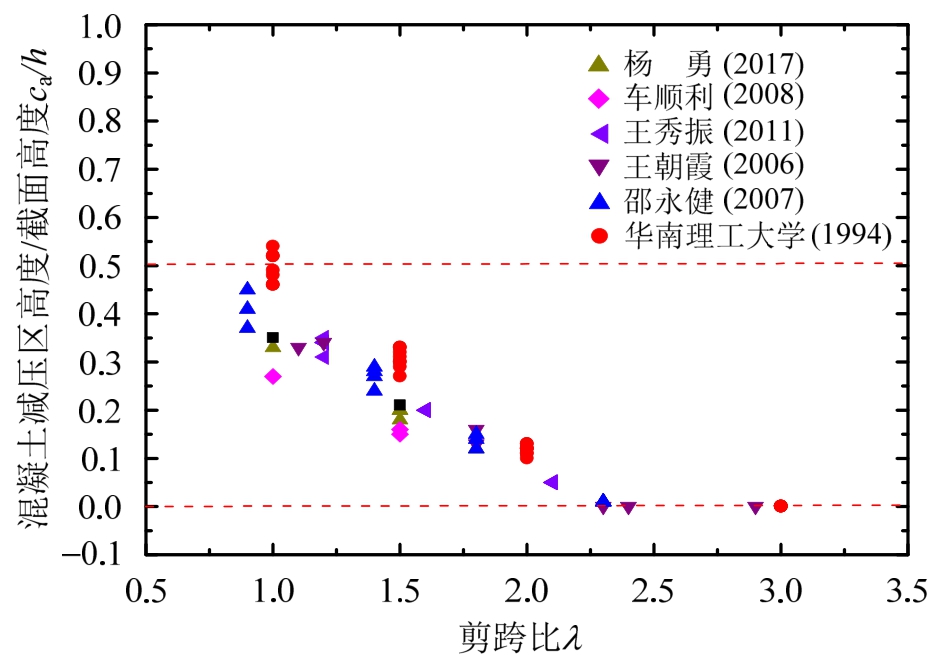
图12 剪压区高度-剪跨比关系图
Fig.12 Height of shear compression area versus aspect ratio
5 结论
(1)2个足尺PSRC梁试件均发生剪切破坏,其中剪跨比为1.0的试件PSRC-1发生斜压破坏,剪跨比为 1.5的试件发生剪压破坏。剪跨比对 PSRC梁受剪性能的影响较大,试件受剪承载力随剪跨比的增加而减小,变形能力与延性系数随剪跨比的增大而增大。
(2)本文提出的基于变形协调桁架-拱模型与Nakamura模型的 PSRC梁受剪承载力计算模型能较好反映PSRC梁的受剪破坏机理及预制、现浇混凝土对试件受剪承载力的贡献,该模型同时适用于计算普通现浇SRC梁的受剪承载力。
(3)规范JGJ 138-2016及AISC 360-2010中建议的SRC梁受剪承载力计算公式均偏于保守,其中由AISC 360-2010中建议的方法计算得出的受剪承载力与试验结果相比离散度较大。
[1]薛建阳.组合结构设计原理[M].北京: 中国建筑工业出版社, 2010: 99―101.Xue Jianyang.Composite structure design principle[M].Beijing: China Architecture & Building Press, 2010:99―101.(in Chinese)
[2]程万鹏, 宋玉普, 张秀娟.预制装配式部分钢骨混凝土框架梁柱节点承载能力的试验研究[J].大连交通大学学报, 2014, 35(4): 52―55.Cheng Wanpeng, Song Yupu, Zhang Xiujuan.Experiment study of bearing capacity for beam and column joints of precast and discontinuous steel reinforced concrete[J].Journal of Dalian Jiaotong University, 2014, 35(4): 52―55.(in Chinese))
[3]程万鹏, 宋玉普, 王军.预制装配式部分钢骨混凝土框架梁柱中节点抗震性能试验研究[J].大连理工大学学报, 2015, 55(2): 171―178.Cheng Wanpeng, Song Yupu, Wang Jun.Experimental study of seismic performance for interior beam-column joints of precast and discontinuous steel reinforced concrete[J].Journal of Dalian University of Technology,2015, 55(2): 171―178.(in Chinese)
[4]张雪松, 李忠献.低周反复循环荷载作用下装配整体式钢骨混凝土框架节点抗震性能试验研究[J].东南大学学报(自然科学版), 2005, 35(sup1): 1―4.Zhang Xuesong, Li Zhongxian.Seismic behavior of joints of prefabricated steel reinforced concrete integral frame under low cyclic and reciprocal loading[J].Journal of Southeast University (Natural Science Edition), 2005, 35(sup1): 1―4.(in Chinese)
[5]Hong W K, Park S C, Kim J M, et al.Composite beam composed of steel and precast concrete (modularized hybrid system, MHS).Part I: Experimental investigation[J].Structural Design of Tall & Special Buildings, 2010,19(3): 275―289.
[6]杨勇, 于云龙, 杨洋, 等.部分预制装配型钢混凝土梁受剪性能试验研究[J].建筑结构学报, 2017, 38(6):53―60.Yang Yong, Yu Yunlong, Yang Yang, et al.Experimental study on shear performance of partially precast steel reinforced concrete beams[J].Journal of Building Structures, 2017, 38(6): 53―60.(in Chinese)
[7]杨勇, 薛亦聪, 于云龙, 等.部分预制装配型钢混凝土梁受弯性能试验研究[J].建筑结构学报, 2017, 38(9):46―53.Yang Yong, Xue Yicong, Yu Yunlong, et al.Experimental study of partially precast steel reinforced concrete beams under positive bending[J].Journal of Building Structures, 2017, 38(9): 46―53.(in Chinese)
[8]Yang Y, Yu Y, Guo Y, et al.Experimental study on shear performance of partially precast Castellated Steel Reinforced Concrete (CPSRC)beams[J].Steel &Composite Structures, 2016, 21(2): 289―302.
[9]过镇海.钢筋混凝土原理[M].北京: 清华大学出版社,2013: 246―253.Guo Zhenhai.Principle of reinforced concrete[M].Beijing: Tsinghua University Press, 2013: 246―253.(in Chinese)
[10]郑山锁, 胡义, 车顺利, 等.型钢高强高性能混凝土梁抗剪承载力试验研究[J].工程力学, 2011, 28(3): 129―135.Zheng Shansuo, Hu Yi, Che Shunli, et al.Experimental study on the shear capacity of SRHSHPC beams[J].Engineering Mechanics, 2011, 28(3): 129―135.(in Chinese)
[11]吴轶, 蔡健, 杨春, 等.基于软化拉-压杆模型内置钢构架型钢混凝土深梁受剪承载力预测[J].工程力学,2009, 26(11): 134―139.Wu Yi, Cai Jian, Yang Chun, et al.Prediction of shear strength of steel truss reinforced concrete deep beams based on softened strut-and-tie model[J].Engineering Mechanics, 2009, 26(11): 134―139.(in Chinese)
[12]邓明科, 马福栋, 李勃志, 等.基于修正拉-压杆模型的型钢混凝土深梁受剪承载力分析[J].工程力学,2017, 34(12): 95―103.Deng Mingke, Ma Fudong, Li Bozhi, et al.Analysis on shear capacity of SRC deep beams based on modified strut-and-tie model[J].Engineering Mechanics, 2017,34(12): 95―103.(in Chinese)
[13]冯鹏, 强翰霖, 叶列平.材料、构件、结构的“屈服点”定义与讨论[J].工程力学, 2017, 34(3): 36―46.Feng Peng, Qiang Hanlin, Ye Lieping.Discussion and definition on yield points of materials, members and structures[J].Engineering Mechanics, 2017, 34(3): 36―46.(in Chinese)
[14]AISC 360―2010, Specification for structural steel buildings[S].Chicago: American Institute of Steel Construction.
[15]JGJ 138-2016, 组合结构设计规范[S].北京: 中国建筑工业出版社, 2016.JGJ 138-2016, Code for design of composite structures[S].Beijing: China Architecture & Building Press, 2016.(in Chinese)
[16]Nakamura S I, Narita N.Bending and shear strengths of partially encased composite I-girders[J].Journal of Constructional Steel Research, 2003, 59(12): 1435―1453.
[17]Pan Z, Li B.Truss-arch model for shear strength of shear-critical reinforced concrete columns[J].Journal of Structural Engineering, 2013, 139(4): 548―560.
[18]Bentz E C, Vecchio F J, Collins M P.Simplified modified compression field theory for calculating shear strength of reinforced concrete elements[J].ACI Structural Journal,2007, 103(4): 614―624.
[19]Kim J H, Mander J B.Influence of transverse reinforcement on elastic shear stiffness of cracked concrete elements[J].Engineering Structures, 2007,29(8):1798―1807.
[20]Ichinose T.A shear design equation for ductile RC members[J].Earthquake Engineering & Structural Dynamics, 1992, 21(3):197―214.
[21]Choi K K, Park H G.Unified shear strength model for reinforced concrete beams- Part II: Verification and simplified method[J].ACI Structural Journal, 2007,104(2):153―161.
[22]车顺利.型钢高强高性能混凝土梁的基本性能及设计计算理论研究[D].西安: 西安建筑科技大学, 2008.Che Shunli.Research on basic behaviors and design theory of steel reinforced high strength and high performance concrete beams[D].Xi’an: Xi’an University of Architecture and Technology, 2008.(in Chinese)
[23]王秀振.型钢再生混凝土梁受剪性能试验研究[D].西安: 西安建筑科技大学, 2011.Wang Xiuzhen.Experimental study on shear behavior of steel reinforced recycled concrete beams[D].Xi’an:Xi’an University of Architecture and Technology, 2011.(in Chinese)
[24]王朝霞.型钢混凝土梁的裂缝和变形的研究[D].西安: 西安建筑科技大学, 2006.Wang Zhaoxia.Study on cracks and deflections of steel reinforced concrete beams[D].Xi’an: Xi’an University of Architecture and Technology, 2006.(in Chinese)
[25]邵永健.型钢轻骨料混凝土梁的力学性能及设计方法的试验研究[D].西安: 西安建筑科技大学, 2007.Shao Yongjian.Experimental study on mechanical performance and design method of steel reinforced lightweight aggregate concrete beams[D].Xi’an: Xi’an University of Architecture and Technology, 2007.(in Chinese)
[26]中国建筑科学研究院.混凝土结构研究报告选集[M].北京: 中国建筑工业出版社, 1994: 478―489.China Academy of Building Research.Research report in reinforced concrete structure[M].Beijing: China Architecture & Building Press, 1994: 478―489.(in Chinese)