混凝土是最常用的土木工程材料，经历火灾(高温)作用后将发生不同程度的损伤劣化，致使其力学性能，如弹性模量和强度等将产生严重退化。另外，在地震、爆炸及冲击等动态荷载作用下，混凝土力学性能与静态加载下有着明显区别，如强度呈现明显增强趋势，即所谓的应变率效应。近年来，受自然灾害及人为因素引起的火灾爆炸事故频繁发生，对人员安全和财产安全造成重大损失。在城市环境内，火灾通常伴随偶然性爆炸同时发生，从而对建筑结构造成更严重的损伤和破坏[1]。工程结构的耐火抗爆性能研究成为迫切需要，受到越来越多相关领域专家学者的重视。因此，对火灾(温度效应)和冲击荷载(率效应)联合作用下混凝土宏观力学性能的研究具有重要的工程和科学意义。
常温下关于混凝土材料动态加载破坏行为的应变率效应及机制，国内外研究者开展了丰硕的物理试验及数值模拟工作，如：Watstein[2]研究了不同配合比的混凝土在快速加载下的力学性能；胡时胜等[3]采用改进的直锥变截面霍普金森压杆(SHPB)进行了混凝土材料的冲击压缩试验，结果表明：混凝土材料不仅具有敏感的应变率效应，还具有十分明显的损伤软化效应。
对于混凝土材料高温损伤问题，研究者亦做了大量卓有成效的工作。如：Ma等[4]统计了部分文献中无应力立方体试件高温后剩余抗压强度、抗弯强度、劈拉强度和弹性模量的试验结果。众多研究者对火灾高温后混凝土的应力-应变关系进行了测试，发现随着温度升高，混凝土应力-应变曲线趋于平缓，峰值应力向右下偏移[5]。李亮等[6]建立了考虑温度影响的混凝土热-力耦合本构关系模型。沈玲华等[7]考察了不同胶凝材料对精细混凝土高温后力学性能的影响。Willam等[8]考虑温度损伤与力学损伤的相互作用、温度膨胀与收缩两个问题，对混凝土材料的温度退化进行了数值研究。Xotta等[9]将混凝土视为由骨料、砂浆和界面过渡区组成的三相复合材料，对混凝土代表体积单元的应力-应变关系和高温下的损伤演化进行了二维和三维数值模拟。
上述研究工作主要集中于火灾(高温)和爆炸、冲击荷载等独立作用。近年来，研究者开始关注火灾高温和冲击荷载联合作用下混凝土材料的力学行为，如：陶俊林等[10]、刘传雄等[11]、何远明等[12]、许金余等[13]、王宇涛等[14]和李志卫等[15]采用加热装置和分离式霍普金森压杆(SHPB)对高温时及高温后混凝土材料的动态压缩性能进行了测试。这些试验结果表明：在高温动态压缩条件下，温度变化是影响混凝土力学性能的主要因素，应变率影响是次要因素；经不同高温作用后混凝土动态破坏强度不断降低，峰值应变不断增加，应力-应变曲线趋于平缓，出现塑性流动现象，且温度越高越为明显。这些试验研究工作促进了火灾(高温)和冲击荷载作用下混凝土力学性能的认识。尽管如此，对于混凝土在高温作用与动态加载联合作用下的“热-力”耦合作用内在机制及损伤演化规律的认识依然不清晰，缺乏深入探讨。细观力学数值分析方法，能够考虑混凝土内部组成的非均质特征，应是揭示混凝土损伤演化过程及破坏机理的有效手段。
鉴于此，本文从细观尺度出发，以高温下混凝土动态压缩破坏为例，考虑高温下细观组分力学性能的退化行为及动态加载的率效应，建立了混凝土二维及三维细观力学模型，研究高温与应变率耦合作用下混凝土宏观力学性能及细观破坏机制。
1 混凝土热-力耦合模型建立
混凝土宏观非线性及破坏行为与其微/细观结构密切关联，在数值计算中需要考虑混凝土内部组成的非均质特性[16]。为揭示高温下混凝土动态破坏机理，本文从细观角度出发，将混凝土看作由骨料、砂浆基质及两者间界面过渡区组成的三相复合材料，对高温下混凝土动态单轴压缩破坏行为进行数值模拟研究。这里，将该“热-力”单向耦合数值模拟分为两个步骤。
1)第一步(温度场模拟)：非均质混凝土中热传导行为模拟―确定混凝土的温度场空间分布。
2)第二步(力学反应)：把第一步的“输出结果”作为第二步动态力学破坏模拟的“初始条件”，依据温度场分布，确定高温下非均质混凝土当前的有效力学参数，进而对其动态力学性能进行模拟。
1.1 细观几何模型
假定骨料颗粒为圆形(球形)，采用Monte-Carlo方法进行骨料投递，随机生成试件边长为 150 mm的混凝土二维和三维随机骨料试件，分别如图1(a)和图1(b)所示。图1中，圆形区域代表圆形骨料颗粒，包含两种等效粒径：中石(粒径d=30 mm)颗粒数为 6，小石(d=12 mm)颗粒数为 56；环形区域表示界面过渡区(ITZ)，考虑到计算量的影响，界面厚度设为 1 mm；灰色区域代表砂浆基质。需要说明的是，热传导模拟中，采用热传导单元来划分网格；力学模拟中，二维和三维细观力学模型分别采用四边形等参单元及六面体线性等参单元来划分网格，网格划分尺寸为1 mm。
图1 混凝土细观力学模型及网格划分
Fig.1 Meso-scopic models of concrete specimens and meshing
1.2 本构模型与力学参数
1.2.1 热传导行为与热工参数
经典的热传导方程为：
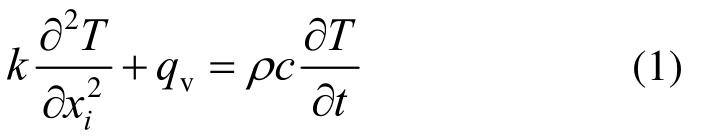
式中：k为导热系数；T/(℃)为温度；qv为单位体积热源强度；ρ为介质密度；c为比热容；xi为空间坐标；t为时间。
混凝土的配合比、水分含量及骨料类型等因素影响着混凝土材料的热工系数，主要包括比热容、导热系数、介质密度及热膨胀系数等[17―18]，多以温度相关的表达式来表征，即考虑了热工参数的温度相关性[19―20]，具体如下：
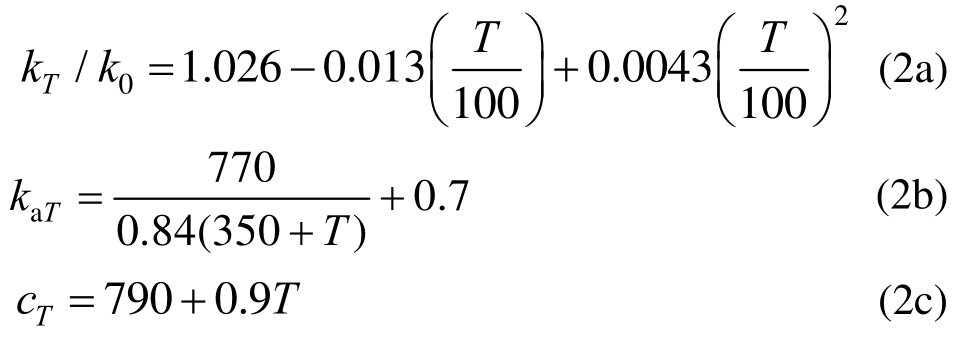
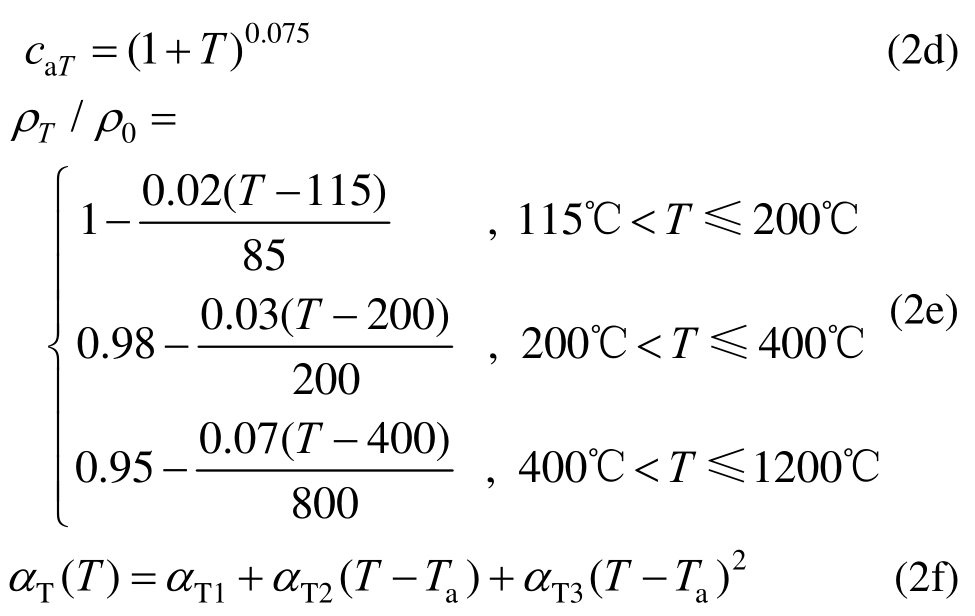
式中：kT、cT、ρT分别为高温下砂浆及界面的导热系数、比热容、介质密度；kaT、caT分别为高温下骨料的导热系数、比热容；k0、ρ0为室温下砂浆及界面的导热系数、介质密度。αT为热膨胀系数，Ta为参考温度(即20℃室温)；αT1、αT2、αT3为模型参数，具体数值详见表1。根据文献[21―23]及部分参数假定，采用的混凝土各细观组分热工参数(室温下，即20 ℃)取值详见表2。
表1 热膨胀系数模型参数[18]
Table 1 Parameters for thermal expansion coefficients
?images/BZ_84_1578_1697_1579_1707.png
表2 室温下混凝土各细观组分热工参数
Table 2 Thermal parameters for meso-constituents under room temperature (20°C)
?
1.2.2 力学本构关系模型与力学参数
1)温度退化效应
试验研究[24]表明混凝土高温下的弹性模量、抗压强度和抗拉强度均随温度升高而显著下降，并且混凝土高温下强度受强度等级、骨料类型、配合比和升温速度的影响，高温下混凝土的应力-应变曲线形状与常温下基本一致。
由于砂浆基质和界面相在高温下的力学性能试验研究薄弱，没有可以直接借用的计算公式，这里暂假定高温下砂浆基质和界面相力学性能退化规律与混凝土相同，采用图2 CEB规范[20]给出的混凝土力学性能随温度退化关系表征，具体如下：
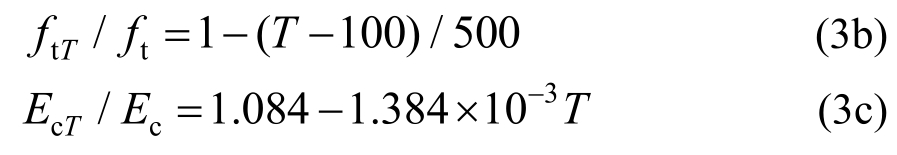
式中：fcT、ftT、EcT为高温下混凝土的抗压强度、抗拉强度、弹性模量；fc、ft、Ec为室温下混凝土的抗压强度、抗拉强度、弹性模量。其中，式(3a)为拟合公式。
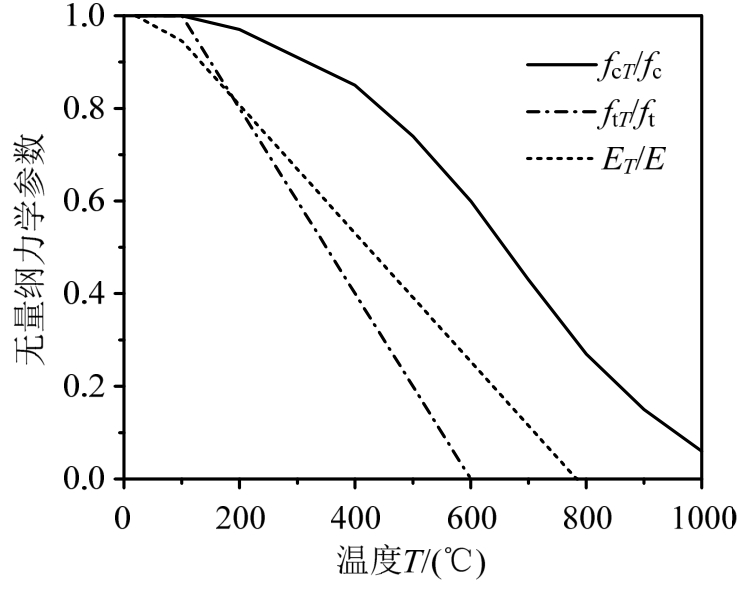
图2 高温下混凝土力学性能退化
Fig.2 Ratio between mechanical properties
2)应变率效应
目前关于高温下混凝土材料的应变率效应还没有普遍认识，对各细观组分高温下的应变率效应则更极为少见。这里，参考 Zhai等[25]相关研究工作，暂假定高温下细观应变率效应与常温下一致。
相比于抗压和抗拉强度，其他力学参数，诸如弹性模量、泊松比及断裂能等应变率敏感性较弱。本文数值模拟中，仅仅考虑强度的放大效应，即采用强度放大系数 DIF(动态强度/静态强度)来表示。CEB规范[20]中用来表征混凝土动态抗压强度提高因子(CDIF)的公式为：
式中：fcd为应变率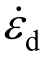
时的混凝土动态抗压强度；fcs为静态抗压强度(
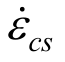=30×10-6 s-1)； lgγ=6.156α-0.49，其中α=(5+3fcu/4)-1，fcu/MPa是混凝土立方体抗压强度。针对拉伸强度增大行为(TDIF)，这里采用修正的CEB模型来表征，为：
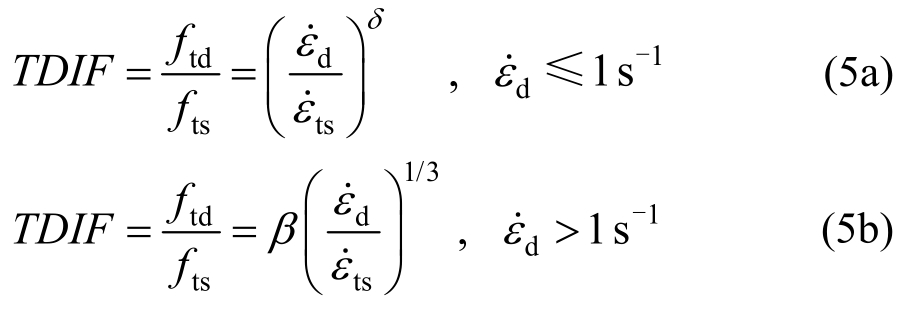
式中：ftd为应变率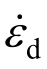
时的混凝土动态抗拉强度；fts为静态抗拉强度
其中
为准静态下混凝土轴心抗压强度。
3)塑性损伤本构关系模型
在常温下，骨料强度较高，一般不会发生破坏；而在高温下，相关研究表明[26]：骨料的峰值应力、弹性模量均有不同幅度的降低，且经历的温度越高，降低的幅度越大。一般来说，可采用理想弹塑性模型来描述高温后骨料的力学行为，采用文献[27]中材料参数。
Lee和Fenves[28]提出了可描述混凝土塑性永久变形及损伤特征的塑性损伤模型。同文献[16]，砂浆基质、界面过渡区与混凝土力学行为类似，可采用该塑性损伤模型来描述其力学行为。该混凝土材料本构模型可以描述单调加载、周期性往复加载、低围压下动力加载等问题，因此得到众多学者极为广泛的应用。在下文关于高温后混凝土材料动态力学行为的数值模拟中，将采用同时耦合温度退化效应及应变率效应的塑性损伤本构模型来描述砂浆基质与界面过渡区的力学行为。
本文中采用的混凝土各细观组分主要力学参数(室温下，即20 ℃)，包括弹性模量、泊松比及拉伸/压缩强度等，详见表3。
表3 室温下混凝土各细观组分力学参数
Table 3 Mechanical parameters for meso-constituents under room temperature (20 ℃)
注：骨料压缩强度为屈服强度。
?
1.3 边界与加载条件
1.3.1 热传导
火灾对结构最直接的作用是表面加热，本文对混凝土试件进行四面受火分析，采用图3所示国际标准化组织(ISO834)推荐的抗火试验及火灾模拟曲线T=T0+3 45lg10(8t+1)[29]，式中T0/(℃)表示初始环境温度，T/(℃)表示t/min时刻的温度幅值。
1.3.2 动态加载
高温下，混凝土单轴动态压缩破坏行为模拟的加载和边界条件为：试件底边采用法向固定约束；两侧为自由边界；顶部为荷载输入边界，采用速度v加载控制。试件的应变率为
(这里，h为混凝土试件高度)。
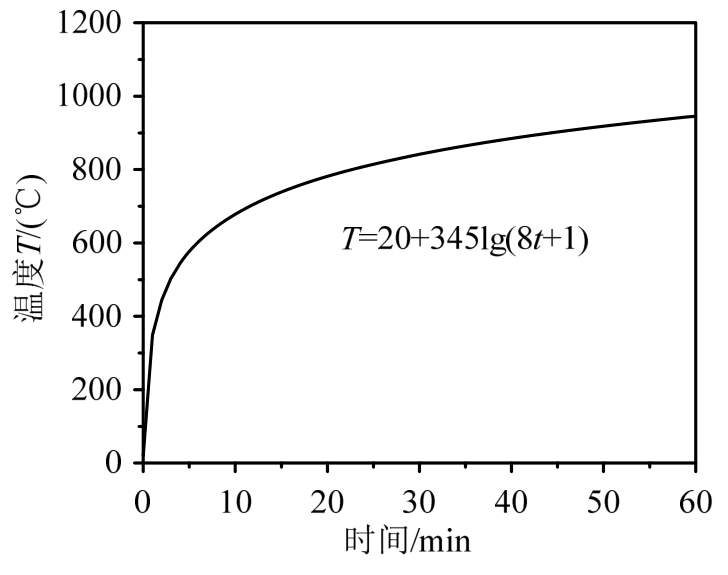
图3 ISO834标准温升曲线
Fig.3 ISO834 standard temperature curve
2 数值计算结果及分析
2.1 温度场分布
图4为混凝土试件在四面受火时不同时刻温度场分布，时间间隔为15 min，最高温度达到945 ℃。总体而言，在某一个时刻温度由外到内逐渐降低，随着升温时间的增加混凝土试件的温度逐渐升高并向内部传递。由于混凝土的传热性能差，形成极不均匀的温度场，靠近加热边界处的升温更加明显。在细观尺度模型中由于考虑了混凝土的非均质性以及骨料的随机分布，不同时刻试样内部的温度场分布是不对称的，因而不均匀的温度场分布会对混凝土材料内部的力学性能产生影响。
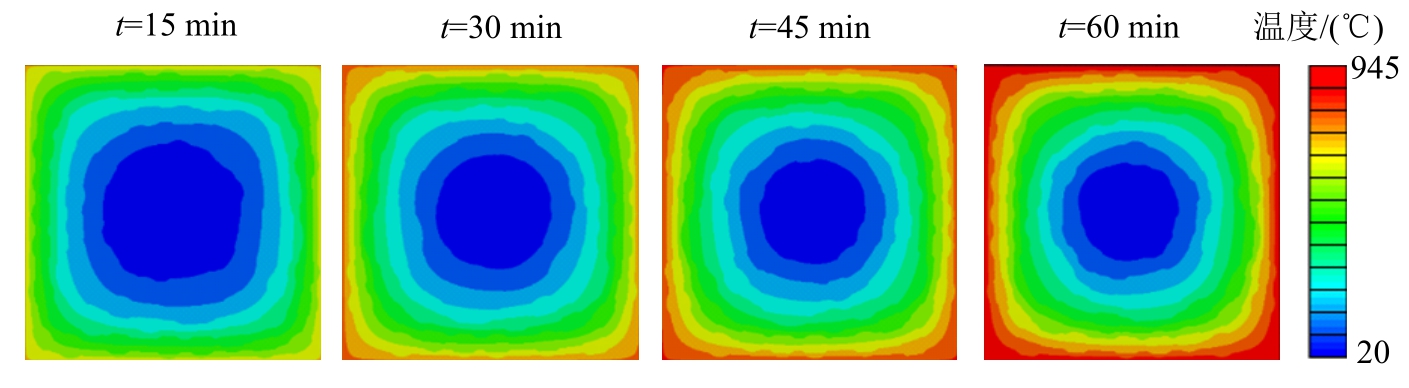
图4 四面受火混凝土试件不同时刻温度场分布
Fig.4 Temperature field within concrete specimen subjected to four-side ISO 834 fire
2.2 模拟方法验证
为验证本文细观数值分析模型与方法的可靠性和准确性，对 Zhai等[30]关于混凝土高温后的动态力学性能进行模拟分析。这里，分别对 600℃与1000℃高温后名义应变率为 0 .0001 s-1和0.003 s -1的两组混凝土试件进行动态压缩破坏模拟，数值及试验获得的动态压缩应力-应变曲线如图5所示。由图5可知，本文数值模拟获得的应力-应变关系曲线与试验结果吻合良好，能够很好地模拟高温下混凝土动态压缩宏观力学行为。
图5 模拟的应力-应变关系与试验结果对比
Fig.5 Comparison of simulated stress-strain curves with experiment results
2.3 高温下混凝土动态压缩破坏模式
基于上述已验证的细观数值分析方法，对混凝土试件在高温下的冲击破坏行为进行模拟分析，工况为：加热60 min，名义应变率为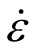
= 1 s -1。图6(a)和图6(b)分别表征了混凝土试件细观结构高温下的二维及三维压缩破坏过程，给出了时间分别为t= 2 .7 ms 、t=3 .5 ms 、t=4 .2 ms 、t=5 .0 ms 时刻的损伤破坏形态。可以看出，混凝土试件最先在加载方向两端边界(即为高温后非均质混凝土中力学性能退化显著的区域)出现严重破坏(以损伤因子来表征其强弱)，随加载时间增大，损伤越来越明显，并沿界面及砂浆区域向试件内部开展。
基于2.1节所述的热传导过程，本文对名义应变率分别为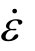
=1×10-5 s-1、1×10-4 s-1、1×10-2 s-1、1 s-1及 100 s-1的混凝土试件压缩破坏过程进行了数值研究。图7给出了常温及高温下不同名义应变率下混凝土试件的损伤破坏模式。从图7可以看出，常温下，试件内部损伤分布均匀，随名义应变率增大，裂纹沿界面延伸扩展且数量增加，呈现出网状交叉路径；高温下，由于不均匀的温度场，试件周边温度损伤尤为严重，故而损伤严重区域主要集中在加载方向的上下端，随名义应变率增大，裂纹变宽增多并向内部延伸；随升温时间增大，损伤由加载边界逐渐向混凝土试件内部传递分散；常温下及高温下裂纹都主要出现在更为薄弱的砂浆及界面区域；名义应变率较小时，试件为裂纹破坏，名义应变率较大时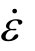=100 s-1，混凝土试件呈粉碎状破坏。此现象与艾晓芹[31]以及Ren等[32]试验结果较为一致。
2.4 峰值应力处应变率空间分布
图6 加热60 min后混凝土试件应变率为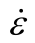
=1 s-1时的压缩损伤过程
Fig.6 Damage process of concrete specimen with strain rate of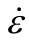
=1 s-1 exposured to fire for 60 minutes
图7 高温下不同应变率下混凝土试件压缩破坏模式
Fig.7 Compressive failure patterns of concrete specimen under different strain rates at elevated temperature
图8 峰值应力处混凝土试件的应变率分布
Fig.8 Strain rate distribution at peak stress of concrete specimen at elevated temperature
图8给出了经历不同加热时间后的混凝土试件在不同应变率下达到峰值应力时的应变率空间分布。可以看出，由于混凝土试件细观结构的非均质性，其内部应变率分布是不均匀的，应变率较大区域主要集中在相对薄弱的界面和砂浆部分。横向观察图 8，同一名义应变率下，常温下应变率较为分散地分布在整个截面；高温下，随加热时间递增，混凝土试件高温劣化愈发严重，获得更大的应变率，应变率较大区域更加集中，并且由边界处逐渐向试件内部传递。纵向观察图8可知，同一温度下，随名义应变率增大，混凝土试件应变率空间分布更加均匀，应变率较大区域明显减少，并且集中分布于加载端边界。
2.5 宏观应力-应变关系
图9给出了不同应变率及不同高温加热时间下混凝土试件的动态压缩应力-应变关系。可见，无论常温下还是高温下，混凝土试件均表现出显著的应变率效应，峰值应力随应变率的增大而增大，峰值应变轻微增大，应力-应变曲线形状不变。值得注意的是，在高应变率(如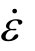=100 s-1)下，峰值应力及峰值应变出现突增现象，这是因为：高应变率时，惯性影响起主导控制作用。经历高温作用后，应力-应变曲线趋于平缓，峰值应力显著减小，峰值应变显著增大，出现了塑性流动，说明高温对混凝土有明显的劣化作用。此外，可以看出，相比于应变率效应，混凝土强度受温度退化效应影响更为显著，与何远明[12]等众多研究者试验所得结果一致。
图9 不同应变率下混凝土试件应力-应变关系
Fig.9 Stress-strain curves of concrete specimen under different strain rates at elevated temperature
图10所示为混凝土试件在峰值应力处割线模量随应变率变化关系。可见，随着温度升高，割线模量明显减小，当加热60 min后，即最高温度达到945℃时，割线模量仅约为室温下的1/6。另外可知，相同温度下，随名义应变率增大，割线模量变化微小。总体而言，相比于应变率效应，割线模量受温度退化效应影响更为显著。
2.6 动态压缩强度增大系数
采用动态压缩强度增大系数(CDIF)，即动态压缩强度与准静态压缩强度(本文取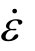 =1× 10-5 s -1时强度)之比来描述材料强度随应变率增大而提高的现象。图11给出了在不同温度下混凝土CDIF与应变率间的三维散点关系，并对其进行拟合，比较了高温下CDIF随应变率的变化关系。由图可知，名义应变率较小时，随温度升高，CDIF呈减小趋势；当应变率超过一定值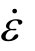=1 s-1时，CDIF表现出先增大后减小的趋势，但此规律尚不明确；当应变率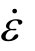=100 s-1时，动态增大系数急剧增加，这与 Li和Meng[33]提到的临界应变率现象相同。其他研究者相关结论尚不一致，Zhai等[30]及何远明等[12]认为CDIF随温度增大而增大，而贾彬[34]却得到相反结论。
图10 峰值应力处割线模量
Fig.10 Secant modulus at peak stress
图11 不同温度下CDIF与应变率关系
Fig.11 Relationship between CDIF and strain rate at elevated temperature
具体数值可参见表4，并与CEB规范[20]公式计算值进行比较，由表可知，与 CEB公式整体趋势一致，由于 CEB规范中取值偏于安全保守，模拟所得数值较CEB计算值偏大。
表4 高温时不同应变率下的混凝土CDIF
Table 4 Simulated CDIFs of concrete under different strain rates after different heating durations
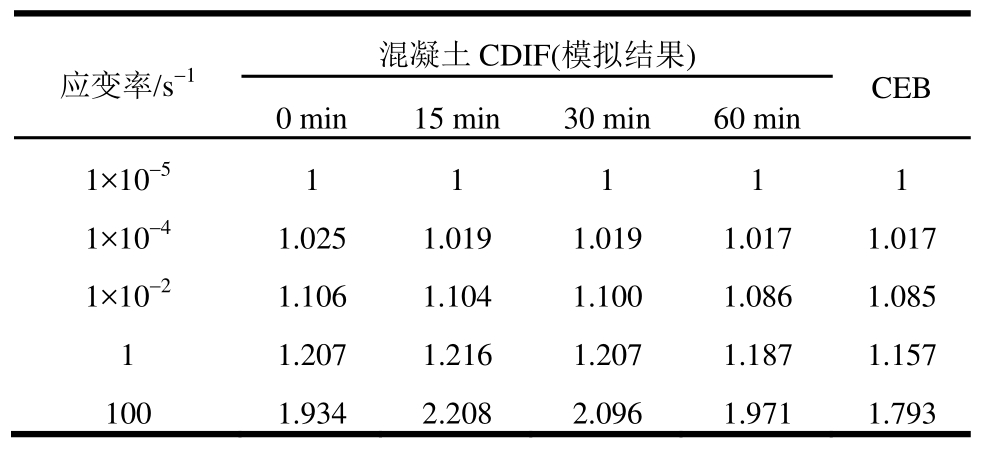
应变率/s-1 混凝土CDIF(模拟结果)CEB 0 min 15 min 30 min 60 min 1×10-5 1 1 1 1 1 1×10-4 1.025 1.019 1.019 1.017 1.017 1×10-2 1.106 1.104 1.100 1.086 1.085 1 1.207 1.216 1.207 1.187 1.157 100 1.934 2.208 2.096 1.971 1.793
3 结论
通过对高温下混凝土动态压缩行为细观数值模拟及方法验证，研究了高温下混凝土动态压缩破坏模式及破坏过程，对比了高温下不同应变率下的应力-应变关系，分析了高温下动态压缩强度增大系数(CDIF)变化规律，得到以下结论：
(1)本文细观数值方法与试验结果吻合良好，能够很好地模拟高温下混凝土动态压缩行为。
(2)常温下冲击压缩，试件内部损伤分布均匀，呈现出网状交叉路径；高温下冲击压缩，混凝土温度破坏集中在力学性能薄弱的加载端，随升温时间增大，逐渐向内部传递分散。
(3)同一名义应变率时，常温下的应变率分布(峰值应力处)较为分散，而高温下更加集中，并且由边界向试件内部传递；同一温度下，随名义应变率增大，应变率分布更加均匀，应变率较大区域明显减少，集中分布于加载端。
(4)经历高温后的混凝土静动力压缩应力-应变曲线总体上较常温下更加平缓，且加热时间越长越为明显，出现了塑性流动现象。
(5)相比于应变率效应，温度退化效应对混凝土力学性能影响更为显著，当最高温度达到945 ℃时，压缩强度约为室温下的 1/4，割线模量仅约为室温下的1/6。
[1]赵建魁, 方秦, 陈力, 等.爆炸与火荷载联合作用下RC梁耐火极限的数值分析[J].天津大学学报(自然科学与工程技术版), 2015, 10(48): 873―880.Zhao Jiankui, Fang Qin, Chen Li, et al.Numerical analysis of fire resistance of RC beams subjected to explosion and fire load[J].Journal of Tianjin University(Science and Technology), 2015, 10(48): 873―880.(in Chinese)
[2]Watstein D.Effect of straining rate on the compressive strength and elastic properties of concrete[J].ACI Journal Proceedings, 1953, 49(4): 729―744.
[3]胡时胜, 王道荣, 刘剑飞.混凝土材料动态力学性能的实验研究[J].工程力学, 2001, 18(5): 115―118.Hu Shisheng, Wang Daorong, Liu Jianfei.Experimental study of dynamic mechanical behavior of concrete[J].Engineering Mechanics, 2001, 18(5): 115―118.(in Chinese)
[4]Ma Q, Guo R, Zhao Z, et al.Mechanical properties of concrete at high temperature-A review[J].Construction and Building Materials, 2015, 93: 371―383.
[5]Nassif A.Postfire full stress-strain response of fire-damaged concrete[J].Fire and Materials, 2006,30(5): 323―332.
[6]李亮, 李彦.基于热力学原理的混凝土热-力耦合本构模型[J].北京工业大学学报, 2016, 42(4): 554―560.Li Liang, Li Yan.Thermo-mechanical coupling constitutive model of concrete based on thermodynamics[J].Journal of Beijing University of Technology, 2016,42(4): 554―560.(in Chinese)
[7]沈玲华, 王激扬, 徐世烺, 等.不同胶凝材料的精细混凝土高温后力学性能[J].工程力学, 2015, 32(增刊1):248―253, 260.Shen Linghua, Wang Jiyang, Xushilang, et al.Mechanical property of fine grained concrete with different cementing material after exposure to high-temperature[J].Engineering Mechanics, 2015,32(Suppl 1): 248―253, 260.(in Chinese)
[8]Willam K, Rhee I, Xi Y.Thermal degradation of heterogeneous concrete materials[J].ASCE Journal of Materials in Civil Engineering, 2005, 17(3): 276―285.
[9]Xotta G, Mazzucco G, Salomoni V A, et al.Composite behavior of concrete materials under high temperatures[J].International Journal of Solids and Structures, 2015,64/65: 86―99.
[10]陶俊林, 秦李波, 李奎, 等.混凝土高温动态压缩力学性能实验[J].爆炸与冲击, 2011, 31(1): 101―106.Tao Junlin, Qin Libo, Li Kui, et al.Experiment of dynamic compressive behaviour of concrete at high temperature[J].Explosion and Shock Waves, 2011,31(1): 101―106.(in Chinese)
[11]刘传雄, 李玉龙, 吴子燕, 等.高温后混凝土材料的动态压缩力学性能[J].土木工程学报, 2011, 44(4): 78―83.Liu Chuanxiong, Li Yulong, Wu Ziyan, et al.Dynamic compression behavior of heated concrete[J].China Civil Engineering Journa, 2011, 44(4): 78―83.(in Chinese)
[12]何远明, 霍静思, 陈柏生, 等.高温下混凝土SHPB动态力学性能试验研究[J].工程力学, 2012, 29(09):200―208.He Yuanming, Huo Jingsi, Chen Bosheng, et al.Impact tests on dynamic behavior of concrete at elevated temperatures[J].Engineering Mechanics, 2012, 29(9):200―208.(in Chinese)
[13]许金余, 刘健, 李志武, 等.高温中与高温后混凝土的冲击力学特性[J].建筑材料学报, 2013, 16(1): 1―5.Xu Jinyu, Liu Jian, Li Zhiwu, et al.Impact mechanical properties of concrete at and after exposure to high temperature[J].Journal of Building Materials, 2013,16(1): 1―5.(in Chinese)
[14]王宇涛, 刘殿书, 李胜林, 等.高温后混凝土静动态力学性能试验研究[J].振动与冲击, 2014, 33(20): 16―19.Wang Yutao, Liu Dianshu, Li Shenglin, et al.Static and dynamic mechanical properties of concrete after high temperature treatment[J].Journal of Vibration and Shock, 2014, 33(20): 16―19.(in Chinese)
[15]李志卫, 肖建庄, 谢青海.高温后高强混凝土受压动态损伤[J].工程力学, 2017, 34(2): 78―84.Li Zhiwei, Xiao Jianzhuang, Xie Qinghai.Compressive dynamic damage of high-strength concrete after elevated temperatures[J].Engineering Mechanics, 2017, 34(2):78―84.(in Chinese)
[16]Du X, Jin L, Ma G.Numerical simulation of dynamic tensile-failure of concrete at meso-scale[J].International Journal of Impact Engineering, 2014, 66(4): 5―17.
[17]漆雅庆.火灾下钢筋混凝土构件的非线性有限元分析研究[D].广州: 华南理工大学, 2011.Qi Yaqing.Nonlinear finite element analysis research of reinforced concrete structure in fire[D].Guangzhou:South China University of Technology, 2011.(in Chinese)
[18]Grassl P, Pearce C.Mesoscale approach to modeling concrete subjected to thermomechanical loading[J].Journal of Engineering Mechanics, 2010, 136(3): 322―328.
[19]Jin L, Zhang R, Du X.Characterization of the temperature-dependent heat conduction in heterogeneous concretes[J].Magazine of Concrete Research, 2017,70(7): 325―339.
[20]Comite Euro-International D B.CEB-FIP model code 1990[S].Trowbridge, Wiltshire, UK: Redwood Books,1993.
[21]Khan M I.Factors affecting the thermal properties of concrete and applicability of its prediction models[J].Building & Environment, 2002, 37(6): 607―614.
[22]Vosteen H D, Schellschmidt R.Influence of temperature on thermal conductivity, thermal capacity and thermal diffusivity for different types of rock[J].Physics &Chemistry of the Earth, 2003, 28(9): 499―509.
[23]
Erný R, Madĕra J, Podĕbradská J, et al.The effect of compressive stress on thermal and hygric properties of Portland cement mortar in wide temperature and moisture ranges[J].Cement & Concrete Research, 2000,30(8): 1267―1276.
[24]李凌志.火灾后混凝土材料力学性能与温度、时间的关系[D].上海: 同济大学, 2006.Li Lingzhi.Research of the relation between mechanics performance of concrete material after fire and temperature & time[D].Shanghai: Tongji University,2006.(in Chinese)
[25]Zhai C, Chen L, Xiang H, et al.Experimental and numerical investigation into RC beams subjected to blast after exposure to fire[J].International Journal of Impact Engineering, 2016, 97: 29―45.
[26]朱合华, 闫治国, 邓涛, 等.3种岩石高温后力学性质的试验研究[J].岩石力学与工程学报, 2006, 25(10):1945―1950.Zhu Hehua, Yan Zhiguo, Deng Tao.et al.Testing study on mechanical properties of tuff, graniteand and breccia after high temperatures[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(10): 1945―1950.(in Chinese)
[27]邱一平, 林卓英.花岗岩样品高温后损伤的试验研究[J].岩土力学, 2006, 27(6): 1005―1010.Qiu Yiping, Lin Zhuoying.Testing study on damage of granite samples after high temperature[J].Rock and Soil Mechanics, 2006, 27(6): 1005―1010.(in Chinese)
[28]Lee J, Fenves G L.Plastic-damage model for cyclic loading of concrete structures[J].ASCE Journal of Engineering Mechanics, 1998, 124(8): 892―900.
[29]International Organization for Standardization.ISO834-1 Fire Resistance Test on Elements of Building Construction[S].1999.
[30]Zhai C, Chen L, Fang Q, et al.Experimental study of strain rate effects on normal weight concrete after exposure to elevated temperature[J].Materials &Structures, 2017, 50: 40.
[31]艾晓芹.混凝土高温后静动态力学性能研究[D].西安: 长安大学, 2015.Ai Xiaoqin.The static and dynamic mechanical properties of concrete after high temperature[D].Xi’an:Chang’an University, 2015.(in Chinese)
[32]Ren W, Xu J, Su H.Dynamic compressive behaviour of concrete after exposure to elevated temperatures[J].Materials & Structures, 2016, 49(8): 3321―3334.
[33]Li Q M, Meng H.About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test[J].International Journal of Solids and Structures, 2003, 40(2): 343―360.
[34]贾彬.混凝土高温静动力学特性研究[D].重庆: 重庆大学, 2011.Jia Bin.Static and dynamic mechanical behavior of concrete at elevated temperature[D].Chongqing:Chongqing University, 2011.(in Chinese)