连梁是地震作用下联肢剪力墙结构体系中重要的耗能元件,是延性剪力墙结构的第一道抗震防线,其强度、刚度和耗能能力对结构体系的抗震性能影响很大[1-6]。传统钢筋混凝土连梁在往复荷载作用下耗能能力较差,滞回曲线存在明显的“捏拢”效应[7]。20世纪 90年代起,国外学者开始应用钢连梁来代替钢筋混凝土连梁。Fortney等[8-9]学者提出了一种截面削弱型可更换连梁,通过削弱腹板中间区域的厚度,使腹板中间区域在地震时首先屈服,达到保护其余部分的目的。Chung等[10-11]通过在钢连梁中部加入摩擦阻尼器来增强连梁的耗能能力。2014年,纪晓东等[12]基于损伤控制的思想提出了可更换钢连梁的联肢剪力墙。已有研究结果表明:相比钢筋混凝土连梁,钢连梁具有更好的延性和耗能能力,是剪力墙结构中较为理想的耗能元件,但不足之处在于钢连梁的腹板在剪切屈服后容易发生面外弹塑性失稳,在一定程度上降低了钢连梁的耗能能力。
为了解决钢连梁的腹板在剪切屈服后发生面外屈曲导致钢连梁耗能能力降低的问题,本文基于钢结构屈曲约束的基本思想和技术[13-17],提出了一种腹板屈曲约束钢连梁的连梁结构形式,如图1所示。在钢连梁的腹板两侧设置约束板,采用对拉螺杆对钢连梁和约束板的接触面施加一定的压应力,从而保证往复剪切荷载作用下钢连梁的腹板剪切屈服后承载力能够持续强化。约束板内的螺孔直径大于螺杆直径,可以保证约束板在面内不承担剪切荷载。相比在腹板上设置加劲肋的传统方式,合理设计的腹板屈曲约束钢连梁的腹板在接近钢材极限剪应变前仍然不发生面外屈曲,且不存在加劲肋焊接残余应力的影响,从而保证钢连梁具有优越的耗能能力。本文通过对5个腹板屈曲约束钢连梁试件进行拟静力试验加载,研究了不同约束方式对钢连梁在往复荷载作用下的承载力强化特性和耗能能力,并考察了腹板屈曲约束钢连梁的和耗能能力。
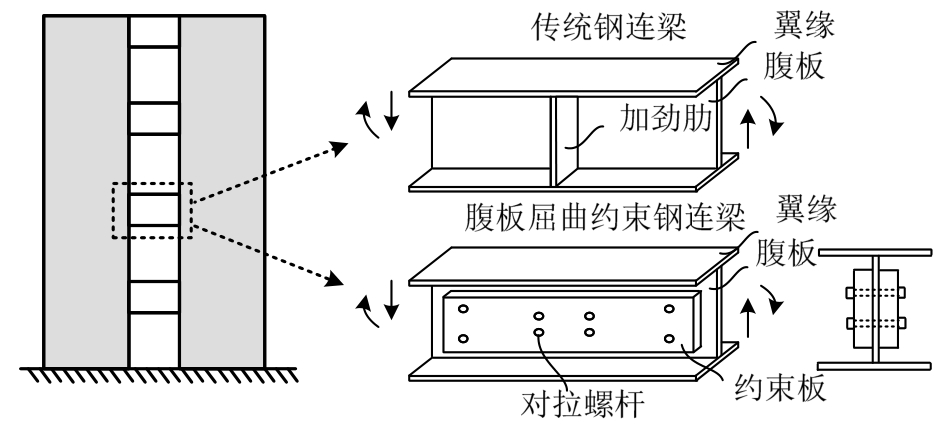
图1 腹板屈曲约束钢连梁的基本构造
Fig.1 Buckling-restrained steel coupling beam with shear yielding failure mode
1 试验概况
1.1 试件设计
以某实际剪力墙结构中的钢连梁为原型,采用3∶8的缩尺比例设计钢连梁试件,钢连梁截面为焊接工字钢 H290×200×6×10(截面高度×翼缘宽度×腹板厚度×翼缘厚度mm),钢连梁长度均为660 mm,试件详细尺寸如图 2所示。钢连梁翼缘宽厚比为9.7,腹板高厚比为45.0,满足《建筑抗震设计规范》(GB 50011―2010)的规定。LS试件的腹板加劲肋厚度为 6 mm,钢筋混凝土板中混凝土强度等级为C35,木板材质为松木,钢连梁两端设置20 mm厚的端板。


图2 试件详细尺寸
Fig.2 Test specimen size
试件变化参数主要包括约束板厚度、约束板材质、对拉螺杆设置位置,共5个试件,详细试件参数如表1所示。现有工程中的工字型截面钢连梁一般采用设置加劲肋的方式防止腹板在剪切荷载作用下过早屈曲,本次试验设计了腹板带有加劲肋的试件LS和腹板不带加劲肋的试件L0,用于考察加劲肋对腹板屈曲的约束效果。另外,设计了25 mm和50 mm两种厚度的钢筋混凝土约束板,用于研究板厚对钢连梁腹板约束作用的影响。木材具有轻质、易加工等优点,是组合结构中常用的材料,本次试验设计了以木板作为约束板的试件 LW25-8,厚度为25 mm,用于对比木板和钢筋混凝土板作为约束板对钢连梁腹板的约束效果。
表1 试件详细参数
Table 1 Parameters of specimens

?
试件翼缘强度等级为 Q345,加劲肋和腹板强度等级为Q235钢材,表2和表3中所示为钢材和木材材性试验结果。由表 4可知约束板混凝土的立方体抗压强度平均值为43.0 MPa。试件翼缘、腹板、端板之间均采用双面角焊缝连接,焊脚高度满足《钢结构设计规范》(GB 50017―2003)的要求。
表2 钢材材性试验结果
Table 2 Test results of steel
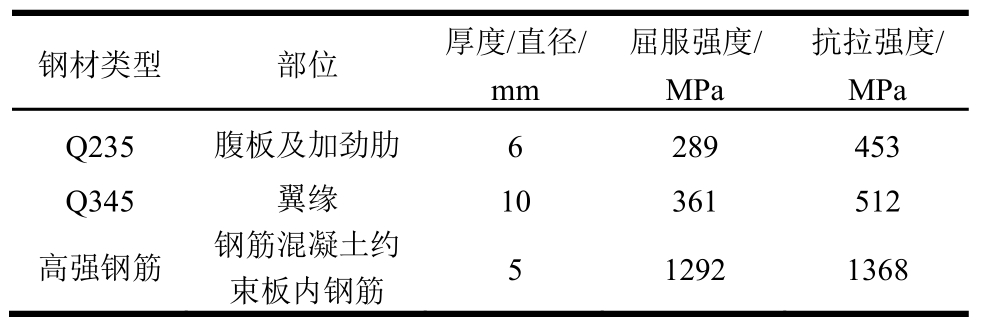
钢材类型 部位 厚度/直径/屈服强度/抗拉强度/mmMPaMPa Q235 腹板及加劲肋 6 289 453 Q345 翼缘 10 361 512高强钢筋 钢筋混凝土约5 1292 1368束板内钢筋
表3 木材材性试验结果
Table 3 Test results of wood
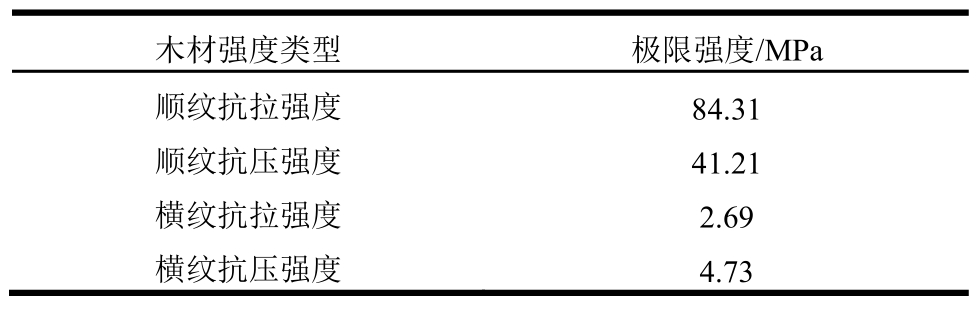
木材强度类型 极限强度/MPa顺纹抗拉强度 84.31顺纹抗压强度 41.21横纹抗拉强度 2.69横纹抗压强度 4.73
表4 混凝土材性试验结果
Table 4 Test results of concrete

试件编号 立方体抗压强度fcu/MPa C1 42.2images/BZ_63_1800_3039_1803_3040.pngC2 43.0 C3 44.5平均值 43.0
1.2 加载装置
试验采用自行设计的可拆卸式钢连梁剪切试验加载装置,如图3所示。试件沿竖直方向放置,底座通过地锚以及止推挡板固定在地面上,钢连梁下端板通过螺栓固定在底座上,上端板通过螺栓与顶梁固定。采用1000 kN的电液伺服作动器对顶梁施加水平荷载。顶梁和底座之间采用两个两端铰接的二力杆相连形成平行四边形约束机构,保证加载时试件两端没有转角。该装置能够模拟钢连梁在地震作用下受到的往复剪力和弯矩。
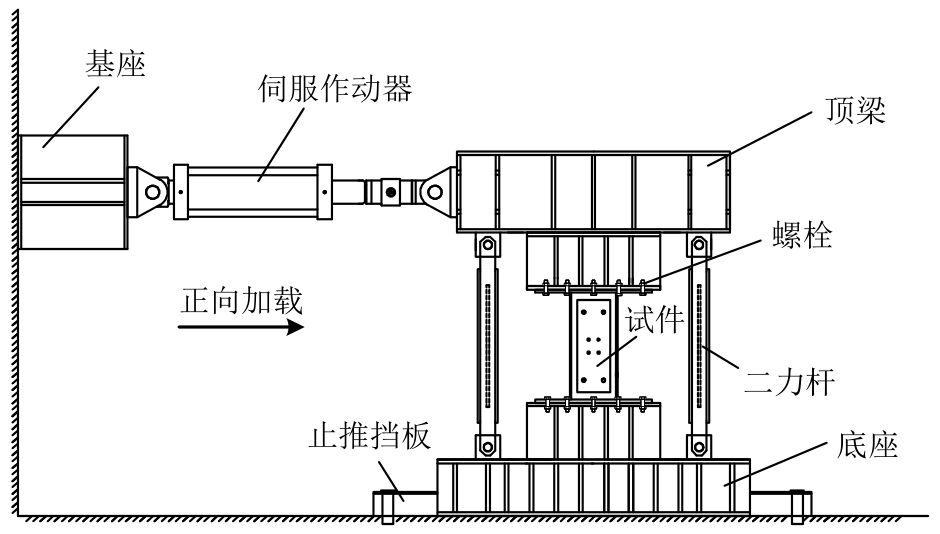
图3 加载装置
Fig.3 Loading setup
1.3 加载制度
所有试件均施加拟静力往复剪切荷载,加载制度参考《建筑抗震试验方法规程》(JGJ 101―2015),如图4所示。试件屈服前每级荷载循环1次,屈服后每级荷载循环3次。位移角定义为试件两端剪切位移与试件长度之比。

图4 加载制度
Fig.4 Loading system
1.4 位移量测方案
所有试件均采用图5所示的量测方案。采用位移计2和4测量试件的水平位移,试件的水平位移取为位移计2和4的平均值。由于加工误差等原因,顶梁可能产生微小的转动,因此采用位移计1和3测量试件的竖向位移,根据两个位移计的位移差可以得到整个加载过程中顶梁的转角。
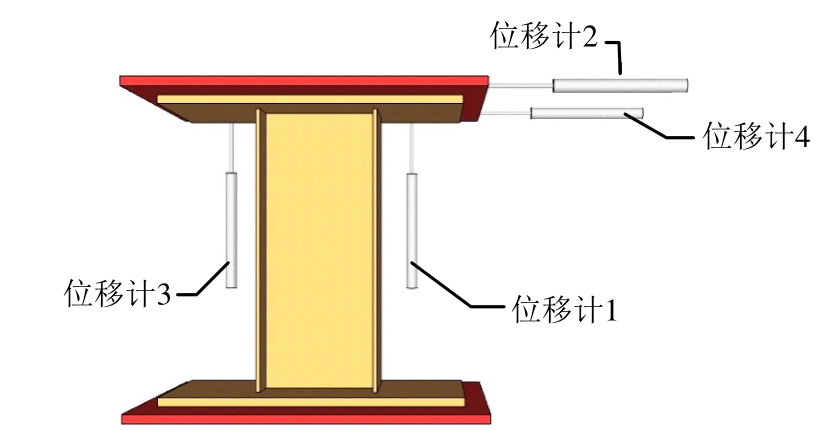
图5 试件测点布置
Fig.5 Measuring point arrangement
2 损伤破坏模式
试件在加载过程中先后出现4种损伤模式,分别为翼缘-端板焊缝断裂、木板或钢筋混凝土约束板弯曲破坏、腹板屈曲,腹板-端板焊缝断裂。由于腹板剪切屈服后受到较强的面外约束,在达到极限承载力之前,试件主要的破坏集中在翼缘-端板焊缝部位,这是由于钢连梁端部翼缘的焊缝在往复拉、压和局部弯曲作用下导致其发生低周疲劳破坏。为了延缓这种破坏,除了试件LS外,其余试件的翼缘和端板间焊缝的焊脚高度加大了0.5倍。所有试件的最终破坏形态如图6所示,各约束板最终破坏形态如图7所示。

图6 各试件最终破坏形态
Fig.6 Final failure modes of each specimen

图7 各试件约束板最终破坏形态
Fig.7 Final failure modes of each constraint plate
3 试验结果分析
3.1 滞回性能
图8所示为试件的剪力-位移角滞回曲线,由图8可以看出,设置钢筋混凝土约束板或木约束板的试件滞回曲线非常饱满,具有较强的约束效果和耗能能力。试件LC25-8和LC50-8在加载后期,随着位移角的增大,试件的受剪承载力强化明显,直到破坏前没有出现较大的承载力下降。LC25-8和LC50-8的对比结果表明,约束板厚度对约束效果存在一定影响。对比试件LW25-8和试件LC25-8的滞回曲线可知,在同等约束板厚度的情况下,木板的约束效果优于钢筋混凝土板。
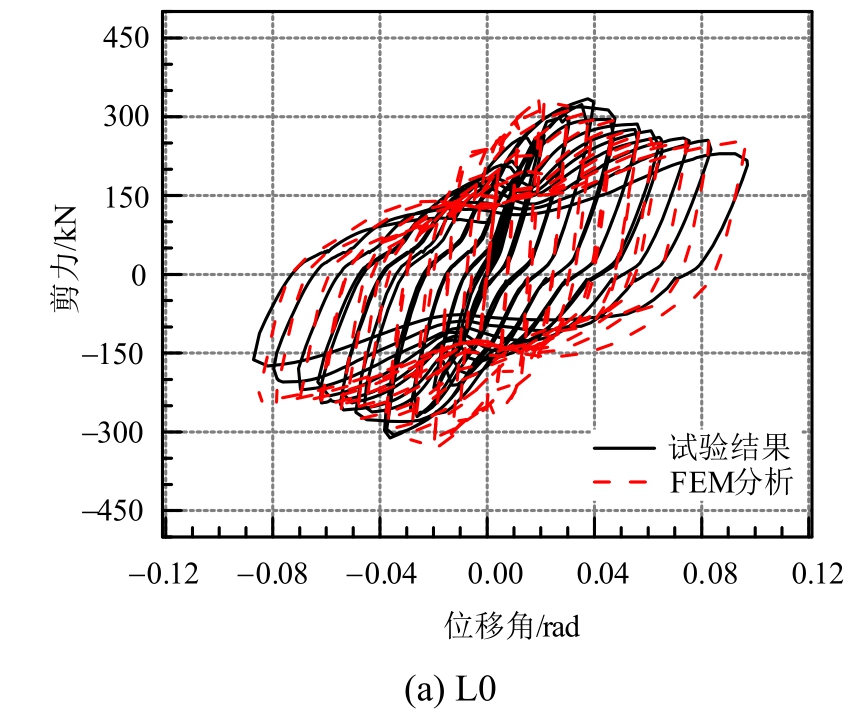

图8 试件剪力-位移角滞回曲线
Fig.8 Hysteretic curves of shear force-drift ratio
3.2 骨架曲线
图9所示为各试件的剪力-位移角骨架曲线,屈服剪力计算值Vy和极限剪力计算值Vu。计算值根据钢连梁的腹板钢材材性试件的屈服强度、极限强度和腹板截面积进行计算,公式如下:

式中:fy为腹板钢材材性件的屈服强度;fu为腹板钢材材性件的极限强度;Aw为腹板的截面积。
从图9可以看出,设置约束板后钢连梁的极限承载力明显提高,接近腹板材料达到极限时的极限剪力理论值。
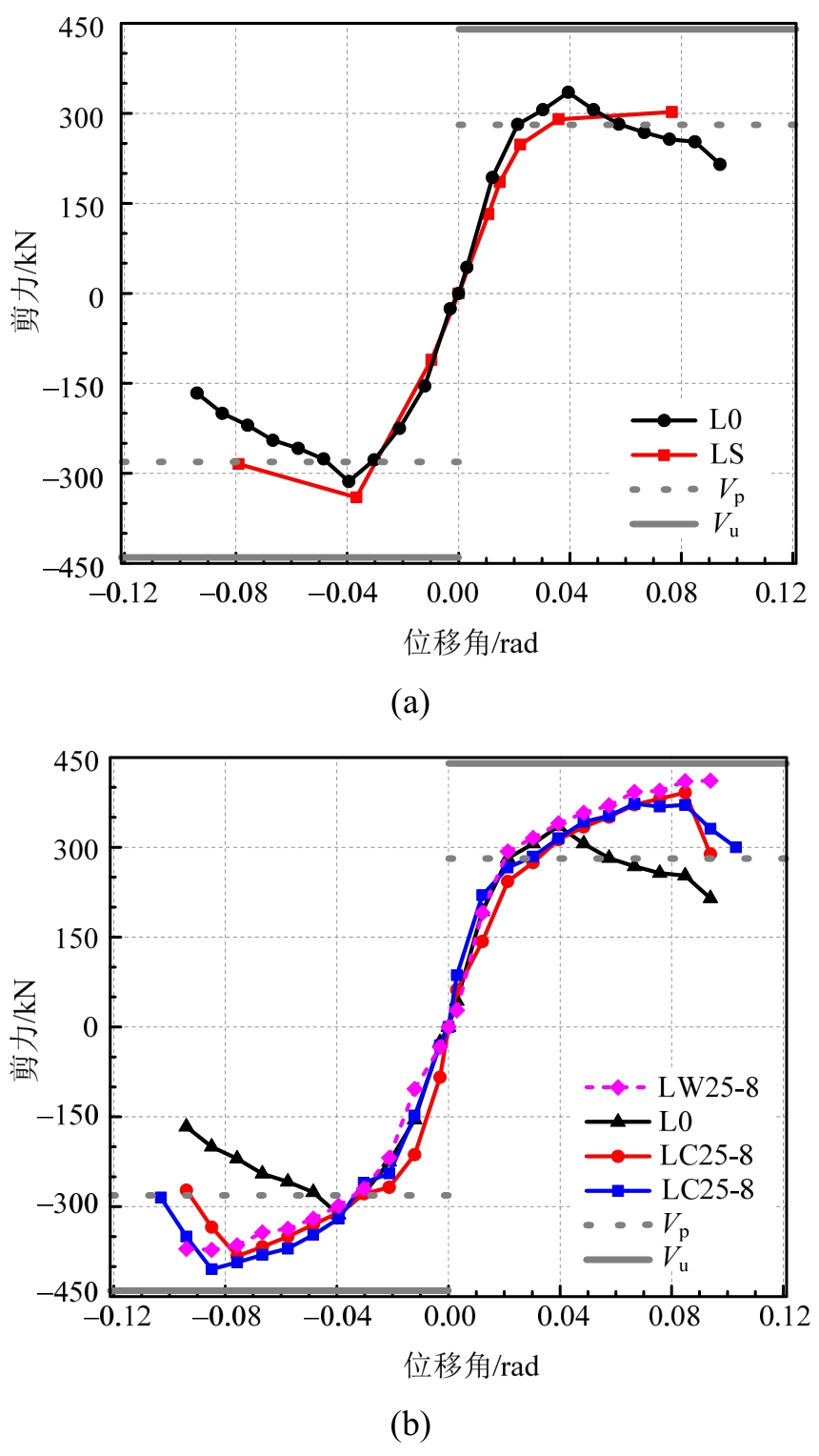
图9 试件剪力-位移角骨架曲线
Fig.9 Skeleton curves of shear force-drift ratio
3.3 受剪承载力及超强系数
表5中所示为各试件的受剪承载力与超强系数。超强系数定义为试验极限剪力与屈服剪力计算值之比,Ω=Vr/Vy,Vr为试验测量的最大剪切荷载,超强系数反映了钢连梁的承载力强化程度。从表5可以看出,纯钢腹板的试件和腹板设置加劲肋的试件的超强系数较小,加劲肋对钢连梁腹板剪切屈服后的屈曲约束效果不明显,而设置25 mm厚的木约束板的试件LW25-8的超强系数最大,略高于设置50 mm厚的钢筋混凝土约束板的试件LC50-8,表明木约束板对钢连梁腹板剪切屈服后的约束效果最好。
表5 试件受剪承载力和超强系数
Table 5 Shear force and the over strength factor
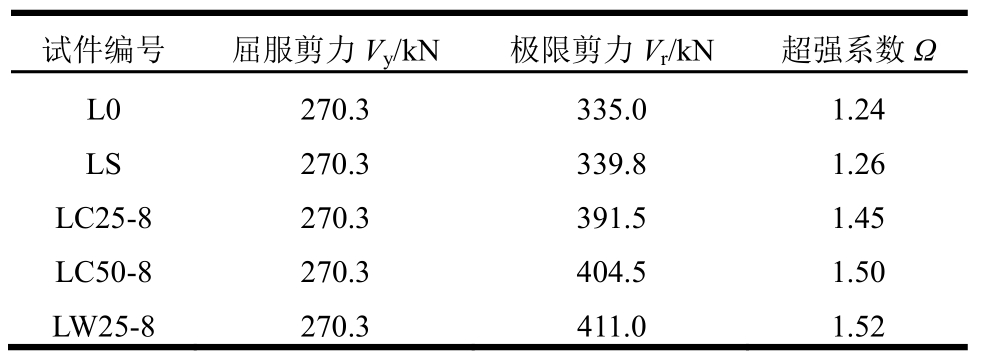
试件编号 屈服剪力Vy/kN 极限剪力Vr/kN 超强系数Ω L0 270.3 335.0 1.24 LS 270.3 339.8 1.26 LC25-8 270.3 391.5 1.45 LC50-8 270.3 404.5 1.50 LW25-8 270.3 411.0 1.52
3.4 耗能能力
耗能能力是反映结构抗震性能的一项重要指标,表征了结构吸收地震能量的能力大小。耗能能力一般通过等效粘滞阻尼系数来反映,所有试件的等效粘滞阻尼系数随位移角的变化规律如图10所示。

图10 各试件等效粘滞阻尼系数与位移角关系
Fig.10 Relationship between equivalent viscous damping coefficient and drift ratio
由图10可以看出,试件的等效粘滞阻尼系数随加载级的增大而逐渐增大,前2个加载级1/330和1/82.5时结构基本处于弹性阶段,耗散的能量值较小。腹板设置25 mm厚木约束板的试件LW25-8的耗能性能最好,约束板对试件剪切屈服后的耗能能力的提升效果明显。
4 有限元分析
4.1 单元选取
基于大型通用有限元程序 ABAQUS建立腹板屈曲约束钢连梁的三维精细化有限元模型。约束板采用实体单元C3D8;钢筋采用桁架单元T3D2,只承受拉、压荷载,且没有转动自由度,钢筋与钢筋混凝土约束板采用嵌入方式组合;钢板采用壳单元S4R;由于本文的分析重点在于钢腹板的屈曲约束,故不对拉螺杆进行实体建模,而采用节点耦合的方式将约束板和钢连梁的腹板连接起来。
4.2 网格划分
为兼顾计算精度与计算成本,约束板单元尺寸取为10 mm,钢梁单元尺寸取为20 mm。通过进行网格尺寸收敛性分析证明了该网格划分精度已经达到要求。
4.3 初始缺陷
钢材的加工、运输及安装过程中难免产生初始缺陷,为了在 ABAQUS中更加准确的模拟初始缺陷,首先进行特征值屈曲分析,并将特征值屈曲分析的一阶模态按照 1/1000的比例施加于钢连梁的腹板上。
4.4 接触设定
采用面面接触模型模拟钢腹板与两侧约束板之间的相互作用,并忽略钢腹板与约束板的切向摩擦力,即认为目标单元的表面是理想光滑的。
4.5 边界约束条件
有限元模型中边界约束条件与试验保持一致。约束板与钢腹板在对拉螺杆布置处耦合3向平动自由度,释放转动自由度。在模型上部端板处施加与试验一致的水平位移时程以及竖向转角时程。模型边界约束条件如图11所示。

图11 边界约束条件
Fig.11 Edge-restraint condition
4.6 材料本构模型
混凝土本构模型采用 ABAQUS自带的塑性损伤模型,并采用《混凝土结构设计规范》(GB 50010―2010)中提供的混凝土单轴应力-应变曲线。钢材选用带强化段的三折线本构模型,此模型定义方式简单,且可取得模拟结果精度较高。本文模型中fy、Es、εk、εu及fu采用钢材材性试验实测值,模型曲线与实际材性试验对比如图12所示。
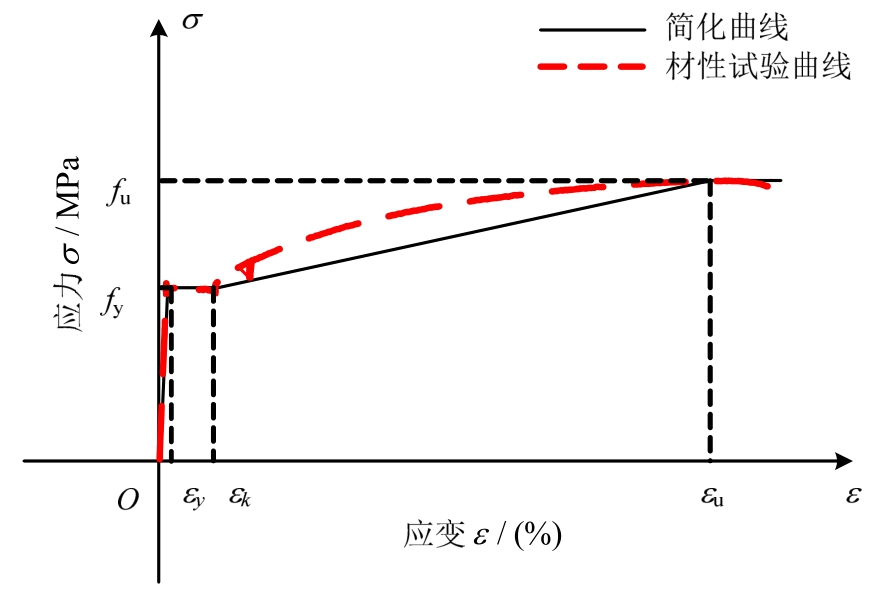
图12 带强化段的钢材三折线本构模型
Fig.12 Three fold constitutive model with reinforced segment
木材在弹性阶段为典型的正交各向异性材料,具有关于三个相互垂直坐标轴的材料弹性对称性,其本构方程如式(2)中所示。

式中:E1、E2和E3分别为木材L、R和T三向的弹性模量;G12、G13和G23分别为木材L-R,R-T和T-L平面内的剪切模量;vij为泊松比;σij和εij、γij为应力和应变分量。
强度准则采用Yamada-Sun强度准则,如式(3)所示。

式中:X、Y和Z分别为三个正应力轴方向的抗拉或抗压强度值;当应力σ11、σ22和σ33为拉或压应力时,即分别选用相应的抗拉或抗压强度;Sij为i-j平面内的抗剪强度。
Yamada-Sun强度准则考虑了多个应力分量的组合作用故计算精度高,且能区别材料的破坏模式,因此本文选用其作为木材的强度准则。此时,式(3)中的x、y和z则分别表示木材的顺纹纵向(L),横纹径向(R)和切向(T)。
4.7 模拟结果
有限元计算得到的各试件的剪力-位移角滞回曲线与试验实测滞回曲线的对比如图8所示。从图中可以看出,本文建立的有限元模型可以较好地模拟腹板屈曲约束钢连梁在往复剪切荷载作用下的受力行为。相比试验实测滞回曲线,有限元计算得到的滞回曲线更为饱满,主要原因为试验中钢连梁的损伤首先出现在钢腹板与翼缘的连接焊缝,然后沿焊缝扩展,导致钢连梁的腹板有效截面减小,使钢腹板不能发生有限元计算分析中出现的全截面屈服的理想破坏模式;另外焊缝的断裂、连接螺栓的局部破坏在本文建立的有限元模型中也无法反映,因此部分试件的试验实测极限承载力略小于有限元计算所得的极限承载力。
5 腹板屈曲约束设计方法
在腹板屈曲约束钢连梁的设计中,约束板的最小厚度是关键因素,必须满足相应要求,才能保证腹板屈曲约束钢连梁充分发挥其耗能作用。本节将采用接触单元模型在弹塑性范围内对腹板屈曲约束钢连梁的约束板最小厚度问题进行分析。研究参数包括钢腹板高厚比、约束板厚度以及螺栓的排布形式等。其中高厚比分别取30、45、90,约束板厚度由15 mm变化到80 mm(级差5 mm),螺栓排布分别选择 4×2(I)、4×2(II)、4×2(III)、2×2 四种形式,依次编号为排布形式(a)、(b)、(c)、(d),如图13所示。
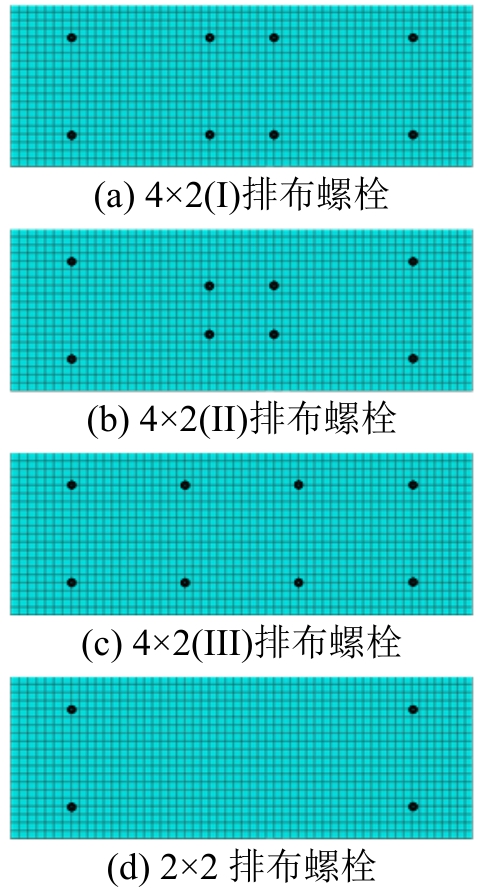
图13 螺栓排布形式
Fig.13 Bolt arrangement
图14(a)所示为采用钢筋混凝土约束板和木约束板的腹板屈曲约束钢连梁的高厚比λ=45时,不同螺栓排布形式下抗剪极限承载力随约束板厚度的变化曲线。图中n×n表示螺栓排布形式,Type C、Type W 分别表示采用钢筋混凝土约束板和木约束板。从图14(a)可以看出,两种不同材质的约束板在相同厚度下,设置木约束板的腹板屈曲约束钢连梁的极限承载力高于同等螺栓排布下设置钢筋混凝土约束板的腹板屈曲约束钢连梁的极限承载力。同时随着约束板厚度的增加,钢连梁的承载力逐渐提高,当约束板的厚度达到35 mm时,各种螺栓排布形式的极限承载力达到最大,此时增加约束板的厚度无法使钢连梁的承载力继续提高。


图14 腹板屈曲约束钢连梁极限抗剪承载力与各参数的关系曲线(λ=45)
Fig.14 Relationship between ultimate shear capacity and parameters of the buckling-restrained steel coupling beam with shear yielding failure mode(λ=45)
图14(b)和图14(c)所示为高厚比λ=45时,两种不同材质约束板的腹板屈曲约束钢连梁的抗剪极限承载力与连接螺栓排布形式的变化曲线,图中 t表示约束板厚度,横坐标 1、2、3、4分别代表上文提到的4种螺栓排布形式,由图14可知,约束板厚度为35 mm时,可保证钢腹板极限应力达到其全截面屈服水平;采用4×2(I)螺栓排布形式并设置木约束板的钢连梁承载力最高,采用4×2(III)螺栓排布形式并设置钢筋混凝土约束板的钢连梁承载力最低,两者相差约2.6%。当约束板厚度小于35 mm时,采用4×2(III)螺栓排布形式的钢连梁承载力最低,其次是采用 2×2螺栓排布形式的钢连梁,采用 4×2(I)和4×2(II)的螺栓排布形式的钢连梁承载力接近。
对于高厚比λ=90的腹板屈曲约束钢连梁,由图15(a)可知采用 2×2螺栓排布形式的钢连梁的极限承载力明显低于采用另外三种螺栓排布形式的钢连梁。采用 4×2(I)、4×2(II)和 4×2(III)三种螺栓排布形式时,当约束板厚度达到45 mm时,极限承载力基本趋于稳定。因此,对于高厚比较大的钢连梁,需要采用较厚的约束板和较紧密的螺栓排布形式,才能达到钢连梁腹板全截面屈服的设计目标。

图15 腹板屈曲约束钢连梁极限抗剪承载力与各参数的关系曲线(λ=90)
Fig.15 Relationship between ultimate shear capacity and parameters of the buckling-restrained steel coupling beam with shear yielding failure mode(λ=90)
由图15可知,对于高厚比λ=90的腹板屈曲约束钢连梁而言,由于腹板较薄,腹板局部屈曲对极限承载力影响更为显著,随着约束板板厚的增加,钢连梁的承载力有较大的提升。采用 4×2(I)和4×2(III)螺栓排布形式的钢连梁的承载力接近,采用2×2螺栓排布形式的钢连梁承载力最低,可见当约束板板厚较小时,螺栓排布应当加密。在腹板高厚比λ=90的情况下,约束板材质对钢连梁的极限承载力影响较小。
对于高厚比λ=30的腹板屈曲约束钢连梁,由于腹板较厚,不易发生面外屈曲,其极限承载力为钢腹板全截面屈服时的承载力。如图16所示,约束板厚度基本不影响腹板屈曲约束钢连梁的极限承载力,采用 4×2(III)螺栓排布形式的钢连梁的极限承载力略低于采用其余三种螺栓排布形式的钢连梁的极限承载力。因此,对于高厚比小于 30的腹板屈曲约束钢连梁,约束板的屈曲约束效果不明显,无需设置约束板。
定义最小约束刚度比η为腹板屈曲约束钢连梁整体屈曲荷载与钢腹板受剪屈服荷载之比,其计算公式为:
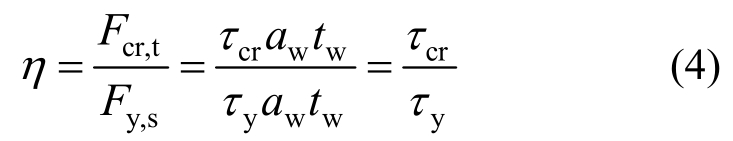
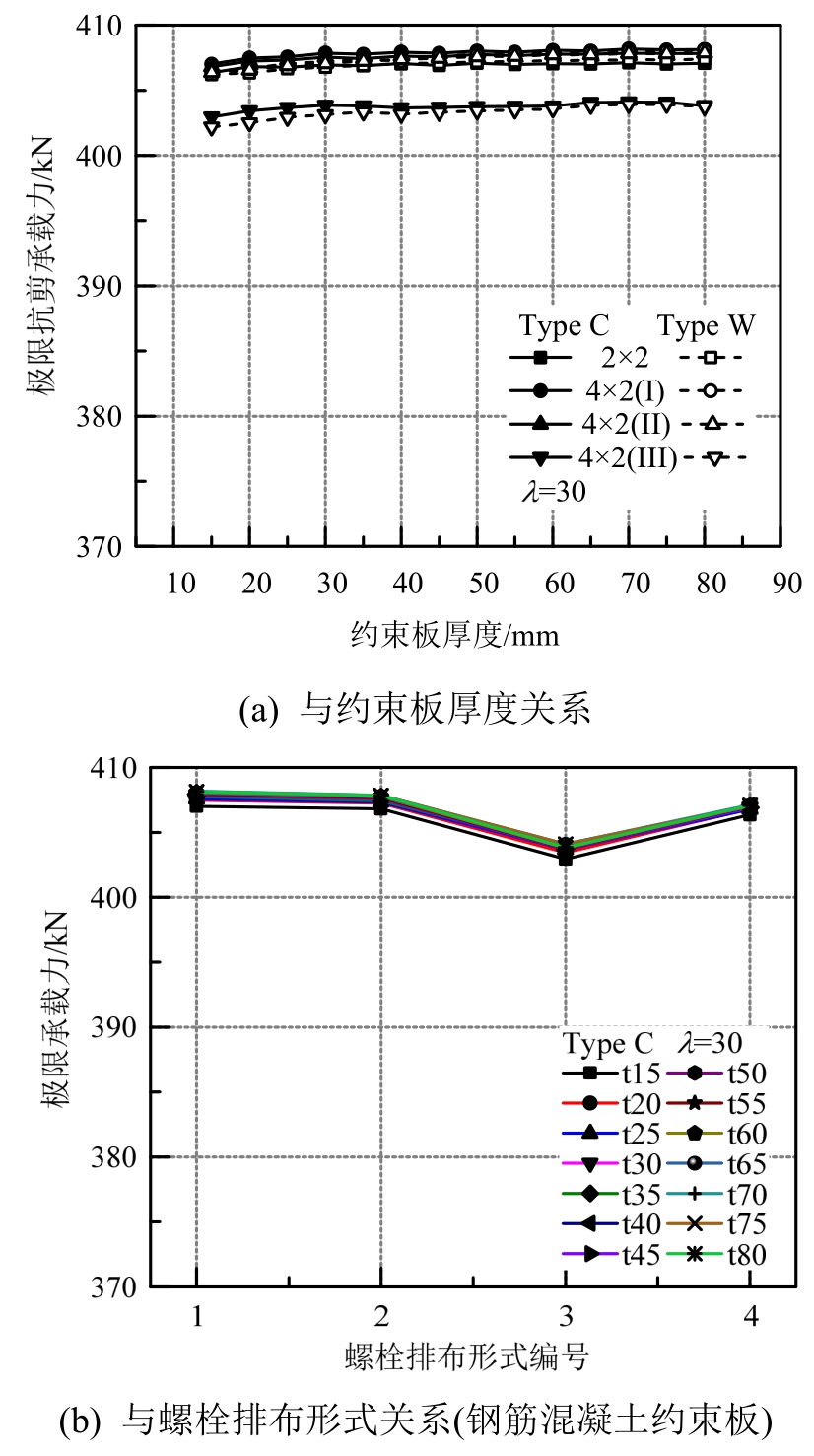
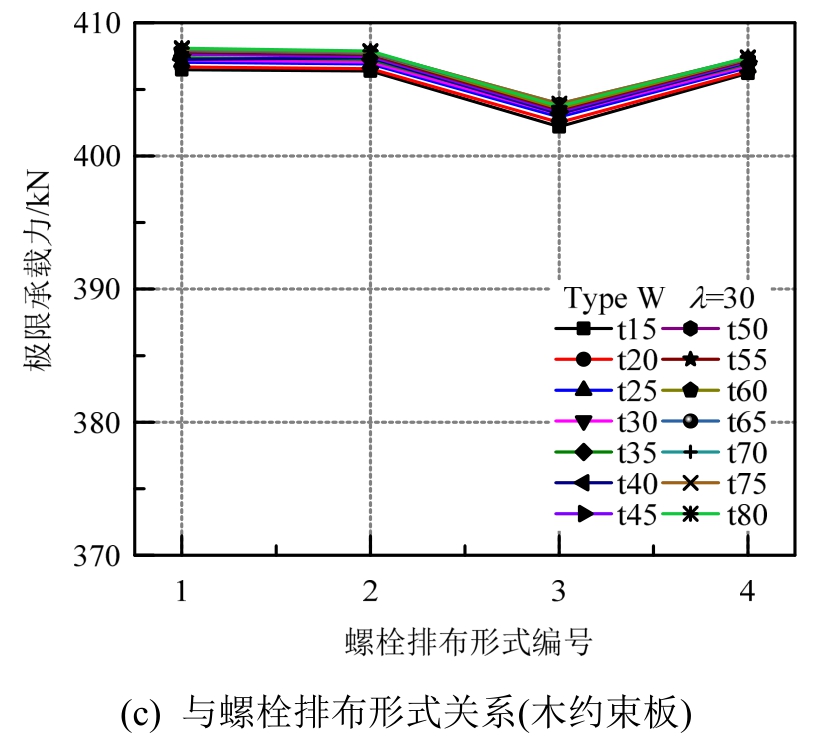
图16 腹板屈曲约束钢连梁极限抗剪承载力与各参数的关系曲线(λ=30)
Fig.16 Relationship between ultimate shear capacity and parameters of the buckling-restrained steel coupling beam with shear yielding failure mode(λ=30)
式中:Fcr,t为腹板屈曲约束钢连梁的整体屈曲荷载;Fy,s=τyawtw为钢腹板受剪屈服荷载,τy为钢腹板剪切屈服强度,aw为钢腹板高度,tw为钢腹板厚度。
表6所示为有限元计算得到的不同腹板高厚比下,采用不同连接螺栓排布形式并设置两种不同材质的约束板的腹板屈曲约束钢连梁所对应的约束板的最小约束刚度比。
表6 约束板最小约束刚度比
Table 6 Critical restraint stiffness ratio
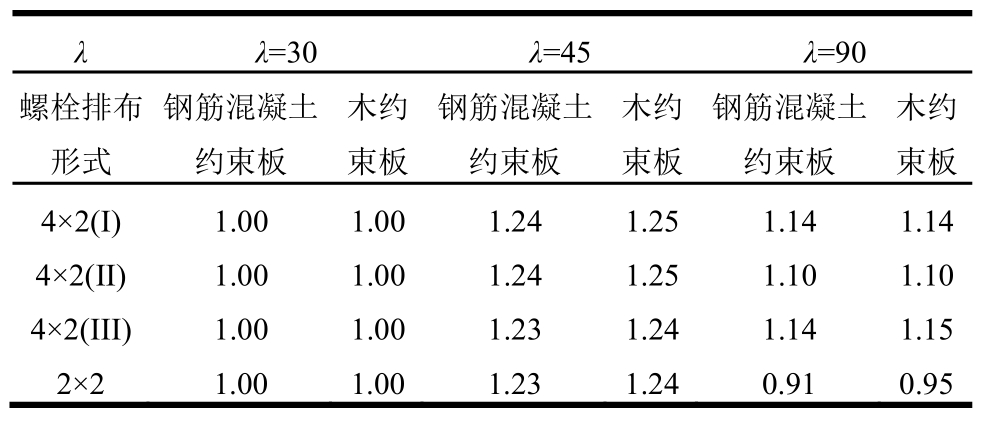
λ λ=30λ=45λ=90螺栓排布 钢筋混凝土 木约 钢筋混凝土 木约 钢筋混凝土 木约形式 约束板 束板 约束板 束板 约束板 束板4×2(I)1.00 1.00 1.24 1.25 1.14 1.14 4×2(II)1.00 1.00 1.24 1.25 1.10 1.10 4×2(III)1.00 1.00 1.23 1.24 1.14 1.15 2×2 1.00 1.00 1.23 1.24 0.91 0.95
由表6可知,对不同高厚比的钢腹板,所需要的约束板最小约束刚度比不同,其对应的约束板厚度也不同。原因在于钢腹板越厚,发生局部屈曲的可能性越小。当钢腹板高厚比小于 30时,理论上已经不要侧向变形约束即可实现全截面屈服。当钢腹板高厚比为 45时,当约束板厚度满足最小约束刚度比的限值时,无论连接螺栓如何排布,均可以保证钢腹板全截面屈服。当钢腹板高厚比为90时,螺栓排布形式对约束板最小约束刚度比的影响较大。同时可以看出,约束板材质对约束板最小约 束刚度比影响不大。
综上所述,当腹板屈曲约束钢连梁的钢腹板高厚比为45时,所需最小约束板厚度为35 mm,高厚比为90时,最小约束板厚度为45 mm。高厚比在45~90之间时,最小约束板厚度在35 mm~45 mm之间取值。高厚比小于 30时,无需设置约束板。为方便设计,可将高厚比在30~45之间的腹板屈曲约束钢连梁约束板厚度取为35 mm。约束板最小厚度的具体取值如表7所示。
表7 约束板最小厚度取值
Table 7 Minimum thickness of constraint plate

钢腹板高厚比 约束板最小厚度/mm λ≤30 0 30<λ≤45 35 45<λ≤90 2/9λ+25 90 45
在约束板设计过程中需要注意,钢筋混凝土约束板的板内配筋应当符合《混凝土结构设计规范》(GB 50010―2010)中相关规定。约束板周边缝隙的大小应根据大震下结构允许的最大弹塑性层间位移角限值确定。
6 结论
本文完成了5个腹板屈曲约束钢连梁剪切荷载作用下的拟静力往复加载试验,变化了约束板厚度和约束板材质等参数,得到了腹板屈曲约束钢连梁在往复剪切荷载作用下的剪力-位移角滞回特性,并基于有限元参数分析提出了设计建议,可以得出以下结论:
(1)本试验的连梁破坏模式主要为大应变条件下的翼缘、端板间焊缝断裂和约束板的弯曲破坏。
(2)试件的超强系数平均值为 1.38,大于《建筑抗震设计规范》GB 50011―2010最低要求1.1,腹板设置 25 mm厚的木约束板的试件超强系数最大,达到1.52。
(3)腹板无约束的纯钢梁试件剪切屈服后的稳定性最差,设置25 mm厚木约束板的试件剪切屈服后的稳定性最好。各试件屈服剪应变大致相同,腹板无约束的纯钢梁试件的极限剪应变最小,设置25 mm厚木约束板的试件的极限剪应变最大,接近腹板钢材的材料极限剪应变。
(4)建立的腹板屈曲约束钢连梁的有限元模型具有较高的计算精度,基于有限元参数分析结果提出的约束板最小厚度的建议取值可为实际工程设计提供参考。
[1]史庆轩, 田建勃, 王南, 等.钢-混凝土组合连梁研究现状及其发展[J].建筑结构, 2014, 44(9): 1―8.Shi Qingxuan, Tian Jianbo, Wang Nan, et al.Research status and development of the steel-concrete composite coupling beam[J].Building Structure, 2014, 44 (9): 1―8.(in Chinese)
[2]马志林, 史庆轩, 王伟.钢筋混凝土联肢剪力墙弹塑性分析[J].建筑科学与工程学报, 2010, 27(1): 60―64.Ma Zhilin, Shi Qingxuan, Wang Wei.Elasto-plastic analysis of reinforced concrete coupled shear walls[J].Journal of Architecture and Civil Engineering, 2010,27(1): 60―64.(in Chinese)
[3]张云鹏, 曹万林, 张建伟, 等.内藏钢桁架深连梁联肢剪力墙抗震性能试验研究[J].世界地震工程, 2010,26(2): 19―24.Zhang Yunpeng, Cao Wanlin, Zhang Jianwei, et al.Experimental study on seismic behavior of a coupled shear wall with deep coupling beam and concealed steel trusses[J].World Earthquake Engineering, 2010, 26(2):19―24.(in Chinese)
[4]滕军, 马伯涛, 李卫华, 等.联肢剪力墙连梁阻尼器伪静力试验研究[J].建筑结构学报, 2010, 31(12): 92―100.Teng Jun, Ma Botao, Li Weihua, et al.Pseudo-static test for coupling beam damper of coupled shear wall structure[J].Journal of Building Structures, 2010,31(12): 92―100.(in Chinese)
[5]武敏刚, 吕西林.钢骨联肢剪力墙抗震性能试验研究[J].结构工程师, 2004, 20(5): 52―56.Wu Mingang, Lu Cilin.Seismic behavior of steel-encased coupled shear walls subjected to cyclic loading[J].Structural Engineers, 2004, 20(5): 52―56.(in Chinese)
[6]Park R, Paulay T.Reinforced concrete structure[M].New York: Wiley, 1975: 645―655.
[7]侯炜, 陈彬, 郭子雄, 等.内嵌钢板混凝土组合连梁抗震性能试验研究[J].土木工程学报, 2017, 50(2): 9―18.Hou Wei, Chen Bin, Guo Zixiong, et al.Experimental study on seismic behavior of embedded steel plate reinforced concrete coupling beams[J].China Civil Engineering Journal, 2017, 50(2): 9―18.(in Chinese)
[8]Fortney P J, Shahrooz B M, Rassati G A.Large scale testing of a Replaceable “fuse” steel coupling beam[J].Journal of Structural Engineering, 2007, 133(7): 1801―1807.
[9]Rassati G A, Fortney P J, Shahrooz B M.Design of innovative coupling Beams for use in hybrid coupling core wall systems[C].NSF CMMI Research and Innovation Conference 2009, Honolulu, Hawaii, 2009:22―25.
[10]Chung H S, Moon B W, Lee S K, et al.Seismic performance of friction dampers using flexure of RC shear wall system[J].The Structural Design of Tall and Special Buildings, 2009, 18(7): 807―822.
[11]师骁, 王彦栋, 曲哲, 等.含摩擦阻尼器钢连梁的往复加载试验[J].工程力学, 2016, 33(增刊): 156―160.Shi Xiao, Wang Yandong, Qu Zhe, et al.Cyclic test of steel coupling beam with friction damper[J].Engineering Mechanics, 2016, 33(Suppl): 156―160.(in Chinese)
[12]纪晓东, 马琦峰, 王彦栋, 等.钢连梁可更换消能梁段抗震性能试验研究[J].建筑结构学报, 2014, 35(6): 1―11.Ji Xiaodong, Ma Qifeng, Wang Yandong, et al.Cyclic tests of replaceable shear links in steel coupling beams[J].Journal of Building Structures, 2014, 35 (6): 1―11.(in Chinese)
[13]刘青, 李国强, 陆烨.内嵌屈曲约束钢板剪力墙钢框架的性能参量及计算方法[J].工程力学, 2016, 33(10):105―115.Liu Qing, Li Guoqiang, Lu Ye.Mechanical properties and calculation of steel the buckling restrained steel plate shear walls embedded steel frame[J].Engineering Mechanics, 2016, 33(10): 105―115.(in Chinese)
[14]于金光, 王雪军, 郑春明, 等.密肋网格防屈曲钢板剪力墙结构性能试验研究[J].土木工程学报, 2017,50(10): 54―61.Yu Jinguang, Wang Xuejun, Zheng Chunming, et al.Experiment study on behavior of ribbed grid buckling-restrained steel plate shear walls[J].China Civil Engineering Journal, 2017, 50(10): 54―61.(in Chinese)
[15]Wei M W, Liew J Y R, Fu X Y.Panel action of novel partially connected buckling-restrained steel plate shear walls[J].Journal of Constructional Steel Research, 2017,128(1): 483―497.
[16]Jin S, Ou J, Liew J Y R.Stability of buckling-restrained steel plate shear walls with inclined-slots: theoretical analysis and design recommendations[J].Journal of Constructional Steel Research, 2016, 117(2): 13―23.
[17]Li G Q, Sun F F, Pang M D, et al.Structural shear wall systems with metal energy dissipation mechanism[J].International Journal of High-rise Buildings, 2016, 5(3):195―203.