螺栓端板连接是一种在钢框架、轻型门式刚架中广泛应用的节点形式。相较于焊接连接方式,螺栓连接避免了焊接节点在地震作用下的脆性开裂并有效地减少了现场施工作业量,是提高建筑工程装配率的优先节点形式之一[1-3]。
已有的研究表明端板连接能够传递一定的弯矩[4-5]。在弯矩作用下,端板或柱壁面外的弯曲塑性破坏是控制节点承载力的一种主要模式[6-8],其屈服承载力的理论分析方法主要基于塑性铰线假定[9]。针对不同的截面形式、连接方法,很多学者进行了公式推导及试验研究。欧洲规范[10]给出了H型截面梁柱端板连接节点中柱壁上不同位置处螺栓在圆形和非圆形塑性铰线两种模式下相应的计算公式,然而这种计算方法没有考虑螺栓孔尺寸的影响。Gomes模型[11]针对H型钢弱轴连接形式给出了计算公式。日本学者Tagawa等[12]采用角钢和钢板加强H型截面梁柱端板连接节点并进行试验,并考虑了两种可能的屈服线模式进行分析计算,计算结果与试验结果较为吻合。
除此之外,近年来由于单边螺栓的发展[13-15]促进了端板连接 H型截面梁-方管柱节点的应用,并发展出了相应的承载力计算方法。Yeomans模型用于计算Flowdrill(由荷兰学者Hoogenboom发明的一种单边螺栓)连接的钢管柱承载能力,被纳入CIDECT设计指南9[16],英国钢结构协会(The Steel Construction Institute,SCI)在设计手册[17]中也给出了类似的计算模型及方法。王志宇等[18-19]分别采用普通螺栓和两种不同直径的 Hollo bolt(英国Lindapter International公司研发的单边螺栓)进行方管柱节点的受拉区的试验,将试验结果与Yeomans模型和SCI模型比较,表明由于这两种模型均不能准确考虑螺栓尺寸影响使得承载力计算结果偏低,因此王志宇根据试验结果提出了两种可能的屈服线破坏模式并给出相应的计算公式。Mourad[20]针对Huck高强度盲孔螺栓(Huck HSBB)提出了两种不同屈服模式的计算模型,并且认为螺栓水平间距与方管柱宽度的比值对屈服模式有决定性影响。Lee等[21]在方管柱受拉区部分的试验中采用新型的单边螺栓Ajax ONESIDE,试验结果与Mourad模型计算结果吻合程度较高。
上述文献均表明,端板连接节点受拉区板件屈服承载力计算的一般步骤是首先假定塑性铰线在板面的分布,需要考虑边界约束条件、端板尺寸以及螺栓孔径等因素的影响,通常计算比较若干种可能的模式,取其中计算得到的较小值作为承载力。整个计算过程繁琐,且不一定能准确考虑各种因素对塑性铰线分布的影响。此外,实际存在的薄膜效应使板件屈服后承载力继续上升,荷载-变形曲线上通常并没有明显的屈服平台,而上述各文献未针对有限元或试验所得的结果给出统一的屈服承载力判定标准,尽管采用了同一理论计算方法,但不同研究者实际上考虑的是不同程度的受力状态。如Tagawa等[12]以切线刚度降为1/3初始刚度时对应的荷载为屈服承载力,而王志远等[18]则采用了初始刚度线与后屈服刚度线的交点作为屈服荷载。这些方法操作简单,但所假定的“屈服状态”不完全符合塑性铰线理论中的全截面塑性基本假定。
本文提出分块组合法,建立开孔板件受面外集中荷载作用时的屈服承载力的通用计算方法。基本思路是将多孔板分割成若干个矩形单孔板,分别计算各板块的屈服承载力,叠加后得到整个多孔板的屈服承载力。图1以端板连接节点受拉区常用的简化模型为例进行说明。在相邻螺孔间的中心沿平行及垂直于柱长方向进行分割,将柱壁分为4个单元。由于构造与受力均沿分割线对称,可知单元在分割线面外方向的平动位移不受约束,该边界条件可假定为滑动铰支边。此外由于柱侧壁的约束作用,柱壁两侧边(AD、BC)的边界条件简化为固支边界。需要注意的是柱壁的上下侧边界(AB、CD)可认为自由边,但由于在实际结构中柱长较大,使该边界距离螺孔远,由后文分析可知在这种情况下,无论何种边界条件,都不会对计算结果产生影响。分割端板可采用同样的方法,由于梁翼缘的约束,水平方向分割线所在边界简化为固支边,而竖向分割线按是否存在加劲肋分别简化为固支边或滑动铰支边。端板四周不受任何约束的边界则简化为自由边。
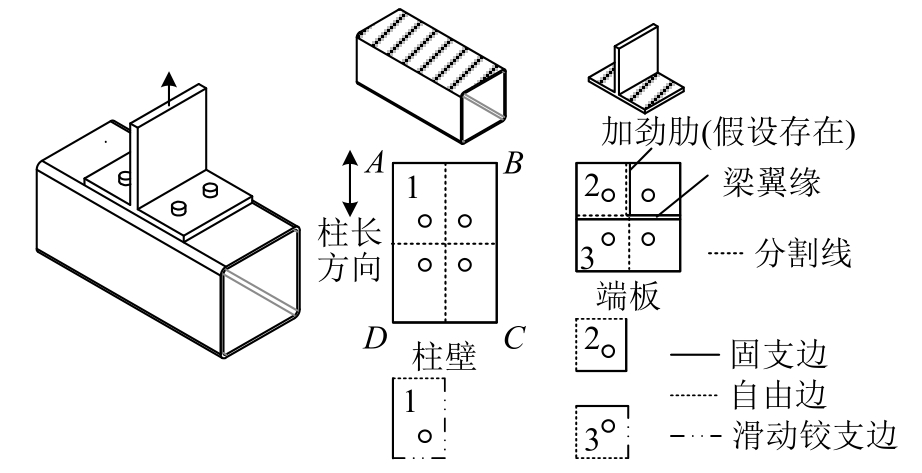
图1 节点受拉区板件的分块组合法示意图
Fig.1 Illustration of segmentation method for joint tension zone
分割后,可以更直观准确地分析如边界条件、孔径等因素对板件塑性铰线分布和屈服承载力的影响。此外,当孔位布置复杂[22]而使塑性铰线的假定困难时,这种方法仍然简单易行,因而适用性更广。
1 基本假定
采用分块组合法进行单孔板的计算基本假定如下:
1)螺栓孔为刚性环,仅有垂直于板面的竖向位移δ。
2)钢材为理想刚塑性材料。
3)极限状态时板件微小变形,不考虑后期薄膜效应。
2 矩形单孔板的塑性极限状态分析
在面外荷载F(图2)的作用下,矩形单孔板存在受弯屈服和冲切两种破坏模式,对应的承载力分别记为Fy和Fc,其塑性极限承载力Fu为两者中的较小值,式(1)。冲切承载力可按式(2)确定[11],本文主要讨论受弯屈服破坏模式,后文针对四边固支、有自由边和有滑动铰支边三种情况分别进行分析。每一种情况都从标准单孔板(即板为正方形且孔位于板的中心)推至一般单孔板(即板为矩形或孔位于板的一般位置)。
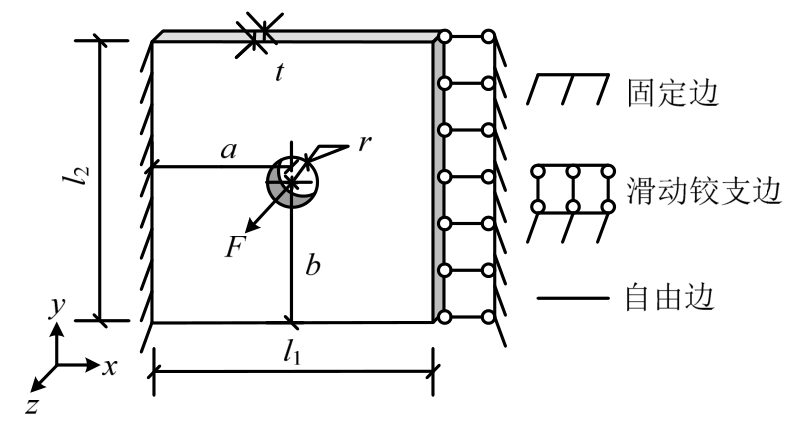
图2 单孔板边界条件示意图
Fig.2 Boundary conditions of a plate with a single hole
式中:Fy为屈服破坏承载力;Fc为冲切破坏承载力:
式中:fy为材料屈服强度;C为冲切区域的边界线长度,如图3所示。C=min{C1, C2},C1为区块冲切的边界长度(图3中点线和点划线);C2 为栓孔冲切的边界长度(图3中虚线);t为板的厚度。
2.1 四边固支单孔板
四边固支标准单孔板的屈服模式可假设为圆形[12,18-19,21],设内力虚功为Ec。在圆形屈服模式中,塑性铰线由板面,边界以及孔周处这三个部分组成,如图4(a)所示。
截取一段中心角为ψ的扇形板进行圆形塑性功的推导,图4(b)。板面上塑性铰线从孔中心沿直径方向延伸至边界。设有(n+1)条塑性铰线将该扇形区域板面划分为n分相同的微小板块,每一块扇形中心角θ,如板块A与板块B为相邻的两个微小板块,它们的交线即为其中一条塑性铰线。记该塑性铰线长度为lp,相邻微小板块变形后夹角为φ。边界和孔周的塑性铰线分别为微小板块在对应的半径R和r处的弧,长度分别记为lp,r、lp,R,转角为φr、φR。
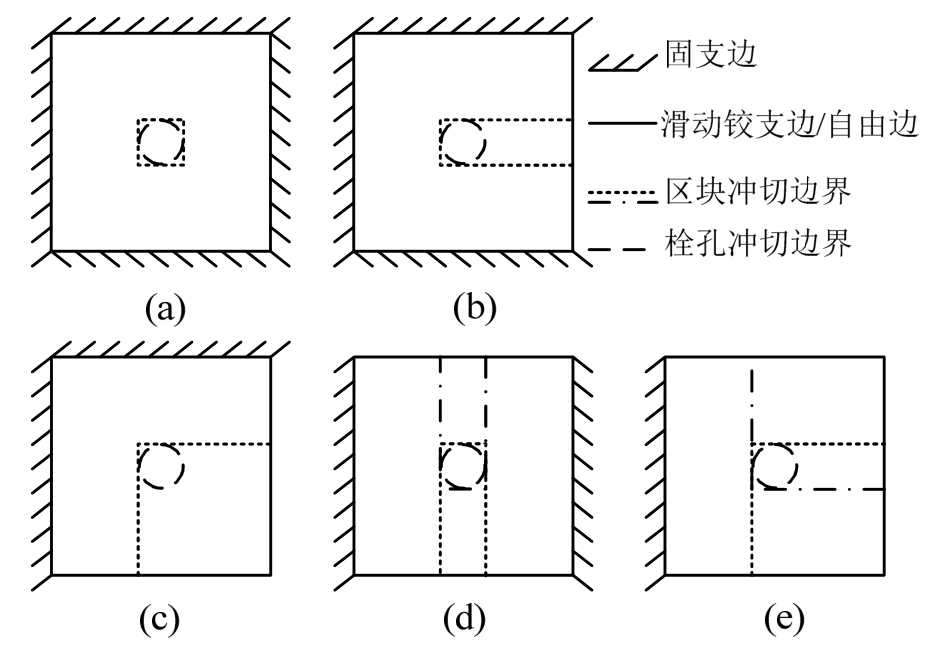
图3 板件的冲切区域
Fig.3 Punching shear area of a plate
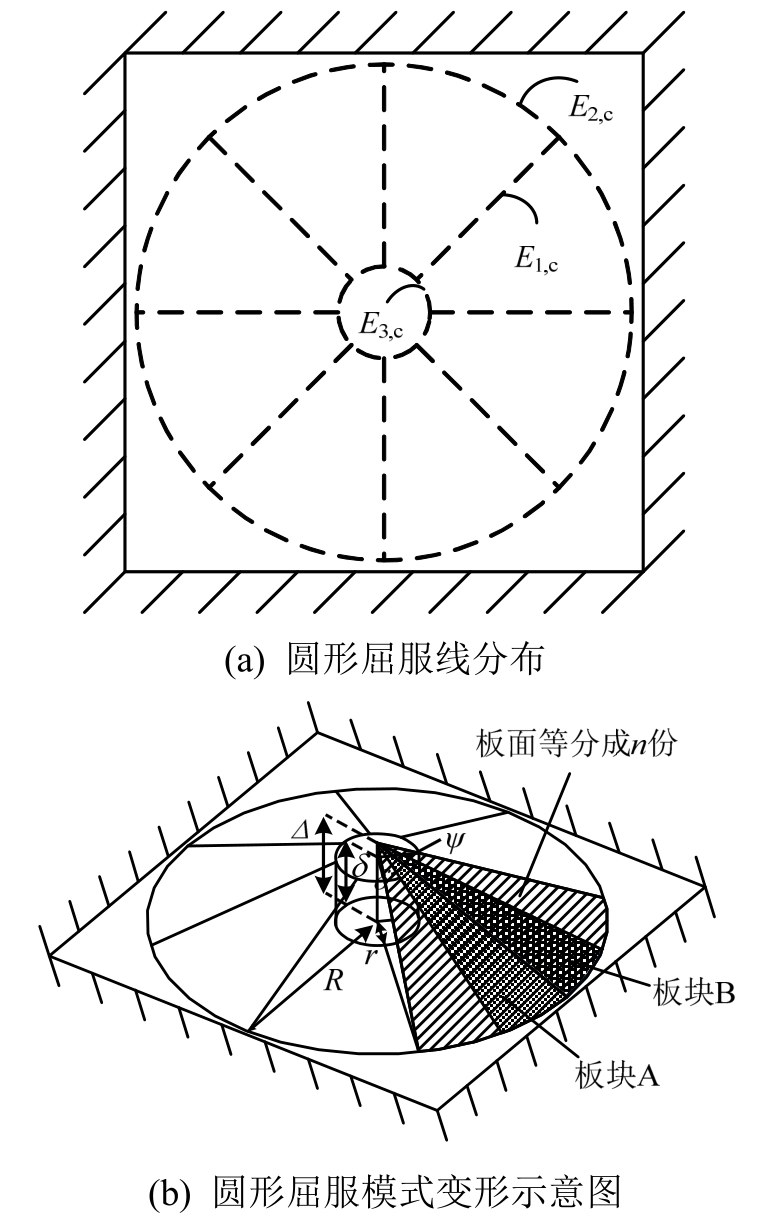
图4 圆形屈服模式
Fig.4 Circular yield pattern
内力虚功分别记为E1,c、E2,c、E3,c,各部分计算公式及结果如下:
详细推导过程见附录。
式中:n为板面划分的数目;δ为孔周平面外虚位移,![]() φ为相邻板面变形后的夹角;ψ为变形前扇形的中心角;mp为单位长度单位转角的塑性功,
φ为相邻板面变形后的夹角;ψ为变形前扇形的中心角;mp为单位长度单位转角的塑性功,![]()
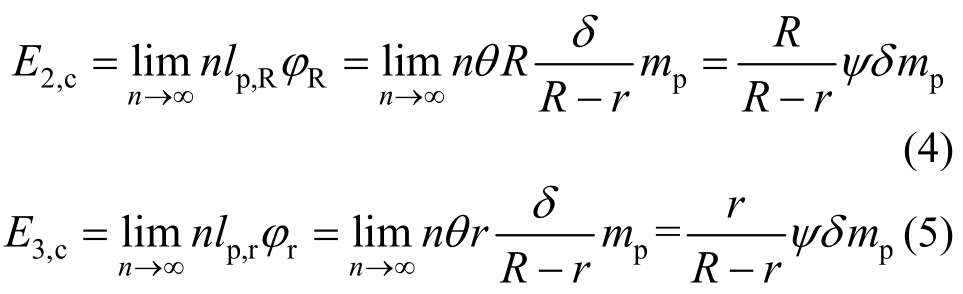
式中:θ为微小扇形板块的中心角,ψ=nθ;R为孔中心到边界塑性铰线的距离;r为孔中心到孔周塑性铰线的距离,下取为孔半径。
对于四边固支的情况而言ψ=2π,则圆形屈服线模式下的虚功为:
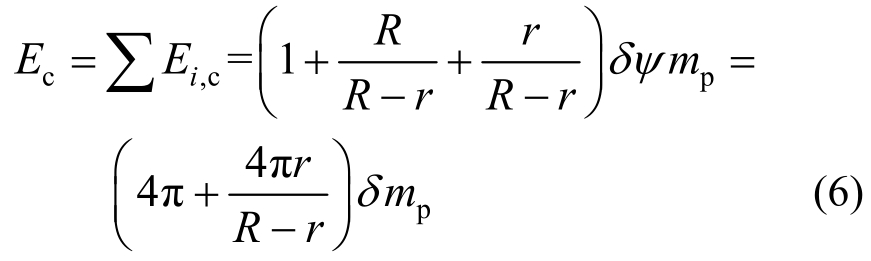
式(3)~式(6)中可以发现:① 塑性功E1,c与圆形半径无关;② 在其他条件一致的情况下,R增大,孔周与边界塑性铰线的内力虚功减小;③ 在其他条件一致的情况下,r减小,孔周与边界塑性铰线的内力虚功减小。根据塑性理论,假设的最终机构上塑性铰线所做内力虚功越小,该模型就越接近真实情况。在图4(a)所示的塑性铰线模式中,R可进一步增大,直至外边界塑性铰线与板外边界重合,由②可知,塑性功可能会减小。因此假设图5所示的非圆形屈服模式,同时为保证形成机构,板面及孔周的塑性铰线也将改变,设此时内力虚功为Er,见式(7)。
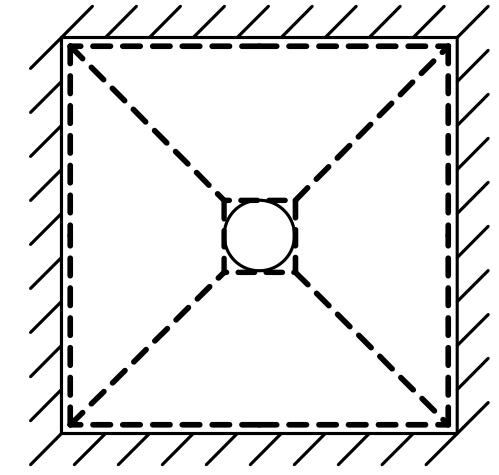
图5 非圆形屈服模式
Fig.5 Non-circular yield pattern
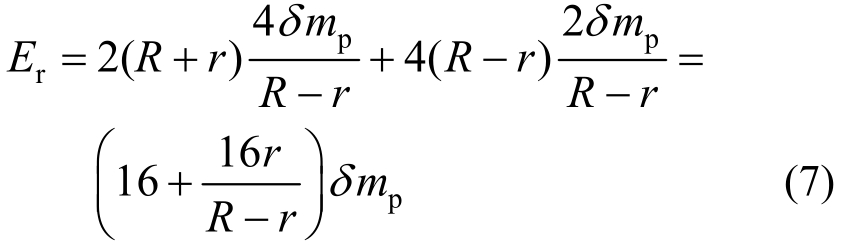
式(8)表明圆形屈服线模式下的塑性功更小。故根据内外功平衡,可得屈服承载力计算式(9)。为了验证理论公式,以长度l1=l2=90 mm,厚度t=5 mm的板为对象建立有限元模型,以r/R为变量进行计算分析。采用有限元软件 ABAQUS对单孔板进行分析,材料为理想弹塑性。板件的有限元模型中选取了C3D8R单元,其厚度分4层以上。在孔中心设置了参考点,与孔壁耦合,通过对参考点施加平面外的位移进行加载。
采用式(1)、式(2)、式(9)计算,当算例中r/R=1/15时理论计算为冲切破坏,其余情况为受弯屈服破坏。不同r/R的理论公式计算结果与有限元计算结果的比值如图6所示,说明圆形屈服模式理论计算结果与有限元计算结果更为吻合。由于板件内膜应力的存在,板件达到塑性极限后,承载力仍会进一步上升。有限元计算得到的板件屈服承载力取参考点荷载-位移曲线中切线刚度由小变大的拐点所对应的荷载,此时板件屈服但薄膜效还未起作用。图7为有限元计算得到的当开孔方板的屈服承载力时,该板中间截面的 MISES应力分布,进入塑性的区域(MISES应力为235 MPa)更接近于圆形,进一步说明圆形屈服模式更为准确。
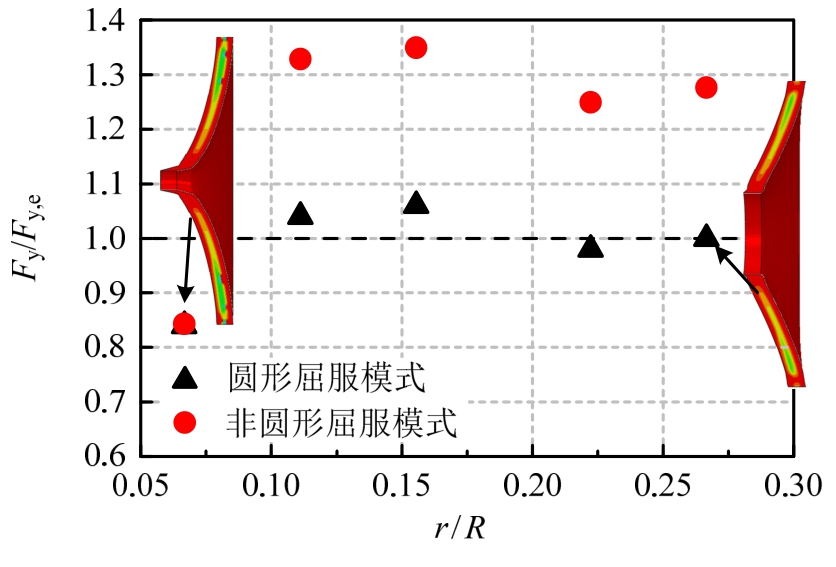
图6 四边固支标准单孔板屈服承载力理论和有限元结果比值
Fig.6 Ratios of yield loads of standardized plate with 4 fixed edges calculated by theoretical model to those by FE model
注:Fy、Fy,e为理论计算、有限元屈服承载力
一般单孔板的屈服承载力计算可类比于标准单孔板,也将其均分为中心角为θ的微小扇形板,每块微小扇形板的内力虚功计算式为(10),根据内外力平衡,屈服承载力由式(11)。为简化计算,将积分运算近似为有限求和,将一般单孔板沿孔中心与边界端点的连线分为4部分,每一部分分别计算承载力后叠加,R取为每一部分孔中心到四边的距离dc。

图7 达到屈服承载力时板中间截面Mises应力分布
Fig.7 Mises stress distribution at center section of plate when fully yielded
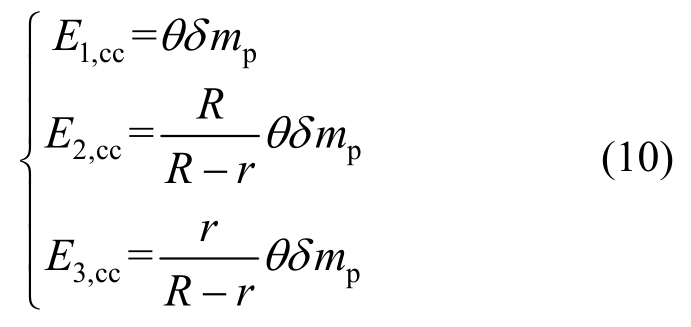
式中,E1,cc、E2,cc、E3,cc为一般单孔板θ角微小扇形区域板面上、边界处及孔周处内力虚功:
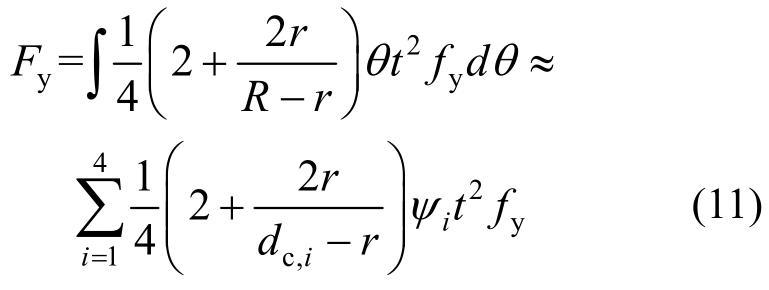
式中:dc,i为孔中心到四固支边的距离;ψi为孔中心到固支边两端点的夹角。
建立有限元模型进行验证,参数选为l1=90 mm,a=30/45 mm,b=22.5 mm,r=10 mm,t=5 mm,以长度l2为变量,理论计算的结果与有限元计算的结果比较如图8所示。理论计算结果精度较高,误差均小于10%,但是总体偏小。从有限元分析结果可知造成这一偏差的主要原因是:一般单孔板分为4部分计算,式中R的近似取值使得每一部分的塑性铰线不再连续,与实际情况并不吻合。如图9,①、②、③部分的R取值与计算假定较为符合,而④中理论计算所用的R明显大于有限元计算中R,造成了结果偏小。

图8 四边固支单孔板屈服承载力理论和有限元结果比值
Fig.8 Ratios of yield loads of the plate with 4 fixed edges calculated by theoretical model to those by FE model

图9 达到屈服承载力时四边固支板中间截面处Mises应力分布(l1=90,l2=135)
Fig.9 Mises stress distribution at center section of plate with 4 fixed edges when fully yielded (l1=90,l2=135)
通过多个有限元模型计算可以发现:塑性发展的区域基本呈椭圆,其圆心位于孔中心,长、短轴垂直于边界,轴长分别为孔圆心到该轴方向上较近板边的距离的两倍。在式(11)可按上述规律对R进行一定的塑性发展距离的修正,使理论计算结果与有限元结果吻合程度更高。在实际计算时,考虑到塑性铰线计算得到的是承载力上限解,致使原本的计算结果偏高并且考虑到未修正的结果也较为准确,因此简便起见,可不加以修正。
2.2 有自由边单孔板
单孔板有自由边和固支边时,共有如图10所示的4种组合方式,在塑性功计算时,设其有两部分组成,分别为孔中心与固支边端点连线所夹区域(即图10阴影部分)与孔中心与自由边端点连线所夹区域(即图10非阴影部分)上塑性铰线所作的内力虚功。
以三边固支,r=0的标准单孔板为例分析这类单孔板的塑性铰线模型。基于前文分析知当R增大时,塑性功减小,更接近真实情况,故在固支边和自由边相交处,与四边固支情况不同,由于没有另一固支边的限制,设R可在此处延伸至边界,此时边界处的塑性铰线与固支边界相切。此外,由于板件的连续性,单孔板受力变形后,在固支边和自由边相交处的板件同样保持连续,因此非阴影区变形后应是与图11微小板块B相切的拱形板件。

图10 有自由边开孔板的边界条件
Fig.10 Boundary conditions of plate with free edges
阴影区域的内力虚功计算与2.1节所述方法一致。非阴影区域计算内力虚功时,假定塑性变形集中在图11两条虚线所示的塑性铰线上,同时塑性铰线两侧板面B均与板面A相切。为了确定塑性铰线的位置,可以取s作为变量。当s=0时,塑性铰线为变形后孔中心到固支边与自由边交点的直线;当s=∞,塑性铰线为过变形后孔中心与W平面垂直的直线,此时两条塑性铰线重合。这两条塑性铰线的内力虚功E计算式为式(12),计算结果见图12,随着s的增大,内力虚功显著减小。

图11 三边固支标准单孔板变形图
Fig.11 Deformation of standardized plate with 3 fixed edges
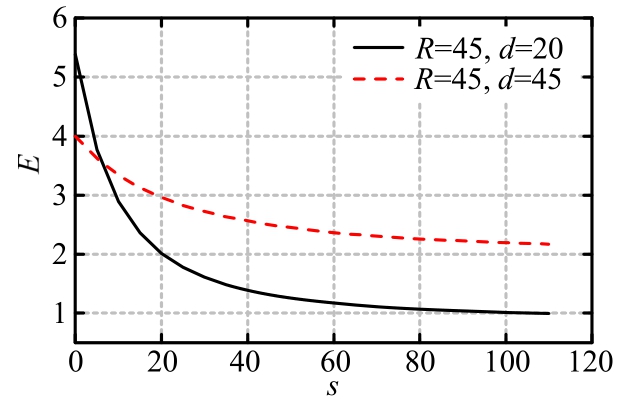
图12 三边固支标准单孔板非阴影部分塑性铰线上虚功
Fig.12 Virtual work of yield lines at non-shaded area of standardized plate with 3 fixed edges
由此确定孔中心与自由边端点连线所夹区域的塑性铰线如图10虚线所示。
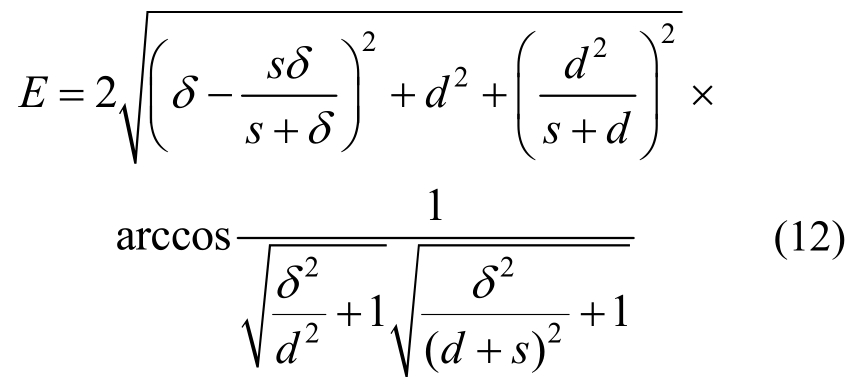
此类单孔板塑性铰线所做虚功,按式(13)进行计算,这里将积分运算转化为有限求和,处理方法同2.1节的一般单孔板。根据内外力平衡,屈服承载力可按式(14)进行计算。

式中:dc为孔中心到固支边的距离;ψ为孔中心到固支边两端点的夹角;df为孔中心与自由边两端点连线所夹区上域塑性铰线的长度;l为塑性铰线到固支边的距离,见图10。
建立有限元模型验证。取参数l1=l2=90 mm,t=5 mm,分别计算了r=5/10 mm时板件的屈服承载力,结果如图13,表明理论计算结果与有限元计算结果非常接近,相差在 3%以内,理论计算时,df近似取为孔中心到自由边距离。
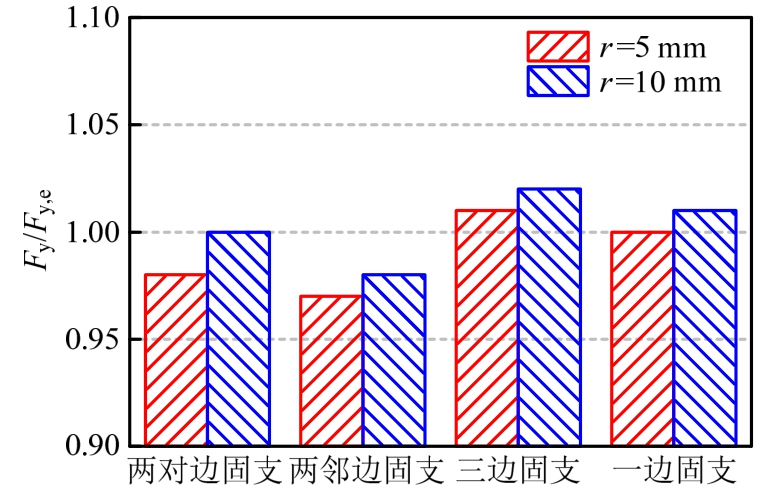
图13 有自由边的标准单孔板屈服承载力理论和有限元比值
Fig.13 Ratios of yield loads of standardized plate with free edges calculated by theoretical model to those by FE model
对一般单孔板,先假定在塑性极限状态时,其变形与标准单孔板一致,因此计算承载力的公式类比式(14),改写为式(15):
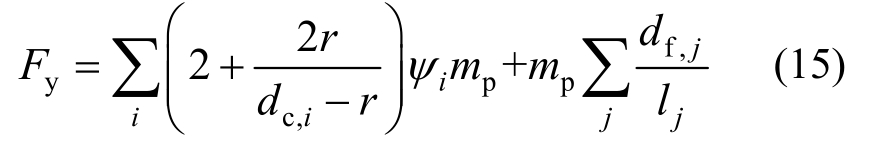
式中:dc,i为孔中心到各固支边的距离;ψi为孔中心到固支边两端夹角;df, j为孔中心与自由边端点连线所夹区域塑性铰线的长度;lj为对应于塑性铰线到固支边的距离。
采用有限元进行验证,模型参数为l1=90 mm,a=30/45/60 mm,b=22.5 mm,r=10 mm,t=5 mm,以长度l2为变量应用式(15)进行理论计算,计算结果与有限元计算结果比较为图14修正前结果,误差随着边长l2的增长而明显增大,部分已经远大于坐标轴范围。理论计算结果会随l2的增大呈线性增长,而有限元结果在l2到达某一数值后不再改变。
以图15有限元模型计算结果为例说明这一现象。根据有限元模型的边界条件(两对边固支),其变形假定为图10(a)。从实际的计算的位移云图中显示距孔较远端的自由边位移为0,更符合图10(c)的屈服铰线假定。因此在计算屈服承载力时,当l2增大到一数值时,远端的自由边应按固支边处理。
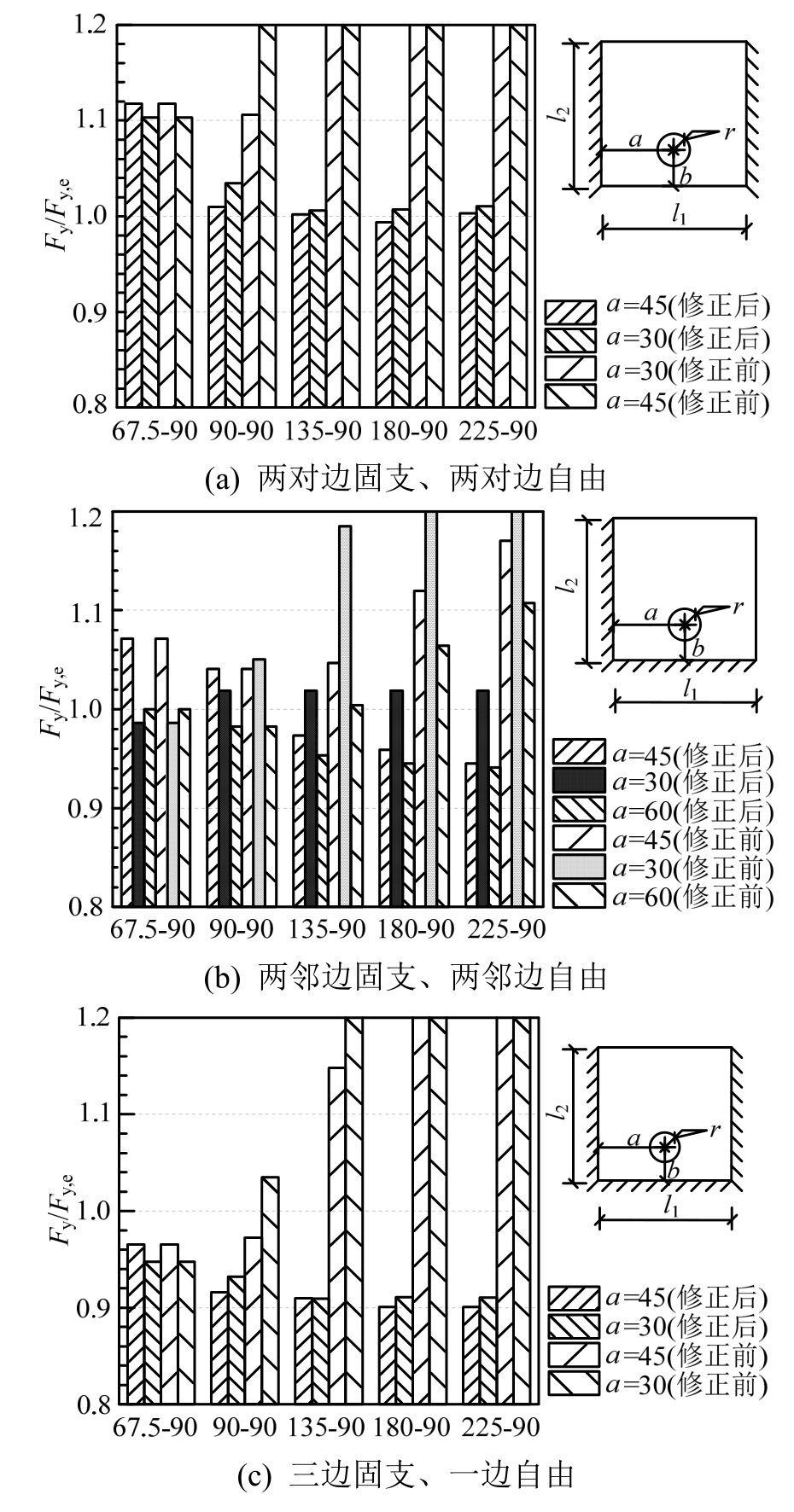
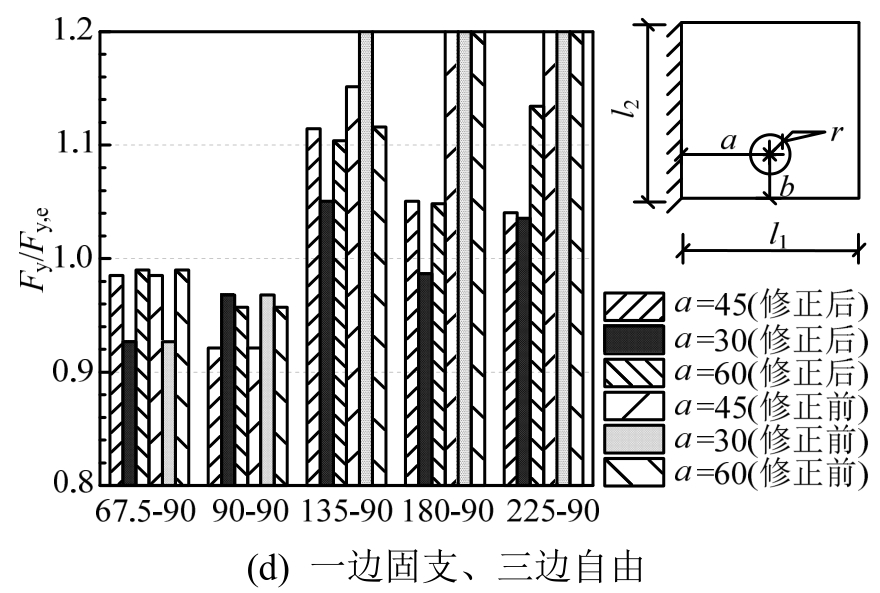
图14 有自由边单孔板屈服承载力理论和有限元比值
Fig.14 Ratios of yield loads of plate with free edges calculated by theoretical model to those by FE model

图15 达到屈服承载力时两对边固支、两对边自由的板位移云图(l1=90,l2=135)
Fig.15 Displacement distribution of plate with opposite edges fixed and other two free when fully yielded (l1=90,l2=135)
计算有自由边的一般开孔板的屈服承载力时,将自由边分别按自由边和固支边分别计算,得到屈Fy,1和Fy,2,取小值计为屈服承载力Fy,如式(16),按这一方法对上述算例进行修正,得到图14修正后结果,误差明显减小。
2.3 有滑动铰支边单孔板
当单孔板有滑动铰支边时,其与自由边、固支边共有10种可能的组合方式,如图16所示。内力虚功由三部分组成。第1部分、第2部分为孔中心与固支边、自由边端点连线所夹区域,这两部分屈服承载力计算方法与2.1节、2.2节所述一致。第三部分是孔中心与滑动铰边端点连线所夹区域,这区域所作的虚功由板面、孔周与边界3项组成。由于滑动铰支边不能限制板件的平面外位移(图17),因而可认为单孔板在塑性极限状态下,滑动铰支边可等同于自由边处理。因此这部分板面上的塑性铰线虚功与第二部分相同。孔周和边界的内力虚功按孔中心与固支边所夹区域的计算方法计算,但由于滑动铰支边本身存在平面外变形,塑性铰线的转角会相应减小,采用γ进行修正,取γ=0.5。

图16 有滑动铰支边单孔板的边界条件
Fig.16 Boundary condition of plate with sliding edges
标准单孔板的内力虚功和屈服承载力计算公式为式(17)、式(18),并建立有限元模型验证。选择单孔板参数l1=l2=90 mm,a/l1=b/l2=0.5,施加与图16对应的边界条件,理论计算与有限元计算比较的结果如图18所示,表明理论计算结果与有限元计算结果较为接近,误差在10%以内。
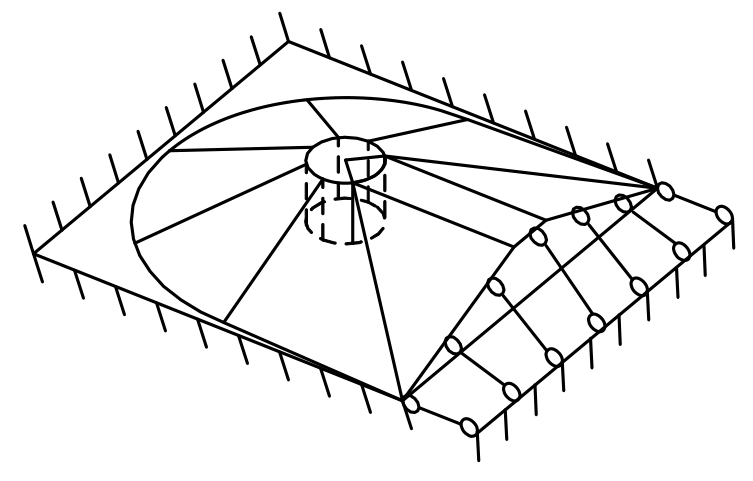
图17 滑动铰支边板的变形图
Fig.17 Deformation of plate with sliding edges
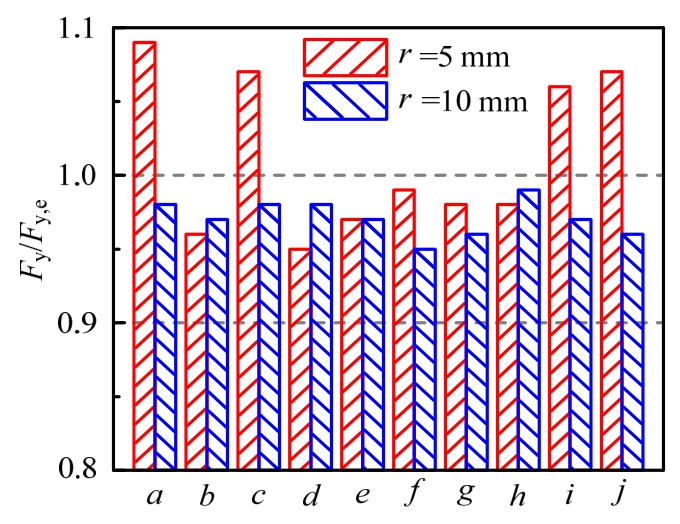
图18 有滑动铰支边标准单孔板屈服承载力理论和有限元比值
Fig.18 Ratios of yield loads of standardized plate with sliding edges calculated by theoretical model to those by FE model
注:图18中a~j分别对应图16(a)~图16(j)

式中:dc为孔中心到固支边的距离;ψi为孔中心到固支边两端夹角;ψk′为孔到滑动铰支边与固支边的交点与滑动铰支边处板面铰线间的夹角,图16;df,、ds为孔中心与自由边、滑动固支边端点连线所夹区域塑性铰线的长度;l为自由边、滑动铰支边处板面塑性铰线到固支边的距离。
对于一般单孔板,也可先假设其变形与标准单孔板相同,其屈服承载力按式(19)计算。当孔与滑动铰支边或自由边距离较大时,计算结果会明显偏大,这种情况的产生原因、解决方法与2.2节所述一致。
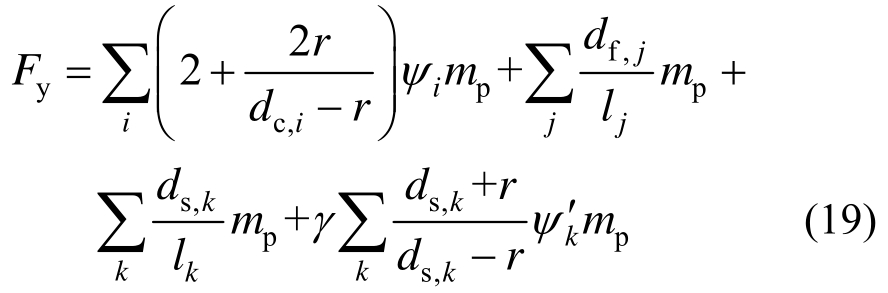
式中:dc,i为孔中心到各固支边的距离;ψi、ψk′为分别为孔到固支边两端夹角、孔到滑动铰支边与固支边交点的连线与滑动铰支边处塑性铰线间的夹角(见图16);df,j、ds,k为孔中心与自由边、滑动固支边端点连线所夹区域塑性铰线的长度;lj、lk为分别为对应于自由边、滑动铰支边处板面塑性铰线到固支边的距离。
2.4 单孔板屈服承载力的计算流程
通过上述对开孔板件塑性极限状态的分析,可总结开孔板屈服承载力的计算流程,如图19所示,其中i代表板件边界的编号,由于是矩形板,i最大为 4。图中设计参数应包括开孔板件的几何参数,材料屈服强度以及边界条件。
3 端板连接节点受拉区柱壁承载力计算
3.1 方钢管柱节点的受拉区件承载力计算
以王志宇等[18-19]试验为有限元模型的参照,建立了如图20所示的模型。采用ABAQUS作为有限元分析软件,材料为理想弹塑性,单元为实体单元C3D8R,沿方管柱壁厚度方向划分6层。方管柱上下截面固支,4个螺栓孔耦合在一参考点,施加平面外的位移。模型参数如下:l=550 mm,b=150 mm,p1=100mm,p2=60/90 mm,t=5/8 mm,r=8.75/13 mm,采用理想弹塑性材料模型,fy=348 MPa
计算时,将柱壁从相邻两孔连线中心线处划分为4部分。以①部分为例,根据实际情况可以认为上边和左边为固支边;由于对称性,下边和右边为滑动铰支边。
各类计算参数计算如下:
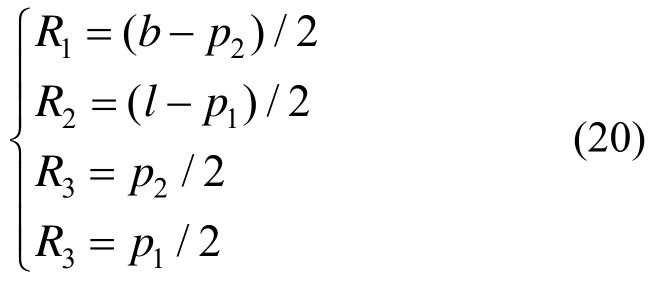

图19 单孔板的屈服承载力计算流程图
Fig.19 Flow chart for yield load calculation of plates with a single hole
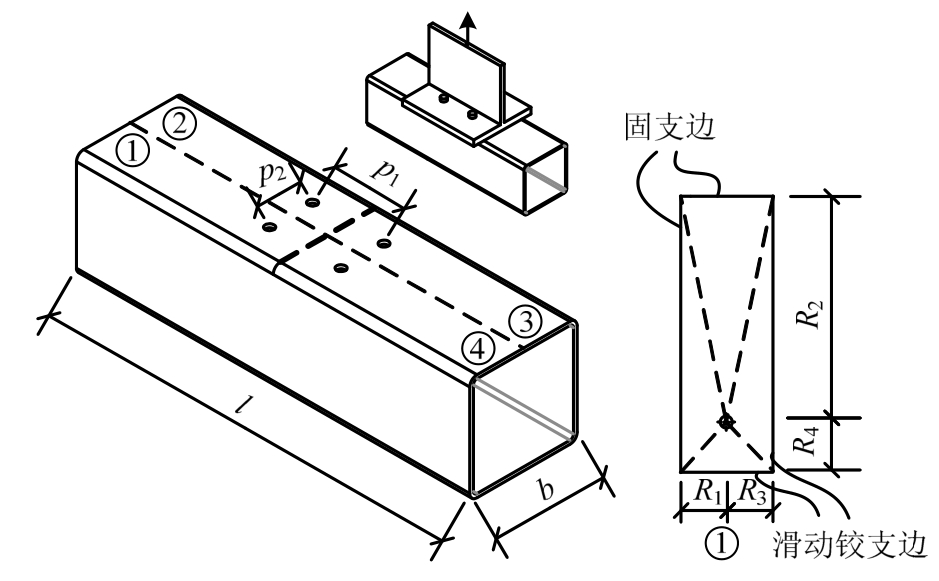
图20 方管柱节点受拉区计算模型
Fig.20 Calculation models of T-stub-to-SHS connection

由于王志宇试验中的普通螺栓不具有其预紧力,不符合刚性环假定,故仅考虑Hollo-bolt的试验数据。柱壁承载力的计算结果如表1所示,发现理论计算与有限元结果非常接近,最大误差在10%左右。但与试验结果计算结果相比,本文采用的计算方法偏大。值得注意的是当采用HB16时,其计算结果较HB10而言相对准确。这一结果的原因在于Hollo-bolt的螺栓预紧力难以保证[23-24],特别是直径较小的Hollo-bolt不具有预紧力,其与普通螺栓一样无法保证计算假定。
表1 柱壁屈服承载力理论计算与有限元和试验结果对比
Table 1 Yield load comparison of column wall between the theoretical models and FE models/tests

注:试件编号规则:螺栓规格-板厚-螺栓间距(p2),螺栓规格有 HB10和 HB16。带*试件在原文献[18]并不存在,本文根据其参数变化规律和命名规则建立了对应模型。
试件编号 分块 有限元 分块组合法/试验 理论计算/组合法/kN计算/kN有限元 结果/kN试验结果CHB10-5-60 78.4 80.0 0.98 55.2 1.42 CHB10-5-90 97.1 106.8 0.91 81.3 1.19 CHB10-8-60 200.7 203.0 0.99 176.4 1.14 CHB10-8-90 248.6 279.0 0.89 219.3 1.13 CHB16-5-60 87.8 88.7 0.99 81.6 1.08 CHB16-5-90 117.3 124.1 0.95 132.2 0.89 CHB16-8-60 224.8 223.2 1.01 196.4 1.14 CHB16-8-90* 300.2 323.0 0.93 ― ―
当预紧力较小时,刚性环假定失效,无法形成孔周的塑性铰线。因此不考虑该部分的塑性铰线内力功,得到表2的理论计算结果,与试验结果吻合较好。此外,表 2给出了原文献[18]的计算结果及其与试验的对比,发现采用本文提出的方法可以给出与原文献计算精度相当的理论结果,但本文方法使用更简便且通用性较好。
表2 柱壁屈服承载力理论计算与试验结果对比(不考虑预紧力作用)
Table 2 Yield load comparison of column wall between theoretical models and FE models/tests (no pretension)
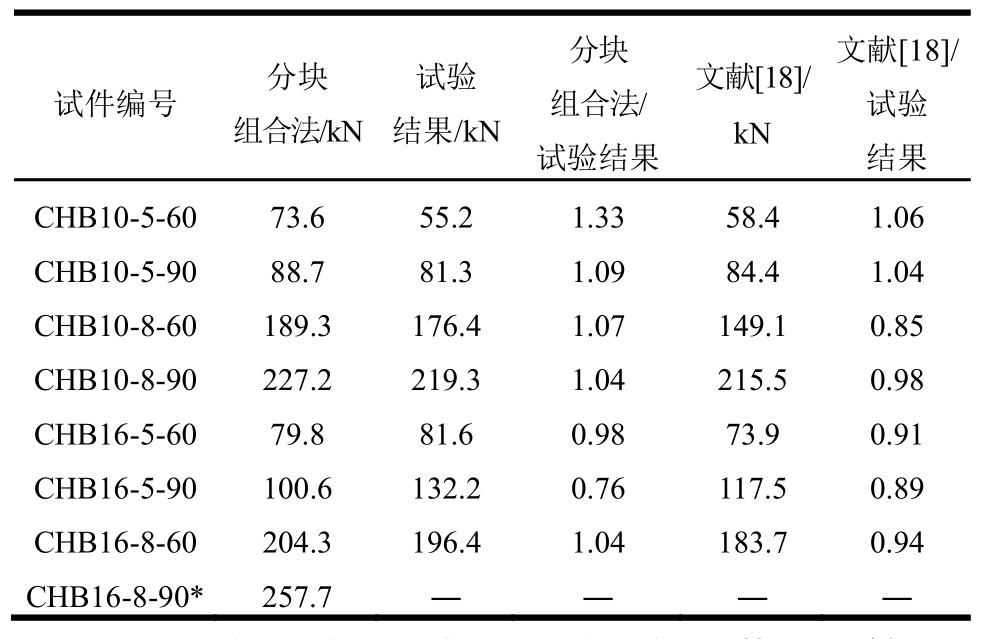
分块 试验 分块 文献[18]/文献[18]/试件编号 组合法/kN结果/kN组合法/kN试验试验结果 结果CHB10-5-60 73.6 55.2 1.33 58.4 1.06 CHB10-5-90 88.7 81.3 1.09 84.4 1.04 CHB10-8-60 189.3 176.4 1.07 149.1 0.85 CHB10-8-90 227.2 219.3 1.04 215.5 0.98 CHB16-5-60 79.8 81.6 0.98 73.9 0.91 CHB16-5-90 100.6 132.2 0.76 117.5 0.89 CHB16-8-60 204.3 196.4 1.04 183.7 0.94 CHB16-8-90* 257.7 ― ― ― ―
3.2 加强型H型柱节点的受拉区件承载力计算
Tagawa等[12]设计了一种新型的节点形式,在节点位置增设角钢对其进行加强。作者对图 21所示的节点受拉区进行了力学性能研究。
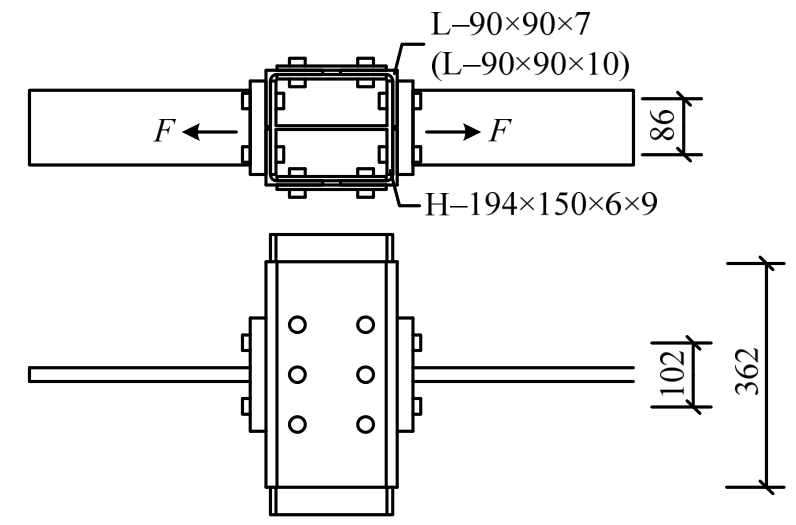
图21 加强型节点受拉区试验试件
Fig.21 Tension zone specimens of stiffening joint
采用本文提出的分块组合法对该节点形式进行屈服承载力的计算。将角钢与H型钢柱分别进行计算,板件分割的方式、边界条件以及尺寸的选取如图22所示。
表3给出了文献[12]以及采用分块组合法的计算结果,并将结果标记在图23中的荷载-位移曲线上。发现文献[12]的结果均小于采用分块组合法的理论计算结果,但从荷载-位移曲线中可以看到,后者的计算结果与薄膜效应的起点更为接近,更接近塑性屈服承载力的上限值。
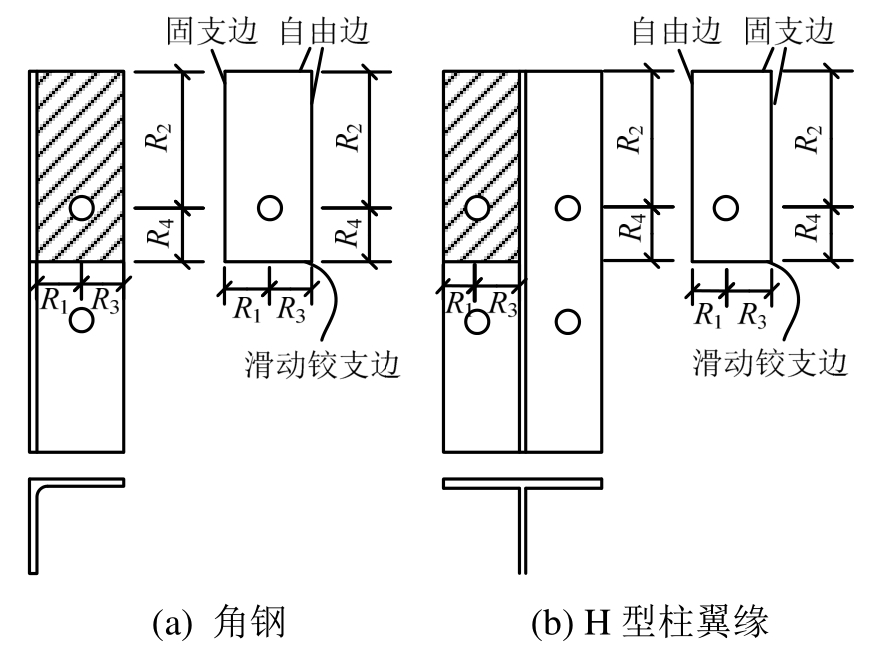
图22 加强型节点受拉区板件的计算模型
Fig.22 Plate calculation models of joint tension zone
表3 加强型节点受拉区的屈服承载力计算
Table 3 Yield load of joint tension zone

注:试件编号规则:T-0表示无加强角钢,T-7/T-10分别表示加强角钢规格为 L-90×90×7 以及 L-90×90×7。
试件编号 文献[12]/kN 分块组合法/kN T-0 162.6 219.1 T-7 326.5 355.9 T-10 445.2 523.7
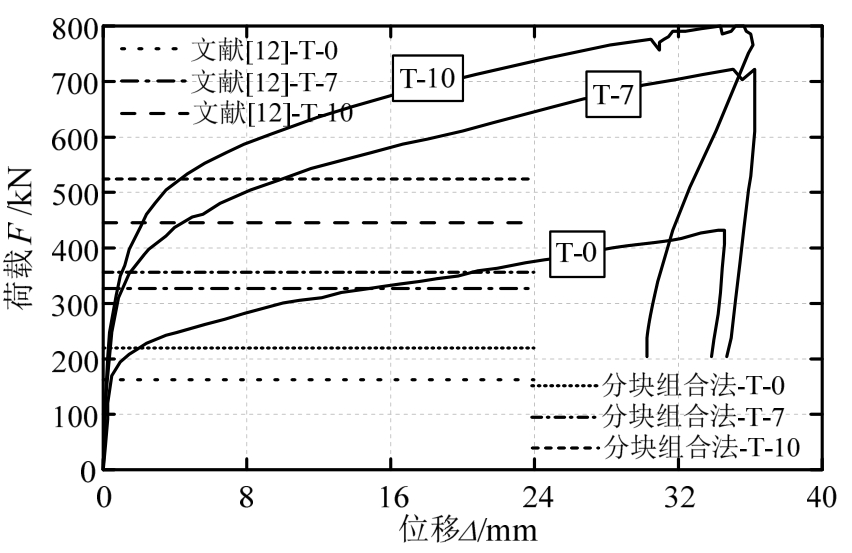
图23 加强型节点受拉区试件的荷载-位移曲线
Fig.23 Tested load-displacement curves of joint tension zones
注:图中荷载位移曲线是通过软件GetData获取。
4 结论
本文提出了分块组合法方法,是一种用于计算端板螺栓连接节点屈服承载力的通用方法,并将理论公式计算结果与有限元数值计算结果以及已有的相关试验结果进行了分析对比。本文可得到以下结论:
(1)分块组合法方法主要思想是先将板件(柱壁、端板等)分割成若干块,确定每一块板的边界条件并计算相应屈服承载力,最后叠加各部分的屈服承载力得到整块板件的屈服承载力。
(2)单孔板四边固支时,采用式(11)进行计算。当固支边距离孔较远时,理论公式的计算假定与实际并不符合,但通过计算发现这种影响较小。
(3)单孔板有自由边或滑动铰支边时,屈服承载力计算采用式(15)、式(19)计算,当自由边或滑动铰支边距离孔较远时,将其视为固支边处理,得到的屈服承载力与原屈服承载力比较,取两者小值。
结合上述结论,文中给出了单孔板屈服承载力的计算流程,通过该计算流程,不仅有效减小对具体屈服模式的依赖,同时也可得到准确的结果。本文中讨论的是在理想状态条件下各类开孔板屈服承载力的计算方法,但实际节点连接的边界条件、受力与理想情况不尽相同,如本文计算中忽略了柱壁中存在的轴向应力,会使计算结果存在一定的偏差。此外对于基本假定 1,本文中没有严格讨论满足刚性环假定的预紧力范围,并且该假定中仅有垂直于板面的竖向位移在少数情况下不符合实际,如三边自由一边固支的情况下,实际情况中孔的位移并不严格垂直于板面而是会绕固定边的转动,这使得本文公式高估了其屈服承载力,但这些情况在实际工程中存在性很低。最后,计算中仅考虑了理想刚塑性材料,实际情况中由于从板面材料进入屈服到板中心截面屈服存在一个过程,板中心截面屈服时,边缘材料的强化使得理论公式计算的结果偏小,但考虑到板件较薄这种影响并不明显可以忽略。
附录:板面塑性功E1,c推导
从图4(b)中易得塑性铰线长度lp:
相邻板块间转角都相同,计算板块1、板块2间转角,标记图4 (b)关键点A~F以及O、O1,并建立直角坐标系,如附图1所示。坐标原点为O点,x轴过BC中点,z轴过点O1。
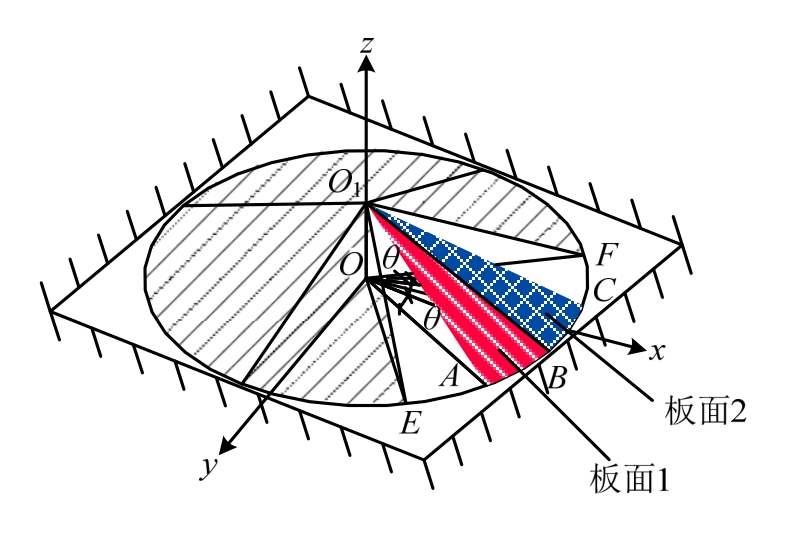
附图1 圆形屈服模式变形图
Attached fig.1 Deformation of circular yield pattern
已知从图中扇形区域EOF的中心角为ψ,顶点为O点。O点向上移动Δ距离,得到新的类扇形区域,记为O1EF。板块1、板块2变形前为OAB与OBC,O点向上移动Δ后,变为O1AB与O1BC。其中O1B为塑性铰线。由于θ很小,AB与BC近似为直线。
通过几何关系可得,扇形O1AB与O1BC的法向量分别为s1、s2:
由此可知O1AB与O1BC的夹角为φ:
由此该条塑性铰线上所做功E为:
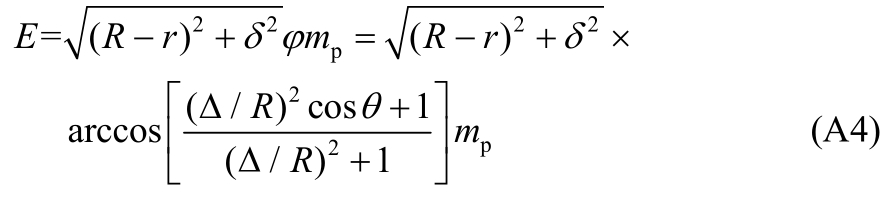
式中,θ=ψ/n,并令Δ/R=t,板面塑性功E1,c计算如下:

注意到关系式δ/(R-r)=Δ/R,则:
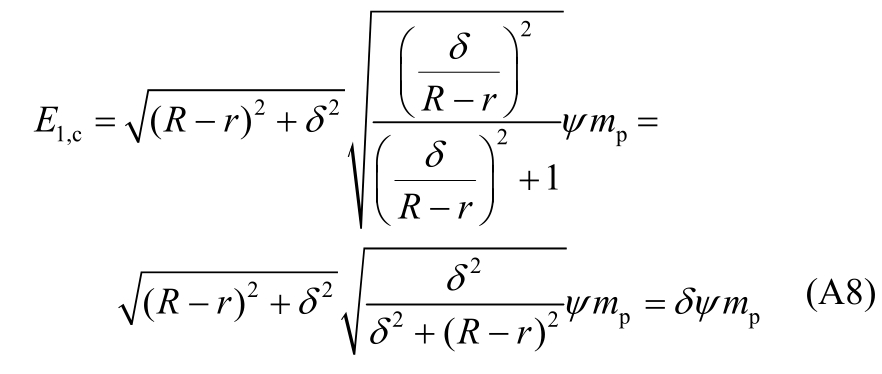
[1]郝际平, 孙晓岭, 薛强, 等.绿色装配式钢结构建筑体系研究与应用[J].工程力学, 2017, 34(1): 1―13.Hao Jiping, Sun Xiaoling, Xue Qiang, et al.Research and applications of prefabricated steel structure building systems[J].Engineering Mechanics, 2017, 34(1): 1―13.(in Chinese)
[2]杨俊芬, 陈雷, 程锦鹏, 等.一种新型装配式梁柱节点抗震性能试验研究[J].工程力学, 2017, 34(12): 75―86.Yang Junfen, Chen Lei, Cheng Jinpeng, et al,Experimental study on seismic behavior of a new type of fully assembled beam-column joints[J].Engineering Mechanics, 2017, 34(12): 75―86.(in Chinese)
[3]Wang J, Uy B, That H T, et al.Behaviour and design of demountable beam-to-column composite bolted joints with extended end-plates[J].Journal of Constructional Steel Research, 2018, 144: 221―235.
[4]石永久, 王萌, 王元清, 等.钢框架端板连接半刚性节点受力性能分析[J].工程力学, 2011, 28(9): 51―58.Shi YongJiu, Wang Meng, Wang Qingyuan, et al.Aanlysis on the behavior of steel frame[J].Engineering Mechanics, 2011, 28(9): 51―58.(in Chinese)
[5]胡方鑫, 施刚, 石永久, 等.工厂加工制作的特殊构造梁柱节点抗震性能有限元分析[J].工程力学, 2015,32(6): 69―75.Hu Fangxin, Shi Gang, Shi Yongjiu, et al.Finite element analysis on seismic performance of specifically pre-fabricated beam-column connections[J].Engineering Mechanics, 2015, 32(6): 69―75.(in Chinese)
[6]Beena K, Naveen K, Shruti S.Experimental and numerical investigations of bolted CFST beams–CFST columns connections[J].Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2018:1―14.
[7]Yin H, Shi G.Finite element analysis on the seismic behavior of fully prefabricated steel frames[J].Engineering Structures, 2018, 173: 28―51.
[8]王萌, 柯小刚, 吴照章.可更换延性耗能连接组件的钢框架节点抗震性能研究[J].工程力学, 2018, 35(12):151―163.Wang Meng, Ke Xiaogang, Wu Zhaozhang.Seismic behavior of steel frame connections with replaceable high ductility and energy dissipation components[J].Engineering Mechanics, 2018, 35(12): 151―163.(in Chinese)
[9]Park R, Gamble W L.Reinforced concrete slabs[M].Canada: John Wiley & Sons, 2000.
[10]prEN 1993-1-8: 2005, Eurocode 3: design of steel structures: part 1―8: design of joints[S].Brussels,Belgium: CEN, 2005.
[11]Gomes F, Jaspsrt J-P, Maquoi R.Moment capacity of beam-to-column minor-axis joints[C]// Istanbul, Turkey:IABSE, 1996: 319―326.
[12]Tagawa H, Liu Y.Stiffening of bolted end-plate connections with steel member assemblies[J].Journal of Constructional Steel Research, 2014, 103: 190―199.
[13]徐婷, 王伟, 陈以一.国外单边螺栓研究现状[J].钢结构, 2015(8): 27―33.Xu ting, Wang wei, Chen yiyi.A review on Foreign research status of one-side bolt[J].Steel Construction,2015(8): 27―33.(in Chinese)
[14]He R, Shu X, Zhang Z.Experimental Study on the Tensile Performance of High-strength Blind-bolted T-stub with Endplate Tapping[J].Journal of Engineering Science and Technology Review, 2018, 11(5): 109―118.
[15]Li B, Wang J, Lu Y, et al.Seismic response tests and analytical assessment of blind bolted assembly CFST frames with beam-connected SPSWs[J].Engineering Structures, 2019, 178: 343―360.
[16]Kurobane Y, Packer J A, Wardenier J, et al.Design guide for structural hollow section column connections[M].Köln: TÜV-Verlag, 2004: 80―84.
[17]SCI/BCSA, Joints in steel construction: simple connections[S].London, UK: The Steel Construction Institute (SCI)&The British Constructional Steelwork Association (BCSA), 2005.
[18]王志宇, 王清远, 刘晓凯, 等.基于屈服线理论的螺栓端板连接方钢管柱承载力计算模型研究[J].建筑结构学报, 2016(6): 160―173.Wang zhiyu, Wang qingyuan, Liu xiaokai, et al.Yield line theory based loading capacity analytical model of bolted endplate connections to square hollow section columns[J].Journal of Building Structures, 2016(6):160―173.(in Chinese)
[19]Wang Z Y, Wang Q Y.Yield and ultimate strengths determination of a blind bolted endplate connection to square hollow section column[J].Engineering Structures, 2016, 111: 345―369.
[20]Eldin A E M.Behaviour of blind bolted moment connections for square HSS columns[D].Canada:McMaster University, 1993: 141―150.
[21]Lee J, Goldsworthy H M, Gad E F.Blind bolted T-stub connections to unfilled hollow section columns in low rise structures[J].Journal of Constructional Steel Research, 2010, 66(8): 981―992.
[22]陈学森, 施刚, 赵俊林, 等.基于组件法的超大承载力端板连接节点弯矩-转角曲线计算方法[J].工程力学,2017, 34(5): 30―41.Chen xuesen, Shi gang, Zhao junlin, et al.Calculation of Moment- rotation curves of ultra-large capacity end-plate connections based on component method.Engineering Mechanics, 2017,34(5): 30―41.(in Chinese)
[23]Ancon Building Products Pty Ltd.Lindapter hollo-bolt brochure[EB/OL].https://www.ancon.com.au/products/lindapter-weld-free-steel-connectors/product-range/hollobolt, 2013-07-15.
[24]徐婷, 王伟, 陈以一.单边螺栓连接性能试验报告[R].上海: 同济大学钢与轻型结构研究室, 2015.Xu Ting, Wang Wei, Chen Yiyi.Test report fot connection performance of one-side bolt[R].Shanghai:Steel and Lightweight Structures in Tongji University,2015.(in Chinese)