工程结构在不利荷载，如地震作用下，表现出强非线性性质。基于结构非线性响应识别结构特征，不仅运用于结构损伤诊断，更能反映结构构件的工作状态，对于验证或者校准结构的数值模型有着重要的意义。然而结构由于复杂的非线性特征，对非线性系统的有效识别是结构健康监测领域亟待解决的问题。
近年来，不少学者提出了基于观测非线性结构响应的识别方法[1―2]。在工程应用中，观测到全部结构响应是非常困难的，因此，对部分观测下系统识别的研究具有重要意义[3―5]。Hoshiya和 Saito[6]提出扩展卡尔曼滤波方法(EKF)，利用一阶泰勒展开简化非线性系统，但此方法依赖于线性近似的有效性，适用于弱非线性系统。Julier等[7―8]提出了结合无迹变换与卡尔曼滤波的无迹卡尔曼滤波(UKF)方法，避免了EKF线性简化及求解雅克比矩阵等问题，被广泛运用于非线性系统识别。
传统的EKF和UKF方法，都要求已知系统外部激励。在实际工程应用中，会存在较难获得准确外部激励的情况，大多数研究都是在激励已知的情况下识别非线性系统[9―10]。因此，已有许多学者提出了未知激励下识别非线性系统的各种方法[11―13]。Yang等[14]、雷鹰和江永强[15]、Liu等[16]等分别基于EKF研究未知激励下系统识别方法(EKF-UI)。但是，迄今为止国内外对未知激励情况下的UKF方法的研究还非常少，Al-Hussein和Haldar[17―19]基于UKF，利用最小二乘法，求出未知激励，但此方法需要对子结构响应的全部观测；Ding等[20]采用正交多项式对未知激励的分解，将多项式系数作为未知参数进行识别。然而，由于多项式分解是一种近似分解，会导致识别困难。
该文基于传统 UKF方法的递推公式与步骤，推导出未知激励下 UKF方法(UKF-UI)的递推识别公式，在部分观测响应条件下，同时识别非线性系统和作用的未知外部激励，并且采用部分观测的结构加速度响应和位移响应的数据融合，避免识别结果的漂移现象。通过未知地震作用下识别非线性迟滞模型为例，说明提出的方法适用于识别强非线性系统，在部分观测条件下，能有效地识别非线性结构系统参数及外部激励，扩展了传统 UKF算法的适用范围。
1 UKF-UI方法推导
一个n自由度的非线性系统在包含未知激励作用下的运动方程可写成如下形式：
式中：M为结构质量矩阵；
分别为结构位移、速度、加速度响应向量；θ为未知结构参数向量；
为结构非线性恢复力向量；f和f u分别为已知外激励向量和未知外激励向量；η和ηu分别为相应的影响矩阵。
结构扩展状态向量X为：
则式(1)可以写为：
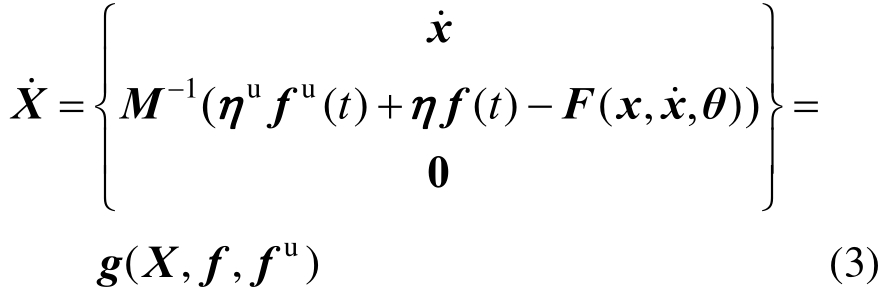
观测方程也可以表达为：
假定结构质量已知且观测量为加速度响应，状态方程和观测方向都与未知激励呈线性关系，则式(3)和式(4)可以写为：
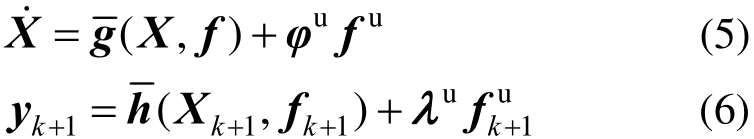
式中：
分别为由式(3)和式(4)推导的非线性方程；φ u为状态方程中未知激励的影响矩阵；λu为测量方程中未知激励的影响矩阵。传统的 UKF方法是在已知外部激励基础上递推识别结构参数，本文提出的UKF-UI方法采用类似的递推识别结构参数和未知激励。
1.1 计算Sigma点
类似传统UKF法，计算2N+1个Sigma点：
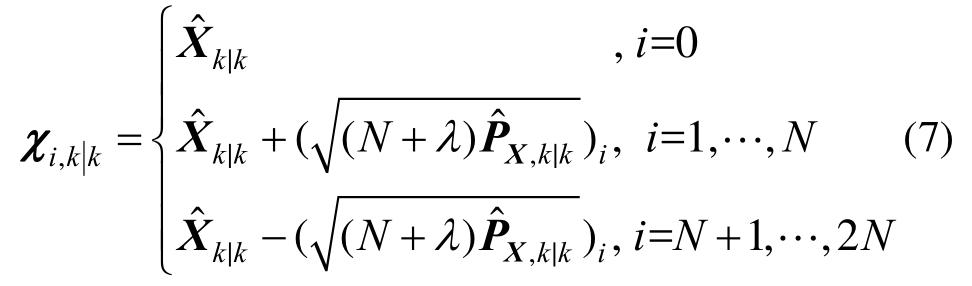
式中：N为状态向量X的维数；
(·)i代表该矩阵第i列向量；λ=α2(N+κ)-N，其中α和κ为调谐参数[21]。
1.2 时间预测
Sigma点
在t=(k+1)时刻的预测为：
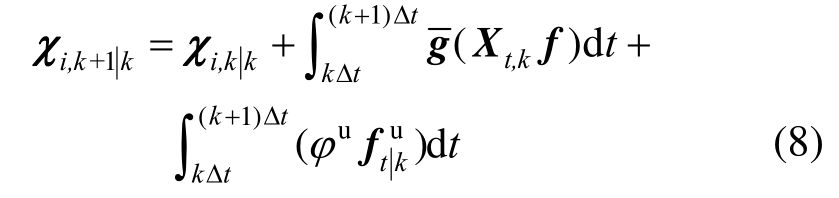
当时间步长很小时，可假设未知激励为t=kΔt时刻的值，则式(8)可写为：
同时，预测状态向量
及误差协方差
在t=(k+1)Δt时刻为：
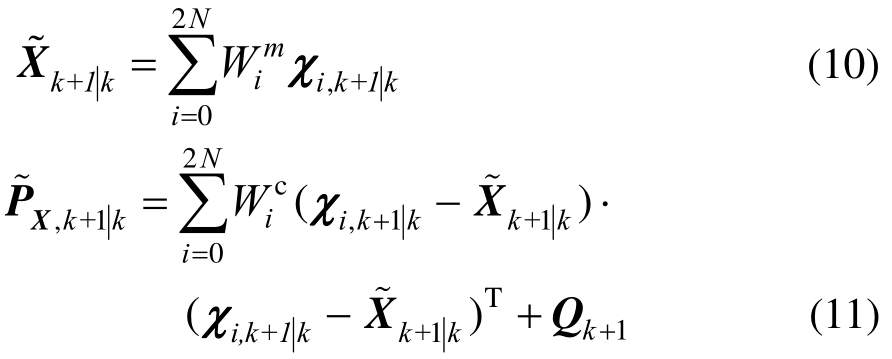
式中：Q为状态噪声的协方差矩阵；Wim和Wic分别为均值和方差的权重：
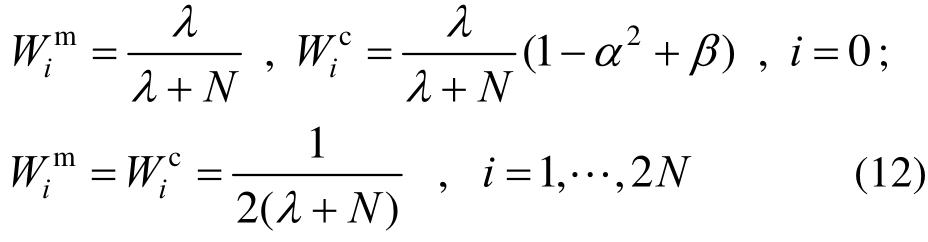
式中：β为非权重系数，用来并入X的概率分布的先验信息，如果是高斯分布，β=2为最优值。
预测的观测向量
和误差协方差矩阵
为：
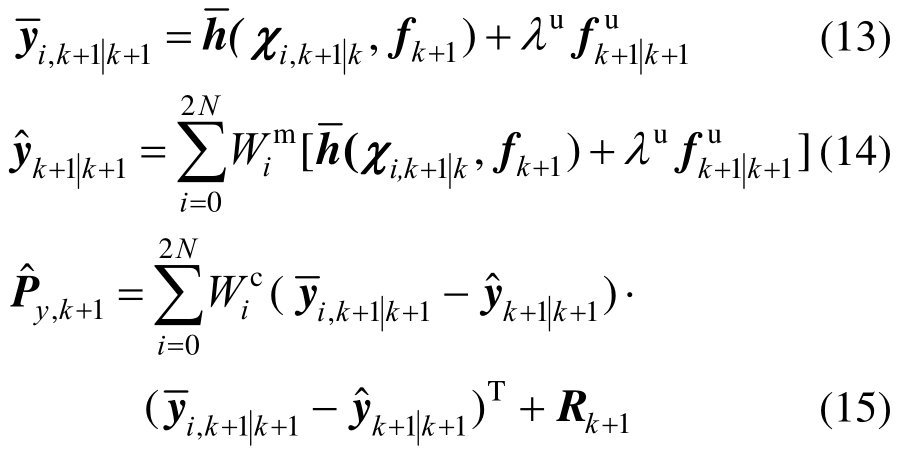
式中，R为观测噪声的协方差矩阵，则交叉项的协方差矩阵
为：
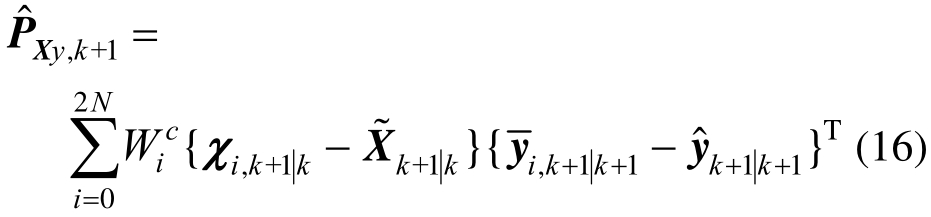
由于
估计的测量值可为：
因此，估计测量误差的表达式为：
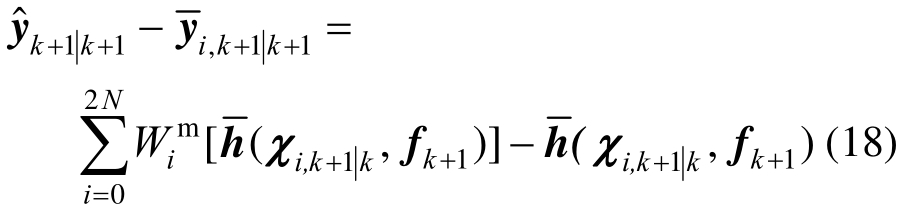
由此可见，式(18)中不含有未知激励
可以直接求得
1.3 估计未知激励及测量更新
根据观测yk+1，扩展状态的更新为：
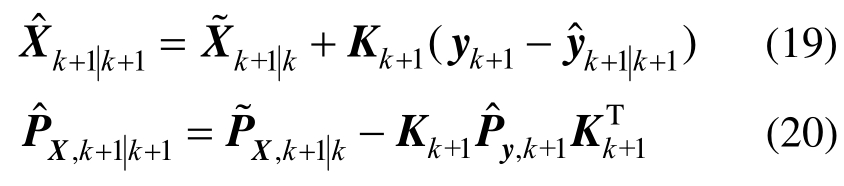
式中，Kk+1为增益矩阵，其表达式为：
由于
未知，则估计测量误差未知，将更新的状态向量代入测量方程，则可得：
因此，观测值和估计值之间的误差可表示为：
此种情况下，当测量点数大于未知力的个数时，
可以通过最小二乘的方法对式(23)误差最小化求得。再将估计的
代入式(19)～式(20)，则得到更新的状态向量和误差协方差。k～k+1部算法流程图如图1所示。通过上述UKF-UI非线性识别方法，在未知激励情况下，通过观测的部分响应，可识别强非线性系统参数及未知外部激励。
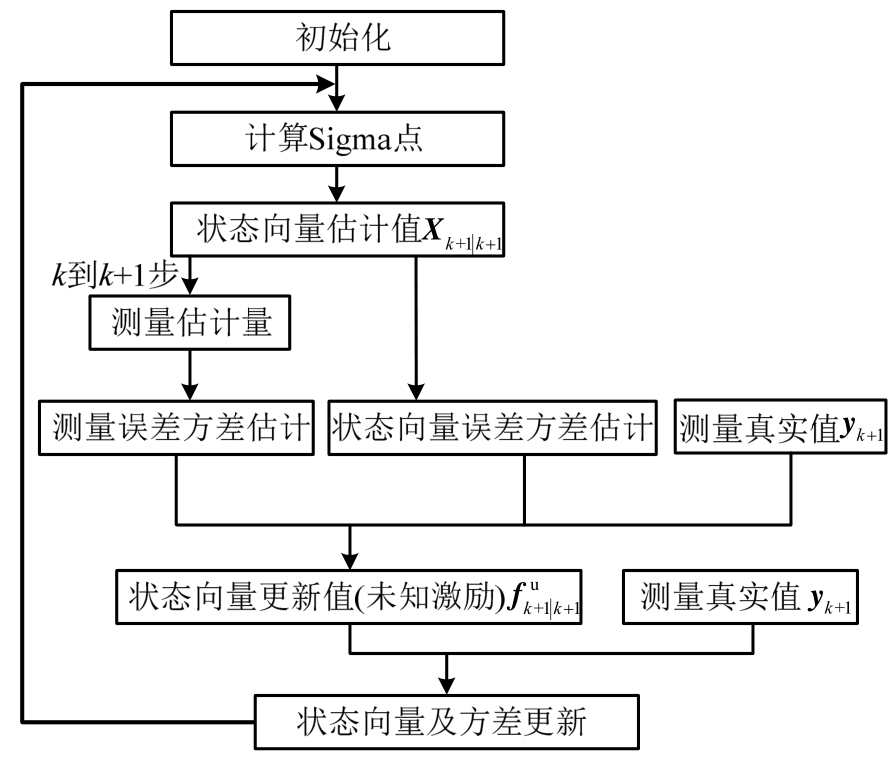
图1 UKF-UI算法流程图
Fig.1 Flow chart of the proposed UKF-UI algorithm
2 数值算例
为验证所提方法对于未知激励情况下识别强非线性系统的有效性，采用数值算例对识别结果进行验证。
2.1 白噪声激励
考虑6层剪切框架模型，受到位于顶层的白噪声激励，框架均考虑为层间恢复力为Bouc-Wen滞回模型的非线性结构，其运动方程为：
式中，zi (t)(i=1 ,2,… ,6)为迟滞位移向量，表达为：
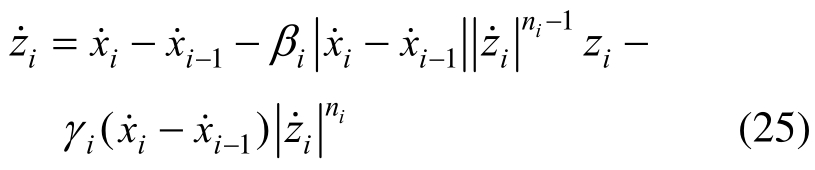
式中：ni、βi和γi为迟滞参数，在本文算例中，参数取值为：βi =800s2 /m2;γi =400s2 /m2;n =2;ki= 2 .4× 1 05 N/m，结构参数分别为：单元质量mi =600 kg，阻尼ci=0 .2 kN⋅ s/m，i= 1 ,2,⋅⋅⋅,6 。
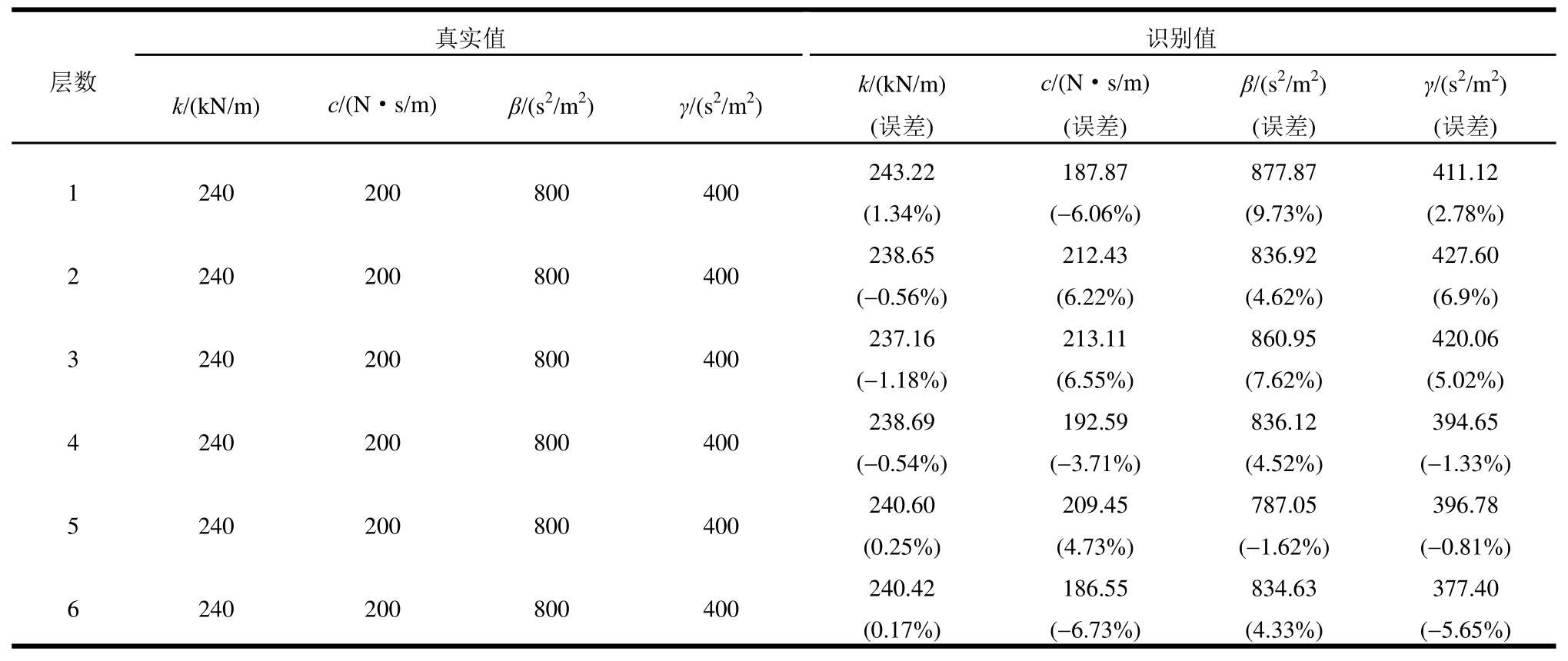
部分观测为观测框架第1、3、5、6层的加速度响应，同时为了消除位移漂移现象，还观测第2层位移，提高识别结果的准确性。所有的加速度及位移的观测均考虑了观测噪声。观测噪声为均方根是相应的信号均方根值的5%，均值为0的高斯宽带白。结构参数识别结果以及识别误差如表1所示。通过识别结果的误差分析可以看出，对结构参数以及非线性迟滞参数的识别都具有良好的准确性，结构刚度识别误差不超过2%，非线性迟滞参数识别误差不超10%，从而验证了所提的UKF-UI方法对识别结构参数以及非线性迟滞参数的有效性。
图2～图5分别为第3层和第4层的位移、速度识别值与真实值对比图，图6为外激励识别值与真实值对比图。对比可知，所提UKF-UI方法能有效识别其他观测的结构位移、速度，以及未知的外部激励。图7～图8为第4层层间迟滞曲线的识别值与真实值对比。通过非线性力与对应的线性力的数值比较，可发现所提UKF-UI方法适用于对强非线性系统的识别。
表1 未知激励下6层迟滞剪切框架识别结果(白噪声激励下)
Table 1 Identification of a 6-story hysteretic frame under unknown excitation (white noise)
真实值识别值层数k/(kN/m)c/(N·s/m)β/(s2/m2)γ/(s2/m2)k/((误k N差/m))c/((N误·差s/)m) β(/(误s2差/m)2 )γ/((误s2/差m)2)1 240 200 800 400 243.22 187.87 877.87 411.12(1.34%)(-6.06%)(9.73%)(2.78%)2 240 200 800 400 238.65 212.43 836.92 427.60(-0.56%)(6.22%)(4.62%)(6.9%)3 240 200 800 400 237.16 213.11 860.95 420.06(-1.18%)(6.55%)(7.62%)(5.02%)4 240 200 800 400 238.69 192.59 836.12 394.65(-0.54%)(-3.71%)(4.52%)(-1.33%)5 240 200 800 400 240.60 209.45 787.05 396.78(0.25%)(4.73%)(-1.62%)(-0.81%)6 240 200 800 400 240.42 186.55 834.63 377.40(0.17%)(-6.73%)(4.33%)(-5.65%)
2.2 地震激励
为更多地验证所提方法的有效性，采用EL-Centro波(PGA=0.2g)地震激励作用下6层剪切框架进行算例验证，6层框架均考虑为 Bouc-Wen滞回模型的非线性结构，其运动方程为：
图2 第3层位移对比图
Fig.2 Comparison of the identified 3rd floor displacement
图3 第3层速度对比图
Fig.3 Comparison of the identified3rd floor velocity
图4 第4层位移对比图
Fig.4 Comparison of the identified 4th floor displacement
图5 第4层速度对比图
Fig.5 Comparison of the identified 4th floor velocity
式中：{I}为单位向量；
为地震加速度；z(t)为层间滞回位移向量。式(25)中，βi、γi、ni为Bouc-Wen滞回参数，此算例中，βi=400s2 /m2；γi=200s2 / m2；ni= 2，其他结构参数分别为：单元质mi=6 00 kg，单元线性刚度ki=2 40 kN/m，阻尼比ci= 0 .2 kN· s/m，i= 1 ,2,⋅⋅⋅,6。
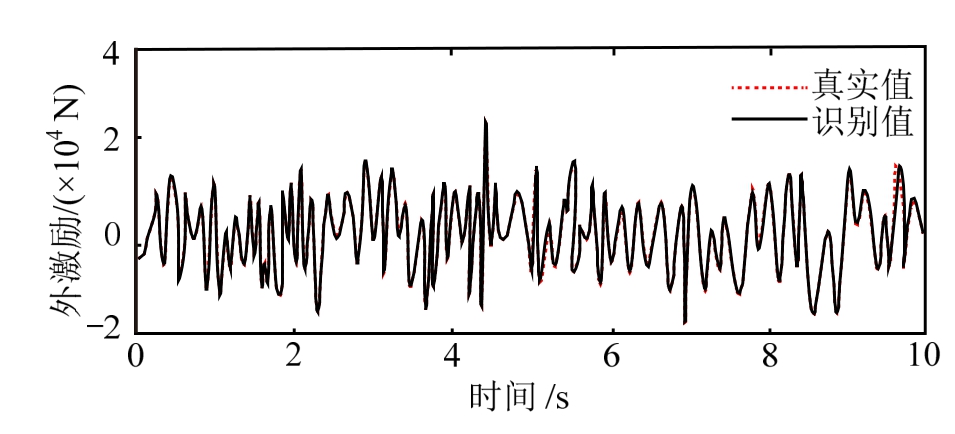
图6 外激励识别对比图
Fig.6 Comparison of identified external excitation
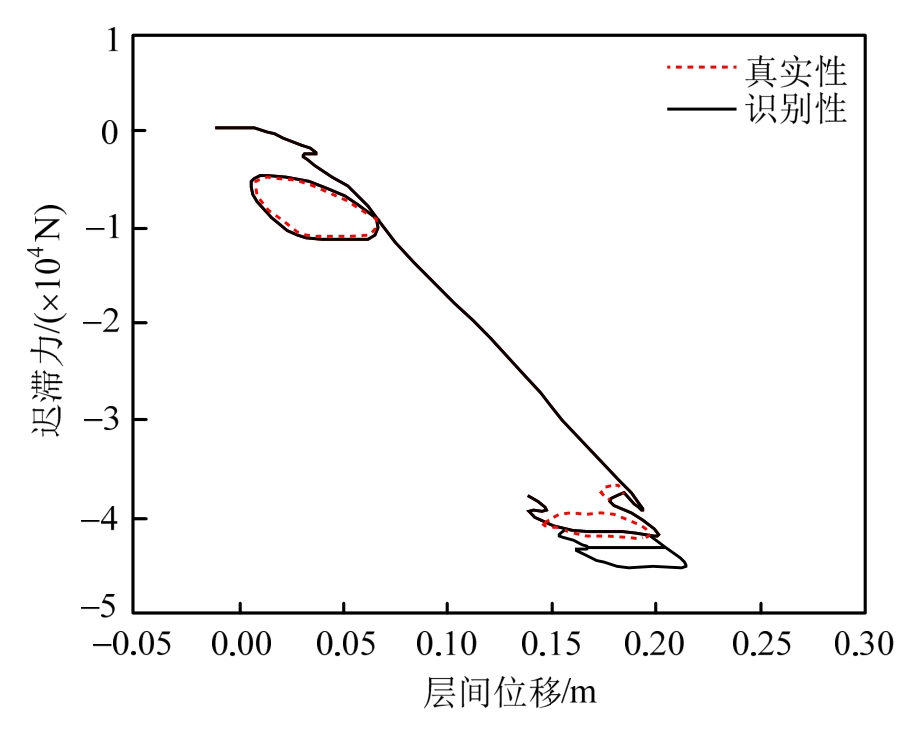
图7 非线性迟滞力对比图
Fig.7 Comparison of story nonlinear restoring force
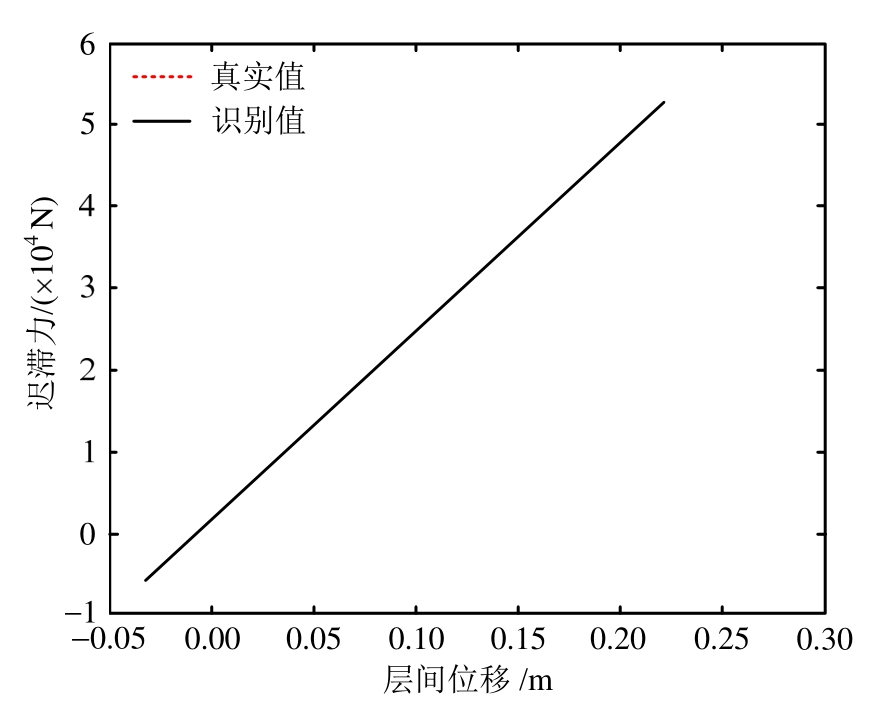
图8 线性力对比图
Fig.8 Comparison of story linear restoring force
部分观测为观测框架第1、2、3、6层加速度，以及第4层位移。算例中观测值均考虑了均方根是相应的信号均方根值的 5%的观测噪声影响。结构参数计算结果及误差如表2所示。由表2可知，提出的UKF-UI方法能有效识别结构参数及非线性迟滞参数。结构参数的识别误差在接受范围之内，其中刚度识别误差在 5%以内，阻尼比以及非线性迟滞参数识别误差不超过10%。
表2 未知激励下6层迟滞剪切框架识别结果(地震激励)
Table 2 Identification of a 6-story hysteretic frame under unknown earthquake ground motion
?
图9和图10分别为第2层位移、速度识别结果比较图，图11为未知激励识别结果比较图。由图可知，提出的方法能有效地识别为观测的结构位移、速度以及未知的外部激励。
图9 第2层位移对比图
Fig.9 Comparison of the identified 2nd floor displacements
图10 第2层速度对比图
Fig.10 Comparison of the identified 2nd floor velocities
图11 外激励识别对比图
Fig.11 Comparison of identified external excitation
图12给出了第5层的非线性迟滞力识别结果比较图，线弹性力识别结果如图13所示。通过非线性力与对应的线性力的数值比较，亦可看出此方法在地震荷载作用下能较好识别迟滞力，解决强非线性系统识别的问题。
由参数识别结果以及对比图可知，本文所提出的UKF-UI方法对于未知激励下的强非线性系统有很好的识别效果，能在部分观测并且考虑观测噪声情况下，同时识别未知激励及强非线性系统结构参数。
图12 非线性迟滞力对比图
Fig.12 Comparison of story nonlinear restoring force
图13 线性力对比图
Fig.13 Comparison of story linear restoring force
3 结论
传统的 UKF方法需要已知外激励，从而限制了使用范围。目前关于未知激励下 UKF的方法研究尚且不足。本文提出未知激励作用下强非线性系统的识别方法(UKF-UI)，在传统无迹卡尔曼滤波方法的基础上推导了UKF-UI的算法方程，通过非线性方程求解方法，求得未知外部激励。融合部分加速度观测和位移观测数据，以消除识别位移结果漂移的现象。目前已有的文献中，鲜有类似的方法。因此提出的方法具有创新性。
本文通过非线性力滞回模型算例验证了此方法在识别强非线性系统以及外部激励的有效性。更进一步，本文所提出的UKF-UI方法将来可进一步应用于复杂结构的识别，通过将子结构之间的作用视为未知激励，对子结构系统进行识别。
本文中，采用数值算例对提出的UKF-UI方法进行验证。今后还需进一步开展试验验证工作，更好验证提出的方法的正确性。
[1]Yun C B, Shinozuka M.Identification of nonlinear structural dynamic systems[J].Journal of Structural Mechanics, 1980, 8(2): 187―203.
[2]Noël J P, Kerschen G.Nonlinear system identification in structural dynamics: 10 more years of progress[J].Mechanical Systems and Signal Processing, 2017, 83:2―35.
[3]李杰, 陈隽.子结构物理参数识别与输入地震动的复合反演研究[J].振动与冲击, 1998, 17(1): 58―62.Li Jie, Chen Jun.Study on composite inversion of ground motion and sub-structural parameter identification[J].Shock and Vibration, 1988, 17(1): 58―62.(in Chinese)
[4]陈隽, 史凯.高层建筑损伤识别中的补偿算法[J].振动与冲击, 2002, 21(2): 24―27.Chen Jun, Shi Kai.Compensation method for damage detection of tall buildings[J].Shock and Vibration, 2002,21(2): 24―27.(in Chinese)
[5]刘以龙, 刘杰, 刘江南.基于子结构分析的动态载荷和模型参数复合反演研究[J].机械强度, 2013, 35(5):553―558.Liu Yilong, Liu Jie, Liu Jiangnan.Research on composite inversion of dynamic loads and structural parameters based on sub-structure analysis[J].Journal of Mechanical Strength, 2013, 35(5): 553―558.(in Chinese)
[6]Hoshiya M, Saito E.Structural identification by extended Kalman filter[J].Journal of Engineering Mechanics-ASCE, 1984, 110(12): 1757―1771.
[7]Julier S J, Uhlmann J K, Durrant-Whyte H F.A new approach for filtering nonlinear systems[C]// Proceeds of American Control Conference, Seattle, WA, USA: IEEE,1995, 3: 1628―1632.
[8]Julier S J, Uhlmann J K.A new extension of the Kalman filter to nonlinear systems[C]// Proceeds of the 11th International Symposium on Aerospace/Defense Sensing,Simulation and Controls.Society of Photo-optical Instrumentation Engineers, Orlando, Florida, USA: 1997:182―193
[9]梅竹, 吴斌, 杨格.钢筋混凝土结构材料本构模型参数的在线识别[J].工程力学, 2016, 33(7): 108―115.Mei Zhu, Wu Bin, Yang Ge.Online parameter identification of concrete constitutive model[J].Engineering Mechanics, 2016, 33(7): 108―115.(in Chinese)
[10]张纯, 陈林, 宋固全, 等.基于l1正则化无迹卡尔曼滤波的结构损伤方法[J].工程力学, 2017, 34(8): 76―84.Zhang Chun, Chen Lin, Song Guquan, et al.Structural damage identification by unscented Kalman filter with l1 regularization[J].Engineering Mechanics, 2017, 34(8):76―84.(in Chinese)
[11]许斌, 贺佳.部分输入未知条件下结构参数及激励识别[J].土木工程学报, 2012, 6(45): 13―22.Xu Bin, He Jia.Structural parameters and dynamic loading identification with partially unknown[J].Journal of Civil Engineering, 2012, 6(45): 13―22.(in Chinese)
[12]李炜明, 朱宏平, 吴贤国, 等.未知激励下框架结构系统辨识的特征系统实现算法[J].振动与冲击, 2010,29(8): 228―231.Li Weiming, Zhu Hongping, Wu Xianguo, et al.System identification based on experimental responses of a frame structure with unknown inputs[J].Shock and Vibration,2010, 29(8): 228―231.(in Chinese)
[13]Astroza R, Ebrahimian H, Li Y, et al.Bayesian nonlinear structural FE model and seismic input identification for damage assessment of civil structures[J].Mechanical Systems & Signal Processing, 2017, 93: 661―687.
[14]Yang J N, Lin S, Huang H W, et al.An adaptive extended Kalman filter for structural damage identification[J].Structural Control and Health Monitoring, 2006, 13(4):849―867.
[15]雷鹰，江永强.输入输出信息有限观测下的结构损伤诊断[J].振动、测试与诊断, 2012, 32(5): 736―740.Lei Ying, Jiang Yongqiang.Structural damage detection with limited measurements of input and output[J].Journal of Vibration, Measurement and Diagnosis, 2012,32(5): 736―740.(in Chinese)
[16]Liu L J, Su Y, Zhu J J.Data fusion based EKF-UI for real-time simultaneous identification of structural systems and unknown external inputs[J].Measurement,2016, 88: 456―467.
[17]Al-Hussein A, Haldar A.Novel unscented Kalman filter for health assessment of structural systems with unknown input[J].Journal of Engineering Mechanics, 2015,141(7): 04015012.1―04015012.13.
[18]Al-Hussein A, Haldar A.Unscented Kalman filter with unknown input and weighted global iteration for health assessment of large structural systems[J].Structural Control and Health Monitoring, 2015, 23(1): 156―175
[19]Alhussein A, Haldar A.Structural damage prognosis of three-dimensional large structural systems[J].Structure& Infrastructure Engineering, 2017, 13(1): 1―13.
[20]Ding Y, Zhao B Y, Wu B, et al.Simultaneous identification of structure and external excitation with improved unscented Kalman filter[J].Advances in Structural Engineering, 2015, 18(11): 1981―1998.
[21]R.Van der Merwe.Sigma-point Kalman filters for probability inference in dynamic state-space models[D].OR, USA: Oregon Health and Science University, 2004.