求解结构动力方程的逐步积分算法，有显式和隐式之分。显式方法中应用最普遍的算法是中心差分法，但它却是有条件稳定的，时间步长受系统的最高频率控制[1]。而隐式逐步积分算法，一般可以容许更大的时间步长。其中经典的平均加速度方法(梯形法)，在线性领域具有无条件稳定的优异性能[2]。然而，在线性领域得到的无条件稳定性结论并不适用于非线性，在非线性分析中该方法也许会发散[3]。研究者在Newmark-β方法族的基础上引入α参数控制算法数值阻尼特性，抑制高频反应，这便是HHT-α算法，但是该方法仍然不能保证在非线性领域的无条件稳定性[4]。在非线性领域，用经典的谱分析方法判别算法的稳定性失效，Belytschko和 Schoeberle[5]指出离散系统的能量有界是算法保持稳定性的充分条件。研究者从能量角度出发构造算法，Hughes等[6]把能量守恒作为约束条件，采用拉格朗日乘子法强迫系统的能量守恒。1992年，Simo和Tarnow[7]在局部物质点层次离散，实现了精细的能量守恒方法。目前，研究者针对不同单元类型构造相应的能量方法。另一方面，精细时程积分法的提出给动力问题的求解提供了一条新的途径[8]，该方法具有高精度和对线性或部分弱非线性保守系统能量守恒的特点，引起了研究者的兴趣[9-10]。
近年来，共旋技术引起研究者的广泛关注，其引入随单元运动的共旋坐标系，可方便地处理工程领域中的几何非线性问题，兼顾了数值计算的精度和效率。Cris fi eld和Shi[11]针对共旋平面桁架单元提出了能量守恒逐步积分算法。随后，Galvanetto和Cris fi eld[12]实现了针对共旋梁单元的近似能量守恒算法。潘天林等[13-14]将桁架能量方法应用于平面桁架和三维网架计算，结果显示能量方法更加适合结构动力非线性分析，随后提出了桁架单元的能量一致积分方法。对三维情形，Crisfield等[15]对末点和中点两种算法形式进行比较，指出中点公式可以实现近似的能量守恒。Chhang等[16-17]针对平面梁单元提出能量方法，虽然该方法没有增加修正参数，但却近似了应变速度场。
梁单元的另一种建模方式是几何精确梁，该理论首先由 Reissner提出[18]，后经 Simo和 Vu-Quoc完善[19]。几何精确梁是一种 Timoshenko类型的梁单元，放弃了在局部坐标系下的小位移和小转动假设。Simo方法可应用于几何精确梁[20]，该方法先时间离散后空间离散，对弱形式方程在一个时间步长内进行算法近似，实现了离散系统的能量守恒。Nguyen和 Sansour[21]没有采用应变-位移关系定义应变场，而是用应变速度场，提出了几何精确梁的能量-动量守恒算法。
本文将以虚功原理为基础，开发二维共旋Timoshenko梁单元的能量守恒逐步积分算法。该算法较传统算法而言，在具备二阶精度的前提下，能够实现离散系统的能量守恒，保证算法在非线性领域的数值稳定性。最后，针对算法编制相应的分析程序，将通过三个算例，验证该算法的有效性和适用性。
1 能量方法推导
Simo能量方法[20]先进行时间离散，然后进行空间离散。Simo等人对动力方程的弱形式进行时间离散后，随即利用试函数的任意性证明其方法能量守恒。这种做法的问题在于，有限元空间离散实际上限制了试函数的任意性，也就是说证明能量守恒所选取的特定试函数可能与有限元离散所采用的形函数不一致，从而导致能量守恒的失效。为了避免这一问题，本文的能量守恒方法按有限元常用的做法，先进行空间离散，然后进行时间离散。
1.1 空间离散
整体坐标系下杆单元节点位置可表示为：
式中：XP、XQ分别表示单元节点位置；θP、θQ分别表示单元节点转角位置；θ3是为了提高计算精度而添加的单元中部转角。局部坐标系下单元的未知量如下：
式中：变量下标含“L”表示该变量定义在局部坐标系中；uL表示单元的轴向变形。局部坐标系随单元的运动而运动，变形前后单元构型如图1所示。
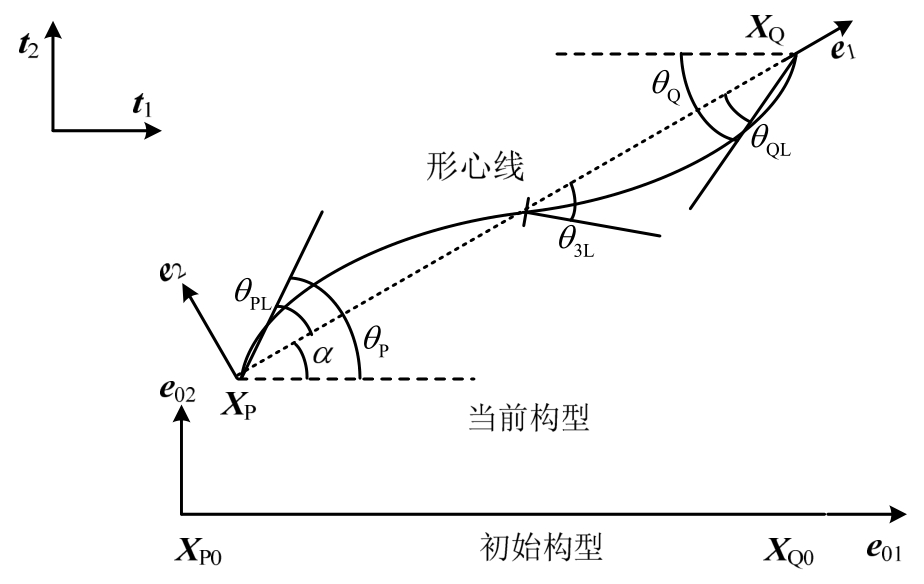
图1 单元构型
Fig.1 Configuration of element
整体未知量与局部未知量之间的关系如下：
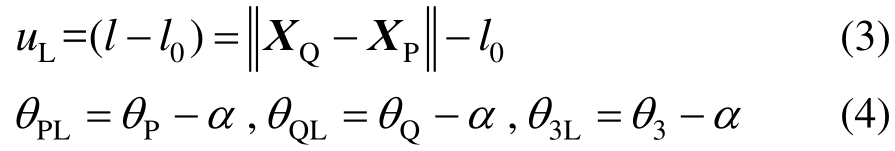
式中：l0表示单元的初始长度；l表示变形后的单元长度；α表示单元的刚体转角，按式(5)计算：
式中，XPQ=XQ-XP，e01、e02表示局部坐标系初始基向量。单元初始倾角能够很容易地被包含进来，在此暂不考虑。整体坐标系基向量用t1、t2表示，局部坐标系的基向量表示如下：
单元的变形在局部坐标系中描述，在局部坐标系下对节点未知量插值获得单元的位移场，采用相关插值，该插值方式见于Zienkiewicz和Taylor书中[22]。轴向变形按式(7)计算：
式中，ξ=2s0 /l0- 1，s0表示对单元初始构型的参数化，s0 ∈[0 ,l0]。转角插值如下：
截面形心线的横向位移按式(9)计算：
式(7)、式(8)、式(9)定义了单元的位移场。由此可以得出整体坐标系下单元形心线的位置X和截面转角θ如下：
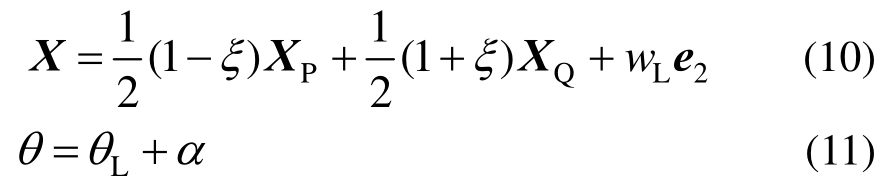
从式(10)可以看出，单元内部位置与节点位置的关系呈非线性，可称之为非线性插值。
在定义位移场之后可导出单元的广义应变场，广义应变定义在初始构型上，轴向应变按式(12)计算：
曲率可表示为：
在局部坐标系下剪切应变、截面转角及形心线斜率的关系见图2，据此计算剪切变形为：
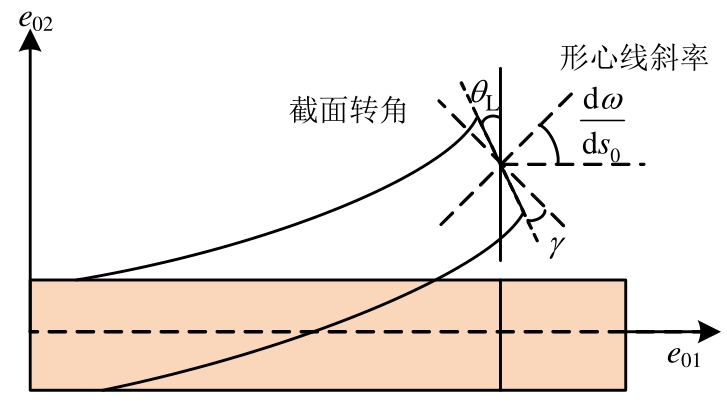
图2 局部变形关系
Fig.2 Local deformation relationship
与上述三种广义应变量功共轭的截面内力分别为截面轴力N、截面弯矩M 、截面剪力Q，对应的内力虚功如下：
式中广义应变的变分可表示如下：
其中：
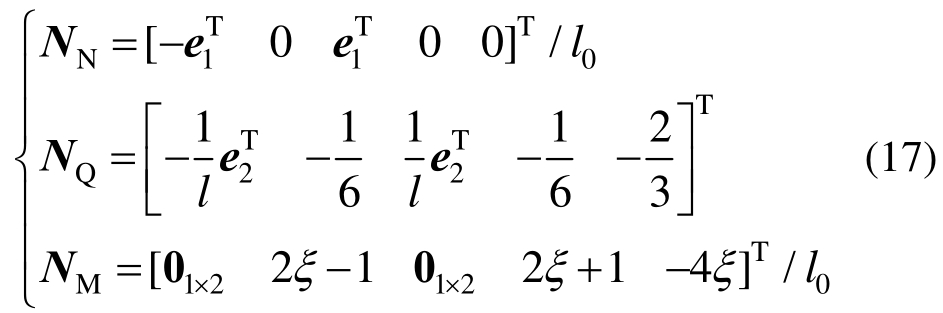
式(16)推导时需要用到单元长度和刚体转角变分，按式(18)计算：
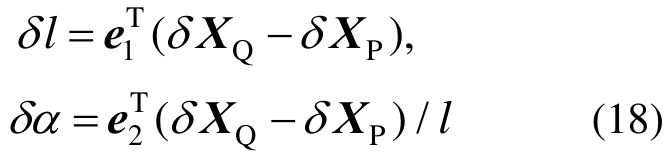
惯性力的虚功可直接在整体坐标系下计算：
式中：v、ω分别表示速度和角速度；t表示时间；A0、I0分别表示截面面积和截面惯性矩；ρ0表示材料密度，式(19)推导过程中需要用到方向向量的变分关系δe2=-e1δα。
虚功方程写为：
由虚位移的独立性和任意性，可获得节点的等效平衡方程：
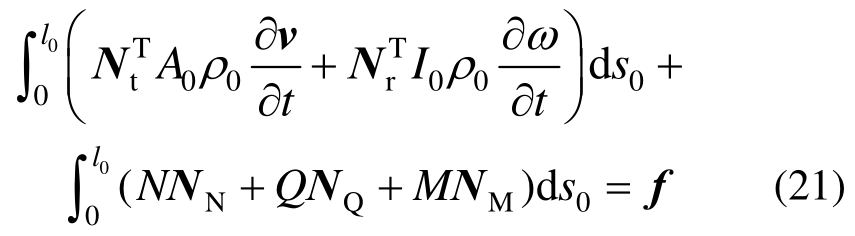
其中：
式中，f表示节点力。式(21)中没有考虑单元中的分布力和分布弯矩，节点位置的变分转置后乘以
和
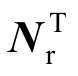便是δX T 和δθ。将式(21)组装之后，可以得到结构整体的等效节点平衡方程：
式中，Fine、Fint、Fext分别表示惯性力、内力和外力向量。
1.2 时间离散
对空间离散之后的等效节点平衡方程式(21)进行时间离散。在梯形法的基础上，为保证时间离散之后系统的能量守恒，在方程中引入多参数修正[23]：
式(24)为微分方程的差分格式，式(25)为运动量之间的假设，假定在时间步长Δt内外荷载不变。式中角标βine、β1、β2表示参数，NN,β1按式(26)计算：
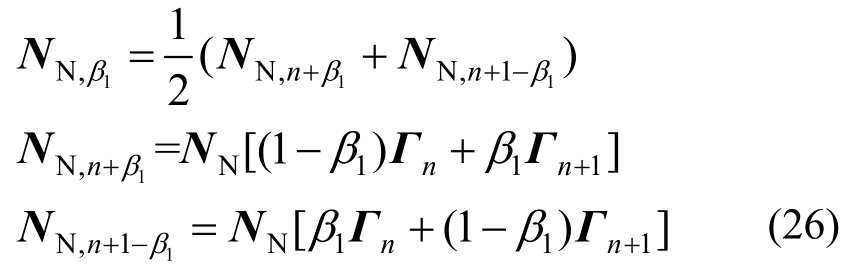
式(26)亦适用于Nt,βine 、NQ,β2。惯性力项的修正系数按式(27)确定：
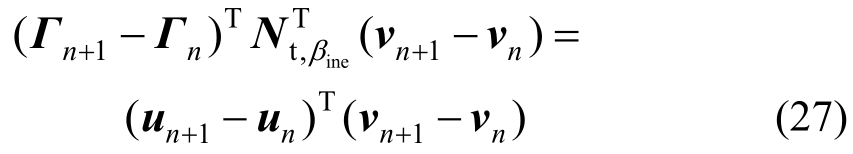
Nr与当前构型无关，无需构造上述格式。内力项修正系数按式(28)：
曲率项因曲率与节点转角关系为线性，无需修正。式(28)可进一步简化为：
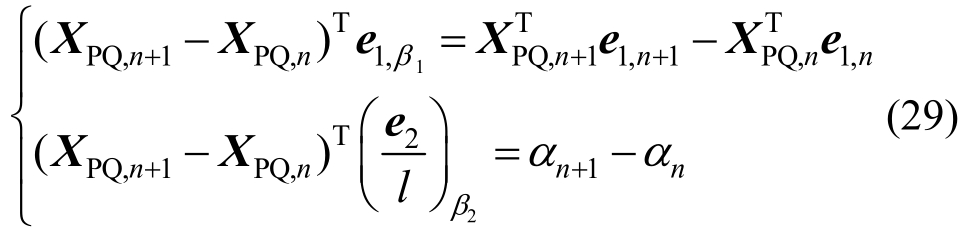
式(24)点乘节点位移增量之后，将式(25)、式(27)和式(28)代入之后得到式(30)：
式中，Nβ、Mβ和Qβ可由截面上纤维的应力数值积分得到。参数β按式(31)确定：
式中，σβ和τβ表示正应力和剪应力，其表达式与式(26)类似，不同之处是以应变为未知量而非Γ。材料线弹性时，对任意β式(31)均成立，可直接取β= 0 .5。
1.3 等效刚度矩阵
式(24)、式(25)以及参数方程联立后是关于节点位置坐标Γn+1和参数的非线性代数方程组，采用嵌套迭代思路求解，即外层迭代求节点位置坐标，内层迭代求解参数。求解时需要线性化列式，对惯性力项和内力项关于节点未知量求偏导获得等效刚度矩阵，可分为三项：质量刚度、材料刚度和几何刚度。为了便于推导，首先在单元层次线性化，然后组装成整体的刚度矩阵。
考虑集中质量时质量矩阵为一对角阵，如下所示：
式中：m表示质量；I表示转动惯量。考虑一致质量矩阵时，因为单元内部位移、速度与节点位移、速度关系的复杂性，需作简化处理，不考虑局部坐标系下截面转角对横向位移的贡献。将质量矩阵表示如下：
其中：
质量刚度为：
内力的雅克比矩阵为：
式(36)可写为：
可分为几何刚度和材料刚度，几何刚度如下：
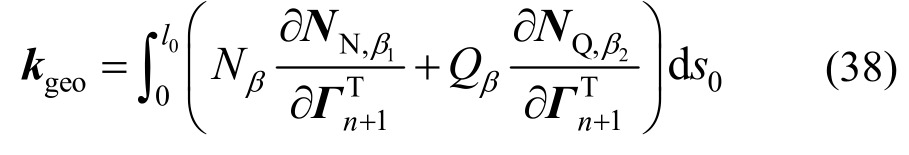
其中：
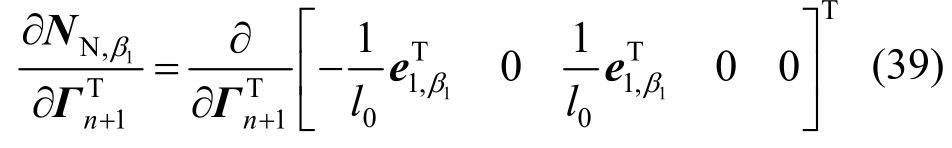
由关系式δe1 =e2δα、式(18)可得：
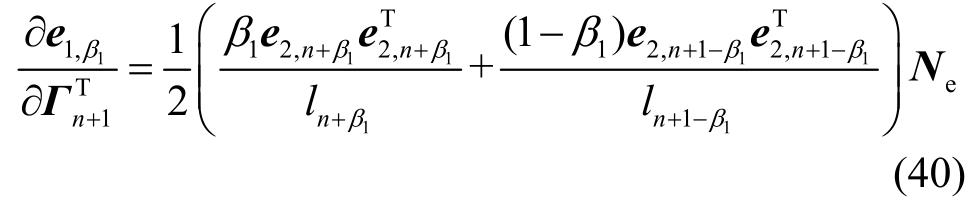
其中：
剪力项几何刚度矩阵推导与上类似，其中：
材料考虑为线性时，材料刚度可以写为：
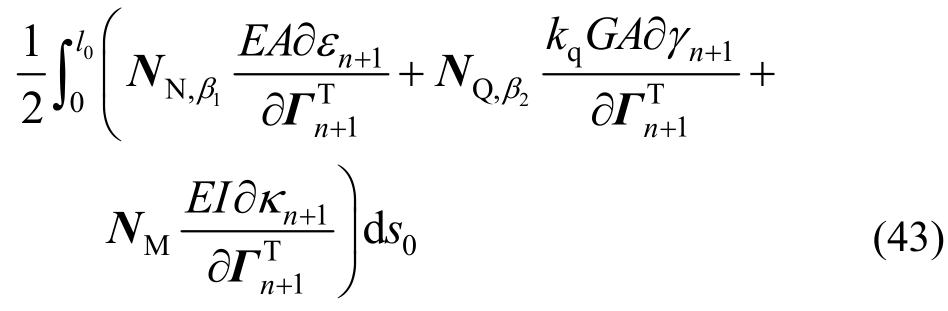
材料非线性时，推导与式(43)类似，只是需采用数值积分形式。
1.4 修正参数求解
在嵌套求解代数方程的每一迭代步中，求解单元刚度矩阵和节点内力时需要先迭代求解参数。以式(29)第二式为例进行说明，取函数如下：
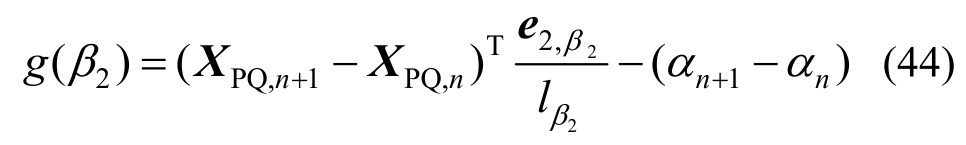
数值模拟表明，在一个计算步内，单元的刚体转角增量和轴向伸长增量在一定范围内时，式(44)所示函数在区间(0,1)为一凸函数，关于β2=0.5对称，有两个零点。用 Newton-Raphson迭代法很容易得到零点对应的参数值，迭代格式如下：
选择上次迭代之后收敛的β作为本次迭代的初始值，可大幅度减少迭代计算量。
本文方法求解结构非线性动力响应时的计算过程与平均加速度等方法类似，区别在每一个迭代步中需要求解参数β。因此，在相同时间步长下，计算量较后二者大。本文方法在一个时间步长内的求解流程如图3所示：
图3 计算流程图
Fig.3 Flowchart of calculation
2 Simo能量守恒算法
Simo方法适用于空间离散时插值函数为线性插值的情形[20]，并不适用于本文。为了便于说明，将其在二维几何精确梁中的应用简单推导如下。弱形式方程经时间离散后，可得：
式中：A0为截面面积；I0为截面惯性矩；ρ0为密度；v为平动速度；ω为角速度；η和φ表示试函数。F表示局部框架下的截面力；M表示截面弯矩；g表示单元上的分布力；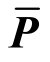
表示节点力，“-”表示该变量为节点处的变量；x表示形心线在整体坐标系中的位置；s0表示对初始单元弧长的参数化；变量下标“n+1/2”表示取n时刻和n+1时刻该变量的平均值；Λ表示对单元截面方向的建模，表达式如下：
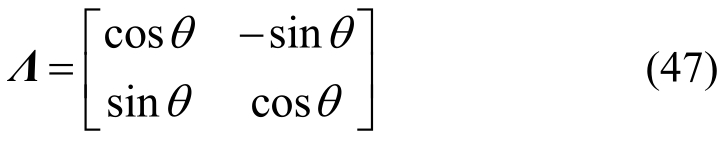
式中，θ表示截面方向，
Det(⋅)表示矩阵的行列式，T90表示θ=π/2时的Λ矩阵。
空间离散时Simo方法插值形式如下：
式(48)中
分别为节点位移增量和节点相对转角增量。式(48)中的插值函数Nu和Nθ并不是
的函数，可称之为线性插值函数，式(46)经空间离散之后点乘节点位移增量即是离散系统能量守恒的表达式。从式(10)可以看出，本文插值形式为非线性插值，这有别于 Simo所采用的插值格式，此时不能采用Simo方法。
值得注意的是，式(48)第二式中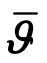
的表达式为：
式中，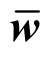
表示节点角速度，转动项的时间离散表达式化简后如下：
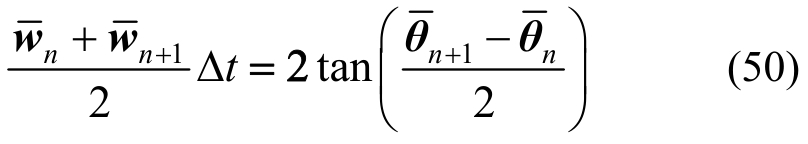
式中，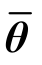
表示节点转角，可以看出相邻时刻节点的角速度平均值乘以时间步长并不等于相邻时刻节点的转角差。在二维情况下，结构作用有常弯矩时(此时物理系统的能量是守恒的)，弯矩乘以对应节点的
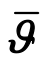后并不等于该弯矩所做功，此时Simo方法无法保证离散系统的能量守恒。在这一情况下导致能量不守恒的根本原因是空间离散限制了证明能量守恒时试函数选取的任意性。
3 数值算例
本部分通过三个算例验证算法的性能，计算程序平台为MATLAB。
3.1 悬臂梁自由振动(材料线弹性)
悬臂梁长2.5 m，宽0.1 m，高0.2 m。弹性模量 200 GPa，泊松比 0.3，剪切因子 5/6，密度ρ=7800 kg/m3。初始条件为节点的速度激励，平动速度按线性分布，如图4所示。结构划分为5个单元，质量矩阵按式(33)选取。计算时长1 s，时间步长0.002 s。采用位移控制，位移残差范数为10-10。
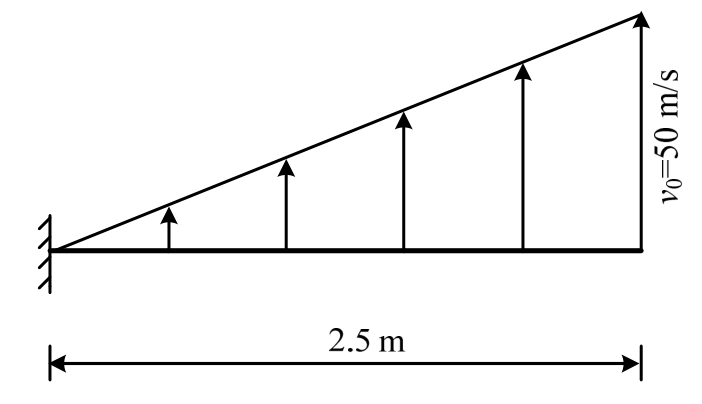
图4 梁初始速度
Fig.4 Initial velocity of beam
在计算中，平均加速度法因发散导致计算失败，隐式中点法也存在发散迹象，而本文方法计算结果稳定，见图5。继续加大时间步长，本文方法依然能够保证稳定，见图6。图7显示出平均加速度法和隐式中点方法能量均不守恒，本文方法很好地保证了系统的能量守恒。
图5 端点竖向位移
Fig.5 Vertical displacement of the beam endpoint
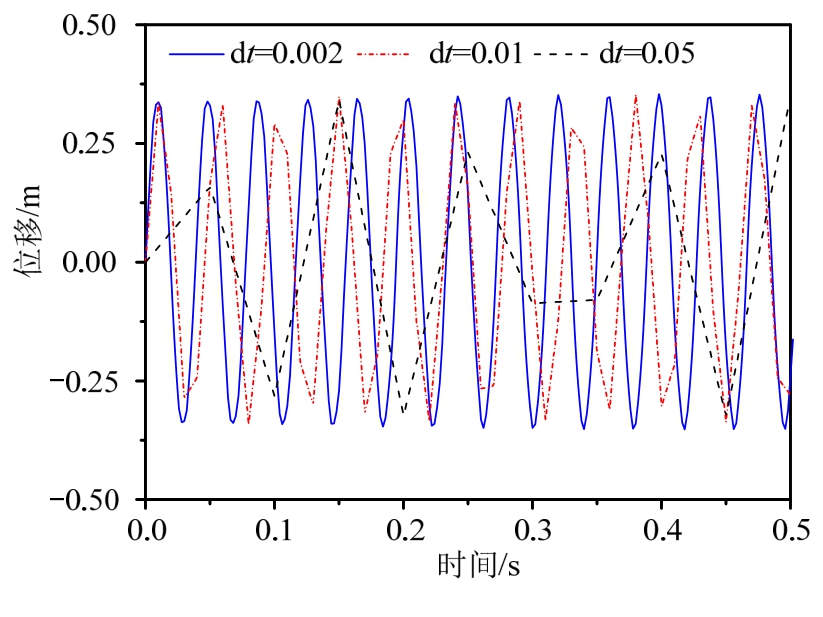
图6 不同时间步长下计算比较
Fig.6 Results comparison of different time step
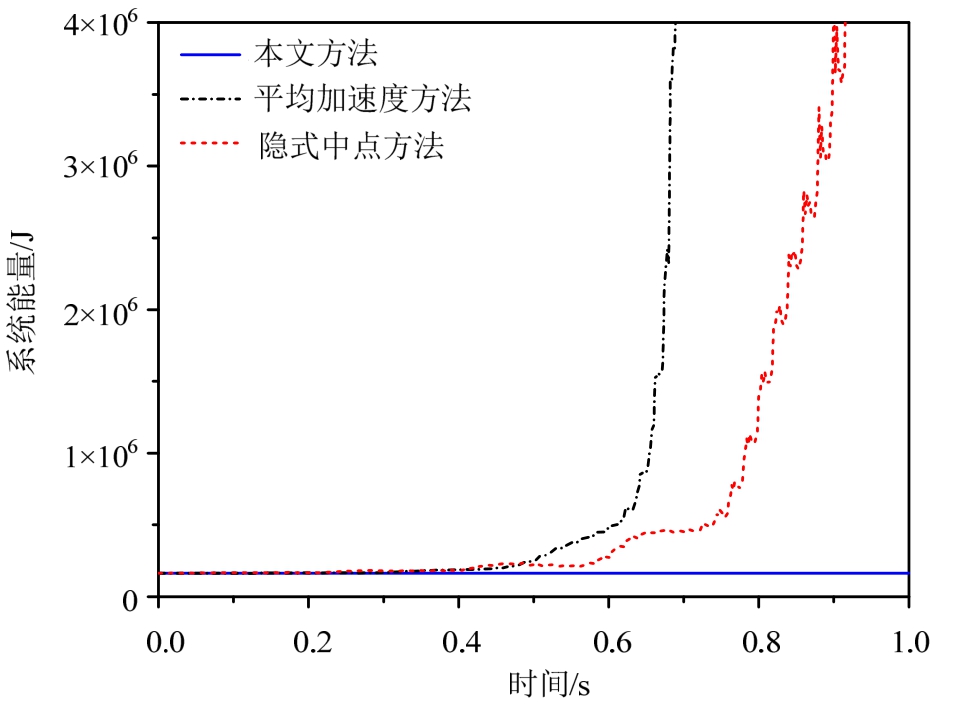
图7 系统能量比较
Fig.7 Comparison of system energy
3.2 固端梁自由振动(材料弹塑性)
固端梁尺寸与上例相同。弹性模量 200 GPa，泊松比0.3，屈服应力400 MPa，屈服后模量为弹性模量的1%。剪切因子5/6，剪切按弹性考虑。梁单元划分为6个单元，中间节点质量500 kg，初始竖向速度 5 m/s，每个单元三个积分点，梯形积分，纤维沿截面高度方向划分为 10层。只考虑轴力弯矩耦合，不考虑弯矩剪力耦合。计算时长 0.15 s，时间步长0.0005 s。
计算结果显示，本文方法与平均加速度方法竖向位移计算结果并无太大差异，但本文方法能够实现系统的能量与塑性耗能的总和不变，见图 8、图9。在累加计算总能量增量时，按式(51)计算与正应变相关的应变能和塑性耗能增量：
式中，在拐点(折返点，即此处应变方向发生改变)处理上认为加载(或卸载)。从严格意义上讲，本文方法应用于弹塑性结构时应称为能量一致积分算法。
图8 中点竖向位移
Fig.8 Vertical displacement of the beam endpoint
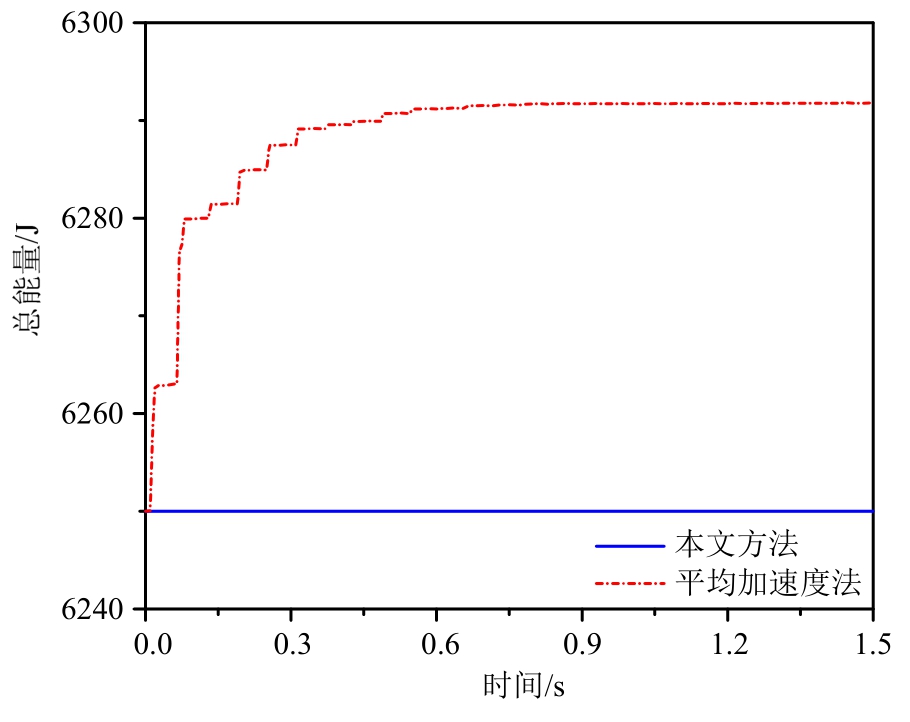
图9 总能量
Fig.9 Total energy
3.3 简支梁受迫振动
简支梁尺寸、材料信息与算例1相同。只在梁中点考虑质量，平动质量 1000 kg，转动惯量为100 kg·m2。在梁中点作用竖向荷载500 kN和外弯矩 5000 kN·m。将梁划分为 6个单元，计算步长为0.002 s，计算时长0.4 s，采用位移增量范数和节点残差力范数作为收敛准则，取值分别为 10-10和10-2。在本算例中，本文方法和Simo方法每个单元均取6个自由度，不在单元内部设置自由度。
本文方法平均迭代步数4.24步，Simo方法平均迭代步4.685步，迭代步上本文方法略优于Simo方法。保守体系的能量可表示为动能、外力势能及应变能之和，设初始状态外力势能为 0，可计算出系统能量的变化，见图10。在本算例中，本文方法可以实现系统的能量守恒，而 Simo方法不能精确地实现能量守恒。
图10 系统能量对比
Fig.10 Comparison of system energy
4 结论
本文从能量角度出发，采用多参数修正方法，实现了 Timoshenko梁单元的能量守恒逐步积分算法。具体结论如下。
(1)本文方法与平均加速度法和隐式中点法相比能够保证弹性动力系统的能量守恒，因而具有更优的数值稳定性。当考虑材料塑性时，本文方法能够保证外力做功增量等于系统能量增量与塑性耗能增量之和。
(2)本文方法适用于共旋Timoshenko梁单元，而此时Simo方法并不适用。在二维情况下与Simo方法相比，本文方法在保守外弯矩作用时仍能保证离散系统能量守恒。
[1]Crisfield M A, Remmers J J, Verhoosel C V.Nonlinear finite element analysis of solids and structures[M].Chichester: John Wiley & Sons, 2012: 144―148.
[2]Newmark N M.A method of computation for structural dynamics[J].Journal of the Engineering Mechanics Division, 1959, 85(3): 67―94.
[3]Crisfield M A, Shi J.An energy conserving co-rotational procedure for non-linear dynamics with finite elements[J].Nonlinear Dynamics, 1996, 9(1): 37―52.
[4]Hilber H M, Hughes T J R, Taylor R L.Improved numerical dissipation for time integration algorithms in structural dynamics[J].Earthquake Engineering &Structural Dynamics, 1977, 5(3): 283―292.
[5]Belytschko T, Schoeberle D.On the unconditional stability of an implicit algorithm for nonlinear structural dynamics[J].Journal of Applied Mechanics, 1975,42(4): 865―869.
[6]Hughes T J R, Caughey T K, Liu W K.Finite-element methods for nonlinear elastodynamics which conserve energy[J].Journal of Applied Mechanics, 1978, 45(6):366―370.
[7]Simo J C, Tarnow N.The discrete energy-momentum method.Conserving algorithms for nonlinear elastodynamics[J].Zeitschrift für angewandte Mathematik und Physik (ZAMP), 1992, 43(5): 757―92.
[8]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报, 1994, 34(2): 131―136.Zhong Wanxie.One precise time-integration method for structural dynamics[J].Journal of Dalian University of Technology, 1994, 34(2): 131―136.(in Chinese)
[9]郭泽英, 李青宁, 张守军.结构地震反应分析的一种新精细积分法[J].工程力学, 2007, 24(4): 35―40.Guo Zeying, Li Qingning, Zhang Shoujun.A new precise integration method for structural seismic response analysis[J].Engineering Mechanics, 2007, 24(4): 35―40.(in Chinese).
[10]Xing Y, Zhang H, Wang Z.Highly precise time integration method for linear structural dynamic analysis[J].International Journal for Numerical Methods in Engineering, 2018, 116: 505―529.
[11]Crisfield M A, Shi J.A co-rotational element/timeintegration strategy for non-linear dynamics[J].International Journal for Numerical Methods in Engineering, 1994, 37(11): 1897―1913.
[12]Galvanetto U, Crisfield M A.An energy-conserving co-rotational procedure for the dynamics of planar beam structures[J].International Journal for Numerical Methods in Engineering, 1996, 39(13): 2265―2282.
[13]潘天林, 吴斌, 郭丽娜, 等.能量守恒逐步积分方法在工程结构动力分析中的应用[J].工程力学, 2014,31(9): 21―27.Pan Tianlin, Wu Bin, Guo Lina, et al.Application of energy conserving step-by-step integration algorithm in dynamic analysis of engineering structures[J].Engineering Mechanics, 2014, 31(9): 21―27.(in Chinese)
[14]潘天林, 吴斌.基于桁架单元的能量一致积分方法[J].工程力学, 2018, 35(10): 1―9.Pan Tianlin, Wu Bin.An energy consistent integration method for truss elements[J].Engineering Mechanics,2018, 35(10): 1―9.(in Chinese).
[15]Crisfield M A, Galvanetto U, Jelenić G.Dynamics of 3-D co-rotational beams[J].Computational Mechanics,1997, 20(6): 507―519.
[16]Chhang S, Sansour C, Hjiaj M, et al.An energymomentum co-rotational formulation for nonlinear dynamics of planar beams[J].Computers & Structures,2017, 187: 50―63.
[17]Chhang S, Battini J M, Hjiaj M.Energy-momentum method for co-rotational plane beams: A comparative study of shear flexible formulations[J].Finite Elements in Analysis and Design, 2017, 134: 41―54.
[18]Reissner E.On one-dimensional finite-strain beam theory: the plane problem[J].Zeitschrift für angewandte Mathematik und Physik (ZAMP), 1972, 23(5): 795―804.
[19]Simo J C, Vu-Quoc L.On the dynamics in space of rods undergoing large motions-a geometrically exact approach[J].Computer Methods in Applied Mechanics and Engineering, 1988, 66(2): 125―161.
[20]Simo J C, Tarnow N, Doblare M.Non-linear dynamics of three-dimensional rods: Exact energy and momentum conserving algorithms[J].International Journal for Numerical Methods in Engineering, 1995, 38(9): 1431―1473.
[21]Nguyen T L,Sansour C,Hjiaj M .Long-term stable time integration scheme for dynamic analysis of planar geometrically exact Timoshenko beams[J].Journal of Sound and Vibration, 2017, 396: 144―171.
[22]Zienkiewicz O C, Taylor R L.The finite element method for solid and structural mechanics (sixth edition)[M].Oxford: Butterworth- heinemann, 2005: 308―311.
[23]潘天林.能量一致积分方法及其在混合试验中的应用[D].哈尔滨: 哈尔滨工业大学, 2016: 63―68.Pan Tianlin.Energy consistent integration Method and its applications to Hybrid testing[D].Harbin: Harbin Institute of Technology, 2016: 63―68.(in Chinese)