复阻尼模型具有每周期能量耗散与外激励频率无关的优点,但其自由振动解中存在发散项,导致时域数值计算结果不能稳定收敛[1-2]。复阻尼模型的时域发散性,是时域运动方程解集本身含有不稳定子集而导致的,故对所有逐步积分算法,均会出现发散现象[3]。损耗因子、地震持续时间等均影响复阻尼模型的时域稳定性,当结构的损耗因子增大时,复阻尼模型的时域计算结果发散程度将增大[4-5];当地震持续时间较长时,复阻尼模型的时域数值计算结果将出现发散现象[6]。在保留复阻尼模型优点的基础上,寻找一种改进复阻尼模型以保证结构的时域计算结果稳定收敛,具有重要意义。
朱镜清和朱敏[7-8]、Kang[9]直接舍弃通解中发散项的计算方法,保证了计算结果的稳定性,但这种直接剔除发散项的做法在数学处理上是不合理的[10-11]。周正华等[12]构造出等效于复阻尼模型的粘弹性阻尼模型;胡海岩[13]采用三参数粘弹性阻尼模型等效复阻尼模型;Reggio和Angelis[14]将Maxwell-Wiechert本构模型等效于复阻尼本构模型;Wang[15]采用Rayleigh阻尼模型等效复阻尼模型,上述等效复阻尼模型均能保证时域计算结果的稳定收敛,但计算过程较为复杂,且存在一定的计算误差。
在复阻尼模型的频域运动方程基础上可得到滞变阻尼模型的时域运动方程,通过将滞变阻尼模型和复阻尼模型进行对比分析,本文发现滞变阻尼模型保留了结构稳态响应时每周期耗散能量与外激励频率无关的优点,同时保证了结构时域计算结果稳定收敛。针对滞变阻尼模型的特点,本文分别提出了滞变阻尼模型的时域理论计算方法和时域数值计算方法。与复阻尼模型的时域数值计算方法相比,滞变阻尼模型的时域理论计算方法和时域数值计算方法可有效避免时域发散现象。同时,滞变阻尼模型的时域理论计算结果和时域数值计算结果与复阻尼模型的频域计算结果近似相等,进一步证明了本文方法的正确性。
1 滞变阻尼模型
复阻尼模型的频域运动方程为
式中:m为结构的质量;k为结构的刚度;η为结构的损耗因子;ϖ为结构的振动频率;X(iϖ)和G(iϖ)分别为x( t)和g( t)的傅里叶变换,G(iϖ)通过复化对偶原则[10]可计算得到![]() 为虚数单位,
为虚数单位,![]()
在复阻尼模型的基础上,为确保由方程(1)得到的传递函数关于正、负激励频率共轭,对阻尼项进行修正,同时剔除右端复化对偶项,可得到滞变阻尼模型的频域运动方程为[16]:
其中:
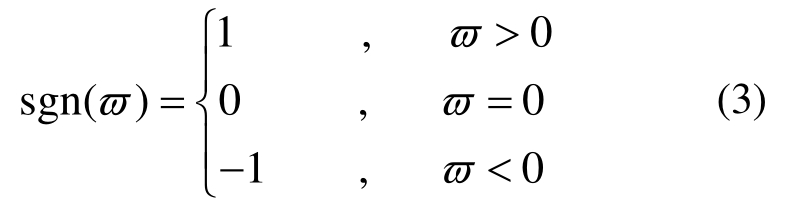
式(2)为基于滞变阻尼理论的单自由度结构频域运动方程。对式(2)进行傅里叶变换,可得到滞变阻尼模型的时域运动方程:
式中,xH(t)为x( t)的希尔伯特变换。
对式(4)进行希尔伯特变换,可得:
式(4)和式(5)合并为:
其中:
基于复阻尼模型的时域运动方程为:
式(6)和式(8)在形式上是一致的。
复化对偶原则为:
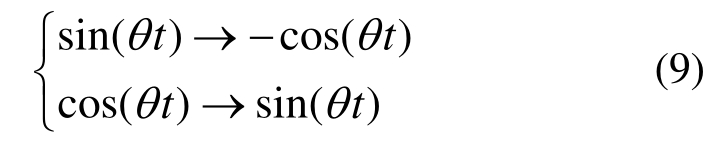
式中,θ为频率。
滞变阻尼模型的转化原则为:
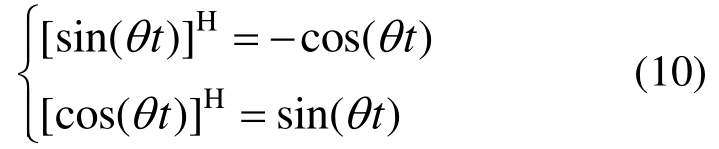
式中:[sin(θt)]H 为 sin(θt)的希尔伯特变换;[cos(θt)]H 为cos(θt)的希尔伯特变换。
由对比可知,式(9)和式(10)是一致的。
设单自由度结构体系在激励频率为θ的谐波作用下,结构的稳态位移响应为:
基于滞变阻尼模型的阻尼力为:
在滞变阻尼模型中,阻尼力与位移的关系与复阻尼模型相同。阻尼力在一个周期内消耗的能量为:
由式(13)可知,每周期阻尼力耗散的能量与外激励频率无关。
综上所述,基于滞变阻尼模型的时域运动方程与基于复阻尼模型的时域运动方程是一致的。基于复阻尼模型的时域运动方程(式(8))自由振动解中存在发散项,而发散项的希尔伯特项是不存在的。滞变阻尼模型在保留复阻尼模型优点的同时,还存在一些差异,即增加了动力响应希尔伯特项必须成立的约束条件。因此,滞变阻尼模型保留了结构稳态响应时每周期耗散能量与外激励频率无关的优点,同时保证了结构时域计算结果稳定收敛。
1.1 单自由度体系的时域理论计算方法
1.1.1 滞变阻尼模型的自由振动响应
基于滞变阻尼模型的单自由度体系自由振动方程为:
式中,ω为结构的无阻尼自由振动频率![]()
采用复平面法求解式(14),假定其解为:
对式(15)进行希尔伯特变换,可得:
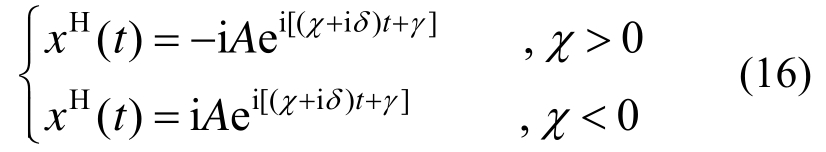
将式(15)和式(16)代入式(14),得:
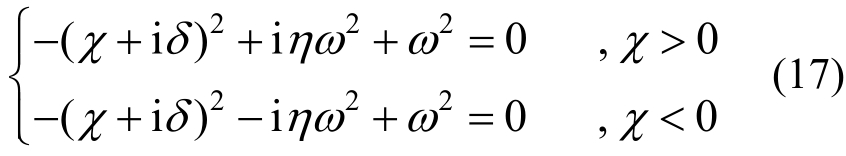
式(17)进一步转化为:
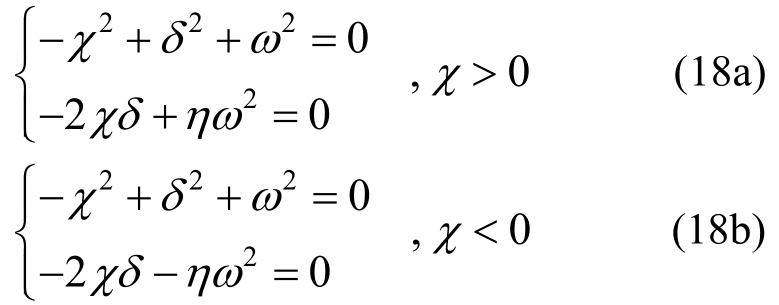
求解式(18),得到χ和δ:
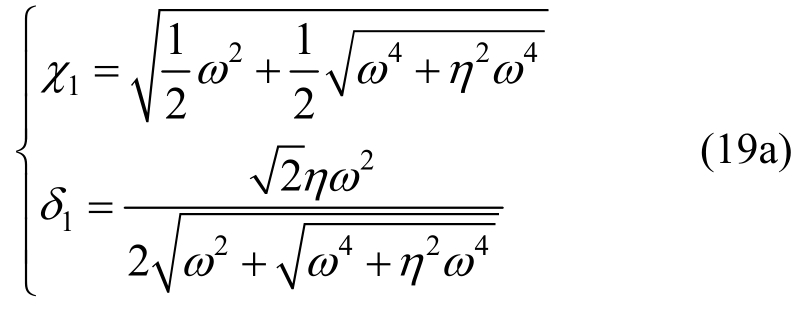
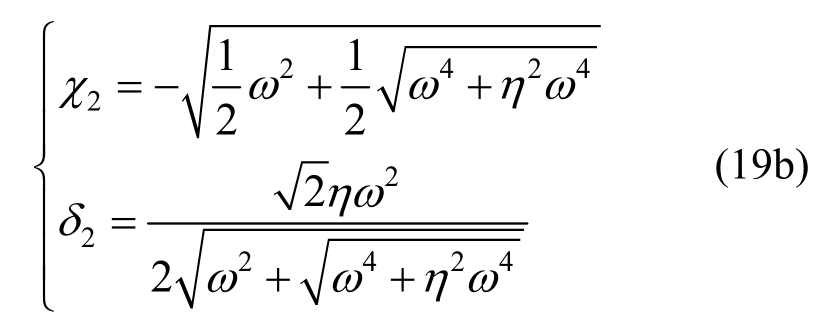
将式(19)代入式(15),得到自由振动解为:
其中:
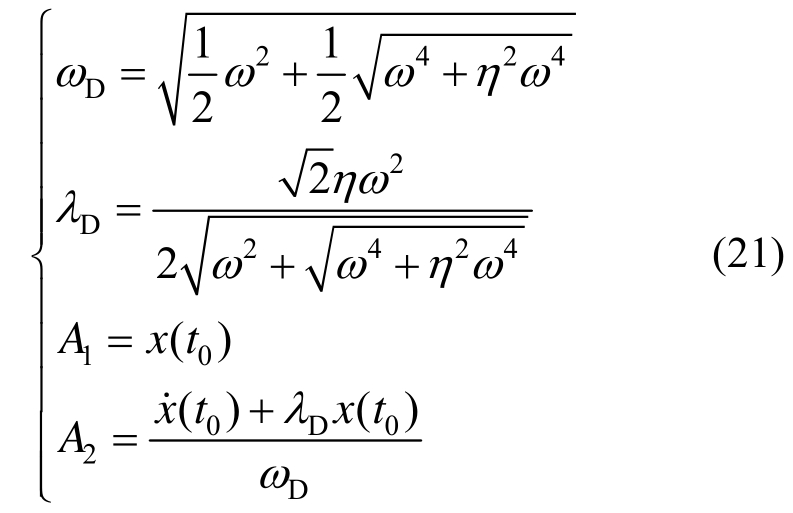
1.1.2 地震作用下滞变阻尼模型的动力响应
地震作用下单自由度体系的时域运动方程为:
地震作用加速度可采用三角级数展开:
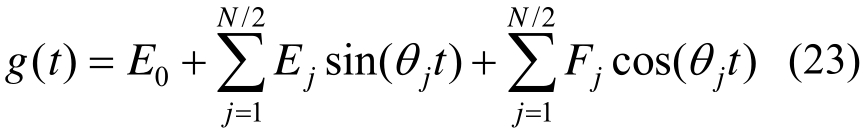
式中:E0为常数;Ej和Fj为三角插值公式系数;θj为谐波频率。
式(22)可转化为:
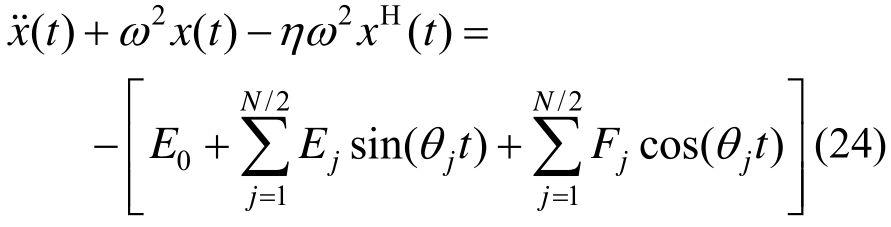
由叠加原理得:
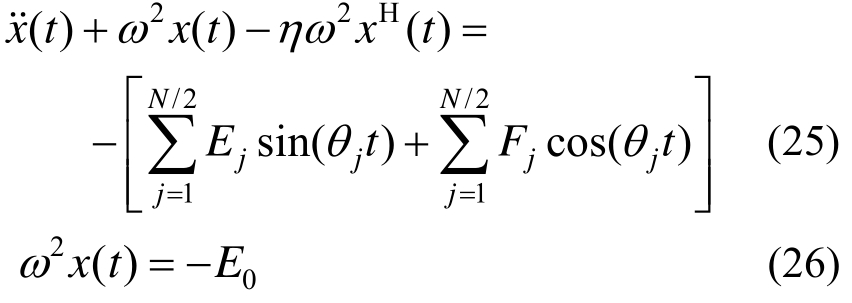
式(25)的特解为:
进一步得:
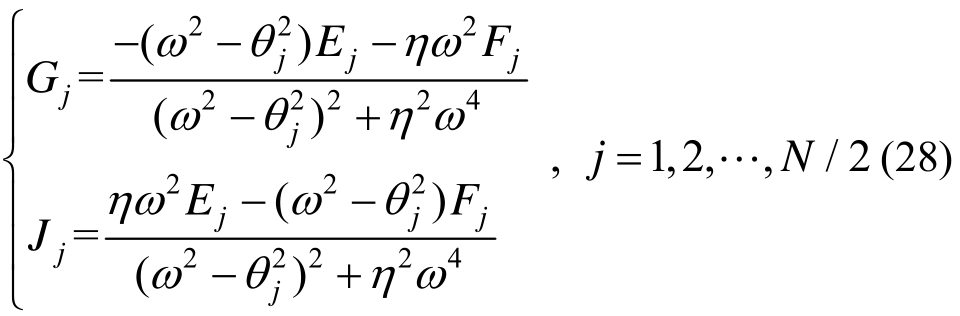
式(26)的特解为:
式(24)的齐次方程通解与自由振动解形式相同,则式(24)的通解为:
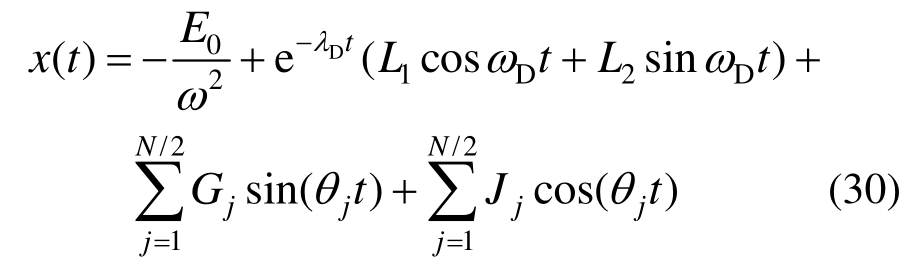
其中:

1.2 单自由度体系的时域数值计算方法
地震作用下滞变阻尼模型的时域方程为:
采用数值积分方法进行计算时,按照时间步长Δt 进行离散,任意时刻可表示为tk=kΔ t(k=0 ,1,2…),利用tk时刻结构的动力响应,计算tk+1时刻结构的动力响应。
结构的振动响应可以由一系列简单谐波叠加表示[17],假定tk时刻和tk+1时刻结构的位移响应是谐波振动响应,可表示为:
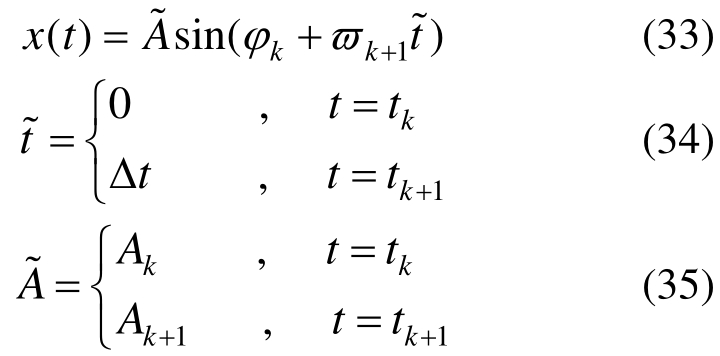
式中:ϖk+1为tk时刻到tk+1时刻结构的振动频率;Ak 为tk时刻结构的瞬时振幅;φk为tk时刻结构的瞬时相位;Ak+1为tk+1时刻结构的瞬时振幅;φk+1为tk+1时刻结构的瞬时相位。
进一步计算出tk时刻结构位移的希尔伯特、结构的速度和加速度,见式(36)。
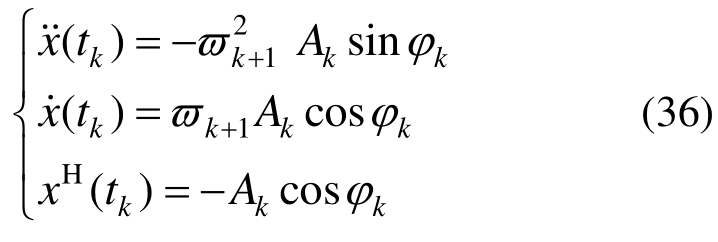
将式(36)代入式(32),可得:
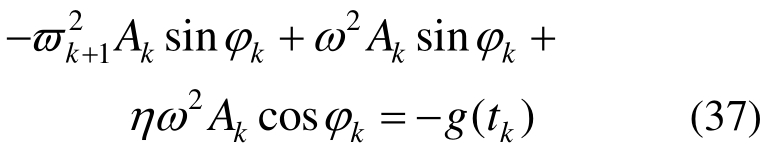
由式(37)计算出tk时刻到tk+1时刻结构的振动频率:
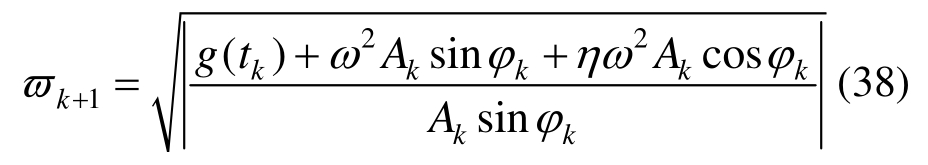
采用常平均加速度法,tk+1时刻结构的速度和位移为[18-19]:
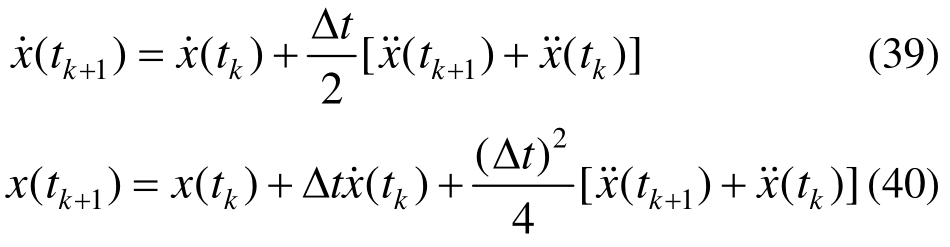
结构位移的希尔伯特变换与速度关系为:
由式(39)和式(41)可得:
将式(40)和式(42)代入式(32),得:
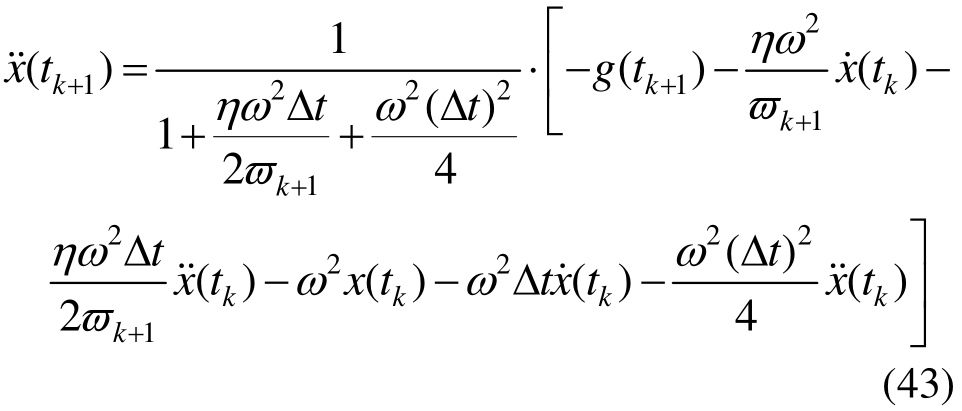
由式(39)和式(40)可计算出![]() 进而得到tk+1时刻的瞬时相位和瞬时振幅:
进而得到tk+1时刻的瞬时相位和瞬时振幅:

重复式(38)~式(44),可完成单自由度体系动力响应的时程迭代计算。
在时域迭代计算过程中,若x ( tk)=0,式(38)无法计算;若ϖk+1=0,式(43)无法进行计算。为此,当ϖk+1=0或x( tk)=0时,可假定tk时刻到tk+1时刻结构的振动频率等于tk-1时刻到tk时刻结构的振动频率,即ϖk+1 =ϖk,以完成时程迭代计算。
关于初值的确定,假定t0时刻振动频率可采用有阻尼自由振动频率:
t0时刻:
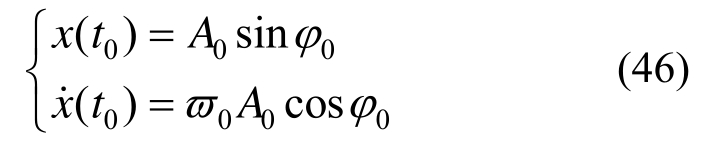
由式(45)和式(46)可得:

综上所述,相比滞变阻尼模型的理论计算方法,滞变阻尼模型的时域数值解增加了计算步骤,但不需要将地震加速度进行三角级数展开。因此,时域数值计算方法的计算量相对较小。
1.3 多自由度体系的时域计算方法
地震作用下基于滞变阻尼模型的多自由度体系时域运动方程为:
式中:M为结构质量矩阵;K为结构刚度矩阵;I为与地震动输入有关的向量(N×1),与g( t)方向相同的位移自由度元素为1。
对于单一材料结构,ηK为比例矩阵,满足经典阻尼条件。因此式(48)可直接采用模态叠加法进行计算。
对于由质量矩阵、刚度矩阵得到的N个自振频率,对应的振型向量可组装成振型矩阵:
x(t)可由振型向量线性组合表示,即:
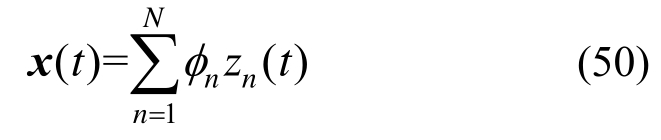
将式(50)代入式(48),可得:
其中:
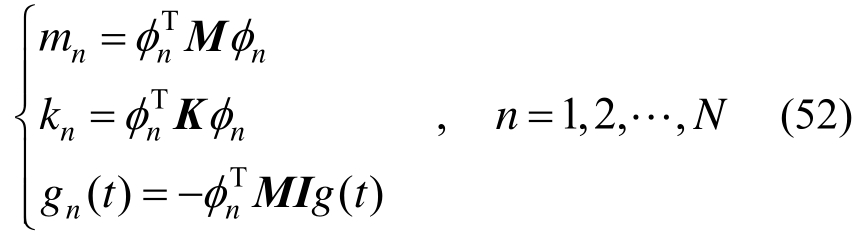
通过模态叠加法,将多自由度体系运动方程解耦得到了单自由度体系运动方程式(51),由1.1节的滞变阻尼模型时域理论解和1.2节的滞变阻尼模型时域数值解计算得到zn ( t)后,即可进而由式(50)计算地震作用下多自由体系的时域计算结果。
2 算例分析
2.1 单自由度体系
2.1.1 自由振动响应
以结构自振频率为4 rad/s,损耗因子为0.1的单自由度体系为例,分别构建模型A和模型B。两种模型仅初始条件不同,模型A的初始位移4 cm,初始速度为6 cm/s,模型B的初始位移0 cm,初始速度为4 cm/s。分别采用滞变阻尼模型的时域理论计算方法(ZJ)和滞变阻尼模型的时域数值计算方法(ZS)计算其自由振动响应,所得结果如图1所示,其中ZS采用的时间步长为0.02 s。
利用希尔伯特变换,可得到模型A和模型B由不同方法计算的位移响应瞬时频率,与自由振动响应的瞬时频率理论值(ZD)对比,如图2所示。理论上,模型A和模型B的自由振动响应仅包含一种频率,即有阻尼自由振动频率,其大小为4.005 rad/s。

图1 不同方法计算的位移响应
Fig.1 The displacement responses of different methods
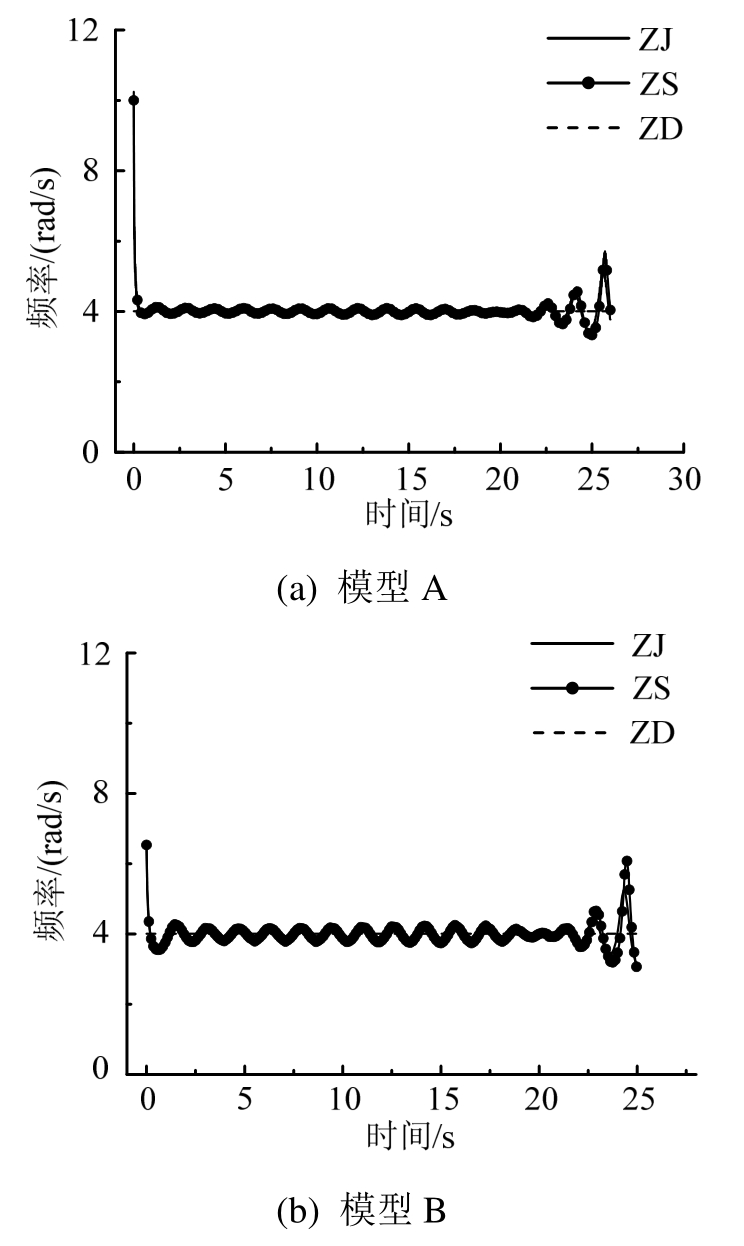
图2 不同方法计算的瞬时频率
Fig.2 The instantaneous frequencies of different methods
由图1可知,ZJ和ZS的自由振动响应结果稳定收敛,且近似相等(图1中两条曲线基本重合),证明了ZJ和ZS的正确性。由图2可知,在0~0.06 s内和 20 s以后,ZJ和 ZS的瞬时频率明显不等于4.005 rad/s,这是由于希尔伯特变换计算瞬时频率时端点效应的影响,可忽略;在0.06 s~22 s内,ZJ和ZS的瞬时频率近似等于4.005 rad/s,进一步证明了ZJ和ZS的正确性。图1(a)和图1(b)对比可知,模型A的ZJ和ZS吻合度较高,衰减过程中波峰和波谷处的位移差异最大为7.2%;模型B的ZJ和ZS计算结果仍基本一致,但两者之间的差异较模型A稍有加大,波峰和波谷处的位移差异最大为11%。这是因为模型B的初始位移为零,ZS引入了tk时刻到tk+1时刻结构振动频率等于tk-1时刻到tk时刻结构振动频率的假定,降低了计算精度,但影响很小。
2.1.2 地震作用下动力响应
以结构自振频率为6 rad/s,损耗因子为0.1的单自由度体系为例,初始时刻结构处于静止状态。分别采用ZJ和ZS计算单自由度体系在地震作用下的动力响应,并与复阻尼模型的频域计算方法(FFZ)、复阻尼模型的时域数值计算方法(FZ)进行对比,计算结果如图3所示。其中,FZ采用的时间步长为0.02 s(下同),FFZ避免了发散现象,可视为复阻尼模型的精确解[20]。
由图3知,地震持续时间较短时,ZJ、ZS、FFZ和FZ的计算结果近似相等;地震持续时间较长时,FZ存在明显的发散现象,与实际情况不符,说明FZ仅能计算地震持续时间较短情况下结构的动力响应;ZJ、ZS和FFZ的计算结果稳定收敛,且近似相等(图3中三条曲线基本重合),ZJ和ZS的位移峰值Xmax与FFZ的位移峰值Xmax近似相等,其相对误差δ在5%以内(见表1),该计算结果进一步证明了ZJ和ZS的正确性。
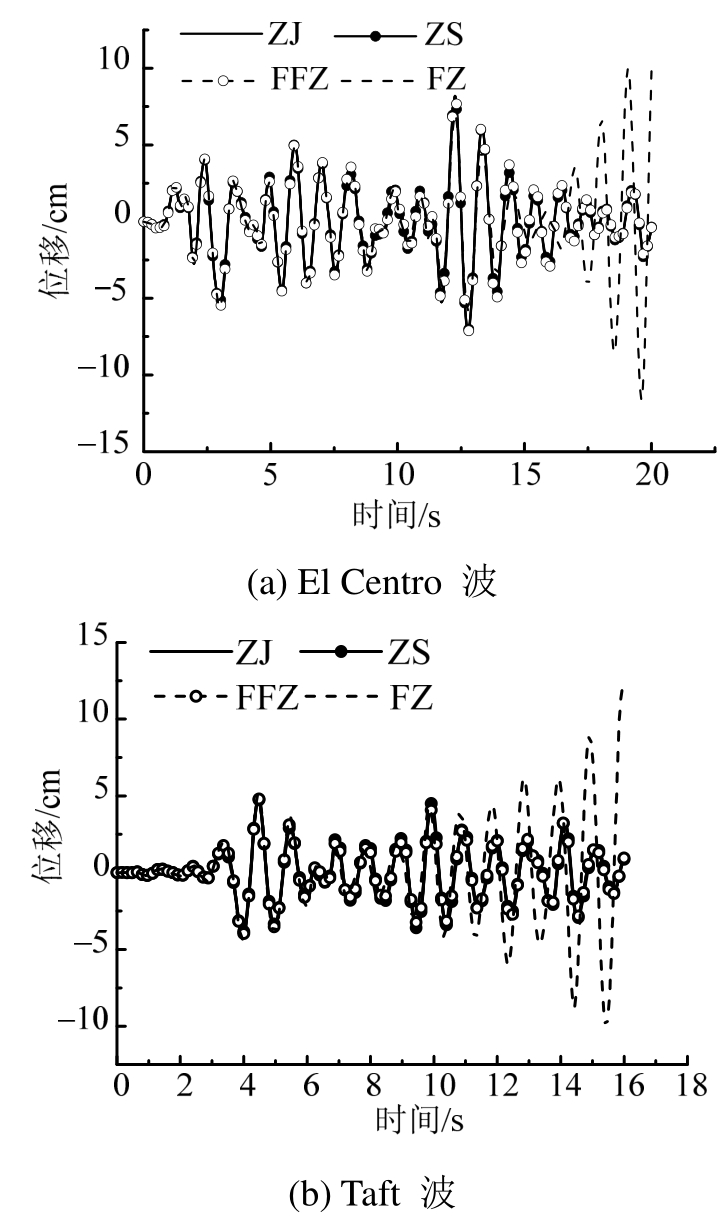
图3 不同方法计算的结构位移响应
Fig.3 The structural displacement responses of different methods
表1 不同方法计算结果的对比
Table 1 Comparison of calculated results with different methods
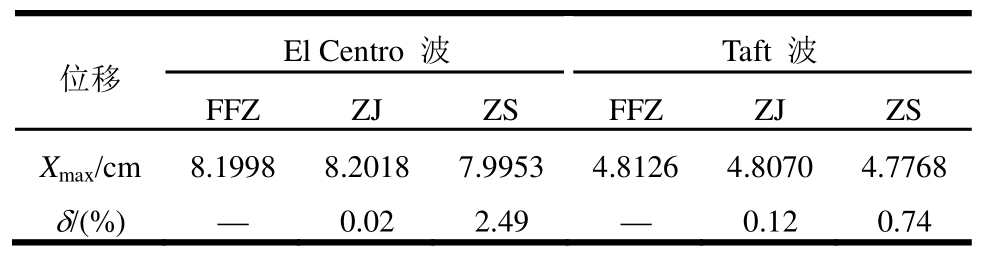
位移 El Centro 波 Taft 波FFZ ZJ ZS FFZ ZJ ZSimages/BZ_30_1708_2431_1710_2432.pngXmax/cm 8.1998 8.2018 7.9953 4.8126 4.8070 4.7768 δ/(%)— 0.02 2.49 — 0.12 0.74
复阻尼模型的频域数值计算方法仅可计算结构稳态反应的结果,避开了结构的瞬态反应,进而解决了结构自由振动响应引起的发散问题,因此复阻尼模型的频域数值计算方法仅适用于初始状态为静止的结构。由上文可知,本文提出的ZJ和ZS可直接计算结构的自由振动响应,且计算结果稳定收敛,可计算初始为非零状态的结构动力响应。此外,ZJ和ZS为时域计算方法,不需要在地震加速度记录后增加零值区段,计算过程更为直观。
2.2 多自由度体系
如图4所示,以3层剪切型框架结构为例[20],材料为钢筋混凝土,结构的阻尼比ξ=0.05,损耗因子为η=0.1[21-22],阻尼矩阵为:
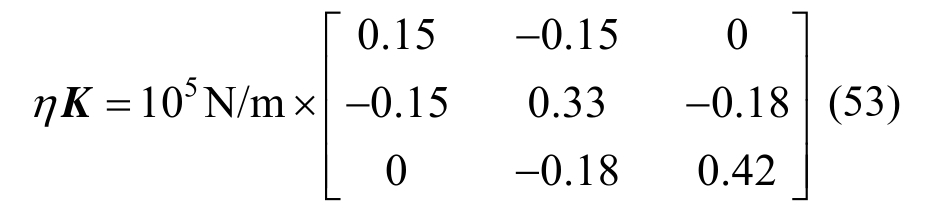
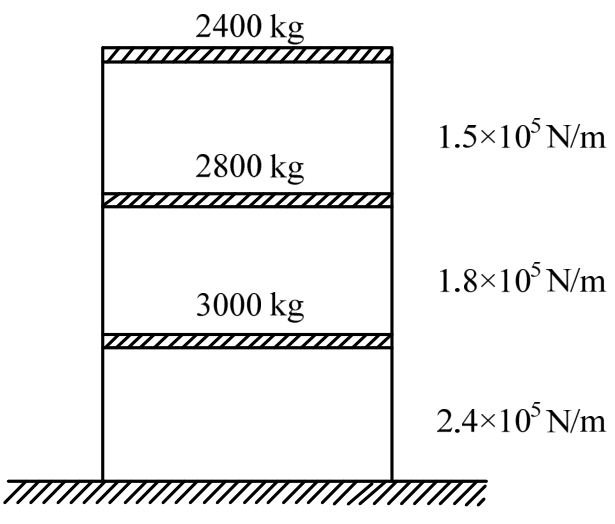
图4 钢筋混凝土框架质量和刚度分布图
Fig.4 The mass and stiffness distribution of reinforced concrete frame
初始时刻框架结构处于静止状态,分别采用ZJ、ZS、FFZ和FZ计算框架结构在地震作用下的动力响应,并以顶层位移为代表对比4种求解方法的计算结果(见图5)。图5表明,与单自由度体系在地震作用下的动力响应规律相同,随着地震持续时间增加,FZ的计算结果出现发散现象,ZJ、ZS和FFZ的计算结果稳定收敛,且位移时程曲线近似相等,ZJ和ZS的位移峰值Xmax与FFZ的位移峰值Xmax 近似相等,其相对误差δ在5%以内(见表2),这进一步证明了ZJ和ZS的正确性。
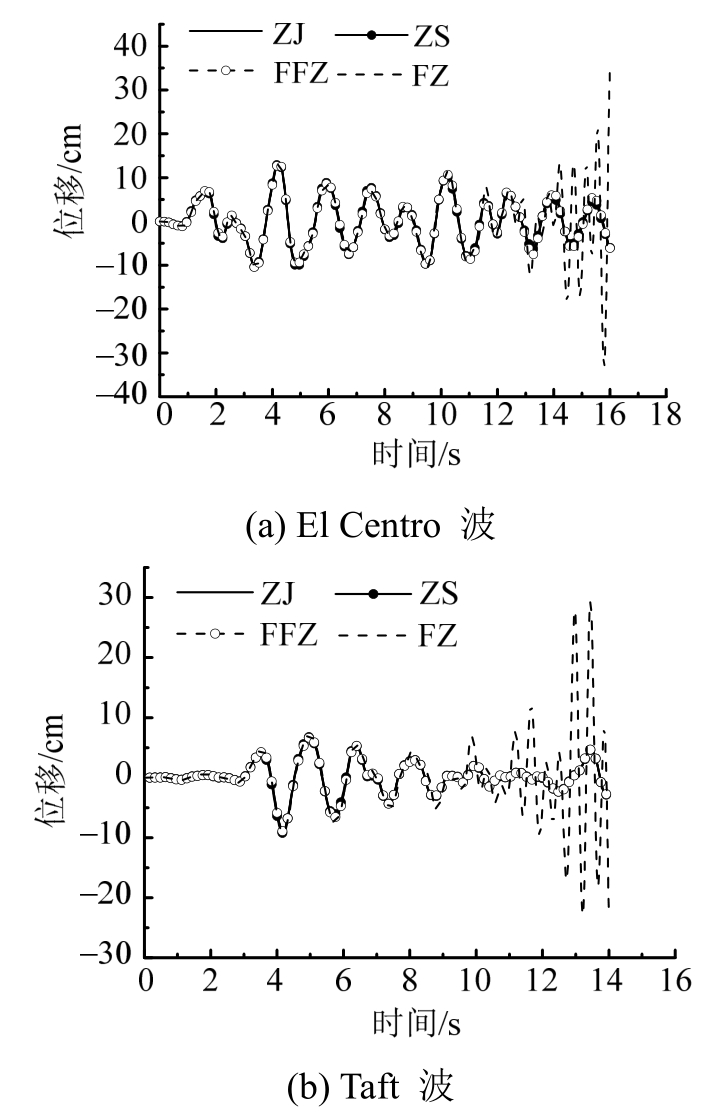
图5 不同方法计算的钢筋混凝土框架结构顶点位移响应
Fig.5 The top displacement responses of reinforced concrete frame with different methods
表2 不同方法计算钢筋混凝土框架结构位移响应的对比
Table 2 Comparison of calculated displacement responses of reinforced concrete frame with different methods
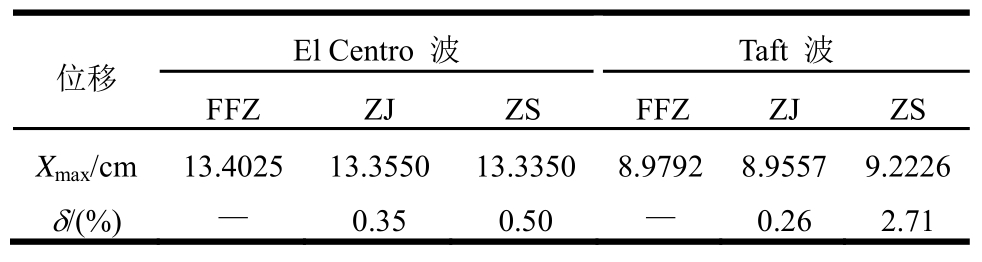
位移 El Centro 波 Taft 波FFZ ZJ ZS FFZ ZJ ZS Xmax/cm 13.4025 13.3550 13.3350 8.9792 8.9557 9.2226 δ/(%) — 0.35 0.50 — 0.26 2.71
3 结论
经理论推导和算例分析,得到以下结论。
(1)在复阻尼模型的频域运动方程基础上可得到滞变阻尼模型的时域运动方程,滞变阻尼模型和复阻尼模型的对比分析结果表明,滞变阻尼模型保留了结构稳态响应时每周期耗散能量与外激励频率无关的优点,同时其时域计算结果是稳定收敛的。
(2)针对滞变阻尼模型的特点,依据复平面法和地震加速度的三角级数表达式,提出了滞变阻尼模型的时域理论计算方法;与此同时,假定时间步长内结构的振动响应为简谐振动响应,以常平均加速度法为例,提出了滞变阻尼模型的时域数值计算方法。算例分析表明,相比滞变阻尼模型的时域理论计算方法,滞变阻尼模型时域数值计算方法的计算精度略有下降,但地震作用下峰值位移的误差在5%以内,满足工程精度要求。
(3)本文提出的滞变阻尼模型的时域理论计算方法和时域数值计算方法可有效避免时域发散现象,且与复阻尼模型的频域计算结果近似相等,证明了这两种计算方法的合理性;相比复阻尼模型的频域数值计算方法,本文方法还可计算初始为非零状态的结构动力响应。
[1]Bert C W.Material damping: An introductory review of mathematical models, measures and experimental techniques[J].Journal of Sound and Vibration, 1973,29(2): 129-135.
[2]Pan Y, Wang Y.Frequency-domain analysis of exponentially damped linear systems[J].Journal of Sound and Vibration, 2013, 332(7): 1754-1765.
[3]朱敏, 朱镜清.逐步积分法求解复阻尼结构运动方程的稳定性问题[J].地震工程与工程振动, 2001, 21(4):59-62.Zhu Min, Zhu Jingqing.Studies on stability of step-by-step methods under complex damping conditions[J].Earthquake Engineering and Engineering Vibration,2001, 21(4): 59-62.(in Chinese)
[4]张辉东, 王元丰, 江辉.不同参数取值对复阻尼模型结构抗震性能的影响[J].建筑结构学报, 2009, 30(6):94-100.Zhang Huidong, Wang Yuanfeng, Jiang Hui.Effect of different parameters on seismic performance of complex damping structures[J].Journal of Building Structures,2009, 30(6): 94-100.(in Chinese)
[5]张辉东, 王元丰.复阻尼模型结构地震时程响应研究[J].工程力学, 2010, 27(1): 109-115.Zhang Huidong, Wang Yuanfeng.Study on seismic time-history response of structures with complex damping[J].Engineering Mechanics, 2010, 27(1): 109-115.(in Chinese)
[6]潘玉华, 王元丰.含复阻尼振动系统的逐步积分法稳定性研究[J].土木工程学报, 2010(增刊1): 206-210.Pan Yuhua, Wang Yuanfeng.Stability of step-by-step methods in solving complex damping vibration systems[J].China Civil Engineering Journal, 2010(Suppl 1):206-210.(in Chinese)
[7]朱镜清, 朱敏.复阻尼地震反应谱的计算方法及其它[J].地震工程与工程振动, 2000, 20(2): 19-23.Zhu Jingqing, Zhu Min.Calculation of complex damping response spectra from earthquake records[J].Earthquake Engineering and Engineering Vibration, 2000, 20(2):19-23.(in Chinese)
[8]朱敏, 朱镜清.复阻尼地震反应谱计算的再研究[J].地震工程与工程振动, 2001, 21(2): 36-40.Zhu Min, Zhu Jingqing.Further studies on calculation of complex damping seismic response spectra[J].Earthquake Engineering and Engineering Vibration,2001, 21(2): 36-40.(in Chinese)
[9]Kang J H.Hysterically damped free and forced vibrations of axial and torsional bars by a closed form exact method[J].Journal of Sound and Vibration, 2016,378: 144-156.
[10]何钟怡.复本构理论中的对偶原则[J].固体力学学报,1994, 15(2): 177-180.He Zhongyi.The dual principle in theory of complex constitutive equations[J].Chinese Journal of Solid Mechanics, 1994, 15(2): 177-180.(in Chinese)
[11]何钟怡, 廖振鹏, 王小华.关于复阻尼理论的几点注记[J].地震工程与工程振动, 2002, 22(1): 1-6.He Zhongyi, Liao Zhenpeng, Wang Xiaohua.Some notes on theory of complex damping[J].Earthquake Engineering and Engineering Vibration, 2002, 22(1): 1-6.(in Chinese)
[12]周正华, 廖振鹏, 丁海平.一种时域复阻尼本构方程[J].地震工程与工程振动, 1999, 19(2): 38―44.Zhou Zhenghua, Liao Zhenpeng, Ding Haiping.A time-domain complex-damping constitutive equation[J].Earthquake Engineering and Engineering Vibration,1999, 19(2): 38-44.(in Chinese)
[13]胡海岩.结构阻尼模型及系统时域动响应[J].振动工程学报, 1992, 5(1): 8-15.Hu Haiyan.Structural damping modal and system dynamic response at time domain[J].Journal of Vibration Engineering, 1992, 5(1): 8-15.(in Chinese)
[14]Reggio A, Angelis M D.Modelling and identification of structures with rate-independent linear damping[J].Meccanica, 2015, 50(3): 617-632.
[15]Wang J.Rayleigh coefficients for series infrastructure systems with multiple damping properties[J].Journal of Vibration and Control, 2015, 21(6): 1234-1248.
[16]Inaudi J A, Kelly J M.Linear hysteretic damping and hilbert transform[J].Journal of Engineering Mechanics,1995, 121(5): 626-632.
[17]Manikanahally D N, Crocker M J.Vibration analysis of hysteretically damped mass-loaded beams[J].Journal of Sound and Vibration, 1989, 132(2): 177-197.
[18]李鸿晶, 王通, 廖旭.关于 法机理的一种解释[J].地震工程与工程振动, 2011, 31(2): 55-62.Li Hongjing, Wang Tong, Liao Xu.An interpretation on Newmark beta methods in mechanism of numerical analysis[J].Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(2): 55-62.(in Chinese)
[19]周惠蒙, 吴斌, 王涛, 等.基于速度的显式等效力控制方法的研究[J].工程力学, 2016, 33(6): 15-22.Zhou Huimeng, Wu Bin, Wang Tao, et al.Explicit equivalent force control method based on velocity[J]..Engineering Mechanics, 2016, 33(6): 15-22.(in Chinese)
[20]潘玉华, 王元丰.复阻尼结构动力方程的高斯精细时程积分法[J].工程力学, 2012, 29(2): 16-20.Pan Yuhua, Wang Yuanfeng.Gauss precise time-integration of complex damping vibration systems[J].Engineering Mechanics, 2012, 29(2): 16-20.(in Chinese)
[21]刘庆林,傅学怡.基于复阻尼假定的不同材料阻尼特性混合结构抗震分析反应谱CCQC法[J].土木工程学报,2011, 44(3): 61-71.Liu Qinglin, Fu Xueyi.A response spectrum CCQC method for seismic analysis of structures of multiple material damping characteristics based on complex damping assumption[J].China Civil Engineering Journal, 2011, 44(3): 61-71.(in Chinese)
[22]Lage Y, Cachão H, Reis L, et al.A damage parameter for HCF and VHCF based on hysteretic damping[J].International Journal of Fatigue, 2014, 62: 2-9.