海底管道作为输送海洋油气的主要装备,其结构安全是保障营运的关键。管道所处海底环境特殊,其失效形式主要分腐蚀破坏、机械损伤和疲劳损伤三种。据统计[1],由海洋捕鱼拖网作业[2]及船舶抛锚[3]等第三方活动引发的冲击损伤已成为诱发管道破坏的第二大因素(占32%)。近年来,随着人类对海洋资源的大力开发,由船舶紧急抛锚及平台作业等第三方活动引发的坠物落水事故逐渐增多。海底管道易受到坠物的冲击损伤,甚至发生泄露事故,带来巨大的经济损失和不可估量的生态环境带破坏。如何抵御坠物的冲击直接关系到管道的安全。
早期,学者们对于管道在冲击荷载下响应问题的研究主要从模型试验和理论分析两个方面开展。Ghosh等[4]和Jones等[5]通过模型试验分析了冲击荷载下的管道力学特性,为理论分析奠定了基础。Ellinas等[6]基于管道冲击试验结果提出了冲击荷载与管道损伤深度的半经验公式,但其仅适用于小变形的情况。Bai等[7]对Ellinas提出的公式进行了修正,但其结论适用于管道线弹性区。Jones等[8]和Wierzbicki等[9]提出了管道在冲击荷载下的理论分析模型,用于获取其在受冲击过程中的动态响应。在此基础上,粟京[10]从能量的角度求解了管道受撞击后的凹痕深度,但仅考虑了坠物与管道间的作用,忽略了管道与土体的相互作用[11—12]。Yu等[13]基于局部伽辽金法提出了用于计算管道受船锚撞击损伤的数值模型,但该方法尚未引入海床与管道相互作用。近年来,随着计算机的发展,数值分析逐渐成为管道受撞击损伤分析的主要手段,并可考虑管土相互作用的影响。杨秀娟等[14]基于ANSYS/ LS-DYNA较为系统地分析了管道受坠物的碰撞损伤,但未考虑海床土体性质对损伤的影响。Lou等[15]用有限元法模拟及分析了悬空管道受坠物撞击的情况,土体性质对其动态响应的影响较小。Gao等[16]和王懿等[17]分析了船锚的入泥深度,为管道埋深提供了设计参考,但未引入船锚与管道的撞击模型。
实际工程中,常对管道进行埋深处理以保障其安全。已有研究很少涉及埋置管道的撞击损伤分析。DNV-RP-F107[18]中仅考虑到碎石层对冲击能量的吸收作用,对于埋深并未说明。美国船级社规范中仅给出埋深的建议值。巴西、日本等国家对此提出的标准也不全面[19]。我国海洋工程领域对于挖沟埋深的标准没有明确规定,设计工作主要凭经验完成。在管道工程中,不同的埋深及土体性质直接关系到其安全性和经济性,如何考虑上述因素的影响对管道的安全设计尤为关键。
基于大变形有限元技术的耦合欧拉-拉格朗日法,本文建立了数值模型,解决坠物与埋置管道撞击过程中引起的土体大变形问题[20]。结合物理模型试验,研究了海床柔性、土体性质及埋置深度对管道受撞击损伤的影响,同时考虑坠物形状和摩擦的影响,为管道的工程设计提供依据。论文首先介绍了物理模型试验及结果分析;其次建立数值模型,并与试验结果进行了对比;最后对影响因素进行了参数化研究,得出了结论。
1 物理模型试验
1.1 试验设备及仪器
物理模型试验的布置如图1所示。试验仪器包括:1)重物释放装置,由型材构成支撑结构主体,并配有滑轮、绞盘、挂钩等,可实现重物在2 m范围内任意高度处自由下落;2)土体槽,长×宽×高为1 m×0.6 m×0.8 m。由亚克力板加工制成,用于进行砂土固结及埋置管道试样;3)三坐标测量仪,用于获取管道受撞击后的截面变形大小。

图1 模型试验布置示意图
Fig.1 Schematic diagram of model experiment layout
试验比尺为1∶10。管道试样长1 m,对应原型10 m长度的管道,其几何及材料参数如表1所示。坠物模型为实心铁球,质量为1 kg、2 kg和3 kg,分别对应1000 kg、2000 kg和3000 kg的原型球状坠物。
表1 管道试样几何尺寸及材料特性
Table 1 Geometry and mechanic properties of specimen
直径/mm 壁厚/mm 长度/mm 弹性模量/GPa 屈服强度/MPa 63 1 1000 210 205
1.2 试验工况及步骤
为研究管道在坠物撞击荷载下的变形特性及其影响因素,设计10组试验(如表2)。在A、B两种管道安置条件下各进行5组试验。其中条件A代表管道裸置在混凝土地面上的情况(图2(a)),模拟管道裸置于刚性海床上的工况;条件B代表管道埋置在砂土中一定深度的情况(图2(b))。
表2 试验设计
Table 2 Experiment design

管道安置条件 工况 质量m/kg 释放高度H/mm 埋置深度d/mm A 1 1 1000 — 2 2 1000 — 3 3 1000 — 4 3 800 — 5 3 600 — B 6 1 1000 20 7 2 1000 20 8 3 1000 20 9 3 800 20 10 3 600 20
试验时,根据工况设计将坠物升至指定高度处。待坠物完全静止后再释放,使其自由下落,与管道发生垂直碰撞。碰撞后,利用三坐标测量仪获取碰撞区域管道的变形。
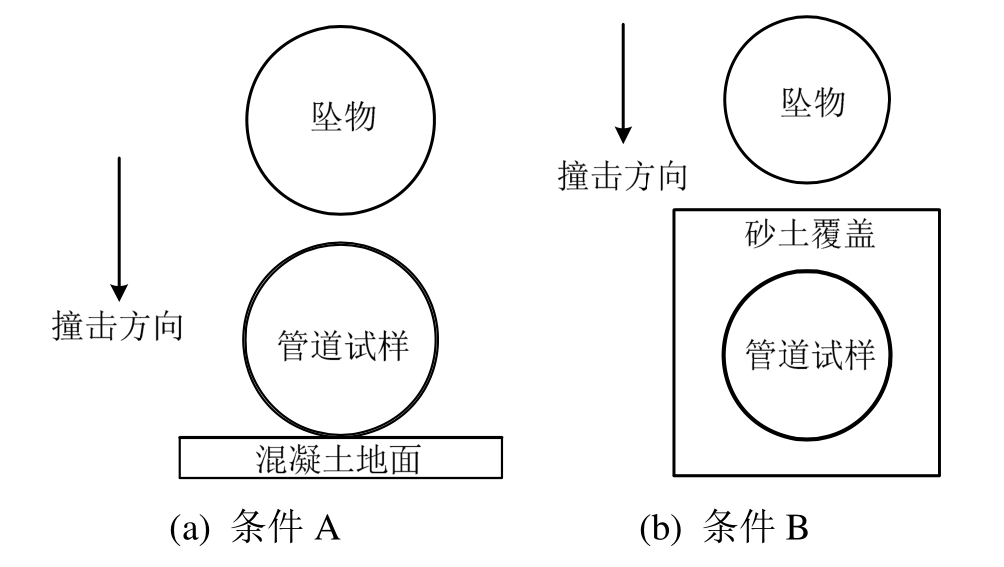
图2 管道安置条件示意图
Fig.2 Schematic diagram of pipeline placement conditions
1.3 试验结果与分析
管道经撞击后,表面会产生凹陷。最大凹陷处的横截面如图3所示,圆心到A、B两点距离的差值即为凹痕深度δ[21]。
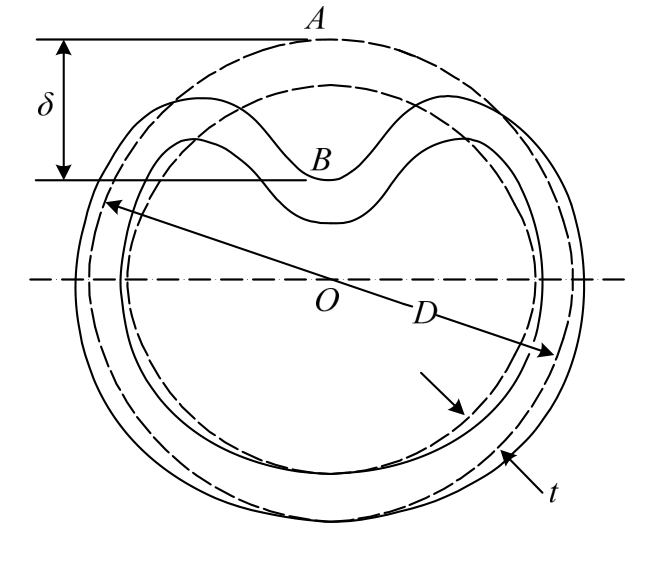
图3 管道凹痕深度定义
Fig.3 Definition of pipeline dent depth
表3为DNV-RP-F107[18]中关于管道损伤的分级标准,其中管道的凹痕深度与管道外径的比值δ/D超过5%则有泄露的危险。本文以此作为衡量管道损伤程度的指标。
表3 管道撞击承载能力及损伤分级
Table 3 Damage classification of steel pipelines

凹痕深度/管道外径/(%) 损伤描述 <5 轻微损伤 5~10 重大损伤 存在泄露风险 10~15 重大损伤 存在泄露及破裂风险 15~20 重大损伤 存在泄露及破裂风险 >20 破裂
图4(a)、图4(b)给出了管道凹痕深度随坠物释放高度、质量的变化。由结果可知,管道的凹痕深度取决于撞击能量的大小以及管道的安置条件。安置条件相同时,管道凹痕深度随着坠物质量、释放高度的增加而明显增大;撞击能量相同时,由条件A及条件B的凹痕深度对比可知,管道的埋深能抵御一部分坠物的冲击能量,对管道起到保护作用。
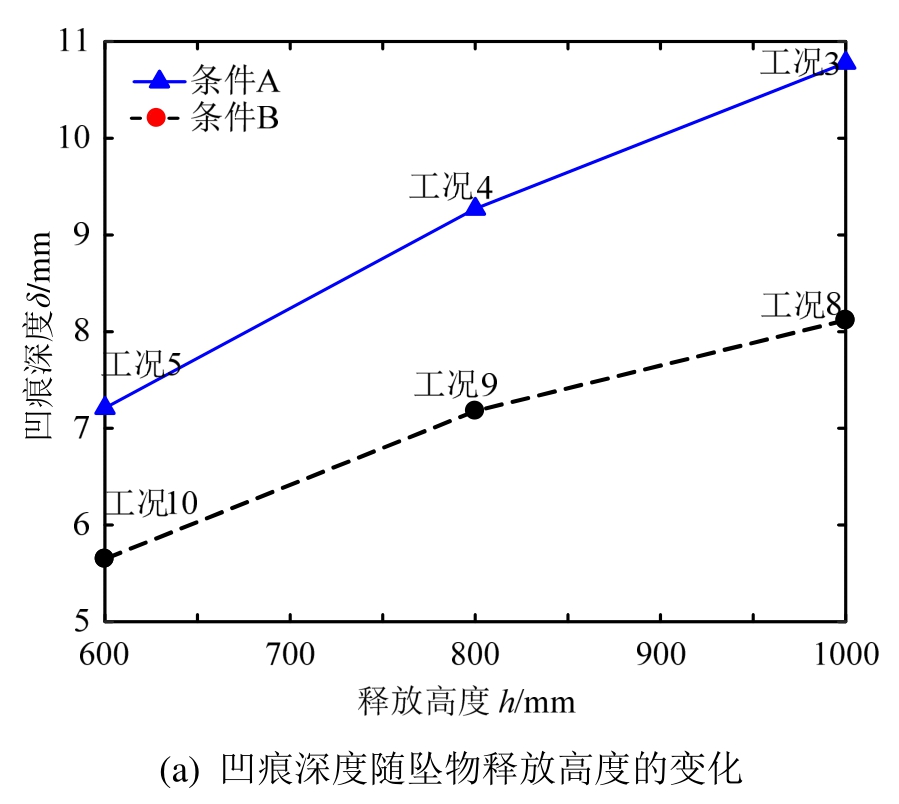
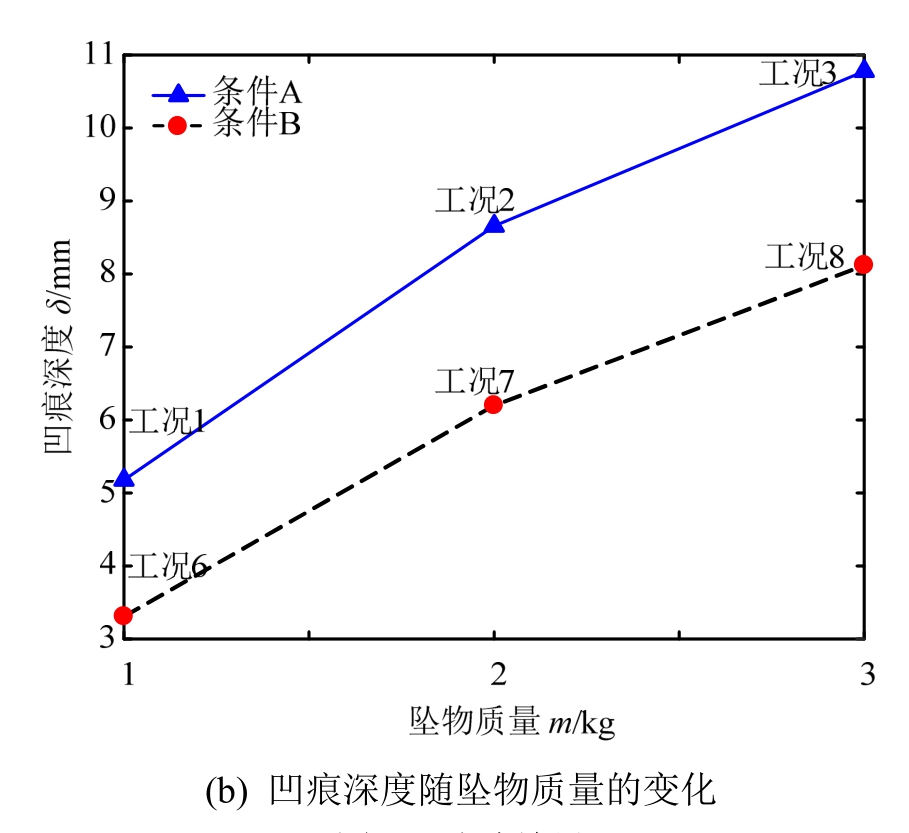
图4 试验结果
Fig.4 Experimental results
2 有限元数值模型
2.1 撞击能量的确定
DNV-RP-F107中指出,坠物在水中的下落速度取决于物体的形状及在水中的质量,并将逐渐趋于稳定。其终止速度vt可表示为:
式中:m为物体质量;g为重力加速度;A为物体的挡水面积;ρw为海水密度;ρd为物体密度;Cd为拖曳系数。
相应地,其撞击能量则取决于物体的终止速度及质量,可表示为:

式中:Ee为有效撞击动能;Et为物体本身的动能;Ea为附加水质量的动能;ma为物体的附加水质量;ρw为海水密度;Ca为附加质量系数;V为物体在水中的体积。
附加水质量在物体体积较大时有显著的影响,需予以考虑,以等效密度[22]的形式赋予物体,如式(4)所示:

式中:ρe为物体的等效密度;ρd为物体密度;ρw为水的密度。
2.2 非线性求解过程
管道受坠物的冲击过程需考虑坠物、管道、土体之间的相互作用,涉及到复杂的接触非线性问题。采用罚函数法来处理,其将接触非线性问题转化为材料非线性问题。根据坠物、管道、土体之间相互作用的特点,将接触面约束条件引入惩罚势能泛函,接触问题则等价于无约束的优化问题,其相应的泛函的极值条件为:
式中:U为应变能;W为外功;Πp为接触面约束条件对应的约束项。
整个系统的运动学方程为:
式中:M、C、K、KP分别为系统的质量矩阵、阻尼矩阵、整体切向刚度矩阵、接触刚度矩阵;F、F分别为节点外荷载向量、等效节点接触力向量;u为单元节点位移矩阵。
对于爆炸、冲击等瞬态问题,宜采用用显式的中心差分法对式(6)进行求解,得到节点位移u后,根据几何方程及物理方程可解得每个单元的应力应变。
2.3 耦合欧拉-拉格朗日算法
有限元分析中,拉格朗日法以物体的坐标为自变量,可准确描述物体的边界。但在物体变形较大时,网格就会发生严重的畸变。欧拉法是以空间坐标为自变量,是对空间的离散,材料在网格中流动,即使材料发生严重变形也不会影响到网格的形状。缺点是无法准确描述材料的边界。
耦合欧拉-拉格朗日算法[23](Coupled Eulerian- Lagrangian method,CEL)结合了拉格朗日法及欧拉法的优点。既克服了单元的扭曲变形,同时也可准确描述材料的边界。在土体结-构物相互作用分析中,对于土体采用欧拉算法去描述。欧拉网格在整个分析过程中保持恒定,土体材料在欧拉网格中流动,并以欧拉体积分数(EVF)来获取其位置。EVF代表材料填充网格的程度,EVF=1代表完全填充,EVF=0代表无填充。对于结构物,则采用拉格朗日算法去描述,并通过结构物的边界来追踪土与结构物接触面的变化。
2.4 模型建立
海底管道有限元模型的尺寸及材料特性参考已建成的海底管道工程实例。管道外径为D=0.611 m,壁厚为t=0.011 m。管道钢材料的弹性模量Es=210 GPa,泊松比μ=0.3,屈服强度σy= 518 MPa,密度ρs=7850 kg/m3。管道模型在分析中的变形较小,采用四节点拉格朗日单元S4R描述,并对撞击区域的网格进行加密。
坠物在碰撞过程中的变形可以忽略,采用拉格朗日单元描述,并施加刚体约束。
海床土体考虑其为饱和土体,并采用Mohr-Coulomb(MC)模型描述其本构关系[24—25]。能够很好地模拟土体在与结构物相互作用时的弹塑性变形,其屈服准则的控制方程为:
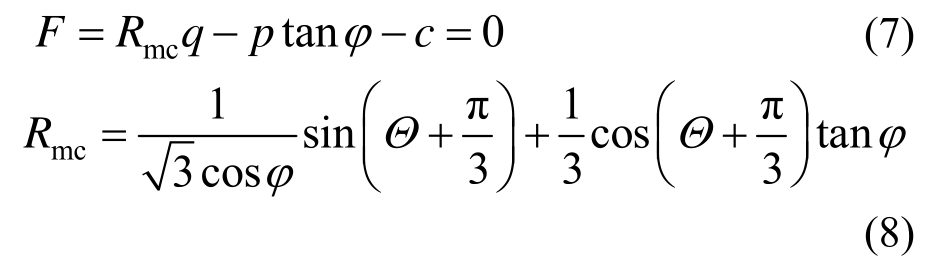
式中:![]() 为偏应力;J2为第二偏应力不变量;
为偏应力;J2为第二偏应力不变量;![]() 为平均应力;σ为应力张量;φ为q p- 应力面上Mohr-Coulomb屈服面的倾斜角,为材料的摩擦角,
为平均应力;σ为应力张量;φ为q p- 应力面上Mohr-Coulomb屈服面的倾斜角,为材料的摩擦角,![]() c为材料的粘聚力;Θ为极偏角,定义为
c为材料的粘聚力;Θ为极偏角,定义为![]() 为第三偏应力不变量。
为第三偏应力不变量。
图5为本文所建立的有限元数值模型。为消除边界效应对计算结果的影响,海床长度即模型y方向的长度取20D、宽度即模型x方向的长度取12D、厚度即模型z方向上管道底部至xOy面边界的距离取6D。海床土体在分析过程中变形较大,采用八节点欧拉单元EC3D8R对其进行描述,并加密与管道临近区域土体网格的密度,在粗细网格区域之间采用过渡网格处理。同时,在撞击分析步之前需对海床土体进行地应力平衡,使其在初始时刻处于一种收敛的应力状态,从而影响撞击过程中土体及管道的响应[26]。

图5 基于CEL法的坠物与埋置管道作用有限元模型
Fig.5 Finite element model of dropped object and buried pipeline based on CEL method
2.5 模型验证
为验证数值模型的可靠性,按模型试验的尺寸及材料特性建模并与试验结果进行对比。如图6(a)~ 图6(b)所示,数值模拟结果与试验结果吻合较好。数值模型对于条件A下的工况的预测效果要优于条件B下的工况。其原因可能是由于不同工况下砂土试样的固结程度难以均保持完全一致,使得土体强度存在差异,从而使得数值结果与试验结果有所偏差,但其误差均在10%以内。

图6 管道凹痕深度对比
Fig.6 The comparison of pipeline dent depths
选取有代表性的工况3和工况6的管道横截面做对比,检验管道变形的模拟效果。如图7(a)~图7(b)所示,二者变形规律较为一致:对于撞击能量较小,有土层保护的工况6,截面变形十分吻合,表面出现微小的凹痕;对于撞击能量较大,且无土层保护的工况3,二者的截面均表现为椭圆形特征,并有向“桃形”发展的趋势。但二者管道顶部区域的形状存在微小偏差,可能是由于物理模型中管道试样的初始几何误差所造成的。对比结果证实了数值模型的有效性。
3 结果讨论分析
3.1 海床柔性及土体性质对撞击损伤的影响

图7 管道最大变形处横截面对比
Fig.7 comparison of circumferential profiles of pipelines at the maximum deformation position
对于裸置在海床上的管道,为研究海床柔性及 土体性质对其动态响应及损伤的影响,以均质粘土海床为研究对象,计算管道在不同土壤条件下与质量为3000 kg的球状坠物(v=vt=8.832 m/s)时撞击时的损伤情况。管道凹痕深度的计算结果如图8所示。可以看出:1)凹痕深度随着速度的增加呈线性增加趋势;2)在撞击速度较小时,土体强度对管道的损伤影响较小。但随着撞击速度的增加,土体强度的影响作用逐渐明显,凹痕深度随着土体强度的增加而增加;3)总体上,考虑管土相互作用时管道的凹痕深度要明显小于忽略其相互作用的情况(即刚性海床的情况),二者最大相差21%,实际差值38 mm。说明海床土体对撞击能量有耗散作用,可减缓损伤的程度。
为了研究海床土体对于撞击能量的耗散机理,图9和图10分别给出了不同土体强度的海床对于能量的耗散情况及管道的纵截面情况。由图9可见,土体耗散的能量随着撞击速度的增加而增加,随土体强度的增加而有所减少。这是因为撞击速度较大时,土体强度较低时,管土相互作用更为明显。这 一点可从图10中得到验证,柔性的海床土体使管道呈现出整体变形的趋势,且随着土体强度的降低而增大,该过程耗散了一部分撞击能量,从而减缓了管道的局部损伤程度。这一现象与Zeinoddini 等[26]得出的结论较为一致。

图8 海床土体强度对裸置裸置管道凹痕深度的影响
Fig.8 The effect of soil strength on dent depth of bare pipeline

图9 土体强度对海床土体能量耗散的影响
Fig.9 The effect of soil strength on energy dissipation
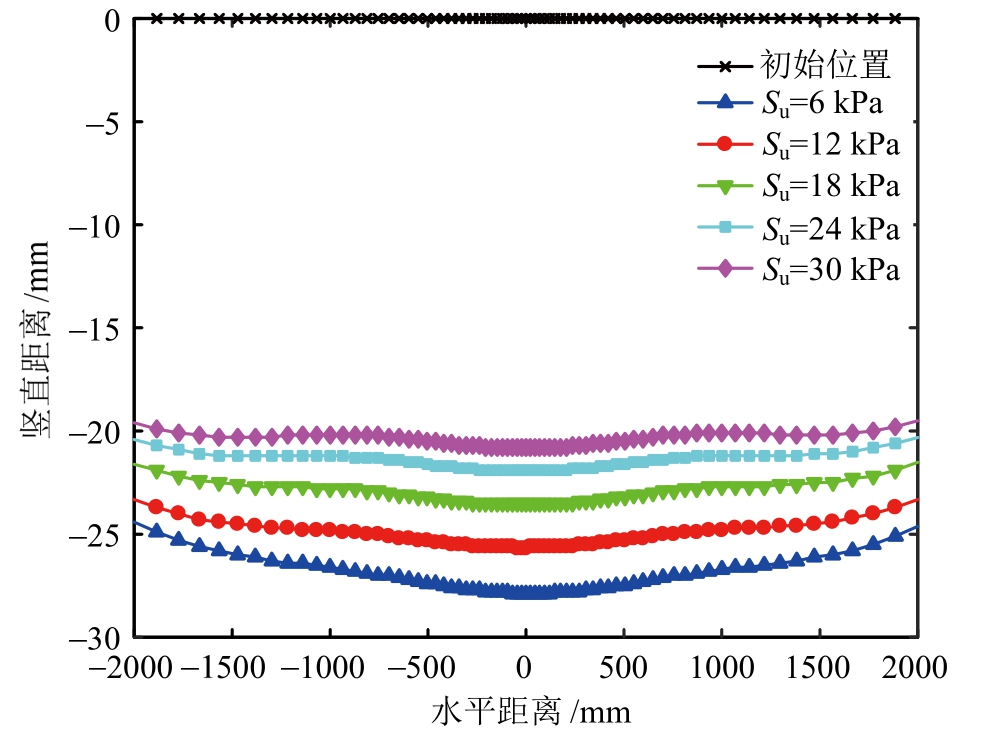
图10 不同土体强度下管道底部节点垂向位移的纵向分布
Fig.10 The distribution of vertical displacements for pipeline bottom nodes along the longitudinal axis with different soil strengths
3.2 粘土海床性质及埋深对于撞击损伤的影响
工程实践表明,深海海底的粘土多为正常固结粘土,其不排水抗剪强度Su随深度近似线性增加,如图11所示,Su(·)为嵌入深度z的函数,表示嵌入深度为z时粘土的不排水抗剪强度;Su0为海床表面处土体的不排水抗剪强度;k为强度增加梯度。已有的研究均将粘土海床简化成强度均匀的土体,忽略了其强度随深度增加的特性,这对管道的安全埋深设计影响较大,应予以考虑。
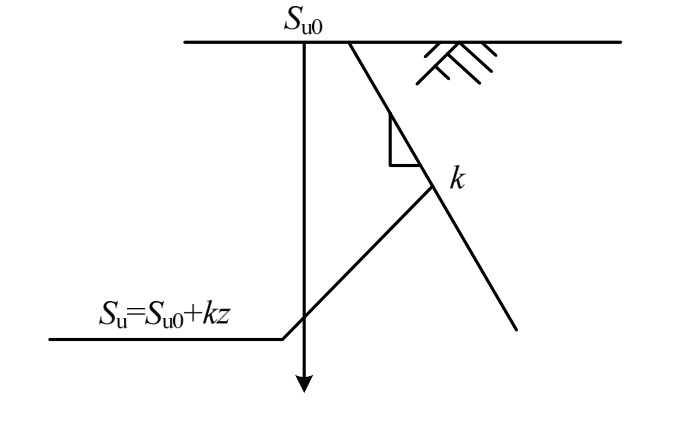
图11 正常固结粘土不排水抗剪强度随嵌入深度变化
Fig.11 Undrained shear strength with penetration depth of the normally consolidated clay
在纯拉格朗日分析中,网格划分在材料上,随材料同时发生变形,因而可将土体强度与网格坐标相关联来实现土体强度随嵌入深度的变化。而对于CEL模型,网格在分析中固定不动,使用上述方法无法奏效。参见图12,本文将温度引入分析步中:以将温度为间接变量,首先建立起温度与深度的函数关系,其次编制用户子程序VUSDFLD,在分析过程中提取每一时间步中温度的信息,最后赋值给场变量(FV),使土体强度与场变量相关联,从而 实现了正常固结土强度随着深度而变化。

图12 方法流程图
Fig.12 Flow diagram of methodology

图13 正常固结粘土不排水抗剪强度分布等值线
Fig.13 Undrianed shear strength distribution contour of the normally consolidated clay
图13为数值模型中正常固结粘土强度分布的等值线。可见:1)总体上等值线从上至下分布均匀,表明土体的强度呈线性增加,其承载能力相应提高;2)坠物旁侧的土体强度等值线向上隆起,坠物底部的等值线则向下运动。表明随着坠物不断嵌入海床,其旁侧的土体发生较大形变,并向四周流动。表层强度较低的一部分土体被坠物压入较深处,坠物底部的土体承载力则由不同强度的土体所共同构成。故相对于均质粘土,正常固结粘土的承载力较高,与实际相符。 定义δ=0时所对应的深度为管道的安全埋深为,以研究土体强度对管道损伤的影响。图14为不同k值的正常固结粘土条件下,管道与质量为3000 kg的球状坠物(v=vt=8.832 m/s)撞击时,凹痕深度随埋深的变化。可以看出:1)凹痕深度随着管道埋深及土体强度的增加明显下降。对于Su=18+3k的正常固结粘土海床,埋深从0.25 m增至1.5m时,管道凹痕深度由120 mm降低为0;随着k值从1增加到9,管道的安全埋深从1.75 m降低到0.75 m。这是由于强度越高的土体,承载力越强,发生相同形变时吸收的能量越多。这一过程耗散了更多的冲击能量;2)而对于强度为Su=18+k海床土体,即使埋深超过1 m,其管道凹痕为77 mm,仍不能有效保护管道。除增加埋深外,还应考虑其他保护措施,如设置混凝土保护层、或在海床表面设置碎石层以耗散撞击能量;3)与均质粘土海床相比(k=0),正常固结粘土海床对管道的保护效果更好,二者的安全埋深最大可相差1.25 m,工程上可以节省资金投入;4)综合考虑不同土质的影响,2 m的埋深可有效的保护管道。

图14 正常固结土性质对管道损伤的影响
Fig.14 The effect of soil property on pipeline damage for normally consolidated clay
对于新近开挖埋设的海底管道,其管道周围的回填土体处于欠固结状态,土体较为松散。同正常固结土相比,在同一荷载作用下,其体积变形大,杨氏模量小,表现出“软”的力学特性,损失了部分承载能力。为了研究该现象,设正常条件下海床土体的不排水抗剪强度为Su=18 kPa,则欠固结状态下,管道周围土体的强度分别取2/3Su、1/3Su,计算管道在上述土体条件下与质量为3000 kg的球状坠物(v=vt=8.832 m/s)撞击时所受的损伤大小,结果如图15所示。

图15 欠固结土性质对管道损伤的影响
Fig.15 The effect of soil property on pipeline damage for underconsolidated clay
由图15可见,新近埋设管道的回填土的土体性质对其损伤情况影响较大,在工程中应格外注意:回填土处于欠固结状态时,土体强度较低,仅增加埋深无法有效保护管道,如Su=12 kPa时,在埋深d=2 m的条件下,管道的凹痕深度δ为50 mm左右,仍然处于失效状态。此时可采用在海床表面铺设碎石垫层等手段来对冲击能量进行耗散,从而有效保护管道。
3.3 摩擦系数对撞击损伤的影响
为研究摩擦对埋置管道损伤的影响,计算不同摩擦系数下管道与质量为3000 kg的球状坠物(v=vt=8.832 m/s)撞击时的凹痕深度。为简化计算,海床土体考虑为均质粘土(Su=18 kPa),结果如图16所示。对于埋置管道,坠物与土体间的摩擦系数对于管道的损伤存在一定影响:1)摩擦系数越大,管道损伤越小。 f=0.6时,其安全埋深为1.75 m,而f=0.1时,即使埋深d=2 m,仍存在10mm的凹痕;2)埋深较小时,摩擦对于损伤的影响不大。埋深d=0.25时,摩擦系数分别为f=0.60及f=0.10时,管道的凹痕深度差值仅4 mm;但随着埋深的增加,摩擦作用逐渐明显,埋深d=1 m时,二者的差值达到22 mm。这是由于埋深较大时,坠物与管道接触前,需克服更多的土体阻力。

图16 摩擦系数对凹痕深度的影响
Fig.16 The effect of friction coefficient on dent depth
3.4 坠物类型对于撞击损伤的影响
不同作业区的海底管道,会受到来自不同种类坠物的撞击损伤:1)在平台作业区,坠物一般为集装箱、配重块等方形或球状物体,钻杆等管状物 体[18];2)在锚泊作业区,坠物则一般以船锚为主。为研究上述两种作业区条件下,管道的损伤及响应规律,本文以质量同为3000 kg的球体、立方体、霍尔锚[27]、锥体为研究对象,使其以相同的初速度(v=vt=8.832 m/s)与埋置管道进行碰撞,计算管道的凹痕深度。当坠物为球体、立方体时,可代表平台作业区的情况;坠物为霍尔锚时,则代表锚泊作业区的情况;坠物为锥体时,则可代表两种作业区条件下,坠物以尖端与管道接触的极限情况。为简化计算,海床土体考虑为均质粘土(Su=18 kPa),结果如图17所示。
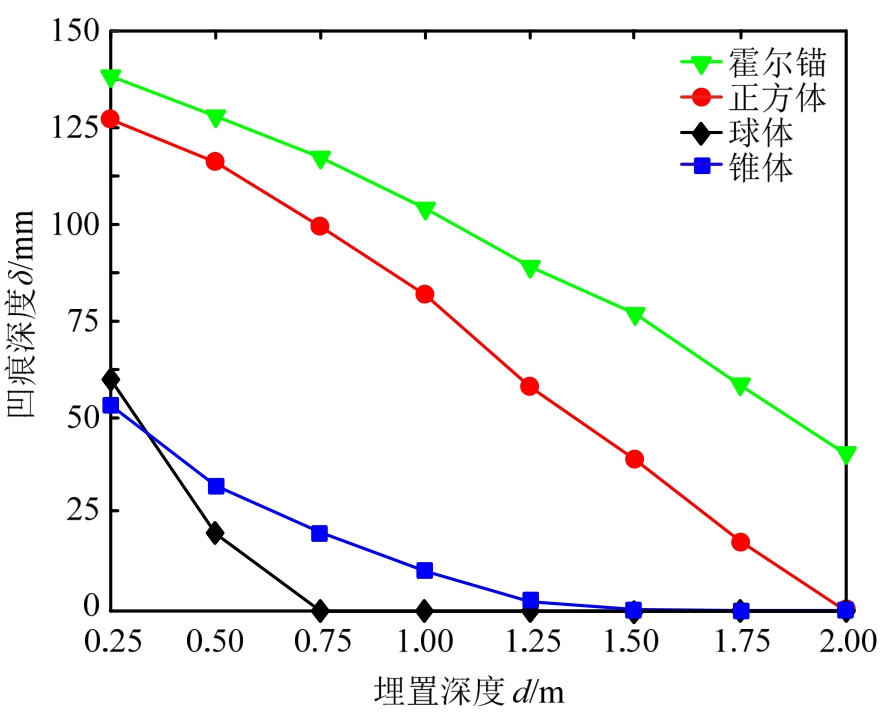
图17 坠物类型对凹痕深度的影响
Fig.17 The effect of dropped object category on dent depth
可以看出,管道凹痕深度的大小取决于坠物同土体、管道间的接触面积:1)随着接触面积的增大,管道的局部凹痕深度明显减小。在平台作业区条件下,对于接触面积较大的立方体坠物,管道的埋深在超过1.25 m后几乎没有损伤,而对于接触面积较小的球体及锥体坠物,仍然有较大的凹痕深度。与此相比,在锚泊作业区条件下,埋深d=0.25 m时,霍尔锚所造成的损伤略大于立方体坠物,而随着埋深的增加,其造成的损伤开始低于立方体坠物且不断降低。这是由于随着埋深的增加,其锚冠端部的凸缘部分与土体开始接触,增加了接触面积,其侵入土体时受到的阻力骤增,损耗了大部分能量;2)随着埋深的增加,坠物形状造成的管道损伤越发明显。在埋深d=0.25 m时,锥体、球体坠物对管道造成的凹痕深度的差值为12 mm。当埋深d=2 m时,球体坠物已不再对管道造成损伤,而锥体坠物仍对管道造成了37 mm的凹痕深度。可见,设计安全埋深时,应以尖锐的坠物为目标,进行极限工况设计。
总体上看,平台作业区内坠物与土体的接触面积较小,管道的撞击损伤更为严重,因此,以该作业区条件下的坠物(球体、立方体、锥体)为研究对象,其结果更具有代表性。
图18为埋深d=1.0 m时,不同坠物撞击管道的横截面变形。可见:正方体坠物对管道造成的损伤程度较小,截面呈近似椭圆形。球体及锥体坠物对管道造成的损伤程度较大,凹痕深度从两侧至中心逐渐增大,截面近似呈“桃形”。
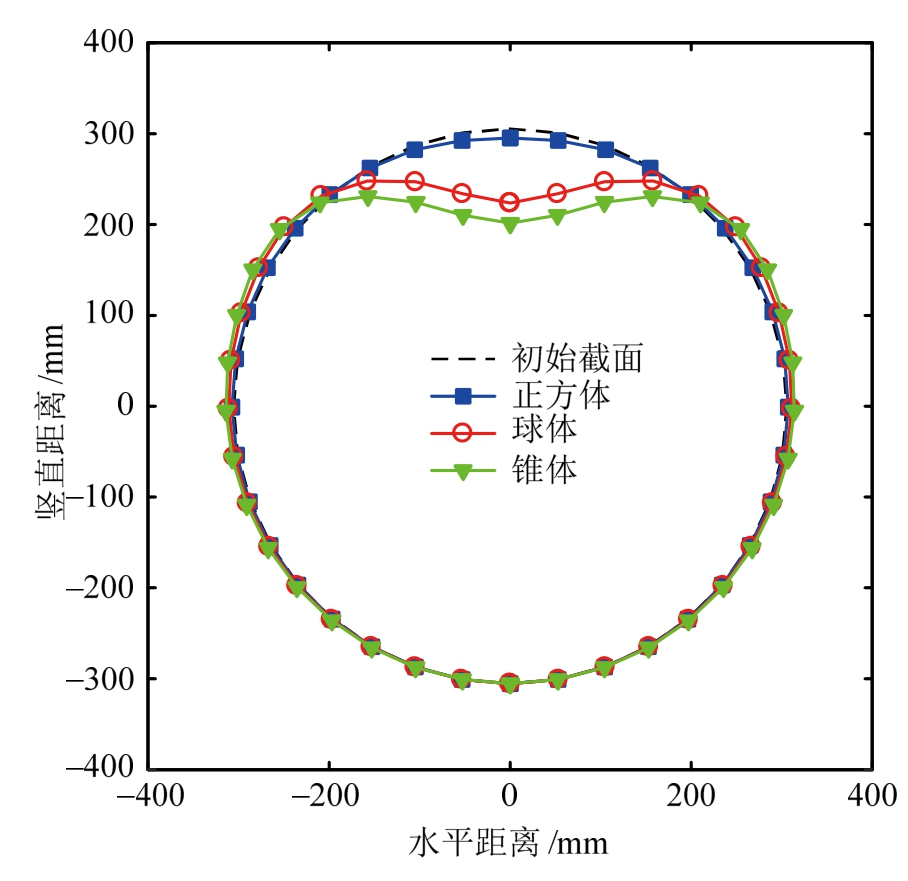
图18 坠物形状对管道横截面的影响
Fig.18 The effect of dropped object shape on pipeline circumferential profile
图19为埋深d=1.0 m时,不同坠物撞击管道的纵截面情况。可以看出:1)对于锥体、球体坠物,形状尖锐,土体阻力较小,撞击的能量作用在管道上,管道轴线方向上的损伤范围及垂直轴线方向上的损伤深度均较大。损伤深度从两端至中心逐渐增大,呈“V”形;2)对于正方体坠物,形状平滑,土体阻力较大,损伤范围及深度均较小,损伤深度在撞击中心区域较为一致。

图19 坠物形状对管道纵截面的影响
Fig.19 The effect of dropped object shape on pipeline longitudinal profile
4 结论
海床土体是影响管道受坠物撞击损伤的重要影响因素,通过物理模型试验及有限元数值模拟对其开展研究,得到以下结论:
(1)对于裸置管道,柔性的海床土体可耗散一部分能量,将其转化为管道的整体变形,减轻管道的局部损伤。与刚性海床相比,管道凹痕深度最多可减少21%。而随着海床土体强度的增加,其刚度逐渐增大,耗散的能量则逐渐减少。
(2)针对粘土海床,通过软件二次开发,模拟了正超固结粘土强度随深度变化的规律,该方法可推广到海洋岩土工程的相关分析中。
(3)对于埋置管道,正常固结粘土海床对管道的保护效果更好,与均质粘土海床相比,前者的安全埋深最多可减少1.25 m。管道凹痕深度随土体强度及埋深的增加而明显减小。综合考虑上述土质的影响,2 m左右的埋深可提供有效的保护。
(4)对于埋置管道,坠物与土体之间的摩擦系数对管道的损伤存在一定的影响,摩擦系数的增加会耗散更多的撞击,从而减少管道的损伤程度。摩擦作用随着埋深的增大而趋于明显。
(5)对于埋置管道,坠物的形状越为尖锐,所受土体的阻力越小,管道的损伤程度越为严重。管道与不同形状的坠物碰撞时,其变形特征存在差异:对于锥体、球体坠物,形状尖锐,凹痕深度从撞击中心至管道两端递减。对于正方体坠物,形状平滑,管道的凹痕深度在撞击区域较为一致。这在管道的检修工作中,需特别注意。
[1]方娜, 陈国明, 朱红卫, 等.海底管道泄露事故统计分析[J].油气储运, 2014, 33(1): 99—104.Fang Na, Chen Guoming, Zhu Hongwei, et al.Statistical analysis of leakage accidents of submarine pipeline [J].Oil Gas Storage Transport, 2014, 33(1): 99—104.(in Chinese)
[2]Longva V, Sævik S, Levold, et al.Dynamic simulation of subsea pipeline and trawl board pull-over interaction [J].Marine Sturcutres, 2013, 34(4): 156—184.
[3]Gao Q, Duan M, Liu X, et al.Damage assessment for submarine photoelectric composite cable under anchor impact [J].Applied Ocean Research, 2018, 73: 42—58.
[4]Ghosh S K, Jhonson W, Reid S R, et al.On thin rings and short tubes subjected to centrally opposed concentrated loads [J].International Journal of Mechanical Sciences, 1981, 23(4): 183—194.
[5]Jones N, Birch S E, Birch R B, et al.An experimental study on the lateral impact of fully clamped mild steel pipes [J].Proceedings of the institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 1992, 206(2): 111—127.
[6]Ellinas C P, Walker A C.Damage on offshore tubular bracing members [C]// IABSE Colloquium on Ship Collisions With Bridges and Offshore Structures.Copenhagen, 1983: 253—261.
[7]Bai Y, Pedesren P T.Elastic-plastic behaviour of offshore steel structures under impact loads [J].International Journal of Impact Engineering, 1993, 13(1): 99—115.
[8]Jones N, Shen W Q.A Theoretical study of the lateral impact of fully clamped pipelines [J].Proceedings of the institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 1992, 206(2): 129—146.
[9]Wierzbicki T, Suh M S.Indentation of tubes under combine loading [J].International Journal of Mechanical Sciences, 1988, 30(3/4): 229—248.
[10]粟京.DNV96版《海底管道系统规范》对冲击防护的新规定[J].石油工业技术监督, 1999, 15(2): 15—17.SU Jing.New states of the shock protection in DNV96 version of marine pipe system standard [J].Technology Supervision in Petroleum Industry, 1999, 15(2): 15—17.(in Chinese)
[11]任艳荣, 刘玉标, 顾小芸.弹塑性海床上的管土相互作用分析[J].工程力学, 2004, 21(2): 84—88.Ren Yanrong, Liu Yubiao, Gu Xiaoyun.Analysis of pipe/soil interaction on elastic-plastic seabed [J].Engineering Mechanics, 2004, 21(2): 84—88.(in Chinese)
[12]Robert D J.A modified Mohr-Coulomb model to simulate the behavior of pipelines in unsaturated soil [J].Computers and Geotechnics, 2017, 91: 146—160.
[13]Yu J X, Zhao Y Y, Li T Y, et al.A three-dimensional numerical method to study pipeline deformations due to transverse impacts from dropped anchors [J].Thin-Walled Structures, 2016, 103: 22—32.
[14]杨秀娟, 闫涛, 修宗祥, 等.海底管道受坠物撞击时的弹塑性有限元分析[J].工程力学, 2011, 28(6): 189—194.Yang Xiujuan, Yan Tao, Xiu Zongxiang, et al.Elastic-plastic finite element analysis of submarine pipeline impacted by dropped objects [J].Engineering Mechanics, 2011, 28(6): 189—194.(in Chinese)
[15]Lou M, Ming H Q.Dynamic response analysis of the submarine suspended pipeline impacted by dropped objects based on LS-DYNA [J].Marine science bulletin, 2015, 17(2): 39—55.
[16]Gao P, Duan M L, Gao Q, et al.A prediction method for anchor penetration depth in clays [J].Ships and offshore structures, 2016, 11(7): 782—789.
[17]王懿, 贾旭, 黄俊, 等.基于CEL的船舶抛锚入泥度分析[J].石油机械, 2014, 42(12): 44—47.Wang Yi, Jia Xu, Huang Jun, et al.Analysis of penetration depth of dropped anchor based on CEL [J].China Petroleum Machinery, 2014, 42(12): 44—47.(in Chinese)
[18]DNV-RP-F107 Risk assessment of pipelines protection [S].Oslo: Det Norske Veritas, 2010.
[19]庄元, 宋少桥.海底管线埋深问题研究[J].大连海事大学学报, 2013, 39(1): 61—64.Zhuang Yuan, Song Shaoqiao.Study on the depth of submerged pipeline [J].Jounral of Dalian Maritime University, 2013, 39(1): 61—64.(in Chinese)
[20]李书兆, 李亚, 鲁晓兵.桩基贯入过程中土体大变形分析与流动机理研究[J].工程力学, 2017, 34(6): 157—165.Li Shuzhao, Li Ya, Lu Xiaobing.Large deformation analysis and flow mechanism study of the soil during pile penetration [J].Engineering Mechanics, 2017, 34(6): 157—165.(in Chinese)
[21]Cosham A, Hopkins P.The effect of dents in pipelines-guidance in the pipeline defect assessment manual [J].International Journal of Pressure Vessels and Piping, 2004, 81(2): 127—139.
[22]王自力, 蒋志勇, 顾永宁.船舶碰撞数值仿真的附加质量模型[J].爆炸与冲击, 2002, 22(4): 321—326.Wang Zili, Jiang Zhiyong, Gu Yongning.The added mass model of ships collision simulation [J].Explosion and shock waves, 2002, 22(4): 321—326.(in Chinese)
[23]Noh W F.CEL: A time-dependent, two-space- dimensional, coupled eulerian-lagrangian code [C].Methods in Computational Physics.New York: Academic Press, 1964, 3: 117—179.
[24]Jiang H, Xie Y.A note on the Mohr-Coulomb and Drucker-Prager strength criteria [J].Mechanics Research Communications, 2011, 38(4): 309—314.
[25]殷齐麟, 董胜, 樊敦秋.复杂地层中自升式平台插桩的数值模拟[J].工程力学, 2016, 33(9): 204—211.Yin Qilin, Dong Sheng, Fan Dunqiu.Nuerical simulation of penetration of jack-up platform in complex foundation soils [J].Enginnering Meachinics, 2016, 33(9): 204—211.(in Chinese)
[26]Zeinoddin M, Arabzadeh H, Ezzati M, et al.Response of submarine pipelines to impacts from dropped objects: Bed flexibility effects [J].Internationl Journal of Impact Engineering, 2013, 62(4): 129—141.
[27]GBT 546—2016, 霍尔锚[S].北京: 中国标准出版社, 2016.GBT 546—2016, Hall anchor [S].Beijing: Standards Press of China, 2016.(in Chinese)