冷却塔作为一种薄壳高耸结构，是火/核电厂冷却系统的重要设施。近年来，随着我国电力事业的快速发展，诸多冷却塔得已兴建。冷却塔在运营阶段主要受到自重、风、温度和地震四类荷载作用，冷却塔柔性大的特点使得控制这类结构设计的主要荷载是风荷载[1]。1965年英国渡桥电厂的冷却塔群在一次远低于50年一遇的风速中倒塌三座[2]，至此研究者们开始对冷却塔的内外表面风压分布进行了广泛的研究[3—4]，冷却塔在风荷载作用下的结构安全性也成为工程界关注的重点[5]。目前，冷却塔抗风设计的主要手段是风洞试验[6—7]。随着多点高频同步风压测量系统的应用，使得对冷却塔表面各点风压瞬时同步分布的测量成为可能，这对外荷载分布敏感的柔性空间体系而言显得尤其重要，因为其稳定性将会受到瞬时脉动风压的影响[8]。通过刚性测压风洞试验可以得到各测点在相应地面粗糙度下的风压时程数据，但由于仪器的限制，能同步测量的测点通常相对有限，难以达到结构有限元模型节点数目的程度。如何通过有限点同步测量的结果有效地得到整个塔筒外表面风压分布的动态信息(即风场重构)，如风压在时间域、空间域上相关性等，仍是一个值得研究的问题。这在一个实际工程项目中，是由风洞试验到有限元模型风荷载转化过程中的必经之路。
目前，风场重构的研究方法有本征正交分解 法[9]和基于Hermite插值的方法[10]。本文采用径向基函数(Radial Basis Function，RBF)研究冷却塔风场的有效重构问题。RBF最早是由Hardy[11—12]应用在地形学中的多维散乱数据插值，它对空间维数不敏感且插值精度较高，因而在多元插值中得到了广泛的应用。Franke[13]对29种散乱点插值法综合比较，证明多重二次曲面径向基函数方法具有最好的效果。之后，Micchelli[14]证明了RBF插值的可解性。Schaback[15]研究了插值的存在性、唯一性和收敛性问题，这使得RBF插值理论日趋成熟。近几十年来RBF在诸多学科中都成为了热门研究课题之一，广泛应用于曲面拟合、神经网络、图像处理、偏微分方程数值解、机器学习、湍流分析、气象学等领域中[16—17]。
本文采用函数线性组合的曲面拟合方法，选取RBF作为形函数，重构冷却塔塔筒外表面的风场。以一个150 m高的冷却塔为例，将刚性模型测压风洞试验得到的有限测点塔筒外表面风压分布时程数据与重构的风场进行对比验证，并对RBF在冷却塔风场重构问题的适用性作一些分析；最后，分析了RBF在不同密度点集下重构风场的一致性问题。
1 RBF法原理
1.1 RBF基本表达式
RBF是一种在定义域内仅与距离有关的函数。一些常用的径向基函数如下所示[18]： 多重二次曲面径向基函数(MQ RBF)：
高斯径向基函数：
薄样条径向基函数：
对数型径向基函数：
其中：在三维空间中，X=(x, y, z)被称为拟合点，
被称为RBF的源点，
为拟合点和原点之间的距离；在式(1)和式(2)中，常数C被称为RBF的体型常数，代表着拟合函数非线性效果的强弱，a也为常数。在式(1)中，当n=1时，被称为倒数形式的MQ RBF；当n=2时，被称为线性形式的MQ RBF；当n=3时，被称为立方形式的MQ RBF[18]。文献[19]指出，在一定范围内，随着C值增大，采用式(1)和式(2)进行拟合的误差显著减小，拟合效果变得更好；但C值也不是越大越好，而是应以使拟合结果接近风洞试验的结果为准则。因此，在RBF法的应用中，合理确定C值是个关键。
1.2 基于RBF线性组合的风场重构
冷却塔外表面的风压场p(x, y, z, t)是空间和时间的函数，根据RBF法的基本原理，将任意时刻ti下的风压场p(x, y, z, ti)可展开成如下形式的级数：
其中：k为正整数；
是已知的形函数；dlti为待定系数。本文选取倒数形式的MQ RBF作为已知的形函数，根据1.1节的内容，在式(1)中取n=1可得到：
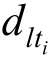求出如下。如果已知时刻ti下m个测点 X1, X2, …, Xm的风压数据，则可建立起如下的线性方 程组：
其中：
且
为ti时刻下测点对应的测量风压。故式(7)的最小二乘解为：
从式(6)可知，Φ是仅与测点和源点空间位置有关的量，根据各时刻下测点对应的风压，可求得各时刻下的 dti 。
各时刻下的
可组成矩阵
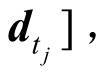再根据重构点和源点的空间位置关系矩阵K，即可求得重构点各时刻下的风压p′(x, y, z, t)，即：
其中：
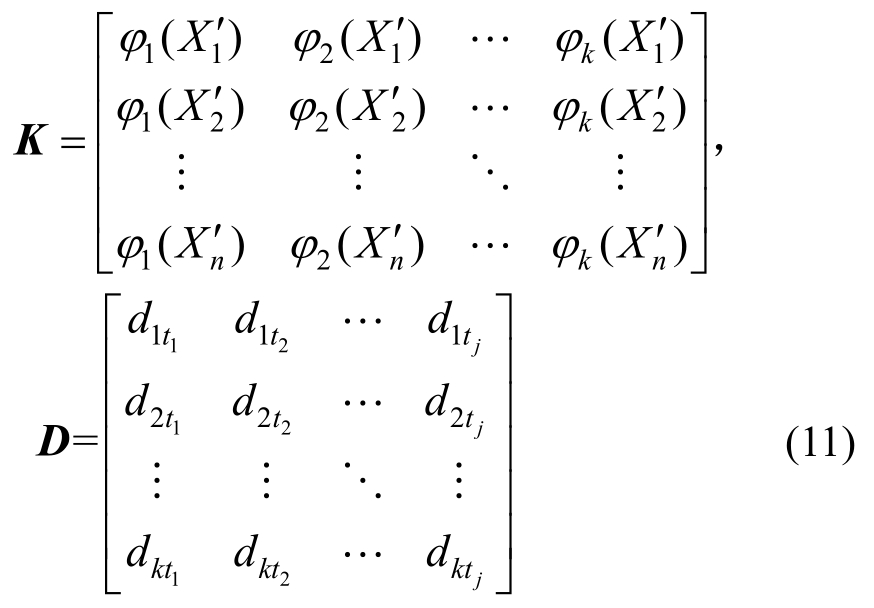
且
为各重构点空间位置，dktj中的k代表选取形函数的个数，tj代表最后一个时刻。
2 RBF法应用
本文以一个典型冷却塔为研究对象，应用RBF法进行冷却塔塔筒外表面的风场重构。
2.1 典型冷却塔风洞试验
选用某地区150 m高的自然通风冷却塔进行风洞试验，该冷却塔几何尺寸为：塔高H=150 m，零米直径112.2 m，出口直径72.0 m，喉部直径66.7 m，支柱采用46对V字型支柱，环板基础。本次试验是在同济大学TJ-3号风洞中完成的，试验对象为1∶250测压模型，在待测模型沿通风筒环向与子午向布置36×12个外表面压力测点、36×4个内表面压力测点，其表面测点分布如图1(a)所示。模拟出的风场为B类紊流场，试验参考点选在模型塔顶处。试验风速为10 m/s，模型通风筒表面粘贴均匀分布的36条3层粗糙纸带(此条件下雷诺数效应模拟为最好)。采用同步扫描测压技术，测压信号采样频率为300 Hz，每个测点采样时长为60 s，即采样样本总长度为18000个数据。
图1 风洞试验模型
Fig.1 Model for wind tunnel test
2.2 基于RBF重构的风场
试验模型的外表面共有432个测点，当k=432时，在式(5)中p(x,y,z,t)的精度最高。原则上源点任意选取，但在试算过程中发现，在冷却塔外表面上均匀选取432个源点时，重构的风场在冷却塔的底部会出现一些稍大的偏差，本文取一种特殊的源点，即取432个测点作为RBF法的源点。由式(6)得到432个倒数形式的MQ RBF。由测点和源点的空间位置关系求得Φ矩阵(432行×432列)，根据风洞试验得到的各测点风压时程数据及式(9)求得各时刻下的 dti，进而得到D矩阵(432行×18000列)。然后将风场重构成均匀分布的10032个点的点集(环向176×子午向57)，由重构点与源点的空间位置关系求得K矩阵(10032行×432列)。最后，根据式(10)得到各重构点各时刻下的风压p′(x, y, z, t)。
2.3 风场重构结果分析
2.3.1 风压系数分布
本文比较的指标是风压系数。根据风洞试验的测点压力数据计算时程风压系数，可按下式求得：
式中：CPit为t时刻测点i处的风压系数；Pit为t时刻作用在测点i处的压力，表面压力相对冷却塔塔壁向内为正、向外为负；P0和P∞分别为试验时参考高度处的平均总压和平均静压。
在结构风工程中，基于风洞试验确定的平均风压系数
和脉动风压系数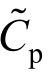
可定义如下[8]：
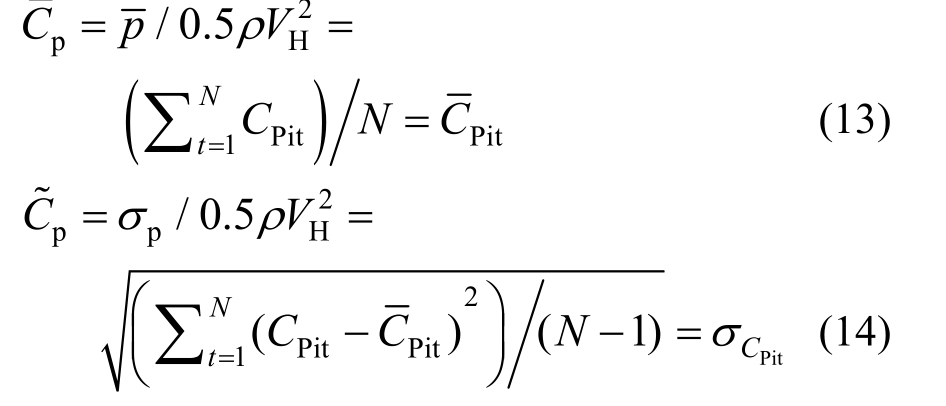
式中：
为各测点的所测风压的平均值及标准差；ρ为空气密度；VH为参考风速；N为样本 总数。
2.3.2 风洞试验与重构风场的对比结果
为判别一种风场重构方法是否合理，首先应该查看的是每个时刻重构风场的风压系数与由风洞试验得到的风压系数的相对误差。原则上讲，应该比较每一位置处的结果，但风洞试验模型仅432个测点，而对应的重构点却有10032个，所以比较每个位置处时程风压系数的相对误差是不现实的。事实上，只要查看某些特征位置处时程风压系数的相对误差就足以反映该重构方法是否合理。本文仅查看冷却塔喉部高度处迎风点和背风点在不同时刻下重构前后风压系数的相对误差。本文主要以冷却塔迎风子午线为0°，沿逆时针旋转取若干条子午线上的风压系数进行比较。对于对称结构，选取半边结构的若干角度即可说明整个冷却塔的风压系数分布情况。本文选择作为对比的子午线角度分别为0°、70°、90°、110°、180°。其中，0°、90°和180°分别为迎风向、横风向和背风向；70°左右子午线上的子午向压力是工程中研究的重点，而110°则是其对称角度。此外，对于冷却塔这种空间结构，重构风场前后环向的风场特性是否保持一致也是值得注意的问题；在RBF中C值的选取方式目前尚未统一，C值与相邻测点的距离有直接关系。文献[19]认为，理论上RBF的C值越大拟合的精度越高，本文选择3个不同的C值，即：最小值Cmin(最小正整数1)、式(9)中的矩阵不出现接近奇异值警告时的最大整数值Cmax(对于本例为5700)、最大整数值的一半0.5 Cmax(对于本例为2850)，比较不同C值对风场重构的影响。因此，本文比较的内容主要分为以下四个方面：
1)重构风场得到的时程风压系数与由风洞试验得到的时程风压系数的比较；
2)重构风场与风洞试验结果在各子午线上风压系数的比较；
3)重构风场与风洞试验结果在若干高度h处的环向上风压系数的比较；
4)RBF中3种不同C值对风场重构影响的比较。
这四个方面的比较结果如图2～图5所示。
图2为各时刻下重构前后喉部高度迎风点和背风点的风压系数相对误差图。从图2可以看出，当C=0.5Cmax时，在整个采样时间内，时程风压系数相对误差基本上都在5%以内，这说明此时重构的风场在每个时刻下的值都是合理的。而当C=Cmin和C=Cmax时，时程风压系数的相对误差均反映出与风洞试验结果有一定的差距。
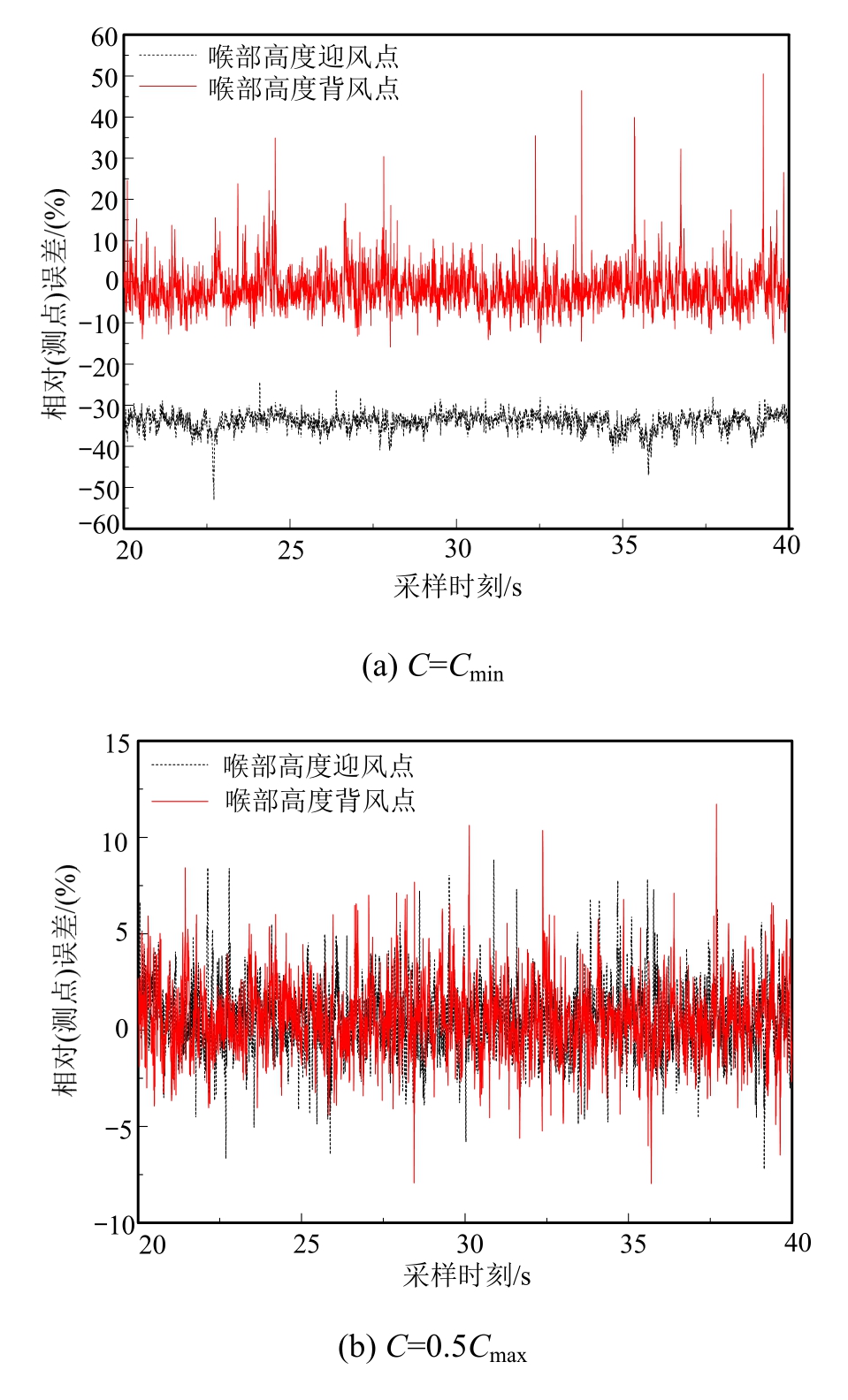
图2 各时刻下重构前后喉部高度迎风点、 背风点的风压系数相对误差
Fig.2 Relative errors of wind pressure coefficients of windward and leeward points at throat height before and after reconstruction at every sample point
图3 重构前后各子午向上脉动风压系数对比结果
Fig.3 Comparison of fluctuating wind pressure coefficient at several meridian lines before and after reconstruction
从图3和图4可以看出，当C=0.5 Cmax时，重构风场的风压系数基本与风洞试验结果完全一致。而当C=Cmin时，重构风场只有在110°和180°子午线上的平均风压系数比较接近风洞试验结果， 而其它子午线上的风压系数都与风洞试验结果有一定的差异。当C=Cmax时，重构风场各子午线上的风压系数与风洞试验结果差异的分布都较为离散。这表明随着C值的增大，重构风场风压系数的随高度的变化变的更加趋于非线性。综合可知，当C=0.5 Cmax时，重构风场各子午线上的风压系数与风洞试验结果一致性最好；而C值取最大值时，并不能再进一步提高与风洞试验结果一致的精度，反而会导致风场的分布更加复杂。
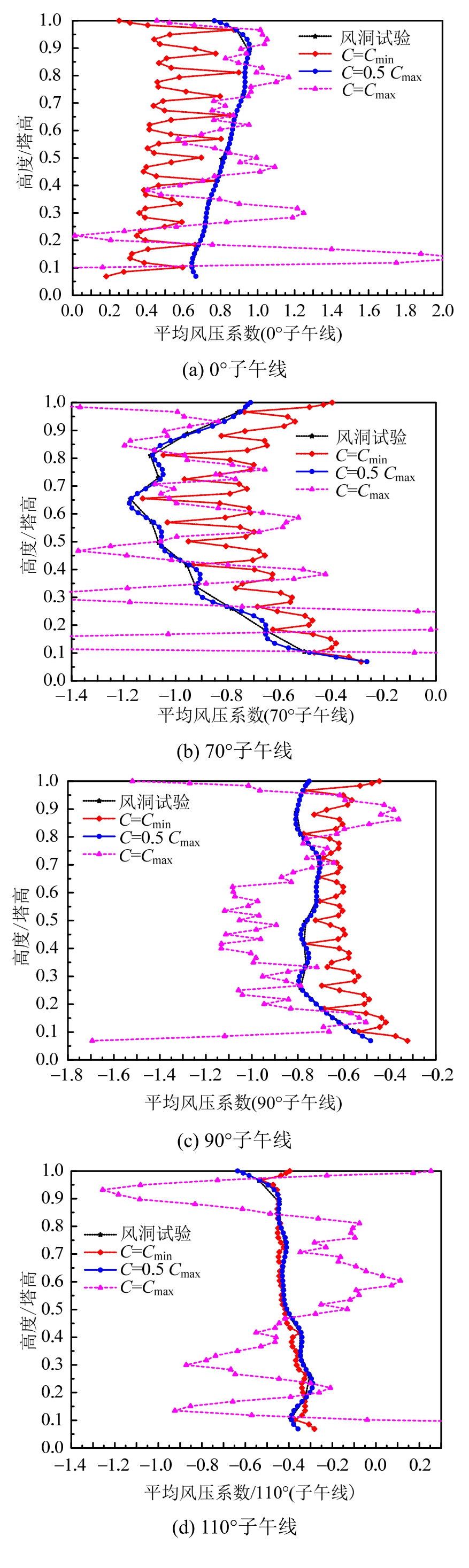
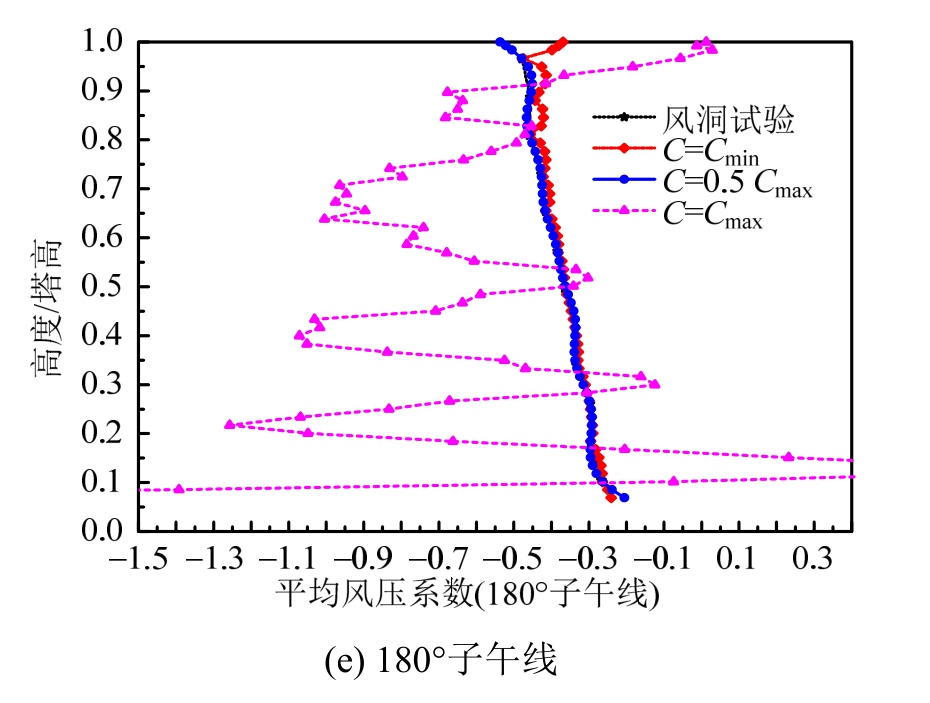
图4 重构前后各子午向上平均风压系数对比结果
Fig.4 Comparison of mean wind pressure coefficient at several meridian lines before and after reconstruction
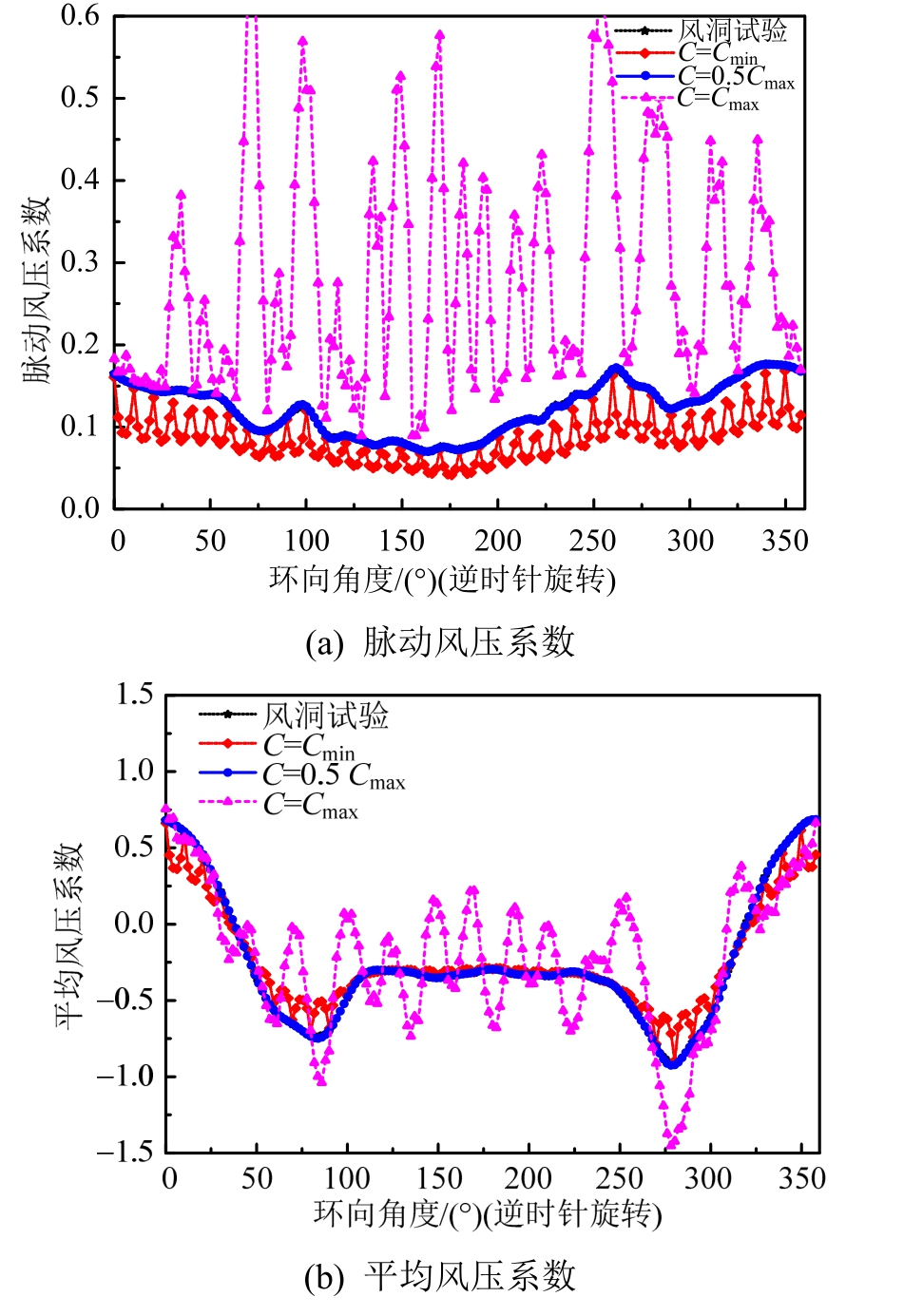
图5 重构前后0.18倍塔高处环向上的风压系数对比结果
Fig.5 Comparison of wind pressure coefficient in latitude direction at h/H=0.18 before and after reconstruction
图5和图6为重构风场前后两个不同高度处环向上风压系数的对比结果。从这两个图中可以看出，当C=0.5 Cmax时，冷却塔底部(0.18倍塔高处)环向上和喉部高度环向上的风压系数基本与风洞试验结果完全一致。而C=Cmin或C=Cmax时，重构的风场与风洞试验结果都有一定的差异。且C=Cmax时，重构的风场的分布最为复杂。因此，C值不宜取得过大。
图6 重构前后喉部高度处环向上的风压系数对比结果
Fig.6 Comparison of wind pressure coefficient in latitude direction at throat height before and after reconstruction
2.3.3 重构风场点集密度不同的对比结果
重构冷却塔风场的方法，应该不论重构点集的疏密，都能与原始风场(风洞试验的结果)保持一致。本文上述重构风场的点集为环向176×子午向57，现在重构另一风场，其点集的密度为环向176×子午向111，即对子午向上加密一倍左右。针对同样的冷却塔模型进行风场重构，其中这两种点集在重构风场过程中取相同的源点，RBF法中C=0.5 Cmax。0°、90°、180°三条子午线上的比较结果如图7和图8所示。
从图7和图8可以看出，两种重构的风场在所有选择的子午线上风压系数都重合在一起，这说明重构的风场无论是沿子午向取57个点还是加密到111个点，都能真实反映原始风场的风压分布特性，从而证明了本文重构冷却塔风场方法的合理性。这部分研究结果也为后续的冷却塔三维风致振动瞬态动力分析指明了方向，即可以在子午线上选择不太密集的点集进行风场重构而不会影响重构风场的精度，这样做的优势是在瞬态动力分析时可使计算机占用的资源相对减少、计算时间大幅度缩减。
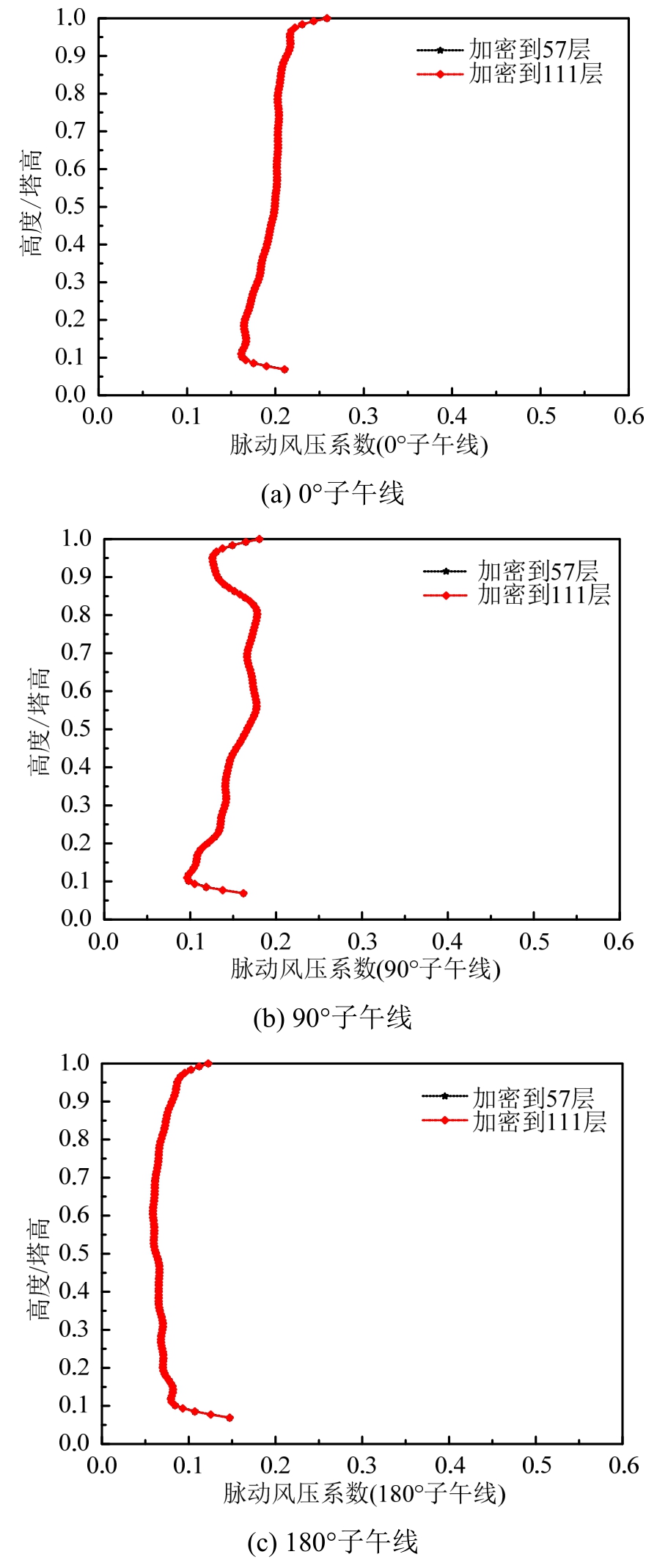
图7 两种不同点集密度重构风场各子午线上脉动风压 系数对比结果
Fig.7 Comparison of fluctuating wind pressure coefficients at several meridian lines between two densities of reconstruction points
图8 两种不同点集密度重构风场各子午线上平均风压 系数对比结果
Fig.8 Comparison of mean wind pressure coefficients at several meridian lines between two densities of reconstruction points
3 结论
本文基于RBF法对冷却塔的塔筒外表面进行了风场重构；通过比较喉部高度处迎风点和背风点相对于重构前对应点时程风压系数的相对误差，分析了3个不同C值对重构风场的影响，得出当C=0.5 Cmax时，在整个采样时间内，绝大部分时程风压系数相对误差均在5%以内；通过比较重构前后不同子午向和环向的风压系数，证明了C=0.5 Cmax时重构前后风压系数的一致性；最后比较了两种不同点集密度重构风场的风场特性。基于以上分析可以得出如下结论：
(1)取C=0.5 Cmax即可使重构前后风压系数基本一致，再增加C值也未必能再进一步提高重构风场与风洞试验结果一致的精度，反而可能会导致重构风场的风压分布更加复杂。虽然该结论是基于150 m冷却塔得到的结果，但由于目前工程中所采用的双曲线型冷却塔形状一般不会有太大变化，因此本文认为，对于任意高度和形状的冷却塔，基于RBF法进行风场重构时，C值都可取为0.5 Cmax。
(2)在均匀布置的重构点达到一定密度时，比如达到测点数的20倍以上时，已能够充分反映原始风场的特性，此时再对重构点进一步加密并不会使重构风场有显著改变。该结论为优化冷却塔结构的风振瞬态动力分析提供了依据。
(3)基于RBF法进行冷却塔的风场重构是一种既简单又有效的方法。该方法不仅适用于冷却塔的风场重构，对其它类型的大型空间结构的风场重构也是适用的。
[1]张军锋, 葛耀君, 赵林.双曲冷却塔结构特性新认识[J].工程力学, 2013, 30(6): 67—76.Zhang Junfeng.Ge Yaojun, Zhao Lin.New perceptions on the structure behavior of hyperboloidal cooling towers [J].Engineering Mechanics, 2013, 30(6): 67—76.(in Chinese)
[2]Niemann H J, Kopper H D.Influence of adjacent buildings on wind effects on cooling towers [J].Engineering Structures, 1998, 20(10): 874—880.
[3]Armitt J.Wind loading on cooling towers [J].Journal of the Structural Division, 1980, 106(3): 623—641.
[4]Sun T F, Zhou L M.Wind pressure distribution around a ribless hyperbolic cooling tower [J].Journal of Wind Engineering & Industrial Aerodynamics, 1983, 14(1): 181—192.
[5]Viladkar M N, Karisiddappa, Bhargava P, et al.Static soil-structure interaction response of hyperbolic cooling towers to symmetrical wind loads [J].Engineering Structures, 2006, 28(9): 1236—1251.
[6]Cheng X, Zhao L, Ge Y, et al.Wind effects on rough-walled and smooth-walled large cooling towers [J].Advances in Structural Engineering, 2017.20(6): 843—864.
[7]田凯强, 秦其伟, 郑云飞, 等.大型冷却塔表面风压分布特性的试验研究[J].工程力学, 2017, 34: 269—272.Tian Kaiqiang, Qin Qiwei, Zheng Yunfei, et al.Experimental research on wind pressure distribution of cooling towers [J].Engineering Mechanics, 2017, 34: 269—272.(in Chinese)
[8]李元齐, 沈祖炎.本征正交分解法在曲面模型风场重构中的应用[J].同济大学学报(自然科学版), 2006, 34(1): 22—26. Li Yuanqi, Shen Zuyan.Application of the proper orthogonal decomposition method to wind field reconstruction of models with curved surfaces [J].Journal of Tongji University (Natural Science), 2006, 34(1): 22—26.(in Chinese)
[9]Huang D, He S, He X, et al.Prediction of wind loads on high-rise building using a BP neural network combined with POD [J].Journal of Wind Engineering & Industrial Aerodynamics, 2017, 170: 1—17.
[10]陶天友, 王浩.基于Hermite插值的简化风场模拟[J].工程力学, 2017, 34(3): 182—188.Tao Tianyou, Wang Hao.Reduced simulation of the wind field based on Hermite interpolation [J].Engineering Mechanics, 2017, 34(3): 182—188.(in Chinese)
[11]Hardy R L.Multiquadric equations of topography and other irregular surfaces [J].Journal of Geophysical Research, 1971, 76(8): 1905—1915.
[12]Hardy R L.Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968-1988 [J].Computers & Mathematics with Applications, 1990, 19(8): 163—208.
[13]Franke R.Scattered data interpolation: Tests of some method [J].Mathematics of Computation, 1982, 157(157): 181—200.
[14]Micchelli C A.Interpolation of scattered data: Distance matrices and conditionally positive definite functions [J].Constructive Approximation, 1986, 2(1): 11—22.
[15]Schaback R.A unified theory of radial basis functions : Native Hilbert spaces for radial basis functions II [J].Journal of Computational & Applied Mathematics, 2000, 121(1/2): 165—177.
[16]Wang L, Wang Z, Qian Z.A meshfree method for inverse wave propagation using collocation and radial basis functions [J].Computer Methods in Applied Mechanics & Engineering, 2017, 322(1): 311—350.
[17]Wang L, Chu F, Zhong Z.Study of radial basis collocation method for wave propagation [J].Engineering Analysis with Boundary Elements, 2013, 37(2): 453—463.
[18]Hu H Y, Chen J S, Hu W.Weighted radial basis collocation method for boundary value problems [J].International Journal for Numerical Methods in Engineering, 2010, 69(13): 2736—2757.
[19]Madych W R.Miscellaneous error bounds for multiquadric and related interpolators [J].Computers & Mathematics with Applications, 1992, 24(12): 121—138.