近年来，基于不确定性分析的边坡稳定性和风险评价受到国内外学者的日益重视。边坡稳定性和风险评价中涉及到不确定性因素如模型不确定性、土体分层不确定性、土体参数空间变异性等[1—2]。传统的单一安全系数法不能有效地考虑土体参数空间变异性对边坡稳定性的影响，亟需发展基于概率理论的可靠度与风险分析方法。目前边坡稳定性可靠度分析方法大多数关注于边坡失效概率计算，对于边坡失稳后果关注度不够，仅仅考虑边坡失效概率的边坡设计方案不一定十分合理[3]。例如，一个位于关键交通枢纽处的边坡，发生浅层滑动(滑体体积较小)与深层滑动(滑体体积较大)对交通的影响是截然不同的。如果该边坡浅层滑动可能性较大，但其产生的后果较小，可忽略不计；相比之下，尽管深层滑动可能性较低，但其后果很严重。如果仅仅根据概率分析结果，工程师可能会选择仅针对浅层滑动进行治理。为了给岩土工程师提供更科学合理的决策依据，亟需在可靠度分析基础上进一步考虑边坡失效后果，即对边坡进行失效风险评估[4]，进而制定基于风险的加固方案。总的来说，边坡风险评估近年来受到越来越多学者的关注，如Huang等[5]基于有限元极限分析提出了以滑块体积作为等效失效后果的边坡定量风险评价方法。Li等[6]在有限元(FEM)框架内提出了基于子集模拟的边坡高效风险评估方法，并探讨了边坡在不同失效概率水平下的风险变化规律。蒋水华等[7]、Cheng等[8]提出了考虑土体参数空间变异性的边坡系统风险评估方法。Li等[9]、Zhang等[10]、Jiang等[11]在极限平衡法(LEM)框架内提出了基于代表性滑面的边坡风险评价方法。
上述研究[9—11]中边坡系统风险评价仅针对边坡变临界滑面(即每次数值模拟中安全系数最小的滑面)。然而对于一次特定的数值模拟，边坡可能同时存在多个满足失效条件(如安全系数FS＜1)的滑面，如果仅基于变临界滑动面进行边坡风险分析显然会低估边坡的系统风险，导致偏危险的设计方案。Cheng等[12]、Reale等[13]、Tun等[14]指出在边坡稳定性分析中应充分考虑最小安全系数以及那些安全系数与最小安全系数接近的滑面。张鲁渝[15]、闫超等[16]、薛海斌等[17]也指出与边坡最小安全系数接近的滑面一般有多条，这些滑面在边坡风险分析中应该得到合理地考虑。因此，非常有必要研究考虑参数空间变异性的边坡多失效模式系统风险分析问题。遗憾的是，由于滑面间存在复杂相关性且其滑块体积在空间上重叠交错[10]，迄今为止很少有学者在边坡系统风险评价中针对此问题进行研究。
另一方面，传统的边坡概率稳定性分析方法大多关注于边坡的系统失效概率，而忽视了对边坡关键失效区域的识别[13,18—22]。识别关键失效区域能为边坡风险的规避、转移提供参考。此外，传统的概率分析结果如边坡系统失效概率等常以数字的形式呈现给工程师，这些结果往往难以被工程师理解，一定程度上限制了概率分析方法在实际工程中的应用[23—24]。
针对上述问题，本文提出了考虑边坡多失效模式的区域概率风险分析方法。首先介绍了土体参数空间变异性模拟方法，给出了区域概率的概念，通过将边坡区域离散为一系列空间上相互独立的区域单元，将滑面失效概率估计转换为每个区域单元的失效概率估计，建立了以区域概率定量表征边坡稳定性的方法，建立了基于区域概率的边坡系统风险评价公式，探讨了该公式的适用性。最后以一不排水黏性土坡为例阐明了所提方法的有效性。
1 边坡土体参数空间变异性模拟
土体参数空间变异性表现为空间任意两点土体特性参数存在自相关性[25]，且随着两点间距离的增加自相关性逐渐减弱，通常采用随机场模型来表征土体参数空间变异性[26]。由于指数型自相关函数形式简单且便于计算，同时考虑到指数型自相关函数不会产生非正定的相关系数矩阵，便于采用乔列斯基分解中点法生成随机场，众多学者采用指数型相关函数表征土体参数的空间相关性[5—6,11,20,27]。本文也采用式(1)所示的指数型自相关函数：
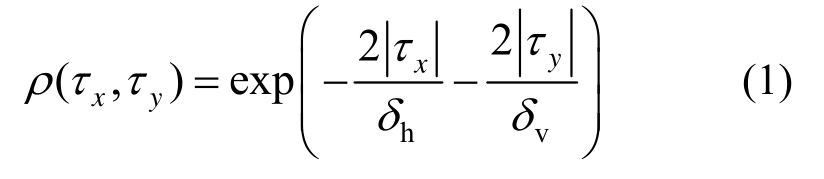
式中：ρ(τx,τy)代表在x方向相距为τx、y方向相距τy的两点间土体力学参数的相关性系数；δh和 δv分别为水平波动范围和垂直波动范围。对于给定的δh和δv，通过式(1)可以获得土体参数相关系数矩阵ρ，对相关系数矩阵进行乔列斯基分解(LTL=ρ )可得土体参数的正态随机场可表示为Xt=μt+σtLU，式中Xt为参数在不同空间位置处的值，μt和σt分别代表土体参数的均值与标准差，U为标准正态随机向量，t代表土体参数类型如不排水抗剪强度c、摩擦角φ等。在实际工程应用中，波动范围δh和δv可通过土体原位测试、室内试验及静力触探试验等得到的土体试验数据统计分析得到[28—29]。
2 区域概率
由于空间变异性等因素的影响，边坡存在多个潜在的破坏模式，边坡可靠度问题是一个系统可靠度问题[30—33]。传统的边坡稳定性分析方法通过求解边坡滑面的失效概率来估计边坡系统失效概率。在边坡稳定性分析中，如果某个滑面FS＜1则表明边坡沿该滑面破坏。在实际工程中，对于地质条件较复杂边坡，边坡的破坏常常伴随多个滑面的同时失效[15,17]。在数值模拟中，由于模型不确定性和岩土体参数不确定性等因素影响，对于一次数值模拟，存在多个可能的失效滑面情况，如图1给出了基于有限元法和极限平衡法进行边坡稳定性分析中某次数值模拟中出现的多个失效滑面，理论上说这些滑面都满足失效条件FS＜1。在边坡稳定性概率方法中，一般根据变临界滑面的安全系数来判断边坡是否失稳，在此基础上定义的边坡的系统失效概率为
式中：X为边坡土体不确定参数；FSmin为边坡最小安全系数；I{FSmin(X)}为示性函数，若FSmin＜1则I{FSmin(X)}=1，若FSmin≥1则I{FSmin(X)}=0。在目前边坡风险分析中，风险评估同样也是基于变临界滑动面。如前所述，边坡失稳可能同时存在多个潜在失效滑动面。因此，在对边坡进行风险评价时，与变临界滑面安全系数接近的滑面或其它安全系数小于1的潜在破坏滑面的风险也应该合理地考虑。遗憾的是，现有研究未能有效地考虑这些滑面的风险。为此，提出了区域概率的概念，将边坡滑面失效概率转化为一系列离散的边坡不同区域的“失效”概率(即边坡破坏时该区域被包含在滑块内的可能性)，下节给出了边坡区域概率的定义及计算过程。
图1 边坡稳定分析一次数值实现中多个失效滑面
Fig.1 Multiple failure slip surfaces in a certain numerical simulation
2.1 区域概率定义
如前所述，在一次确定的数值模拟中可能同时存在多个失效滑面，此时，边坡坡体区域会被这些滑面划分为一系列不规则小区域，这些小区域被包含在不同滑块中的可能性也不相同，本文定义这种可能性为区域失效概率，用来表征边坡不同区域的“失效”概率。下面以图2所示三层土坡为例说明区域概率的概念，为简化说明，假设该边坡仅包含两个可能的失效模式F1、F2，这两个滑面将边坡坡体区域划分为四个区域：区域I、区域II、区域III和模式F1、F2没有包含的区域。当采用数值方法如LEM去分析该边坡的稳定性时，可能出现四种情况：仅F1失稳，仅F2失稳、F1、F2都失稳和F1、F2都不失稳。在边坡稳定性概率分析中，这四种情况可能出现在不同的随机数值实现中，表明区域I～III被包含在边坡失效滑块中的可能性是不同的。可以看出区域I和II的失效概率等于F1和F2的失效概率，而区域III的失效概率等于边坡系统失效概率。以上描述数学表达式为：
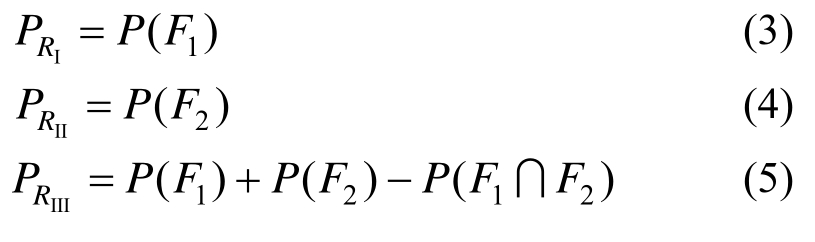
式中：P(F1)P(F2)≤P(F1∩F2)≤min{P(F1)，P(F2)}，P(F1∩F2)的值与模式F1和F2的相关性有关，当F1和F2相互独立时，P(F1∩F2)=P(F1)P(F2)；当F1和F2完全相关时，P(F1∩F2)=min{P(F1)，P(F2)}。当仅有两个失效模式时，用式(5)估计边坡不同区域的失效概率非常简单。遗憾的是，边坡系统一般包含大量的滑动面(如图3所示)，此时用式(5)估计边坡区域概率较为复杂。当有n个模式存在时，式(5)进一步表达为[35]：
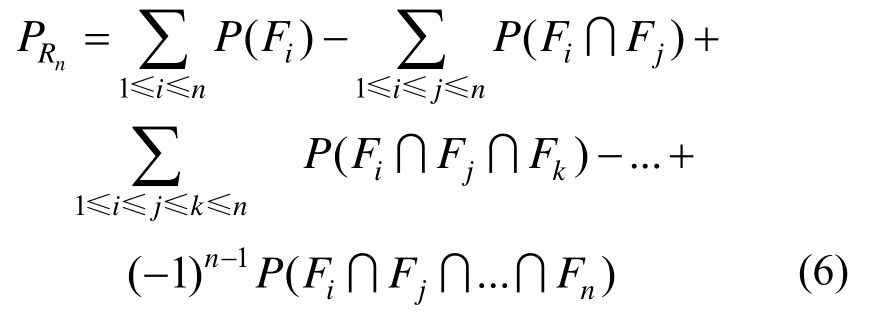
式中：PRn代表被所有n个滑面包含区域的失效概率；P(Fi)代表模式Fi的失效概率。可以看出，随着滑面数目的增加，根据式(6)估计 PRn变得越来越困难。此外，增加的滑面会划分边坡坡体为无数不规 则形状的小区域，导致这些小区域难以用数学方法来描述。同时注意到，区域概率的估计依赖于该区域与失效滑面的相对位置，这进一步使得采用式(6)直接计算 PRn难度增加。
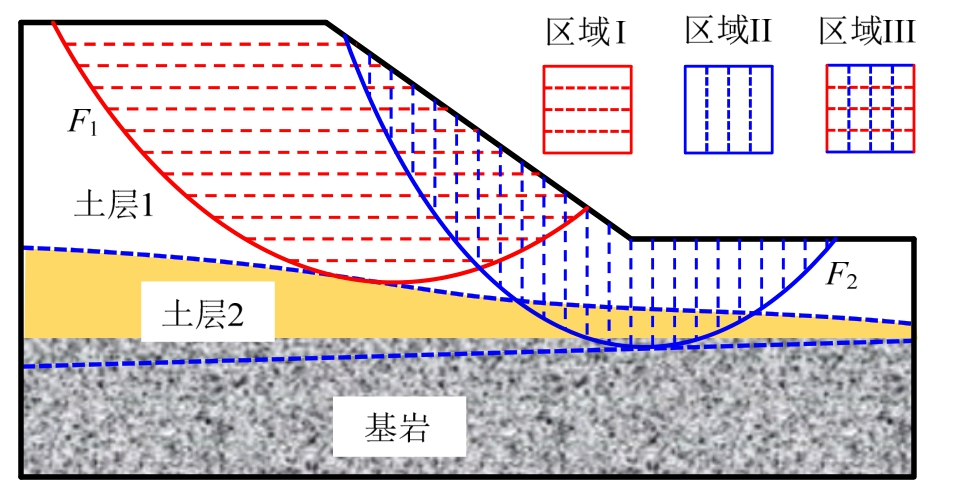
图2 区域概率示意图
Fig.2 Illustration of region probability
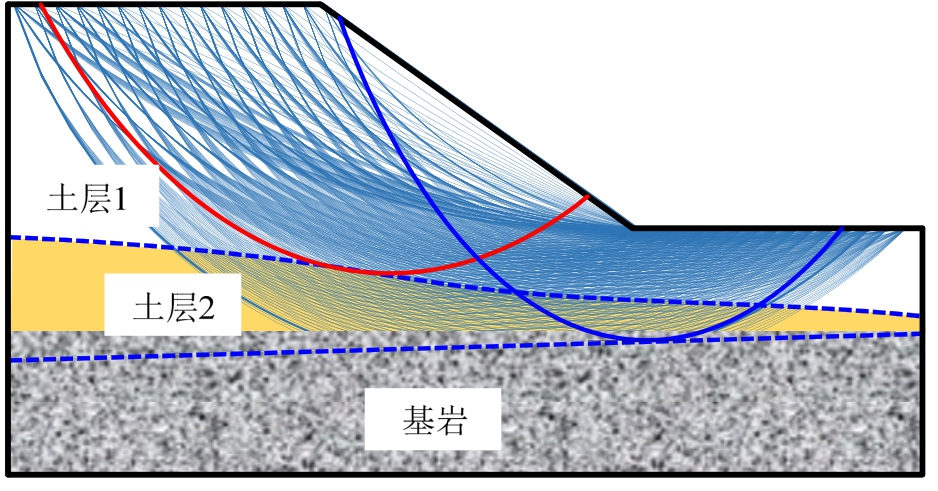
图3 包含大量滑面的区域概率示意图
Fig.3 Region probability for a larger number of failure modes
2.2 区域概率计算
为了方便计算区域概率，将边坡区域离散为一系列规则形状的小区域。图4给出了图2所示边坡离散后的区域。边坡区域离散后，区域失效概率的估计转化为计算每个区域被包含在失效滑体中的次数，这可以通过MCS实现。具体执行过程为：1)将边坡坡体离散为一系列规则小区域。如图4中矩形和三角形代表离散后的小区域，在边坡稳定性分析之前，先估计这些小区域的中心坐标。2)进行边坡稳定性分析，这里采用简化Bishop法计算边坡安全系数，如在图4中计算模式F1和F2的安全系数。3)确定失效滑面(即FS＜1的滑面)，将包含在这些失效滑面中的区域视为失效区域。图4(a)～ 图4(c)中斜线区域表示模式F1失效、F2失效、模式F1和F2同时失效时对应的失效区域。4)执行MCS模拟NT次，计算每个区域的失效次数Ni，区域失效概率计算公式为：
式中，Nk为第k个区域的失效次数。
图4 基于离散后小区域的区域概率估计
Fig.4 Estimation of region probability based on discretized small regions
根据每个小区域的失效概率，可以绘制区域概率图。区域概率图采用不同颜色标识边坡不同位置 的失效可能性。该图可以为岩土工程师提供一个简单、直观的可视化工具，能够在一定程度上帮助工程师进行风险决策。值得指出的是，式(7)表达边坡滑面的失效概率为一系列互不重叠的规则小区域。通过考虑包含在多失效滑面中的区域为失效区域，式(7)不仅能够有效地考虑每次随机模拟数值实现中的所有失效滑面，而且能够回避这些失效滑面的滑块体积在空间上重叠交错的问题，为合理地评价边坡多失效模式系统风险提供了一种可行的工具。
3 边坡系统风险评估
本节介绍基于区域概率的边坡系统风险评价方法。边坡风险定义为边坡失效概率与相应失效后果的乘积。边坡失效后果具有时空差异性，依赖于边坡失效时间、附近建筑物分布及人口密集程度等，准确地量化边坡失效后果比较困难。一般来说，边坡失效后果与边坡滑动体积紧密相关，滑动体积较大的滑坡往往导致更严重的后果[9]，因此，在边坡风险评价中，可采用边坡滑块面积(二维问题)或体积(三维问题)来近似表示边坡失效后果[5—6,9—11,36—37]。本文也采用边坡滑块面积作为近似的边坡失效后果。
3.1 基于区域概率的风险评估方法
根据2.2节估计的边坡区域概率Pk，边坡风险可表示为：
式中：k是边坡坡体离散后的区域单元编号，k=1,2,…,Nr；Nr是离散后的区域数目；Pk是第k个区域的失效概率；Vk是第k个区域的面积(对于三维边坡Vk为体积)，Vk也可视为一个由第k个区域单元失效引起的广义的失效后果指标。式(8)将传统的基于滑面的风险评估转化为基于边坡失效区域的风险评估，与边坡滑面不同的是离散后的边坡区域在空间上相互独立，这样就可有效地避免边坡系统风险评价中多失效滑面间复杂相关性问题，从而可以有效地考虑边坡多失效模式风险评估问题。
3.2 本文方法与现有边坡风险评估方法的比较
边坡风险一般定义为边坡单一失效模式的失效概率与相应失效后果的乘积。以边坡系统中存在的第i个潜在滑面为例，风险计算公式为：
式中：P(Fi)为第i个失效模式的失效概率；Ci是失效模式Fi对应的失效后果，即第i个滑面表示的面积。式(9)适用于边坡单一失效模式的风险评估[5—6]。如前所述，边坡系统通常存在大量潜在滑面，任何一个滑面破坏都可能导致边坡失稳。此时，式(9)的适用性受到限制。为此，Huang等[5]、Li等[6]进一步提出了式(9)更广义的形式：
式中：nf代表NT次MCS产生的失效样本数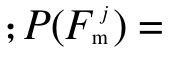
1/NT和
分别代表第j个失效样本对应的变临界滑面失效概率和其失效后果。尽管Li等[9]、Zhang 等[10]、Jiang等[11]也提出了估计边坡多滑面的系统风险计算公式，这些公式虽然在形式上与式(10)不同，但是与式(10)具有相同的内涵，这些公式也仅仅能考虑变临界滑面的失效后果，即每次随机模拟中只考虑1个滑面的风险，难以考虑每次随机模拟中其它潜在滑面的失效后果。简而言之，在边坡系统风险评估中式(10)并不能有效地考虑每次随机模拟中多个潜在失效模式的失效后果。
综上所述，传统方法式(9)仅能考虑单一固定滑面的风险。式(10)仅能考虑变临界确定性滑面的风险，本文所提式(8)能够考虑边坡每次随机模拟中同时出现的多失效滑面风险。在每次随机模拟中，当假设位于单一固定滑面或变临界滑面内的边坡区域为失效区域时，式(8)简化为单一固定滑面或变临界滑面的风险。因此，式(8)可视为广义风险评价计算公式。下面给出证明：
式中：nf,k代表第k区域单元失效的样本数目；NT代表MCS模拟样本数；nf代表MCS产生的失效样本数；Ij(k)为示性函数，若第j失效样本导致第k个区域单元失效，则Ij(k)=1，反之，Ij(k)=0；
和
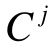分别代表第j个失效样本对应的失效概率和失效后果。在每次随机模拟中，当假设位于变临界滑面内的区域为失效区域时，可以得到
此时式(11)可表达为：
即式(8)与式(10)等价。
在每次随机模拟中，当假设位于单一固定滑面如第i个滑面内的区域为失效区域时，可以得到
此时式(11)中nf代表边坡系统中第i个滑面对应的失效样本数，式(11)可进一步表达为：
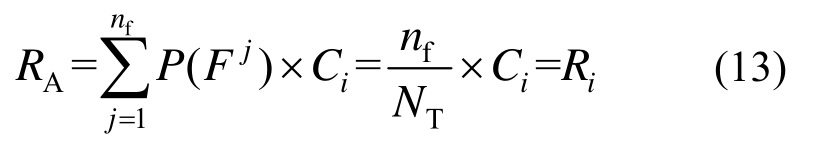
即式(8)与式(9)等价。可见，与式(9)和式(10)相比，式(8)通用性更强。
4 计算流程
为了有效地估计边坡系统多失效模式导致的系统风险，本文提出了考虑边坡多失效模式的区域概率风险分析方法，图5给出了该方法的计算流程图，具体步骤如下：
1)确定边坡土体参数统计值如均值、标准差、相关性、分布类型等，建立边坡稳定性数值分析模型。
2)为了便于随机场离散及边坡区域概率估计，将边坡区域离散为一系列规则形状的小区域。
3)根据步骤1)的信息产生边坡土体参数随机场的NT实现，设j=1。
4)基于参数随机场第j次实现评价边坡稳定性，识别安全系数小于1滑面内的小区域，认为这些小区域在该次边坡随机场实现中失效。
5)重复步骤4)至j=NT，计算边坡区域失效概率，并根据式(8)评价边坡系统风险。
基于上述5个步骤，本文编制了基于MATLAB的计算程序，用户只需要输入边坡土体参数不确定性信息、边坡几何尺寸信息及MCS模拟次数NT，就可以确定边坡的区域概率图和边坡系统风险。
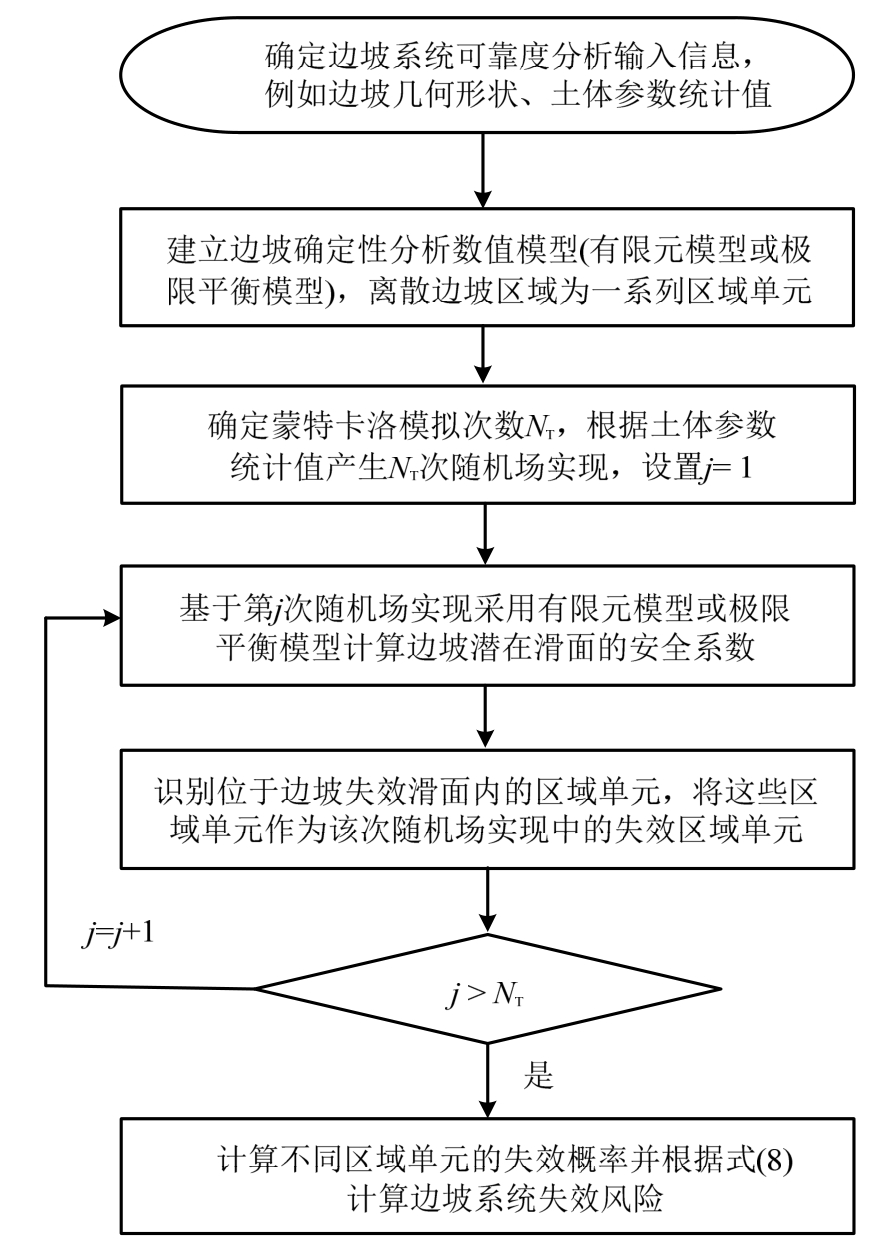
图5 区域概率估计及边坡系统风险评估流程图
Fig.5 Flow chart of assessment of region probability and slope system risk
5 不排水黏性土坡
5.1 算例介绍
本节以单层不排水黏性土坡来验证所提方法的有效性。如图6所示，坡高5 m，坡角约26.6°，边坡底边界之下为基岩。由于土体重度的空间变异性较小，一般视为确定性参数，土体重度γ = 20 kN/m3。土体不排水状态下内摩擦角为0，仅考虑土体不排水抗剪强度参数cu的不确定性，其服从均值μc=23 kPa、变异系数COVc=0.3的对数正态分布。Cho[20]、Jiang等[38]曾研究过不排水抗剪强度参数cu的空间变异性对该边坡系统可靠性的影响。与Cho[20]、Jiang等[38]一致，本文也仅考虑cu的空间变异性，并采用对数正态随机场描述cu的空间变异性。采用本文自编程序计算边坡安全系数，为验证自编程序的正确性，采用自编程序计算边坡(cu在空间上不同位置取均值23 kPa)安全系数为1.356，与商业软件SLOPE/W计算的1.356及Cho[20]、Jiang等[38]、李典庆等[19]给出的结果1.356、1.356、1.354非常吻合。图6所示边坡确定性临界滑面通过边坡底边界，一般地不排水土坡确定性分析临界滑面的位置会通过边坡底边界，随着底边界的降低临界滑面位置也会相应降低，但到达一定高度后(如图6所示高度)临界滑面安全系数的变化十分小。
图6 不排水黏性土坡的几何形状及潜在滑动面
Fig.6 Geometry and potential slip surfaces of undrained cohesive slope
为了在数值模型中有效地考虑不排水抗剪强度参数空间变异性的影响，将边坡区域离散为910个规则形状的小区域(见图6)。为计算方便，将区域概率元与随机场单元取相同大小尺寸。采用对数正态随机场描述不排水抗剪强度参数空间变异性，这里采用式(1)所示的指数型自相关函数描述其相关结构。为了进一步验证自编程序的可靠性，采用与Cho[20]采用一致的相关结构及波动范围，表1给出了采用本文自编程序计算的边坡失效概率与Cho[20]的结果，这进一步说明本文自编程序的准确性。
表1 可靠度分析结果的对比
Table 1 Comparison between reliability results obtained from Cho[20] and this study
δh/m δv/m 计算类型 失效概率 相对误差本文 Cho[18] 40 4.0 概率临界滑面 3.20×10-2 3.16×10-2 0.01 变临界滑面 7.89×10-2 7.60×10-2 0.04 40 8.0 概率临界滑面 6.08×10-2 6.21×10-2 -0.02 变临界滑面 1.10×10-1 1.09×10-1 0.01 80 4.0 概率临界滑面 4.31×10-2 4.22×10-2 0.02 变临界滑面 9.09×10-2 8.94×10-2 0.02
表2 期望稳定性水平与可靠度指标 β 、失效概率Pf之间的关系 （USACE1997［39］）
Table 2 Relationship between reliability index (β)and probability of failure (Pf)(after USACE 1997[39])
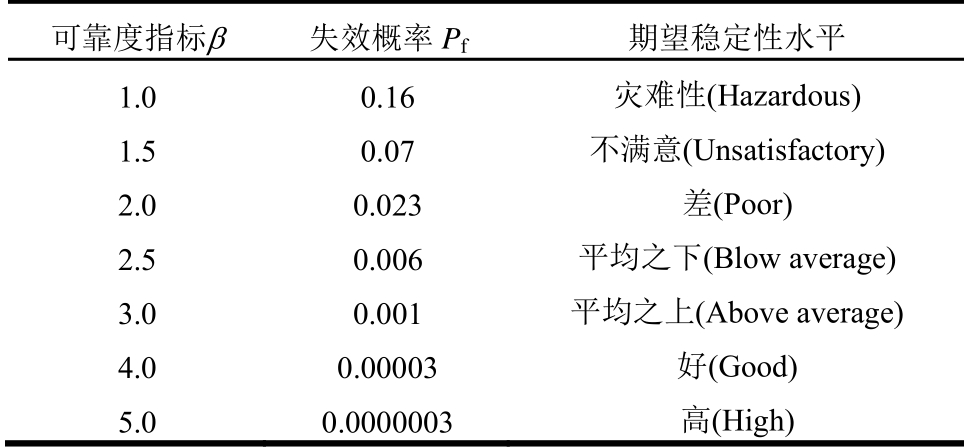
可靠度指标β 失效概率Pf期望稳定性水平 1.0 0.16 灾难性(Hazardous)1.5 0.07 不满意(Unsatisfactory)2.0 0.023 差(Poor)2.5 0.006 平均之下(Blow average)3.0 0.001 平均之上(Above average)4.0 0.00003 好(Good)5.0 0.0000003 高(High)
5.2 区域概率图
本节采用MCS来估计边坡不同区域的失效可能性，MCS模拟次数为1×106次，该模拟次数对失效概率大于1×10-5(失效次数大于10)的区域具有统计意义，能够确保估计的失效概率变异系数小于30%。图7给出了
和δv=4 m时边坡的区域概率图。可以看出，边坡最危险区域集中在边坡坡顶附近。边坡最危险区域的失效概率为6.43×10-3。根据区域概率图，工程师能较容易地 确定边坡潜在最危险区域，进而为边坡加固设计提供指导。此外，该图也可为工程师对于边坡风险认识提供一种直观、有效的分析工具，区域概率图与有限元分析结果呈现形式较为类似，易于为工程师理解。
图7 区域失效概率图(δh=40 m, δv=4 m)
Fig.7 Region failure probability chart (δh=40 m, δv=4 m)
根据区域概率图可以绘制边坡等势概率线，如图7中黑线条所示。等势概率线可用来指导基于目标可靠度水平的边坡加固措施。表2给出了边坡稳定性水平与失效概率之间的对应关系，根据表2和图7结果可以看出，0.001等势概率线以上的区域在平均水平以下，如果以失效概率0.001为目标水平，对于此边坡加固设计来说，所用锚杆长度或锚杆加固影响范围穿过边坡0.001等势概率线区域是十分有效的措施。值得注意的是，严格意义上加固前的等概率区域图只是用来判断加固区域。按照这个加固后，加固区域内的失效概率应该会减小，所以按照加固前的等概率区域图进行加固设计是一种相对偏保守的做法。
5.3 空间变异性对风险的影响
图8(a)和图8(b)分别给出了不同垂直波动范围对不排水黏性土坡失效概率和风险的影响。图8(a)中系统失效概率同时代表考虑边坡多滑面与考虑变临界滑面的边坡系统失效概率，这是由于变临界滑面为多失效滑面中安全系数最小的滑面，对于随机场每次实现，变临界滑面失效意味着考虑多滑面的边坡失效条件也成立，因此二者具有相同大小的失效概率。此外，从图8(a)可以看出随着垂直波动范围的增加，边坡系统失效概率、概率临界滑面(即潜在滑面中失效概率最大的滑面)失效概率及风险临界滑面(即潜在滑面中失效风险最大的滑面)失效概率逐渐增大。边坡系统失效概率明显大于概率临界滑面失效概率及风险临界滑面失效概率，这是由于边坡系统的失效是一系列分量模式失效的结果，概率临界滑面与风险临界滑面仅为边坡系统中失效概率相对较大的分量失效模式。从图8(b)可以看出考虑多滑面的边坡系统风险RA、考虑变临界滑面的边坡风险RV、考虑概率临界滑面的边坡风险RP及考虑风险临界滑面的边坡风险RR都随着垂直波动范围的增加(即空间变异性的减弱)而变大。空间变异性越弱，RA与RV、RP和RR差异越大。以上分析可以看出传统方法(基于变临界滑面的风险和基于概率临界滑面的风险)明显低估了边坡系统风险，这对于边坡稳定性评价及加固设计是非常不利的，这也进一步说明本文方法能够较准确地量化边坡系统风险。
图8 垂直空间变异性对边坡失效概率及其失效风险的 影响
Fig.8 Effects of vertical spatial variability on failure probability and risk for considered slope (δh=40 m)
图9给出了不排水黏性土坡在一次随机数值模拟中同时存在的多个失效模式及各种典型滑动面，可以看出多失效模式引起的后果(滑动面积)明显大于变临界滑动面的后果。概率临界滑面和风险临界滑面的位置有明显的差别，尽管概率临界滑面具有较大的失效概率，但其失效后果明显小于风险临界滑面，在边坡加固治理中风险临界滑面同样应该予以足够的关注。
图9 随机场一次实现对应的特征滑面(δh=40 m, δv=4 m)
Fig.9 Characteristic slip surfaces of slopes associated with one typical random field realization (δh=40 m, δv=4 m)
6 结论
本文提出了考虑边坡多失效模式的区域概率风险分析方法。首先提出了区域概率的概念，建立了以区域概率定量表征边坡稳定性的方法，推导了基于区域概率的边坡系统风险评价公式，探讨了该公式的适用性。最后以一不排水黏性土坡为例阐明了所提方法的有效性。主要结论如下：
(1)区域概率风险分析方法将边坡滑面失效概率转化为一系列离散的边坡不同区域的“失效”概率，该方法为表征边坡的关键失效区提供了一种简单、直接的可视化工具，为工程师制定合理的边坡加固设计方案提供了参考依据。
(2)基于区域概率风险分析方法的边坡系统风险评价公式不仅能够有效地回避边坡风险评价中多滑面间安全系数及滑块体积之间相关性计算问题，而且能够准确地量化边坡多破坏模式的系统风险。此外，该公式也可以计算单个滑面如变临界滑面、概率临界滑面等引起的风险，为从多个角度研究边坡风险提供了一种有效的手段。
(3)土体参数空间变异性对边坡风险影响显著。考虑边坡多失效滑面的风险明显大于单个滑面风险，传统的风险评价方法可能显著低估边坡系统风险，使得边坡设计方案偏危险，这对于边坡工程安全是十分不利的。此外，边坡失效概率最大的滑面不一定是边坡失效风险最大的滑面，从边坡风险的角度考虑，在边坡加固设计中，失效风险较大的滑面也应该予以关注。
[1]Zhu H, Zhang L M, Xiao T, et al.Generation of multivariate cross-correlated geotechnical random fields [J].Computers and Geotechnics, 2017, 86: 95—107.
[2]左自波, 张璐璐, 程演, 等.基于MCMC法的非饱和土渗流参数随机反分析[J].岩土力学, 2013, 34(8): 2393—2400.Zuo Zibo, Zhang Lulu, Cheng Yan, et al.Probabilistic back analysis of unsaturated soil seepage parameters based on Markov chain Monte Carlo method [J].Rock and Soil Mechanics, 2013, 34(8): 2393—2400.(in Chinese)
[3]Huang J, Griffiths D V.Modelling spatial variability in geotechnical engineering [J].Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2016, 10(1): 1.
[4]Lacasse S, Nadim F, Kalsnes B.Living with landslide risk [J].Geotechnical Engineering Journal of the SEAGS & AGSSEA, 2010, 41(4): 1—13.
[5]Huang J, Lyamin A V, Griffiths D V, et al.Quantitative risk assessment of landslide by limit analysis and random fields [J].Computers and Geotechnics, 2013, 53: 60—67.
[6]Li D, Xiao T, Cao Z, et al.Enhancement of random finite element method in reliability analysis and risk assessment of soil slopes using Subset Simulation [J].Landslides, 2016, 13(2): 293—303.
[7]蒋水华, 杨建华, 姚池, 等.考虑土体参数空间变异性边坡失稳风险定量评估[J].工程力学, 2018, 35(1): 136—147.Jiang Shuihua, Yang Jianhua, Yao Chi, et al.Quantitative risk assessment of slope failure considering spatial variability of soil properties [J].Engineering Mechanics, 2018, 35(1): 136—147.(in Chinese)
[8]Cheng H Z, Chen J.Risk assessment of slope failure considering the variability in soil properties [J].Computers and Geotechnics, 2018, 103: 61—72.
[9]Li L, Chu X.Risk assessment of slope failure by representative slip surfaces and response surface function[J].KSCE Journal of Civil Engineering, 2016, 20(5): 1783—1792.
[10]Zhang J, Huang H W.Risk assessment of slope failure considering multiple slip surfaces [J].Computers and Geotechnics, 2016, 74: 188—195.
[11]Jiang S, Huang J, Yao C, et al.Quantitative risk assessment of slope failure in 2-D spatially variable soils by limit equilibrium method [J].Applied Mathematical Modelling, 2017, 47: 710—725.
[12]Cheng Y M, Lansivaara T, Wei W B.Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods [J].Computers and Geotechnics, 2007, 34(3): 137—150.
[13]Reale C, Xue J, Gavin K.System reliability of slopes using multimodal optimization [J].Géotechnique, 2016, 66(5): 413—423.
[14]Tun Y W, Pedroso D M, Scheuermann A, et al.Probabilistic reliability analysis of multiple slopes with genetic algorithms [J].Computers and Geotechnics, 2016, 77: 68—76.
[15]张鲁渝.边坡稳定分析软件ZSlope的开发[J].岩石力学与工程学报, 2004, 23(16): 2830—2835. Zhang Luyu.Development of software zslope for slope stability analysis [J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2830—2835.(in Chinese)
[16]闫超, 刘松玉, 籍晓蕾.一种基于强度折减法的次级滑动面分析方法研究[J].岩土力学, 2016, 37(4): 935—942. Yan Chao, Liu Songyu, Ji Xiaolei.Research on a secondary sliding surface analysis approach based on strength reduction method [J].Rock and Soil Mechanics, 2016, 37(4): 935—942.(in Chinese)
[17]薛海斌, 党发宁, 尹小涛, 等.基于岩土材料软化特性的滑坡多级滑动面分析方法研究[J].岩土力学, 2015, 36(11): 3235—3242. Xue Haibin, Dang Faning, Yin Xiaotao, et al.Research on analytical method of multi-slip surfaces of landslide based on softening characteristics of geomaterial [J].Rock and Soil Mechanics, 2015, 36(11): 3235—3242.(in Chinese)
[18]蒋水华, 李典庆, 周创兵, 等.考虑自相关函数影响的边坡可靠度分析[J].岩土工程学报, 2014, 36(3): 508—518. Jiang Shuihua, Li Dianqing, Zhou Chuangbing, et al.Slope reliability analysis considering effect of autocorrelation functions [J].Chinese Journal of Geotechnical Engineering, 2014, 36(3): 508—518.(in Chinese)
[19]李典庆, 蒋水华, 周创兵, 等.考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J].岩土工程学报, 2013, 35(8): 1413—1422. Li Dianqing, Jiang Shuihua, Zhou Chuangbing, et al.Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method [J].Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1413—1422.(in Chinese)
[20]Cho S E.Probabilistic assessment of slope stability that considers the spatial variability of soil properties.Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(7): 975—984.
[21]Chowdhury R N, Xu D W.Geotechnical system reliability of slopes [J].Reliability Engineering & System Safety, 1995, 47(3): 141—151.
[22]Oka Y, Wu T H.System reliability of slope stability [J].Journal of Geotechnical Engineering, 1990, 116(8): 1185—1189.
[23]Christian J T.Issues of reliability in stability of slopes [J].InGeo-Congress 2013: Stability and Performance of Slopes and Embankments III, 2013: 2246—2261.
[24]Juang C H, Zhang J, Gong W.Reliability-based assessment of stability of slopes [J].IOP Conference Series: Earth and Environmental Science, 2015, 26(1): 12006.
[25]Phoon K, Kulhawy F H.Characterization of geotechnical variability [J].Canadian Geotechnical Journal, 1999, 36(4): 612—624.
[26]杨智勇, 曹子君, 李典庆, 等.颗粒接触摩擦系数空间变异性对颗粒流双轴数值试验的影响[J].工程力学, 2017, 34(5): 235—246. Yang Zhiyong, Cao Zijun, Li Dianqing, et al.Effect of spatially variable friction coefficient of granular materials on its macro-mechanical behaviors using biaxial compression numerical simulation [J].Engineering Mechanics, 2017, 34(5): 235—246.(in Chinese)
[27]祁小辉, 李典庆, 周创兵, 等.考虑土体空间变异性的边坡最危险滑动面随机分析方法[J].岩土工程学报, 2013, 35(04): 745—753.Qi Xiaohui, Li Dianqing, Zhou Chuangbing, et al.Stochastic analysis method of critical slip surfaces in soil slopes considering spatial variability [J].Chinese Journal of Geotechnical Engineering, 2013, 35(4): 745—753.(in Chinese)
[28]闫澍旺, 朱红霞, 刘润.天津港土性相关距离的计算研究和统计分析[J].岩土力学, 2009, 30(7): 2179—2185.Yan Shuwang, Zhu Hongxia, Liu Run.Numerical studies and statistic analyses of correlation distances of soil properties in Tianjin Port [J].Rock and Soil Mechanics, 2009, 30(7): 2179—2185.(in Chinese)
[29]田密, 李典庆, 曹子君, 等.基于贝叶斯理论的土性参数空间变异性量化方法[J].岩土力学, 2017, 38(11): 3355—3362.Tian Mi, Li Dianqing, Cao Zijun, et al.Quantification of inherent spatial variability of soil parameters using Bayesian approaches [J].Rock and Soil Mechanics, 2017, 38(11): 3355—3362.(in Chinese)
[30]邓志平, 李典庆, 曹子君, 等.考虑地层变异性和土体参数变异性的边坡可靠度分析[J].岩土工程学报, 2017, 39(6): 986—995.Deng Zhiping, Li Dianqing, Cao Zijun, et al.Slope reliability analysis considering geological uncertainty and spatial variability of soil parameters [J].Chinese Journal of Geotechnical Engineering, 2017, 39(6): 986—995.(in Chinese)
[31]李静萍, 程勇刚, 李典庆, 等.基于多重响应面法的空间变异土坡系统可靠度分析[J].岩土力学, 2016, 37(1): 147—155, 165.Li Jingping, Cheng Yonggang, Li Dianqing, et al.System reliability analysis of spatially variable soil slopes using the multiple response surfaces method [J].Rock and Soil Mechanics, 2016, 37(1): 147—155, 165.(in Chinese)
[32]王贺, 张洁, 陈飞扬.强降雨条件下花岗岩残积土边坡的时变可靠度[J].武汉大学学报(工学版), 2016, 49(5): 763—767.Wang He, Zhang Jie, Chen Feiyang.Time-dependent reliability of slopes made of completely decomposed granite under intense rainfall [J].Engineering Journal of Wuhan University, 2016, 49(5): 763—767.(in Chinese)
[33]罗正东, 董辉, 陈铖, 等.基于克里金模型的边坡稳定可靠度分析方法[J].岩土力学, 2015, 36(增刊1): 439—444.Luo Zhengdong, Dong Hui, Chen Cheng, et al.An analytic method for slope stability reliability based on Kriging model [J].Rock and Soil Mechanics, 2015, 36(Suppl 1): 439—444.(in Chinese)
[34]Zhu D, Griffiths D V, Huang J, et al.Probabilistic stability analyses of undrained slopes with linearly increasing mean strength [J].Géotechnique, 2017, 67(8): 733—746.
[35]Ang A H S, Tang W H.Probability concepts in engineering: emphasis on applications in civil and environmental engineering [M].Hoboken, New Jersey: John Wiley & Sons, Inc, 2007.
[36]Wenping G, Lei W, Sara K, et al.Robust geotechnical design of earth slopes using fuzzy sets [J].Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(1): 04014084.
[37]Ali A, Huang J, Lyamin A V, et al.Simplified quantitative risk assessment of rainfall-induced landslides modelled by infinite slopes [J].Engineering Geology, 2014, 179: 102—116.
[38]Jiang S H, Li D Q, Cao Z J, et al.Efficient system reliability analysis of slope stability in spatially variable soils using Monte Carlo simulation [J].Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(2): 04014096.
[39]US Army Corps of Engineers.Engineering and design: introduction to probability and reliability methods for use in geotechnical engineering [Z].Engineer Technical Letter 1110-2-547.Washington, DC: Department of the Army, 1997.