框架结构受力明确、空间布置灵活，是工程中常用的一种结构体系。准确预测框架结构在地震作用下的随机响应，对工程设计有着重要意义。由于地震活动发生的时间、空间和强度的不确定性，以随机过程描述地震地面运动更为合理[1]。随机激励广泛存在，高斯白噪声过程常被用来模拟这些随机过程，这是一种理想状态的模拟方式。实际中大部分的随机激励都不能单纯地简化为高斯白噪声过程。以地震动作用为例，实际上90%以上的地震震源都发生在地壳中，地壳中的土质和岩石种类复杂多变，地震波在传播的过程中不断的被削弱和过滤。因此，采用过滤高斯白噪声模拟作用于结构上的地震作用，更具代表性。1960年，日本著名学者Kanai和Tajimi提出了金井清模型[2]，这是首次用过滤高斯白噪声模拟地震动作用的模型。随后Ruiz和Penzien[3]、欧进萍等[4]、杜修力等[5-6]学者提出的过滤高斯白噪声模型，均是对金井清模型的改进。金井清模型考虑了均匀场地土层对地震波的过滤作用，在结构随机振动理论研究方面得到了广泛的应用。
相对于高斯白噪声，过滤高斯白噪声过程通常称为彩噪声。在彩噪声的激励下，结构的响应并不是马尔科夫过程，这样传统的Fokker-Planck (FPK)方程不再适用。通常的做法是把彩噪声作为辅助状态变量，通过马尔科夫增广状态向量的方式来研究。但是这种做法会增大初始系统的维数，产生多维的FPK方程。FPK方程的求解比较困难，精确解只存在于低维的FPK方程并且在非常严格的条件下，而且很多近似方法或者数值法最多只对二维的FPK方程有效，只有极少数的近似法或数值法可以用于求解多维的FPK方程[7—9]。Xie等学者[10-13]用响应统计矩法研究了不同噪声激励下的系统响应；Paola和Floris[14]用高斯矩截断法和
随机微分法，研究了过滤高斯白噪声激励下非线性系统的非高斯响应统计规律；Su和Falzarano[15]用累积矩截断法解决了多维FPK方程难于求解的问题；Floris[16]用累积矩截断法分别研究了1阶、2阶过滤高斯白噪声参数激励下的系统响应。累积矩截断法可以解决过滤高斯白噪声激励下系统响应难于求解的问题，不仅为非平稳振动提供理论分析方法，还推动了过滤高斯白噪声在结构工程领域的应用[17]。
另一方面，实际地震不仅有水平振动分量，而且还有竖向振动分量。但目前关于结构的水平随机地震响应分析，常常仅研究水平地震作用，而忽略了竖向地震作用的影响。其原因一方面是问题的复杂性，另一方面是竖向加速度往往小于重力加速度，其产生的惯性力小于结构自重。但研究表明，竖向地震对结构水平振动的参激作用将使响应进一步增大，加剧结构的破坏。近年来，国内外学者在结构同时受到水平和竖直地震作用方面的研究相对较多，如：Lin等[18]建立了单自由度结构在水平和竖直地震作用下的随机分析模型及数值解法；李创第等[19]在Lin的研究基础上，推导了同时承受水平和竖向地震作用的悬臂梁构件的振动方程，方程中两个方向的地震激励分别采用外部激励和参数激励表示，获得了结构1阶和2阶响应矩渐近稳定条件的解析判别式；Dimentberg[20]用过滤高斯白噪声研究了两个自由度系统在不完全周期参数激励下组合共振的均方稳定性条件。但以上研究，均认为模拟竖直和水平地震作用的参数激励和外部激励是相互独立的。实际上，水平和竖直两个方向的地震激励是地震作用的两个分量，他们不仅是相关的，而且是完全相关的。Guo等[21—22]研究了外部激励和参数激励相关性的影响，得到了非零均值的响应和不对称的概率密度函数。
基于以上研究，为得到更精细化的结构随机地震响应，需要考虑水平和竖向地震动分量间的相关性。本文分别以高斯白噪声、过滤白噪声过程模拟地震动作用，采用累积矩截断法，研究单层框架结构在地震动作用下的随机响应，并讨论地震动作用分量间的相关性对结构响应的影响。
1 结构分析模型
如图1(a)所示无质量结构体系，质点质量为m，水平阻尼系数为c，杆的长度和抗弯刚度分别为l和EI，水平作用力为F，竖直作用力为P，在水平地震动ug(t)和竖向地震动vg(t)的作用，结构发生水 平位移为y(x,t)，如果结构的竖向刚度与水平刚度的比值较大，并仅考虑竖向荷载作用对质点水平响应的影响时，质点m的水平运动方程[23]为：
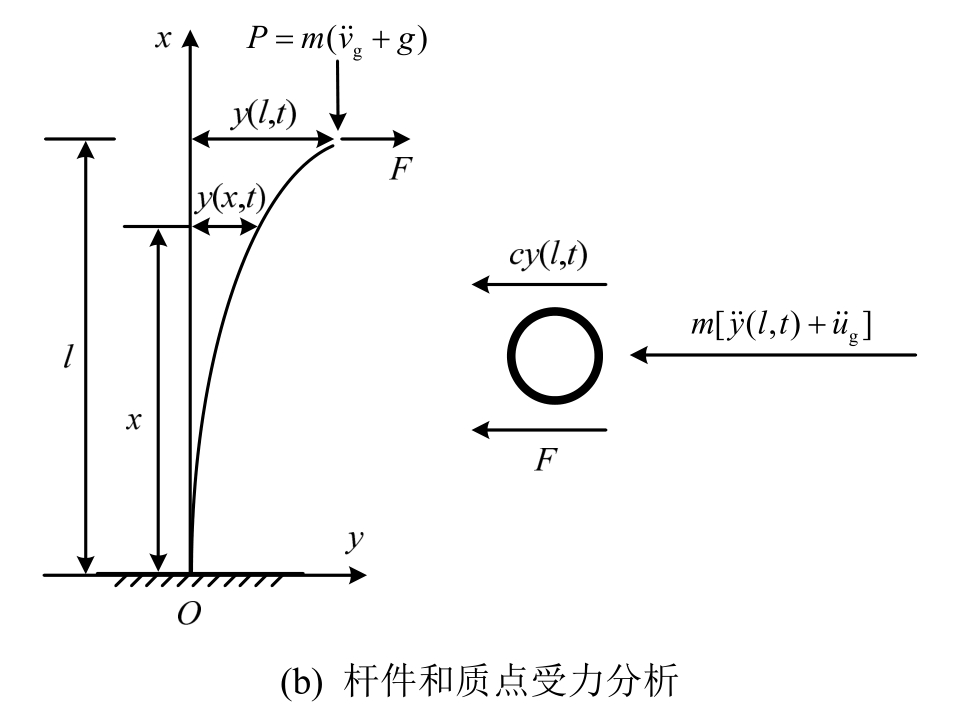
图1 结构构件的建模过程
Fig1 Modeling the structural system
参考文献[23—24]，经过一系列推导，得：
式中：k1、k2、k3是关于结构特性的参数，而且 k1＞0、k2＞0、k3＞0。
无量纲化处理后，推导得结构在水平和竖向荷载作用下振动方程为：
式中，V1(t)和V2(t)分别代表水平和竖向地震动过程。
本文分别采用高斯白噪声和过滤高斯白噪声过程模拟地震作用，考虑地震动作用分量间的相关性对结构随机响应的影响。
2 累积矩截断法
2.1 高斯白噪声激励下框架结构的响应
设Wi表示非零均值的高斯白噪声过程，W1表示外部激励过程，W2表示参数激励过程，其自相关函数和互相关函数分别为：
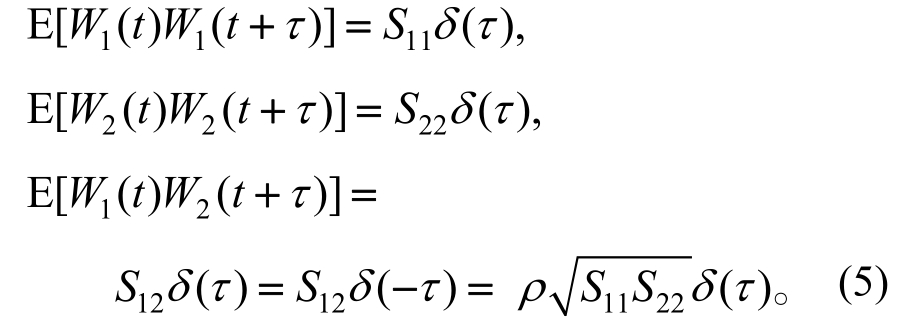
式中：E[·]表示均值；δ(τ)是Diracδ函数；ρ表示外部激励和参数激励的相关性系数，||1ρ≤。
设Duffing系统在相关的外部激励和参数激励作用下运动方程为：
令式(6)中
将系统的运动方程写成
型得：
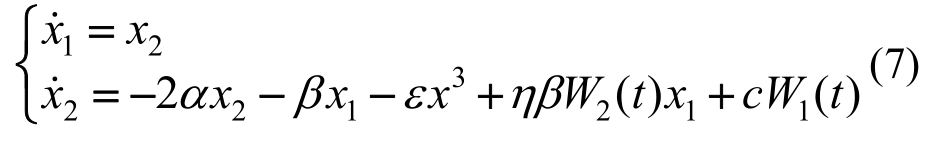
在高斯白噪声激励下，系统响应{x1，x2}是马尔科夫矢量，其满足如下联合矩方程：
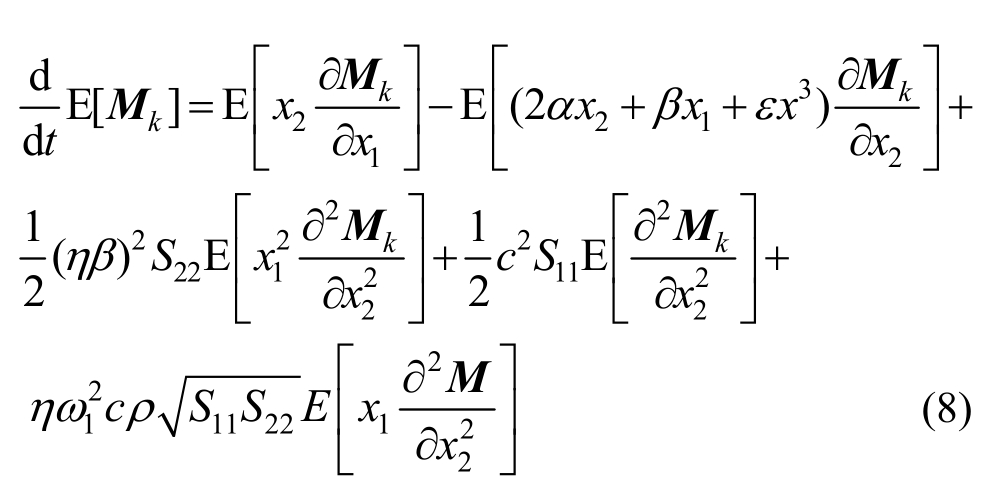
其中，
当外部激励和参数激励完全独立时，其联合矩方程降低为：
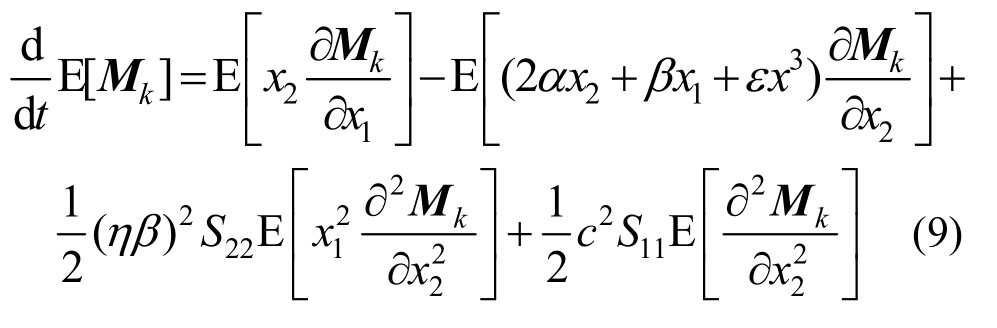
采用经典的四阶龙格—库塔法求解式(8)微分方程组，可以得到系统响应的统计规律。
2.2 过滤高斯白噪声激励下框架结构的响应
设V(t)限宽度功率谱密度函数S(ω)的彩噪声过程，可以采用二阶滤波器模型得到：
其中：
对时间的导数；W(t)是均值为零的高斯高斯白噪声过程，其相关函数为E[W(t)W(t+τ)]=S0δ(τ)；δ(τ)；表示Dirac-delta函数；S0是高斯白噪声的功率谱密度。
根据式(10)，可得过滤高斯白噪声V(t)的功率谱密度函数为：
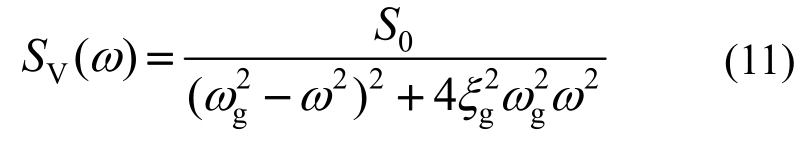
当将式(10)应用于建筑结构地震动分析时，
是地震地面相对于基岩的加速度；ξg和ωg分别为单自由度体系的地表土层阻尼比和固有频率； 是地震基岩加速度，其均值为0、谱密度为S0。于是作用于结构基底的绝对地震加速度ag(t)为：
由式(10)和式(12)可得的平稳谱密度为：
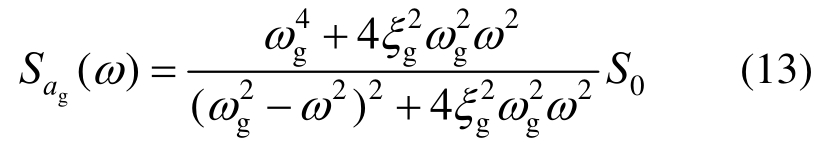
相对于理想高斯白噪声而言，过滤高斯白噪声模拟地震动作用更加合理。假设单自由度结构在地震动作用下发生的水平侧移为x，其运动方程可以表示为：
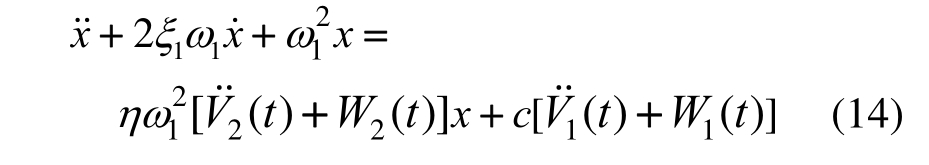
式中，各参数的物理意义同式(4)，地震动作用的水平分量V1和竖向分量V2由地震作用W1和W2通过地表土层的过滤后得到，即：
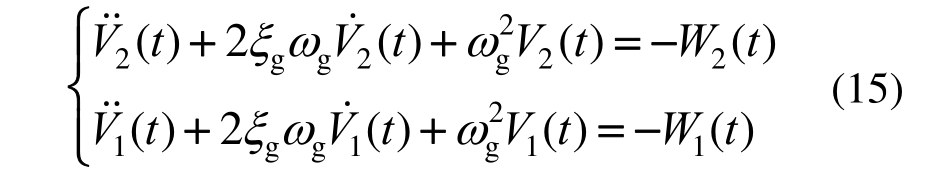
将二阶过滤高斯白噪声作为扩充的状态变量进行分析计算，则式(14)的状态空间矢量
其中
令
则联合式(14)与式(15)转化为
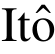型得：
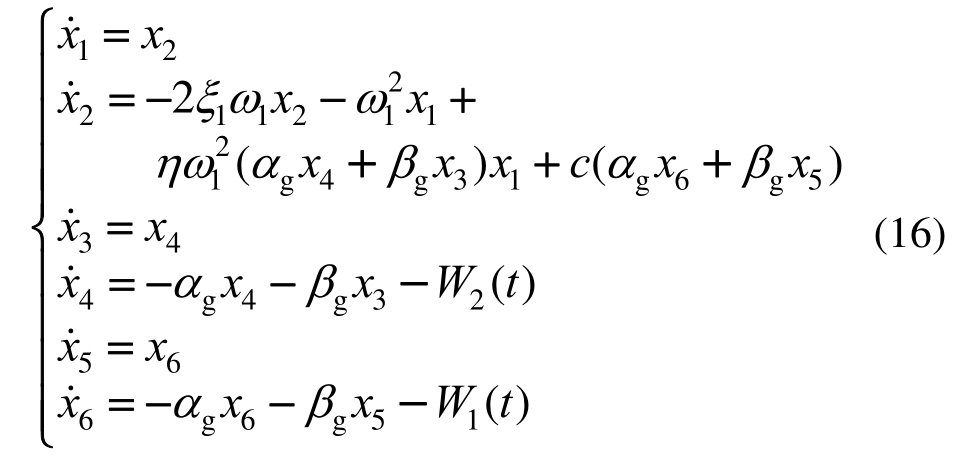
则系统式(14)的联合矩方程为：
其中，
当外部激励和参数激励完全独立时，其联合矩方程降低为：
3 数值分析
3.1 Duffing系统在外部激励和参数激励下的响应
考虑Duffing系统式(6)，参数取值为：a=0.5，β=10，ε=0.5，η=0.238，高斯白噪声谱密度强度分别为S11=0.1，S22=0.05，其中ρ∈[-1，1]。将以上参数代入式(8)，将累积矩二阶截断进行响应求解。为了检验计算结果的准确性，采用等价线性化法，对比结构体系在高斯白噪声激励下的平稳地震响应，如图2所示，证明了累计矩截断法的有效性。
图2 二阶截断响应与平稳响应对比
Fig.2 Comparison between two-order truncation response and stationary response
图3为参数激励和外部激励相关性对系统响应均方值的影响。由图3(a)可知：参数激励和外部。激励相关性对均方响应有影响，随着相关系数的变化，结构位移稳态响应变化规律呈开口向下的抛物线，当参数激励和外部激励完全不相关时，位移响应均方值最大，完全相关时最小。图3(b)为5种相关激励作用下系统在平稳化过程中的位移均方响应，从图中可以看出，激励间的相关性在平稳化过程中对Duffing系统响应的影响不大。讨论外部激 励和参数激励间的相关性对系统随机响应的影响，其结果列于表1。由表1可知，外部激励和参数激励间的相关性使得系统响应偏离其初始的位置，重新建立平衡位置，且相关性越强，偏离的程度越大。
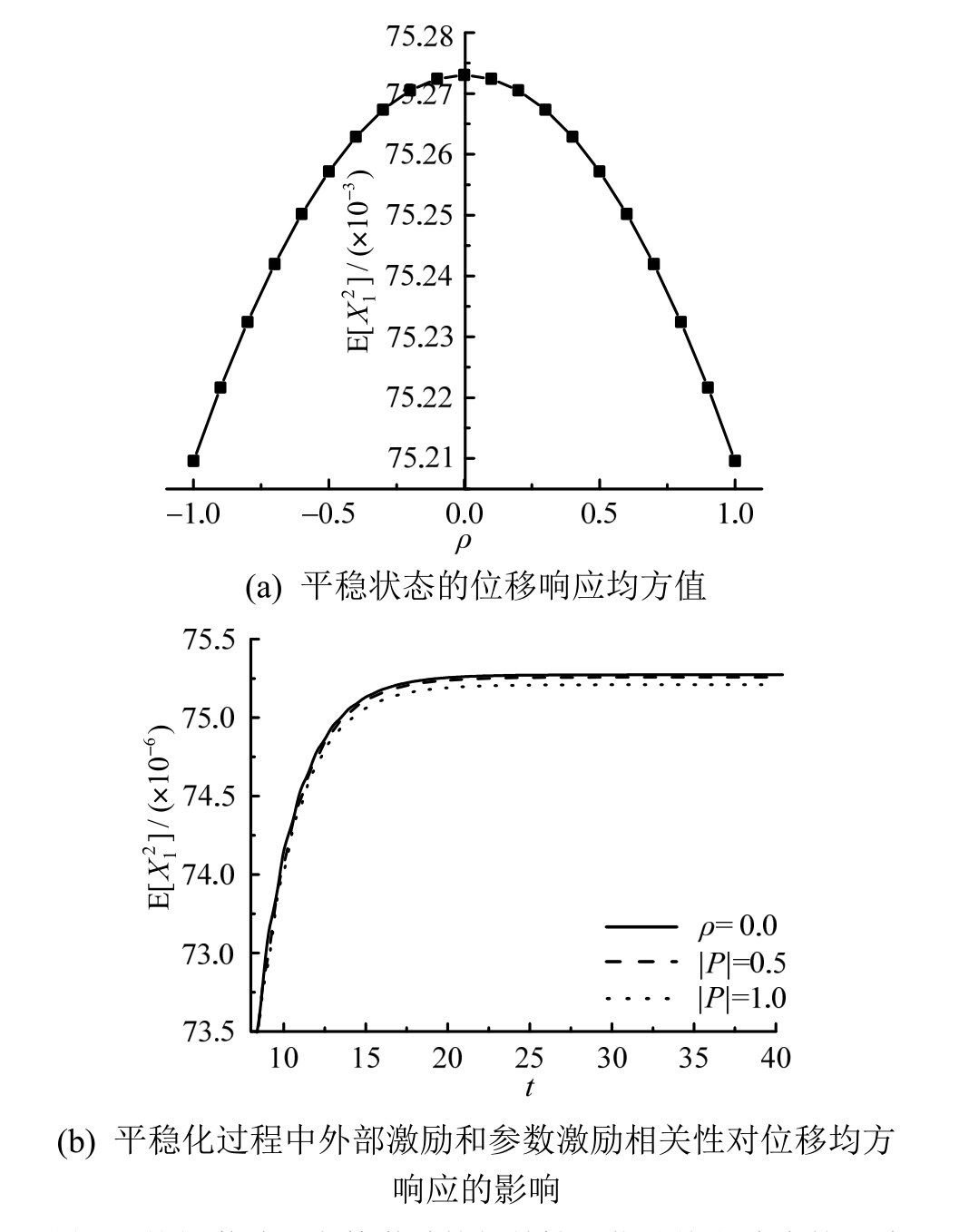
图3 外部激励和参数激励的相关性对位移均方响应的影响
Fig.3 The influence of correlation between external excitation and parametric excitation on mean square value of displacement response
图4为外部激励和参数激励间的相关性对系统平衡位置的影响。图4(a)表明：随着参数激励和外部激励相关性的增大，位移随机响应过程偏离平衡位置的值越来越大，因此，当相关性比较强时，其对系统响应的影响是不可忽略的。图4(b)为5种相关激励作用下系统的位移均方响应，从图中可以看出，正、负相关激励下系统一阶位移响应的平稳化过程是关于初始平衡位置对称分布的。而对于速度响应则不存在此规律，对应的图形在此省略。
3.2 过滤高斯白噪声激励
设有一单自由度结构，其结构阻尼比为ξ1=0.05，结构的修正自振频率为ω1=4π/s，竖向地震作用强度取S22=0.01m2/s3，水平地震强度为S11=0.02m2/s3，ρ∈[-1,1]，考虑结构自重，取μ=0.7，则η=0.238。二阶线性滤波器参数为：
表1 外部激励和参数激励间的相关性对系统响应的影响
Table 1 System response with the change of correlation coefficient
注：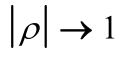
时，激励的相关性越强；
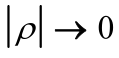时，相关性越弱。
相关性ρ 6 1(E[ ]/ 1 )0 X -×2 1(E[ ]/ 1 )0 X -3× 2 3 2(E[ ]/ 1 )0 X -×-1.0 72.834 75.210 761.916 -0.9 65.561 75.222 761.966 -0.8 58.284 75.232 762.012 -0.7 51.004 75.242 762.052 -0.6 43.723 75.250 762.086 -0.5 36.439 75.257 762.116 -0.4 29.153 75.263 762.140 -0.3 21.866 75.267 762.158 -0.2 14.578 75.271 762.172 -0.1 7.289 75.272 762.180 0.0 0 75.273 762.182 0.1 -7.289 75.272 762.180 0.2 -14.578 75.271 762.172 0.3 -21.866 75.267 762.158 0.4 -29.153 75.263 762.140 0.5 -36.439 75.257 762.116 0.6 -43.723 75.250 762.086 0.7 -51.004 75.242 762.052 0.8 -58.284 75.232 762.012 0.9 -65.561 75.222 761.966 1.0 -72.834 75.210 761.916
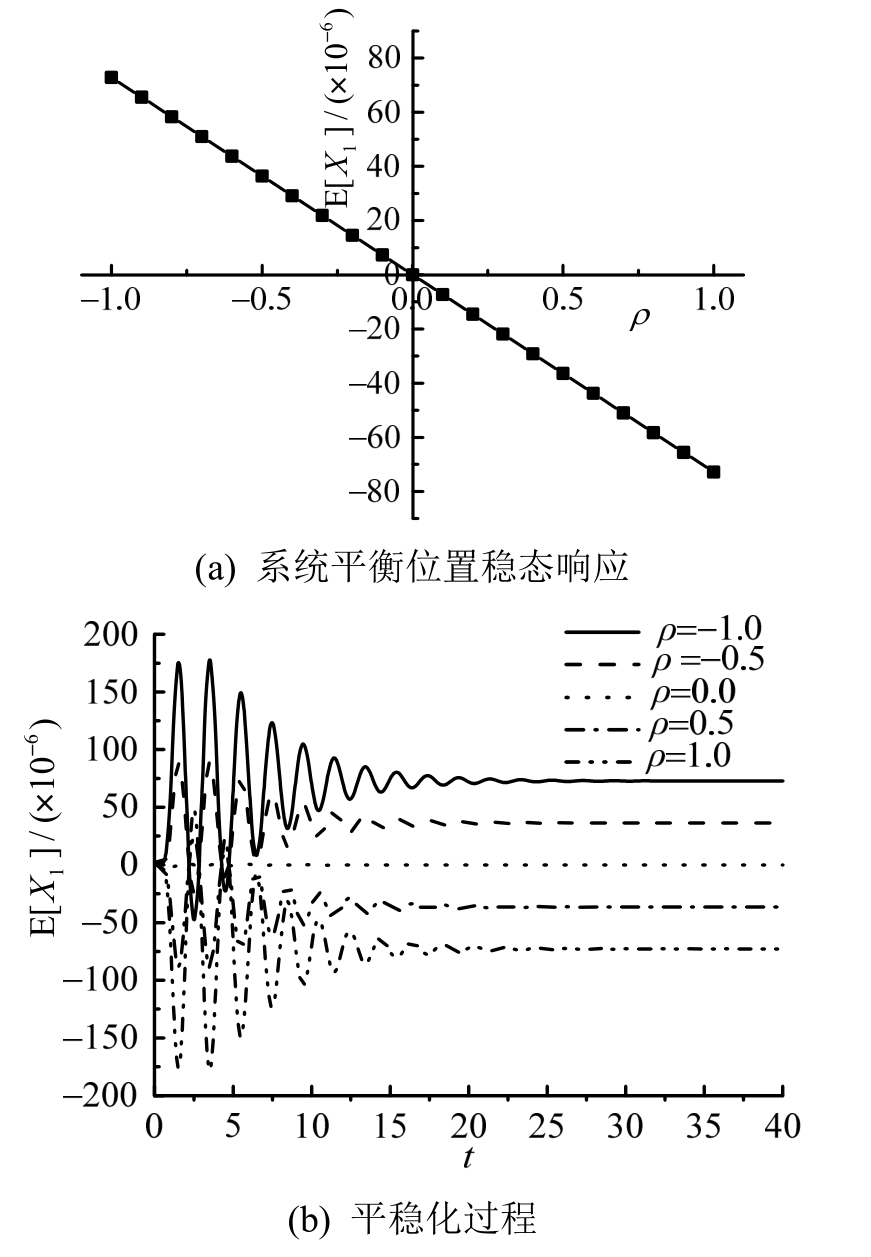
图4 外部激励和参数激励间相关性对系统平衡位置的影响
Fig.4 The influence of the correlation between external and parametric excitations on the statistical mean of displacement
① I类场地：覆盖土层的特征阻尼比ξg=0.64，覆盖土层的特征频率ωg=25.13 s-1；
② IV类场地：覆盖土层的特征阻尼比ξg=0.90，覆盖土层的特征频率ωg=9.67 s-1。将以上参数代入式(17)二阶展开的微分矩方程组进行求解，结果见表2。
表2 考虑地震作用相关性的结构响应(过滤高斯白噪声)
Table2 Structural response considering seismic action correlation (Filter white noise)
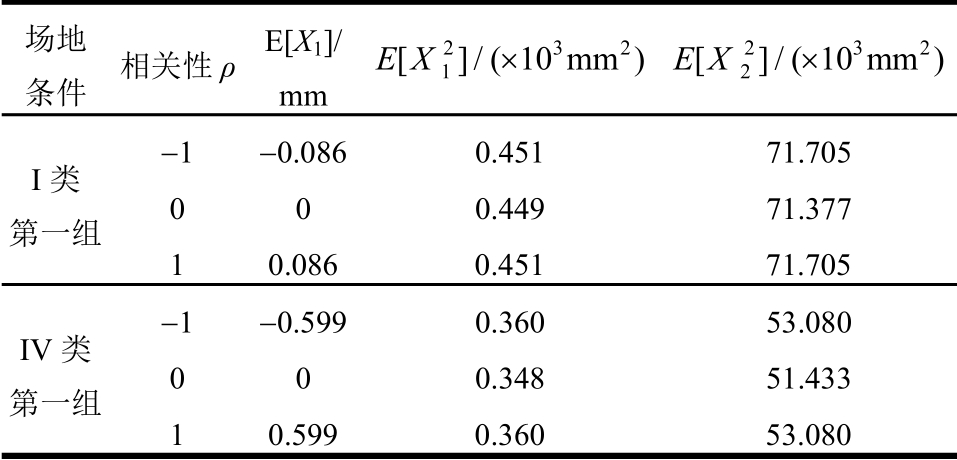
场地 条件 相关性ρ E[X1]/ mm 2 3 2 1([ ]/ 10 m)m EX × 2 3 2 2[ ]/(10 m)m EX ×I类 第一组 -1 -0.086 0.451 71.705 0 0 0.449 71.377 1 0.086 0.451 71.705 IV类 第一组 -1 -0.599 0.360 53.080 0 0 0.348 51.433 1 0.599 0.360 53.080
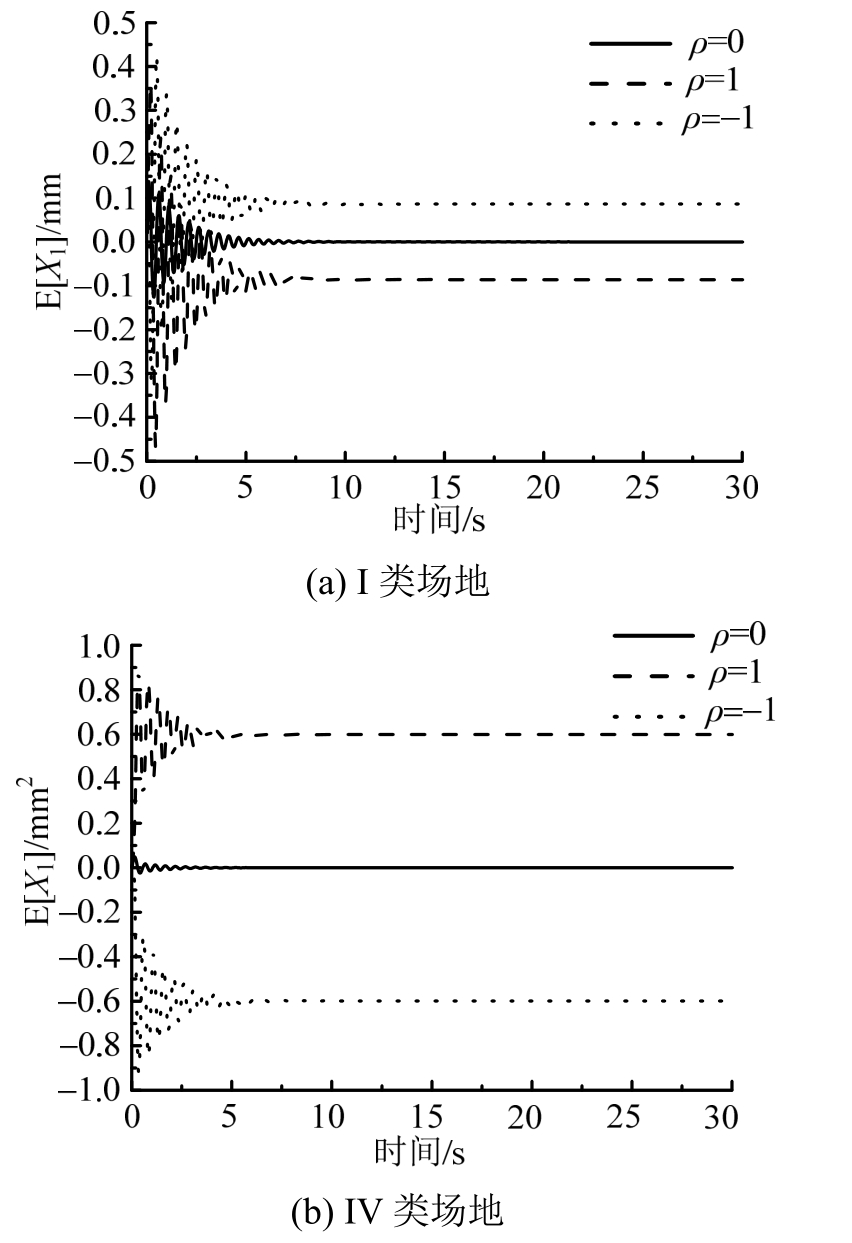
图5 地震作用相关性对结构地震响应平衡位置的影响
Fig.5 The influence of earthquake action correlation on the structural response equilibrium position
采用过滤高斯白噪声过程模拟地震动作用，考虑了场地条件对地震的过滤作用，结构响应更具代表性。实际上，对于地震作用，水平和竖直两个方向的地震激励是地震作用的两个分量，他们不仅是相关的，而且是完全相关的，即完全正相关或完全负相关。表2为水平和竖向地震作用的相关性对系统响应的影响，场地条件采用抗震设计第一组的I类和IV类场地土层。根据表2数据绘制图5、图6。
图5为过滤高斯白噪声激励相关性对结构地震响应平衡位置的影响。与理想高斯白噪声相比，过滤高斯白噪声作用下的结构响应平衡位置受地震作用相关性的影响更显著，即地基土对地震作用相关性的影响具有放大作用；根据图5所示，I类场地上结构地震一阶位移响应偏离初始平衡位置0.086 mm，IV类场地上偏离0.599 mm，IV类场地条件对地震作用相关性影响的放大效应大于I类场地条件的。
图6为地震动间相关性系数对位移均方响应的影响。由图6可知，累积矩2阶截断的位移均方响应趋近于平稳解；对比I类场地条件和IV类场地条件下结构的位移均方值，地震作用相关性对结构响应的影响程度不同。如图6(a)和图(b)所示，坚硬地基上，地震作用相关性使结构位移响应增大了0.44%，软弱地基上的增大了2.00%，软弱地基上的地震激励相关性对结构响应的影响更为明显。因此在抗震设计中，地震作用相关性对结构随机响应的影响需要根据具体场地工况分析。
图6 相关性系数对系统位移均方响应的影响
Fig.6 The influence of correlation coefficient on the system displacement response
综上所述，当结构所在场地被认为是理想刚体时，地震作用相关性对结构响应的影响理论存在但并不显著，但这种情况在现实中是不存在的。地震作用相关性的显著程度受场地条件的影响较大，过滤高斯白噪声考虑地基土层的过滤作用，较为全面的考虑了场地条件对地震响应的影响，更准确地模拟了作用于结构的地震作用，响应更具代表性。
4 结论
本文针对单自由度体系，考虑地震作用分量间的相关性，研究了地震作用下结构的随机响应。结果表明：
(1)外部激励和参数激励间的相关性使得系统的响应偏离其初始的位置，且相关性越强，偏离的程度越大；
(2)相较于高斯白噪声，过滤高斯白噪声作用下结构的位移响应受地震作用相关性的影响更为显著。地震作用的相关性放大了结构的位移响应，且放大的显著程度相对于不同场地条件是存在有差异的。因此在抗震设计中，地震作用相关性的影响不可忽略且需要根据具体工况分析。
对于多自由度结构体系，其相关性的影响规律还有待进一步研究。
[1]Lanzotti A, Renno F, Russo M, et al.Design and development of an automotive magnetorheological semi-active differential [J].Mechatronics, 2014, 24(5): 426—435.
[2]Kanai K.Semi-empirical formula for the seismic characteristics of the ground [J].Earthquake Research Institute, the University of Tokyo, 1957, 35(2): 309—325 .
[3]Ruiz P, Penzien J.Probabilistic study of the behavior of structures during earthquakes [R]. Earthquake Engineering Research Center, UCB, CA, Report No.EERC 69—03, 1969.
[4]欧进萍, 牛荻涛, 杜修力.设计用随机地震动的模型及其参数确定[J].地震工程与工程振动, 1991, 11(3): 45—54.Ou Jinping, Niu Ditao, Du Xiuli.Random earthquake ground motion model and its parameter determination used in asismic design [J].Earthquake Engineering and Engineering Vibration, 1991, 11(3): 45—54.(in Chinese)
[5]杜修力, 陈厚群.地震动随机模型及其参数确定方法[J].地震工程与工程振动, 1994, 14(4): 1—5.Du Xiuli, Chen Houxiong.Random simulation and its parameter determination method of earthquake ground motion[J].Earthquake Engineering and Engineering Vibration,1994, 14(4): 1—5.(in Chinese)
[6]赖明, 叶天义, 李英民.地震动的双重过滤白噪声模型[J].土木工程学报, 1995, 28(6): 60—66.Lai Ming, Ye Tianyi, Li Yingmin.Multi-filtered white noise model for ground motion [J].Chinese Journal of Civil Engineering, 1995, 28(6): 60—66.(in Chinese)
[7]Deng Weihua.Numerical algorithm for the time fractional Fokker-Planck equation [J].Journal of Computational Physics, 2007, 227(2): 1510—1522.
[8]戚鲁媛, 徐伟, 高维廷.色噪声激励Rayleigh-Duffing振子瞬态响应及最优有界控制[J].工程力学, 2013, 30(12): 24—30.Qi Luyuan, Xu Wei, Gao Weiting.Transient response and optimal bounded control of colored noise excited Rayleigh-Duffing oscillator [J].Engineering Mechanics, 2013, 30(12): 24—30.(in Chinese)
[9]杨杰, 马萌璠, 王旭.随机结构动力可靠度计算的条件概率方法[J].工程力学, 2018, A01(增刊1):17—21.Yang Jie, Ma Mengfan, Wang Xu.Conditional probability method for dynamic reliability calculation of random structures [J].Engineering Mechanics, 2018, A01(Suppl 1): 17—21.(in Chinese)
[10]Xie W C.Moment Lyapunov exponents of a two-dimensional system under combined harmonic and real noise excitations [J].Journal of Sound & Vibration, 2007, 303(1): 109—134.
[11]Xie W C.Moment Lyapunov exponents of a two-dimensional system under bounded noise parametric excitation [J].Journal of Sound & Vibration, 2002, 239(1): 139—155.
[12]Loh C H, Ma M J.Reliability assessment of structure subjected to horizontal-vertical random earthquake excitations [J].Structural Safety, 1997, 19(1): 153—168.
[13]Bobryk R V, Chrzeszczyk A.Stability regions for Mathieu equation with imperfect periodicity [J].Physics Letters A, 2009, 373(39): 3532—3535.
[14]Paola M D, Floris C.Iterative closure method for non-linear systems driven by polynomials of Gaussian filtered processes [J].Computers & Structures, 2008, 86(11/12): 1285—1296.
[15]Su Z, Falzarano J M.Gaussian and non-Gaussian cumulant neglect application to large amplitude rolling in random waves [J].International Shipbuilding Progress, 2011, 58(2): 97—113.
[16]Floris C.Mean square stability of a second-order parametric linear system excited by a colored Gaussian noise [J].Journal of Sound & Vibration, 2015, 336(1): 82—95.
[17]刘章军, 王磊, 黄帅.非平稳随机地震作用的结构整体可靠度分析[J].工程力学, 2015(12): 225—232.Liu Zhangjun, Wang Lei, Huang Shuai.Structural reliability analysis of non-stationary random earthquakes [J].Engineering Mechanics, 2015(12): 225—232.(in Chinese)
[18]Lin Y K, Shih T Y.Column response to horizontal-vertical earthquakes [J].Journal of the Engineering Mechanics Division, 1980, 106(6): 1099—1109.
[19]李创第, 李暾.结构在水平与竖向随机地震同时作用下的相关函数和谱密度[J].工程力学, 2008, 25(8): 156—163.Li Chuangdi, Li Tun.Correlation function and spectral density of structures under horizontal and vertical random earthquakes [J].Engineering Mechanics, 2008, 25 (8): 156—163.(in Chinese)
[20]Dimentberg M, Bucher C.Combinational parametric resonance under imperfectly periodic excitation [J].Journal of Sound & Vibration, 2012, 331(19): 4373—4378.
[21]Guo S S.Probabilistic solutions of stochastic oscillators excited by correlated external and parametric white noises [J].Journal of Vibration & Acoustics, 2014, 136(3): 031003.
[22]Guo S S, Er G K, Chi C L.Probabilistic solutions of nonlinear oscillators excited by correlated external and velocity-parametric Gaussian white noises [J].Nonlinear Dynamics, 2014, 77(3): 597—604.
[23]李创第, 邹万杰, 黄天立, 等.结构在水平与竖向地震同时作用的非平稳响应[J].土木工程学报, 2005, 38(6): 25—34.Li Chuangdi, Zou Wanjie, Huang Tianli.The nonstationary response of structure to horizontal and vertical earthquakes [J].China Civil Engineering Journal, 2005, 38(6): 25—34.(in Chinese)
[24]Joseph Emans, Marian Wiercigroch.Cumulative effect of structural nonlinearities: chaotic dynamics of cantilever beam system with impacts [J].Chaos, Solitons and Fractals, 2005(23): 1661—1670.