国内外普遍将名义屈服强度不低于460 MPa的钢材称为高强度钢材[1—2]。相比普通强度钢材，因材料强度的提高，高强钢构件尺寸更小，结构自重减轻，降低了工程造价，提高了结构效率。高强度螺栓承压型连接是钢结构现场施工常用的连接方式[3]，我国现行《钢结构设计规范》[4](下称《钢规》)中针对承压型连接的计算准则如图1所示。点1定义了摩擦型连接的计算准则，实际上此连接尚有较大的承载潜力。点2定义了承压型连接的计算准则，对比点1，承压型连接的计算准则更加充分利用了螺栓的承载能力，理论上可节约高达50%的螺栓。
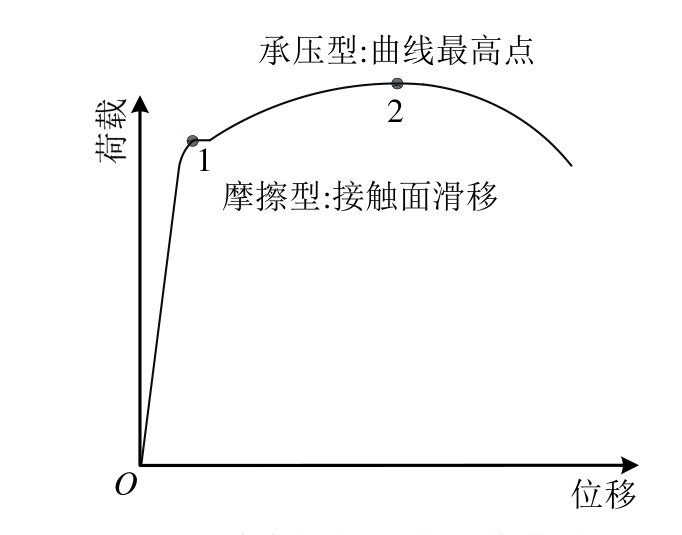
图1 单个螺栓受剪工作曲线
Fig.1 Working curve for an individual bolt
承压型螺栓连接的承载力主要来源于钢板孔壁与螺栓的接触行为，承载力的发展伴随着螺栓孔壁周围材料的应力集中与塑性变形，如图2所示。普通钢延性好，其充分塑性变形能力可降低因螺栓孔边缘应力集中造成的不利影响。随着强度增高，钢材延性变差，导致螺孔周围局部变形能力相比普通钢材有下降[1]，需对高强度钢材承压型连接的受力性能进行研究。
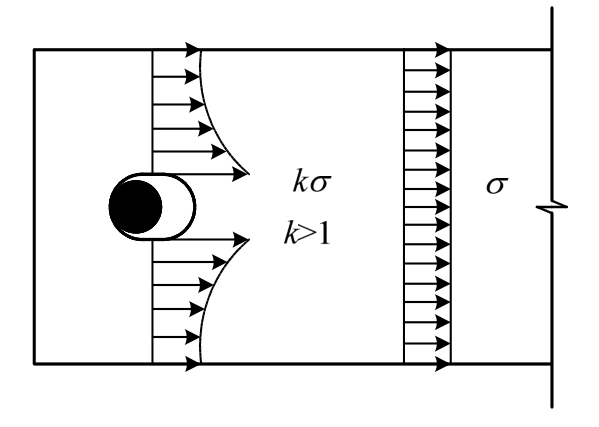
图2 应力集中现象
Fig.2 Stress concentration phenomenon
目前国内外主要采用单螺栓或双螺栓的连接形式来研究承压型连接的受力性能。国外学者Puthli和Fleischer[5]采用S460钢材进行了25组垂直受力方向布置的双螺栓承压性能试验，发现欧洲规范EN 1993-1-8[6]对边距不足情况下承压承载力的折减过于保守，该研究优化了EN 1993-1-8中的折减系数，提高了连接的设计承载力。Može和Beg[7—9]利用S235和S690钢材进行了单螺栓和双螺栓的承压性能试验，发现对于高强钢S690制作的试件，受剪破坏仍然具有延性，可观察到螺栓孔周材料较显著的塑性变形，研究还发现EN 1993-1-8的设计值无论对于普通钢还是高强钢，均过于保守。Kim和Yura[10]采用了强屈比为1.13和1.61的两种钢材进行了单螺栓和双螺栓承压性能试验，研究发现，极限承载力与材料的抗拉强度成正比，建议以材料的抗拉强度作为设计公式的参数。Aalberg和Larsen[11—12]采用了三种极限强度分别为539 MPa，870 MPa和1440 MPa的钢材，进行了单螺栓和双螺栓承压性能试验，发现美国规范ANSI/AISC 360-10[13]对所测试的高强钢承压型连接仍有较好的预测精度。Kamtekar[14]对于单螺栓连接的极限承压承载力进行了理论推导，理论公式对已有普通钢的试验结果有较好的预测精度。国内学者石永久等利用Q460级高强钢进行了双螺栓承压性能试验[15]和有限元分析[16]，并建议国产Q460级高强钢承压强度设计值取为1.4倍钢材最小抗拉强度[17]。
已有研究中针对高强钢的试验数量较少，本文采用3种超500 MPa级国产钢材Q550D、Q690D和Q890D，制作了24组单螺栓双剪试件[18]，16组单螺栓单剪试件，6组单螺栓孔径变化试件，以及4组Q345B单螺栓对比试件。利用上述共50组试件，本文研究了承压承载力的主要影响因素，并和国内外规范进行了对比。
1 承压型连接的特征性参数
现行《钢规》中，螺栓连接板的承压承载力按式(1)设计，式(1)中的参数d和t分别代表螺栓杆直径和钢板厚度。实际设计中，当确定螺栓杆直径d和钢板厚度t后，承压承载力仅取决于承压强度设计值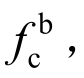
该参数即为计算承压承载力的特征性参数。
式中：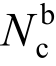
是承压承载力；d是螺栓杆直径；∑t是在不同受力方向中一个受力方向承压构件总厚度的较小值，对于单块钢板，∑t即为t；
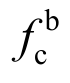是承压强度设计值，为
是钢材的最小抗拉强度。
《钢规》规定，参数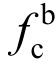
取为1.26倍钢材的最小抗拉强度。结合图1中的对承压型螺栓连接的定义，该参数可利用荷载位移曲线的最高点直接测量获得。试验中，根据不同的设计参数，单螺栓连接可能出现不同的破坏模式，主要包括：孔壁承压破坏、净截面破坏和螺栓受剪破坏。每种破坏模式对应的荷载位移曲线均有最高点，需确定采用何种曲线的最高点来确定参数
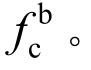我国《钢规》中已有针对净截面破坏和螺栓受剪破坏的设计公式，综合分析《钢规》的设计理念，确定参数
时，应选用孔壁承压破坏对应曲线的最高点确定参数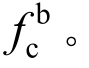
现行EN 1993-1-8和ANSI/AISC 360-10针对承压型螺栓连接的设计公式分别如式(2)～式(4)所示。两个国外规范的设计理念均与《钢规》存在差异。
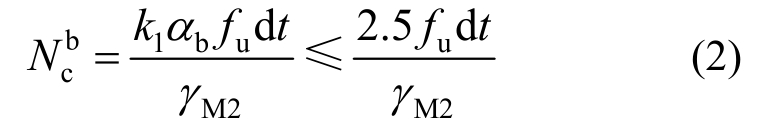
式中：αb取值为min(αb, fub/fu, 1.0)；fub是螺栓材料的极限抗拉强度，对于端部位置的螺栓，αd=e1/3d0；k1取值为min(2.8e2/d0-1.7, 2.5)；e1和e2是欧洲规范中定义的几何参数；d和d0分别为螺栓直径和螺栓孔径；t是钢板厚度；γM2是分项系数，在本文计算时取为1.0。
式中，lc是净距，为受力方向从螺栓孔边缘到相邻孔或连接件边缘的距离。
EN 1993-1-8将端距e1和边距e2的影响考虑进式(2)内，并兼顾了螺栓自身材料强度的影响，公式较《钢规》的公式更为复杂。EN 1993-1-8的公式存在一个上限值2.5fudt，该上限值主要用来限制螺栓孔的变形。利用该上限值与dt(螺栓杆径与钢板厚度的乘积)的比值，可换算得到EN 1993-1-8对应的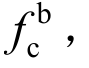
换算值高达2.5fu，达到了《钢规》的2倍。
ANSI/AISC 360-10将承压型连接的设计按两种情况分别考虑，当设计需要考虑限制螺栓孔的变形时，承压承载力按照式(3)计算；当设计不需要考虑限制螺栓孔的变形时，承压承载力按照式(4)计算。ANSI/AISC 360-10的公式建立在净距lc的概念上，净距lc和EN 1993-1-8中的端距e1相差0.5倍的螺栓孔径d0。对于式(3)还是式(4)，换算得到的最大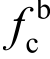
高达2.4fu和3.0fu，均显著地超过我国《钢规》的规定值。
综上所述，我国《钢规》表达形式简洁，便于设计应用，但承压强度设计值取值相比欧洲和美国规范偏保守。
2 试验概况
2.1 试件材料力学性能
所有钢板的厚度均为10 mm，其中，试件板采用Q550D、Q690D和Q890D三种由舞阳钢铁厂生产的高强度钢材制作，为避免过高的热输入量对钢材材性的影响，试件板的加工采用线切割加工。盖板材料为Q890D，尺寸比试件板略大，以保证加载过程中盖板始终保持弹性。试验中补充了4组国产Q345B钢试件作为对比试验。四种钢材根据《金属材料 拉伸试验 第1部分：室温试验方法》(GB/T 228.1-2010)[19]进行了室温拉伸试验，测得材料力学性能如表1所示。
表1 钢材材料参数
Table 1 Material parameters of steel
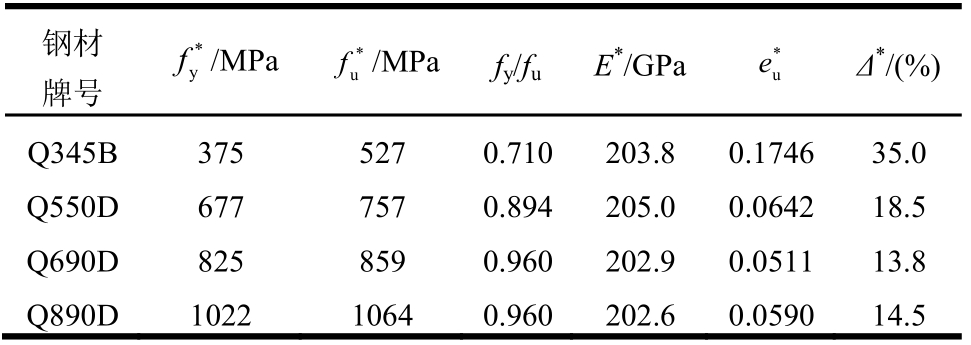
注：fy是屈服强度；fu是极限抗拉强度；E是弹性模量；eu是抗拉强度处的应变；Δ是断后伸长率。
钢材 牌号 *y f/MPa *u f/MPa fy/fuE*/GPa *u e Δ*/(%)Q345B 375 527 0.710 203.8 0.1746 35.0 Q550D 677 757 0.894 205.0 0.0642 18.5 Q690D 825 859 0.960 202.9 0.0511 13.8 Q890D 1022 1064 0.960 202.6 0.0590 14.5
2.2 试件设计与制作
单螺栓试件主要设计的几何尺寸包括端距e1和边距e2，分别描述了螺栓到钢板边缘的距离，如图3所示。端距e1为受力方向上螺栓孔中心至构件边缘的距离，边距e2为垂直受力方向螺栓孔中心至构件边缘的距离。试验中，端距e1设计了1.0d0、1.2d0、1.5d0、2.0d0和2.5d0共5种尺寸，而边距e2则设计了0.8d0、1.1d0、1.5d0和3.0d0共4种尺寸。试验按照类型可分为：单螺栓双剪切面试验、单螺栓单剪切面试验和螺栓孔径变化试验，分别用“SD”、“SS”和“SH”来表示，其中，“SD”和“SS”试验采用M24螺栓，而“SH”试验采用M16螺栓。每根试件的编号采用“XX-e1/d0-e2/d0-钢材等级”的形式，XX按照试验类型可取为SD、SS或SH，表2展示了不同试验的尺寸设置。如试件SD-15-30-550，表示双剪切面的单螺栓试件，采用Q550D钢，端距e1=1.5d0，边距e2=1.5d0。
图3 端距和边距的定义
Fig.3 Definition of end and edge distance
表2 试件尺寸设计
Table 2 Geometry set-up
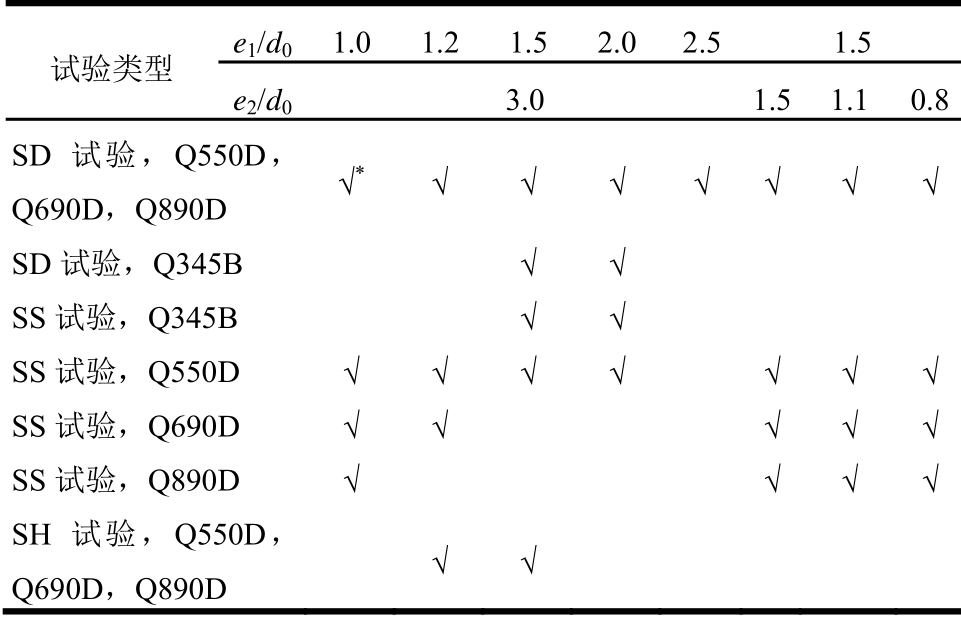
注：在该尺寸处设置了一根试件。
试验类型 e1/d0 1.0 1.2 1.5 2.0 2.5 1.5 e2/d03.0 1.5 1.1 0.8 SD试验，Q550D，Q690D，Q890D √* √ √ √ √ √ √ √SD试验，Q345B √ √ SS试验，Q345B √ √ SS试验，Q550D √ √ √ √ √ √ √SS试验，Q690D √ √ √ √ √SS试验，Q890D √ √ √ √SH试验，Q550D，Q690D，Q890D √ √
2.3 加载方案与测点布置
本文的试验设置如图4所示，一个试件组由试件板、盖板和高强螺栓组成。试验采用12.9级的高强螺栓，包括M24和M16两种螺栓，相应的螺栓孔直径分别为26 mm和18 mm，螺栓不施加预紧力，实测螺栓材料的抗拉强度为1437 MPa。全部试件在同济大学结构工程试验室的万能材料试验机进行加载。试验时，先进行预加载，以闭合螺栓与孔壁之间的间隙，预加载结束后卸载至零，以1.5 mm/min的加载速率进行单调加载，直至试件破坏。试件采用量程为30 mm的位移计来测量试件和盖板间的相对变形，位移计的初始标距为100 mm，如图4所示。
图4 试验设置
Fig.4 Experimental set-up
3 试验结果及分析
3.1 破坏模式
试验中出现的破坏模式可归纳为图5中连接板件的剪出破坏、端部撕裂破坏、净截面破坏和螺栓的受剪破坏4种模式，其中钢板的剪出和端部撕裂破坏均属钢板抗剪强度不足发生的破坏。各试件的破坏模式汇总于表3，试件典型破坏模式照片见图6。通过对比分析不同几何参数与不同等级钢材试件的破坏模式与特征，得到如下结果：
1)剪出破坏和端部撕裂破坏总体特征较为相似，沿受力方向的剪切断裂线均出现在两种破坏模式中，钢板最终因材料的抗剪强度不足而发生破坏；两者的主要区别主要在净截面与板件边缘的变形形态上。对于端部撕裂破坏的试件，净截面有明显的转动变形，且板件边缘出现受拉撕裂断口，而剪出破坏的试件则没有这些特征；
2)不同等级钢材的剪出破坏和端部撕裂破坏的特征相似，破坏均伴随着明显的螺栓孔拉长，极限状态下孔壁前形成断裂线，试件最终受剪破坏。该试验现象表明高强度钢材延性虽低于普通强度钢材，但其试件局部变形能力仍足以克服螺栓孔周围应力集中的不利影响，使承压承载力得到充分利用；
3)剪切面数不影响破坏模式的整体特征，但使得螺栓受剪破坏更容易发生。对比SD-20-30-550(图6(g))和SS-20-30-550(图6(h))两个试件，单剪试件钢板的螺栓孔变形明显小于双剪试件，螺栓在板件承压承载力未充分发挥前剪断；
4)螺栓孔径对破坏模式的影响不明显，相似的螺栓孔变形和剪切断裂线特征出现在两种不同孔径的连接中，例如试件SD-15-30-550(图6(a))和SH-15-30-550(图6(l))。
图5 单螺栓连接可能的破坏模式
Fig.5 Possible failure modes in single-bolt connection
图6 钢板在破坏时的特征
Fig.6 Features of steel plates at failure
表3 所有试件的破坏模式
Table 3 Failure mode for all specimens
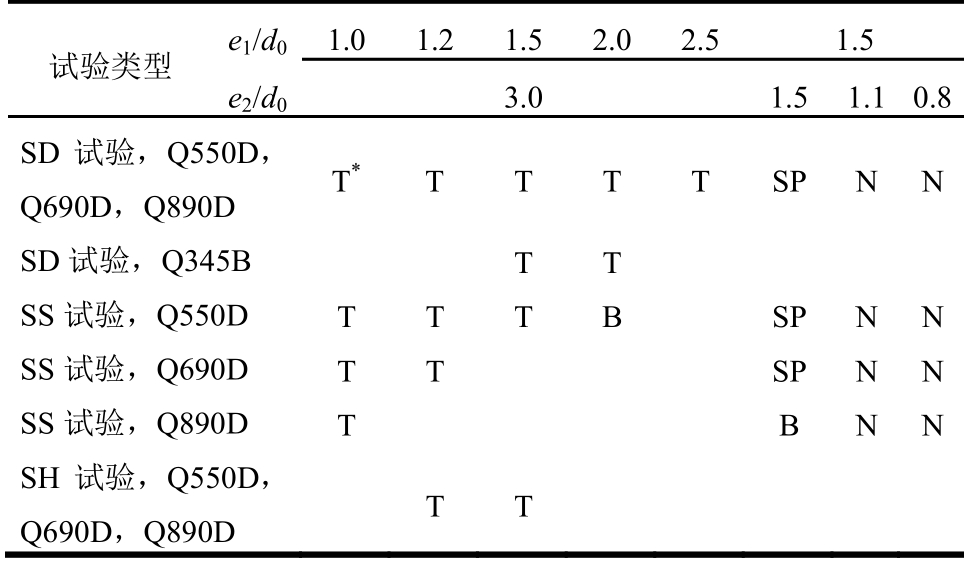
注：T、SP、N和B分别代表图5中的剪出破坏，端部撕裂破坏、净截面破坏和螺栓受剪破坏。
试验类型 e1/d0 1.0 1.2 1.5 2.0 2.5 1.5 e2/d03.0 1.5 1.1 0.8 SD试验，Q550D，Q690D，Q890D T* T T T T SP N N SD试验，Q345B T T SS试验，Q550D T T T B SP N N SS试验，Q690D T T SP N N SS试验，Q890D T B N N SH试验，Q550D，Q690D，Q890D T T
3.2 实测承压强度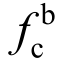
本试验50组试件的极限承载力Nu汇总于表4。为便于比较结果，设置表4中每一行为相同几何尺寸试件，每一列为相同的钢材等级试件。根据式(1)可由受剪破坏试件的极限承载力算得其承压强度值，即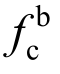
=Nu/dt，并沿用《钢规》中将测得承压强度
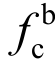以承压强度系数(钢材抗拉强度fu的倍数)的方式表述。通过不同几何尺寸与不同钢材强度等级试件结果的比较可知：
表4 极限承载力与承压强度系数
Table 4 Ultimate strength and bearing strength coefficients
Q690D Q890D Nu/kN b c f /fu Nu/kN b c f /fu 210 1.02 262 1.02 249 1.21 328 1.28 332 1.61 416 1.63 437 2.12 550 2.15 542 2.63 662 2.59 SD-15-15 — — 271 1.49 317 1.54 392 1.54 SD-15-11 — — 242 — 284 — 347 — SD-15-08 — — 125 — 149 — 183 — SS-10-30 — — 186 1.02 207 1.01 264 1.03 SS-12-30 — — 227 1.25 262 1.27 — — SS-15-30 216 1.70 294 1.62 — — — — SS-20-30 273 2.16 380 — — — — — SS-15-15 — — 288 1.59 317 1.54 381 1.50 SS-15-11 — — 248 — 295 — 357 — SS-15-08 — — 133 — 156 — 194 — Sh-12-30 — — 156 1.28 170 1.23 220 1.30 Sh-15-30 — — 201 1.66 220 1.61 282 1.66
1)在相同几何参数情况下，极限承载力随钢板强度增高而增高，但不同钢材强度等级试件的承压强度系数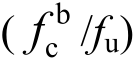
较为接近，最大相差5.8%，可见钢材等级对承压强度系数的影响不明显；
2)在相同钢材强度等级下，试件端距参数e1/d0与承压强度系数呈线性关系(图8)，承压强度系数随e1/d0的增加而增加；
3)在钢材等级和端距e1/d0相同的情况下，边距e2/d0足够避免发生净截面破坏但又不足以限制净截面发生转动变形时，试件会呈现端部撕裂破坏，其承压强度系数要小于剪出破坏。试件SD-15-15(端部撕裂破坏)相比试件SD-15-30(剪出破坏)承压强度系数有所降低，对于Q550D、Q690D和Q890D三种钢材试件分别降低了7.5%、4.3%和5.5%。
3.3 荷载位移曲线
图7给出了加载试件的典型荷载-位移曲线，比较了不同钢材等级、端距e1、边距e2、剪切面数和螺栓孔径对试件承压性能的影响：
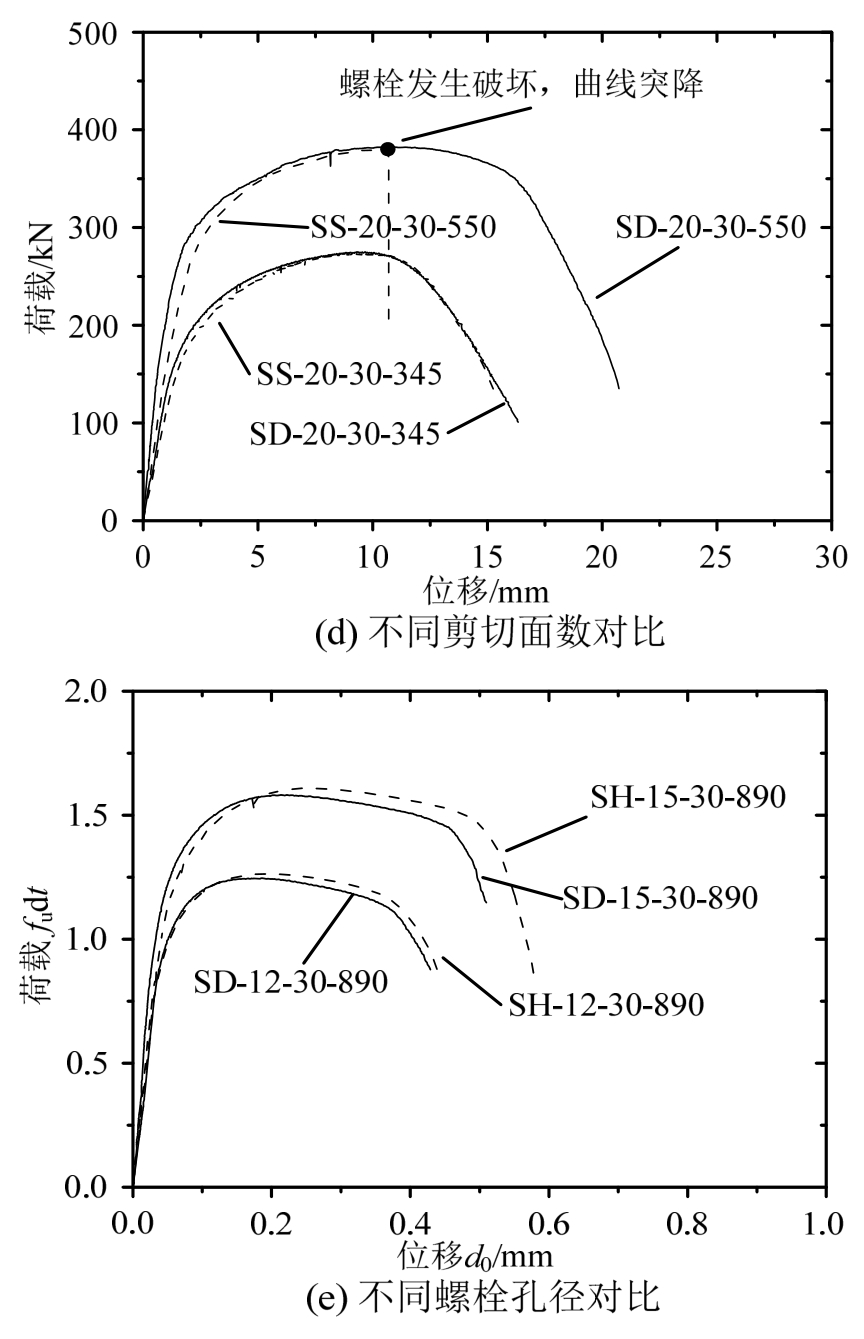
图7 典型荷载位移曲线
Fig.7 Typical load-deformation curves
1)图7(a)对比了4种不同钢材的荷载位移曲线，不同等级钢材试件达到曲线峰值点时的位移比较接近，峰值点后不同等级钢材试件的下降段均较为平缓，高强钢试件呈明显延性破坏性特；
2)图7(b)对比了Q550试件不同端距e1下的荷载位移曲线，可以看出提高端距e1不仅可显著地提高极限承载力，也同时提高连接的变形能力；
3)图7(c)对比了Q690试件不同边距e2下的荷载-位移曲线，结果表明，在边距足够避免净截面破坏时，剪出破坏和端部撕裂破坏的荷载-位移曲线差异较小；但当边距e2进一步降低，发生净截面破坏时，连接试件的承载力与变形能力均大幅降低；
4)图7(d)对比了试件在单、双剪切面条件下的荷载-位移曲线，当不发生螺栓受剪破坏时，单剪切面和双剪切面的荷载位移曲线差异较小。但对于承压承载力较高的高强钢连接试件，当采用单剪切面时试件易发生螺栓受剪破坏，导致连接破坏呈脆性，应在设计中尽量避免；
5)图7(e)为便于比较不同螺栓孔径的荷载-位移曲线，将横纵坐标分别以d0和fudt进行了正则化处理，可以看出，不同螺栓孔径的正则化荷载-位移曲线差异较小，可以忽略不同螺栓孔径对承压强度系数的影响。
4 与已有规范的对比
将试验结果以承压强度系数的形式与EN 1993-1-8、ANSI/AISC 360-10及《钢规》的计算结果进行对比，见图8。按规范计算时，式(2)～式(4)中相应材料的分项系数均按1.0考虑。
由图8的对比结果可以看出，EN 1993-1-8的预测曲线处于试验值的下方，预测偏保守16%～25%。ANSI/AISC 360-10对于考虑限制螺栓孔变形的式(3)，曲线均处于试验值以下，预测偏保守5%～38%；对于不考虑限制螺栓孔变形的式(4)，ANSI/AISC 360-10在e1/d0＜1.5时预测仍然偏保守，但在e1/d0＞1.5时高估了连接试件的承压承载力，说明美国规范不考虑限制螺栓孔变形时，对于e1/d0＞1.5的螺栓连接承压承载力预测偏危险。
图8 现行规范与试验结果对比
Fig.8 Comparison between current codes and experimental results
《钢规》中规定的最小容许端距e1为2d0，设计中对满足e1/d0≥2.0的试件，承压强度系数统一取1.26。对于按《钢规》最小端距要求设计的试件，实测承压承载力约为规范值的1.70倍。对于e1/d0=2.5的试件，实测承压承载力约为规范值的2.05倍，《钢规》预测值较保守。
由图8中不同规范比较可知，《钢规》中螺栓连接承压承载力规定较EN 1993-1-8和ANSI/AISC 360-10更为保守。
图8中的实测承压强度系数与参数e1/d0之间呈线性关系，基于本研究的试验数据以最小二乘法进行线性拟合，得到了承压承载力与端距e1/d0的关系，式(5)。为进一步验证式(5)的适用性，搜集了欧洲规范研究报告[20—22]和文献[7—8]中共191组试验结果与式(5)预测值进行对比，见图9。该191组试验结果采用的钢材的实测屈服强度范围为251 MPa～761 MPa。图9的结果表明，式(5)的预测精度较高，可用来预测不同强度等级的钢材和不同e1/d0对应的承压强度系数。
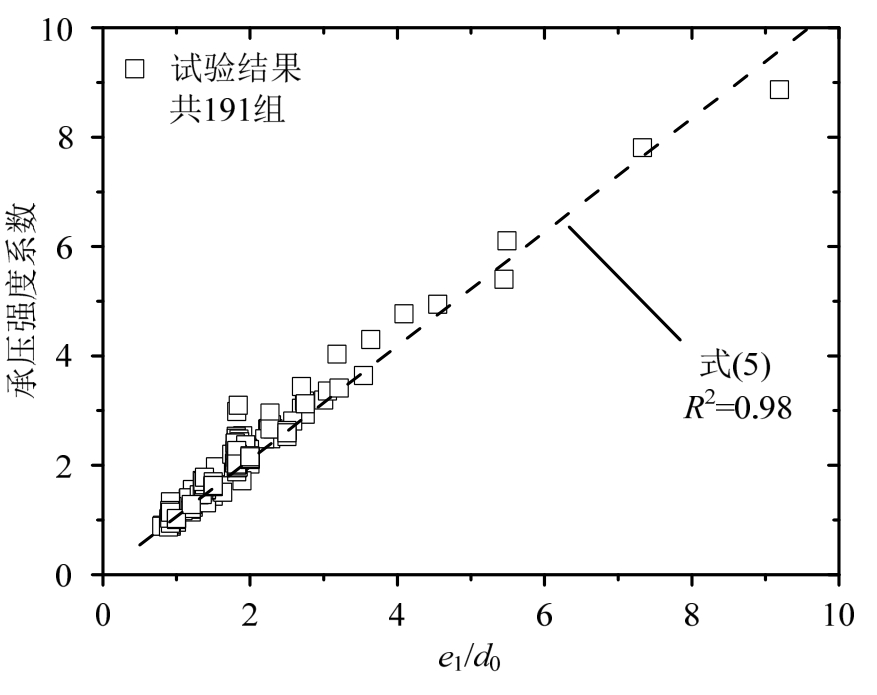
图9 式(5)与其他文献试验结果的对比
Fig.9 Comparison of results from external sources with Eq.(5)
5 承压强度设计值的保证率
《钢规》的式(1)与EN 1993-1-8的式(2)以及ANSI/AISC 360-10的式(3)和式(4)相比，形式上更简洁，设计应用更方便。
可利用式(5)确定螺栓承压强度设计值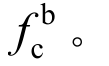
式(5)假定承压承载力与e1/d0之间采用线性的计算模式，需对此计算模式的不确定性进行分析。计算模式的不定性反映了实际抗力与公式计算抗力之间的差异[23]，表达如式(6)所示。利用图9中的191组试验数据和式(5)，可分析计算模式不定性的相关统计参数。图10展示了Kp的频率分布直方图，数据分布接近正态分布，利用χ2拟合检验法进行分布拟合检验，检验结果表明，在显著性水平α=0.05下，可认为变量KP服从正态分布，相应的均值μP和标准差σP分别约为1.095和0.111，变异系数为0.101，正态分布曲线如图10所示。
式中：KP是计算模式不定性；R0是实际抗力；Rc是公式计算的抗力值。
现行《钢规》规定的最小端距e1=2d0，利用式(5)计算所得的承压强度系数约为2.09。小于均值μP两倍标准差σP的分位值约为μP-2σP=0.873，相应的承压强度系数为2.09×0.873≈1.82。利用正态分布的特点，1.82的系数仍具有97.5%的保证率。
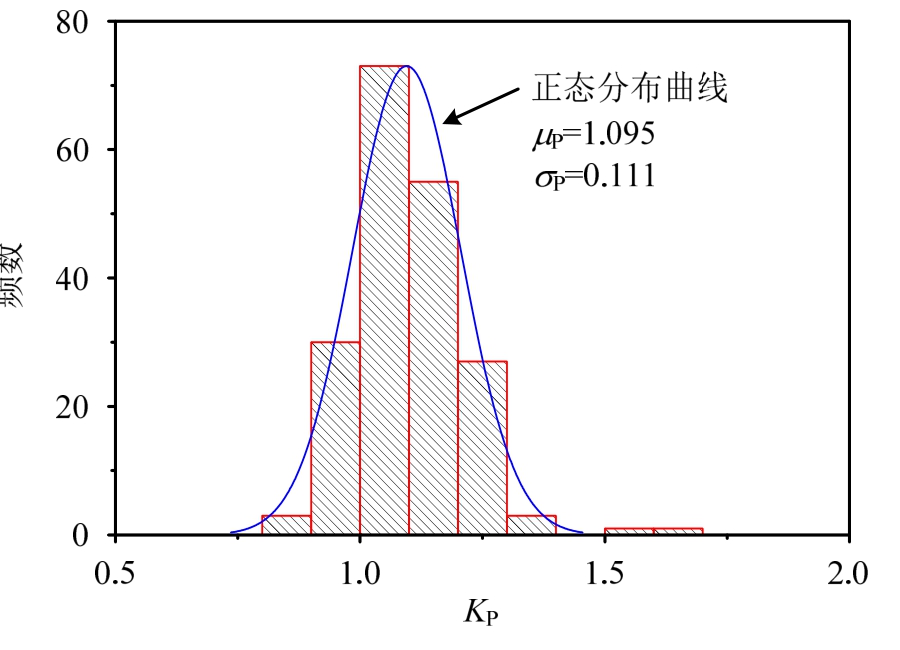
图10 KP直方图分析
Fig.10 Analysis on histogram of KP
对于超500 MPa高强钢，如按照现行《钢规》螺栓承压强度系数取为1.26，则承压强度设计值的保证率为99.99%，较偏于保守。
6 结论
本文主要采用3种超500 MPa级国产钢材Q550D、Q690D和Q890D和一种国产普通强度钢材Q345B，制作了共50组承压型单螺栓试件，综合研究了影响螺栓承压承载力的因素，并和国内外规范计算结果进行了对比，得到主要的结论如下：
(1)高强度钢材延性虽相对普通强度钢材有所下降，但其塑性变形能力仍足以克服应力集中的不利影响，可充分利用高强钢板件的承压承载力；
(2)钢材的强度等级和螺栓孔径对试验破坏模式的影响不显著，测得的承压强度系数在参数e1/d0相同的情况下较接近。单剪切面的构造使得螺栓受剪破坏更容易发生，连接行为呈现脆性。若能保证螺栓受剪破坏不发生，在参数e1/d0相同的情况下，单剪切面测得的承压强度系数与双剪切面无明显差异；
(3)现行《钢规》规定的螺栓承压强度设计值与端距e1=1.2d0试件的实测值较为接近，但较显著地小于e1＞1.2d0试件的实测值。按照《钢规》中最小容许端距进行设计的试件，试验实测值约为《钢规》的规定值的1.7倍左右，存在较大的承载潜力；
(4)欧洲规范对于承压承载力的预测相比本文试验结果总体偏保守。现行美国规范考虑限制螺栓孔变形的预测公式总体偏保守，但不考虑限制螺栓孔变形的公式在e1＞1.5d0时可能不安全；
(5)现行《钢规》中规定的螺栓连接板承压强度设计值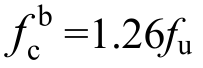
偏于保守，螺栓连接板承压强度设计值取
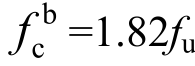仍具有97.5%的保证率。
[1]李国强, 王彦博, 陈素文, 等.高强度钢结构研究现状及其在抗震设防区应用问题[J].建筑结构学报, 2013, 34(1): 1—13.Li Guoqiang, Wang Yanbo, Chen Suwen, et al.State-of-the-art on research of high strength structural steels and key issues of using high strength steels in seismic structures [J].Journal of Building Structures, 2013, 34(1): 1—13.(in Chinese)
[2]施刚, 朱希.高强度结构钢材单调荷载作用下的本构模型研究[J].工程力学, 2017, 34(2): 50—59.Shi Gang, Zhu Xi.Study on constitutive model of high-strength structural steel under monotonic loading [J].Engineering Mechanics, 2017, 34(02): 50—59.(in Chinese)
[3]王朋, 陈海波, 张会武, 等.螺栓连接对基础非均匀沉降输电塔的影响研究[J].工程力学, 2015, 32(10): 209—219.Wang Peng, Chen Haibo, Zhang Huiwu, et al.Effect of bolt joint on the behaviour of transmission tower with non-uniform settlement [J].Engineering Mechanics, 2015, 32(10): 209—219.(in Chinese)
[4]GB 50017—2017, 钢结构设计规范[S].北京: 中国计划出版社, 2017.GB 50017—2017, Code for design of steel structures [S].Beijing: China Planning Press, 2017.(in Chinese)
[5]Puthli R, Fleischer O.Investigations on bolted connections for high strength steel members [J].Journal of Constructional Steel Research, 2001, 57(3): 313—326.
[6]EN 1993-1-8 Eurocode3: Design of steel structures- Part 1-8: Design of joints [S].Brussels: European Committee for Standardization, 2005.
[7]Može P, Beg D.High strength steel tension splices with one or two bolts [J].Journal of Constructional Steel Research, 2010, 66(8/9): 1000—1010.
[8]Može P, Beg D.A complete study of bearing stress in single bolt connections [J].Journal of Constructional Steel Research, 2014, 95: 126—140.
[9]Može P.Bearing strength at bolt holes in connections with large end distance and bolt pitch [J].Journal of Constructional Steel Research, 2018, 147: 132—144.
[10]Kim H J, Yura J A.The effect of ultimate-to-yield ratio on the bearing strength of bolted connections [J].Journal of Constructional Steel Research.1999, 49(3): 255—269.
[11]Aalberg A, Larsen P K.Bearing stregnth of bolted connections in high strength steel [C].Copenhagen: Nordic Steel Construction Conference Committee, 2001: 859—866.
[12]Aalberg A, Larsen P K.The effect of steel strength and ductility on bearing failure of bolted connections [C].Portuguesa: The Third European Conference Committee, 2002: 869—878.
[13]AISC.Specifications for Structural Steel Buildings.ANSI/AISC 360-10 [S].Chicago: American Institute of Steel Construction, Inc, 2010.
[14]Kamtekar A G.On the bearing strength of bolts in clearance holes [J].Journal of Constructional Steel Research, 2012, 79: 48—55.
[15]石永久, 潘斌, 施刚, 等.高强度钢材螺栓连接抗剪性能试验研究[J].工业建筑, 2012, 42(1): 56—61.Shi Yongjiu, Pan Bin, Shi Gang.Experimental study on high strength steel-plate-bolted connections under shear force [J].Industrial Construction, 2012, 42(1): 56—61.(in Chinese)
[16]潘斌, 石永久, 王元清.Q460等级高强度钢材螺栓抗剪连接孔壁承压性能有限元分析[J].建筑科学与工程学报, 2012, 29(2): 48—54.Pan Bin, Shi Yongjiu, Wang Yuanqing.Finite element analysis of bolted connection in Q460 grade high strength steels under static shear [J].Journal of Architectural and Civil Engineering, 2012, 29(2): 48—54.(in Chinese)
[17]石永久, 潘斌, 王元清.高强度钢材螺栓连接孔壁承压性能研究及设计建议[J].青岛理工大学学报, 2013, 34(1): 24—32.Shi Yongjiu, Pan Bin, Wang Yuanqing.Investigation and proposed design rules on bolted connections for high strength steel [J].Journal of Qingdao Technological University, 2013, 34(1): 24—32.(in Chinese)
[18]Wang Yanbo, Lyu Yifan, Li Guoqiang.Behavior of single bolt bearing on high strength steel plate [J].Journal of Constructional Steel Research.2017, 137: 19—30.
[19]GB/T 228.1—2010, 金属材料 拉伸试验 第1部分: 室温试验方法[S].北京: 中国标准出版社, 2010.GB/T 228.1—2010, Metallic material-tensile testing-Part 1: Method of test at room temperature [S].Beijing: China Standard Press, 2010.(in Chinese)
[20]Snijder H H, Ungermann D, Stark J W B, et al.Evaluation of test results on bolted connections in order to obtain strength functions and suitable model factors Part A: results [R].Eurocode 3 Editorial Group, 1988.
[21]Snijder H H, Ungermann D, Stark J W B, et al.Evaluation of test results on bolted connections in order to obtain strength functions and suitable model factors Part B: evaluations [R].Eurocode 3 Editorial Group, 1988.
[22]Snijder H H, Ungermann D, Stark J W B, et al.Evaluation of test results on bolted connections in order to obtain strength functions and suitable model factors Part C: Test data [R].University of Technology Aachen, Institute for Steel Construction, 1988.
[23]施刚, 朱希.国产高强度结构钢设计指标和可靠度分析[J].建筑结构学报, 2016, 37(11): 144—159.Shi Gang, Zhu Xi.Design indexes and reliability analysis of domestic high-strength structural steels [J].Journal of Building Structures, 2016, 37(11): 144—159.(in Chinese)