在现浇钢筋混凝土剪力墙结构中,窗洞口下方的窗下墙一般采用砌体填充墙。由于砌体墙的承载力较低,尽管其在小震作用下对结构的刚度有一定程度的影响,但在中、大震作用下会较早发生破坏,且破坏为脆性,耗能能力较差,对结构在中、大震下的性能影响较小。因此目前在大多数规范中,都把砌体填充墙视为非结构构件[1]。在预制装配式混凝土剪力墙结构中,为进一步提高施工效率,往往将门窗洞口预留在剪力墙中,即将窗下墙与两侧的剪力墙作为一个整体共同预制。此时,窗台墙为钢筋混凝土构件,其承载力、变形和耗能能力均高于砌体填充墙,因此会对结构的受力性能有较大影响。目前的一种常见做法是在窗台墙中设置保温板等减重材料(图1),且在窗台墙和下层连梁间不设置竖向的连接钢筋,以避免形成高度较大的连梁,甚至是深连梁,并减小对结构受力性能的影响。此时,窗台墙与下层连梁可视为并列布置的“双连梁”。与仅有单根连梁的情况相比,双连梁的刚度和承载力均大幅增加。若设计时不考虑窗台墙的作用,则分析模型与结构的实际受力情况不符,从而可能产生超出预期的破坏模式。相反,若合理设计窗台墙,使其具有较低的承载力和较高的延性,则可以在地震作用下率先破坏,耗散地震能量,作为结构的第一道抗震防线。与剪力墙中的连梁相比,窗下墙不需要承担楼板传来的竖向荷载,作为耗能构件更为合适。

图1 试验试件配筋图
Fig.1 Reinforcement details of the specimens
目前,国内外针对装配式混凝土结构抗震性能展开的研究主要集中在结构本身[2-3],对填充墙尤其是窗下墙对结构抗震性能的影响尚未见诸文献。本文参照国家标准图集《预制混凝土剪力墙外墙板》(15G365-1)[4],分别设计制作了一个带有高窗下墙和一个矮窗下墙的剪力墙试件,并进行了拟静力试验,研究了不同高度窗下墙对剪力墙抗震性能的影响[5]。在此基础上,基于商业有限元程序MSC.Marc,提出了带窗下墙预制剪力墙结构的精细有限元数值模拟方法,结合试验结果分析揭示了窗下墙对带开洞预制剪力墙抗震性能的影响,并为进一步深入研究多高层预制装配式混凝土剪力墙结构的抗震性能提供了可供参考的数值模拟方法。
1 试验概况与加载方案
1.1 试验试件设计与制作
本文设计制作了两个缩尺比例均为1∶1.5的两层带窗下墙的预制装配式自保温剪力墙试件,分别为带矮窗下墙的预制剪力墙试件W-1,和带高窗下墙的预制剪力墙试件W-2,构件尺寸及截面配筋如图1所示。两个试件层高均为1800 mm,剪力墙为夹心保温外墙,墙肢长度为400 mm,墙厚为205 mm(外叶板厚40 mm,内叶板厚135 mm,中间保温板厚30 mm)。连梁和窗下墙的净跨度为1800 mm,连梁截面尺寸为205 mm×300 mm。试件属于剪力墙中洞口较大的壁式框架结构。试件W-1窗下墙高380 mm,试件W-2窗下墙高580 mm(对应的原型窗下墙高度分别为600 mm和900 mm,是工程中常用的两种窗台高度)。窗下墙中钢筋配置方式参照15G365-1图集[5],为了尽量降低窗下墙的强度,纵筋近似按我国混凝土结构设计规范中规定的受弯构件最小配筋率设计[6]。在高窗下墙试件W-2的窗下墙内设置了部分保温板以减轻自重。为了考虑真实结构中楼板对连梁刚度的影响,试件在每层连梁高度处均设有500 mm宽的楼板。试件制作时,上下两层墙板在工厂分开预制,然后在试验室进行拼装。剪力墙纵向受力钢筋采用灌浆套筒的方式连接,窗下墙与下层连梁和楼板之间采用坐浆的方法连接,未设置连接钢筋。
试验所采用的混凝土等级为C45,实测立方体抗压强度平均值为48.5 MPa。钢筋等级为HRB400,其实测材料性能如表1所示。
表1 钢筋材性
Table 1 Mechanical properties of the reinforcing bars
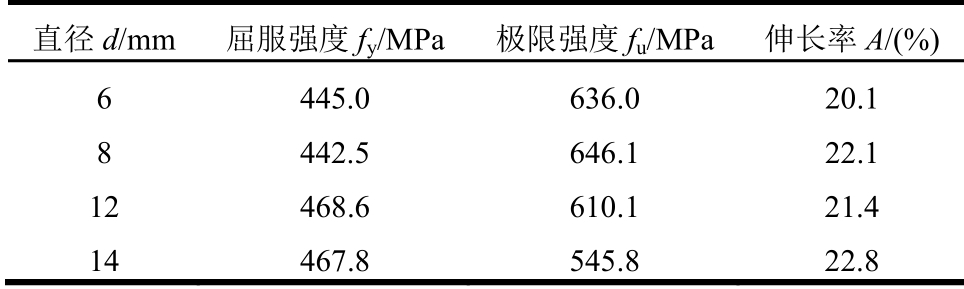
直径d/mm 屈服强度fy/MPa 极限强度fu/MPa 伸长率A/(%)6 445.0 636.0 20.1 8 442.5 646.1 22.1 12 468.6 610.1 21.4 14 467.8 545.8 22.8
1.2 试验设备加载方案

图2 试验装置
Fig.2 Test setup
试验加载装置如图2所示。剪力墙的设计轴压比为0.2,由两个千斤顶分别将193 kN的竖向荷载施加在两侧墙体的顶部,试验过程中保持该竖向荷 载不变。水平荷载由MTS电液伺服作动器施加。水平加载分为两个阶段,在试件屈服之前,水平荷载采用力控制的加载模式,分七级加载,每级荷载反复一次;在试件屈服后采用位移控制的加载模式,每级循环三次,直至试件破坏[7]。加载制度如图3所示。

图3 加载制度示意图
Fig.3 Loading protocol
2 试验现象与结果分析
2.1 试验现象及破坏形态
当试件W-1水平荷载达到20 kN时,首层右侧墙肢根部首先出现一条水平弯曲裂缝。水平荷载达40 kN时,一层连梁左侧底部出现一条垂直弯曲裂缝。加载至80 kN时,左右两侧墙肢根部不断出现新的弯曲裂缝。二层窗下墙和一层连梁作为一个整体共同工作,整体连梁的左右两侧顶、底部不断出现新的弯曲裂缝。加载至140 kN时,整体连梁的左右两侧顶、底部,二层连梁的左右两端,一层墙肢的顶部、底部和二层墙肢的底部出现多条弯曲裂缝,并有部分裂缝发展成弯剪斜裂缝,一层墙肢和连梁节点核心区出现少量斜裂缝。此时,钢筋应变数据显示二层窗下墙两端上部纵筋达到屈服,随后加载改为位移控制。
当试件顶点位移达到20 mm时,出现一声较大声响,同时试件顶部的水平位移突然增大。由于作动器无法适应这一突然的变形增长,荷载由174 kN降低至154 kN。此时,在窗下墙右侧出现一条最大宽度约为5 mm的裂缝,沿45°角斜向下延伸贯通至一层连梁的顶部(图4)。与此同时,填充墙底部坐浆层与一层连梁顶面发生脱离,一根整体连梁分为两根(图5),窗下墙左侧顶部,一层连梁左侧顶部、右侧底部出现多条弯曲和弯剪裂缝,钢筋应变数据也显示连梁端部纵筋应变突然增大,达到屈服。顶点位移达到30 mm时,底层墙肢根部纵筋达到屈服。顶点位移达50 mm时,底层右侧墙肢根部、二层窗下墙右侧底部出现轻微的混凝土保护层剥落现象。顶点位移达80 mm时,底层墙肢根部、连梁左右两端底部和二层窗下墙左右两端顶、底部混凝土均出现大面积压碎,试件承载力降低至峰值荷载的85%左右,试验结束。试件最终破坏状态如图4(a)所示。
试件W-2当水平荷载达到40 kN时,在一层右侧墙肢根部出现第一条弯曲水平裂缝。荷载达60 kN时,一层连梁右侧底部出现第一条竖向弯曲裂缝,二层窗洞角部出现短斜裂缝。加载至140 kN时,窗下墙和下部连梁连接在一起形成的整体连梁左右两端顶、底部出现多条弯曲裂缝,底层墙肢的顶、底部,二层墙肢的底部以及二层连梁的左右两端出现多条弯曲裂缝,并有部分弯曲裂缝逐渐发展为弯剪斜裂缝。此时应变片数据显示窗下墙端部纵筋屈服,此后加载改为位移控制。顶点位移达20 mm时,整体连梁突然出现多条平行的交叉斜裂缝,贯通整个整体连梁的高度。同时,一层连梁与二层窗下墙间坐浆处出现水平裂缝,有脱开迹象。裂缝出现时试件承载力有轻微突降,此后继续加载,承载力又继续上升。钢筋应变数据显示在这一加载级别时一层连梁左端底部纵筋应变突然增大并达到屈服,一层墙肢根部纵筋也已达到屈服。顶点位移30 mm的正向加载的第一个循环时,窗下墙与下部连梁完全脱开,因此反向加载到同一位移级别时,试件承载力明显低于正向。顶点位移达40 mm时,左侧墙肢根部开始出现受压竖向裂缝。顶点位移达70 mm时,两侧墙肢根部混凝土保护层剥落,二层窗下墙左右两侧顶、底部均出现大面积混凝土压碎,试件承载力下降至峰值荷载的85%以下,试验结束。试件的最终破坏形态如图4(b)所示。
由上述试验现象可知,两试件的受力过程均可分为两个阶段。荷载较小时为整体连梁工作阶段,即窗下墙和下部连梁作为整体共同工作。随荷载和位移的增大,二者逐渐脱开,进入双连梁工作阶段。试件受力形态发生变化,内力发生重分布。两试件最终的破坏模式类似,都是墙肢根部和双连梁两端形成塑性铰,且受压区混凝土达到压碎而破坏。两试件的区别在于W-2窗下墙较高,与下部连梁共同形成的整体连梁的跨高比更小,且在截面中部设置了保温板,降低了抗剪强度,因此在整体连梁工作阶段出现大量斜裂缝,有受剪破坏的趋势。但进入双连梁工作阶段后,连梁和窗下墙破坏模式仍以弯曲破坏为主。由于W-2窗下墙刚度与下部连梁相比较大,分配的弯矩也较大,破坏也较严重,而下部连梁与W-1相比破坏程度则较轻。

图4 试件破坏形态
Fig.4 Damage pattern of the specimens

图5 窗下墙与连梁间水平通缝
Fig.5 Horizontal cracks between the window wall and the coupling beam
试件墙肢根部最终的破坏形态如图6所示。可见,对于纵筋采用灌浆套筒连接的剪力墙,破坏时塑性铰区存在2~3条宽度较大的主裂缝。其中,剪力墙与基础间水平拼缝处的裂缝宽度最大,套筒顶部附近也出现一根主裂缝,宽度相对水平拼缝处裂缝较小。除此以外,其破坏形态与现浇钢筋混凝土剪力墙差别不大。

图6 剪力墙墙肢根部破坏形态
Fig.6 Damage pattern of the wall bottom
2.2 试验结果分析
2.2.1 滞回曲线和骨架曲线
试验得到试件W-1、W-2的水平力-顶点位移滞回曲线如图7所示,相应骨架曲线对比如图8所示。

图7 试件水平力-顶点位移滞回曲线
Fig.7 Lateral load-top displacement hysteresis loops of the specimens

图8 试件力-位移骨架曲线
Fig.8 Load-displacement skeleton curves of the specimens
从图7可以看出,两个试件的滞回曲线形状相似,均比较饱满,耗能能力较好。荷载较小时滞回环为梭形,随着位移增大,刚度退化趋于明显,曲线逐渐呈反S形。试件W-1和W-2分别在正向加载至顶点位移为20 mm和30 mm时,窗下墙与下部连梁脱开形成两根连梁。继续反向加载至同一位移时,由于连梁已脱开,因此反向加载的荷载值低于正向加载的最大荷载值。
2.2.2 承载力和变形能力
表2列出了试件受力过程中屈服点、峰值点和极限点几个关键时刻的荷载值。表中屈服点通过等能量法[8]作图得到。极限点取水平力下降至峰值荷载的85%的时刻,若未下降至85%,则取试验结束时刻。表中可见,窗下墙较高的试件W-2正反向加载得到峰值承载力平均值较试件W-1提高约22.83%,变形能力则相对较差,正反向加载位移延性系数平均值较W-1减小约25.32%,极限位移角较W-1减小约19.21%。
2.2.3 刚度退化情况
取每次循环的正反向最大荷载绝对值之和与相应变形绝对值之和的比值作为每一级荷载下割线刚度。两个试件割线刚度随顶点位移的退化曲线如图9所示。窗下墙较高的试件W-2初始刚度较大,随着位移的增大W-1和W-2的刚度均逐渐减小。顶点位移超过30 mm后,随着试件损伤的加剧,两试件刚度间差距逐渐减小,试验末期两者趋于一致。
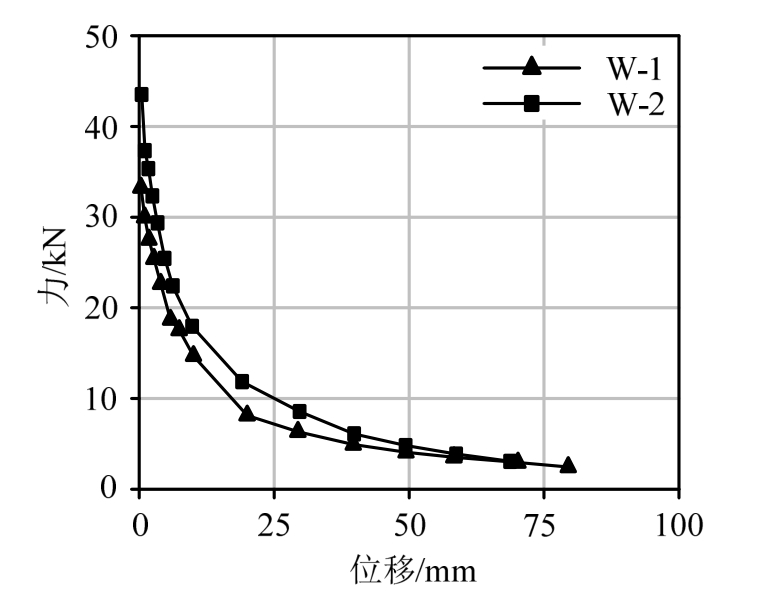
图9 试件刚度退化曲线
Fig.9 Stiffness deterioration curves of the specimens
2.2.4 耗能能力
根据文献[7]的规定采用能量耗散系数E评估试件的耗能能力。计算得到两个试件的能量耗散系数E值分别为1.63和1.58。可见,两试件耗能能力相差不大,窗下墙较高的试件W-2耗能能力略小。
表2 骨架曲线特征值
Table 2 Characteristic values of the skeleton curves

编号 方向 屈服点 峰值点 极限点 Py/kN Δy/mm Pp/kN Δp/mm Pu/kN Δu/mm 位移延性系数 极限位移角 μ=Δu/Δyθu=Δu/H W-1 正向 172 10.7 210.02 70.9 198.2 80.04 7.48 1/43 反向 140 12.0 205.28 69.47 192.93 78.94 6.58 1/44 W-2 正向 220 14.0 286.54 29.38 243.56 60.84 4.35 1/57 反向 170 11.0 223.56 40.04 195.21 67.57 6.15 1/51
3 数值模拟分析
3.1 精细有限元数值模拟方法
为了明确窗下墙对整体结构抗震性能的影响,深入了解预制剪力墙结构的内在损伤机理,有必要提出一种通用性强(同时适用于构件层次和整体结构层次)、计算效率高且计算精度较好的带窗下墙预制剪力墙精细有限元数值模拟方法。大量研究表明,分层壳剪力墙模型可较好地模拟不同类型现浇剪力墙构件的复杂受力行为,且被广泛应用于高层结构和超高层结构的抗震性能研究[9—11]。此外,张微敬等[12]的研究均表明采用灌浆套筒连接方式的预制剪力墙构件与现浇剪力墙构件的抗震性能基本相当。因此,分层壳模型可用于该类预制剪力墙结构的抗震性能研究。
在此,本文基于大型商业有限元程序MSC.Marc,采用分层壳剪力墙模型对带窗下墙的预制剪力墙构件展开相应的数值模拟方法研究。根据试件的截面尺寸和配筋情况指定每一层的材料特性和厚度。试件中的钢筋根据其位置和方向弥散在多个正交的层中。对于钢筋和混凝土的材料本构模型及其模型参数确定方法,本文采用江见鲸和陆新 征[13—14]等建议的本构模型和相应参数确定方法确定。三明治墙板的外叶板和保温板均为非结构构件,因此在模型中不予以考虑。剪力墙墙肢、连梁、楼板和窗下墙均采用75号壳单元模拟,沿着构件厚度方向将截面划分为24层。试验结果表明,在初始受力阶段,窗下墙与下层连梁共同工作形成一根刚度较大连梁,但由于两者之间没有钢筋连接,在较小的位移下即在水平拼缝处开始脱开,形成两根并列布置的“双连梁”。本文在窗下墙和连梁间设置如图7所示的20 mm厚的分缝,即不考虑二者脱开之前的受力状态,直接按照“双连梁”考虑。对于窗下墙中有内置保温板的部分,本文采用了等效厚度的方法予以考虑。具体而言,在建立含保温板窗下墙试件W-2的分层壳模型时,将截面厚度取为内叶板厚度减去内置保温板厚度,即72 mm。基于上述简化,本文最终建立了如图10所示的带窗下墙预制剪力墙构件精细有限元模型。
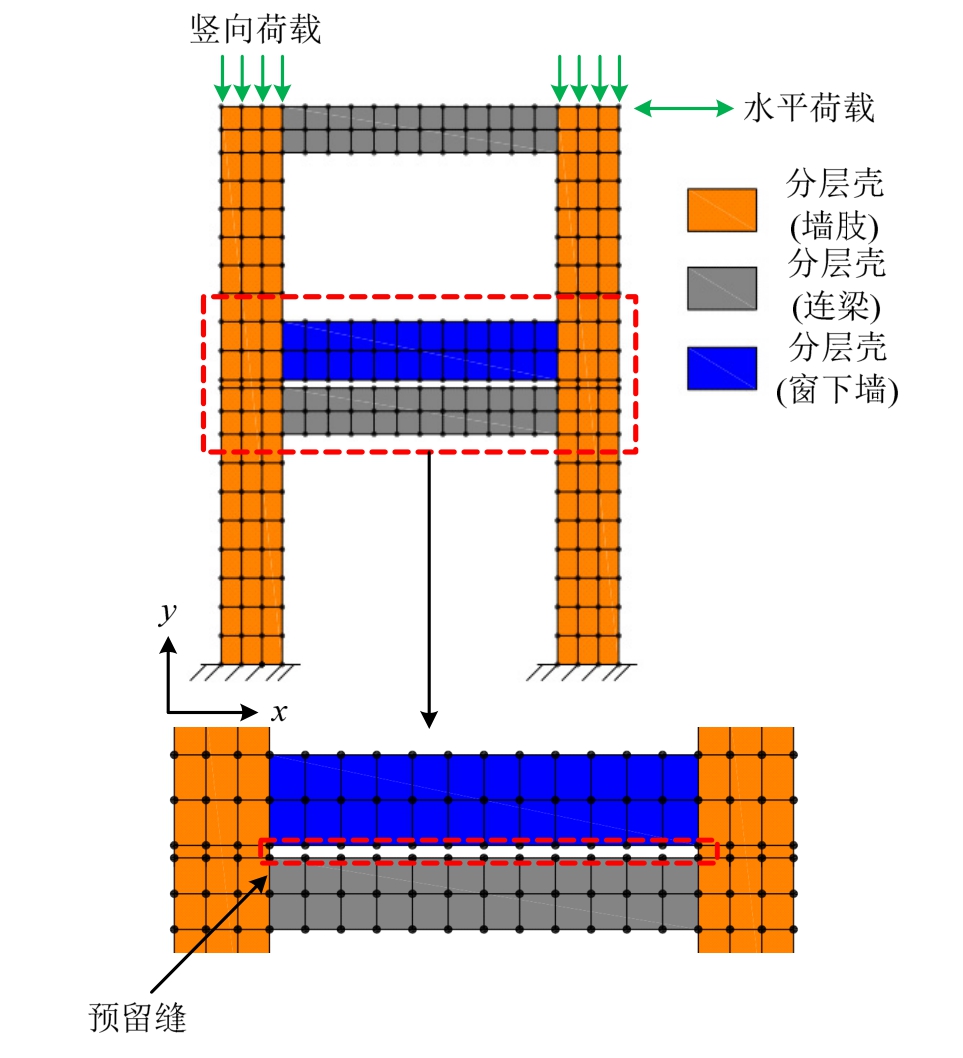
图10 精细有限元模型示意图
Fig.10 Schematic drawing of the refined FEA model
3.2 模拟结果与试验结果对比分析
基于上述精细有限元数值模拟方法,本文对试件W-1和W-2进行了数值模拟分析,并将其结果与试验结果对比,如图11所示。从图中可以看出,基于本文提出的精细有限元数值模拟方法计算所得的滞回曲线与试验曲线整体吻合良好,尽管无法模拟试验过程中窗下墙和连梁脱开形成双连梁的这一过程,但这并不影响该模型较好地把握构件的承载力、变形和耗能特性,表明该模型可以较好地反映窗下墙对预制剪力墙构件抗震性能的影响,具有一定的可靠性。

图11 模拟和试验滞回曲线对比
Fig.11 Comparison between the simulation and test hysteresis loops
上述结果表明在对带窗台预制剪力墙结构进行分析时,可采用本文建议的精细有限元数值模拟方法对该类结构进行抗震性能分析,即:1)采用分层壳模型模拟墙体、连梁和楼板;2)忽略窗下墙与下层连梁间的连接灌浆,将窗下墙与下层连梁视为双连梁采用分层壳模型模拟;3)采用等效厚度的方法考虑内保温板对窗下墙的削弱。值得注意的是,该精细有限元数值模型体系同时还具有较好的计算稳定性和通用性,可用于进一步深入研究该类预制剪力墙结构的抗震性能。
3.3 窗下墙对试件抗震性能的影响性分析
为了进一步明确窗下墙对预制剪力墙构件抗震性能的影响,本文建立了不带窗下墙剪力墙的精细有限元模型,对其进行了低周反复荷载下的数值分析,并将其滞回曲线和骨架曲线与W-1和W-2的模拟曲线对比分别如图12(a)和图12(b)所示。结果表明,矮窗下墙和高窗下墙分别提高了1)剪力墙的初始刚度约14%和24%;2)剪力墙的屈服承载力约10%和25%;3)剪力墙的极限承载力约12%和25.6%;4)剪力墙的等效粘滞阻尼系数约12%和16.7%。因此,对带窗下墙的预制剪力墙结构进行抗震设计时应对窗下墙予以适当的考虑。

图12 不同模型滞回曲线和骨架曲线对比
Fig.12 Comparison of the hysteresis loops and skeleton curves between different models
4 结论
为了研究带窗洞的预制装配式混凝土剪力墙中窗下墙对结构抗震性能的影响,本文对两个带不同高度窗下墙的两层预制剪力墙试件进行了低周反复荷载试验。在此基础上,本文基于商业有限元程序MSC.Marc展开了该类构件的精细有限元数值模拟方法研究。主要结论如下:
(1)两试件在水平荷载作用下的受力过程均可分为两个阶段:荷载较小时,窗下墙和连梁作为一根高连梁共同工作;随荷载和位移的增大,二者之间水平拼缝逐渐脱开,形成两根并列布置的双 连梁。
(2)两试件最后破坏模式类似,都是墙肢根部和双连梁两端形成塑性铰,最后塑性铰范围内受压区混凝土压碎而破坏。试件W-2窗下墙较高,与下部连梁共同形成的整体连梁高度更大,且在截面中部设置了保温板,降低了抗剪强度,因此在第一阶段出现大量的受剪斜裂缝。
(3)纵筋采用灌浆套筒连接的剪力墙,墙肢根部最终破坏时塑性铰区存在2~3条较宽的主裂缝,其中,剪力墙与基础顶面水平拼缝部位裂缝宽度最大,其余裂缝宽度则相对较小。除此以外,其破坏形态与现浇钢筋混凝土剪力墙差别不大。
(4)窗下墙较高的试件W-2峰值承载力也较大,变形能力相对W-1则较差,耗能能力也略差。
(5)窗下墙较高试件W-2初始刚度较大,随着试件损伤程度的增加,两试件刚度间差距也逐渐 减小。
(6)提出了基于分层壳模型的带窗下墙预制剪力墙结构的精细有限元数值模拟方法,将分析结果与试验结果进行了对比分析,结果吻合良好,验证了本文提出的数值模拟方法的合理性和可靠性。
(7)预制剪力墙构件中的窗下墙可显著提高该类构件的刚度、承载力和耗能能力,对带窗下墙的预制混凝土剪力墙结构进行抗震设计时应对窗下墙予以考虑。建议将窗下墙作为连梁进行建模,并利用“双连梁”模型的分析结果进行结构设计。此外,也可采用性能化设计方法,将窗下墙视为结构在中、大震下的耗能构件,从而达到耗散地震能量,减轻结构损伤的目的。
[1]Bolea O.The seismic behaviour of reinforced concrete frame structures with infill masonry in the Bucharest area.Energy Procedia, 2016, 85: 60—76.
[2]孙建, 邱洪兴, 谭志成, 等.采用螺栓连接的工字形全装配式RC剪力墙试验研究[J].工程力学, 2018, 35(8): 172—183, 191.Sun Jian, Qiu Hongxing, Tan Zhicheng, et al.Experimental study on I-shaped precast reinforced concrete shear walls using bolted connections [J].Engineering Mechanics, 2018, 35 (8): 172—183, 191.(in Chinese)
[3]侯和涛, 朱文灿, 曲哲, 等.屈曲约束支撑钢筋混凝土框架结构干式柔性梁柱节点的试验研究[J].工程力学, 2018, 35(6): 151—161.Hou Hetao, Zhu Wencan, Qu Zhe, et al.Experimental study on dry flexible beam-column joint in buckling restrained braced reinforced concrete frame structures [J].Engineering Mechanics, 2018, 35(6): 151—161.(in Chinese)
[4]15G365-1, 国家建筑标准设计图集,预制混凝土剪力墙外墙板[S].北京:中国计划出版社, 2015.15G365-1, Atlas for exterior precast concrete walls [S].Beijing: China planning press, 2015.(in Chinese)
[5]万金亮.窗下墙对预制混凝土剪力墙结构抗震性能影响的试验研究[D].合肥:合肥工业大学,2017 Wan Jinliang.Experimental study on the effects of the window wall on the seismic performance of Precast Concrete shear wall [D].Hefei: Hefei University of Technology, 2017
[6]GB 50010—2010, 混凝土结构设计规范[S].北京:中国建筑工业出版社, 2015.GB 50010—2010, Code for design of concrete structures [S].Beijing: China architecture & Building Press, 2015.(in Chinese)
[7]JGJ/T 101—2015, 建筑抗震试验方法规程[S].北京: 中国建筑工业出版社, 2015.JGJ/T 101—2015, Specificating for seismic test of buildings [S].Beijing: China Architecture & Building Press, 2015.(in Chinese)
[8]Mahin S A, Bertero V V.Problems in establishing and predicting ductility in structural design [J].Proceedings of the Internastional Symposium on Earthquake Structural Engineering, 1976, 1: 613—628.
[9]Lu X Z, Xie L L, Guan H, et al.A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees [J].Finite Elements in Analysis & Design, 2015, 98: 14—25.
[10]解琳琳, 黄羽立, 陆新征, 等.基于OpenSees的RC框架-核心筒超高层建筑抗震弹塑性分析[J].工程力学, 2014, 31(1): 64—71.Xie Linlin, Huang Yuli, Lu Xinzheng, et al.Elasto-plastic analysis for super tall RC frame- core-tube structures based on OpenSees [J].Engineering Mechanics, 2014, 31(1): 64—71.(in Chinese)
[11]陆新征, 林旭川, 叶列平, 等.地震下高层建筑连续倒塌数值模型研究[J].工程力学, 2010, 27(11): 64—70.Lu Xinzheng, Lin Xuchuan, Ye Lieping, et al.Numerical models for earthquake induced progressive collapse of high-rise buildings [J].Engineering Mechanics, 2010, 27(11): 64—70.(in Chinese)
[12]张微敬, 钱稼茹, 于检生, 等.竖向分布钢筋单排间接搭接的带现浇暗柱预制剪力墙抗震性能试验[J].土木工程学报, 2012, 45(10): 9—97. Zhang Weijing, Qian Jiaru, Yu Jiansheng, et al.Tests on seismic behavior of precast shear walls with cast-in-situ boundary elements and vertical distributed reinforcements spliced by a single row of steel bars [J].China Civil Engineering Journal, 2012, 45(10): 89—97.(in Chinese)
[13]江见鲸.混凝土结构有限元分析[M].北京: 清华大学出版社, 2005.Jiang Jianjing.Finite element analysis of concrete structures [M].Beijing: Tsinghua University Press, 2005.(in Chinese)
[14]陆新征.建筑抗震弹塑性分析[M].北京: 中国建筑工业出版社, 2009.Lu Xinzheng.Elasto-plastic analysis of buildings against earthquake [M].Beijing: China Architecture & Building Press, 2009.(in Chinese)