由于不可避免的随机性，可靠度成为结构设计的基础[1-5]，基于分项系数法则的规范可靠度表达式[6]，如式(1)所示，是可靠度原理指导结构设计的直接体现。
式中：γ0为结构重要性系数；γG为恒荷载分项系数；γQi 为第i项可变荷载的分项系数；ψ为组合值系数，
为抗力分项系数；
分别为恒荷载、第i项可变荷载、抗力的标准值。然而，规范表达式给出的目标可靠指标与实际结构中对应于具体各构件的真实可靠度并不一定相同，究其根源，主要原因在于：1)规范表达式确定分项系数时，综合考虑了各类常见构件的影响和多种简单荷载组合的影响，然而实际结构中某一具体构件的可靠度仅属于某一特定类型和某一特定荷载工况。2)为满足普遍适用性，规范表达式直接以抗力和荷载效应为随机变量，将功能函数写为这两类变量的显式、线性函数，且函数形式与构件自身无关；而对具体某一构件进行可靠度分析时，可根据其受力情况得到以材料参数、几何参数和荷载参数作为基本随机变量的隐式功能函数。相对而言，抗力和荷载效应随机变量实质上是材料参数、几何参数和荷载参数等基本随机变量的函数，直接引入其分布类型假设往往具有较大的经验性，会产生较大的误差；而基本随机变量较易统计，由此确定的变量分布模型更趋合理。
因此，规范表达式的功能仅是从宏观上指导某类结构的各类构件的整体可靠度水平，而不能确定某一实际结构中具体各构件的真实可靠度。准确的构件可靠度应该以材料参数、几何参数和荷载参数等物理量为基本变量，以构件退出工作为失效准则，此时构件的功能函数常为基本变量的隐式函数，与规范表达式的可靠度分析有着显著的差异。对单构件可靠度的分析已有大量成熟方法[7-12]，然而结构通常是由许多构件组成的体系，对于基于可靠度的结构维护、优化，计算多个甚至所有构件的可靠度具有实际意义。本文将对多个构件的可靠度计算定义为多构件可靠度分析。对于多构件可靠度分析，无论是继续沿用单构件可靠度分析方法分别对每一构件进行计算，还是如文献[13—14]分别提出的用Monte Carlo法和响应面法进行此类可靠度分析的思路，均面临计算成本过高的局限。近年来，新出现一种向量型层递响应面法[15-17]，该方法可高效建立结构总体节点位移向量显示表达式，能够方便地应用于多构件可靠度分析。然而，该方法推导基于线弹性随机结构，不适用于考虑材料非线性或几何非线性的复杂工程结构。
为此，本文结合自适应点估计法与最大熵原理进行了结构体系中多构件的可靠度分析，并将其与已有方法的计算性能进行详细的对比。
1 基于矩方法的多构件可靠度分析
1.1 双变量降维近似模型
不失一般性，假设Θ={Θ1,Θ2,…, Θs}为结构系统的基本随机向量，结构系统由m个单元组成，结构第r(r=1,2,…,m)个单元的功能函数为：
对Θ引入Rosenblatt变换[18]或Nataf变换[19]，则式(2)可改写为：
式中：当已知Θ的联合概率密度函数时，RN-1代表逆Rosenblatt变换；否则，RN-1代表逆Nataf变换。
由于式(3)维数较高，难以直接分析。本文引入广义降维近似原理[20]，并记Θ取均值µΘ时对应的参考点为uc=RN(µΘ)={uc,1,uc,2,…, uc,s}，对式(3)进行双变量降维近似可得：
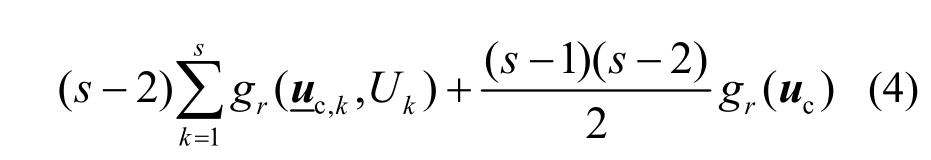
式中：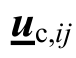
为uc中除uc,i和uc,j外的所有元素构成的向量，同理
为uc中除uc,k外的所有元素构成的向量。
1.2 自适应交叉项判定
对于式(4)中双变量分量函数
若其包含Ui和Uj (i≠j，i, j∈{1,2,3,…,s})的交叉项不存在，则该函数的期望值可由多个单变量函数的期望值来表示，使得求解过程进一步简化。根据文 献[21]，该函数交叉项是否存在应由下式判断。
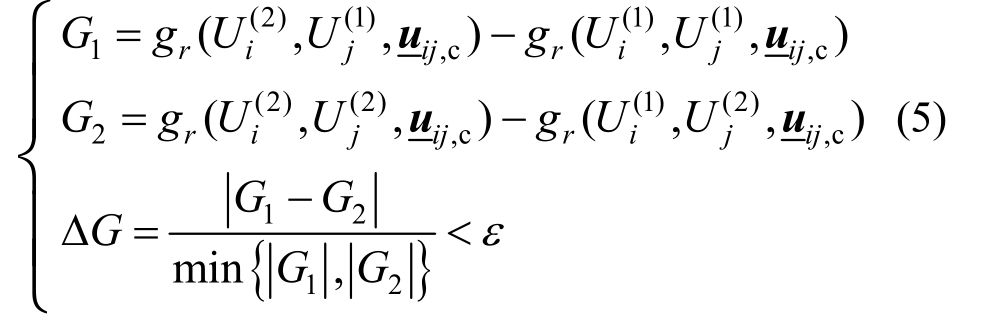
式中：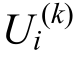
为Ui的第k个样本点；
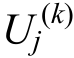为Uj的第k个样本点，k=1,2。本文取ε=1×103。为了进一步保证交叉项判定的准确性，判定准则式(5)应采用两组不同的样本点验证，当且仅当两组样本点处同时满足ΔG＜ε时，即判定Ui和Uj的交叉项不存在，否则认为Ui和Uj的交叉项存在。
根据Ui和Uj交叉项是否存在，定义Ui和Uj交叉项的释性函数为：
1.3 基于交叉项判定的自适应点估计法
基于式(4)的双变量降维近似模型，第r个单元功能函数Zr的前四阶矩可由下式[20]计算：
式中：μZ,r为功能函数的均值；MZ,r,q为功能函数的q阶中心矩，E[]·为期望函数，可表示为如下积分 形式：
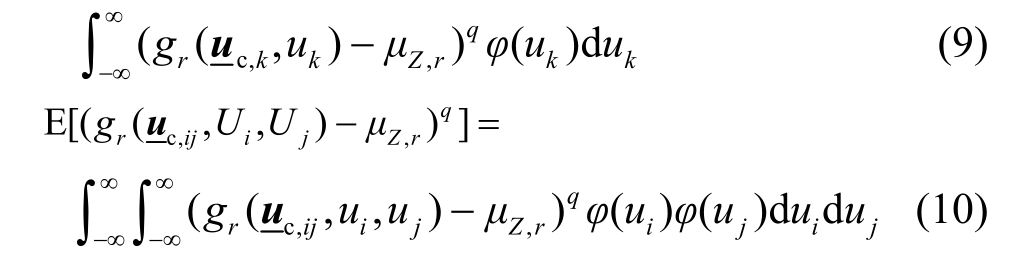
对于双变量分量函数的期望值，当Ui和Uj交叉项不存在，即Ih(Ui,Uj)=0时，式(10)可简化为：
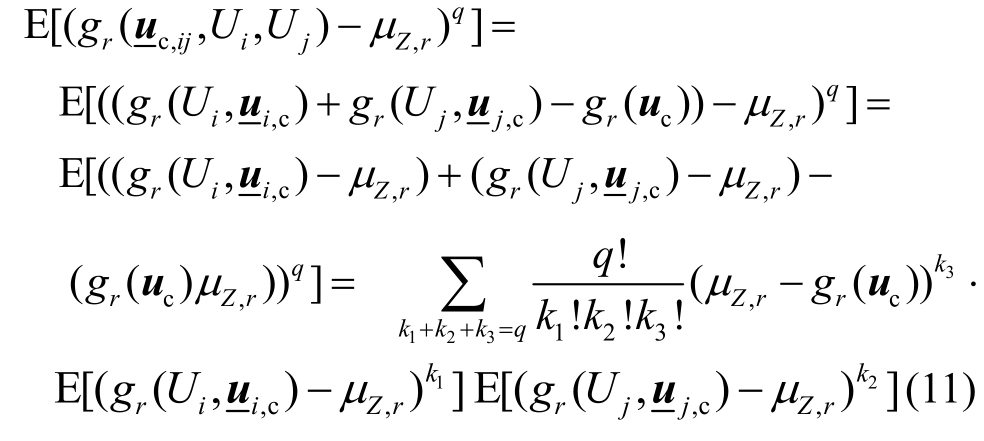
式(11)中仅包含单变量函数的期望值。由此可知，当Ih(Ui,Uj)=0时，双变量函数的期望值可由多个单变量函数的期望值来表示。不仅如此，由于式(9)所示的单变量函数一维积分是先于二维积分进行的必要步骤，因此，最初需要通过二维积分才能得到的双变量函数的期望值，现可以通过调用之前步骤的一维积分值直接得到，而无需额外的结构分析次数。
通过引入Gauss-Hermite数值积分方法，式(9)和式(10)可由下式计算：
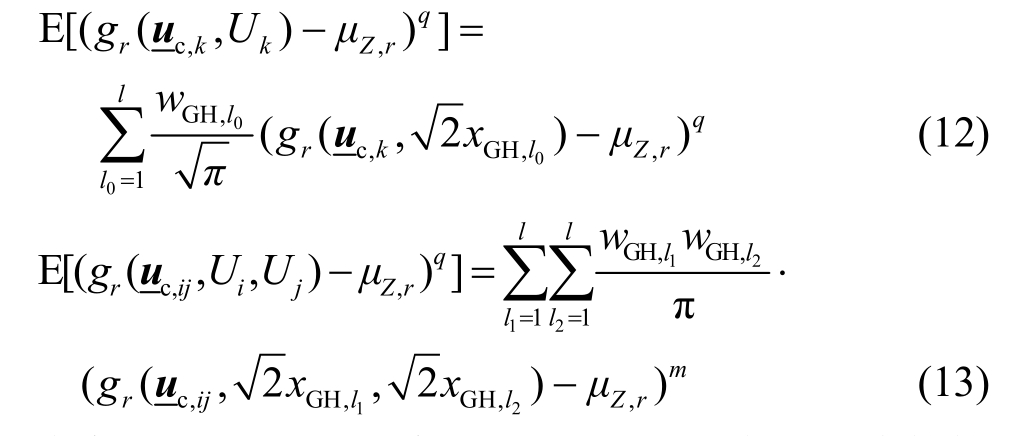
式中：xGH,l0和wGH,l0为Gauss-Hermite求积公式的第l0个节点坐标和权系数，l为Gauss-Hermite积分点的数量，本文中取l=7。
由式(12)和式(13)可知，为得到第r个单元的前四阶矩，首先需要在标准正态空间选出如下所示积分节点，设为点集K：
由点集K得到的有限元分析结果，结合式(7)～ 式(10)，式(12)和式(13)可以得到第r个单元的前四阶矩，并继而计算该单元可靠度。显然，计算结构任意单元的前四阶矩，均仅需在点集K处进行有限元分析。故对于某结构系统而言，无论是求解系统中的单构件，多构件甚至所有构件的可靠度，都仅需在K处进行有限元分析，而求解各个单元前四阶矩的过程中仅包含数值计算，无需额外的有限元分析。所以，采用矩方法进行的多构件可靠度分析，所需有限元分析次数仅与随机变量个数有关，而与构件数量无关。因上述过程未包含交叉项判定，本文定义为直接矩方法。
若通过式(5)的交叉项判定准则，从点集K中筛选掉各单元功能函数中交叉项判定均不存在的二维数值积分点，其剩余点设为点集K*。同理，由点集K*得到的有限元分析结果，结合式(7)～式(13)同样可得到结构任意单元的前四阶矩，继而求得各单元可靠度。上述方法被本文定义为自适应矩方法。
本文对多构件可靠度分析问题提出了直接矩方法和自适应矩方法两种方法，因自适应矩方法的效率较高，本文建议方法为自适应矩方法。又因在自适应矩方法中，交叉项判定结果取决于具体问题，点集K*的规模无法直接由随机变量数判断，而直接矩方法中的点集K仅取决于随机变量数，且点集K为K*的上界，当且仅当所有交叉项均存在时K*=K。所以，为便于深入理解本文建议方法所需计算成本，后文中同样对直接矩方法进行了分析比较。
1.4 基于最大熵原理的可靠度分析方法
1948年，Shannon首次将热力学熵的概念引入信息论中[22]。若随机事件有n个可能结果，每个结果出现的概率为pi (i=1,2,…,n)，为度量此事件的不确定性，Shannon引入下列函数：
式中，c＞0为常数，因此H≥0。H称作Shannon熵。
若随机变量X服从概率密度函数为fX(x)的连续分布，Shannon熵为：
Shannon熵本质上是对事件的不确定性或信息量的度量。
在给定的条件下，所有可能的概率分布中存在一个使信息上取极大值的分布，这称为最大熵原理。在已知的信息附加约束条件下使信息熵最大，所得到的概率分布具有最小偏见，由此可以得到一种构造“最优”概率分布的途径。
为使功能函数Zr的熵取最大值，以功能函数Zr的前4阶原点矩MZ,r,q (q=0,1,2,3,4)为约束条件，利用Lagrange乘子法可得下式：
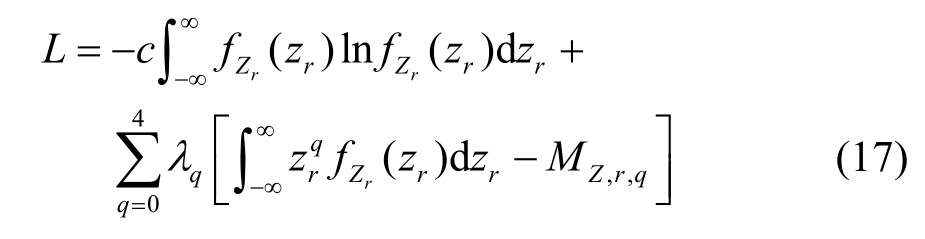
式中：λ0, λ1, ···, λ4为待定系数。在稳定点处有
可得到最大熵密度函数为：
在实际计算中，通常将功能函数Zr标准化为：
并根据最大熵原理，求解对应的Lagrange系数a0, a1, ···, a4，从而估计随机变量Yr的密度函数：
则第r个单元的失效概率为：
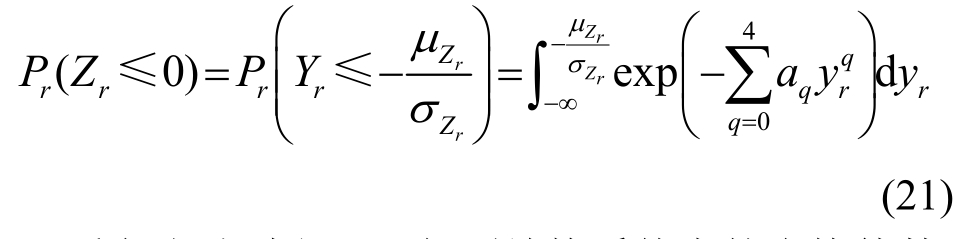
重复上述过程，可得到结构系统中的多构件甚至所有构件的可靠度，显然求解结构各构件可靠度的过程仅包含数值计算，无需额外的有限元分析。
1.5 算法效率分析
对于构件可靠度分析，现有方法主要包括蒙特卡洛法[13]和响应面法[14]。分别对蒙特卡洛法、响应面法及本文提出的两种矩方法进行效率分析和对比。
1.5.1 蒙特卡洛法
蒙特卡洛直接抽样法最少随机抽样次数与失效概率估计值之间的近似对应关系如下：
表1数据可以看出可靠指标为4时蒙特卡洛直接抽样需要106数量级，可靠指标为5时，直接抽样需要108数量级。工程实际运用蒙特卡洛方法时往往每次抽样后需要通过有限元分析确定结构是否失效，而工程结构又要求有较高的可靠度，从而将蒙特卡洛法运用到工程实际将花费大量计算时间和费用。
表1 抽样次数与失效概率的关系
Table 1 Relationship between N1 andfP
β 3.0 4.0 5.0 Pf1.350×10-3 3.167×10-5 2.867×10-7 N17.408×104 3.157×106 3.489×108
1.5.2 响应面法
响应面法采用忽略交叉乘积项的非完全的二次多项式，通过中心复合设计选取样本点。对于s个变量m个构件的结构系统，迭代nl次时取点数为：
1.5.3 矩方法
为了更好地体现本文建议的自适应矩方法的效率优势，将不包含交叉项判定的直接矩方法与建议方法的效率进行对比说明。
直接矩方法计算结构中的构件可靠度时取点数仅取决于随机变量数，采用7点Gauss-Hermite数值积分法估计功能函数的统计矩的s个变量m个构件可靠度问题取点数为：
当采用本文建议的自适应矩方法时，假设判定为不存在的交叉项数为nx，则采用7点Gauss-Hermite数值积分法估计功能函数的统计矩的s个变量m个构件可靠度问题取点数为：
值得指出的是，与直接矩方法相比，当所有交叉项都判定为存在时，即nx=0时，自适应矩方法即退化为直接矩方法。然而，当一个或多个交叉项判定为不存在时，即nx≥1时，根据式(11)，双变量函数的期望值可由多个单变量函数的期望值来表示。因此，自适应矩方法的选点数将少于直接矩方法，且计算精度与直接矩方法完全一致。
1.5.4 效率对比
三种方法所需的有限元分析次数如表2所示。
表2 各方法有限元分析次数
Table 2 Number of finite element analysis by different methods
可靠度方法 有限元分析次数 蒙特卡洛法 N1=100/Pf 响应面法 N2=[(nl-1)×m+1]×(2s+1)矩方法 直接矩方法 N3=Cs2×72+7s+1 自适应矩方法 N4=(Cs2-nx)×72+2nx+7s+1
对比三种方法的效率，蒙特卡洛法虽然精度较好，但是需要大量的计算，不适合工程应用。与蒙特卡洛法相比，响应面法所需的有限元分析次数已经较少，但是响应面法存在的问题有：1)需对每个杆件单独构造响应面函数，当杆件较多时，有限元分析次数随之增加，且计算过程复杂；2)每个响应面函数均需要进行迭代求解，有限元分析次数随迭代次数的增多而迅速增加，且迭代次数难以预估。与其它方法相比，直接矩方法的计算成本较小，所需有限元分析次数与杆件数无关，考虑交叉项判定后的自适应矩方法可以进一步提高计算效率，计算过程简便。
为进一步说明本文建议的自适应矩方法相比于直接矩方法和响应面法的计算优势，保守估计响应面法所需平均迭代次数为4次的情况下，随着随机变量个数及杆件数的变化，自适应矩方法、直接矩方法与响应面法的有限元分析次数对比如图1 所示。
图1 自适应矩方法、直接矩方法与响应面法有限元分析 次数对比
Fig.1 Number of finite element analysis by moment method and response surface method
由图1可以发现，随着结构复杂程度不断增加，杆件数量不断增多，建议方法相比于直接矩方法和响应面法的计算效率优势愈发明显。
1.6 算法步骤
基于建议方法的构件可靠度分析基本步骤 如下：
1)Gauss-Hermite积分点选取：
根据式(14)选取积分点点集K，其中包含（Cs2×72+7s+1)个积分点；
2)交叉项判定：
应对所有随机变量进行两两交叉项判定，对于Ui和Uj交叉项判定，步骤如下：
① 选取以下两组样本点：
③ 将单变量函数的期望值和双变量函数的期望值代入式(7)和式(8)中，计算各构件功能函数的前四阶矩；
5)基于求得的功能函数前四阶矩，按照式(17)～式(21)计算各构件的可靠指标。
由上述算法步骤可知本文建议方法仅需指定样本点处对应的结构分析结果，与结构分析中间过程无关，因此，本算法同样可用于非线性结构的多构件可靠度分析。
2 算例分析
② 利用有限元软件对以上积分点处进行结构分析，并得到各个杆件对应的功能函数值：
2.1 算例1：平面桁架体系多构件可靠度分析
某理想弹塑性平面桁架几何尺寸如图2所示，各杆件截面屈服强度均为σmax，单元截面面积均为A，受到水平荷载F的作用，其中F={F1, F2}= F0·{2,1}。基本随机变量包括F0，σmax，A均服从对数正态分布，其统计参数如表3所示。
③ 再次，根据式(5)计算所有杆件处两组样本点处的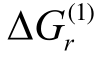
和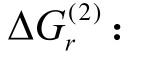
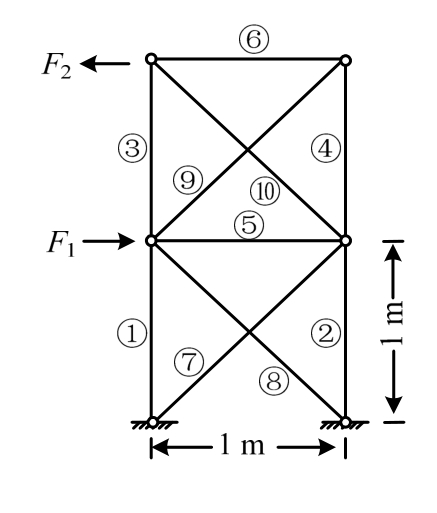
图2 算例1平面桁架
Fig.2 Plane truss in Case 1
当且仅当
和
在所有杆件处同时满足时，认为Ui和Uj的交叉项不存在，即Ih(Ui,Uj)=0，否则，仍认为Ui和Uj的交叉项存在，即Ih(Ui,Uj)=1。将所有Ih(Ui,Uj)=0对应的二维积分点
从点集K中筛选掉，构成实际积分点点集K*；
3)结构有限元重分析：
根据点集K*中样本点进行结构有限元重分析，得到各构件对应样本点处的功能函数值；
4)各构件前四阶矩计算：
① 根据式(12)计算式(7)和式(8)中单变量函数的期望值；
② 根据交叉项判定结果分情况计算式(7)和式(8)中双变量函数的期望值：
a)当交叉项判定为存在时，利用式(13)计算双变量函数的期望值；
b)当交叉项判定为不存在时，利用式(11)计算双变量函数的期望值；
表3 算例1基本随机变量的统计信息
Table 3 Statistical information of basic variables in Case 1
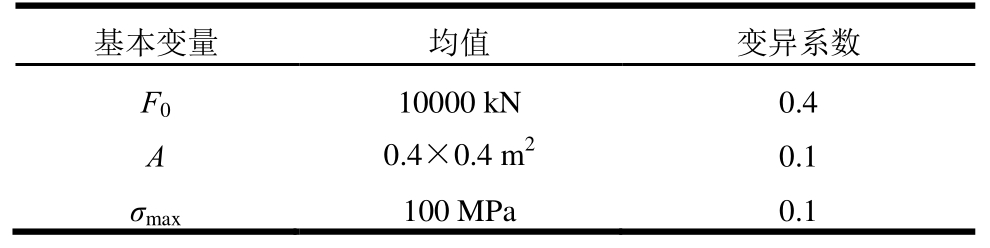
基本变量 均值 变异系数 F010000 kN 0.4 A 0.4×0.4 m2 0.1 σmax100 MPa 0.1
显而易见，所有杆件均为二力杆。通过有限元法可以计算得到在荷载F作用下各杆件的内力，即各杆件的荷载效应Si，i=1,2,…,10。考虑强度失效时，杆件(i)的功能函数为：
根据交叉项判定准则，可得Ih(F0, A)=Ih(F0, σmax)=0，即F0与A的交叉项以及F0与σmax的交叉项不存在。
采用基于有限元的蒙特卡洛法、响应面法、直接矩方法和建议的自适应矩方法，分别计算各杆件的可靠指标，结果列于表4。
表4 算例1各杆件的可靠指标
Table 4 Reliability index of each component in Case 1
杆件编号 蒙特卡洛法 响应面法 直接矩方法 建议方法单元1 3.633 3.603 3.564 3.564 单元2 2.511 2.504 2.516 2.516 单元3 3.202 3.197 3.170 3.170 单元4 2.803 2.803 2.801 2.801 单元5 1.701 1.702 1.721 1.721 单元6 2.803 2.803 2.801 2.801 单元7 2.761 2.758 2.759 2.759 单元8 1.658 1.659 1.676 1.676 单元9 1.956 1.958 1.985 1.985 单元10 2.353 2.352 2.371 2.371
值得指出的是，不含交叉项判定的直接矩方法和包含交叉项判定的建议方法所得到的结果完全一致。因此，交叉项判定的引入对于矩方法结果的精度无任何影响。
以蒙特卡洛法结果为标准解，定义其它可靠度方法的误差为：
式中：βMC为由蒙特卡洛法计算得到的可靠指标；β为其它可靠度方法计算得到的可靠度指标。对响应面法和矩方法进行误差分析，结果示于表5。
表5 算例1不同方法的误差分析
Table 5 Error analysis of different methods in Case 1
杆件编号 响应面法/(%) 直接矩方法/(%) 建议方法/(%)单元1 0.84 1.90 1.90 单元2 0.31 0.20 0.20 单元3 0.18 1.00 1.00 单元4 0.00 0.05 0.05 单元5 0.04 1.18 1.18 单元6 0.00 0.05 0.05 单元7 0.10 0.06 0.06 单元8 0.05 1.11 1.11 单元9 0.08 1.47 1.47 单元10 0.07 0.76 0.76
由表5可知，响应面法的最大误差为0.84%，直接矩方法与建议方法结果完全相同，其最大误差为1.90%，所得结果均能够满足工程所需的精度要求。
各方法的有限元分析次数示于表6，显然，直接矩方法和建议方法的计算效率均优于其它方法。值得指出的是，本文建议的自适应矩方法能够进一步地提高计算效率，且无任何精度损失。
表6 算例1各方法有限元分析次数
Table 6 Number of Finite element analysis by different methods in Case 1
可靠度方法 有限元分析次数 蒙特卡洛法 1×106 响应面法(平均4次迭代) 217 直接矩方法 建议方法 169 75
2.2 算例2：钢框架体系多构件可靠度分析
某三维框架体系如图3(a)所示，为方便起见，先取其中某一榀框架为例进行说明。
如图3(b)所示，某一榀理想弹塑性6层2跨框架结构跨度5 m，层高3 m，受到水平荷载F={F1,F2,F3}=F0·{1,2,3}的作用。对各杆件进行编号1号～30号。弹性模量E=2×105 MPa，底层柱截面尺寸为l1×l1，其它层柱截面尺寸为l2×l2，梁截面尺寸为b×h，截面屈服强度为σy。基本随机变量的统计参数如表7所示。
图3 算例2框架体系
Fig.3 The frame system in Case 2
表7 算例2基本随机变量的统计信息
Table 7 Statistical information of basic variables in Case 2
基本变量 均值 变异系数 分布类型 l1600mm 0.1 对数正态 l2500mm 0.1 对数正态 b 350mm 0.1 对数正态 h 450mm 0.1 对数正态 σy100MPa 0.1 对数正态 F0150kN 0.3 极值I型
考虑杆件的抗弯失效，通过有限元分析可以得到荷载作用下各杆件中最大弯矩为
各杆件单元功能函数可以表示为：
式中，Mu,i为第i根杆件的极限抗弯承载力，由材料的屈服强度σy和对应杆件的截面尺寸确定。
根据交叉项判定准则，可得Ih(l1, l2)=Ih(l1, b)= Ih(l1, h)=Ih(l1, F0)=Ih(l2, b)=Ih(l2, h)=Ih(l2, F0)=Ih(b, F0)=Ih(h, F0)=Ih(σy, F0)=0。共10组交叉项判定为不存在。
分别采用蒙特卡洛法、响应面法和建议方法计算此结构系统中各杆件单元可靠指标，结果列于图4和表8。
图4 例2多层框架多构件可靠度指标
Fig.4 Reliability index of each component in multi-story frame in Case 2
表8 各杆件可靠指标
Table 8 Reliability index of each component in Case 2
杆件编号 蒙特卡洛法 响应面法 建议方法 单元1 2.620 2.623 2.646 单元2 2.573 2.615 2.593 单元3 2.625 2.668 2.645 单元4 2.599 2.632 2.621 单元5 1.679 1.686 1.654 单元6 2.614 2.639 2.637 单元7 4.592 4.710 4.507 单元8 2.901 2.938 2.886 单元9 4.116 4.012 4.173 单元10 3.110 3.168 3.133 单元11 2.679 2.692 2.693 单元12 3.403 3.449 3.429 单元13 4.685 4.792 4.613 单元14 2.401 2.433 2.386 单元15 3.200 3.257 3.181 单元16 4.077 4.162 4.130 单元17 2.511 2.526 2.524 单元18 4.096 4.179 4.147 单元19 3.010 3.038 3.011 单元20 3.016 3.017 3.020 单元21 2.998 3.028 3.008 单元22 3.002 3.042 3.022 单元23 3.018 3.061 3.038 单元24 3.022 3.032 3.027 单元25 3.062 3.099 3.088 单元26 3.066 3.075 3.072 单元27 3.108 3.128 3.119 单元28 3.119 3.110 3.132 单元29 3.140 3.165 3.156 单元30 3.164 3.194 3.182
同理进行误差分析示于表9。
表9 算例2不同方法的误差分析
Table 9 Error analysis of different methods in Case 2
杆件编号 响应面法/(%) 建议方法/(%)单元1 0.11 0.97 单元2 1.65 0.79 单元3 1.64 0.78 单元4 1.28 0.84 单元5 0.41 1.48 单元6 0.95 0.88 单元7 2.58 1.84 单元8 1.29 0.51 单元9 2.51 1.40 单元10 1.85 0.71 单元11 0.51 0.54 单元12 1.36 0.76 单元13 2.29 1.55 单元14 1.34 0.60 单元15 1.76 0.59 单元16 2.08 1.30 单元17 0.59 0.51 单元18 2.02 1.25 单元19 0.93 0.03 单元20 0.03 0.12 单元21 1.01 0.33 单元22 1.35 0.68 单元23 1.43 0.67 单元24 0.33 0.18 单元25 1.22 0.85 单元26 0.31 0.21 单元27 0.66 0.37 单元28 0.28 0.43 单元29 0.79 0.50 单元30 0.94 0.56
由误差分析结果可知，响应面法的最大误差为2.58%，建议方法的最大误差为1.84%。对于多层框架结构，响应面法和建议方法的精度均能够满足工程要求。对于一榀框架，各方法的有限元分析次数示于表10，再一次验证了建议方法的高效性。
表10 算例2一榀框架各方法有限元分析次数
Table 10 Number of Finite element analysis by different methods of the plane frame in Case 2
可靠度方法 有限元分析次数 蒙特卡洛法 1×107 响应面法(平均4次迭代) 1183 直接矩方法 建议方法 778 308
同理，对于整体三维框架体系，其分析过程与一榀框架分析过程完全一致，其所需结构重分析次数如表11所示。由于建议方法所需结构重分析次数与杆件数量无关，建议方法的结构分析次数并无增加，而响应面法所需的结构分析次数随着杆件数量增多而明显增加，进一步体现出对于杆件数量较多的复杂结构体系，建议方法所具有明显的计算效率优势。
表11 算例2三维框架各方法有限元分析次数
Table 11 Number of Finite element analysis by different methods of the three-dimensional frame in Case 2
可靠度方法 有限元分析次数 蒙特卡洛法 1×107 响应面法(平均4次迭代) 6799 直接矩方法 建议方法 778 308
采用算例2中相同的随机变量和结构尺寸，计算结构受三种不同工况下的水平荷载F1= {F1,F2,F3}=F0·{1,2,3},F2={F1,F2,F3}=F0·{2,2,2},F3={F1,F2,F3}=F0·{3,2,1}，分别记为case1、case2、case3。将不同工况下各构件可靠指标按值的大小分组统计如图5所示，由该图5可知，同一结构中各构件可靠指标差别较大，并且若受力工况和位置不同，各构件可靠指标又会发生较大变化。但使用本文建议方法，可以方便高效地计算体系中一个或多个构件的可靠指标。
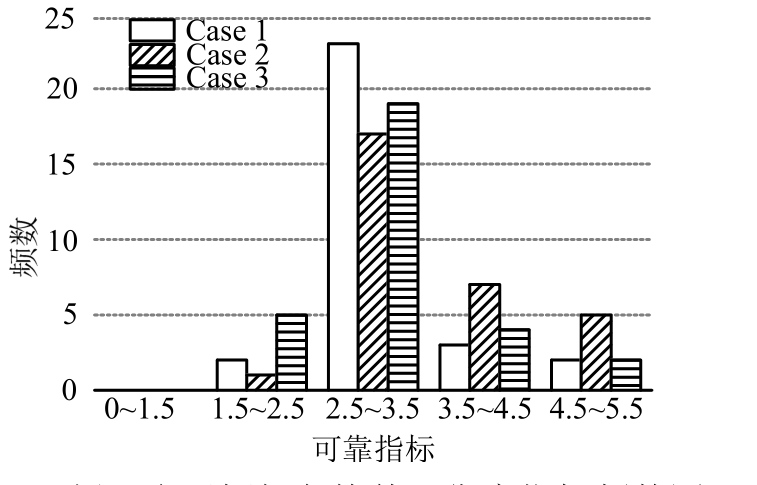
图5 例2多层框架各构件可靠度指标频数图
Fig.5 The frequency of reliability index for each component of the multi-story frame in Case 2
3 结论
本文提出了一种基于自适应点估计和最大熵原理的结构体系多构件可靠度分析方法，并从原理和算例分析两方面对比了本文建议方法与蒙特卡洛法，响应面法等多构件可靠度计算方法的性能，分析表明：
(1)计算精度方面，蒙特卡洛法适用范围广泛，计算结果可靠，其结果可以作为近似的精确解。与蒙特卡洛法相比，响应面法和建议方法的计算结果相对误差均较小，能够满足工程可靠度计算的精度要求。
(2)计算效率方面，蒙特卡洛法计算成本较高，所需的结构分析次数取决于可靠指标的大小；响应面法需要对每个杆件构造对应的响应面函数，当结构体系复杂化，杆件数量增多时，其所需的结构重分析次数也随之增多，且迭代次数无法预估，并存在迭代不收敛的可能。与响应面法相比，直接矩方法所需结构重分析次数与杆件数量无关，计算成本较低，且计算过程简便无需迭代，能够方便的求解所有单元的可靠指标。
此外，建议方法通过引入基于交叉项判定的自适应点估计方法，可以减少一部分结构重分析次数，从而在保证计算精度不变的前提下，进一步提高直接矩方法的计算效率。
[1]赵国藩.工程结构可靠度[M].北京: 水利出版社, 1984: 42—68.Zhao Guofan.Reliability for engineering structures [M].Beijing: Hydraulic Press, 1984: 42—68.(in Chinese)
[2]张明.结构可靠度分析-方法与程序[M].北京: 科学出版社, 2009: 89—93. Zhang Ming.Structural reliability analysis-methods and procedures [M].Beijing: Science Press, 2009: 89—93.(in Chinese)
[3]余波, 陈冰, 吴然立.剪切型钢筋混凝土柱抗剪承载力计算的概率模型[J].工程力学, 2017, 34(7): 136—145.Yu Bo, Chen Bing, Wu Ranli.Probabilistic model for shear strength of shear-critical reinforced concrete columns [J].Engineering Mechanics, 2017, 34(7): 136—145.(in Chinese)
[4]羡丽娜, 何政, 张延泰.考虑年均倒塌概率的结构倒塌安全储备可接受值[J].工程力学, 2017, 34(4): 88—100.Xian Lina, He Zheng, Zhang Yantai.Acceptable structural collapse safety margin ratios based on annual collapse probability [J].Engineering Mechanics, 2017, 34(4): 88—100.(in Chinese)
[5]Shayanfar M A, Barkhordari M A, Barkhori M, et al.An adaptive directional importance sampling method for structural reliability analysis [J].Structural Safety, 2018, 70: 14—20.
[6]GB/50068—2001, 建筑结构可靠度统一标准[S].北京: 中国建筑工业出版社, 2000.GB/50068—2001, Unified Standard for Reliability Design of Building Structures [S].Beijing: China Architecture Industry Press, 2000.(in Chinese)
[7]Grooteman F.Adaptive radial-based importance sampling method for structural reliability [J].Structural Safety, 2008, 30(6): 533—542.
[8]吕大刚, 贾明明, 李刚.结构可靠度分析的均匀设计响应面法[J].工程力学, 2011, 28(7): 109—116.Lü Dagang, Jia Mingming, Li Gang.Uniform design response surface method for structural reliability analysis [J].Engineering Mechanics, 2011, 28(7): 109—116.(in Chinese)
[9]Xuan S N, Sellier A, Duprat F, et al.Adaptive response surface method based on a double weighted regression technique [J].Probabilistic Engineering Mechanics, 2009, 24(2): 135—143.
[10]Gavin H P, Yau S C.High-order limit state functions in the response surface method for structural reliability analysis [J].Structural Safety, 2008, 30(2): 162—179.
[11]Guimarães H, Matos J C, Henriques A A.An innovative adaptive sparse response surface method for structural reliability analysis [J].Structural Safety, 2018, 73: 12—28.
[12]Schöbi R, Sudret B.Structural reliability analysis for p-boxes using multi-level meta-models [J].Probabilistic Engineering Mechanics, 2017, 48: 27—38.
[13]刘春城, 孙显鹤, 牟雪峰, 等.高压输电塔覆冰荷载作用下可靠度分析[J].水电能源科学, 2011(5), 29(5): 156—158.Liu Chuncheng, Sun Xianhe, Mu Xuefeng, et al.Reliability analysis of high voltage transmission tower under icing load [J].Water Resources and Power, 2011(5), 29(5): 156—158.(in Chinese)
[14]熊铁华, 侯建国, 安旭文.覆冰、风荷载作用下南方某输电铁塔可靠度分析[J].武汉大学学报(工学版).2011, 44(2): 207—210.Xiong Tiehua, Hou Jianguo, An Xuwen.Reliability analysis of transmission tower under the wind load and icing load [J].Engineering Journal of Wuhan University.2011, 44(2): 207—210.(in Chinese)
[15]杨绿峰, 李朝阳.结构随机分析的向量型层递响应面法[J].工程力学, 2012, 29(11): 58—64.Yang Lüfeng, Li Zhaoyang.Vectorial hierarchical response surface method for analysis of stochastic structures [J].Engineering Mechanics, 2012, 29(12): 58—64.(in Chinese)
[16]杨绿峰, 李朝阳, 杨显峰.结构可靠度分析的向量型层递响应面法[J].土木工程学报, 2012(7): 105—110.Yang Lüfeng, Li Zhaoyang, Yang Xianfeng.Vectorial cooperative response surface method for structural reliability [J].China Civil Engineering Journal, 2012, 45(7): 105—110.(in Chinese)
[17]杨绿峰, 袁彦华, 余波.基于等概率近似变换的向量型层递响应面法分析结构可靠度[J].工程力学, 2014, 31(7): 185—191.Yang Lüfeng, Yuan Yanhua, Yu Bo.Vector cooperative response surface method for structural reliability analysis based on approximately equivalent probability transformations [J].Engineering Mechanics, 2014, 31(7): 185—191.(in Chinese)
[18]Rosenblatt M.Remarks on a multivariate transformation [J].The Annals of Mathematical Statistics, 1952, 23(3): 470—472.
[19]Liu P L, Der Kiureghian A.Multivariate distribution models with prescribed marginals and covariances [J].Probabilistic Engineering Mechanics, 1986, 1(2): 105—112.
[20]Xu H, Rahman S.A generalized dimension-reduction method for multi-dimensional integration in stochastic mechanics [J].International Journal of Numerical Methods in Engineering, 2004, 61(12): 1992—2019.
[21]Fan W L, Wei J H, Ang H S, et al. Adaptive estimation of statistical moments of the responses of random systems [J].Probabilistic Engineering Mechanics, 2016, 43: 50—67.
[22]Shannon C E.A mathematical theory of communication [J].Bell System Technical Journal, 1948, 27: 379—423.