盾构法隧道因其具有对地面交通和城市居民生活影响小、施工期短以及不受气候条件制约等优点,被广泛应用于我国城市轨道交通的建设过程中[1]。但由于盾构隧道为地下结构,在土体中的受力情况较为复杂,其结构的受力和变形与地基土体的应力场和位移场密切相关,容易受到周围环境变化的影响,严重时会导致隧道变形过大,危及隧道结构安全[2—4]。
我国以上海、广州、南京等城市为首的软土地区建设有多条地铁线路,部分地铁沿线分布有深厚的软弱土层,土体承载能力较低,工程性质较差。由于软土地层中隧道周围土体具有较高的灵敏系数,当隧道结构周边环境发生变化、土体受到扰动,例如基坑开挖时,土体的应力状态由被动态向主动态转化,不能为隧道结构提供稳定的侧向压力,导致隧道侧向发生卸载。一方面,地铁沿线往往伴随着大量的商业开发,基坑开挖导致隧道侧向发生卸载的情况较为普遍;另一方面,我国软土地区盾构隧道结构设计时,按照柔性衬砌的设计理论[5],所设计的管片厚度一般偏小,结构抗变形能力较差,导致盾构隧道在侧向卸载的不利工况下容易产生较大的横向变形。目前,国内学者就卸载对管片影响的研究主要以隧道正上方的卸载为主[4],虽然已有学者通过足尺试验对侧向卸载进行了相关研究[6],但并没有考虑管片不同结构尺寸的影响。
对盾构管片力学特征的研究可以采用试验或数值模拟等方法。目前国内外学者对隧道结构进行试验研究的主要手段可分为足尺试验[6—10]与相似模型试验[11—14]。通过足尺试验进行研究可以获得更加准确与丰富的试验数据,但试验成本过高,不适用于需要进行多组比较的试验。因此,本文采用相似模型试验与数值模拟相结合的方法,研究了管片结构在发生侧向卸载时管片内力与变形的发展规律,以及管片厚度对此过程的影响。最终结果可为软土地区盾构法隧道的受力状态的预测与结构尺寸选择提供参考。
1 试验方案
1.1 原型结构
本次试验以某市地铁三号线盾构隧道为研究对象,管片采用混凝土等级为C50,盾构衬砌圆环外径6.2 m,管片宽度为1.5 m。全环分为6块,1个封顶块、2个邻接块、3个标准块,其中封顶块占圆心角为20.5°,标准块占圆心角68.5°,相邻块占圆心角67.5°。管片采用错缝拼装方式,按22.5°角交替布置,衬砌圆环结构布置如图1所示。封顶块、邻接块、标准块之间通过两根M30的环向弯螺栓连接,螺栓强度等级为5.8级。
为研究管片厚度对隧道结构在发生侧向卸载时抵抗变形能力的影响,试验中选择了厚度分别为300 mm、350 mm、380 mm与400 mm的管片作为研究对象。其中,300 mm和350 mm是目前国内最为常见的管片厚度,而380 mm和400 mm则是考虑为增大管片刚度而提升的管片厚度。

图1 管片结构布置图
Fig.1 Diagram of segment structure
1.2 相似关系
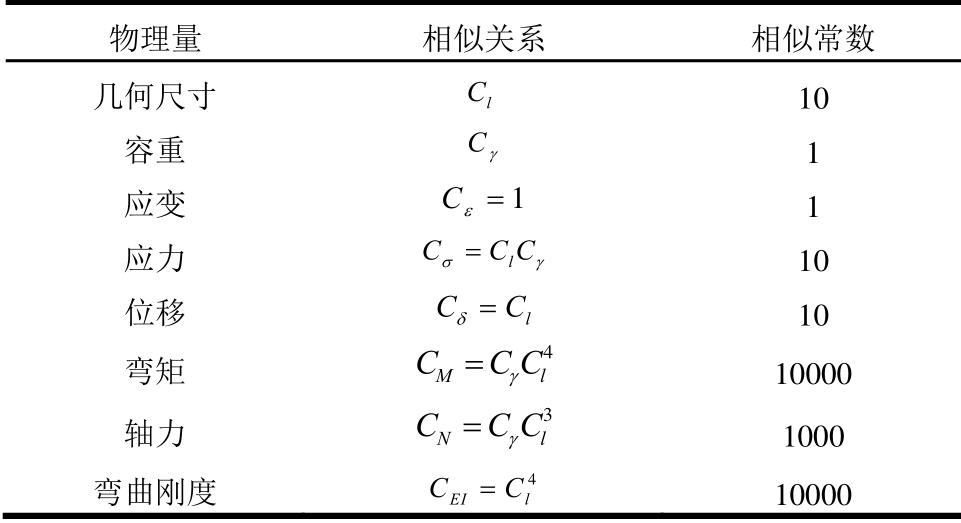
综合考虑模型试验的可靠性、经济性和灵活性,最终确定模型试验以几何相似比(1∶10)及容重相似比(1∶1)为设计基础,并根据三大相似定理,按弹性力学问题求得模型试验相似常数如表1所示。
1.3 模型管片
本次试验主要通过测定管片的径向变形来判断结构的抗变形能力,因此模型管片的弯曲变形是最重要的试验指标,该指标主要与模型管片的尺寸、材料以及纵缝接头的模拟方法有关。在模型管片的制作过程中,模型尺寸根据原型尺寸与几何尺寸相似比确定,重点考虑了模型管片的材料以及纵缝接头模拟的问题。同时,考虑到管片的错缝拼装效应的影响,模型管片采用三环错缝的方式进行拼装。
表1 模型试验相似常数
Table 1 Similar constants of model test
物理量 相似关系 相似常数 几何尺寸lC 10 容重 Cγ1 应变 1C =ε 1 应力l C CC=σ γ 10 位移l C C=δ 10 弯矩 4 Ml C CC=γ 10000 轴力 3 Nl C CC=γ 1000 弯曲刚度 4 EIl C C= 10000
1.3.1 模型管片材料
管片采用的混凝土等级为C50,弹性模量为34.5 GPa,通过相似计算可知,弹性模量相似常数,即需要选择弹性模量接近3.45 GPa的材料。通过市场调查与综合分析,试验最终选用MC尼龙作为模型管片的材料。该材料的弹性模量为2.7 GPa,与原材料的弹性模量相似比,接近目标值,同时该材料具有物理、化学性质稳定的优点,可避免模型管片的性能在试验过程中受环境因素影响而发生改变。模型管片如图2所示。由于MC尼龙材料弹性较好,在试验荷载下始终处于弹性变形阶段,因此本试验也主要研究管片在弹性阶段的力学特性。

图2 模型管片
Fig.2 Model segments
1.3.2 模型管片厚度修正
由材料力学基本概念可知,在纯弯曲情况下,梁发生弯曲变形后的曲率表达式为:
式中:ρ为曲率半径;EI为单环管片截面的抗弯刚度;IZ为惯性矩;b为截面的宽度;t为截面的厚度。
为保证管片衬砌模型与原型间保持弯曲变形的相似关系,需要控制曲率的相似常数。Cρ= Cl=10。由于模型管片所选材料的弹性模量小于目标值,可通过对模型管片的厚度相似比进行修正的方法调整曲率相似常数,可以得到:
式中:Ct为厚度相似系数;CM为弯矩相似系数;Cρ为半径相似系数;CE为弹性模量相似系数;Cb为宽度相似系数;Cl为尺寸相似系数。
计算得:修正后4种原型管片厚度对应的模型管片厚度如表2所示。
表2 模型管片厚度
Table 2 Model segment thickness
原型管片厚度/mm 300 350 380 400 模型管片厚度/mm 32.57 38.00 41.26 43.43
1.3.3 纵缝接头模拟
纵缝接头的存在削弱了管片的局部刚度,在模型试验中可采用开槽的方式进行模拟[14],同时管片的抗弯刚度与接头处的内力相关[15],故不同接头处槽壁的厚度有所不同。考虑到模型管片需在管壁内侧布设测量装置,纵缝接头采用外侧开槽的方式,并根据抗弯刚度等效的原则确定开槽的深度。开槽段对应的管片环中心角为4°,各角度(顺时针)开槽后如图3所示,开槽段槽壁厚度如表3所示。
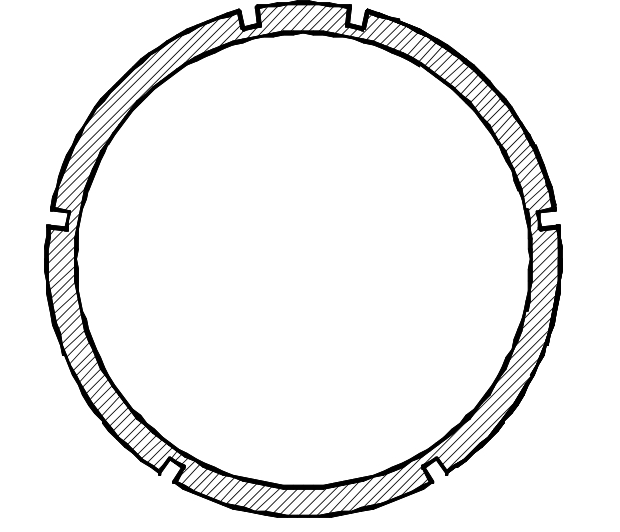
图3 纵缝接头模拟
Fig.3 Simulation of joints at longitudinal seam
表3 开槽处管片厚度
Table 3 Segment thickness at slot
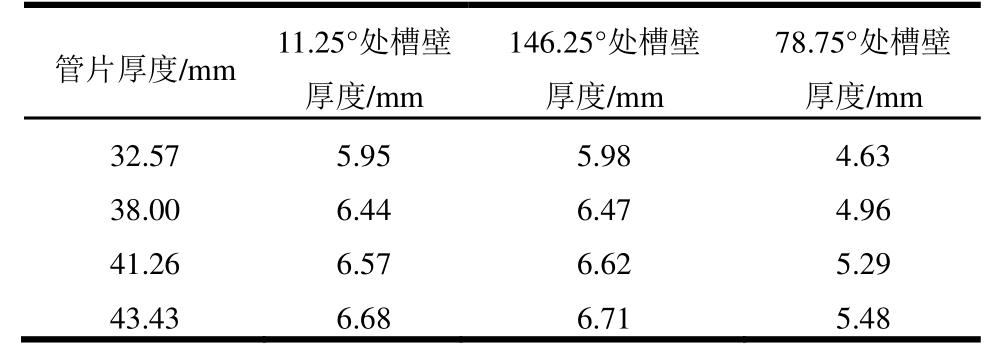
管片厚度/mm 11.25°处槽壁厚度/mm 146.25°处槽壁 厚度/mm 78.75°处槽壁厚度/mm 32.57 5.95 5.98 4.63 38.00 6.44 6.47 4.96 41.26 6.57 6.62 5.29 43.43 6.68 6.71 5.48
1.3.4 环缝接头模拟
管片环与环之间的错台一般由隧道的纵向不均匀沉降引起。由于本次试验不考虑隧道纵向不均匀沉降对管片变形的影响,因此,对环缝接头的模拟方法偏安全考虑,三环错缝拼装的管片环缝接头均采用平均分布的16根长2 cm、直径2 mm的带螺纹螺栓模拟,使环缝接头具有足够大的刚度,接头处管片不发生错动。
1.4 试验装置
为了模拟隧道管片所受到的实际荷载以及荷载的变化情况,试验研制了缩尺盾构管片力学模拟试验装置,整体尺寸为1.65 m×1.65 m×1.5 m。通过外环反力架提供反力支撑,安装有48个最大量程为1 t且受高精度液压系统控制千斤顶,分上、下两层作用于24个环管片外侧布设的持荷梁进行荷载传递。该持荷梁具备足够的刚度,可以使模拟荷载平均作用于三环错缝拼装的模型管片外侧,更接近与真实受力情况。试验装置如图4所示。

图4 试验装置示意图
Fig.4 Diagram of test device
三环错缝拼装的模型管片水平放置,受到由持荷梁传递的分组荷载作用,如图6所示。加载点的布设参考了足尺试验[6],采用24个加载点模拟隧道管片周围的荷载。48个千斤顶分上、下两层布设,24个加载点分为P1、P2和P3三组,等间距作用于模型管片上,如图5所示。其中,P1代表作用于隧道顶部的垂向水土压力和底部的地基反力,共6个加载点;P2代表作用于隧道腰部的水平水土压力,共10个加载点;P3作为荷载的过渡组,共8个加载点。

图5 模型管片受力状态
Fig.5 Loading state of model segment
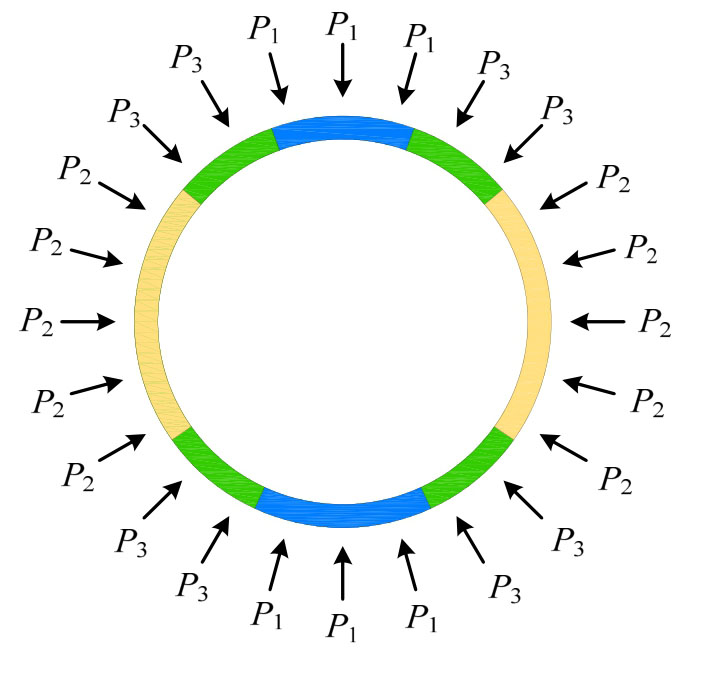
图6 加载点布置
Fig.6 Layout of loading points
1.5 荷载模拟方案
根据地铁沿线的地质情况,选择地质条件较差且具有代表性的计算断面如图7所示。作用于隧道上方的垂向土压力按照土柱理论计算,根据所选计算断面和相似关系计算得P1为35.4 kPa,隧道穿越<2-1A>淤泥质土,侧向压力系数λ的初始设计值根据地质勘测情况取0.75。
试验过程分为两个阶段:1)加载阶段,荷载从0逐渐加载至隧道结构未发生侧向卸载时的正常设计荷载—P1从0加载至35.4 kPa,并保持P2=λP1,P3=(P1+P2)/2,λ=0.75;2)卸载阶段,模拟隧道结构侧向卸载过程—P1=35.4 kPa,P2=λP1,P3=(P1+P2)/2,λ逐渐减小。

图7 计算断面
Fig.7 Computation cross-section
1.6 测量内容
1)模型管片径向变形。在模型管片中间一环布设位移计,以90°为间隔呈放射状布置测点,分别测量模型管片顶底以及腰部共4个部位的径向变形,布置位置如图8(a)所示。
2)模型管片内表面应变。由于管片外侧受持荷梁传递荷载作用,无法在理想部位布设应变传感器,因此仅在三环模型管片的内侧表面相隔45°均匀地粘贴箔式电阻应变片,用于测量管片表面环向应变。三环模型共布置有24个测点,布置位置如图8(b)所示。
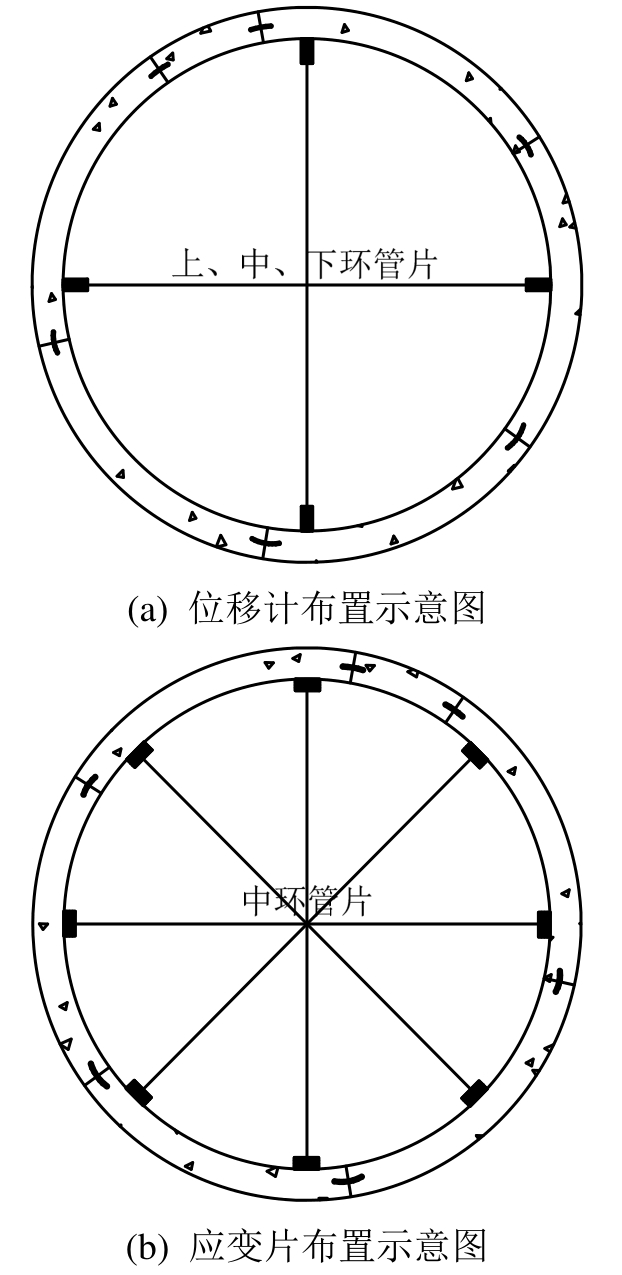
图8 传感器布置示意图
Fig.8 Layout of sensors
2 模型试验结果分析
2.1 侧向卸载过程管片变形分析


图9 管片径向变形
Fig.9 Radial deformation of segment
在试验的加载与卸载阶段,模型管片各角度径向变形转化为实际尺寸后如图9所示(变形背离圆心为正,指向圆心为负)。在试验的加载阶段,管片各角度径向变形随荷载增大而缓慢增加,以300 mm厚度管片为例,加载至正常设计荷载时管片拱顶、 左侧拱腰、右侧拱腰和拱底的变形分别为-10.22 mm、7.1 mm、7.01 mm和-4.55 mm,管片最大径向变形发生在拱顶位置,两侧拱腰位置的径向变形大小接近,拱底位置的径向变形最小。而在试验的卸载阶段,各角度径向变形快速增大,且增大速度呈现逐渐加快的趋势。
重点分析隧道在侧向卸载时的变形情况,如图10所示,隧道直径变形随着侧向压力损失的增加而增大,并逐渐超过控制值。根据《城市轨道交通结构安全保护技术规范》(CJJ/T 202—2013)[16]中规定:隧道径向收敛的控制值应小于20 mm,取隧道直径的收敛变形限值为20 mm。
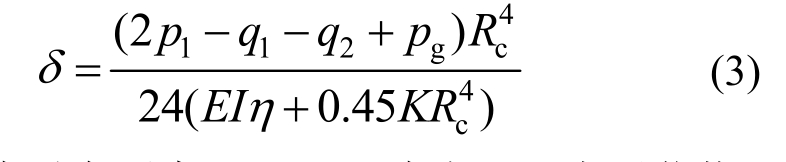
我国地铁设计中常采用弹性均值圆环法(惯用计算法)与修正惯用算法进行管片结构设计,算法给出的管片腰部单侧径向变形计算公式为: 式中:p1为垂向压力;q1、q2为上、下水平荷载;pg为结构自重反力;Rc为管片平均半径;EI为单位长度抗弯刚度;η为刚度折减系数;K为水平向土体抗力系数。
惯用算法与修正惯用算法基于结构力学的基本理论,由式(3)可以推导出管片的变形与侧向压力损失之间呈线性关系。而试验结果则证明,侧向压力损失程度较小时,可以认为变形与侧向压力损失之间为线性关系;而当侧向压力损失较大时,两者之间表现出明显的指数型增大关系。
由于软土地区土体工程性质较差,灵敏系数较高,容易受到周边环境的影响,无法为隧道结构提供稳定的侧向压力,而隧道变形随侧向压力损失呈指数型增大的特点也导致隧道在此工况下容易产生较大的变形,超出控制值。这也从一定程度上解释了以上海、南京为代表的软土地区地铁盾构隧道变形容易超限的原因。
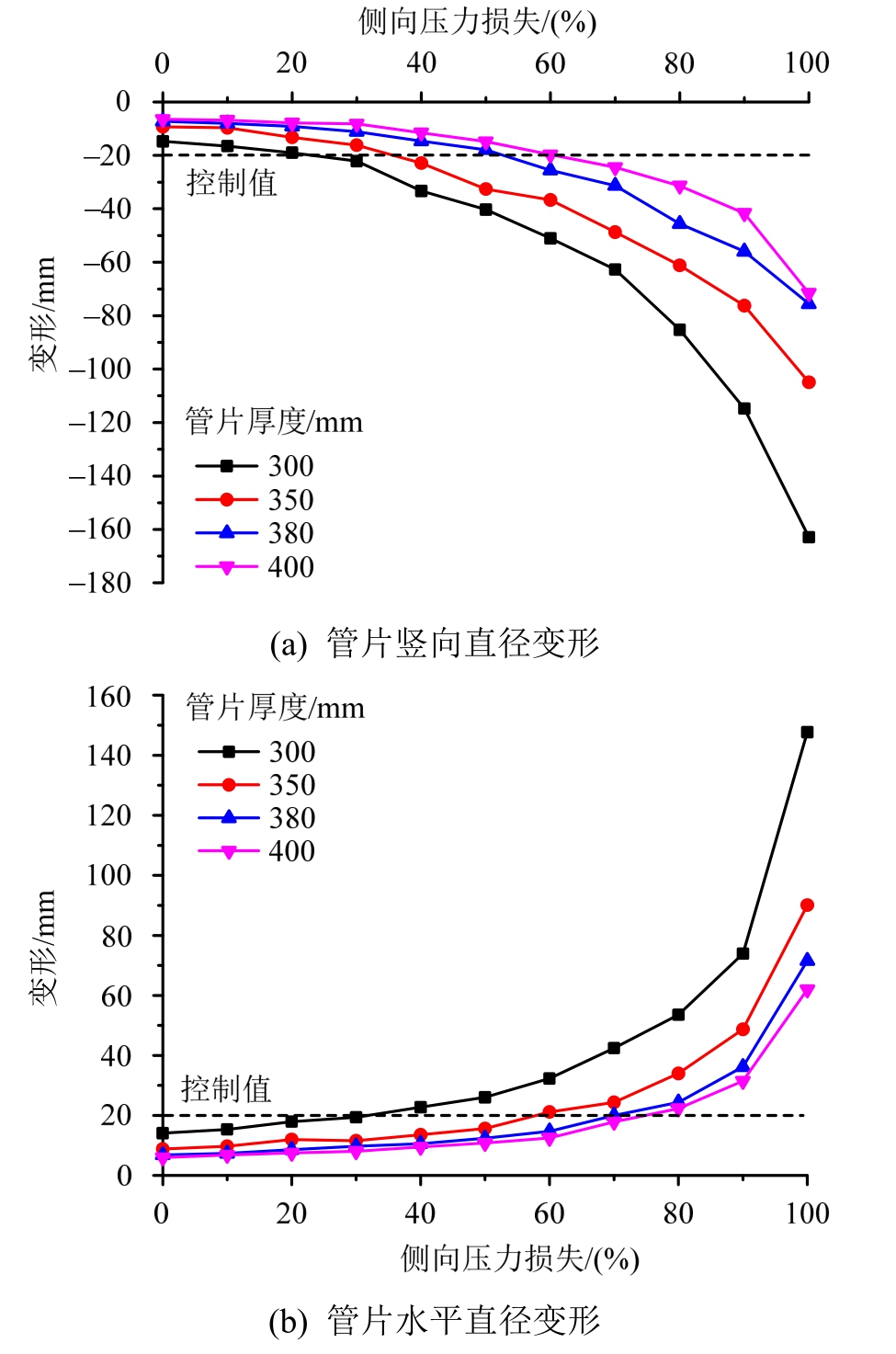
图10 侧向压力损失下管片变形
Fig.10 Deformation of segment under lateral pressure loss
2.2 管片厚度对隧道变形的影响
根据材料力学的基本计算方法可知,管片主截面抗弯刚度 与管片厚度呈三次方关系,即从理论出发,增大管片厚度是提升管片结构抗变形能力的有效手段。
如图11所示,在不同卸载程度下,管片的竖向直径变形与水平直径变形均随着管片厚度的增大而降低。以管片侧向卸载至侧向压力系数为0.675时为例,管片厚度从300 mm增大至350 mm、380 mm和400 mm时管片竖向直径变形分别为-16.52 mm、-9.70 mm、-8.06 mm和-6.83 mm,后三者变形分别为300 mm厚度时的58.7%、48.8%和41.3%,可见,增大管片厚度对管片抗变形能力的提升效果是十分显著的,但这种提升效果会随着管片厚度的增大而趋于平缓。同时,由于模型试验仅能反映管片在弹性阶段的变形特征,试验后期测得的变形数值会较真实情况偏小,因此还需结合数值模拟进行研究。

图11 不同厚度管片变形对比
Fig.11 Comparison on the deformation of segment with different thickness
2.3 管片厚度对应变的影响分析
一方面,在相同荷载条件下,管片厚度的增加,提高了管片本身的刚度,有效降低了管片的变形,但同时也伴随了管片弯矩的增大与轴力的减小,这会导致厚度较大的管片具有更大的偏心距,不利于管片结构的受力[17]。另一方面,从盾构隧道结构应力/应变的角度出发,结构最大应力/应变值能够更为直观地反应出结构的受力状态。
图12所示为上、中、下三环管片各角度内表面应变在侧向压力系数降为0.6时的分布情况。三环管片最大应变值均发生在管片拱腰部位,但由于试验中模型管片采用了错缝拼装的形式,相较于通缝拼装管片,环间螺栓传递剪力所产生的错缝效应改变了管片的局部刚度[13],导致管片内力分布不均匀,最大应变值位置不同。其中,上环与下环管片最大应变位于90°位置,中环管片最大应位于270°位置。
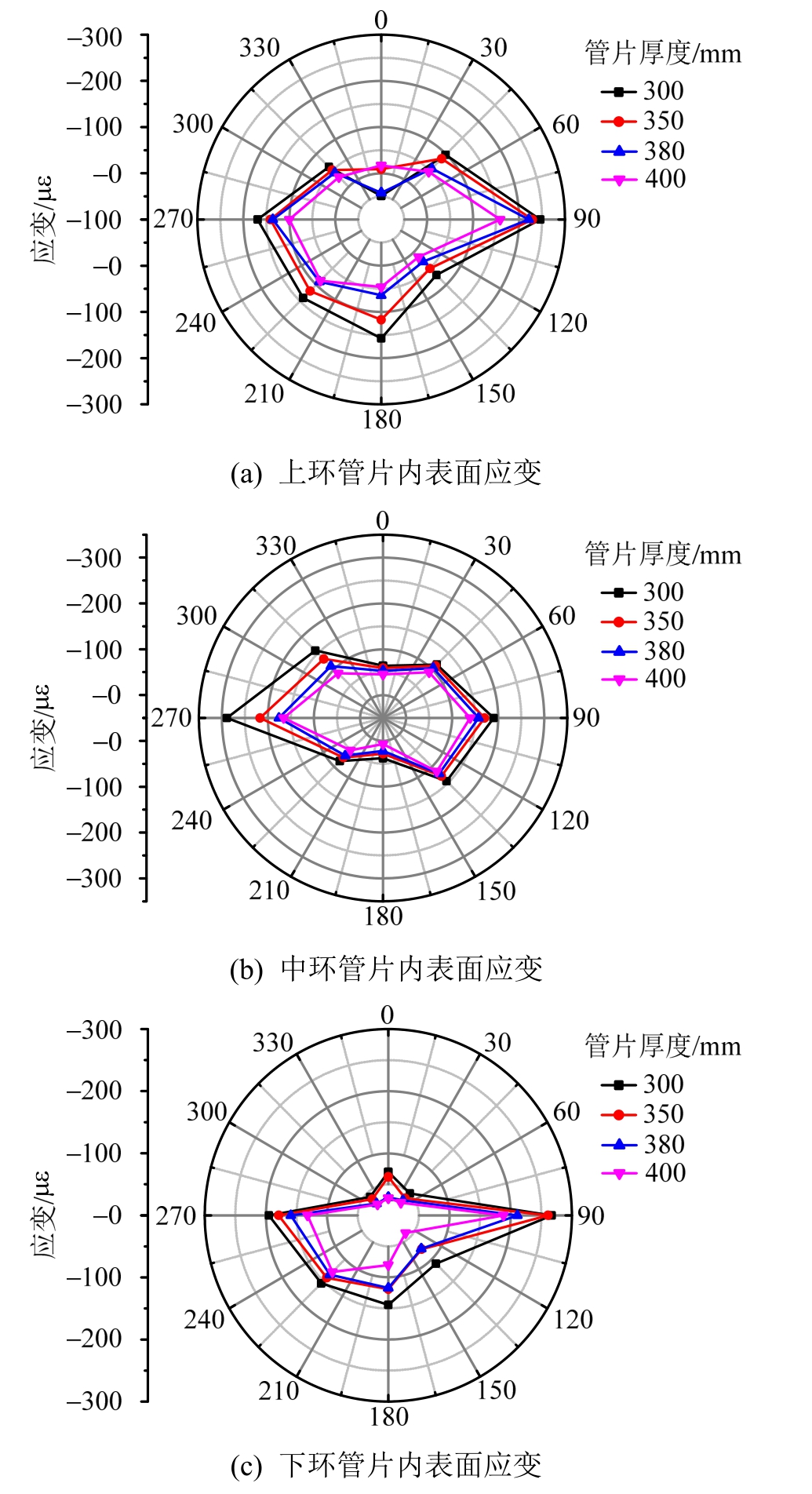
图12 管片内侧应变
Fig.12 Strain on the inner surface of segment
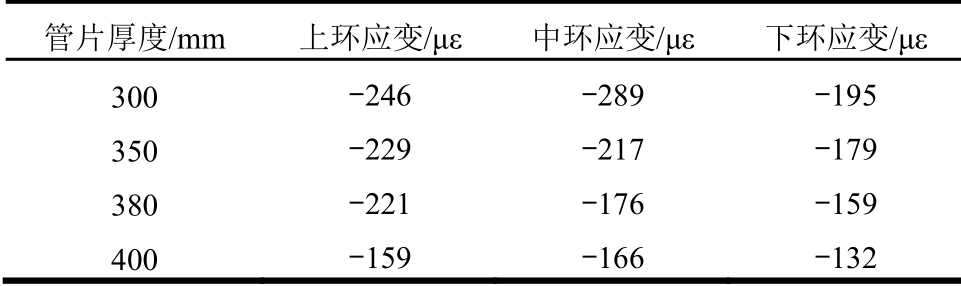
此工况下三环管片最大应变的量值如表4所示。分析可知,随着管片厚度的增大,管片最大压应变值反而减小。当管片厚度从300 mm增大至350 mm、380 mm和400 mm时,最大压应变值分别减小至 300 mm 时的 75.09%~93.09%、60.9%~89.84%及57.44%~67.69%。即从盾构隧道结构应力/应变的角度出发,增大厚度能有效减低管片的应变,混凝土应力更难达到其极限强度,从而使得管片处于更加安全的受力状态。
表4 管片最大应变
Table4 Maximum strain of segment
管片厚度/mm 上环应变/με 中环应变/με 下环应变/με 300 -246 -289 -195 350 -229 -217 -179 380 -221 -176 -159 400 -159 -166 -132
3 数值模拟对比分析
3.1 错缝拼装管片有限元模型
由于试验中模型管片选用的材料为MC尼龙,与钢筋混凝土材料有较大差异,在试验荷载条件下仍处于弹性变形阶段,未出现明显塑性变形或发生破坏,因此相似模型试验的结果也仅能反映盾构管片在弹性阶段的变形特征。对于管片在塑性阶段的变形情况需要结合数值模拟进行计算。
在通用有限元软件ABAQUS中按照原型管片的尺寸建立了4种厚度管片的三环错缝拼装实体有限元模型,考虑了管片凹凸榫、螺栓孔等细部构造。混凝土本构采用拟合德国Rush 建议模型的多段线。隧道所受水土荷载采用荷载-结构模型,计算了管片在不同侧向压力作用下的多个工况。有限元模型如图13所示。

图13 有限元模型
Fig.13 Finite element model
3.2 卸载工况管片厚度的影响
根据模型试验的结果,在管片弹性变形阶段,增大管片厚度能有效提升管片的抗变形能力。以厚度为300 mm管片的竖向直径变形为基准,对模型试验与数值计算的结果进行归一化处理,如图14所示。
对试验结果进行分析,在不同侧向压力条件下 增大管片厚度对管片变形的减小程度较为接近,可取均值处理。管片厚度从300 mm分别增大至350 mm、380 mm和400 mm时对应管片变形分别 减小至300 mm时的63%、49%和42%。

图14 试验与数值计算结果对比
Fig.14 Comparation of testing and numerical results
在数值计算中,管片实体模型混凝土材料采用了多段线本构模型,在应力超过转折应力后结构的抗变形能力逐渐下降,计算结果可以更好地反映出管片在塑性阶段的变形特征。可以看出,当管片侧向压力系数不低于0.66时,数值模拟的结果与相似模型试验的结果十分接近;而当管片侧向卸载程度逐渐加大时,增大管片厚度对管片变形的减小程度也随之增大。
显然,在侧向卸载过程中,当土体向隧道管片提供的侧向压力降低时,厚度较小的管片会先进入塑性变形阶段,并逐渐发生破坏。因而增大管片厚度不仅能提升管片的抗变形能力,还能有效延缓管片进入塑性变形阶段而进一步发生破坏的过程。可以分析出,增大管片厚度在侧向卸载更严重的工况下对管片抗变形能力的提升效果更加明显,更有利于控制变形。
此外,数值计算结果显示,在侧向压力系数降为0.6时,四种厚度中环管片最大应变均发生在270°截面,分别为-312με、-243με、-198με和-181με,即管片厚度从300 mm增大至350 mm、380 mm和400 mm时,最大压应变值分别减小至300 mm时的77.9%%、63.5%及58.0%,符合之前模型试验的结果。
4 结论
通过相似模型试验和数值模拟,可以得到以下结论:
(1)当侧向压力损失较小时,侧向压力损失与盾构隧道径向变形之间呈线性关系,盾构隧道结构处于弹性阶段;当侧向压力损失增大时,侧向压力损失与盾构隧道径向变形之间呈指数型关系,盾构隧道结构进入塑性阶段。
(2)增大管片厚度对管片抗变形能力的提升效果是十分显著的,但这种提升效果会随着管片厚度的增大而趋于平缓。
(3)在侧向卸载更严重的工况下,增大管片厚度对管片抗变形能力的提升效果更加明显,有利于提升管片在软土地区不良地质下的安全储备。
(4)随着盾构管片厚度的增大,虽然其结构最大偏心距也随之增大,但从结构应力/应变的角度出发,管片最大应变值反而降低,从而使得管片处于更加安全的受力状态。
[1]周顺华.城市轨道交通结构设计与施工[M].北京: 人民交通出版社, 2011: 16.Zhou Shunhua.Structural design and construction in urban mass transit [M].Beijing: China Communications Press, 2011: 16.(in Chinese)
[2]陈仁朋, 王诚杰, 鲁立, 等.开挖对地铁盾构隧道影响及控制措施[J].工程力学, 2017, 34(12): 1—13.Chen Renpeng, Wang Chengjie, Lu Li, et al.Influence of excavation on exist metro shield tunnel and control measures [J].Engineering Mechanics, 2017, 34(12): 1—13.(in Chinese)
[3]温科伟, 刘树亚, 杨红坡.基于小应变硬化土模型的基坑开挖对下穿地铁隧道影响的三维数值模拟分析[J].工程力学, 2018, 35(增刊1): 80—87.Wen Kewei, Liu Shuya, Yang Hongpo.Three- dimensional numerical simulation analysis of the influence of pit excavation based on hardening soil-small strain model on metro tunnel [J].Engineering Mechanics, 2018, 35(Suppl 1): 80—87.(in Chinese)
[4]葛世平, 谢东武, 丁文其.大面积加卸载对软土地铁隧道的影响[J].土木工程学报, 2011, 44(增刊2): 127—130.Ge Shiping, Xie Dongwu, Ding Wenqi.Effects of loading and unloading large-scale area loadacting on soft soil metro line [J].China Civil Engineering Journal, 2011, 44(Suppl 2): 127—130.(in Chinese)
[5]刘建航, 侯学渊.盾构法隧道[M].北京: 中国铁道出版社, 1991: 104.Liu Jianhang, Hou Xueyuan.Shield tunnel [M].Beijing: China Railway Publish House, 1991: 104.(in Chinese)
[6]柳献, 张浩立, 鲁亮, 等.卸载工况下盾构隧道结构承载能力的试验研究[J].城市轨道交通研究, 2015, 18(5): 38—43.Liu Xian, Zhang Haoli, Lu Liang, et al.Experiment of the bearing capacity of shield tunnel in unloading conditions [J].Underground Engineering and Tunnels, 2015, 18(5): 38—43.(in Chinese)
[7]刘四进, 封坤, 何川, 等.大断面盾构隧道管片接头抗弯力学模型研究[J].工程力学, 2015, 32(12): 215—224.Liu Sijin, Feng Kun, He Chuan, et al.Study on the bending mechanical model of segmental joint in shield tunnel with large cross-section [J].Engineering Mechanics, 2015, 32(12): 215—224.(in Chinese)
[8]封坤, 何川, 邹育麟.大断面越江盾构隧道管片拼装方式对结构内力的影响效应研究[J].工程力学, 2012, 29(6): 114—124.Feng Kun, He Chuan, Zou Yulin.Study on the effect of assembling method on the innerforce of segmental lining for cross-river shield tunnel with large cross-section [J].Engineering Mechanics, 2012, 29(6): 114—124.(in Chinese)
[9]Blom C B M, van der Horst E J, Jovanovic P S.Three-dimensional structural analyses of the shield-driven “Green Heart” tunnel of the high-speed line South [J].Tunnelling and Underground Space Technology, 1999, 14(2): 217—224.
[10]Liu X, Liu Z, Ye Y, et al.Mechanical behavior of quasi-rectangular segmental tunnel linings: Further insights from full-scale ring tests [J].Tunnelling and Underground Space Technology, 2018, 79: 304—318.
[11]鞠杨, 徐广泉, 毛灵涛, 等.盾构隧道衬砌结构应力与变形的三维数值模拟与模型试验研究[J].工程力学, 2005, 22(3): 157—165.Ju Yang, Xu Guangquan, Mao Lingtao, et al.3D numerical simulation of stress and strain properties of concrete shield tunnel lining and modeling experiments [J].Engineering Mechanics, 2005, 22(3): 157—165.(in Chinese)
[12]叶飞, 杨鹏博, 毛家骅, 等.基于模型试验的盾构隧道纵向刚度分析[J].岩土工程学报, 2015, 37(1): 83—90.Ye Fei, Yang Pengbo, Mao Jiahua, et al.Longitudinal rigidity of shield tunnels based on model tests [J].Chinese Journal of Geotechnical Engineering, 2015, 37(1): 83—90.(in Chinese)
[13]王士民, 申兴柱, 何祥凡, 等.不同拼装方式下盾构隧道管片衬砌受力与破坏模式模型试验研究[J].土木工程学报, 2017, 50(6): 114—124.Wang Shimin, Shen Xingzhu, He Xiangfan, et al.A model test for the mechanical property and failure mode of lining segments with different assembly types of shield tunnel [J].China Civil Engineering Journal, 2017, 50(6): 114—124.(in Chinese)
[14]黄大维, 周顺华, 王秀志, 等.模型盾构隧道管片纵缝接头设计方法[J].岩土工程学报, 2015, 37(6): 1068—1076. Huang Dawei, Zhou Shunhua, Wang Xiuzhi, et al.Design method for longitudinal segment joints of shield tunnel model [J].Rock and Soil Mechanics, 2015, 37(6): 1068—1076.(in Chinese)
[15]徐国文, 王士民, 汪冬兵.基于接头抗弯刚度非线性的壳-弹簧-接触-地层模型的建立[J].工程力学, 2016, 33(12): 158—166.Xu Guowen, Wang Shimin, Wang Dongbing.Shell-spring-contact-ground model based on segment joint stiffness nonlinearity [J].Engineering Mechanics, 2016, 33(12): 158—166.(in Chinese)
[16]CJJ/T 202—2013, 城市轨道交通结构安全保护技术规范[S].北京: 中国建筑工业版社, 2014.CJJ/T 202—2013, Technical code for protection structures of urban rail transit [S].Beijing: China Architecture & Building Press, 2014.(in Chinese)
[17]黄钟晖, 廖少明, 刘国彬.上海软土盾构法隧道管片厚度的优化[J].岩土力学, 2000, 21(4): 326—330.Huang Zhonghui, Liao Shaoming, Liu Guobin.The optimization of the segment thickness of shield tunnel in Shanghai soft soils [J].Rock and Soil Mechanics, 2000, 21(4): 326—330.(in Chinese)