不锈钢材料除其外表光洁美观、全寿命周期长且能够很好适应严苛的外部环境[1]等优点外，还具有强度高、延性好，耐火性能佳等特点，越来越被广泛应用于建筑及桥梁结构中[2]。越来越多的学者也在关注于不锈钢构件承载力以及稳定性的研究[3—10]，但不锈钢材料的抗震性能研究有限[11]。
在地震荷载下，结构构件通常需要突然承受巨大而短暂的往复作用力[12]，反应在材料层面为大应变的超低周疲劳[13]。已有研究[14—18]显示不锈钢材料在循环荷载下表现了良好的力学性能，但主要是基于高周或低周且应变较小的荷载工况中，与地震作用带来的大应变超低周荷载有一定差别。国内外相关学者也曾提出一些简化的计算模型[19—24]用于模拟不锈钢材料在循环载荷下的本构响应，并标定了部分奥氏体型牌号不锈钢材料的循环本构参数[25—27]。但是不锈钢材料种类繁多，不同钢种性能差异明显[28]，已标定参数不一定适用于所有不锈钢牌号。对于国内常用奥氏体型S30408(以下简称304)不锈钢循环本构研究较少，更鲜有双相型S220503(以下简称2205)不锈钢材料的循环本构研究。
本文共设计了奥氏体型和双相型不锈钢共24个材性试件，采用多种加载制度，研究两种工程常用牌号不锈钢的力学特性，分析其单调性能、滞回性能等。采用三种本构模型对单调拉伸荷载下应力应变关系进行拟合，得到该荷载下两种材料的本构模型参数；通过Ramber-Osgood模型对骨架曲线进行拟合，得到两种材料的循环强化参数；采用Chaboche[29]塑性本构模型，标定了两种牌号不锈钢的循环荷载下本构参数，并结合有限元软件ABAQUS对本文试验结果进行模拟，为今后准确计算结构在地震荷载下的响应提供参考。
1 试验及本构参数研究
1.1 试验设计
按照《金属材料拉伸试验 第一部分：室温试验方法》(GB/T 228.1—2010)[30]的要求，对不锈钢棒材进行常温单轴拉伸试验和往复加载试验。不锈钢材料主要成分表见表1，试样尺寸(两种材料相同)如图1。棒材沿轧制方向分别取自板厚为18 mm的奥氏体型和16 mm的双相型板件。两种材料各12根，各3根进行单向拉伸试验，9根进行循环加载试验，共设置9种不同往复加载制度，标记为304/2205L1-L9，采用位移控制，加载制度详见图2。
表1 奥氏体型304和双相型2205不锈钢化学成分表/(%)
Table 1 Chemical constituents of austenitic 304 and duplex 2205 stainless steel
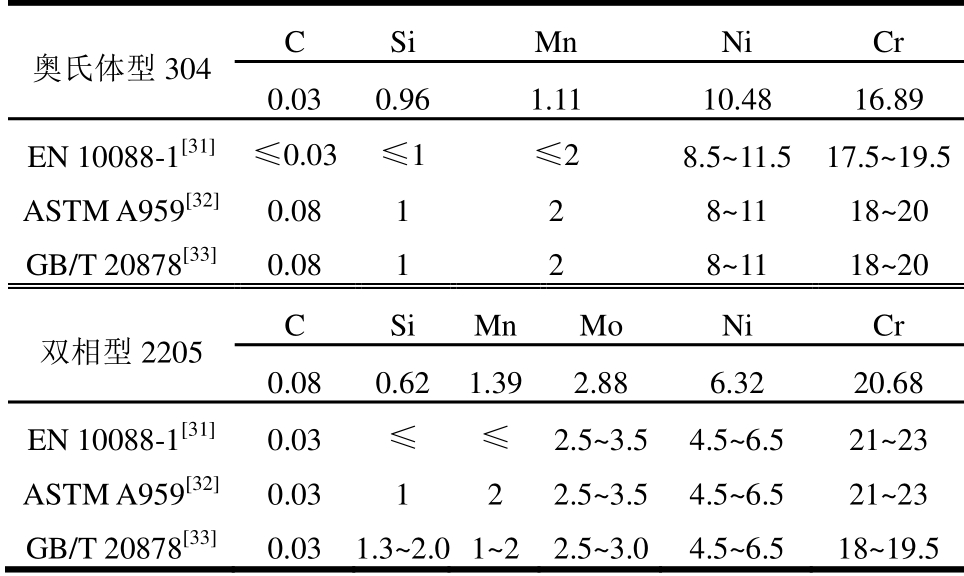
奥氏体型304 C Si Mn Ni Cr 0.03 0.96 1.11 10.48 16.89 EN 10088-1[31] ≤0.03 ≤1 ≤2 8.5～11.5 17.5～19.5 ASTM A959[32] 0.08 1 2 8～11 18～20 GB/T 20878[33] 0.08 1 2 8～11 18～20 双相型2205 C Si Mn Mo Ni Cr 0.08 0.62 1.39 2.88 6.32 20.68 EN 10088-1[31] 0.03 ≤ ≤ 2.5～3.5 4.5～6.5 21～23 ASTM A959[32] 0.03 1 2 2.5～3.5 4.5～6.5 21～23 GB/T 20878[33] 0.03 1.3～2.01～2 2.5～3.0 4.5～6.5 18～19.5
图1 单调拉伸和循环荷载下圆棒尺寸和试件图 /mm
Fig 1 Coupons under monotonic and cyclic loading
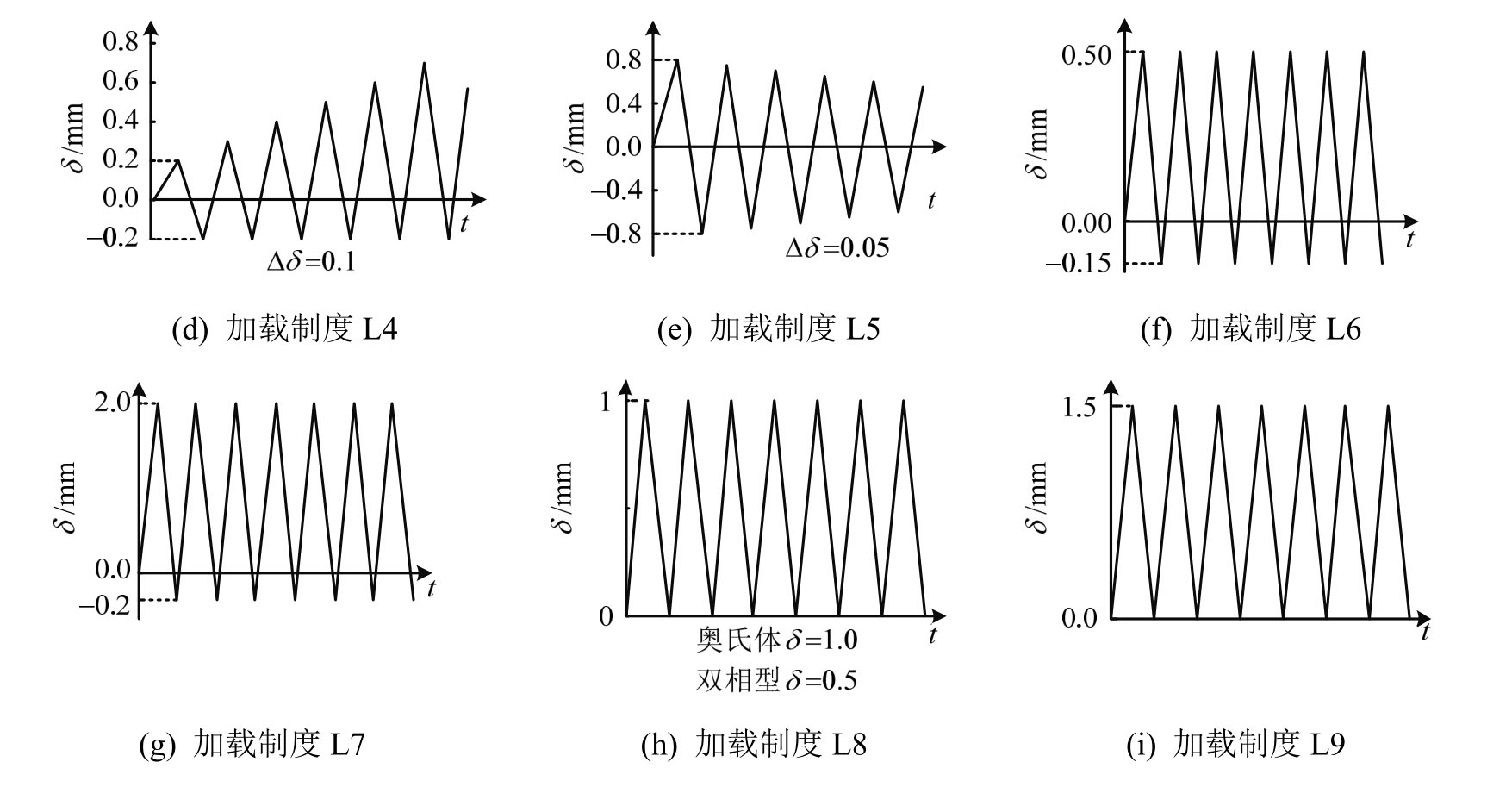
图2 循环加载制度
Fig.2 Cyclic loading system
1.2 试验加载设备
单调拉伸试验采用如图3(a)所示的Zwick/Roell Z100型电子拉压扭万能拉伸试验机进行加载。该试验机最大吨位为10 t，并携带可自动调整量程的双侧引伸计(标距段25 mm)，从而保证了试验精度要求。整个试验过程中保持2 mm/min的匀速加载，由计算机自动采集仪记录全过程荷载-变形和荷载-位移曲线。
循环加载试验采用如图3(b)所示的低周疲劳试验机，该机器最大加载能力为50 kN；采用横梁位移控制，试验机1 s采集50个数据点，加载速率为0.1 HZ。试验中，试样标距段的变形采用引伸计测量，引伸计标距为18 mm。
图3 单调拉伸和循环加载试验机
Fig.3 Test set up of monotonic and cyclic loading
1.3 单轴拉伸试验结果分析及参数拟合
通过圆棒单轴拉伸试验得到了各试件的工程应力-应变曲线，如图4所示，主要力学指标见表2。结果表明，在单调拉伸荷载下，两种不锈钢材料均表现出了明显的非线性行为，和普通碳素钢相比无明显屈服平台；而与304不锈钢相比，2205不锈钢抗拉强度更高；两种牌号不锈钢材料断面收缩率均在65%以上，断后伸长率也都在40%以上，表明二者均具有良好的塑性变形能力；奥氏体型不锈钢断后伸长率在60%以上，表现出更好的延性。
图4 单轴拉伸工程应力-应变
Fig.4 Engineering stress-strain relationship curves
本文采用当前常用的三种本构模型对实测曲线进行拟合，得出能够准确描述所采用不锈钢材料的全周期单调加载力学性能的表达式：
1)美国规范[34]采用的单段Ramberg-Osgood表达式，简写为“R-O”；
2)Gardner和Nethercot[35]提出的修正两段表达式，简写为“G-R-O”；
3)Quach等[36]提出的三段表达式，简写为“Q-R-O”。
试件加载过程中，随着荷载增大，试件截面积减小，采用下式计算材料真实应力-应变：
在ABAQUS有限元分析中，定义材料塑性参数时，需采用塑性应变指标，按式(2)计算：
图5为上述三个模型拟合材性试验真实应力-应变关系曲线结果，拟合参数见表3，结果表明：
1)R-O模型会高估不锈钢材料的应变硬化能力，特别是当应力值较高的时候，偏差尤其显著。不锈钢材料的延性很好，应考虑大应变高应力时的应力-应变关系，因此单段的Ramberg-Osgood模型不建议单独作为描述不锈钢材料的本构模型。
2)G-R-O模型能够较准确拟合奥氏体型和双相型不锈钢单调拉伸情况下应力-应变关系曲线，表3中参数为本模型拟合所得。
3)Q-R-O模型也同样能够较为准确地拟合出不锈钢应力-应变关系曲线，但由于在计算极限抗拉强度和对应的应变等指标时的准确性难以保证，拟合结果与试验实测曲线存在一定的偏差，且参数较多，应用过程较为繁琐，所以本文未使用此模型。
图5 不同本构模型拟合真实应力-应变曲线
Fig.5 Fitting curves with different constitutive models
表2 单轴拉伸试验参数
Table 2 Results of uniaxial tensile tests
注：E0为初始弹性模量；σ0.01和σ0.2分别为残余应变为0.01%和0.2%时对应的弹性应力值ε0.2为σ0.2对应的应变值；σu为极限荷载；εu为极限荷载对应的极限应变值；Z为断面收缩率；A为断后伸长率。
试件编号 E0/MPa σ0.01/MPa σ0.2/MPa ε0.2/(%) σu/MPa εu/(%) Z/(%) A/(%)304-1 304-2 304-3 AVG.265000 207000 275000 249000 190.7 184.3 196.0 190.3 278.84 268.54 274.16 273.85 0.32 0.33 0.29 0.31 708.69 709.58 712.88 710.38 46.31 50.24 47.33 47.96 76.15 76.11 75.82 76.02 63.16 62.80 61.08 62.35 COV/(%) 12.04 2.51 1.40 5.58 0.25 4.41 0.19 1.45 2205-1 2205-2 2205-3 AVG.195000 230000 254000 226000 297.7 273.3 326.1 299 519.48 545.71 530.24 531.81 47.21 42.62 42.98 44.27 763.12 755.07 745.98 754.72 20.11 16.89 16.78 17.92 66.67 68.20 66.67 67.19 47.01 41.79 41.06 43.29 COV/(%) 10.70 7.22 2.02 4.71 0.93 8.63 1.07 6.12
表3 单轴拉伸本构模型拟合参数
Table 3 Fitting parameters of uniaxial tensile constitutive model
注：E0.2为残余应变为0.2%时对应的弹性模量；σ1.0为残余应变为1%时对应的应力值；ε1.0为σ1.0时对应的应变值；ε2.0为σ2.0时对应的应变值；n为应变硬化指数；n′为应变硬化系数；a、b为Q-R-O本构模型中的参数。
试件编号 E0.2/MPa σ1.0/MPa ε1.0/(%) σ2.0/MPa ε2.0/(%) n n′ a b 304-1 304-2 304-3 AVG.15779 15559 14525 15288 329.98 332.87 340.04 334.30 1.12 1.16 1.12 1.13 361.48 363.84 372.04 365.78 2.14 2.18 2.18 2.16 7.89 7.96 8.93 8.26 2.78 2.93 3.02 2.91 336 340 347 341 1511 1444 1517 1491 COV /(%) 3.57 1.26 1.66 1.23 0.87 5.72 3.5 1.24 2.21 2205-1 2205-2 2205-3 AVG.38666 48418 36758 41614 611.96 619.03 607.78 612.92 1.32 1.33 1.28 1.31 643.73 648.14 639.96 643.94 2.34 2.34 2.28 2.32 5.38 4.33 6.16 5.29 2.25 2.31 2.32 2.96 624 628 620 624 1450 1507 1494 1484 COV/(%) 13.39 0.75 1.47 0.51 1.10 14.18 1.41 0.49 1.63
1.4 循环加载试验结果分析及本构参数拟合
1.4.1 骨架曲线
以往的工程计算中常采用单调拉伸曲线作为材料本构，但在循环荷载作用下，不锈钢的受力性能与单调加载下的受力性能有很大差别，往往会低估了材料的实际承载性能。图6可见单调加载曲线与滞回曲线存在明显区别。循环骨架曲线能够直观地表现出循环荷载与单调荷载作用下不锈钢材料的力学行为差别。
采用式(3)Ramberg-Osgood模型对循环加载骨架曲线进行拟合：
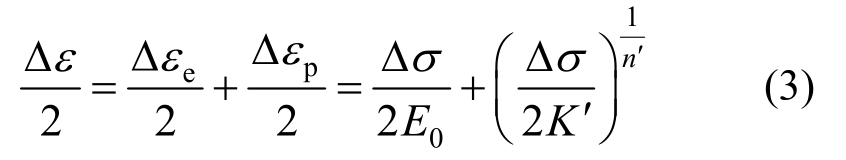
式中：Δε代表总应变幅；Δεe代表弹性应变幅；Δεp代表塑性应变幅；Δσ是稳定的应力幅；E是钢材的弹性模量；K′是循环强化系数；n′是循环强化指数。根据试验数据可对参数K′和n′进行拟合。
表4 Ramberg-Osgood模型循环强化拟合参数
Table 4 Cyclic hardening parameters of Ramberg-Osgood model
试件编号 K′/MPa n′ 304-L1 500.1 0.125 304-L2 827.2 0.313 304-L4 854.6 0.334 304-L5 576.1 0.152 AVG. 764.5 0.234 COV/(%) 22.41 39.88 2205-L1 511.5 0.0969 2205-L2 560.8 0.0927 2205-L4 528.3 0.0918 2205-L5 545.7 0.0924 AVG. 536.6 0.0935 COV/(%) 3.41 2.16
表4为不锈钢材料的强化参数，可以看出奥氏体型循环强化参数较双相型大，从图6骨架曲线与单调曲线的对比中也可以看出，两种材料均出现了较大幅度的应变硬化，但奥氏体型的循环强化现象远大于双相型；表4中双相型循环强化系数离散性较小，而奥氏体型较大，说明奥氏体型不锈钢的循环强化现象受加载制度影响更大。图7显示Ramberg-Osgood模型对骨架曲线的拟合结果吻合度很高，且在工程常用的应变范围(图7所示14%)内，循环强化作用可使双相型不锈钢抗拉强度提高10%～20%，奥氏体型提高50%以上，其中L1、L2、L5加载制度下奥氏体型抗拉强化提高达70%。不锈钢在循环与单调荷载下的力学反应差别较大，故不可用单调拉伸工况下的本构模型来代替循环加载。
图6 加载制度L2下滞回曲线与单调拉伸曲线对比
Fig.6 comparison of hysteresis curve and monotonic stretch curve of L2 loading system
图7 奥氏体型和双相型不锈钢循环骨架曲线
Fig.7 Cyclic skeleton curve of austenite and duplex stainless steel
1.4.2 滞回性能
循环荷载下不锈钢材料滞回曲线如图8所示，所有试件滞回曲线饱满，循环强化现象明显，表明两种材料均具有良好的耗能能力。从滞回曲线的发展规律可以看出不锈钢的滞回行为准则综合了各向同性强化及随动强化两者的特征，并且随动强化起主要影响作用。材料的强化幅度前期较高，后期较小但依然强化明显，并且不同应变幅值下，强化程度不同。
图8 奥氏体型和双相型不锈钢滞回曲线及模拟曲线
Fig.8 Hysteretic curve and simulation curve of austenite and dual phase stainless steel
1.4.3 参数标定及数值模拟
根据Chaboche塑性本构模型[29]标定两种材料的循环本构参数，包括各向同性强化和随动强化两者的特征。
各向同性强化是屈服面σ0的大小和等效塑性应变εp的函数：
式中：σ|0 表示在等效塑性应变为零时的应力，本文取σ0.01；Q∞为屈服面最大变化值；biso为屈服面随着塑性应变的增加而变化的比率。
在第i圈的屈服面，定义为：
式中：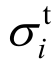
为最大拉应力；
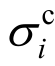为最大压应力。
第i圈的等效塑性应变
定义为：
式中，
为塑性应变变化范围，可用公式计算：
式(4)通过根据每一个数据点
以及biso，结果见表5。
随动强化模型定义了背应力αk，表达式为：
式中：Ckin,k和γk为常数，γk定义了随塑性应变增加而变化背应力的变化率，比率
为背应力的最大变化值。由于曲线的形状对于不同的应变范围有较大的变化，所以采用背应力叠加的方式可以得到更为准确的曲线，如式(9)所示，本文选取k=4。
数据点
式中：
是通过应变轴时的塑性应变值，对于每一个数据点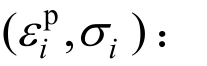
式中：σs为第一个数据点σ1和最后一个数据点σn的平均值。利用
和
进行拟合，拟合结果见表5。
利用ABAQUS中的“cycle hardening”材料属性对循环荷载下不锈钢棒材试验曲线进行模拟，根据表5中拟合得到的材料参数，可得到有限元计算结果。图8为试验曲线与有限元曲线的对比，可以看出有限元可以较为准确地模拟实际曲线情况，标定得到的参数可以较精准地应用，从而为今后准确计算结构在地震荷载下的反应提供了重要参考。
3 结论
本文通过对12个奥氏体型和12个双相型不锈钢圆棒进行单调和循环加载试验，研究不锈钢材料的力学行为及本构模型，主要结论如下：
(1)不锈钢材料在单调拉伸荷载下，双相型不锈钢的断后伸长率大于45%，奥氏体型不锈钢的断后伸长率高于60%，表明不锈钢材料具有很好的延性。
表5 奥氏体型和双相型不锈钢循环本构模型参数
Table 5 Parameters of cyclic constitutive model of austenite and duplex stainless steel
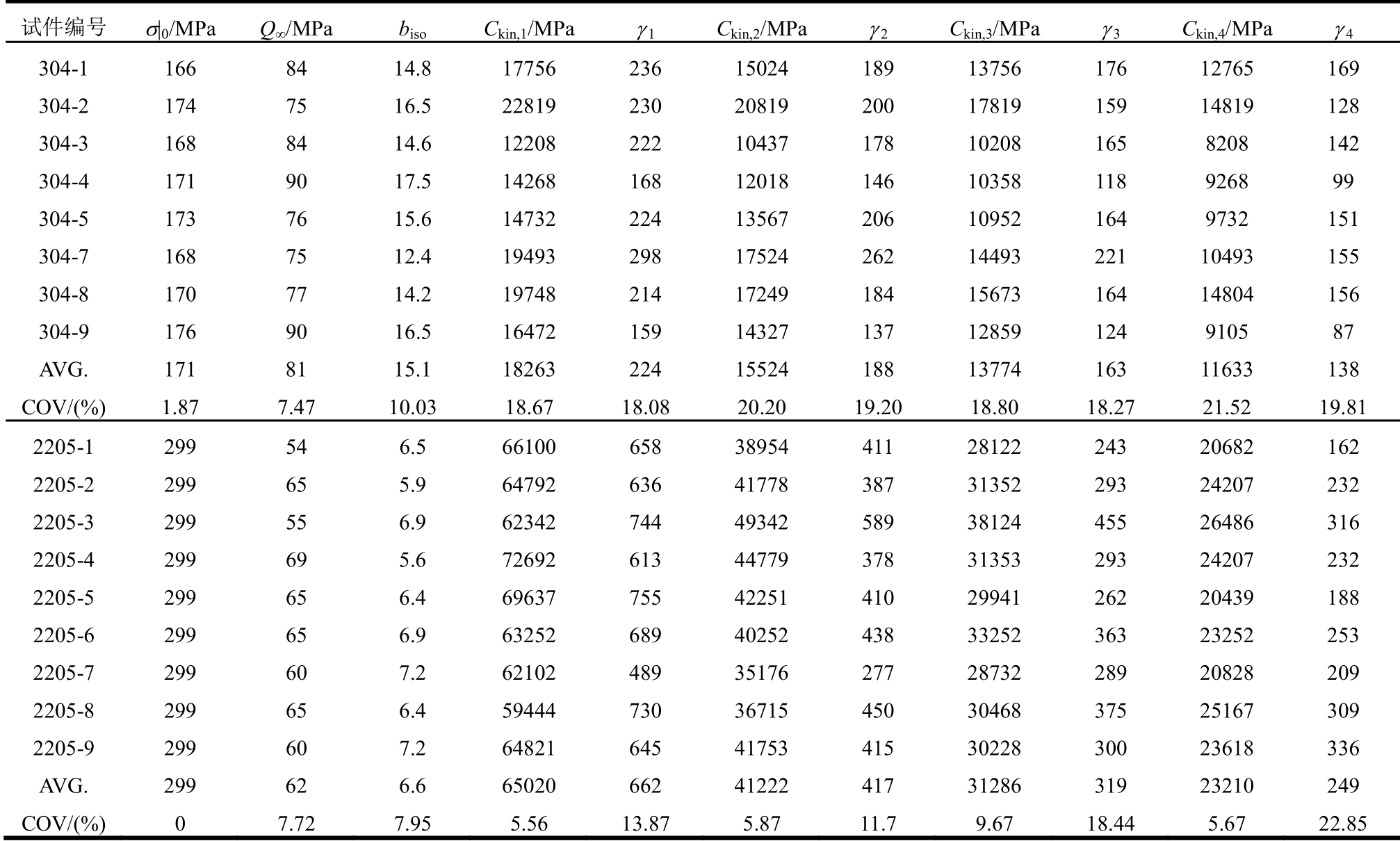
试件编号 σ|0/MPa Q∞/MPa bisoCkin,1/MPa γ1Ckin,2/MPa γ2Ckin,3/MPa γ 3Ckin,4/MPa γ4 304-1 166 84 14.8 17756 236 15024 189 13756 176 12765 169 304-2 174 75 16.5 22819 230 20819 200 17819 159 14819 128 304-3 168 84 14.6 12208 222 10437 178 10208 165 8208 142 304-4 171 90 17.5 14268 168 12018 146 10358 118 9268 99 304-5 173 76 15.6 14732 224 13567 206 10952 164 9732 151 304-7 168 75 12.4 19493 298 17524 262 14493 221 10493 155 304-8 170 77 14.2 19748 214 17249 184 15673 164 14804 156 304-9 176 90 16.5 16472 159 14327 137 12859 124 9105 87 AVG. 171 81 15.1 18263 224 15524 188 13774 163 11633 138 COV/(%) 1.87 7.47 10.03 18.67 18.08 20.20 19.20 18.80 18.27 21.52 19.81 2205-1 299 54 6.5 66100 658 38954 411 28122 243 20682 162 2205-2 299 65 5.9 64792 636 41778 387 31352 293 24207 232 2205-3 299 55 6.9 62342 744 49342 589 38124 455 26486 316 2205-4 299 69 5.6 72692 613 44779 378 31353 293 24207 232 2205-5 299 65 6.4 69637 755 42251 410 29941 262 20439 188 2205-6 299 65 6.9 63252 689 40252 438 33252 363 23252 253 2205-7 299 60 7.2 62102 489 35176 277 28732 289 20828 209 2205-8 299 65 6.4 59444 730 36715 450 30468 375 25167 309 2205-9 299 60 7.2 64821 645 41753 415 30228 300 23618 336 AVG. 299 62 6.6 65020 662 41222 417 31286 319 23210 249 COV/(%) 0 7.72 7.95 5.56 13.87 5.87 11.7 9.67 18.44 5.67 22.85
(2)单调荷载作用下，R-O模型对不锈钢应力-应变曲线前期(应变5%以内)拟合程度较好，后期出现偏高的情况；G-R-O模型能够较准确拟合两种不锈钢材料单调拉伸应力-应变关系曲线；Q-R-O模型拟合结果与G-R-O模型接近，但参数较G-R-O模型多，应用过程相对繁琐，故本文建议使用G-R-O模型。
(3)不锈钢材料在循环荷载与在单调荷载下的响应有很大差别，循环强化现象明显；骨架曲线对于准确模拟循环荷载下不锈钢受力行为起到重要作用，Ramberg-Osgood模型拟合结果与试验骨架曲线吻合度高，表明本文标定出的循环强化参数准确可靠。
(4)两种牌号不锈钢滞回环饱满，均表现出良好的耗能能力；标定出的循环本构参数可以很好地模拟试验滞回曲线，表明参数准确可靠，可为模拟结构体系地震作用下的响应分析在提供必要的数据支持。
[1]Baddoo N R.Stainless steel in construction: A review of research, applications, challenges and opportunities [J].Journal of Constructional Steel Research, 2008, 64(11): 1199—1206.
[2]方志, Ivan Campbell T.不锈钢和CFRP混合配筋预应力混凝土梁的延性和变形性能[J].工程力学, 2005, 22(3): 190—197. Fang Zhi, Ivan Campbell T.Ductility of concrete beams prestressed with CFRP [J].Engineering Mechanics, 2005, 22(3): 190—197.(in Chinese)
[3]杨璐, 徐东辰, 尚帆, 等.双相型不锈钢焊接工字形截面轴压柱整体稳定性能试验研究[J].建筑结构学报, 2015, 36(7): 99—105. Yang Lu, Xu Dongchen, Shang Fan, et al.Experimental study on the overall stability of duplex stainless steel welded I-section columns under axial compression.[J].Journal of Building Structures, 2015, 36(7): 99—105.(in Chinese)
[4]杨璐, 徐东辰, 尚帆, 等.双相型不锈钢焊接箱形截面轴压构件整体稳定性能试验研究[J].东南大学学报(自然科学版), 2015, 45(2): 364—369. Yang Lu, Xu Dongchen, Shang Fan, et al.Experimental study on the overall stability of biaxial stainless steel welded box section axial compression members [J].Journal of Southeast University (Natural Science Edition), 2015, 45(2): 364—369.(in Chinese)
[5]张涌泉.双相型不锈钢轴心受压构件承载力试验研究与理论分析[D].南京: 东南大学, 2016. Zhang Yongquan.Experimental research and theoretical analysis of the bearing capacity of dual phase stainless steel axially compression members [D].Southeast University, 2016.(in Chinese)
[6]杨璐, 张有振, 周晖, 等.双相型S22053不锈钢角焊缝连接拉伸试验研究[J].土木工程学报, 2016(11): 19—25. Yang Lu, Zhang Youzhen, Zhou Hui, et al.Tensile test study on fillet weld connections of S22053-grade duplex stainless steel [J].China Civil Engineering Journal, 2016(11): 19—25.(in Chinese)
[7]尚帆, 杨璐, 赵梦晗, 等.不锈钢工字形截面轴心受压构件整体稳定性能有限元研究[J].工程力学, 2016, 33(3): 112—119. Shang Fan, Yang Lu, Zhao Menghan, et al.FEA study on the overall stability performance of a stainless steel I-section axial compression member [J].Engineering Mechanics, 2016, 33 (3): 112—119.(in Chinese)
[8]尚帆, 杨璐, 赵梦晗, 等.不锈钢箱形截面轴心受压构件整体稳定性有限元研究[J].建筑结构, 2016(6): 66—70.Shang Fan, Yang Lu, Zhao Menghan, et al.The FEA study of the overall stability of the stainless steel box section axial compression members finite element study [J].Building Structure, 2016(6): 66—70.(in Chinese)
[9]袁焕鑫, 王元清, 杜新喜, 等.不锈钢焊接工字形截面短柱轴压局部稳定性能试验研究[J].建筑结构学报, 2015, 36(5): 38—45. Yuan Huanxin, Wang Yuanqing, Du Xinxi, et al.Experimental research on local stability of stainless steel welded I-section short columns under axial compression [J].Journal of Building Structures, 2015, 36 (5): 38—45.(in Chinese)
[10]Yang L, Zhao M, Chan T M, et al.Flexural buckling of welded austenitic and duplex stainless steel I-section columns [J].Journal of Constructional Steel Research, 2016, 122: 339—353.
[11]王元清, 赵义鹏, 徐春一, 等.不同种类螺栓的不锈钢端板连接节点抗震性能试验研究[J].天津大学学报(自然科学与工程技术版), 2017(增1): 140—146. Wang Yuanqing, Zhao Yipeng, Xu Chunyi, et al.Experimental research on seismic performance of stainless steel end plate connections with different bolts.[J].Journal of Tianjin University (Natural Science and Engineering Edition), 2017 (Suppl1): 140—146.(in Chinese)
[12]石永久, 王萌, 王元清.循环荷载作用下结构钢材本构关系试验研究[J].建筑材料学报, 2012, 15(3): 293—300. Shi Yongjiu, Wang Meng, Wang Yuanqing.Experimental study on constitutive relationship of structural steel under cyclic loading study of [J].Journal of construction Materials, 2012, 15(3): 293—300.(in Chinese)
[13]Nip K H, Gardner L, Davies C M, et al.Extremely low cycle fatigue tests on structural carbon steel and stainless steel [J].Journal of Constructional Steel Research, 2010, 66(1): 96—110.
[14]Roy S C, Goyal S, Sandhya R, et al.Low cycle fatigue life prediction of 316 L(N)stainless steel based on cyclic elasto-plastic response [J].Nuclear Engineering and Design, 2012, 253(2012): 219—225.
[15]Ye D, Matsuoka S, Nagashima N, et al.The low-cycle fatigue, deformation and final fracture behaviour of an austenitic stainless steel [J].Materials Science & Engineering A (Structural Materials: Properties, Microstructure and Processing), 2006, 415(1/2): 104—117.
[16]王留兵.Z2CND18.12N奥氏体不锈钢低周疲劳及热机疲劳性能研究[D].天津: 天津大学化工学院.2010—06. Wang Liubing.Z2CND18.12N austenitic stainless steel in low cycle fatigue and thermo mechanical fatigue of the performance of [D].Tianjin: Chemical Engineering Tianjin University 2010-6.(in Chinese)
[17]于敦吉.奥氏体不锈钢循环塑性的微观机理和宏观本构描述[D].天津: 天津大学, 2014—11. Yu Dunji.A study of micro-mechanisms and macro- constitutive modeling of the cyclic plasticity of austenitic stainless steels [D].Tianjin: Tianjin University, 2014—11.(in Chinese)
[18]罗云蓉, 于清远.建筑用抗震钢高应变低周及超低周疲劳性能研究进展[J].四川建筑科学研究, 1008-1933(2011)03-139-07. Luo Yunrong, Yu Qingyuan.Advances in research on high strain low cycle fatigue properties of low cycle Jichao [J].Building Science Research of Sichuan, 1008-1933 (2011)03-139-7.(in Chinese)
[19]Ramberg W, Osgood W R.Determination of stress-strain curves by three parameters [R].Technical note No.503, National Advisory Committee on Aeronautics (NACA), 1941.
[20]Mirambell E, Real E.On the calculation of deflections in structural stainless steel beams: an experimental and numerical investigation [J].Journal of Constructional Steel Research, 2000, 54(1): 109—133.
[21]Gardner L, Nethercot D A.Experiments on stainless steel hollow sections-Part 1: Material and cross-sectional behavior [J].Journal of Constructional Steel Research, 2004, 60(9): 1291—1318.
[22]Quach W M, Teng J G, Chung K F.Three-stage full-range stress-strain model for stainless steels [J].Journal of Structural Engineering ASCE, 2008, 134(9): 1518—1527.
[23]Nathaniel G C, Krawinkler H.Uniaxial cyclic stress-strain behavior of structural steel [J].Journal of Engineering Mechanics, 1985, 111(9): 1105—1120.
[24]Chaboche J L.Time independent constitutive theories for cyclic plasticity [J].International Journal of Plasticity, 1986, 2(2): 149—188.
[25]王萌, 杨维国.奥氏体不锈钢滞回本构模型研究[J].建筑材料学报, 2015(11): 107—114. Wang Meng, Yang Weiguo.Austenitic stainless steel hysteretic constitutive model [J].Journal of Architectural Materials, 2015 (11): 107—114.(in Chinese)
[26]王元清, 常婷.循环荷载下奥氏体不锈钢的本构关系试验研究[J].东南大学学报(自然科学版), 2012, 42(6): 1175—1179. Wang Yuanqing, Chang Ting.Experimental study on constitutive relation of austenitic stainless steel under cyclic loading [J].Journal of Southeast University (Natural Science Edition), 2012, 42(6): 1175—1179.(in Chinese)
[27]Nip K H, Gardner L, Davies C M.et al.Extremely low cycle fatigue tests on structural carbon steel and stainless steel [J].Journal of Constructional Steel Research, 2010, 66(1): 96—110.
[28]段文峰, 邓泽鹏, 刘文渊, 等.不锈钢S30408材料本构模型试验研究[J].钢结构, 2016, 31(5): 37—40.Duan Wenfeng, Deng Zeping, Liu Wenyuan et al.The constitutive model test of stainless steel S30408 materials study [J].Steel Structure, 2016, 31(5): 37—40.(in Chinese)
[29]Chaboche J L.Time-independent constitutive theories for cyclic plasticity [J].International Journal of Plasticity, 1986, 2(2): 149—188
[30]GB/T 228.1—2010, 金属材料拉伸试验 第一部分: 室温试验方法[S].北京: 中国标准出版社, 2010.GB/T 228.1—2010, metal material tensile test Part 1: room temperature test method [S].Beijing: China Standard Press, 2010.(in Chinese)
[31]EN 10088—1: 2005, Stainless steels-Part 1: List of stainless steels [S].CEN, 2005.
[32]ASTM A959—11, Standard guide for specifying harmonized standard grade compositions for wrought stainless steels [S].West Conshohocken, PA: ASTM International, 2011.
[33]GB/T 20878—2007, 不锈钢和耐热钢 牌号及化学成分[S].北京: 中国标准出版社, 2007.GB/T 20878—2007, Stainless and heat-resisting steels- Designation and chemical composition [S].Beijing: Standards Press of China, 2007.(in Chinese)
[34]SEI/ASCE 8—02, Specification for the design of cold-formed stainless steel structural members [S].New York: American Society of Civil Engineers (ASCE), 2002.
[35]Gardner L, Nethercot D A.Experiments on stainless steel hollow sections-Part 1: Material and cross-sectional behavior [J].Journal of Constructional Steel Research, 2004, 60(9): 1291—1318.
[36]Quach W M, Teng J G, Chung K F.Three-stage full-range stress-strain model for stainless steels [J].Journal of Structural Engineering ASCE, 2008, 134(9): 1518—1527.