在高放废物的地质处置中，膨润土由于具有渗透性低，导热性能优良，吸附性好，高膨胀性等特点，被视为良好的缓冲材料[1]。将高压实的膨润土砌块进行拼接，填充在废物罐和围岩间，可实现工程屏障的功能。在施工过程中，罐体与砌块、围岩与砌块，以及砌块与砌块之间，不可避免地会留下接缝。利用膨润土吸水膨胀的特性可以填充接缝，但是接缝作为薄弱环节对缓冲层整体性能的影响还需要探讨。
接缝的存在会使相关区域的膨胀力延迟出现，并且会产生一个优先流动的水力通道[2]。陈宝等[3]通过精确控制试样与活塞之间的预留缝隙来模拟施工接缝，并观测了水化后的微观结构，指出接缝会降低膨胀力和防渗性能。鉴于施工接缝对缓冲材料性能的减弱，许多学者建议往施工接缝内回填粘土材料[4—5]。Zhang等[6]研究了膨润土粉末，膨润土泥浆，以及膨润土颗粒3种形式的接缝回填材料的愈合性能，指出不同的接缝材料力学性能上会有差异，但整体来看，都具有渗透性强，导热性略低于砌块，具有可压缩性等特点。
由于缓冲材料的工作周期较长，在处置库的设计中需要数值计算加以辅助，国内已有学者[7—8]对不同边界条件下的缓冲材料水热传递和膨胀性能进行了计算，并依托China-Mock-up大型试验装置，进行了结果的分析和预测。但是目前的计算主要对象仍为完整的膨润土材料，对接缝存在的影响数值研究较少。本文以含接缝的GMZ01膨润土缓冲材料为研究对象，接缝填充材料为膨润土粉末，使用Comsol Multiphysics有限元程序求解自定义方程，模拟组合砌块在热源和外界水头作用下的热-水-力的耦合演化过程，分析了接缝的愈合效应，以及接缝的类型、拼接方式、宽度和干密度等对缓冲材料渗透性能的影响。
1 热-水-力耦合控制方程
在处置库工作的过程中，土体的含水率和温度会在热源和外界水头的作用下发生变化，使土体产生变形，改变土体的结构和孔隙率，渗流和导热性能也随之改变，物性参数需要在计算中实时更新。
砌块和接缝的成分都为GMZ01膨润土，因此砌块和接缝可以采用相同的对流控制方程，区别只在于干密度不同，相应的计算参数不同。
1.1 热传导控制方程
本文计算中不考虑空气流动所携带的热量，并认为在某一点处，土颗粒和水的温度瞬间达到平衡，因此只有一个温度变量T，得到热传导的控制方程：
式中：▽为Hamilton算子；H表示粒子点处的单位体积热容量；λk为热传导系数；ρl为液态水的密度；Cl为水的比热容；u为水的流速矢量；El为水的体积蒸发速率；L为水的蒸发潜热；q是热源强度。有计算表明高压实膨润土砌块的浸润过程中，蒸发效应对热传导和水分迁移影响较小[9—10]，取El=0。流速场u通过渗流计算得到。
试验结果表明[11]，导热系数λk /(W/(m· )℃)与膨润土的干密度ρd和饱和度Sω近似成线性关系：
式中：干密度ρd单位为g/cm3，下同。
单位体积总热容H /(J/(m3·℃))：
式中：n为孔隙率；Cps和Cpl分别表示土颗粒和液态水的质量比热。
1.2 渗流控制方程
由于膨润土质地致密，渗流缓慢，可通过Richards渗流方程[12]进行计算：
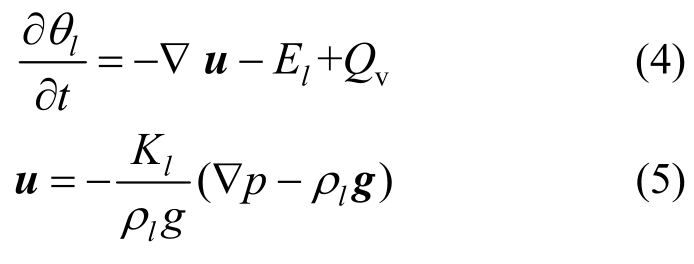
式中：θl为水的体积分数；g为重力加速度的矢量；El为蒸发项；Qv为源项。p/MPa为水压力；Kl/(m/s)为渗透系数：
式中：kr为相对渗透率，与饱和度有关，根据试验结果可取[13]，kr=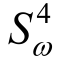
。Ks为饱和渗透系数，尽管国内外针对接缝材料渗透系数的研究较少，但是针对各类膨润土已有的研究表明[5,14]，相同温度下，饱和渗透系数Ks与膨润土的干密度的指数线性相关：
固有渗透率Kint主要取决于多孔介质的孔隙结构，与流体性质和温度无关，单位m2，常用于温度变化环境下的渗流计算，与渗透系数Ks的关系为：
式中：μl为水的动力粘度，与温度相关：
式中：温度T的单位为℃，下同。结合式(7)～式(9)可得Kint与干密度的关系：
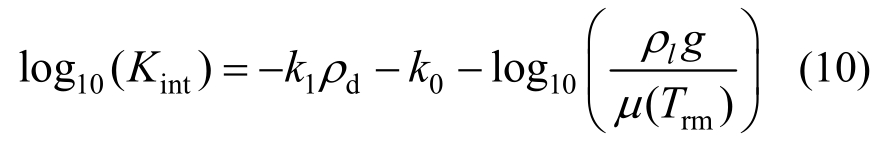
式中：Trm为试验时室温；k0和k1取值见表1。
假设气压恒定，通过水压p的正负判断土体的饱和状态，水压p力为负时，存在吸力s=-p。吸力s与土体饱和度、温度和干密度有关：
式中：σ (T)表示水的表面张力系数对吸力的影响，根据蔡国庆等[15]提出的公式简化为线性关系：
sr与Sω的关系使用van Genuchten(VG)模型[16]描述：
参数a和b根据Chen等[17]在20 ℃下对压实膨润土砌块的土水特征曲线试验结果进行拟合得到。计算过程中忽略气压的变化。
表1 对流计算的相关参数
Table 1 Parameters of diffusion models
参数 数值 文献来源及说明初始含水率 0.11 表1[18] 水的密度ρl /(kg/m2) 1000 表1[8] 土颗粒比重ρs2.7 表1[8] 水的比热Cpl /(J/(kg·℃)) 4200 表1[8] 土颗粒比热Cps /(J/(kg· ))℃ 900 表1[8] 渗透率参数k03.51 结合[7,14] 渗透率参数k16.0 结合[7,14] 参考温度T0 /( )℃ 20 本文拟定 参考干密度ρd0 /(g/cm3) 1.7 第2节[8] 热传导参数λkd0 /(W/(m· ))℃ -0.5 拟合[11] 热传导参数λkd1 /(W/(m· ))℃ 0.6 拟合[11] 热传导参数λk1 /(W/(m· ))℃ 1.07 拟合[11] VG模型参数a /m-1 0.009 拟合[17] VG模型参数b 1.3386 拟合[17] 吸力参数l 2 简化[15] 吸力参数σ01 简化[15] 吸力参数σ1 /(℃-1) 0.004 简化[15] 室温Trm /( )℃ 20 本文拟定
2 力学模型和应力路径
Barcelona basic model (BBM)模型作为描述非饱和土力学行为的经典模型，可用于缓冲材料力学行为的计算[7—8]，但是接缝材料所需参数不够完善，且BBM模型难以在通用的数值软件中实现。本文针对土体湿化这一特定过程，分析了砌块和接缝可能经历的应力路径，对计算模型进行了合理简化。
2.1 膨胀过程
膨润土在体积不变的情况下，完全饱和后产生的膨胀力为最大膨胀力PsM，PsM与膨润土的干密度、初始含水率、蒙脱石含量、试验方法等有关。缓冲材料处在密闭的空间中，接近于恒体积法的试验条件，根据叶为民等[18]恒体积试验结果，得到初始含水量11%，初始温度为20℃的GMZ01膨润土膨胀力与干密度的关系式为：
设砌块和接缝的干密度分别为1.7 g/cm3和1.1 g/cm3，由式(14)可得接缝材料PsMj为0.068 MPa，砌块PsMb为5.83 MPa。膨润土的膨胀力Ps随着吸力的减小而增大，吸力为0时达到最大值PsM[19]：
牛文杰等[1]测定了干密度1.7 g/cm3的砌块自由膨胀率与吸力的关系，见图1。
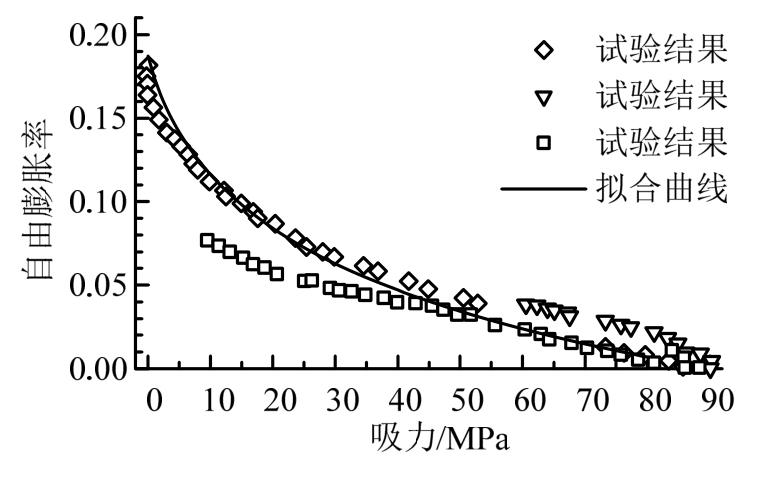
图1 砌块自由膨胀率和吸力的关系
Fig.1 Relationship between free swelling ratio and suction of block
砌块在低围压下因吸力变化产生的变形全部为弹性变形[20]：
式中：s/MPa为吸力值；κs为吸力作用的弹性变形指数；pv0为拟合参数。设初始状态砌块的比体积和吸力分别为vb0和sb0，对式(16)积分得到自由膨胀状态下vb和s的关系：
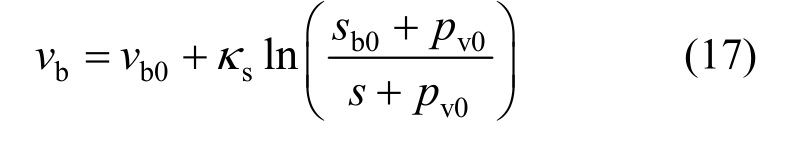
将式(17)与图1拟合得到κs=0.10，pv0=5.0 MPa。设土体所受外界平均压应力为p，定义等效膨胀力
将式(15)代入式(17)，并用PsE替换Ps，得到砌块在有荷膨胀过程中的应力-应变关系：
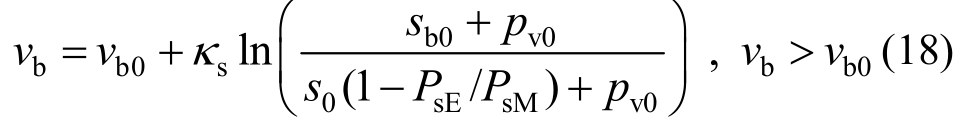
土骨架受热会产生膨胀，一般粘土矿物的热膨胀系数αs在0.5×10-5℃-1～1.8×10-5℃-1之间[21]，本文假设：
由式(19)可知，干密度1.7的砌块温度升高70 ℃热膨胀应变约为1.2×10-3，相对浸润膨胀较小。
2.2 压缩过程
图2中p′为平均主应力，v为比体积，v=1+e，e为孔隙率，砌块和接缝的初始比体积分别为vb0和vj0。λ(0)为土体饱和状态的压缩指数，有：
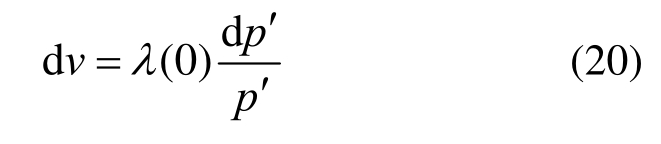
非饱和状态下，压缩指数λ(s)随吸力减小而增大，因此松散的土体在高围压下会发生湿陷。
图2 砌块和接缝材料湿化过程的应力路径
Fig.2 Stress path of block and joint material during wetting
图2通过v-logp′曲线，描述了湿化过程中由于产生膨胀力和相互间的变形协调而可能经历的应力路径，路径1和路径2分别代表接缝和砌块应力路径的两种极端情况：路径1表示接缝先吸水饱和，但由于接缝的膨胀力太小，接缝和砌块不发生变形，随后砌块开始吸水，产生较大膨胀力，接缝以压缩模量λ(0)到达JF点；路径2表示砌块先吸水膨胀，将接缝沿回弹曲线挤压并到达屈服面，随后以压缩模量λ(s)到达JD点，最后接缝吸水饱和，发生湿陷，到达JF点。实际上砌块和接缝会同时经历饱和的过程，因此实际应力路径应该在1和2之间，材料完全饱和后，到达的终点与路径无关[21]，因此计算中忽略λ(s)的变化。数值计算中接缝压缩指数取λ(0)，得到接缝的压缩过程中的应力-应变关系：
式中：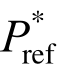
为参考应力；N(0)为参考比体积，通过压缩试验[22]得到；vjpc为先期固结压力对应的比体积，假定v>vjpc时土体为线弹性，弹性模量等于v=vjpc时的弹性模量。因此可得：
式中：pcj为接缝的先期固结压力，令式(22)中的 p′=0，应有vj = vj0，因此可得：
砌块弹性压缩指数[8]为κ，得：
在数值计算中可以直接输入应力-应变关系，也可以使用公式求导后得到弹性模量进行输入。
2.3 温度的影响
Bolzon等[23]提出温度升高会提升土的弹性模量，张发忠等[24]在不同温度下对膨润土进行饱和膨胀试验，发现膨胀率随温度的升高而降低，尽管其中的微观因素复杂，但在计算中可以通过对弹性模量进行温度修正来实现。设温度修正系数ET，有：
ET取值见表2。
2.4 屈服准则
接缝由于强度较低，可能出现屈服，计算中使用Mohr-Coulomb屈服准则，通过大小主应力和粘聚力c内摩擦角φ判断是否屈服。砌块则使用弹性模型。陈皓[25]研究表明，膨润土的粘聚力c会随着干密度和温度升高而升高，内摩擦角φ则主要与饱和度有关，近似有：
式中：c0、cd、cT、φ0、φT通过对纯GMZ01膨润土高含水率试样测试结果[25]拟合得到，参数取值见表2，粘聚力的拟合结果见图3。
表2 力学模型的相关参数
Table 2 Parameters of mechanical models
参数 数值 文献来源及说明 饱和压缩指数λ(0) 0.133 表2[8] 参考应力 *ref P /MPa 1.0 参考[25] 参考比体积N(0) 1.90 参考[25] 接缝初始比体积vj02.455 计算得到 砌块初始比体积vb01.588 计算得到 弹性压缩指数κ 0.0244 表2[8] 吸力作用弹性压缩指数κs0.10 表2[8] 砌块最大膨胀力PsMb /MPa 5.83 式(4)[17] 膨胀变形参数Pv0 /MPa 5.0 拟合[1] 砌块和接缝的泊松比ν 0.3 图7[22] 热膨胀系数αs /(℃-1) ρd×10-5 表3[21]
续表
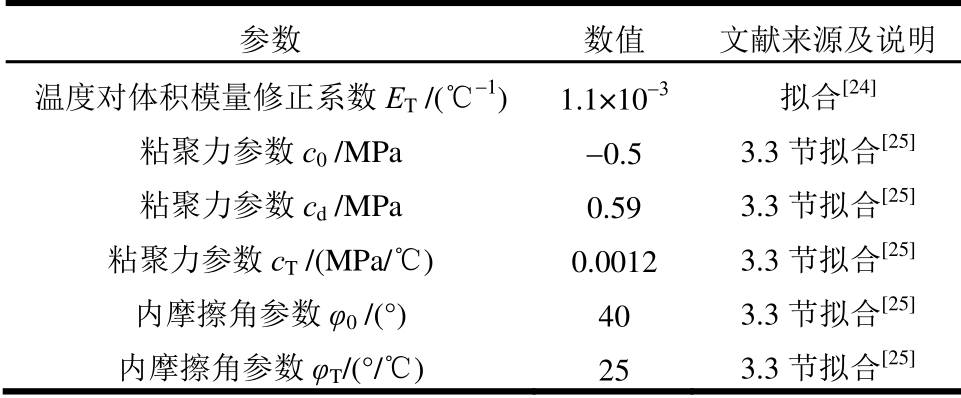
参数 数值 文献来源及说明温度对体积模量修正系数ET /(℃-1) 1.1×10-3 拟合[24] 粘聚力参数c0 /MPa -0.5 3.3节拟合[25] 粘聚力参数cd /MPa 0.59 3.3节拟合[25] 粘聚力参数cT /(MPa/ )℃ 0.0012 3.3节拟合[25] 内摩擦角参数φ0 /(°) 40 3.3节拟合[25] 内摩擦角参数φT/(°/ )℃ 25 3.3节拟合[25]
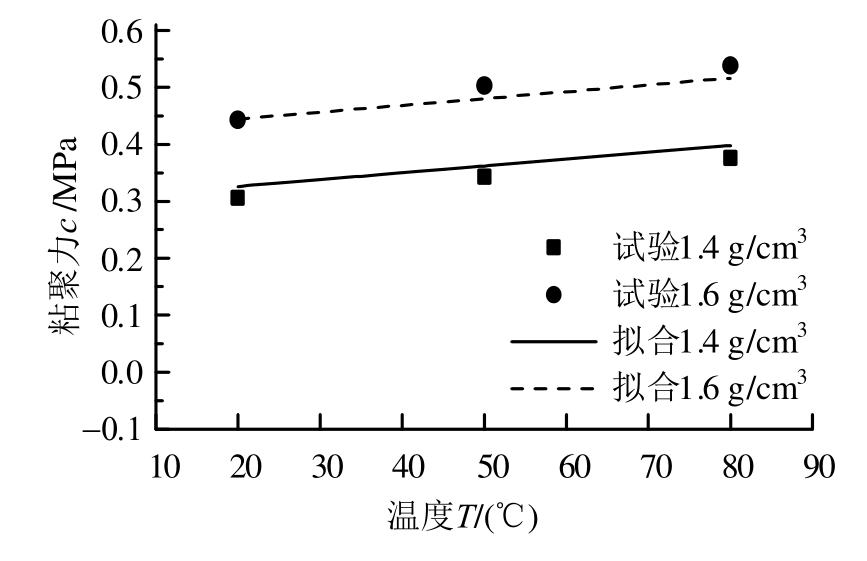
图3 粘聚力与干密度、温度的关系
Fig.3 Relationship of cohesion and dry density/ temperature
3 物理模型和边界条件
处置库模型尺寸参考China-Mock-up试验[5]，整体为半径450 mm的圆柱体，中心部分是半径150 mm的热源，外侧为围岩。缓冲层厚度为300 mm，由砌块和接缝拼接而成。罐体与砌块，围岩与砌块，砌块与砌块之间均有接缝材料填充，其中接缝的形式分为环向、径向和横向3种，环向与横向接缝的宽度为10 mm，径向接缝中心处宽度也为10 mm，内层6块砌块，外层12块砌块，均匀布置，砌块的初始干密度为1.70 g/cm3，接缝为1.10 g/cm3，缓冲材料的平均干密度为1.60 g/cm3，满足一般设计要求。由于砌块环向是等间距布置，取1/6模型进行计算，高度取300 mm，模型的左右两侧和上下两侧均为对称边界条件。中心部分的热源设置“温度”为90℃，缓冲层初始温度和环境温度均为20℃，外边界设置为“热通量”，与环境的换热系数h为8 W/m2℃。砌块和接缝材料的初始质量含水率均为0.11，外边界设置“压强”为2 MPa，内侧设置为“无流动”。不考虑热源和围岩的变形，土体内外侧均设置为“辊支承”。
图4中B1、B2、B3、B4为砌块内的点，J1、J2为横向接缝内的点，J3、J4为径向接缝内的点，用于记录计算过程中的相关数据。模型使用Comsol自带的几何模块进行绘制，网格3456个域单元、3480个边界元和1208个边单元。各个域之间选择“形成联合体”，保证接触面两侧的位移是连续的，各物理场可以通过接触面传递。砌块的应力-应变采用非线性弹性模型计算，注意需要将体积模量转化为变形模量，泊松比为定值，膨胀力以添加“外部应力”的方式加以实现，接缝使用弹塑性模型，选择“Mohr-Coulomb”屈服准则，塑性势选择关联流动。各物理场均采用二次离散，使用“MUMPS”求解器进行瞬态求解，时间步进采用向后差分公式，初始步长10 d～8 d。
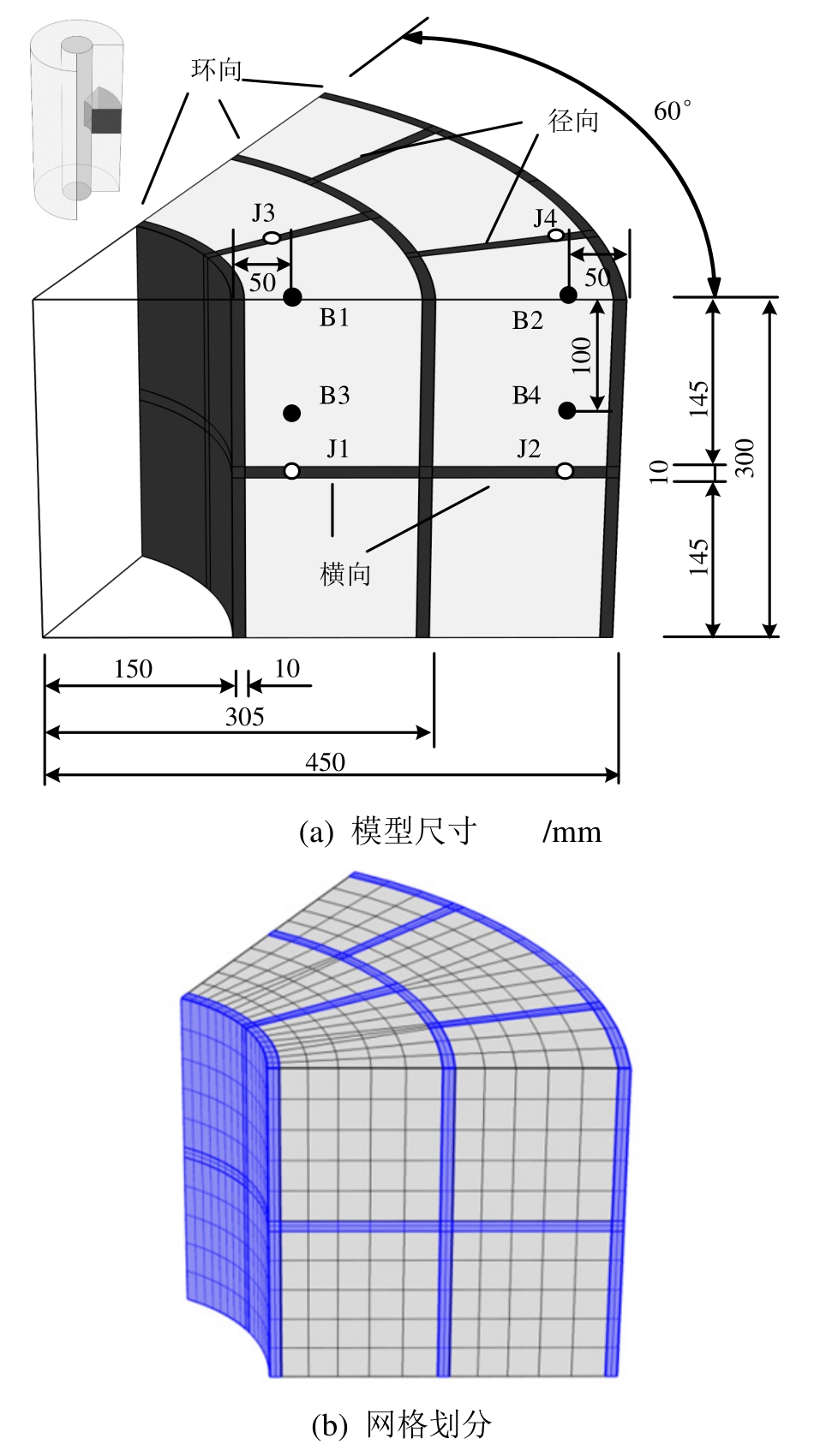
图4 数值计算模型及网格示意图
Fig.4 Diagram of numerical model and mesh
4 计算结果分析
4.1 热-水-力的演化规律及愈合过程
1)干密度的演化规律
在演化过程中，干密度是膨润土体应变直接体现，同时干密度也决定了土体的导热、渗流和强度性质。图5中实心标志代表接缝，空心标志代表砌块，无标志的虚线和实线分别表示同样边界条件下，无接缝的模型中B1和B2点的计算结果。可知在外界水头的作用下，接缝和砌块都从外向内逐渐饱和，在初期，外层砌块吸水产生膨胀力，产生较大的膨胀变形，将接缝和内层砌块挤压。缓冲材料完全饱和后，内外层砌块的干密度均变为1.62 g/cm3左右，接缝的干密度被压缩为1.47 g/cm3左右，接缝的干密度相较于初始状态的1.1 g/cm3有显著提升，相应的物理性质也会发生变化，缓冲材料整体变得更为均匀。接缝的最终干密度可能与砌块的膨胀力有关，砌块的膨胀力越大，接缝的最终干密度越高。
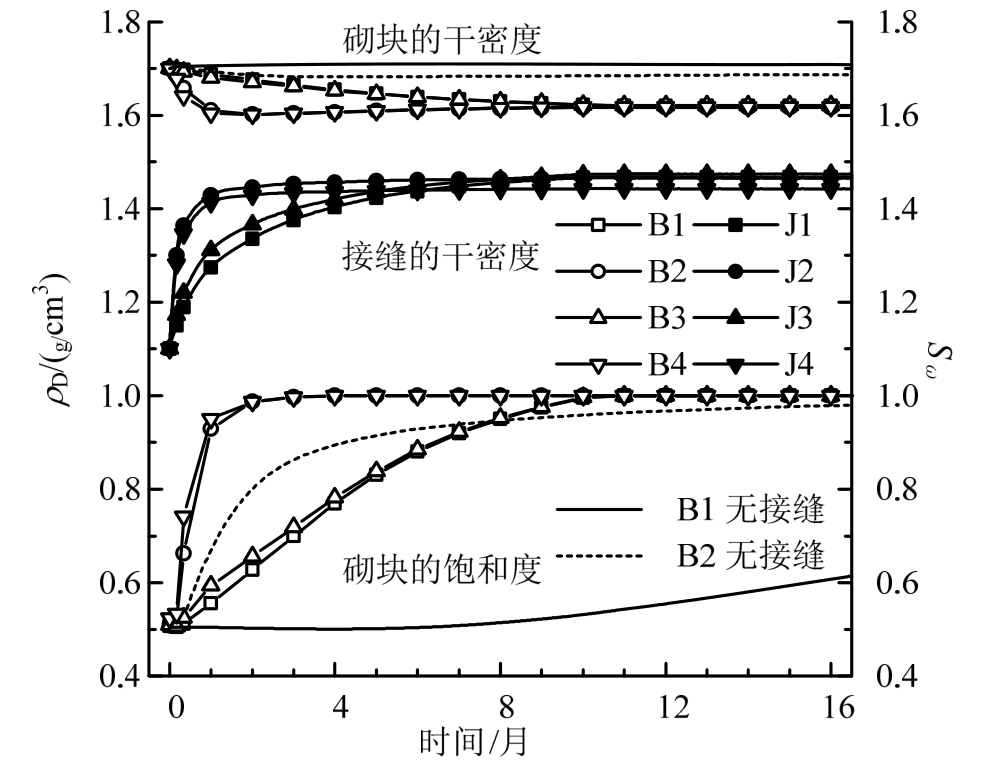
图5 干密度、饱和度随时间的演化规律
Fig.5 Evaluation of dry density and saturation with time
2)应力-应变的演化规律
缓冲材料内的应力由膨润土吸水膨胀产生。有接缝材料在12 月时完全饱和，应力停止增长，最终材料内的膨胀力约为2.5 MPa，而无接缝材料的膨胀力会一直增长到砌块的最大膨胀力PsM=5.8 MPa。接缝的存在会使整体的膨胀力有一定的减小，但仍能满足膨胀力＞2 MPa的一般设计要求[26]。而且结合图5可以发现，尽管有接缝的材料饱和较快，但由于接缝的存在，膨润土的应力增长延迟出现。
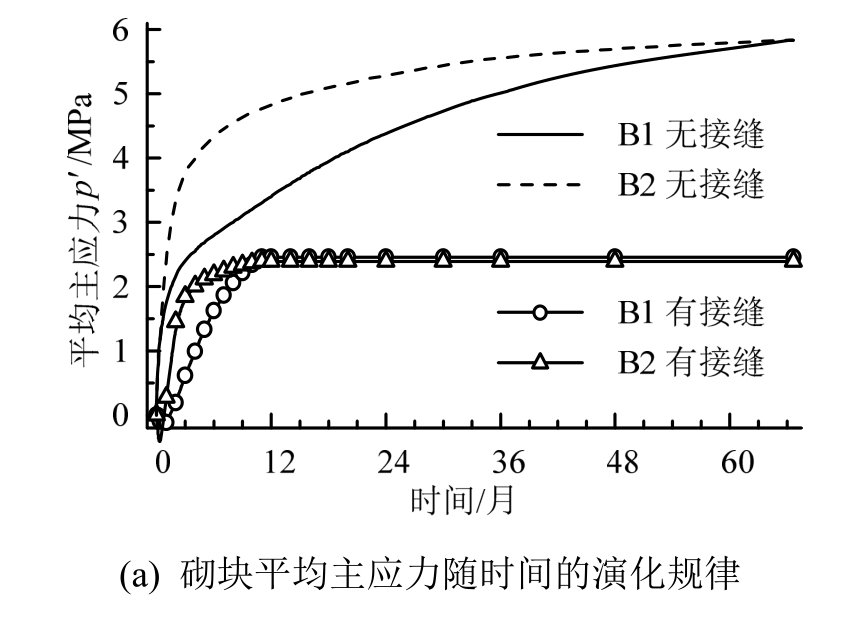
图6 应力和塑性应变演化规律
Fig.6 Evaluation of stress and plastic strain with time
由图6(b)可知，接缝的应力增长规律与砌块类似，外侧的接缝应力增长较快。虽然说屈服条件与大、小主应力有关，但是由于接缝基本处于单方向受压的状态，因此小主应力增长不明显，因此塑性应变εp的增长与p′具有时间上的同步性和幅值上的相关性，值得注意的是，外侧径向接缝J4虽然应力增长较快，但是由于应力值相对较低，并没有产生塑性应变。结合图5可以计算出接缝的最大压缩体应变为0.255，而最大塑性应变为0.011，在当前的设计参数下，塑性应变相对较小，应变分布见图7。塑性应变的主要方向为径向和横向的接缝由于挤压向外侧流动，可以起到填补围岩裂隙的作用。
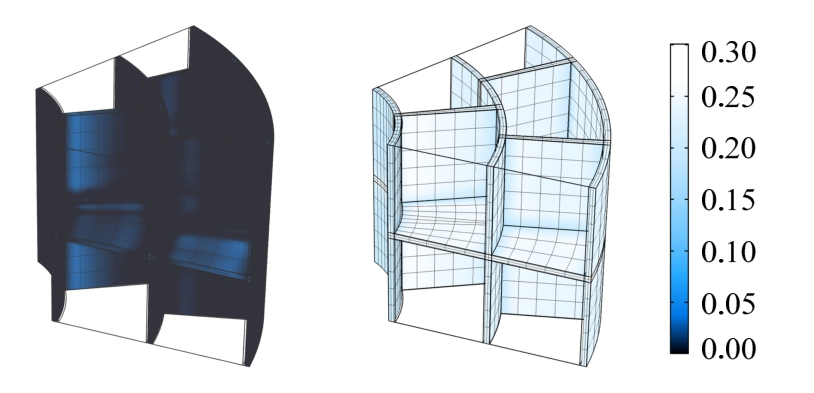
图7 t=360 d接缝塑性应变和总应变分布
Fig.7 Joint’s plastic and total strain distribution at 360 d
3)饱和度和渗透率的演化规律
由图5可知，接缝的存在会显著加速砌块的饱和过程，结合图8推断主要原因有两方面：① 接缝的渗透率远高于砌块，形成水力通道；② 砌块膨胀后孔隙率增大，渗透系数升高。缓冲材料最重要的作用之一就是阻止污染物的渗透，因此认为接缝愈合的主要特征为接缝与砌块的渗透率相差小于一个数量级，即Kintj＜10Kintb，或根据式(10)换算得到干密度相差小于0.167。
图8中无标记的虚线和实线分别代表r=0.2 m和r=0.4处环形截面的平均渗透率，可以看出尽管砌块的渗透率会有所增大，但是由于接缝的渗透率从初始的8.0×10-18 m2，降低到愈合后的5.0×10-20 m2左右，整体的平均渗透率从10-18 m2量级降低到10-20 m2，且外层接缝先于内层愈合。有试验表明［27］，对于微小粒径的污染物，其迁移速率几乎正比于渗流速度，也就是说尽管缓冲材料内存在不均匀性，但可近似的认为污染物整体扩散的速度正比于环向截面的平均渗透率。
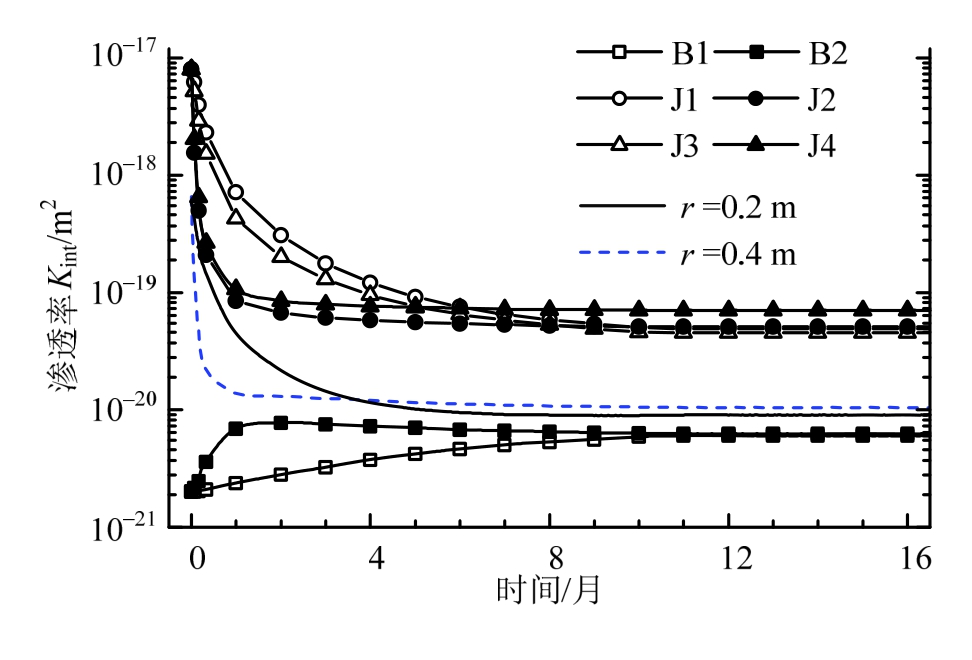
图8 渗透率随时间的演化规律
Fig.8 Evaluation of permeability with time
图9中箭头表示渗流速度的矢量，箭头长短与流速大小的对数成正比，可以看到接缝中的流速远大于砌块，且随着时间推移，渗流速度明显降低。
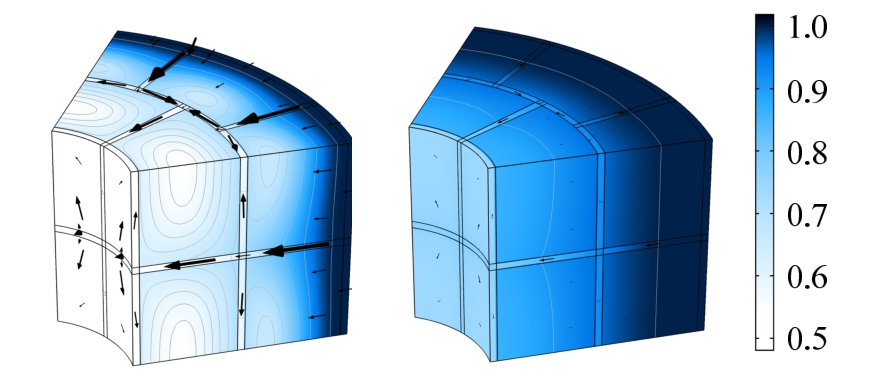
图9 t=30 d和t=180 d饱和度分布
Fig.9 Saturation distribution at 30 d and 180 d
表3 导热系数随时间的演化规律 /( W/(m℃)
Table 3 Evaluation of heat conductivity with time
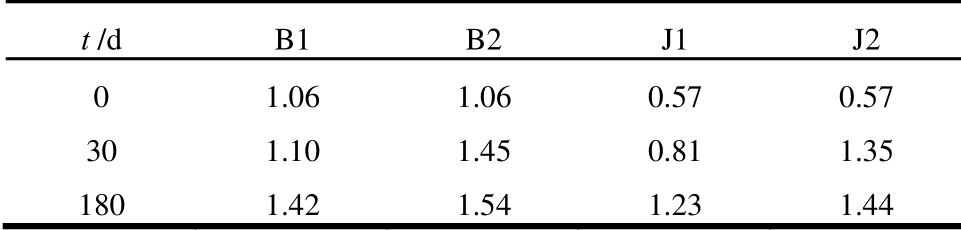
t /d B1 B2 J1 J2 0 1.06 1.06 0.57 0.57 30 1.10 1.45 0.81 1.35 180 1.42 1.54 1.23 1.44
4)温度的演化规律
图10中箭头表示热通量的矢量，箭头长短与热通量大小的对数成正比，由图可知，虽然接缝的导热系数要略小于砌块，但是对整体的温度分布并未造成显著影响。由表3可知，随着饱和度的升高，砌块和接缝的热传导系数均有一定的提升，接缝的导热系数升高较为显著，在180 d时已经和砌块接近，整体能够达到国际原子能机构建议的大于1 W/m· ℃的要求。
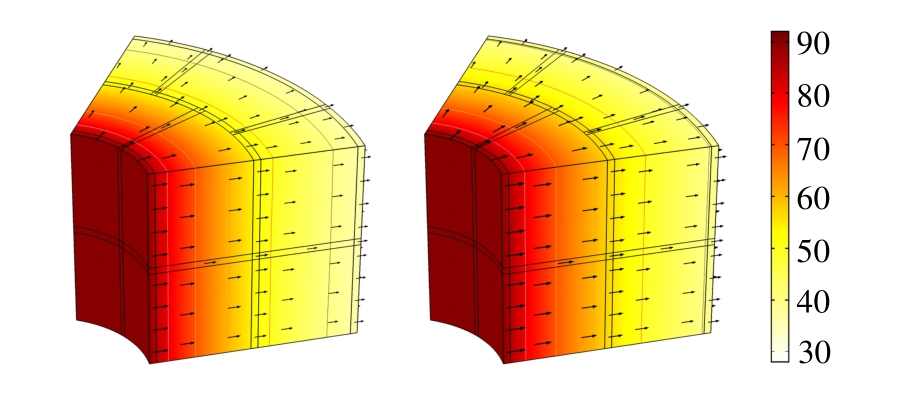
图10 t=30 d和t=180 d温度分布 /(℃)
Fig.10 Temperature distribution at 30 d and 180 d
4.2 接缝对渗流过程的影响
由上文的分析可知接缝的存在对缓冲材料整体的渗透率有较大的影响，而渗透率是影响污染物迁移速率的关键因素。膨润土产生的膨胀力、干密度以及相关物性参数的变化，均与饱和度的变化密切相关，因此需要研究接缝对渗流过程的影响。
1)接缝类型的影响
如图4(a)所示，在缓冲材料中有环向、径向和横向3种类型的接缝存在，为比较不同类型接缝对渗流的影响，保持缓冲材料整体尺寸不变，分别计算只有某一种接缝的模型，如图11所示。环向a接缝宽度10 mm，环向b接缝宽度5 mm，径向接缝角度2°，横向接缝宽度10 mm。
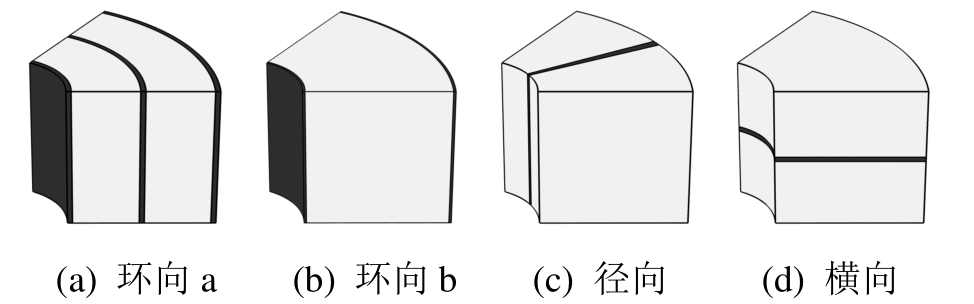
图11 分别只含环向、径向、横向接缝的计算模型
Fig.11 Models contain circumferential, radial, lateral joints respectively
表4 不同接缝形式对渗流的影响
Table 4 Influence of joints form on Seepage
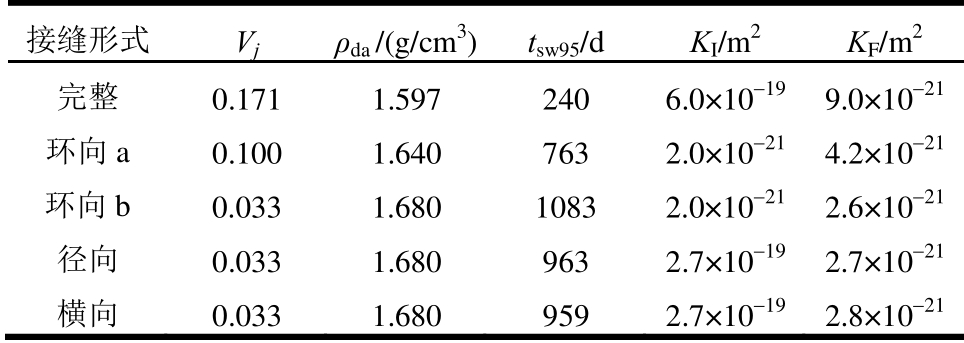
注：“完整”指4.1节所计算模型，含有全部类型的接缝。
接缝形式 Vjρda/(g/cm3) tsw95/d KI/m2 KF/m2 完整 0.171 1.597 240 6.0×10-19 9.0×10-21环向a 0.100 1.640 763 2.0×10-21 4.2×10-21环向b 0.033 1.680 1083 2.0×10-21 2.6×10-21径向 0.033 1.680 963 2.7×10-19 2.7×10-21横向 0.033 1.680 959 2.7×10-19 2.8×10-21
表4中，Vj表示接缝体积比缓冲材料总体积，ρda为缓冲材料平均干密度，由接缝和砌块的干密度体积加权平均得到。tsw95表示r=0.2 m砌块中心点饱和度到达95%所需的时间，KI和KF分别表示初始状态和完全饱和后r=0.2 m处截面的平均渗透率，tsw95和KF可以反映砌块整体的渗透性能。应当注意，渗流计算中由于方程和参数的选定均由室内试验得到，而现场地下水的情况复杂，tsw95的计算结果与现场试验会存在区别，但是可以作为横向比较指标。由图12可知，环向接缝的主要作用是给砌块膨胀提供空间，使砌块的干密度降低，进而渗透率升高；径向和横向接缝都法向于罐体表面，在给砌块提供膨胀空间的同时，还能起到水力通道的作用。因此相同体积比的情况下，法向接缝对渗流的影响大于环向接缝。
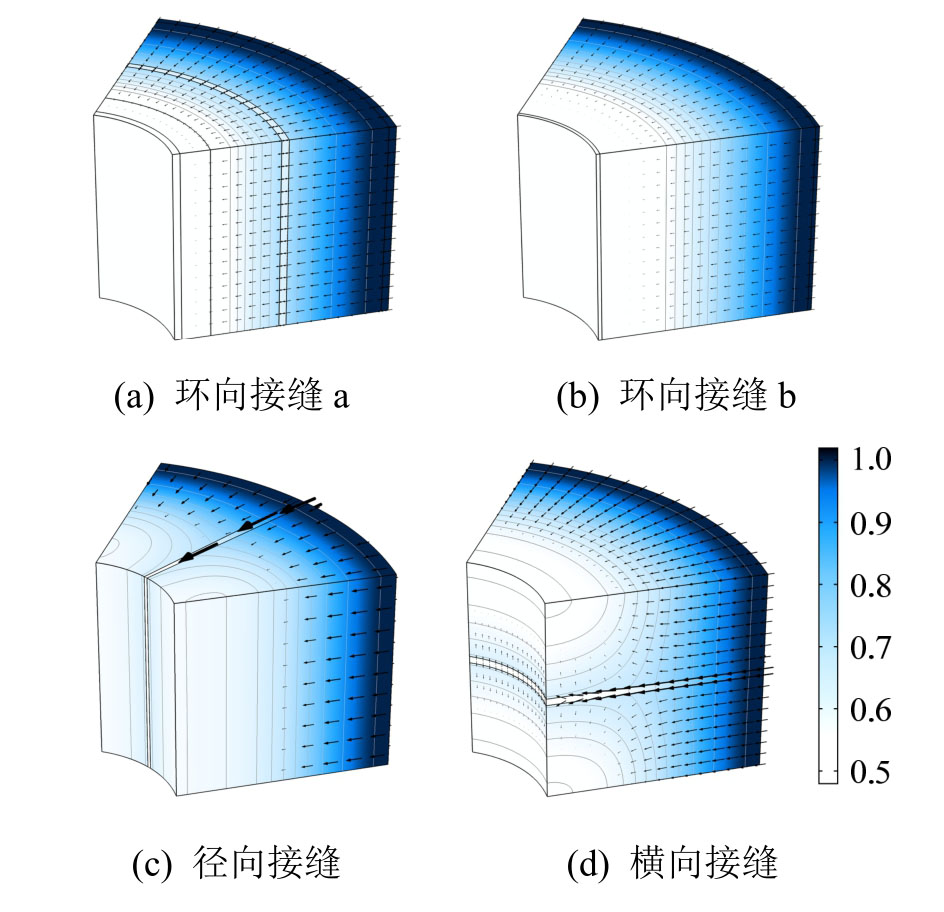
图12 不同接缝类型t=180 d饱和度分布
Fig.12 Saturation distribution at t=180 d with different joints
2)径向接缝数量的影响
考虑到在实际工程中，砌块与罐体、围岩间的环向接缝不可避免，因此本节计算中环向接缝宽10 mm不变，只改变径向接缝的数量，不考虑横向接缝。径向接缝的角度φj=2°，以圆柱体轴心为中心均匀分布，如图13所示，计算结果见表5。可知尽 管接缝都满足了愈合的标准，但随着接缝数量的增加，接缝干密度降低，平均渗透率升高。为保证材料的阻隔性能，应尽量减少径向接缝的数量。
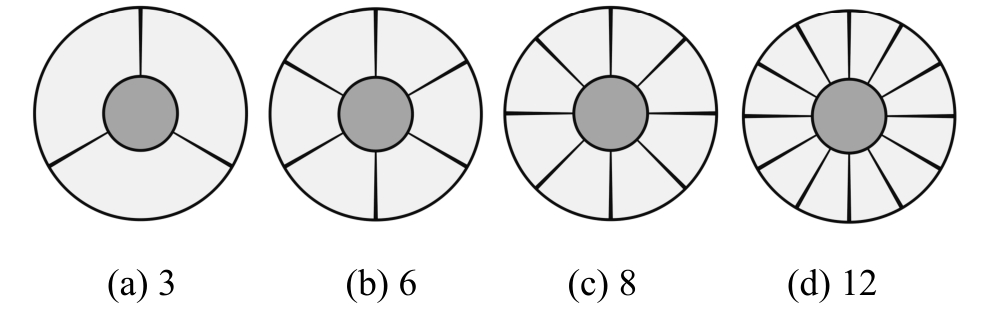
图13 不同径向接缝数量的模型
Fig.13 Models with different number of radial joints
表5 径向接缝数量对渗流的影响
Table 5 Influence of radial joints number on seepage
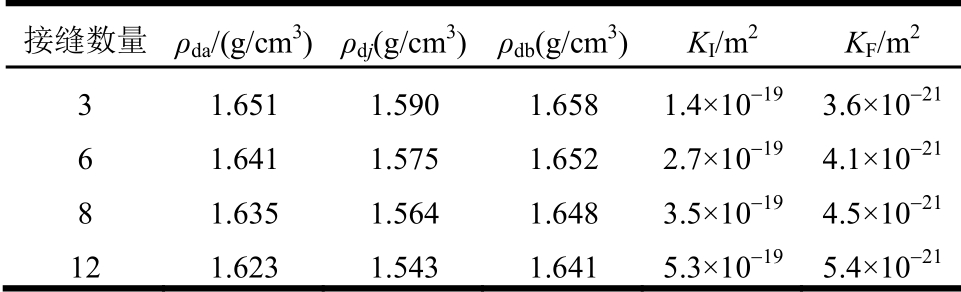
注：ρdj、ρdb分别为饱和后r=0.2 m处接缝和砌块的干密度。
接缝数量 ρda/(g/cm3)ρdj(g/cm3)ρdb(g/cm3) KI/m2 KF/m2 3 1.651 1.590 1.658 1.4×10-19 3.6×10-21 6 1.641 1.575 1.652 2.7×10-19 4.1×10-21 8 1.635 1.564 1.648 3.5×10-19 4.5×10-21 12 1.623 1.543 1.641 5.3×10-19 5.4×10-21
3)径向接缝宽度的影响
本节计算模型同图13(b)，接缝数量和环向接缝宽度不变，改变径向接缝的角度φj以研究径向接缝宽度的影响，结果见表6，结合表5可知径向接缝的宽度对渗流的影响与接缝数量类似，随着接缝宽度的增加，接缝的最终干密度降低，平均渗透率升高，施工中要注意控制精度，接缝不宜过宽。
表6 径向接缝宽度对渗流的影响
Table 6 Influence of radial joints width on seepage
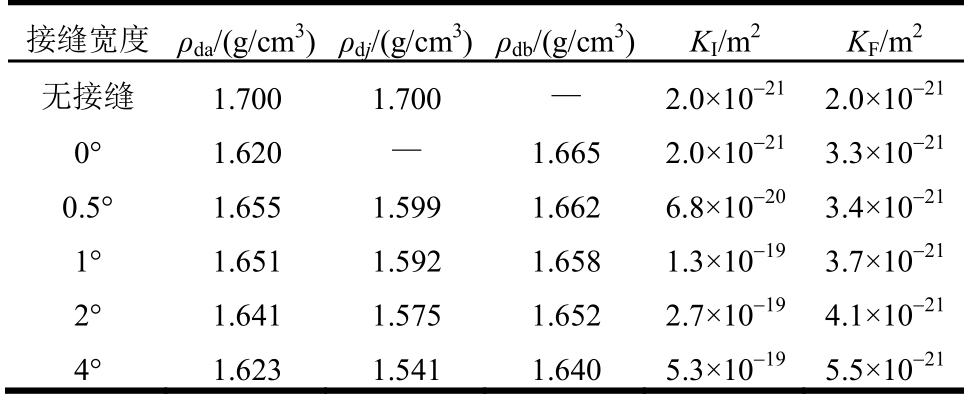
接缝宽度 ρda/(g/cm3)ρdj/(g/cm3)ρdb/(g/cm3) KI/m2 KF/m2无接缝 1.700 1.700 — 2.0×10-21 2.0×10-21 0° 1.620 — 1.665 2.0×10-21 3.3×10-21 0.5° 1.655 1.599 1.662 6.8×10-20 3.4×10-21 1° 1.651 1.592 1.658 1.3×10-19 3.7×10-21 2° 1.641 1.575 1.652 2.7×10-19 4.1×10-21 4° 1.623 1.541 1.640 5.3×10-19 5.5×10-21
4)砌块拼接形式的影响
内层和外层径向接缝的平均宽度均为10 mm，交错a和对齐a的布置参考FEBEX项目[28]的方案，交错b和对齐b为笔者设计，示意图见图14。因为横向接缝的影响与径向接缝类似，本节计算不考虑横向接缝，计算结果见表7。
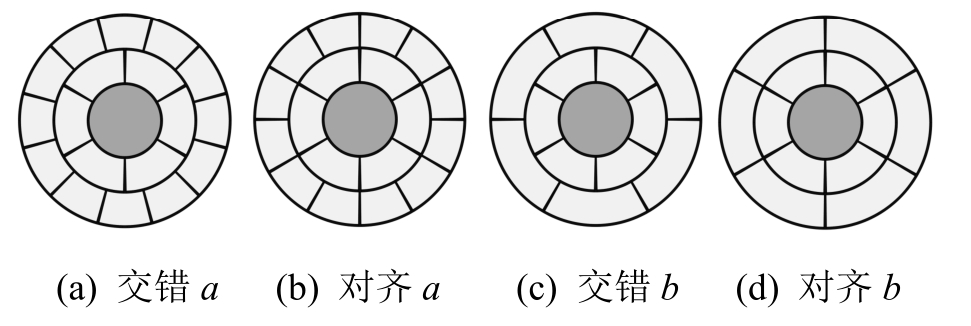
图14 不同砌块拼接形式模型
Fig.14 Models of different blocks splicing forms
表7 砌块拼接形式对渗流的影响
Table 7 Influence of blocks splicing form on seepage
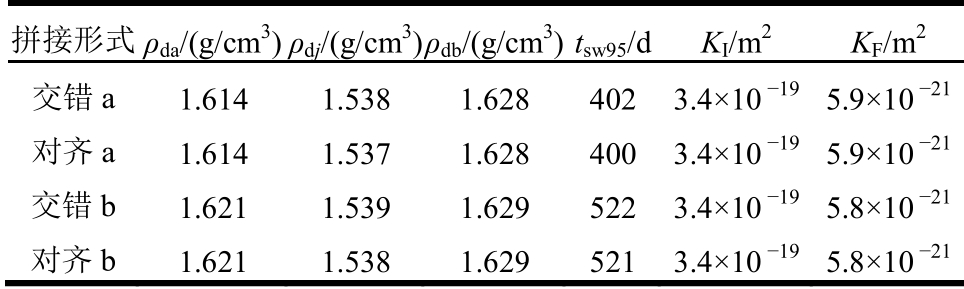
拼接形式ρda/(g/cm3)ρdj/(g/cm3)ρdb/(g/cm3)tsw95/d KI/m2 KF/m2交错a 1.614 1.538 1.628 402 3.4×10 -195.9×10 -21对齐a 1.614 1.537 1.628 400 3.4×10 -19 5.9×10 -21交错b 1.621 1.539 1.629 522 3.4×10 -19 5.8×10 -21对齐b 1.621 1.538 1.629 521 3.4×10 -19 5.8×10 -21
分析表7的数据发现，外层接缝是否与内层接缝对齐对整体的渗流几乎没有影响，分析可能是因为接缝的愈合效应使缓冲层整体均匀性得到了改善，从而接缝的水力通道效应得以减弱。
5)接缝和砌块干密度的影响
本节计算模型同图13(b)，保持接缝数量和宽度不变，改变砌块和接缝材料的干密度。材料主要的参数对比见表8，其余参数通过对应的公式计算得到。
表8 材料主要计算参数对比
Table 8 Comparison of materials’ main parameters
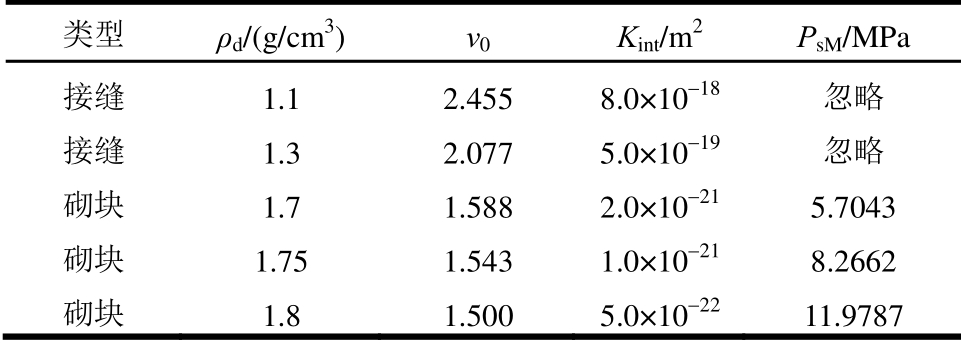
类型 ρd/(g/cm3) v0Kint/m2 PsM/MPa 接缝 1.1 2.455 8.0×10-18 忽略 接缝 1.3 2.077 5.0×10-19 忽略 砌块 1.7 1.588 2.0×10-21 5.7043 砌块 1.75 1.543 1.0×10-21 8.2662 砌块 1.8 1.500 5.0×10-22 11.9787
由表9知，因为接缝的渗透率远大于砌块，接缝干密度对缓冲层的初始平均渗透率KI起决定性作用，随着接缝的愈合，完全饱和后的平均渗透率KF主要由砌块的干密度决定。分析其原因，可能是因为干密度较高的砌块会产生更大的膨胀力，将接缝材料挤压的更为密实，整体的渗透率也因此得到极大的降低。因此增大砌块的干密度可以显著增强缓冲层的防渗性能。
表9 材料干密度对渗流的影响
Table 9 Influence of materials dry density on seepage
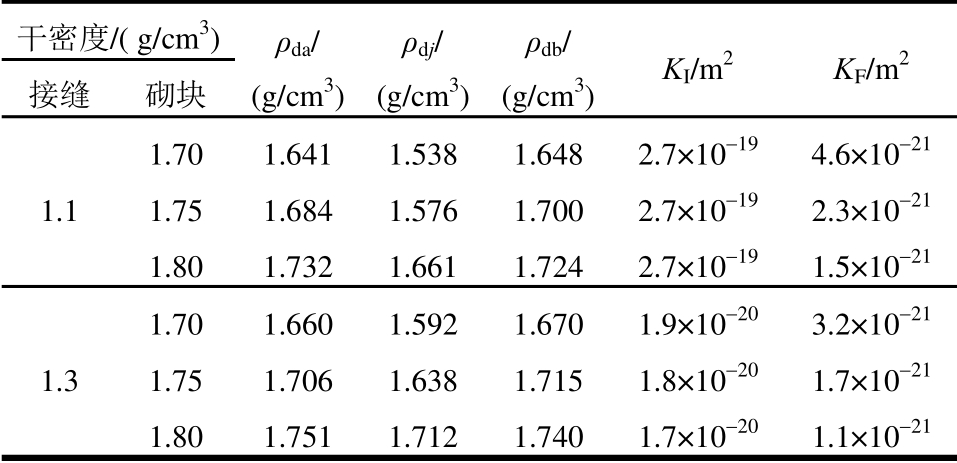
干密度/( g/cm3) ρda/ (g/cm3)ρdj/ (g/cm3)ρdb/ (g/cm3) KI/m2 KF/m2 接缝 砌块 1.1 1.70 1.641 1.538 1.648 2.7×10-19 4.6×10-21 1.75 1.684 1.576 1.700 2.7×10-19 2.3×10-21 1.80 1.732 1.661 1.724 2.7×10-19 1.5×10-21 1.3 1.70 1.660 1.592 1.670 1.9×10-20 3.2×10-21 1.75 1.706 1.638 1.715 1.8×10-20 1.7×10-21 1.80 1.751 1.712 1.740 1.7×10-20 1.1×10-21
结合4.2节中各表的数据，将平均干密度ρda与平均渗透率KF进行回归，得到ρda与KF的拟合关系式：
拟合曲线如图15所示，确定系数R2=0.9739。可知在多种接缝同时存在的情况下，最终平均渗透 率和平均干密度近似成指数关系，平均干密度越高平均渗透率越低，与已有试验结果的规律相似[3]。
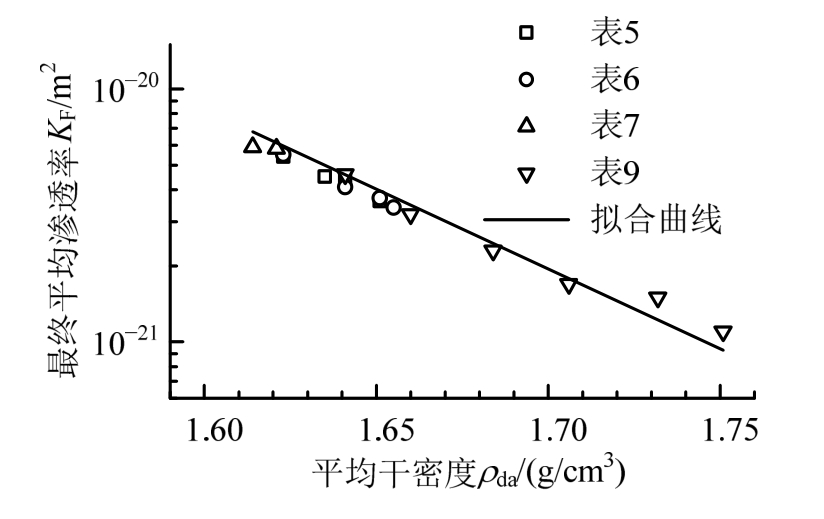
图15 最终平均渗透率与平均干密度的关系
Fig.15 Relationship between final permeability and average dry density of buffer material
4.3 材料干密度对应力应变的影响
本节计算模型同图13(b)，参数见表8，分析了材料干密度对接缝的体应变，大、小主应力和粘聚力的影响。
工程屏障的产生剪切破坏最可能的原因就是地震，接缝极有可能成为破坏过程中的薄弱环节，较好的粘聚力可以保证缓冲材料的整体性。干密度为1.1 g/cm3和1.3 g/cm3的接缝材料初始粘聚力分别为0.15 g/cm3和0.27 MPa，经历了愈合过程之后，接缝的粘聚力有了显著的提升，缓冲层的整体强度也因此提高。
由表10可知，膨胀力与砌块干密度有关，在处置库的设计中，需要足够的膨胀力使接缝愈合，并利用接缝材料产生的塑性变形修复砌块与围岩间的缝隙[1]，增强整体的密封性能，而且要满足抑制微生物生长的要求，但过高的膨胀力会导致缓冲材料刚度过大，在地震时起不到缓冲的作用，甚至会造成废物罐的开裂，引起更大的泄漏，国际原子能机构[22]的建议是膨胀产生的应力在2 MPa～ 10 MPa之间。而干密度1.8 g/cm3的砌块产生的大主应力高达12.3 MPa，由此可见砌块的干密度不宜过大。
表10 材料干密度对应力和粘聚力的影响
Table 10 Influence of materials dry density on stress and cohesion
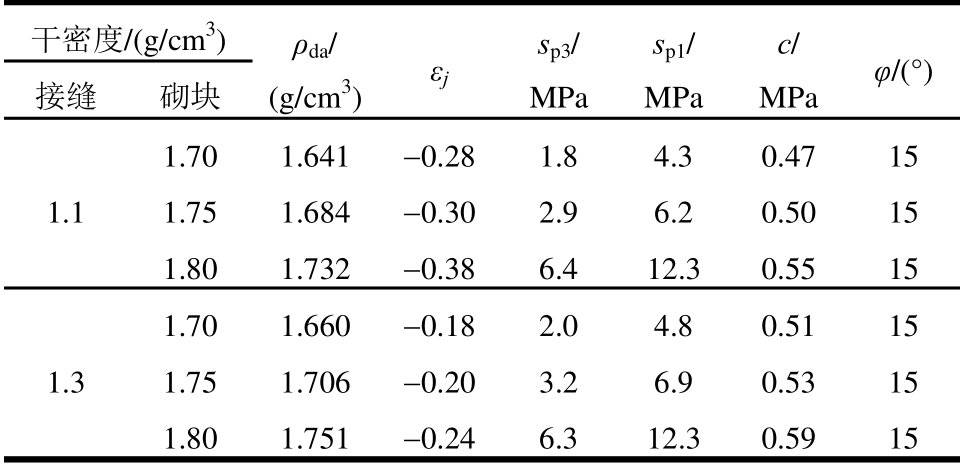
干密度/(g/cm3) ρda/ (g/cm3) εjsp3/ MPa sp1/ MPa c/ MPa φ/(°)接缝 砌块 1.1 1.70 1.641 -0.28 1.8 4.3 0.47 15 1.75 1.684 -0.30 2.9 6.2 0.50 15 1.80 1.732 -0.38 6.4 12.3 0.55 15 1.3 1.70 1.660 -0.18 2.0 4.8 0.51 15 1.75 1.706 -0.20 3.2 6.9 0.53 15 1.80 1.751 -0.24 6.3 12.3 0.59 15
5 结论
本文利用多场耦合软件对缓冲材料的水化过程进行了数值模拟，重点分析了不同的接缝参数和拼接形式对渗流过程的影响，得到以下结论：
(1)缓冲材料中接缝的存在对计算结果有较大影响，会使缓冲材料整体渗透性显著提高，膨胀应力有所降低，但对导热性能的影响较小。
(2)膨润土具有高膨胀性，饱和过程中接缝会出现愈合效应，即接缝材料的干密度升高，与此同时砌块的干密度会稍有降低，缓冲材料的均匀性得到改善，平均渗透率较愈合前显著降低，约为两个数量级。
(3)径向和横向接缝的存在对缓冲材料的渗透性能影响尤为显著，在设计时要尽量避免此类接缝的存在。
(4)砌块和接缝的干密度决定了缓冲材料最终平均渗透率，整体的平均干密度和平均渗透率呈指数关系，而在平均干密度相同的情况下，砌块的拼接形式对整体渗透性影响不大。
(5)增大材料干密度可以增加整体的抗剪强度，同时也会增大膨胀应力，为保证废物罐的安全，砌块的干密度不宜过大。
研究展望：缓冲材料工作性能的时间效应，接缝对处置库抗震性能的影响，核素在处置库中的扩散规律等诸多问题，应当在今后的研究中加以 考虑。
[1]牛文杰, 叶为民, 陈宝.高压实膨润土的非饱和渗透膨胀模型 [J].岩土力学, 2009, 30(增2): 88—92. Niu Wenjie, Ye Weimin, Chen Bao.Experimentally derived model for suction-induced permeability, swell and microstructure behaviour of unsaturated compacted bentonite [J].Rock and Soil Mechanics, 2009, 30(Suppl 2): 88—92.(in Chinese)
[2]Bai Bing, Shi Xiaoying.Experimental study on the consolidation of saturated silty clay subjected to cyclic thermal loading [J].Geomechanics and Engineering, 2017, 12(4): 707—721.
[3]陈宝, 陈建琴, 曹永超.接缝对高压实膨润土工程屏障自封闭性能的影响 [J].岩石力学与工程学报, 2012, 31(3): 618—624. Chen Bao, Chen Jianqin, CAO Yongchao.Influence of joint on self-sealing behaviour of highly compacted bentonite in engineering barrier [J].Chinses Journal of Rock Mechanics and Engineering, 2012, 31(3): 618—624.(in Chinese)
[4]Ferrari A, Seiphoori A, Rüedi J, et al.Shot-clay MX-80 bentonite: An assessment of the hydro-mechanical behaviour [J].Engineering Geology, 2014, 173(2): 10—18.
[5]Chen L, Liu Y M, Wang J, et al.Investigation of the thermal-hydro-mechanical (THM)behavior of GMZ bentonite in the China-Mock-up test [J].Engineering Geology, 2014, 172(8): 57—68.
[6]Zhang H, Wang X, Ping L, et al.Sealing and healing of compacted bentonite block joints in HLW disposal [J].Chinese Journal of Rock Mechanics & Engineering, 2016.35(Suppl 2): 3605—3614
[7]Chen L, Wang J, Liu Y, et al.Numerical thermo-hydro-mechanical modeling of compacted bentonite in china-mock-up test for deep geological disposal [J].Journal of Rock Mechanics and Geotechnical Engineering, 2012, 4(2): 183—192.
[8]Zhao J, Chen L, Collin F, et al.Numerical modeling of coupled thermal-hydro-mechanical behavior of GMZ bentonite in the China-Mock-up test [J].Engineering Geology, 2016, 214(30): 116—126.
[9]Bai B.Fluctuation responses of saturated porous media subjected to cyclic thermal loading [J].Computers & Geotechnics, 2006, 33(8): 396—403.
[10]Bai Bing, Rao Dengyu, Xu Tao, et al.SPH-FDM boundary for the analysis of thermal process in homogeneous media with a discontinuous interface [J].International Journal of Heat and Mass Transfer, 2018,117: 517—526.
[11]刘月妙, 蔡美峰, 王驹, 高放废物处置库缓冲材料导热性能研究[J].岩石力学与工程学报, 2007, 26(增2): 3891—3896. Liu Yuemiao, Cai Meifeng, Wang Ju.Thermal properties of buffer material for high-level radioactive waste disposal [J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 2): 3891—3896.(in Chinese)
[12]Richards L A.Capillary conduction of liquids in porous mediums [J].Physics, 1931, 1(5): 318—333.
[13]Ye W M, Cui Y J, Qian L X, et al.An experimental study of the water transfer through confined compacted GMZ bentonite [J].Engineering Geology, 2009, 108(3-4): 169—176.
[14]Lloret A, Villar M V.Advances on the knowledge of the thermo-hydro-mechanical behavior of heavily compacted FEBEX bentonite [J].Physics and Chemistry of the Earth, Parts A/B/C, 2007, 32(8): 701—715
[15]蔡国庆, 赵成刚, 刘艳.非饱和土土-水特征曲线的温度效应 [J].岩土力学, 2010, 31(4): 1055—1060. Cai Guoqing, Zhao Chenggang, Liu Yan.Temperature effects on soil-water characteristic curve of unsaturated soils [J].Rock and Soil Mechanics, 2010, 31(4): 1055—1060.(in Chinese)
[16]van Genuchten.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J].Soil Science Society of America Journal, 1980, 44(44): 892—898.
[17]Chen B, Qian L, Ye W.et al.Soil-water characteristic curves of Gaomiaozi bentonite [J].Chinese Journal of Rock Mechanics and Engineering, 2006.25(4): 788—793.
[18]叶为民, T.Schanz, 钱丽鑫,等.高压实高庙子膨润土GMZ01的膨胀力特征 [J].岩石力学与工程学报, 2007, 26(增2): 3861—3865. Ye Weimin, T.Schanz, Qian Lixin, et al.Characteristics of welling pressure of densely compacted Gaomiaozi bentonite GMZ01 [J].Chinses Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 2): 3861—3865.(in Chinese)
[19]Alonso E E, Vaunat J, Gens A.Modelling the mechanical behaviour of expansive clays [J].Engineering Geology, 1999, 54(1/2): 173—183.
[20]Alonso E E, Gens A, Josa A.A constitutive model for partially saturated soils [J].Géotechnique, 1990, 40(3): 405—430.
[21]Mckinstry H A.Thermal expansion of clay minerals[J].American Mineralogist, 1965, 50: 212—222.
[22]刘月妙, 蔡美峰, 王驹,等.高放废物地质处置库预选缓冲材料压缩性能研究[J].铀矿地质, 2007, 23(2): 91—95. Liu Yuemiao, Cai Meifeng, Wang Ju, et al.Compressibility of buffer material for HLW disposal in China [J].Uranium Geology, 2007, 23(2): 91—95.(in Chinese)
[23]Bolzon G, Schrefler B A, Zienkiewicz O C.Elastoplastic soil constitutive laws generalized to partially saturated states[J].Géotechnique, 1996, 46(2): 279—289.
[24]张发忠, 方振东, 秦冰, 等.不同温度下膨润土膨胀变形行为研究[J].后勤工程学院学报, 2017, 33(2): 23—27. Zhang Fazhong, Fang Zhendong, Qin Bing, et al.Study on bentonite’s swelling strain behaviour at different temperatures [J].Journal of Logistical Engineering University, 2017, 33(2): 23—27.(in Chinese)
[25]陈皓.高放废物地质库缓冲材料在高温高压下的变形强度特性研究[D].广西: 广西大学, 2015. Chen Hao.Research of strength and volume change of buffer material in high temperature and pressure from high-level radioactive waste repository [D].Guangxi: Guangxi University, 2015.(in Chinese)
[26]Reijonen H M, Alexander W R, Marcos N, et al.Complementary considerations in the safety case for the deep repository at Olkiluoto, Finland: support from natural analogues [J].Swiss Journal of Geosciences, 2015, 108(1): 111—120.
[27]Bai B, Xu T, Guo Z.An experimental and theoretical study of the seepage migration of suspended particles with different sizes [J].Hydrogeology Journal, 2016, 24(8): 1—16.
[28]Villar M V, Lloret A.Dismantling of the first section of the FEBEX in situ, test: THM laboratory tests on the bentonite blocks retrieved [J].Physics & Chemistry of the Earth, 2007, 32(8): 716—729.