超高性能混凝土(Ultra High Performance Concrete，UHPC)是一种具有超高强度、高韧性、高耐久性和高抗冲击性能的新型水泥基复合材料。掺加一种大掺量短钢纤维(纤维体积掺量为2%～6%)的UHPC[1]，能有效地提高材料受拉强度、延性[2]和与钢筋的黏结性能[3]，自然养护条件下其抗压强度为120 MPa～160 MPa，抗拉强度为6 MPa～ 15 MPa，与钢筋的黏结强度为26 MPa～87 MPa。由于大掺量纤维创造了材料局部延性断裂区域，与钢筋混凝土结构相比，在UHPC结构中，配筋率可以非常高，达10%到20%。因此，这种UHPC可用于重载结构(超高层建筑结构的底部等)、大跨结构(如大跨度桥梁等)、抗震[4]、抗爆[5]和抗冲击结构等。
目前，国内外对UHPC的研究多集中于材料性能方面，对构件受力性能方面的研究相对有限。Yoo等[6]设计了4种玻璃纤维筋UHPC梁，研究在不同玻璃纤维筋配筋率下梁的抗弯性能，通过试验研究及理论分析建立了玻璃纤维筋UHPC梁的挠度计算公式。杨剑[7]通过6根碳纤维增强塑料(CFRP)预应力筋活性粉末混凝土(RPC)梁试验，研究梁的跨中极限变形，探讨梁的裂缝分布及其发展。邓宗才等[8]使用高强钢筋替换普通钢筋，研究配筋率、截面形式对梁抗弯性能的影响规律。Singh等[9]通过有限元数值模拟，对钢纤维掺量为2.25%的UHPC配筋梁进行非线性分析，经试验值与模拟值比较发现，混凝土塑性损伤(CDP)模型能很好地预测UHPC梁的承载力。
上述研究中，UHPC材料中的钢纤维体积掺量为2%左右，对于大掺量钢纤维UHPC对梁受弯能力的影响缺乏研究。Kaptijn等[10]将这种大掺量纤维UHPC用于桥面板，板厚仅45 mm，配置3层钢筋，板中间配筋率为5.6%，板边缘配筋率为10%，有效地减轻了桥面板的自重。
为了减小大跨高比梁的自重并提高其受弯承载力，本文选取3%、5%两种纤维体积掺量配制UHPC，并配置高强钢筋；为验证规范[11]关于普通钢筋混凝土适筋梁的界限配筋率是否适用于配筋UHPC梁，设计制作了跨高比均为16的2根适筋梁及2根超筋梁，对其进行两点对称静力加载试验，观察梁的破坏形态；分析钢纤维体积掺量、纵筋配筋率对梁抗裂性能、裂缝开展、承载能力等性能的影响；通过截面分析建立高强钢筋UHPC梁正截面受弯承载力计算模型。
1 试验概况
1.1 试验材料与构件设计
试验材料采用水泥、硅灰、石英砂、钢纤维等，其配合比见表1。钢纤维平均长度为7.2 mm，长径比为43，抗拉强度大于2850 MPa。水泥基材料的搅拌过程为：先将不同粒径的石英砂放入搅拌机中，干拌1 min；加入水泥和硅灰，继续干拌2 min，使各个材料分散均匀；加入水和减水剂，搅拌7 min；最后边搅拌边加入钢纤维，并持续搅拌5 min。
表1 UHPC的配合比
Table 1 Mix proportions of UHPC
水泥 水 硅灰 石英砂 减水剂 钢纤维/(%)1.00 0.23 0.26 1.26 0.03 3/5
由于UHPC不含粗骨料，其成分类似于活性粉末混凝土(RPC)，故根据RPC规程[12]，其立方体试块尺寸选用100 mm×100 mm×100 mm；棱柱体试块尺寸为100 mm×100 mm×300 mm；轴心抗拉试件为狗骨形试件，尺寸如图1所示。试验测定的UHPC基本力学性能见表2。梁纵筋采用HRB500，箍筋和架立筋均采用HRB400，其实测力学性能指标见表3，其中弹性模量按规范[11]取值。
图1 狗骨形受拉试件尺寸
Fig.1 Details of axial tension specimen
表2 UHPC力学性能
Table 2 Mechanical properties of UHPC
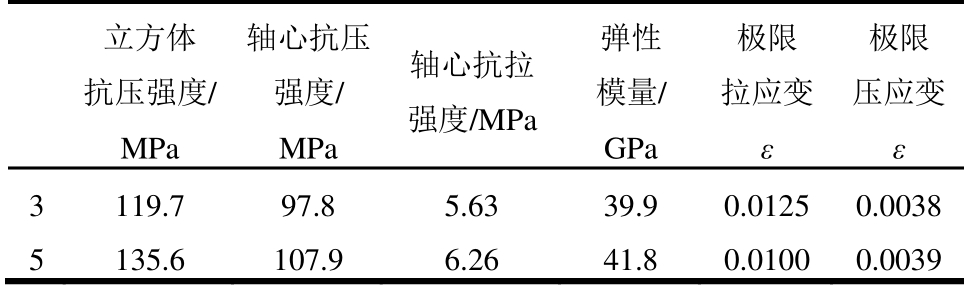
立方体 抗压强度/ MPa 轴心抗压强度/ MPa 轴心抗拉 强度/MPa 弹性 模量/ GPa 极限 拉应变ε 极限 压应变ε 3 119.7 97.8 5.63 39.9 0.0125 0.0038 5 135.6 107.9 6.26 41.8 0.0100 0.0039
表3 钢筋力学性能
Table 3 Mechanical properties of reinforcement
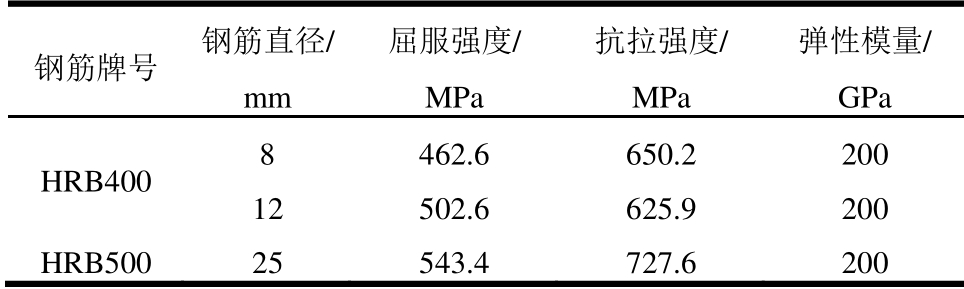
钢筋牌号 钢筋直径/ mm 屈服强度/ MPa 抗拉强度/ MPa 弹性模量/ GPa HRB400 8 462.6 650.2 200 12 502.6 625.9 200 HRB500 25 543.4 727.6 200
4根UHPC梁的截面尺寸均为170 mm×300 mm，计算跨度为4.8 m，跨高比为16。模型缩尺比例为1/2。为消除剪力对梁受弯性能影响，试件中有一段长度为1.6 m的纯弯段，段内不设箍筋；同时为消除架立筋充当受压钢筋的影响，纯弯段内无架立筋。为了防止试验梁发生剪切破坏，在剪跨区配置足够多的抗剪箍筋。4根梁的截面、构造和配筋见图2所示，混凝土保护层厚度为10 mm。图中尺寸的单位均为mm，试验梁截面信息如表4所示。
表4 试验梁截面信息
Table 4 Member section of specimens
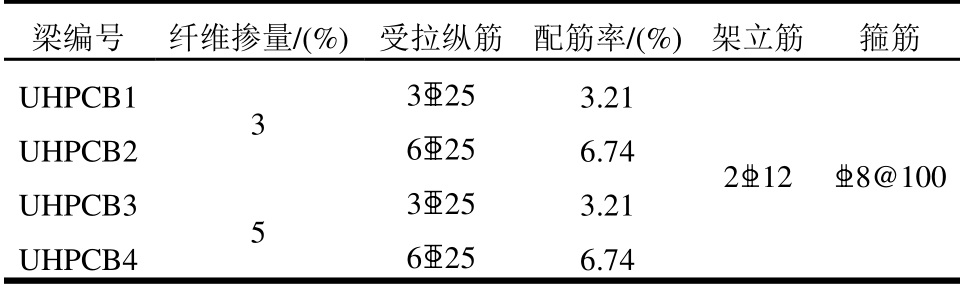
梁编号 纤维掺量/(%) 受拉纵筋 配筋率/(%)架立筋 箍筋 UHPCB1 3 3■25 3.21 2■12 ■8@100 UHPCB2 6■25 6.74 UHPCB3 5 3■25 3.21 UHPCB4 6■25 6.74
1.2 试件制作及养护
试件制备主要过程为：UHPC制备→浇筑试 件→静置并自然养护7 d→拆模→自然养护至试验，自然养护过程中应使试件保持湿润，进行足够的水化反应。
图2 试件尺寸及配筋
Fig.2 Dimension and reinforcement details of specimens
1.3 加载装置及加载制度
试验在西安建筑科技大学结构工程与抗震教育部重点试验室进行，静力加载装置见图3所示，试验全貌见图4。
加载试验参照《混凝土结构试验方法标准》[13] (GB/T 50152—2012)进行，试验开始前进行预加载以检验装置和仪表仪器是否正常工作。预加载值不超过试验梁预估承载力的5%(小于试验梁的开裂荷载)，确定各个设备工作正常后卸载，并开始正式加载。试验采用分级加载，加载到达试验梁预估开裂荷载80%之前，每级加载值为极限荷载预估值的5%；接近开裂荷载时每级加载值不超过5 kN。当试验梁开裂后，每级加载值为试验梁极限荷载预估值的10%，接近极限荷载时，缓慢加载直至梁破坏。每级持荷时间10 min～15 min。在加载过程中采用TDS-530静态数据采集仪采集应变及位移数据；在 持荷阶段，用强光手电查找裂缝，采用裂缝对比卡比对裂缝宽度，记录试验现象。
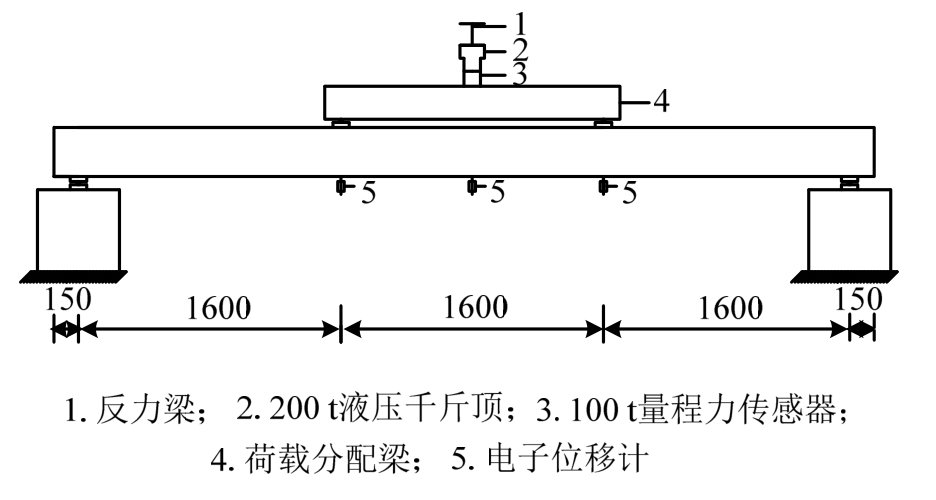
图3 试验装置示意图
Fig.3 Sketch of test device
图4 试验全貌
Fig.4 Photo of test
1.4 测试内容及方法
主要测试内容及方法有：1)在梁跨中及加载点位置布置位移计(图3)，测试其挠度。2)沿梁截面高度布置位移计(图5)，将位移计测得的两点距离变化量与两点原距离之比值作为两点所在高度处的平均应变；梁跨中底部粘贴混凝土应变片，测试其受拉应变。3)在梁底部跨中受拉钢筋上粘贴应变片，测试纵向受拉钢筋应变。4)为了能有效观察记录裂缝，试验梁两侧涂抹白灰并绘制网格，通过网格线观察裂缝发展形态及位置，通过裂缝对比卡，记录各级荷载下的裂缝宽度，在试验梁上绘出裂缝分布与开展情况。5)录试验梁的开裂荷载、极限荷载，观察试验现象和破坏形态。
图5 位移计布置图
Fig.5 The displacement meters setting
2 试验现象
4根试验梁纯弯区段的最终破坏形态及裂缝开展情况如图6所示。
图6 梁纯弯段破坏形态及裂缝分布图
Fig.6 Crack patterns of specimens at failure
2.1 破坏形态
试件UHPCB1、UHPCB3纵向受拉钢筋先屈服，受拉区竖向裂缝向上延伸开展，中性轴位置逐渐上升，受压区高度降低，最终受压区UHPC被压酥起皮，梁宣告破坏，破坏形态为适筋破坏。
试件UHPCB2、UHPCB4达到极限荷载时，第一排受拉钢筋应变均达到屈服应变，表明钢筋已屈服，第二排受拉钢筋未屈服但接近屈服(图8(b)、图8(d))，受压区混凝土受挤压破溃，梁宣告破坏，破坏形态为部分超筋破坏。部分超筋破坏梁纯弯段区出现由加载点向下延伸的斜裂缝(见图6(d))，这是因为加载至极限荷载时，加载点附近UHPC在集中荷载作用下产生压应力集中场(加载点处的集中力向下扩散形成向下的压力流，类似于楼盖结构中次梁与主梁相交处主梁产生的斜裂缝)，使纯弯区段产生较大的剪力，对于大跨高比梁，纯弯区段的受剪截面相对较小，又无抵抗竖向剪力的箍筋，故产生斜裂缝。这是大跨高比受弯试验梁(纯弯段不配箍筋)不同于一般跨高比梁可能出现的一种破坏现象。
2.2 裂缝的发展及分布
当梁达到开裂荷载时，梁在底面率先出现细微裂缝，随后裂缝开始在梁侧面出现。在正常使用阶段(约0.4～0.7的极限荷载)，4根梁出现的裂缝均为细微裂缝，裂缝宽度不足0.25 mm；随着荷载的增加，竖向裂缝逐渐向受压区方向延伸开展。
梁UHPCB1纯弯区段两侧面的竖向裂缝数量分别为41条、36条；梁UHPCB2纯弯区段两侧面的裂缝数量分别为36条、35条；梁UHPCB3纯弯区段区两侧面的裂缝数量分别为27条、25条；梁UHPCB4纯弯段区两侧面的裂缝数量分别为21条、22条。分别对比梁UHPCB1与梁UHPCB3、梁UHPCB2与梁UHPCB4这两组试验梁的裂缝数量，可以发现随着钢纤维掺量由3%提高到5%，裂缝数量显著减少，表明梁的抗裂性能显著提高。同时分别对比梁UHPCB1与梁UHPCB2、梁UHPCB3与梁UHPCB4这两组梁的裂缝数量，可以发现纵筋配筋率对梁裂缝数量的影响不大；但是观察图6中各梁裂缝的开展可以看出，纵筋配筋率对各梁裂缝长度的影响显著，纵筋配筋率高的梁裂缝长度较短，纵筋配筋率低的梁裂缝长度较长。这也表明，为了保持梁截面受力平衡，较高纵筋配筋率的梁，需要较高受压区高度UHPC承受压力来平衡拉区受拉钢筋拉力。
3 试验结果及分析
3.1 荷载-挠度曲线
4根试验梁的荷载-跨中挠度曲线如图7所示。各试验梁的开裂、屈服和极限荷载及相应的弯矩如表5所示，其中开裂荷载为梁跨中出现第一条竖向裂缝对应的荷载；屈服荷载为梁跨中全部纵筋屈服(试件UHPCB1与UHPCB3)或第一排纵筋屈服(试件UHPCB2与UHPCB4)对应的荷载；极限荷载为梁截面受压区UHPC酥裂起皮对应的荷载，由于此时梁尚未完全破坏(试验加载采用人工控制，为防止操作失误造成事故，未加载至梁完全破坏)，故梁的荷载-跨中挠度曲线没有出现下降段。
UHPC简支梁的荷载-挠度曲线(见图7)有如下特点：
1)高强钢筋UHPC适筋梁(图7(a))的荷载-挠度曲线大致分为三个阶段：从开始加载到受拉区UHPC开裂为第一阶段，从开裂到纵向受拉钢筋屈服为第二阶段，从钢筋屈服到破坏为第三阶段。
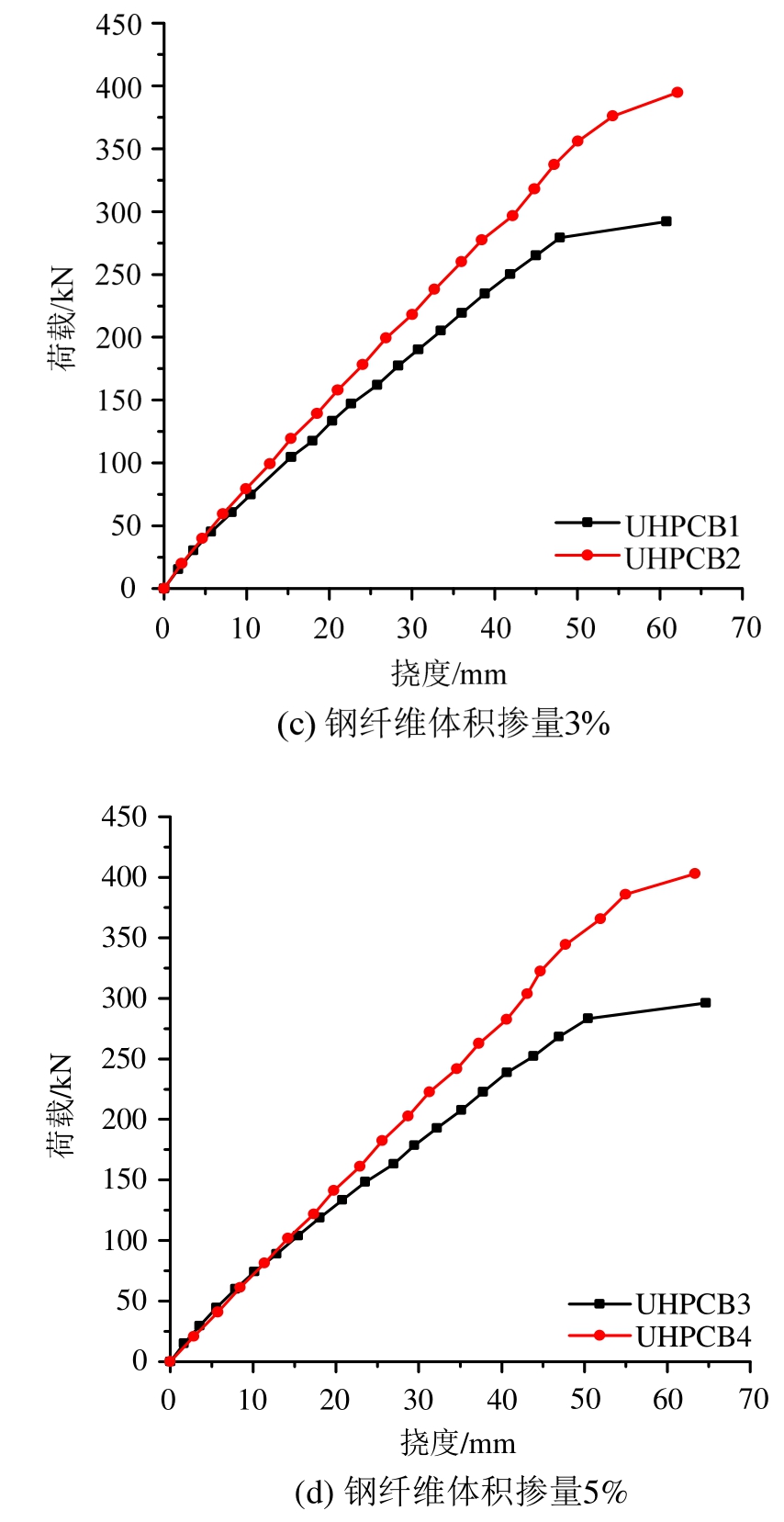
图7 跨中荷载-挠度曲线
Fig.7 Loading-deflection curves at mid-span
表5 梁的实测荷载
Table 5 Measured load of specimens
注：表中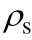
为纵向钢筋配筋率；
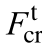为实测开裂荷载；
为实测开裂弯矩；
为实测屈服荷载；
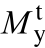为实测屈服弯矩；
为实测极限荷载；
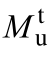为实测极限弯矩。
梁编号 sρ/ (%)t cr F / kN t cr M / (kN·m)tyF/kN t y M / (kN·m)tuF/ kN t u M / (kN·m)UHPCB1 3.21 45 36.0 279 223.2 292 233.6 UHPCB2 6.74 45 36.0 372 297.6 394 315.2 UHPCB3 3.21 48 38.4 284 227.2 296 236.8 UHPCB4 6.74 50 40.0 385 308.0 404 323.2
2)高强钢筋UHPC部分超筋破坏梁(图7(b))的荷载-挠度曲线相比适筋梁，受拉纵向钢筋未全部屈服，故只有两阶段：从开始受力到受拉区UHPC开裂为第一阶段，从开裂到试验梁破坏为第二阶段。
3)纤维掺量变化对梁受弯承载力的提高作用不明显(图7(a)、图7(b))，这是因为试件制作过程中，纤维体积掺量为5%的UHPC性能未达期望要求(抗压强度应达到150 MPa)，两种钢纤维掺量的UHPC抗压强度差异不大(10%，见表2)，故导致梁的受弯承载力亦差异不大。
4)纵向钢筋配筋率对梁受弯承载能力影响显著(图7(c)、图7(d))，纵筋配筋率由3.21%提高到6.74%，两个梁的受弯承载力分别提高了34.9%、36.5%。
3.2 平截面假定验证
UHPC梁的正截面承载力计算是建立在平截面假定基础上的，故应对平截面假定进行验证。各梁跨中截面沿高度的平均应变分布如图8所示，可见基本呈线性变化，平截面假定成立。
由表3可知，HRB500钢筋的屈服应变约为2700×10-6。由图8可知，在破坏时，试件UHPCB1、UHPCB3的钢筋拉应变已远大于其屈服应变；试件UHPCB2、UHPCB4的第一排钢筋拉应变超过其屈服应变，第二排钢筋拉应变接近其屈服应变。这表明，试件UHPCB2、UHPCB4接近于受弯界限破坏；如果这两个试件的纯弯段配置足够的抗剪箍筋，则可能发生受弯适筋破坏。
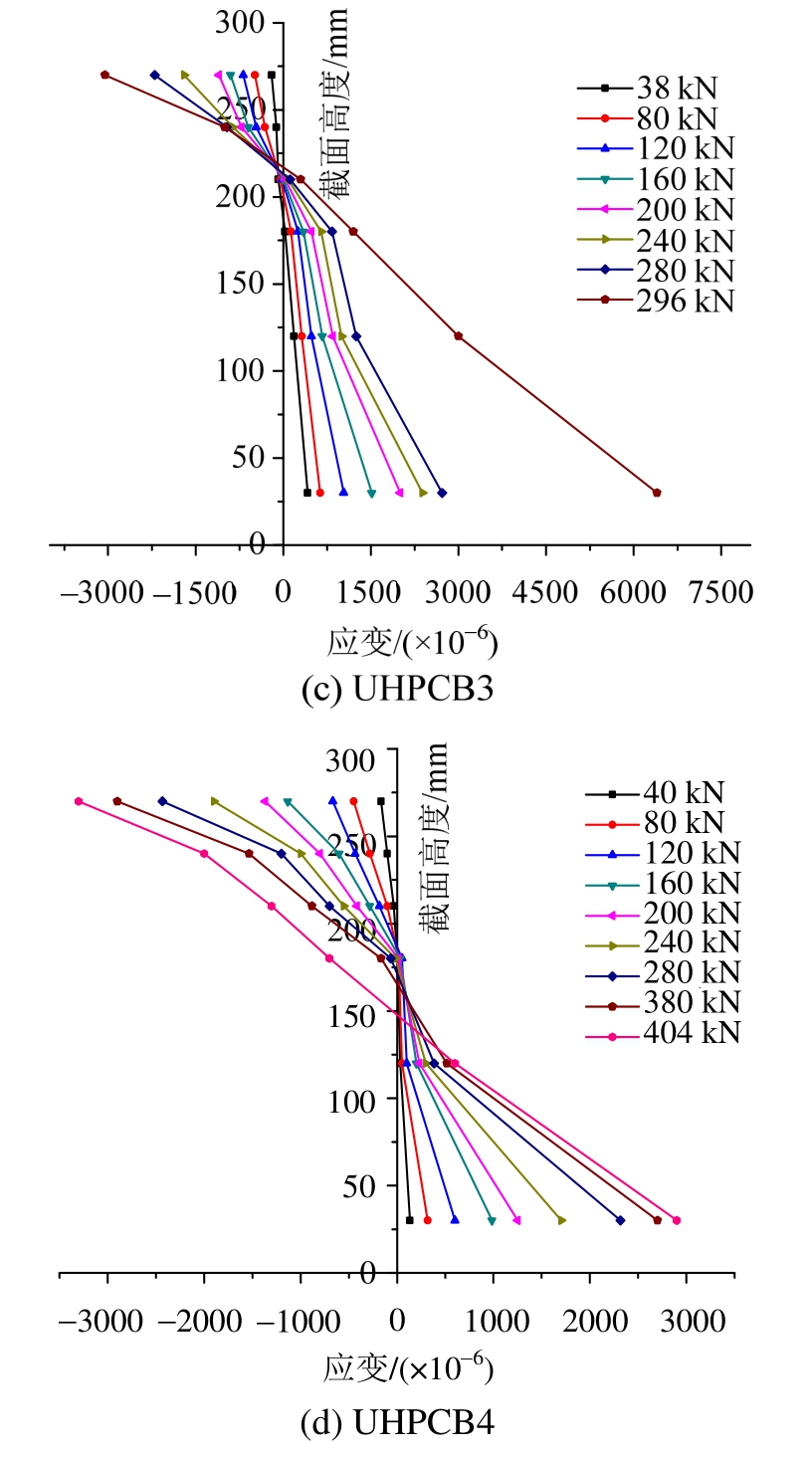
图8 UHPC梁截面应变分布
Fig.8 Strain profiles at mid-span section of specimens
3.3 界限配筋率
试件设计时，取UHPC抗压强度平均值为100 MPa，并换算为设计值；钢筋采用HRB500；按混凝土规范[11]确定的梁界限配筋率为5.56%。试件UHPCB2、UHPCB4的实际配筋率均为6.74%，理论上为超筋梁。试验结果(图8(b)、图8(d))表明，这两根梁为部分超筋破坏梁，第二排钢筋应变接近其屈服应变，接近于界限破坏。已有研究[10]表明：变形钢筋与UHPC界面的黏结强度很高(达87 MPa)，不易发生劈裂黏结破坏，故钢筋强度可充分利用，配筋率可提高到10%～20%。本文由于UHPC的性能未达到预期要求，故相应的梁配筋率未达到10%。
4 UHPC梁正截面承载力计算
4.1 基本假定及UHPC材料本构模型
高强钢筋UHPC梁正截面承载力计算的基本假定与普通钢筋混凝土梁相似，主要区别在于UHPC开裂后，钢纤维在开裂面的桥接作用，可以承受一定的拉应力，所以UHPC梁截面受拉区可考虑纤维承受部分拉应力。
由于钢纤维的掺入及细集料的使用，UHPC的材料本构模型较普通混凝土变化明显。经分析比较，采用由Lok等[14]提出的钢纤维混凝土受压本构模型(图9(a))和理想弹塑性受拉本构模型(图9(b))。
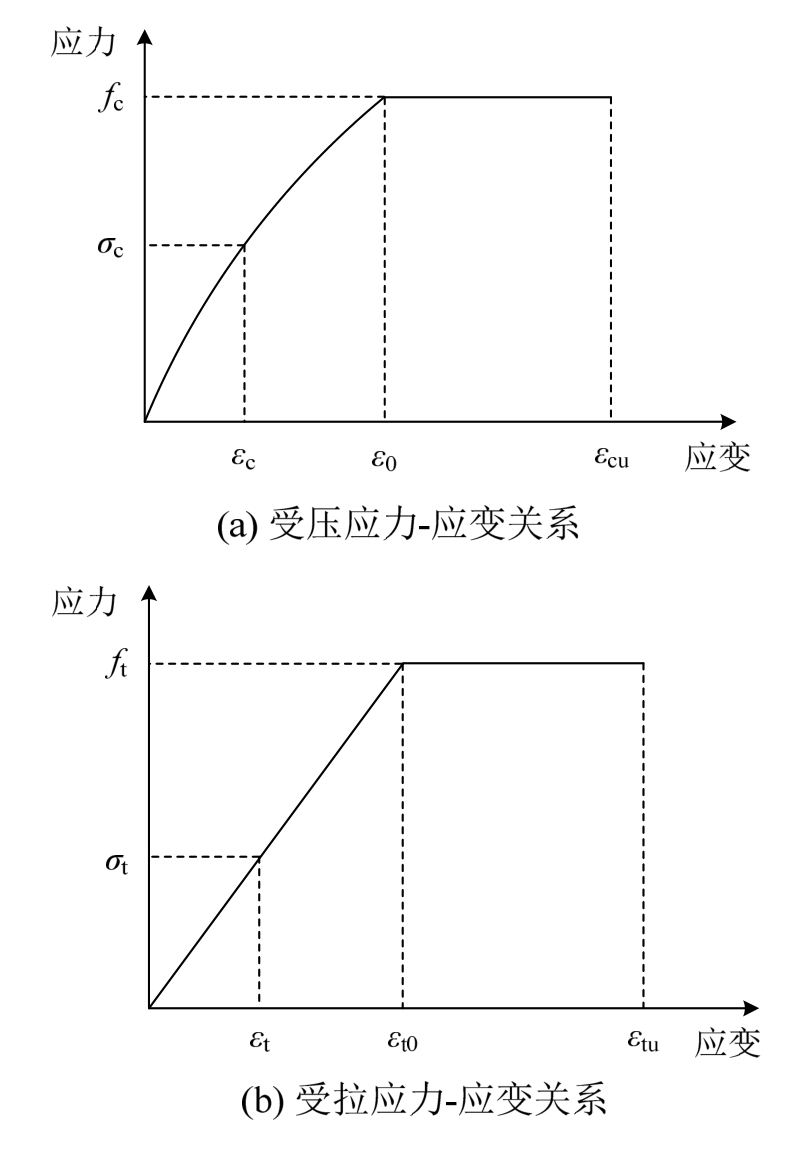
图9 UHPC本构关系
Fig.9 Stress-strain relationship of UHPC
基本假定如下：
1)沿梁截面高度的平均应变分布符合平截面假定，即截面平均应变沿高度呈线性分布。
2)截面受拉区的拉力由钢筋和UHPC共同承担，UHPC的受拉本构关系为：
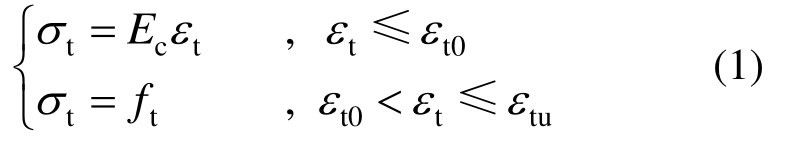
式中：Ec为UHPC弹性模量；σt为UHPC拉应变为εt时的拉应力；ft为UHPC的峰值拉应力；εt0为UHPC的峰值应变；εtu为UHPC的极限拉应变。
3)UHPC受压应力-应变关系采用由Lok等[14]建议的应力-应变关系，即：
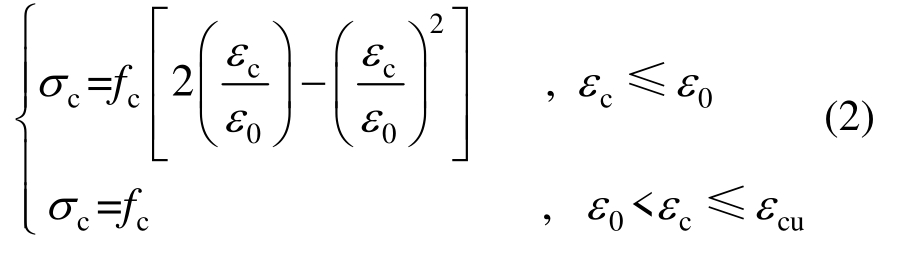
式中：σc为UHPC应变为εc时的压应力；fc为UHPC轴心抗压强度；ε0为UHPC压应力达到fc时的压应变，文献[15]给出了峰值应变的经验公式
为UHPC极限压应变，文献[16]建议
4)纵向受拉钢筋与UHPC材料间无滑移。
5)纵向钢筋的应力-应变关系采用理想弹塑性模型，其表达式为：
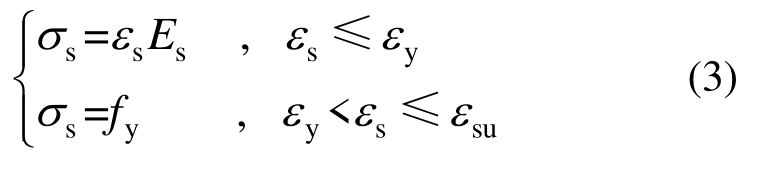
式中：fy为钢筋的抗拉或抗压屈服强度；σs为对应于钢筋应变为εs时的钢筋应力值；εy为钢筋的屈服应变，即
为钢筋的弹性模量。
4.2 受弯承载力计算
根据基本假定，可得在承载能力极限状态时截面的应力、应变分布(图10)。此时，截面受压区边缘UHPC达到了其极限压应变εcu。假定此时截面受压区高度为k1h，则距截面中性轴距离为y的UHPC纤维处的应变可按下式计算：
钢筋的拉力及其距中和轴的距离ys可分别按下式计算：
式中：h0为有效截面高度；k1为截面受压区高度与截面高度之比。
受拉区混凝土的拉力Tc可按下式计算：
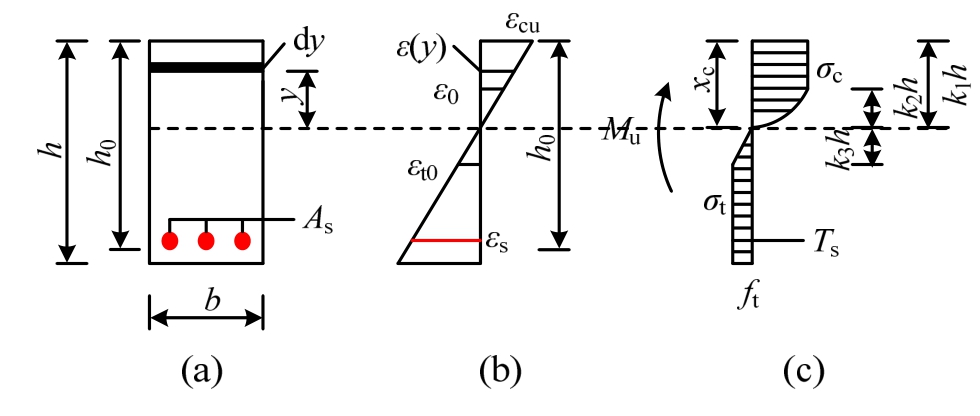
图10 矩形截面受弯分析
Fig.10 Strain and stress profiles at ultimate state
根据截面的平衡条件，可写出以下两个平衡方程：
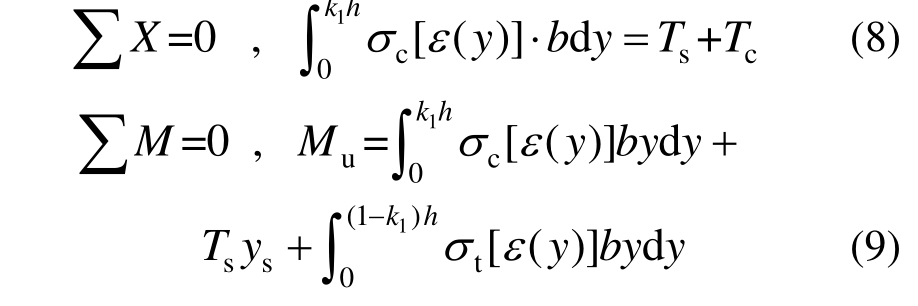
图10(c)截面应力图中既有弹性区域也有塑性区域，假定各区域的高度进行截面分析，并将式(1)、(2)代入式(8)可得：
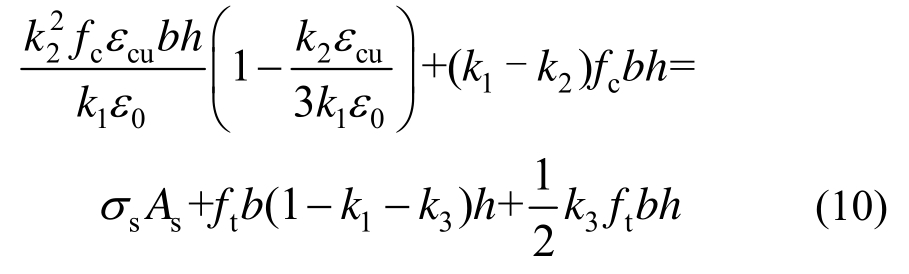
方程两边同除以bh，得：
将式(1)、式(2)代入式(9)可得：
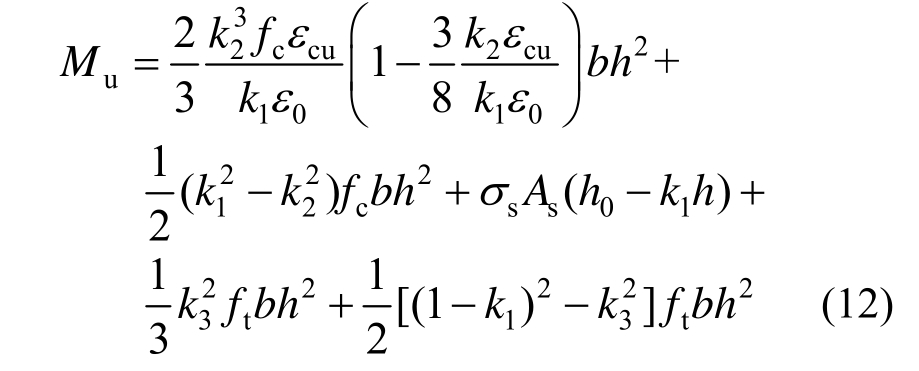
再由平截面假定得：
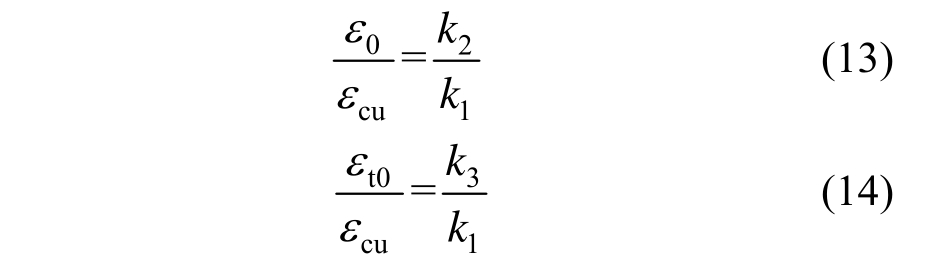
将式(13)、式(14)代入式(12)，简化后得：
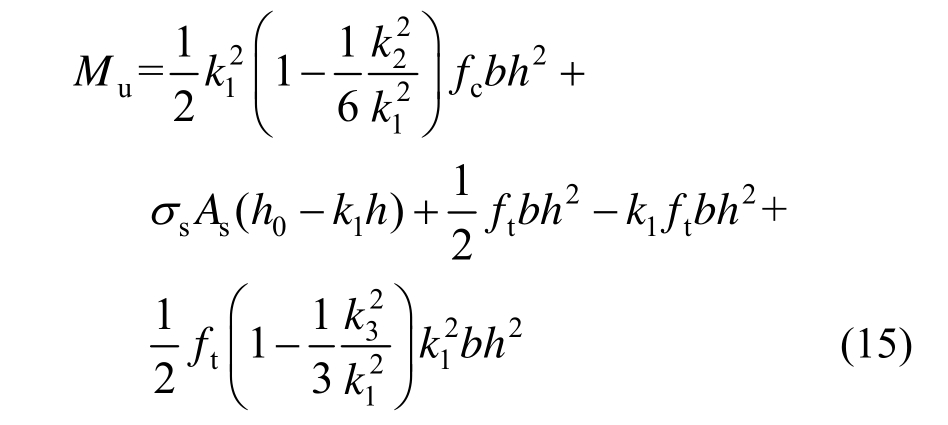
式中：ρ为毛截面配筋率，
为截面待定高度系数；b为截面宽度。
由文献[16]的经验式
则有：
式中：Et为峰值压应力处的割线模量；Ec为UHPC弹性模量，假定UHPC为各向同性材料，则
UHPC峰值抗拉强度ft，可通过下式估算[17]：
将式(17)代入式(16)，对于UHPC材料，其轴心抗压强度基本可达100 MPa以上。则
将其近似取0.04计算，故
与1相比可略去不计，所以式(15)左边第五项可用
代替。令截面受压区高度xc=k1h，将上述结果代入式(15)，简化得：
式中，xt为截面受拉区高度，
系数k1可以联立式(11)、式(13)、式(14)求解，并对其简化可得：
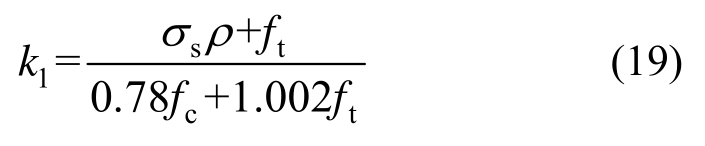
为了验证上述承载力计算模型的可行性，从文献[8,16]、[18—20]选出25组UHPC、RPC及FRC试验梁进行验证，试验梁数据见表6。理论计算值与试验值对比见表6。
表6 试件主要参数、极限弯矩计算值与试验值比较
Table 6 Main parameters of specimens, comparison of ultimate moment calculated and experimental values
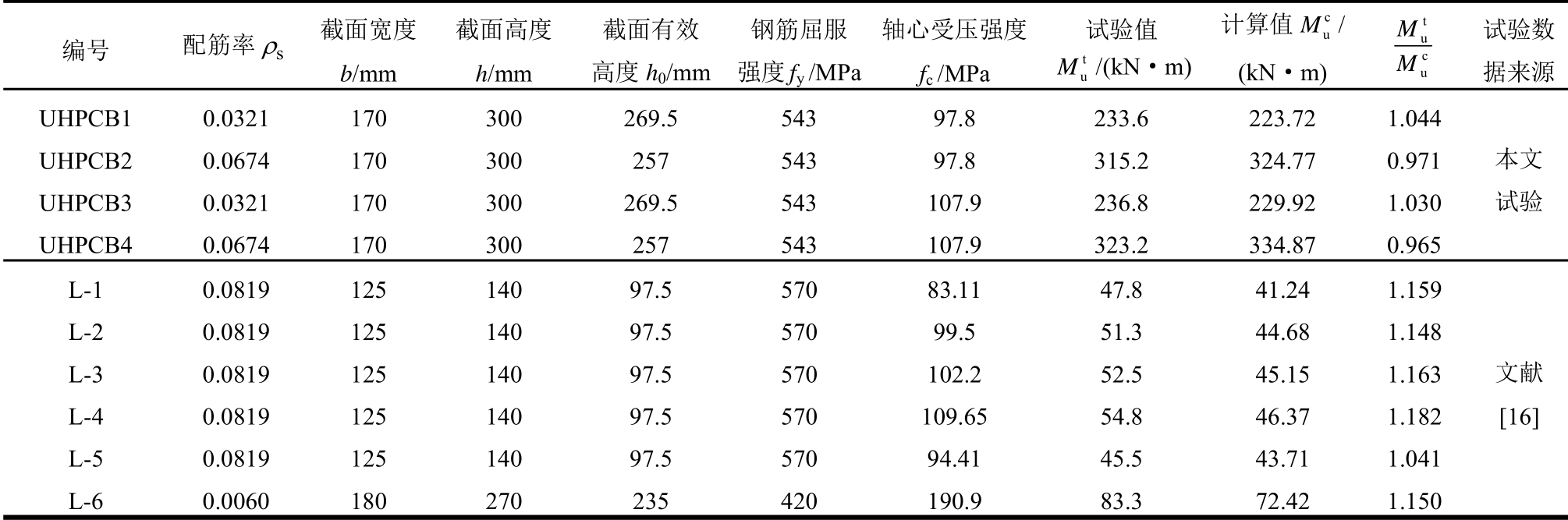
编号 配筋率sρ 截面宽度b/mm 截面高度 h/mm 截面有效 高度h0/mm钢筋屈服强度fy /MPa轴心受压强度fc /MPa 试验值 t u M/(kN·m)计算值 c u M / (kN·m)tucu M M 试验数据来源UHPCB1 0.0321 170 300 269.5 543 97.8 233.6 223.72 1.044 本文 试验 UHPCB2 0.0674 170 300 257 543 97.8 315.2 324.77 0.971 UHPCB3 0.0321 170 300 269.5 543 107.9 236.8 229.92 1.030 UHPCB4 0.0674 170 300 257 543 107.9 323.2 334.87 0.965 L-1 0.0819 125 140 97.5 570 83.11 47.8 41.24 1.159 文献[16]L-2 0.0819 125 140 97.5 570 99.5 51.3 44.68 1.148 L-3 0.0819 125 140 97.5 570 102.2 52.5 45.15 1.163 L-4 0.0819 125 140 97.5 570 109.65 54.8 46.37 1.182 L-5 0.0819 125 140 97.5 570 94.41 45.5 43.71 1.041 L-6 0.0060 180 270 235 420 190.9 83.3 72.42 1.150
续表
注：
极限弯矩计算值。
编号 配筋率 sρ 截面宽度b/mm 截面高度 h/mm 截面有效 高度h0/mm钢筋屈服强度fy /MPa轴心受压强度fc /MPa 试验值 t u M/(kN·m)计算值 c u M / (kN·m)tucu M M 试验数据来源L-7 0.0090 180 270 235 420 192.2 92.2 84.33 1.093 文献[16]L-8 0.0120 180 270 235 420 196.1 116.5 96.54 1.207 L-9 0.0131 180 270 215 420 190.9 105.7 91.49 1.155 L-10 0.0196 180 270 215 420 196.1 131.6 112.99 1.165 L-11 0.0144 150 300 275 528.7 62.67 90.45 102.63 0.881 文献[18]L-12 0.0144 150 300 275 528.7 58.2 89.1 100.94 0.883 L-13 0.0147 150 200 182 518.3 115.1 48.1 51.55 0.933 文献 [8]L-14 0.0221 150 200 182 518.3 115.1 62.8 67.96 0.924 L-15 0.0414 150 200 162 518.3 115.1 92.8 88.37 1.050 L-16 0.0496 150 200 162 518.3 115.1 101.6 100.63 1.010 L-17 0.0287 150 250 228 534 116.7 124.3 131.91 0.942 文献[19]L-18 0.0489 150 250 201 534 116.7 157.5 157.38 1.001 L-19 0.0678 150 250 193 534 116.7 180.6 184.64 0.978 L-20 0.0287 150 250 228 432 116.7 128.65 113.04 1.138 L-21 0.0122 150 200 168 476.5 102.28 38.25 38.41 0.996 文献[20]L-22 0.0309 150 200 164 478.3 102.28 63.5 67.46 0.941 L-23 0.0307 150 200 166 467.6 102.28 64.5 67.31 0.958 L-24 0.0590 150 200 154 465.2 102.28 87 93.77 0.928 L-25 0.0967 150 200 139 465 102.28 101 107.84 0.937
将UHPC梁相关参数代入式(18)、式(19)，可得弯矩计算值
计算时适筋梁钢筋强度取其屈服强度
部分超筋梁钢筋强度根据其实测钢筋应变及本构关系确定。计算值
、试验值
及试验值与计算值的比值如表6所示。由表6可得，本文试件受弯承载力试验值与计算值之比的均值为1.003，标准差为0.040，变异系数为0.040；文 献[8, 16]、[18—20]相关试件受弯承载力试验值与计算值之比的均值为1.039，标准差为0.101，变异系数为0.097。表6所有梁受弯承载力试验值与计算值之比的均值为1.034，标准差为0.101，变异系数为0.098。可见所有试件受弯承载力计算值与试验值吻合的较好，且精度满足工程计算要求。
5 结论
(1)试验表明，大跨高比受弯试验梁(纯弯段不配箍筋)出现部分超筋破坏时，梁纯弯段区出现由加载点向下延伸的斜裂缝。这是因为加载至极限荷载时，加载点附近UHPC在集中荷载作用下产生压应力场，使梁纯弯区段产生较大的剪力，对于大跨高比梁，梁纯弯区段受剪截面相对较小，又无抵抗竖向剪力的箍筋，故产生斜裂缝。这是大跨高比受弯试验梁(纯弯段不配箍筋)不同于一般跨高比梁可能出现的一种破坏现象。
(2)当钢纤维掺量从3%提高到5%时，UHPC梁纯弯区段裂缝数量显著减少，开裂荷载提高了6.0%～11%，表明增加钢纤维掺量能改善梁的抗裂性能；极限荷载仅提高了1.4%～2.5%，表明增加钢纤维体积掺量对其极限荷载影响较小。这是因为纤维体积掺量为5%的UHPC性能未达期望要求，致使两种钢纤维掺量的UHPC抗压强度差异不大，故导致两种纤维掺量梁的抗裂性能、受弯承载力亦差异不大。
(3)试验表明，高强钢筋用于UHPC梁，二者优势互补，协调性强；增加高强纵向钢筋的配筋率，能有效提高UHPC梁的受弯承载力（提高了34.9%～ 36.5%）。
(4)试验及分析表明，UHPC梁截面平均应变沿高度分布总体呈线性，平截面假定基本成立。按现行混凝土结构设计规范规定的界限配筋率判断为超筋梁，梁破坏时截面受拉区第一排钢筋应变超过其屈服应变，第二排钢筋应变接近其屈服应变，其破坏模式接近于受弯界限破坏；如果这种梁的纯弯段配置足够的抗剪箍筋，则可能发生受弯适筋破坏。因此，现行规范规定的界限配筋率不适用于UHPC梁，具体限值有待进一步研究确定。
(5)基于截面平衡条件、平截面假定以及钢筋和UHPC材料的本构关系，建立了UHPC梁受弯承载力计算模型；该模型能较好地反映UHPC的受弯性能，受弯承载力计算值与试验值吻合较好。
[1]Russell H G.Ultra-high performance concrete: A State- of-the-art report for the bridge community [R].Research, development, and technology turner-fair bank highway research center, McLean, Virginia, 2013: 16—19.
[2]金凌志, 李月霞, 祁凯能, 等.高强钢筋RPC简支梁抗剪承载力及延性研究[J].工程力学, 2015, 32(S1): 209—214.Jin Lingzhi, Li Yuexia, Qi Kaineng, et al.Research on shear bearing capacity and ductility of high strength reinforced RPC beam [J].Engineering Mechanics, 2015, 32(S1): 209—214.(in Chinese)
[3]徐世烺, 王洪昌.超高韧性水泥基复合材料与钢筋粘结本构关系的试验研究[J].工程力学, 2008, 25(11): 53—61.Xu Shilang, Wang Hongchang.Experimental Study on bond-slip between ultra-high toughness cementitious composites and steel bar [J].Engineering Mechanics, 2008, 25(11): 53—61.(in Chinese)
[4]邓明科, 卜新星, 潘姣姣, 等.型钢高延性混凝土短柱抗震性能试验研究[J].工程力学, 2017, 34(1): 163—170.Deng Mingke, Bu Xinxing, Pan Jiaojiao, et al.Experimental study on seismic behavior of steel reinforced high ductile concrete short columns [J].Engineering Mechanics, 2017, 34(1): 163—170.(in Chinese)
[5]赖建中, 朱耀勇, 谭剑敏.超高性能混凝土在埋置炸药下的抗爆试验及数值模拟[J].工程力学, 2016, 33(5): 193—199.Lai Jianzhong, Zhu Yaoyong, Tan Jianmin.Experimental and simulation of ultra-high-performance concrete subjected to blast by embedded explosive [J].Engineering Mechanics, 2016, 33(5): 193—199.(in Chinese)
[6]Yoo D Y, Banthia N, Yoon Y S.Predicting service deflection of ultra-high-performance fiber-reinforced concrete beams reinforced with GFRP bars [J].Composites Part B Engineering, 2016, 99(6): 381—397.
[7]杨剑.CFRP预应力筋超高性能混凝土梁受力性能研究[D].长沙: 湖南大学, 2007.Yang Jian.Flexural behavior of ultra high performance concrete beams prestressed with CFRP tendons [D].Changsha: Hunan University, 2017.(in Chinese)
[8]邓宗才, 王义超, 肖锐, 等.高强钢筋UHPC梁抗弯性能试验研究与理论分析[J].应用基础与工程科学学报, 2015, 23 (1): 68—78.Deng Zongcai, Wang Yichao, Xiao Rui, et al.Flexural test and theoretical analysis of UHPC beams with high strength rebars [J].Journal of Basic Science and Engineering, 2015, 23(1): 68—78.(in Chinese)
[9]Singh M, Sheikh A H, Ali M S M, et al.Experimental and numerical study of the flexural behaviour of ultra-high performance fibre reinforced concrete beams [J].Construction & Building Materials, 2017, 138(5): 12—25.
[10]Kaptijn N, Blom J.A new bridge deck for the Kaag Bridges the first CRC (Compact Reinforced Composite)application in civil infrastructure [J].Science and Engineering of Composite Materials, 2002, 10(6): 397—402.
[11]GB 50010—2010，混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010-2010, Code for design of concrete structures [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[12]GB/T 31387—2015, 活性粉末混凝土[S].北京, 中国标准出版社, 2015.GB/T 31387—2015, Reactive powder concrete [S].Beijing: China Standard Press, 2015.(in Chinese)
[13]GB/T 50152—2012, 混凝土结构试验方法标准[S].北京: 中国建筑工业出版社, 2012.GB/T 50152—2012, Standard for test method of concrete structures [S].Beijing: China Architecture & Building Press, 2012.(in Chinese)
[14]Lok T S, Xiao J R.Flexural strength assessment of steel fiber reinforced concrete[J].Journal of Materials in Civil Engineering, 1999, 11(3): 188—196.
[15]曾建仙, 吴炎海, 林清.掺钢纤维活性粉末混凝土的受压力学性能研究[J].福州大学学报, 2005, 33(S1): 132—137.Zeng Jianxian, Wu Yanhai, Lin Qing.Researches on the compressive mechanics properties of steel fiber RPC [J].Journal of Fuzhou University, 2005, 33(Sl): 132—137.(in Chinese)
[16]Al-Hassani H M, Khalil W I, Danha L S.Prediction of the nominal bending moment capacity for plain and singly reinforced rectangular RPC beam sections [J].Engineering & Technology Journal, Part(A), 2015, 33(5): 1113—1130.
[17]Soranakom C, Yekani-Fard M, Mobasher B.Development of design guidelines for strain softening fiber reinforced concrete [C].7th International Symposium of Fiber Reinforced Concrete: Design and Applications BEFIB 2008, Editor: R.Gettu, Sept.2008: 513—523.
[18]黄伟, 张丽, 吴明超.HRB500级高性能钢筋钢纤维混凝土梁受弯性能试验研究[J].工业建筑, 2011, 41(11): 76—80.Huang Wei, Zhang Li, Wu Mingchao.Experimental investigation on flexural behavior of steel fiber RC beams with grade HRB500 reinforcement of low-cost and high-performance [J].Industrial Construction, 2011, 41(11): 76—80.(in Chinese)
[19]曹霞, 常婧, 王艳俊.高强钢筋RPC梁受弯构件正截面承载力试验研究[J].河南理工大学学报: 自然科学版, 2015, 34(1): 109—115.Cao Xia, Chang Jing, Wang Yanjun.Experimental study on flexural capacity of normal section of high strength reinforced reactive powder concrete beam [J].Journal of Henan Polytechnic University: Natural Science, 2015, 34(1): 109—115.(in Chinese)
[20]李莉.活性粉末混凝土梁受力性能及设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2010.Li Li.Mechanical behavior and design method for reactive powder concrete beams [D].Harbin: Harbin Institute of Technology, 2010.(in Chinese)