在混凝土结构工程中推广应用高强热轧钢筋可以节约资源、减少环境污染，是实现节能减排的重要途径。随着HRB500钢筋和HRB600钢筋相继引入《混凝土结构设计规范》(GB 50010—2010)[1]和《钢筋混凝土用钢第2部分：热轧带肋钢筋》(GB/T 1499.2—2018)[2]，以高强热轧钢筋作受拉纵筋的混凝土框架梁端弯矩调幅性能成为人们研究的重点之一。
由于过去纵向受力钢筋屈服强度相对较低，框架梁端弯矩调幅被认为主要集中在塑性铰形成之后，并与塑性铰转动能力成正比[3]。以HRB500钢筋和HRB600钢筋作框架梁受拉纵筋时，由于钢筋屈服强度提高，一是从截面受拉区混凝土进入塑性、受拉边缘混凝土开裂、裂缝发展直至纵向钢筋受拉屈服这一过程变长，这一阶段对应的弯矩调幅幅度变大；二是相对受压区高度相同时，框架梁端控制截面的屈服曲率变大，塑性铰出现会推迟，塑性铰的转动能力减小；三是锚固于节点内的框架梁端纵向受拉钢筋应变渗透引起的附加转角会增大，对弯矩调幅的影响更加明显。因此重视塑性铰形成前这一阶段框架梁端控制截面的弯矩调幅幅度、考虑应变渗透对框架梁端控制截面弯矩调幅的影响具有重要的理论意义及实用价值。
基于此，完成了12榀HRB500钢筋、HRB600钢筋作纵筋的单层两跨框架梁端弯矩调幅试验。考察了受拉纵筋屈服强度、梁端控制截面相对受压区高度、梁柱节点内梁端受拉纵筋应变渗透引起的附加转角对梁端塑性铰形成前后两阶段弯矩调幅的影响，建立了考虑各关键参数影响的两阶段弯矩调幅系数计算公式。
1 试验概况
1.1 试件设计及制作
12榀混凝土框架试件中，KJ-A-1～KJ-A-6框架梁纵向受拉钢筋采用HRB600钢筋，KJ-B-1～KJ-B-6框架梁纵向受拉钢筋采用HRB500钢筋。框架梁截面尺寸为b×h=180 mm×300 mm，计算跨度均为3000 mm，梁端控制截面相对受压区高度分0.1、0.2、0.3、0.4四档；框架柱纵向钢筋采用HRB400钢筋，柱高1500mm(从底梁顶算起)，截面宽度为250 mm，截面高度分250 mm、350 mm及450 mm三档；混凝土采用C40、C50和C60三种强度等级。各框架设计参数及配筋见表1，试件制作过程如图1所示。
表1 12榀试验框架设计参数及配筋
Table1 Design parameters and reinforcements of 12 test frame specimens
注：1)箍筋混凝土保护层厚度均为25mm；HRB500钢筋用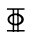
表示，HRB600钢筋用
表示；2)为保证框架梁端控制截面能充分调幅，框架梁跨中配置了足够的纵向受力钢筋；
3)为保证框架梁端控制截面预定相对受压区高度的实现，框架梁底正弯矩纵筋在距柱边(含中柱和边柱)1.5h0(h0为梁截面有效高度)截断；
4)为保证试验过程中框架梁斜截面受剪破坏迟于正截面受弯破坏，试验框架配置了足够的箍筋；
5)框架梁架立钢筋为2φ10(HPB300钢筋用φ表示)。
试件 编号 受拉纵筋牌号 混凝土强度等级 中柱两侧梁端控制截面 边柱内侧梁端控制截面 跨中受拉纵筋 柱截面高度/mm 相对受压区高度 受拉纵筋 相对受压区高度 受拉纵筋KJ-A-1 HRB600 C40 0.29 218+120 0.10 212 322 250 KJ-A-2 C40 0.38 3 22 0.17 314 420 2/2 350 KJ-A-3 C50 0.25 220+122 0.12 214 322 350 KJ-A-4 C50 0.36 420 2/2 0.16 314 422 2/2 450 KJ-A-5 C60 0.28 3 22 0.12 214 520 2/3 450 KJ-A-6 C60 0.39 422 2/2 0.15 218 520 2/3 250 KJ-B-1 HRB500 C40 0.31 3■20 0.10 2■14 3■20 250 KJ-B-2 C40 0.41 4■20 2/2 0.17 2■18 2■20+2■22 350 KJ-B-3 C50 0.25 3■22 0.10 2■16 2■20+2■22 350 KJ-B-4 C50 0.40 4■22 2/2 0.15 2■18 4■22 2/2 450 KJ-B-5 C60 0.38 2■20+2■22 0.10 2■14 3■20+2■22 450 K J-B-6 C60 0.40 3■20+2■22 0.15 2■18 6■22 3/3 250
图1 试件制作
Fig.1 Fabrication of specimens
1.2 材料力学性能
根据《金属材料拉伸试验 第1部分：室温试验方法》(GB/T 228.1—2010)[4]对试验用HRB500钢筋、HRB600钢筋进行拉拔试验，各直径钢筋力学性能见表2。每榀试验框架预留9块(3组，每组3块)边长为150 mm×150 mm×150 mm的标准立方体试块，与框架同期同条件养护，各强度等级混凝土力学性能见表3。
表2 钢筋力学性能
Table 2 Mechanical properties of steel bars
钢筋 牌号 直径d/mm 屈服强度fy/MPa 屈服应变εy/με 极限强度fu/MPa 弹性模量 Es/(×105 MPa)HRB500 12 569 2845 740 2.00 14 569 2845 740 2.00 16 555 2775 710 2.00 18 590 2950 749 2.00 20 581 2905 732 2.00 22 543 2715 713 2.00 HRB600 12 704 3520 915 2.00 14 714 3570 928 2.00 16 645 3225 839 2.00 18 631 3155 825 2.00 20 654 3270 837 2.00 22 618 3090 901 2.00
表3 混凝土力学性能
Table 3 Mechanical properties of concrete
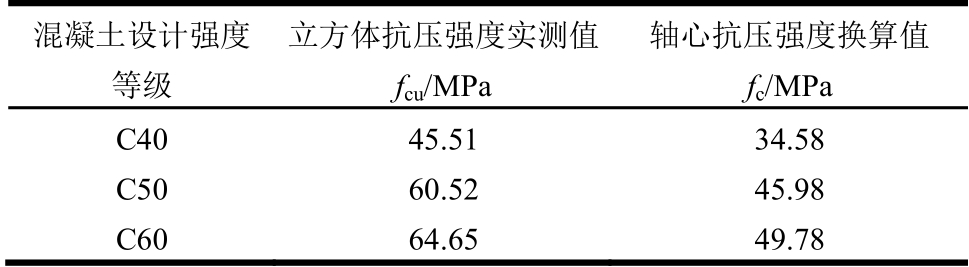
注：fc=αc1fcu，对于C50及以下普通混凝土αc1=0.76；对于C80混凝土αc1=0.82，中间按线性插值。
混凝土设计强度 等级 立方体抗压强度实测值fcu/MPa 轴心抗压强度换算值fc/MPa C40 45.51 34.58 C50 60.52 45.98 C60 64.65 49.78
1.3 加载装置及测点布置
两跨框架梁每跨均采用三分点对称加载[5]，加载装置如图2所示。为了考察梁端塑性铰区及柱截面高度范围内框架梁受拉纵筋在加载过程中拉应变的发展规律，从每个框架梁端的受拉纵筋中选择一根钢筋，在其柱截面高度范围内和柱边缘外侧1.5 h0(h0为截面有效高度)范围内密布间距为40 mm的钢筋应变片(宽度1 mm、标距2 mm)。对该钢筋沿纵肋一侧开设长×宽为4 mm×4 mm的槽口(如图3所示)，并将应变片沿筋长粘贴在槽底以保证加载过程中应变片的存活率，同时能最大限度地减少对纵筋粘结性能的影响。在框架柱端控制截面处每根纵筋上均粘贴钢筋应变片，用以计算框架内力。
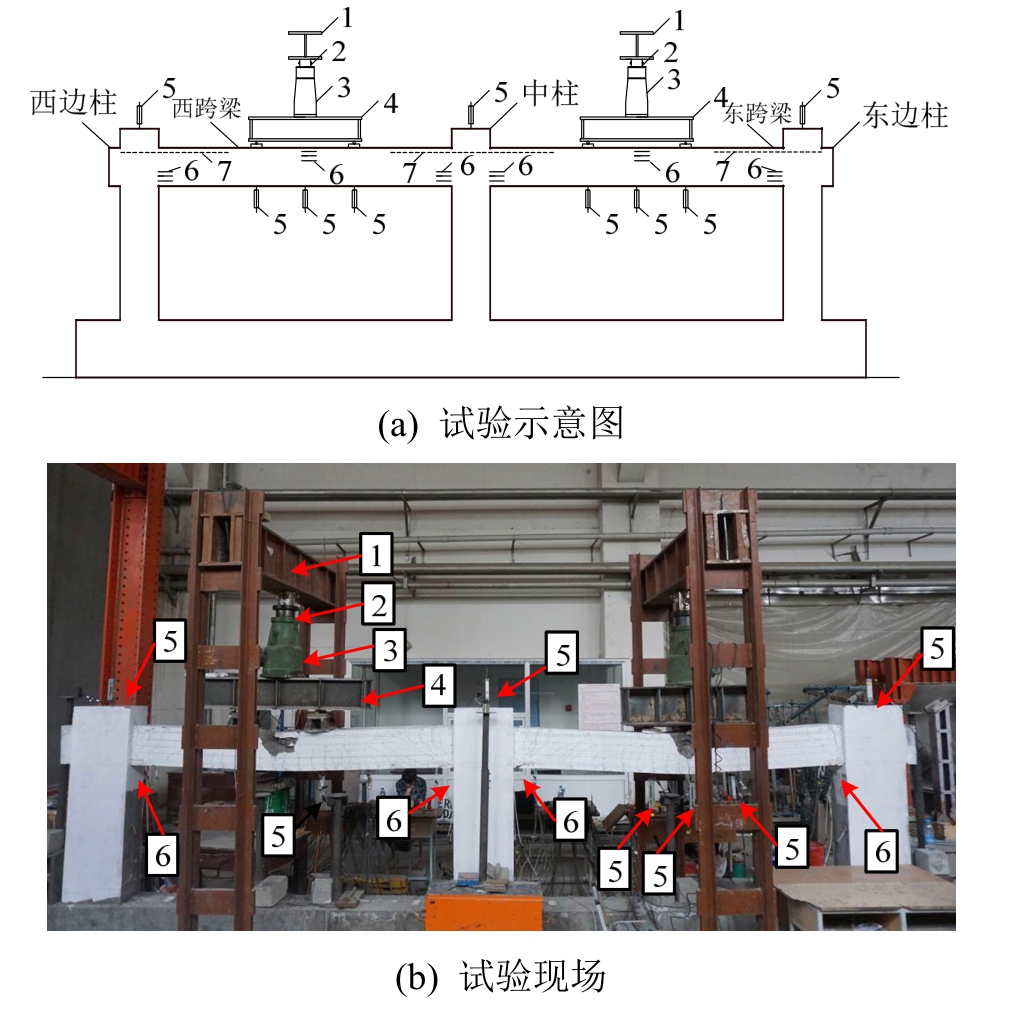
图2 试验框架加载装置
Fig.2 Test setup
1-反力梁；2-加载传感器；3-2000kN千斤顶；4-分配梁； 5-位移计；6-混凝土应变片；7-钢筋应变片
图3 钢筋剖槽贴应变片
Fig.3 Strain gauges in notch of steel bars
2 试验结果及分析
2.1 梁端控制截面附近区域及柱截面高度范围内钢筋应变实测结果
当框架梁端控制截面受压边缘达到混凝土极限压应变时，即认为该控制截面达到其设计用承载能力极限状态(简称极限状态)。在受拉纵筋屈服时刻及极限状态下，各框架梁端控制截面以外1.5 h0范围内及框架柱截面高度范围内受拉钢筋应变实测值如图4～图15所示。图4～图15的(b)图中横坐标零点为中柱截面中点；图4～图15的(a)图和图4～图15的(c)图中横坐标零点为边柱截面外边缘。
2.2 梁端塑性铰转角
图4 KJ-A-1框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.4 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-1
通过对梁端受拉纵筋剖槽密布应变片的方法能准确地捕捉塑性铰区域范围，基于钢筋拉应变实测值及平截面假定计算确定塑性铰区内各测点曲率，如图4～图15所示。令φy为截面受拉钢筋屈服 时对应的曲率、φu为截面达到极限状态时对应的曲率，按与实际塑性铰区长度范围内塑性曲率分布曲线所围面积相等的原则，对应高度为(φu-φy)的矩形区段的长度即为等效塑性铰长度[6-12]，等效矩形分布如图4～图15所示。各框架梁端等效塑性铰长度及相对塑性转角见表4。
图5 KJ-A-2框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.5 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-2
图6 KJ-A-3框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.6 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-3
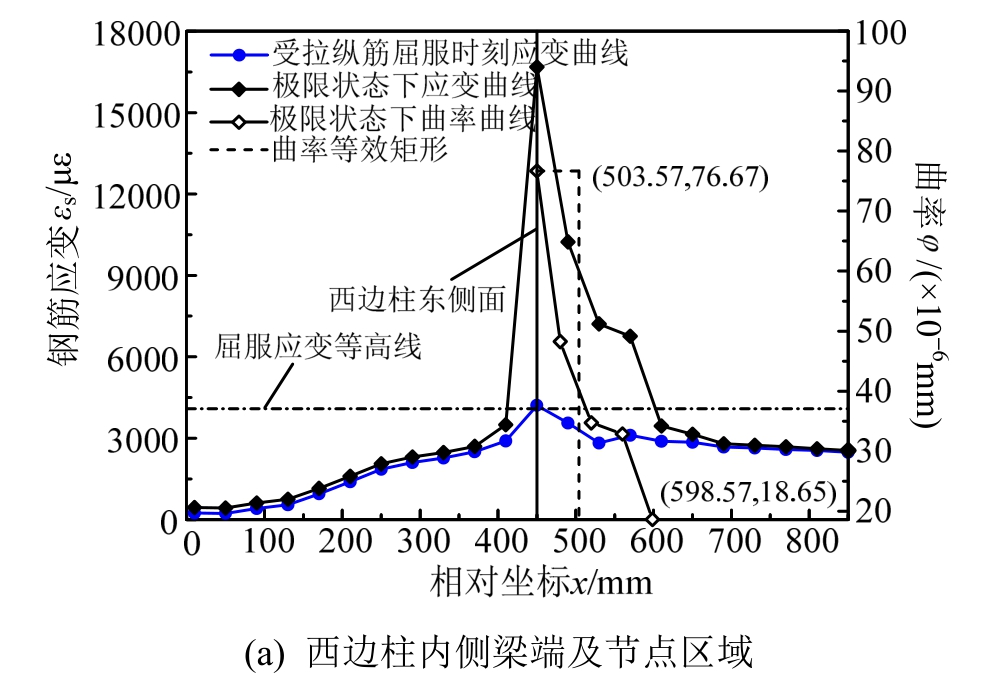
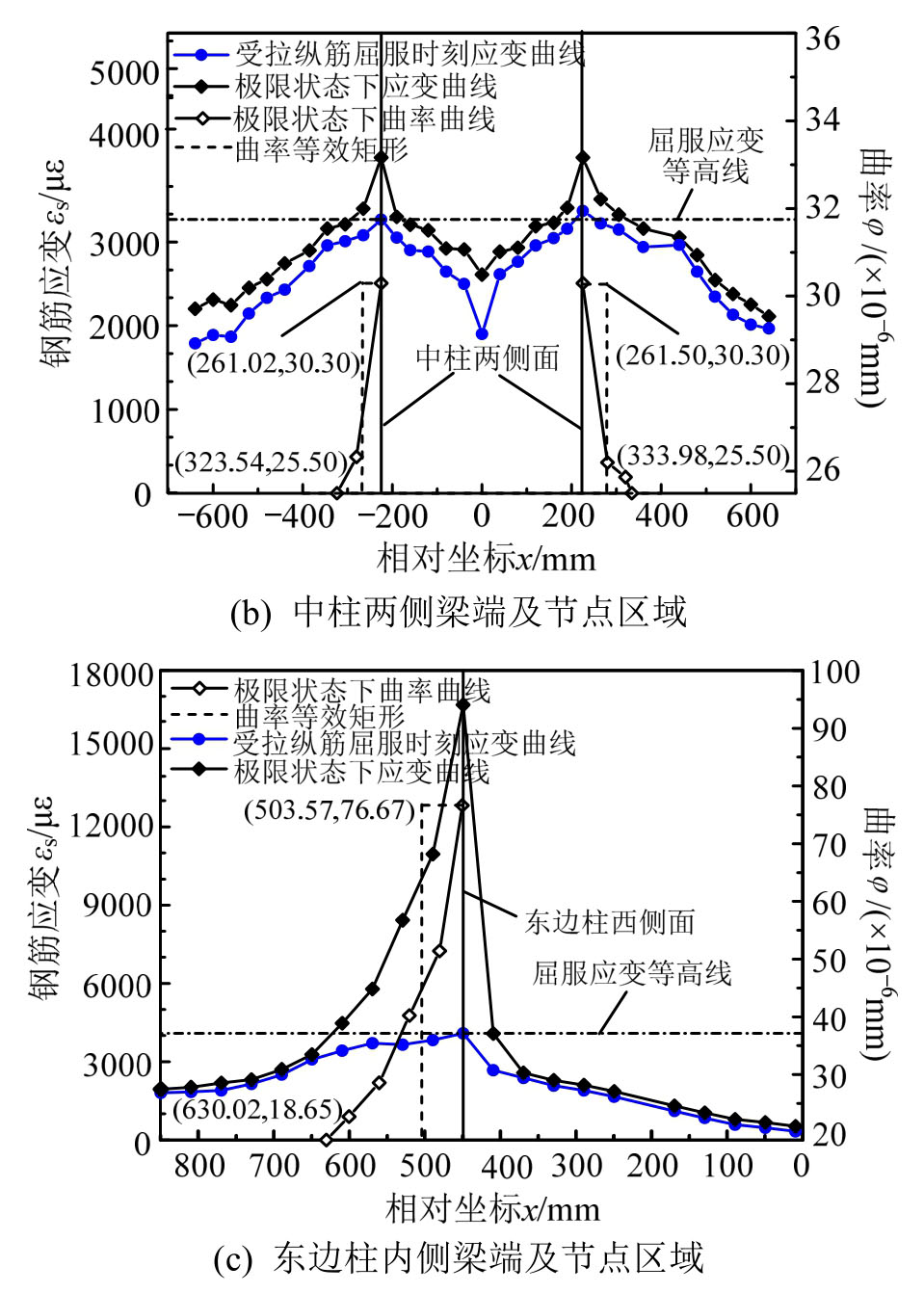
图7 KJ-A-4框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.7 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-4
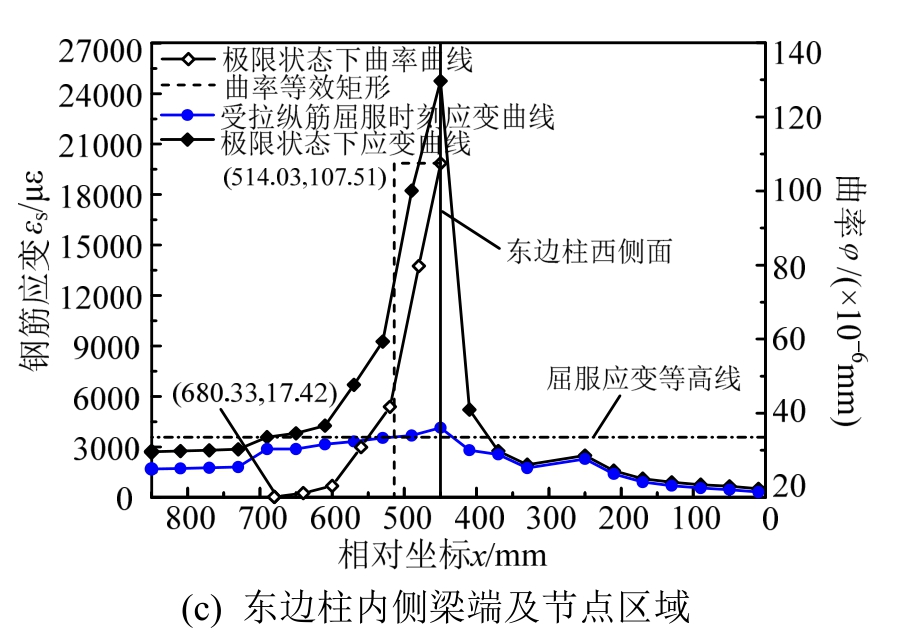
图8 KJ-A-5框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.8 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-5
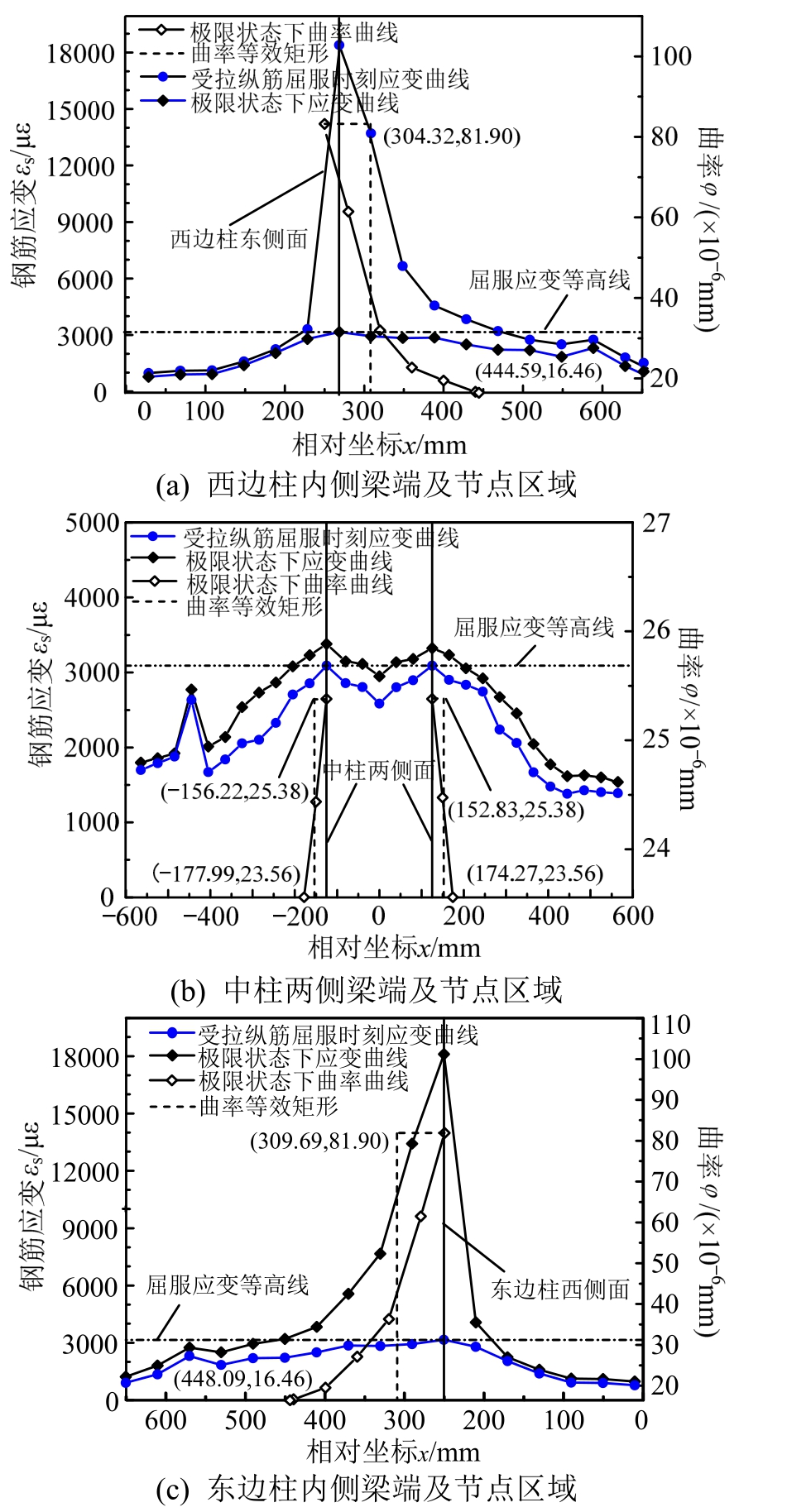
图9 KJ-A-6框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.9 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-A-6
图10 KJ-B-1框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.10 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-1
图11 KJ-B-2框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.11 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-2
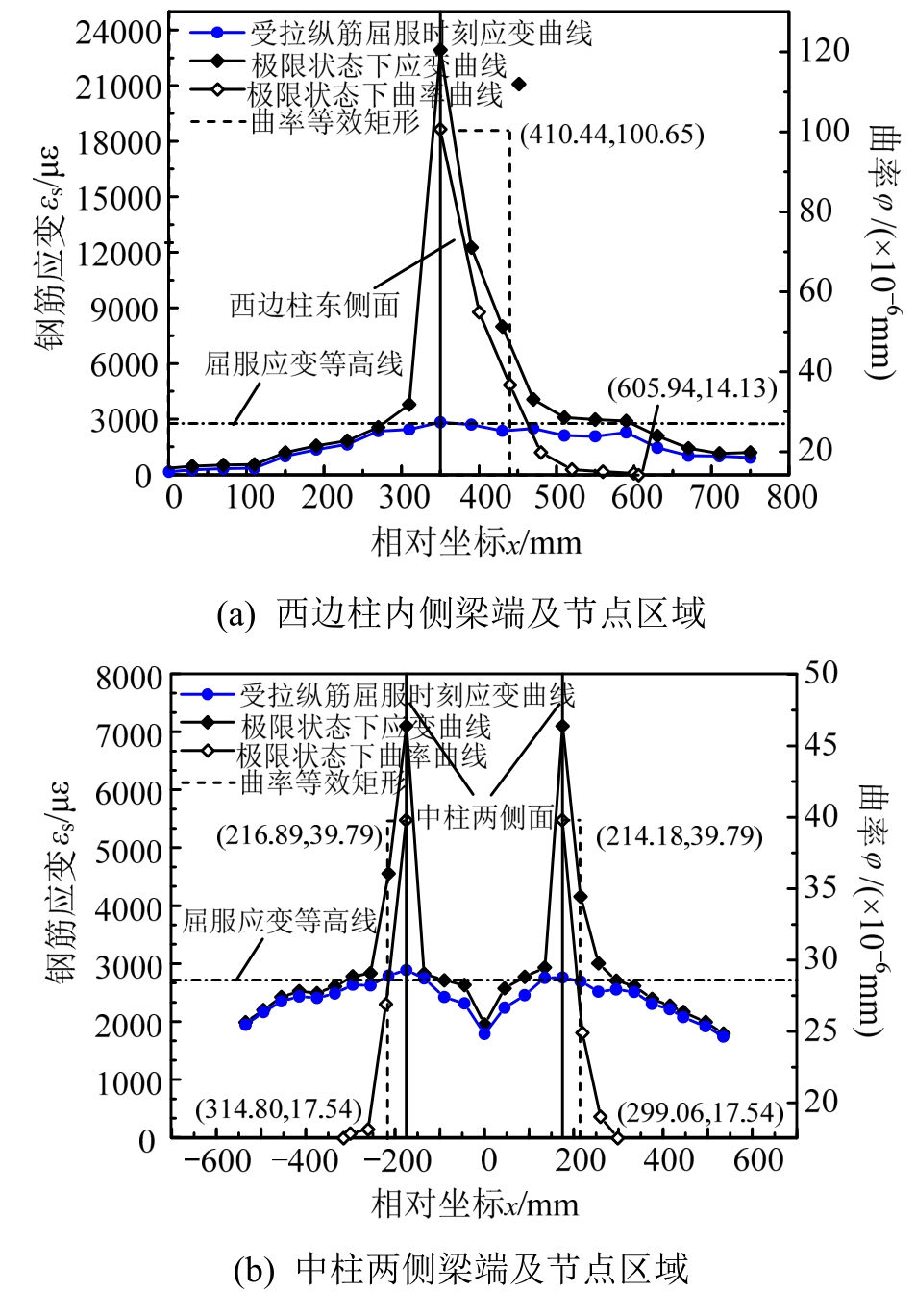
图12 KJ-B-3框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.12 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-3
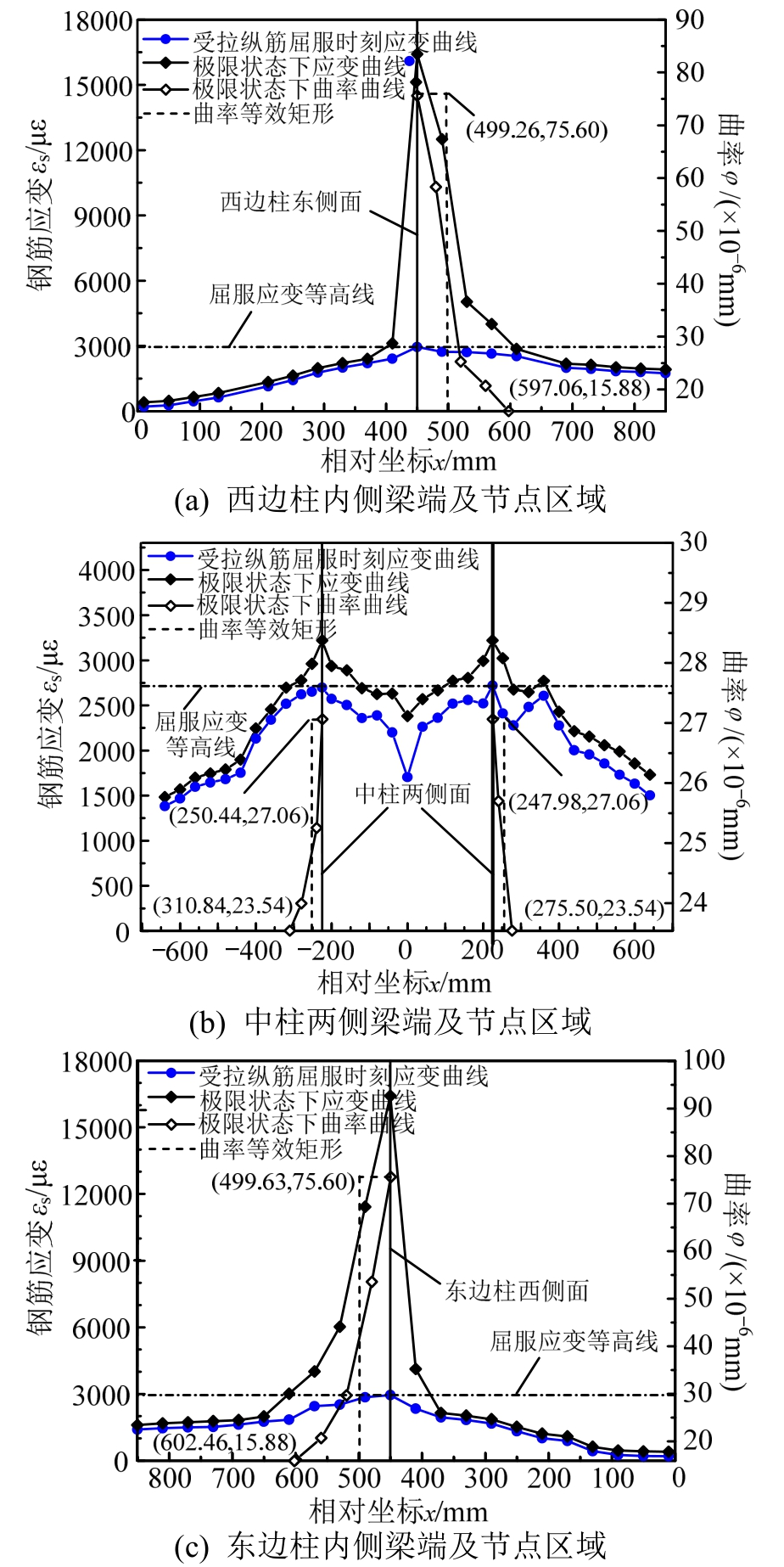
图13 KJ-B-4框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.13 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-4
图14 KJ-B-5框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.14 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-5
图15 KJ-B-6框架梁端附近区域及柱截面高度范围内钢筋拉应变分布及曲率分布
Fig.15 Strain distribution and curvature distribution of the reinforcement anchored in columns and in plastic hinge regions of KJ-B-6
表4 各框架梁端等效塑性铰长度及相对塑性转角
Table 4 Equivalent length of plastic hinges and relative plastic rotations for each test specimen
试件 编号 中柱两侧梁端 边柱内侧梁端 等效塑性铰长度 p l/mm 屈服曲率φy/ (×10-6mm-1)极限 曲率φu/ (×10-6mm-1)相对塑性转角 (θp/h0)/(×10-6mm-1)等效塑性铰长度 p l/mm 屈服 曲率φy/ (×10-6mm-1)极限 曲率φu/ (×10-6mm-1)相对塑性转角 (θp/h0)/(×10-6mm-1)西侧 东侧 西侧 东侧 西边柱 东边柱 西边柱 东边柱KJ-A-1 43.36 42.72 21.33 34.71 2.23 2.20 56.56 58.67 17.29 104.14 18.89 19.63 KJ-A-2 34.51 37.29 23.21 26.29 0.41 0.44 50.77 46.13 19.73 59.62 7.79 7.08 KJ-A-3 35.28 38.72 19.50 37.25 2.41 2.64 61.67 61.55 17.60 103.12 20.29 20.28 KJ-A-4 36.02 36.50 25.50 30.30 0.72 0.73 53.57 58.96 18.65 76.67 11.95 13.15 KJ-A-5 39.13 41.80 19.77 34.93 2.28 2.44 64.03 57.78 17.42 107.51 22.18 20.02 KJ-A-6 31.22 27.83 23.56 25.38 0.18 0.16 54.32 59.69 16.46 81.90 13.67 15.02 KJ-B-1 39.97 39.02 20.08 32.19 1.86 1.82 48.17 50.55 14.63 94.08 14.72 15.47 KJ-B-2 30.06 31.88 21.42 22.76 0.17 0.18 53.37 48.94 16.54 67.13 10.38 9.52
续表
试件 编号 中柱两侧梁端 边柱内侧梁端 等效塑性铰长度 p l/mm 屈服曲率φy/ (×10-6mm-1)极限 曲率φu/ (×10-6mm-1)相对塑性转角 (θp/h0)/(×10-6mm-1)等效塑性铰长度 p l/mm 屈服 曲率φy/ (×10-6mm-1)极限 曲率φu/ (×10-6mm-1)相对塑性转角 (θp/h0)/(×10-6mm-1)西侧 东侧 西侧 东侧 西边柱 东边柱 西边柱 东边柱KJ-B-3 41.89 39.18 17.54 39.79 3.59 3.35 60.44 60.93 14.13 100.65 20.11 20.27 KJ-B-4 25.44 22.98 23.54 27.06 0.37 0.34 49.26 49.63 15.88 75.60 11.31 11.40 KJ-B-5 27.85 31.33 23.69 29.20 0.64 0.72 67.15 66.45 14.08 111.35 25.12 24.86 KJ-B-6 26.28 30.40 21.33 23.26 0.23 0.27 44.06 46.01 16.00 71.96 9.48 9.90
2.3 由应变渗透引起的梁端附加转角
应变渗透是指在外荷载作用下框架梁端控制截面受拉钢筋在梁柱节点内的锚固区段存在拉伸应变的现象[13]。该拉伸应变使得节点内的受拉纵筋在梁端控制截面存在一定滑移值，该滑移值与梁端控制截面受拉区高度的比值即为应变渗透引起的附加转角。中柱两侧梁端及边柱内侧梁端受拉纵筋应变渗透分别如图16(a)、图16(b)所示。
图16 节点内锚固钢筋应变渗透
Fig.16 Strain penetration of reinforcement anchored in joints
如果忽略梁柱节点内混凝土变形，则节点内锚固钢筋在中柱两侧梁端控制截面及边柱内侧梁端控制截面的滑移量可分别按式(1)、式(2)计算。本文参考白绍良等[14-15]对直角弯折梁筋在边节点中的锚固性能试验结果，认为边柱内锚固钢筋水平段长度不小于0.4la(la为钢筋基本锚固长度)、竖直段长度不小于15d(d为钢筋直径)时，竖直段钢筋应力不大，近似认为弯弧末端处钢筋滑移量δ为零。结合控制截面实际受压区高度，则可按式(3)计算由钢筋应变渗透引起的附加转角数值。
式中：Δ为锚固钢筋相对滑移量；a为中柱内受拉纵筋锚固长度，如图16(a)所示；b为边柱内受拉纵筋直锚段长度，如图16(b)所示；x0为截面实际受压区高度；θ为应变渗透引起的附加转角。
当采用高强热轧钢筋作受拉纵筋时，由于钢筋屈服强度相对较高，由节点内钢筋应变渗透引起的附加转角会增大，应变渗透对框架梁端控制截面弯矩调幅的提高作用增强。基于实测钢筋应变值，分别计算试验框架梁端受拉纵筋屈服时刻及极限状态下应变渗透引起的附加转角值θy和θu，见表5。
表5 各框架梁端控制截面两特征时刻应变渗透引起的附加转角值
Table 5 Additional rotations due to strain penetration at two characteristic points
试件 编号 中柱两侧梁端 边柱内侧梁端 x0,y/mm θy/(×10-3rad) x0,u/mm θu/(×10-3rad) x0,y/mm θy/(×10-3rad) x0,u/mm θu/(×10-3rad)西侧 东侧 西侧 东侧 西侧 东侧 西侧 东侧 KJ-A-1 106.67 2.39 2.32 93.06 2.94 2.92 56.39 1.97 2.13 31.11 4.34 4.37 KJ-A-2 126.87 3.79 3.77 123.43 4.22 4.21 79.06 3.31 3.31 54.42 5.40 5.51 KJ-A-3 101.53 2.96 2.96 87.37 3.27 3.28 57.11 2.58 2.57 31.46 5.23 5.22 KJ-A-4 111.76 4.81 4.99 107.60 5.29 5.34 68.61 3.82 3.78 42.52 6.22 6.31 KJ-A-5 103.69 4.11 4.10 87.46 4.82 4.89 55.09 3.67 3.61 29.79 6.62 6.66 KJ-A-6 118.84 2.70 2.72 116.82 2.95 2.96 68.34 2.24 2.25 38.89 4.15 4.11 KJ-B-1 115.30 2.15 2.16 101.57 2.81 2.78 65.59 1.73 1.78 34.17 4.12 4.16 KJ-B-2 124.37 3.49 3.56 122.90 4.20 4.16 81.62 3.01 2.98 48.25 5.24 5.33
续表
注：x0,y为控制截面受拉纵筋屈服时刻截面实际受压区高度；x0,u为控制截面受压边缘达到混凝土极限压应变时刻截面实际受压区高度。
试件 编号 中柱两侧梁端 边柱内侧梁端 x0,y/mm θy/(×10-3rad) x0,u/mm θu/(×10-3rad) x0,y/mm θy/(×10-3rad) x0,u/mm θu/(×10-3rad)西侧 东侧 西侧 东侧 西侧 东侧 西侧 东侧 KJ-B-3 105.19 2.76 2.74 81.55 3.06 3.09 63.67 2.24 2.28 32.25 4.71 4.73 KJ-B-4 124.67 4.59 4.67 121.01 5.18 5.19 74.28 3.22 3.08 42.85 5.37 5.48 KJ-B-5 117.36 4.00 4.03 113.27 4.78 4.81 57.89 3.06 2.99 28.42 6.05 6.04 KJ-B-6 123.80 2.57 2.55 121.56 2.87 2.83 75.62 1.99 1.94 44.50 3.82 3.93
3 弯矩调幅分析
将试验框架梁端弯矩调幅分两阶段进行计算分析：一是由梁端控制截面受拉区混凝土进入塑性至受拉纵筋屈服这一塑性发展过程引起的弯矩调幅幅度βI；二是由塑性铰形成至控制截面受压边缘达到混凝土极限压应变引起的弯矩调幅幅度βII。其中，受拉纵筋屈服强度fy、梁端控制截面相对受压区高度ξ、节点内受拉纵筋应变渗透引起的梁端附加转角θ以及混凝土抗压强度fc[16-20]对两阶段弯矩调幅的影响是本文所关注的。
3.1 弯矩调幅全过程
由框架柱端控制截面处每根纵筋的实测应变值及截面内力平衡条件可计算确定框架梁端控制截面实际弯矩值；由外荷载可计算确定框架梁端控制截面的弹性弯矩值，则各级荷载作用下梁端控制截面弯矩调幅系数按式(4)计算。
其中：Me,i、Mt,i分别为加载至第i级荷载时，梁端控制截面弹性弯矩计算值和弯矩实测值；Me,u为极限荷载作用下，梁端控制截面弹性弯矩计算值。需要指出，由于框架中柱两侧梁端和边柱内侧梁受拉纵筋不会同时屈服，各梁端区域形成塑性铰后框架计算简图会发生变化，其他控制截面弯矩调幅对象应根据变化后简图计算。
加载过程中各框架梁端控制截面弯矩调幅系数随梁端控制截面弯矩实测值变化全过程如图17～图28所示。随着荷载逐渐增加，A点为框架梁端上部混凝土开裂，B点为框架梁端受拉钢筋屈服，梁端附近形成塑性铰，弯矩调幅开始进入第二阶段。弯矩由梁端控制截面向其他截面调整，直到梁端控制截面受压边缘达到混凝土极限压应变的C点。各框架梁端控制截面特征时刻弯矩调幅系数计算结果见表6。
3.2 第一阶段弯矩调幅
3.2.1 相关参数对第一阶段弯矩调幅的影响
图29为fc、ξ和lah/d相同时，第一阶段弯矩调幅系数βI随fy的变化情况。由于钢筋屈服强度的提高，由受拉区混凝土进入塑性到混凝土开裂、裂缝发展再至受拉纵筋屈服这一过程变长，故βI随fy的增大而增大。以HRB500钢筋作受拉纵筋的框架梁端第一阶段弯矩调幅系数为基准，引入钢筋屈服强度对第一阶段弯矩调幅影响系数ηsI，按式(5)计算。
图17 KJ-A-1框架梁端控制截面弯矩调幅全过程
Fig.17 Process of moment redistribution at the critical section of KJ-A-1
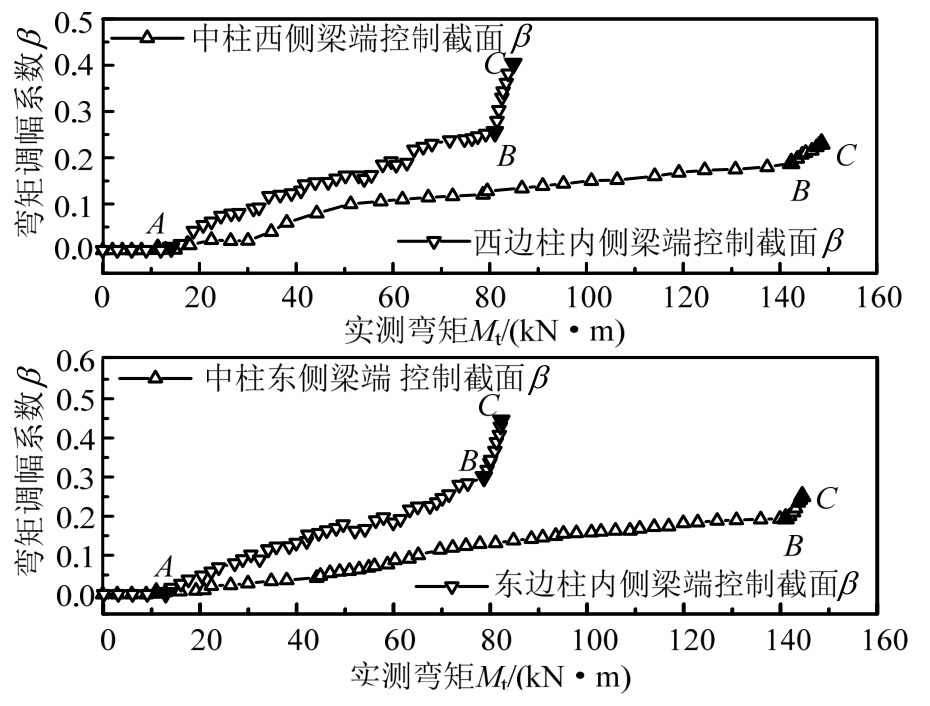
图18 KJ-A-2框架梁端控制截面弯矩调幅全过程
Fig.18 Process of moment redistribution at the critical section of KJ-A-2
图19 KJ-A-3框架梁端控制截面弯矩调幅全过程
Fig.19 Process of moment redistribution at the critical section of KJ-A-3
图20 KJ-A-4框架梁端控制截面弯矩调幅全过程
Fig.20 Process of moment redistribution at the critical section of KJ-A-4
图21 KJ-A-5框架梁端控制截面弯矩调幅全过程
Fig.21 Process of moment redistribution at the critical section of KJ-A-5
图22 KJ-A-6框架梁端控制截面弯矩调幅全过程
Fig.22 Process of moment redistribution at the critical section of KJ-A-6
图23 KJ-B-1框架梁端控制截面弯矩调幅全过程
Fig.23 Process of moment redistribution at the critical section of KJ-B-1
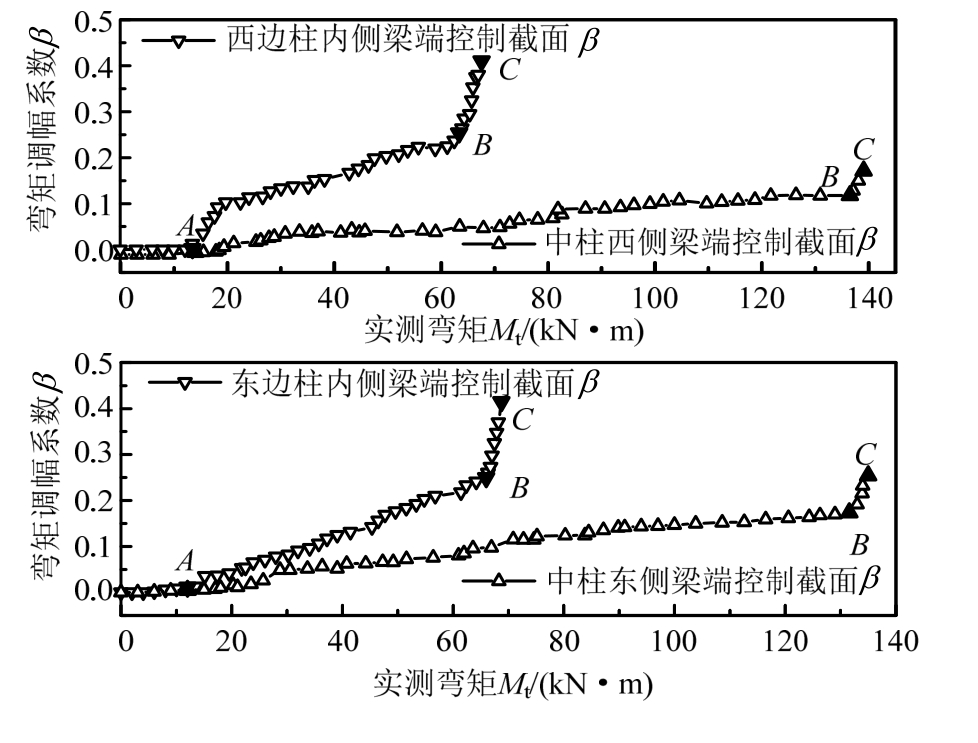
图24 KJ-B-2框架梁端控制截面弯矩调幅全过程
Fig.24 Process of moment redistribution at the critical section of KJ-B-2
图25 KJ-B-3框架梁端控制截面弯矩调幅全过程
Fig.25 Process of moment redistribution at the critical section of KJ-B-3
图26 KJ-B-4框架梁端控制截面弯矩调幅全过程
Fig.26 Process of moment redistribution at the critical section of KJ-B-4
图27 KJ-B-5框架梁端控制截面弯矩调幅全过程
Fig.27 Process of moment redistribution at the critical section of KJ-B-5
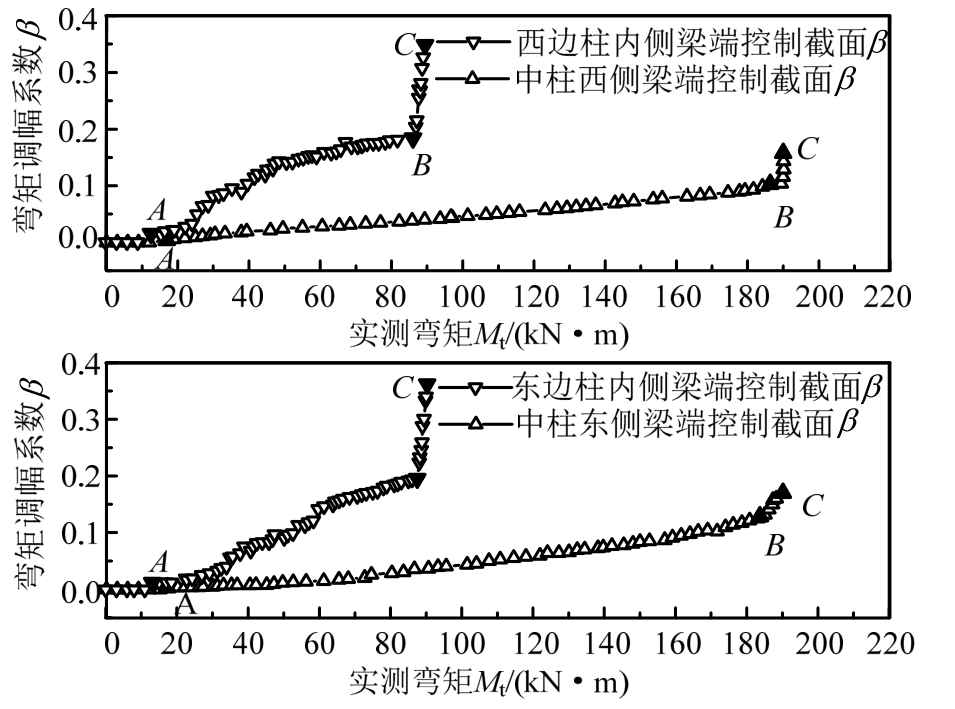
图28 KJ-B-6框架梁端控制截面弯矩调幅全过程
Fig.28 Process of moment redistribution at the critical section of KJ-B-6
表6 各试验框架梁端控制截面特征时刻弯矩调幅计算结果
Table 6 Moment redistribution of critical sections at each characteristic point of test specimens
编号 出铰 顺序 梁端控制截面位置 中柱两侧梁端 边柱内侧梁端 控制截面 受拉纵筋屈服时刻 控制截面受压边缘达到 混凝土极限压应变时刻 控制截面 受拉纵筋屈服时刻 控制截面受压边缘达到 混凝土极限压应变时刻 弹性 计算值Me,y/(kN·m)实测值 Mt,y/(kN·m)βy/(%)弹性 计算值Me,u/(kN·m)实测值 Mt,u/(kN·m)βu/(%)弹性 计算值Me,y/(kN·m)实测值 Mt,y/(kN·m)βy/(%)弹性 计算值Me,u/(kN·m)实测值 Mt,u/(kN·m)βu / (%)KJ-A-1 1 西侧 143.89 114.44 18.45 159.62 117.84 26.17 67.53 40.07 29.24 93.90 44.20 52.93东侧 143.89 112.54 19.64 159.62 116.06 27.29 65.39 38.66 30.07 88.90 42.25 52.47 KJ-A-2 1 西侧 178.63 142.29 18.82 193.09 148.58 23.05 117.38 81.06 25.53 142.30 84.92 40.32东侧 178.63 141.14 19.42 193.09 144.59 25.12 122.92 78.61 29.97 147.84 82.24 44.37 KJ-A-3 2 西侧 191.27 149.55 20.23 206.27 153.62 25.53 87.48 55.00 28.20 115.17 57.29 50.26东侧 191.27 146.15 21.87 206.27 149.54 27.50 84.72 53.97 28.05 109.63 55.66 49.23 KJ-A-4 2 西侧 186.19 146.05 19.47 206.19 154.12 25.25 126.54 76.22 32.02 157.15 80.92 48.51东侧 191.19 148.92 20.50 206.19 153.10 25.75 133.34 79.74 33.38 160.55 84.37 47.45 KJ-A-5 2 西侧 198.79 153.01 20.01 228.79 159.87 30.13 99.32 52.60 33.34 140.14 55.04 60.73东侧 203.79 149.67 23.65 228.79 155.62 31.98 106.13 57.01 33.42 146.94 58.50 60.19 KJ-A-6 1 西侧 220.16 185.37 14.75 235.89 190.73 19.14 104.71 72.40 25.63 126.08 75.45 40.16东侧 220.16 188.27 13.75 231.96 192.19 17.14 102.58 69.72 25.63 128.22 74.59 41.82 KJ-B-1 1 西侧 128.17 106.84 14.51 147.00 110.20 25.03 58.98 38.00 26.29 79.81 40.75 48.94东侧 124.24 101.44 15.51 147.00 110.20 25.45 61.12 40.67 25.03 81.68 42.77 47.63
续表
注：出铰顺序1表示中柱两侧梁端先形成塑性铰；出铰顺序2表示边柱内侧梁端先形成塑性铰。
编号 出铰 顺序 梁端控制截面位置 中柱两侧梁端 边柱内侧梁端 控制截面 受拉纵筋屈服时刻 控制截面受压边缘达到 混凝土极限压应变时刻 控制截面 受拉纵筋屈服时刻 控制截面受压边缘达到 混凝土极限压应变时刻 弹性 计算值Me,y/(kN·m)实测值 Mt,y/(kN·m)βy/(%)弹性 计算值Me,u/(kN·m)实测值 Mt,u/(kN·m)βu/(%)弹性 计算值Me,y/(kN·m)实测值 Mt,y/(kN·m)βy/(%)弹性 计算值Me,u/(kN·m)实测值 Mt,u/(kN·m)βu / (%)KJ-B-2 2 西侧 166.09 136.39 16.40 181.09 139.00 23.24 92.47 63.44 25.33 114.62 67.64 40.98东侧 163.09 131.58 17.40 181.09 135.00 25.45 95.24 65.99 24.92 117.38 68.74 41.44 KJ-B-3 2 西侧 170.43 135.32 18.43 190.43 140.17 26.39 79.18 48.66 26.50 115.17 53.57 53.49东侧 170.43 136.75 17.68 190.43 140.60 26.16 84.72 52.92 27.61 115.17 54.82 52.40 KJ-B-4 2 西侧 186.27 148.18 18.46 206.27 151.13 26.73 105.24 70.89 25.90 132.61 72.39 45.41东侧 186.27 149.21 17.96 206.27 152.78 25.93 102.19 66.52 28.89 123.48 70.97 42.53 KJ-B-5 2 西侧 175.19 141.34 16.91 200.19 146.91 26.61 83.95 45.64 30.27 126.53 49.92 60.54东侧 175.19 140.19 17.93 195.19 144.39 26.02 86.99 50.32 28.30 129.57 53.39 58.80 KJ-B-6 1 西侧 209.72 186.36 10.35 225.61 189.98 15.79 111.60 86.31 18.38 137.60 89.67 34.83东侧 212.90 183.51 12.85 228.79 189.88 17.01 115.20 87.47 19.58 141.60 90.29 36.24
当fy和fc相同时，令δ1=100/θy、δ2=0.01/ξ0.5，则δ1βI随ξ的变化情况如图30所示、βI/δ2随屈服时刻应变渗透引起的梁端附加转角θy的变化情况如图31所示。可以看出，第一阶段弯矩调幅系数随ξ的增加而减小(见图30)，随θy的增大而增大(见 图31)。
图29 fy对βI的影响
Fig.29 Effect of fy on βI
图30 ξ对δ1βI的影响
Fig.30 Effect of ξ on δ1βI
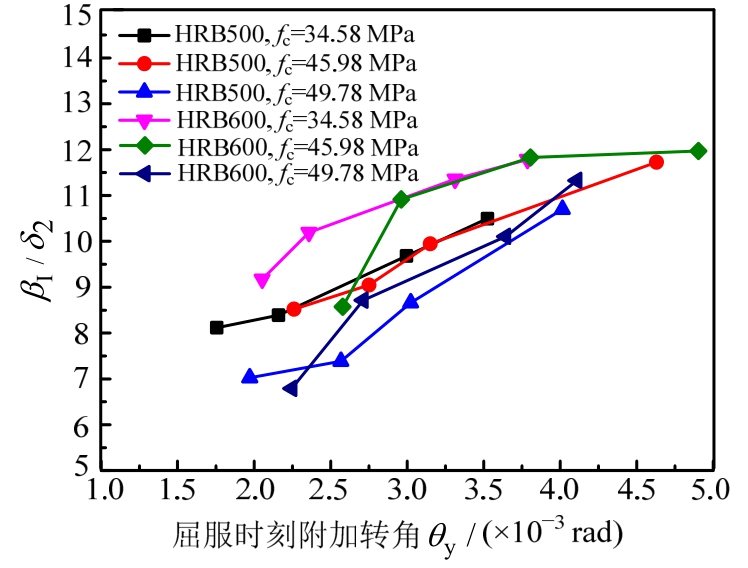
图31 θy对βI/δ2的影响
Fig.31 Effect of θy on βI/δ2
图32为fy、ξ、lah/d相同时，第一阶段弯矩调幅系数βI随fc的变化情况。由图可知，C40～C60混凝土抗压强度的变化对第一阶段弯矩调幅幅度影响并不明显。
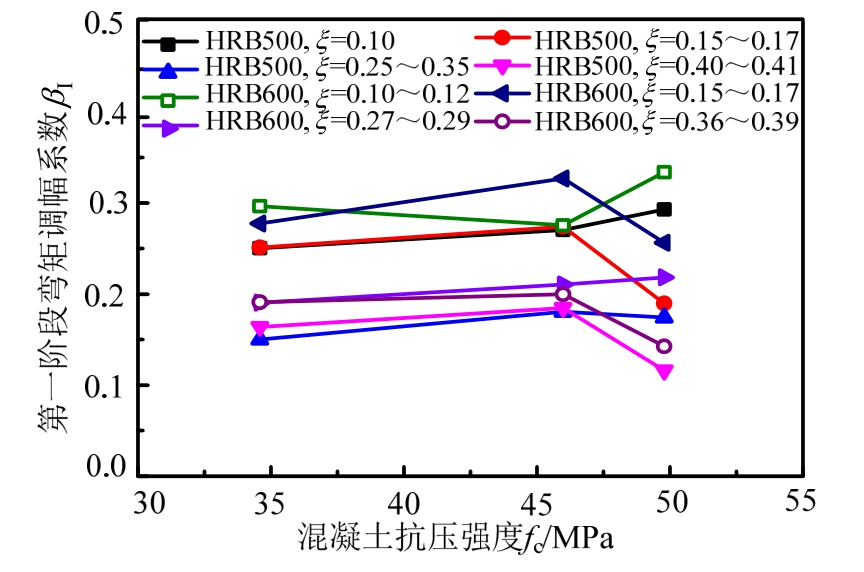
图32 fc对βI的影响
Fig.32 Effect of fc on βI
3.2.2 第一阶段弯矩调幅系数公式建立
以梁端控制截面相对受压区高度ξ和屈服时刻应变渗透引起的梁端附加转角θy为横坐标、以梁端控制截面第一阶段弯矩调幅系数βI为纵坐标建立坐标系，将各试验框架梁端控制截面第一阶段弯矩调幅系数试验值置于该坐标系中，则混凝土强度等级为C40～C60、相对受压区高度介于0.1～0.4的HRB500钢筋、HRB600钢筋作纵向受拉钢筋的框架梁端第一阶段弯矩调幅系数βI拟合曲面分别如图33(a)、图33(b)所示，经拟合按下式计算：
式中，ηsI为钢筋屈服强度对第一阶段弯矩调幅影响系数，按式(5)计算。统计分析表明，拟合公式计算值βI,c与试验值βI,t之比的平均值
=1.011，标准差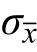
=0.095，变异系数
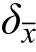=0.094，计算值和试验值对比如图33(c)所示。
图33 梁端控制截面第一阶段弯矩调幅系数拟合曲面
Fig.33 Fitting surfaces of first-stage moment redistribution
3.3 第二阶段弯矩调幅
框架梁端总塑性转角θp,Σ包括梁端塑性铰转角θp和由应变渗透引起的梁端附加塑性转角两部分，按下式计算：
式中，θy、θu 分别为梁端受拉纵筋屈服时刻和极限状态下应变渗透引起的梁端附加转角。
3.3.1 相关参数对第二阶段弯矩调幅的影响
图34为fc、ξ和lah/d相同时，第二阶段弯矩调幅βII随fy的变化情况。钢筋屈服强度的提高使截面屈服曲率增大，塑性铰转动能力降低，故βII随fy的增大而减小。以HRB500钢筋作受拉纵筋的框架梁端第二阶段弯矩调幅系数为基准，引入钢筋屈服强度对第二阶段弯矩调幅影响系ηsII，按下式计算：
当fy和fc相 同 时，令τ1=100/(θu-θy)0.3、τ2=0.01/ξ0.5，可得τ1·βII随ξ的变化情况如图35所示、βII/τ2随(θu-θy)变化情况如图36所示。由于ξ的增大使截面极限曲率减小，塑性铰转动能力降低，故βII随ξ的增大而减小(见图35)。由于梁端附加塑性转角(θu-θy)的增加对总塑性转角有有利贡献，故βII随(θu-θy)的增加而增大(见图36)。
图34 fy 对βII的影响
Fig.34 Effect of fy on βII
图35 ξ对τ1βII的影响
Fig.35 Effect of ξ on τ1βII
图36 (θu-θy)对βII/τ2的影响
Fig.36 Effect of (θu-θy)on βII/τ2
当fy、ξ和lah/d相同时，第二阶段弯矩调幅βII随fc的变化情况如图37所示。可以看出，在C40～C60间第二阶段弯矩调幅幅度变化规律并不明显。
图37 fc对βII的影响
Fig.37 Effect of fc on βII
3.3.2 第二阶段弯矩调幅系数公式建立
以总塑性转角θp,Σ为横坐标、以梁端控制截面第二阶段弯矩调幅系数βII为纵坐标建立坐标系，则混凝土强度等级C40～C60、相对受压区高度介于0.1～0.4的HRB500钢筋、HRB600钢筋作纵向受拉钢筋的框架梁端第二阶段弯矩调幅系数βII拟合曲线分别如图38(a)、图38(b)所示，经拟合按下式 计算：
其中，ηsII为钢筋屈服强度对第二阶段弯矩调幅影响系数，按式(8)计算。统计分析表明，拟合曲面计算值βII,c与试验值βII,t之比的平均值βII,c与试验值βII,t之比的平均值
=1.042，标准差
=0.145，变异系数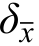
=0.139，计算值和试验值对比如图38(c)所示。
HRB500钢筋、HRB600钢筋作纵向受拉钢筋的框架梁端控制截面总弯矩调幅系数按下式计算：
其中：βI按式(6)计算，βII按式(9)计算。经分析，计算值βtol,c与试验值βtol,t之比的平均值=1.011，标准差=0.067，变异系数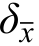=0.066。
图38 梁端控制截面第二阶段弯矩调幅系数拟合曲线
Fig.38 Fitted curves of second-stage moment redistribution
4 结论
(1)提出了将HRB500钢筋、HRB600钢筋作纵筋的混凝土框架梁端弯矩调幅分为塑性铰形成前后两阶段考察的思想。第一阶段为从受拉混凝土进入塑性、经历开裂和裂缝发展至受拉纵筋屈服引起的弯矩调幅；第二阶段为从受拉纵筋屈服到控制截面受压边缘达到混凝土极限压应变引起的弯矩调幅。
(2)随钢筋屈服强度的提高，由应变渗透引起的框架梁端附加转角增大，应变渗透增大了梁端控制截面弯矩调幅幅度。
(3)建立了混凝土强度等级为C40～C60、相对受压区高度介于0.1～0.4的HRB500钢筋、HRB600钢筋作纵向受拉钢筋的框架梁端控制截面两阶段弯矩调幅系数计算公式。第一阶段弯矩调幅系数随梁端控制截面相对受压区高度的增加呈幂函数减小趋势、随受拉纵筋屈服强度和受拉纵筋屈服时刻应变渗透引起的梁端附加转角的增加呈线性增长趋势；第二阶段弯矩调幅系数随总塑性铰转角的增大呈幂函数增长趋势、随受拉纵筋屈服强度的提高呈线性减小趋势。
(4)框架柱端控制截面拉区混凝土进入塑性后对弯矩调幅是有影响的，在后续工作中将开展相关研究。
[1]GB 50010—2010, 混凝土结构设计规范[S].北京：中国建筑工业出版社, 2010.Code for design of concrete structures [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[2]GB/T 1499.2—2018, 钢筋混凝土用钢 第2部分：热轧带肋钢筋[S].北京: 中国标准出版社, 2018 Steel for the reinforcement of concrete-Part 2:Hot rolled ribbed bars [S].Beijing: Standards Press of China, 2018.(in Chinese)
[3]Eligehausen R, Langer P.Rotation capacity of plastic hinges and allowable degree of moment redistribution.Universität Stuttgart - Universitätsbibliothek, 1987.
[4]GB/T 228.1—2010, 金属材料拉伸试验 第1部分：室温试验方法[S].北京: 中国建筑工业出版社, 2010.Metallic materials-tensile testing-Part 1: Method of test at room temperature [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[5]GB/T 50152—2012, 混凝土结构试验方法标准 [S].北京: 中国建筑工业出版社, 2012.Standard methods for testing of concrete structures [S].Beijing: China Architecture & Building Press, 2010.(in Chinese)
[6]王英, 周威, 郑文忠.跨中集中荷载下两跨UPC矩形截面连续梁塑性铰性能[J].土木工程学报, 2008, 41(5): 26—32.Wang Ying, Zhou Wei, Zheng Wenzhong.Performance of plastic hinge in a two-span continuous rectangular cross-section beam prestressed with unbonded tendons under concentrated load at mid span[J].China Civil Engineering Journal, 2008, 41(5): 26—32.(in Chinese)
[7]郑文忠, 王钧, 韩宝权, 等.内置H型钢预应力 混凝土连续组合梁受力性能试验研究[J].建筑结构学报, 2010, 31(7): 23—31.Zheng Wenzhong, Wang Jun, Han Baoquan, et al.Experimental research on mechanical behavior of continuous prestressed composite concrete beams with encased H-steel [J].Journal of Building Structures, 2010, 31(7): 23—31.(in Chinese)
[8]解恒燕, 郑文忠.内置钢箱-混凝土连续组合梁受力性能试验[J].哈尔滨工业大学学报, 2010, 42(2): 186—192.Xie Hengyan, Zheng Wenzhong.Experimental research on mechanical behavior of continuous encased steel box concrete beam [J].Journal of Harbin Institute of Technology, 2010, 42(2): 186—192.(in Chinese)
[9]Haskett M, Oehlers D J, Ali M S M, et al.Rigid body moment-rotation mechanism for reinforced concrete beam hinges [J].Engineering Structures, 2009, 31(5): 1032—1041.
[10]Wibowo A, Wilson J, Lam N, et al.Yield Penetration Displacement of Lightly Reinforced Concrete Columns [J].Applied Mechanics & Materials, 2016, 845: 119—125.
[11]陈明政, 魏世宏, 黄林青.三类预应力混凝土框架试验研究[J].工程力学, 2008(增刊1): 169—174.CheN Mingzheng, Wen Shihong, Huang Linqing.Test investigation of three types pre-stressed concrete frame [J].Engineering Mechanics, 2008(Suppl 1): 169—174.(in Chinese)
[12]王文炜, 吴文清, 李淑琴, 等.简支梁转变为连续梁的弯矩调幅试验研究及其简化计算方法[J].工程力学, 2010, 27(5): 147—152, 158.Wang Wenwei, Wu Wenqing, Li Shuqin, et al.Experimental study and calculation method on moment redistribution induced by transforming simply supported beams into continuous beams [J].Engineering Mechanics, 2010, 27(5): 147—152, 158.(in Chinese)
[13]Zhao J, Sritharan S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures [J].Aci Structural Journal, 2007, 104(2): 133—141.
[14]白绍良, 傅剑平, 汤华.框架中间层端节点梁筋直角弯折 锚固端设计概念及方法的改进 [J].重庆建筑工程学院学报, 1994, 16(3): 1—12.Bai Shaoliang, Fu Jianping, Tang Hua.Improvements for the design concept and approach of the anchorage end 90-degree bent beam reinforcement in frame exterior joints [S].Journal of Chongqing Architecture University, 1994, 16(3): 1—12.(in Chinese)
[15]白绍良, 傅剑平, 周中元.末端带直角弯折的梁筋在端节点中的锚固性能试验研究[J].重庆建筑工程学院学报, 1994, 16(2): 1—12.Bai Shaoliang, Fu Jianping, Zhou Zhongyuan.Experimental study on static anchorage behavior of beam bars with 90-degree hook in exterior joints of RC frames [S].Journal of Chongqing Architecture University, 1994, 16(2): 1—12.(in Chinese)
[16]Farahbod F, Mostofinejad D.Experimental study of moment redistribution in RC frames strengthened with CFRP sheets [J].Composite Structures, 2011, 93(3): 1168—1177.
[17]李龙起, 周东华, 廖文远, 等.腹板开洞钢-混凝土连续组合梁塑性铰及内力重分布试验研究[J].工程力学, 2015, 32(11): 123—131.Li Longqi, Zhou Donghua, Liao Wenyuan, et al.Experimental study on plastic hinge and international force redistribution for continuous steel-concrete composite beams with web openings [J].Engineering Mechanics, 2015, 32(11): 123—131.(in Chinese)
[18]Lou T, Lopes S M R, Lopes A V.Factors affecting moment redistribution at ultimate in continuous beams prestressed with external CFRP tendons [J].Composites Part B, 2014, 66(11): 136—146.
[19]Bagge N, O’Connor A, Elfgren L, et al.Moment redistribution in RC beams - A study of the influence of longitudinal and transverse reinforcement ratios and concrete strength [J].Engineering Structures, 2014, 80(5): 11—23.
[20]Lou T, Lopes S M R, Lopes A V.Neutral axis depth and moment redistribution in FRP and steel reinforced concrete continuous beams [J].Composites Part B, 2015, 70(3): 44—52.