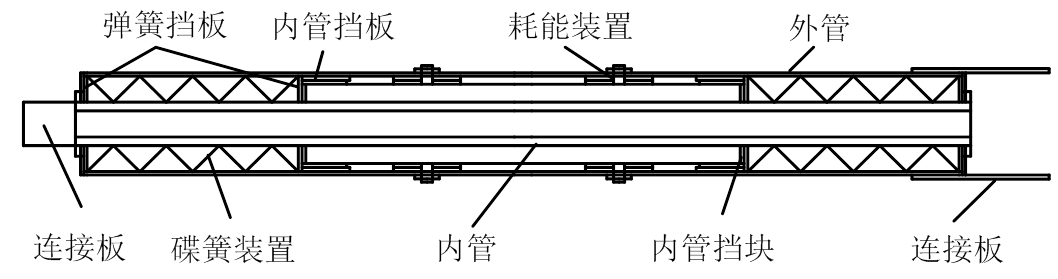
图1 PS-SCED支撑构造
Fig.1 Configuration of PS-SCED brace
摘 要:为减小斜拉桥横桥向的地震响应,提出一种设置预压弹簧自复位耗能支撑的斜拉桥横向减震体系及支撑参数的设计方法。以一座斜拉桥为研究对象,对支撑参数进行了设计,并对塔梁固结体系和采用支撑的减震体系进行地震时程分析,从关键位置的地震响应、耗能能力等方面对支撑体系的抗震性能进行了研究。结果表明,横桥向采用预压弹簧自复位耗能支撑的斜拉桥减震体系利用支撑良好的滞回耗能特性,有效减小桥塔位移和应变,改善桥塔受力,减小主梁的残余位移。附加预压弹簧自复位耗能支撑对斜拉桥地震响应有良好减震控制效果,是一种合理的抗震体系。
关键词:斜拉桥;预压弹簧自复位耗能支撑;减震设计;横向;抗震性能
近二十年来,斜拉桥设计和施工技术取得飞速的发展,斜拉桥成为许多国家高速公路系统的组成部分。大跨斜拉桥纵桥向一般采用漂浮体系,并在塔梁间设置减震装置来对其地震响应进行控制[1-2]。而在横桥向由于考虑风荷载作用,一般塔梁、墩梁间采用固定约束方式,斜拉桥横向刚度较大,这意味着在地震作用下主梁直接将惯性力传递到桥塔下部,往往导致塔底内力过大,强震作用下桥塔容易发生损伤和破坏。若地震力过大,支座被剪断,主梁在横桥向滑动可以降低主梁传递到斜拉桥下部的地震力,但主梁和墩塔间的位移将明显增加,且主梁与桥塔易发生碰撞,针对此,有学者提出在塔梁、墩梁间设置钢阻尼器,通过钢阻尼器良好的滞回耗能特性来耗散地震能量减小地震响应[3―4],但钢阻尼器在地震过后可能存在残余变形,桥墩和桥塔处梁不能恢复原位。
因此,本文以一座斜拉桥为研究对象,提出一种设置预压弹簧自复位耗能(pre-pressed spring self-centering energy dissipation, PS-SCED)支撑[5―7]的斜拉桥横向减震体系,及支撑参数设计方法,并对附加支撑的斜拉桥结构的横向抗震性能进行了研究。
PS-SCED支撑主要由内管、外管、碟簧装置和摩擦装置组成[8―9],其主要构造如图1所示。于内外管焊接摩擦板并埋置摩擦块,利用贯穿摩擦装置的高强螺栓对其施加预紧力。支撑内外管发生相对运动时,摩擦装置被激活,耗散地震输入能量。碟簧设于内管两侧,并在初始状态对其施加预压力,无论支撑受拉或受压,碟簧始终保持受压状态,其恢复力随支撑位移增大而增大。

图1 PS-SCED支撑构造
Fig.1 Configuration of PS-SCED brace
PS-SCED支撑滞回曲线如图2所示。初始加载,支撑内外管未发生相对位移时,支撑刚度k1由内外管共同提供,当荷载大于支撑起滑力(碟簧预压力P0和摩擦装置摩擦力F0之和)后支撑内外管开始相对滑动,此时支撑刚度k2仅由碟簧提供;初始卸载时,摩擦力方向改变,内外管还未发生相对位移时,刚度k3由内外管共同提供;当荷载减小为Pmax-2F0时,内外管开始滑动,此时刚度k4由碟簧提供。
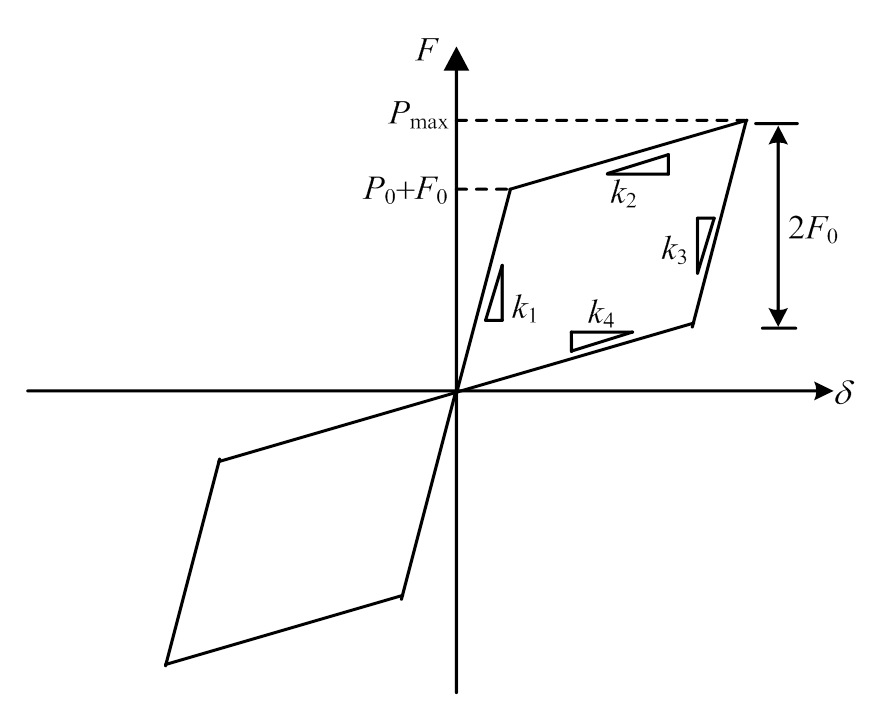
图2 PS-SCED支撑滞回曲线
Fig.2 Hysteretic curve of PS-SCED brace
PS-SCED支撑简化模型由弹簧单元和杆单元并联组成。数值模拟时,弹簧单元采用双折线弹性本构模型,杆单元采用理想弹塑性本构模型,两者叠加呈旗形滞回曲线,如图3所示。
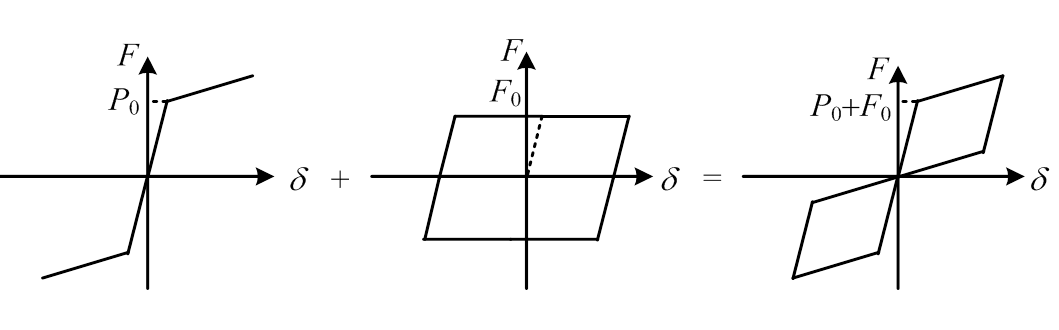
图3 PS-SCED支撑简化模型
Fig.3 Simplified model of PS-SCED brace
利用支撑简化模型,数值模拟预压力为270 kN,摩擦力分别为200 kN和300 kN的PS-SCED支撑滞回响应,并与支撑拟静力试验结果[8―9]做对比分析。试验加载过程采用位移控制,分级加载,每级幅值增加2 mm,循环加载3次,加至幅值为14 mm时结束。
PS-SCED支撑数值模拟与试验滞回曲线对比结果如图4所示。可以看出,支撑简化分析模型模拟出的滞回曲线与试验吻合较好,说明简化分析模型能够较好描述支撑的滞回特性。
表1列出了在不同加载位移情况下,PS-SCED支撑承载力数值模拟与试验结果对比情况。可以看出,摩擦力为200 kN时,支撑受拉方向承载力数值模拟与试验结果误差小于6%;支撑受压方向承载力误差在6%~10.1%之间。摩擦力为300 kN时,支撑在较大受拉位移处承载力数值模拟与试验结果误差在2%~10%之间,在较小受拉位移处两者误差较大为16.11%;支撑受压时两者承载力误差在1%~6%之间。说明支撑简化模型可以较好反映支撑实际受力情况。
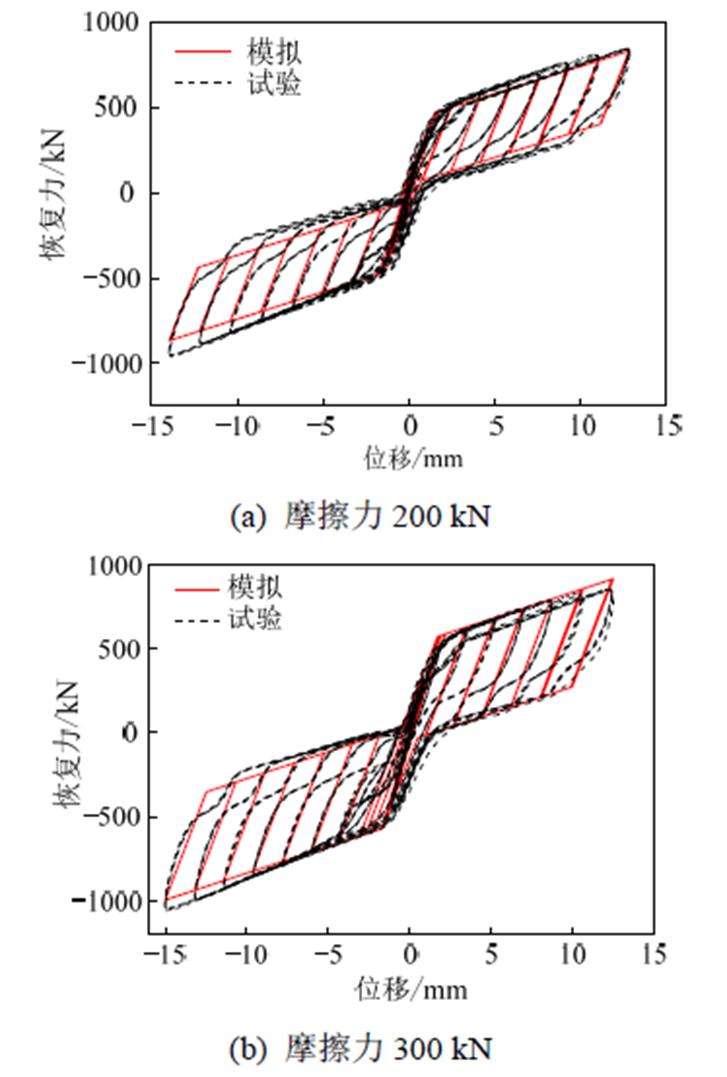
图4 PS-SCED支撑数值模拟与试验滞回曲线对比
Fig.4 Comparison of hysteretic curves between simulation and tests of PS-SCED brace
表1 PS-SCED支撑承载力数值模拟与试验结果对比
Table 1 Comparison of bearing capacity between simulation and tests of PS-SCED brace
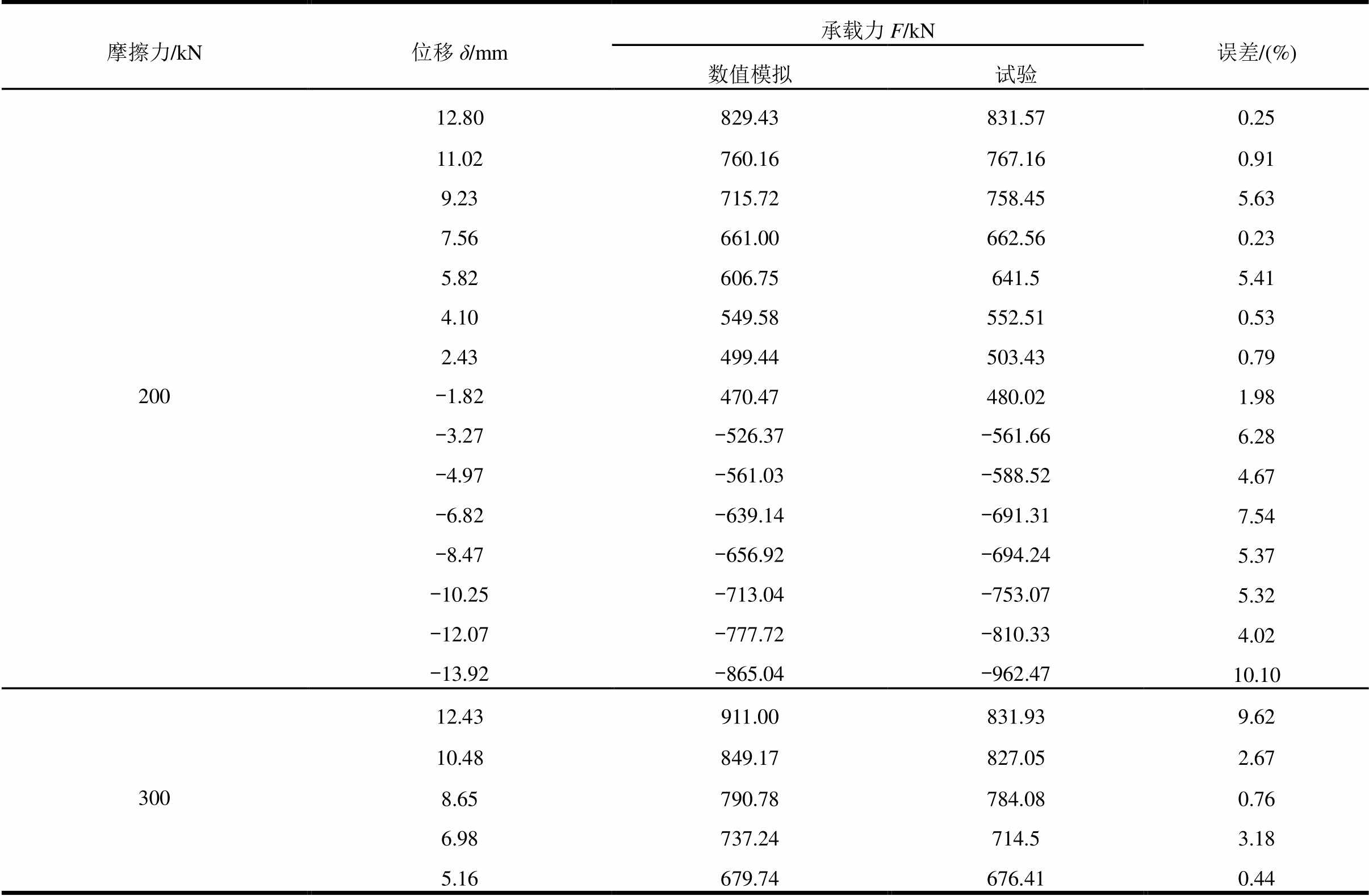
摩擦力/kN位移δ/mm承载力F/kN误差/(%) 数值模拟试验 20012.80829.43831.570.25 11.02760.16767.160.91 9.23715.72758.455.63 7.56661.00662.560.23 5.82606.75641.55.41 4.10549.58552.510.53 2.43499.44503.430.79 -1.82470.47480.021.98 -3.27-526.37-561.666.28 -4.97-561.03-588.524.67 -6.82-639.14-691.317.54 -8.47-656.92-694.245.37 -10.25-713.04-753.075.32 -12.07-777.72-810.334.02 -13.92-865.04-962.4710.10 30012.43911.00831.939.62 10.48849.17827.052.67 8.65790.78784.080.76 6.98737.24714.53.18 5.16679.74676.410.44
续表
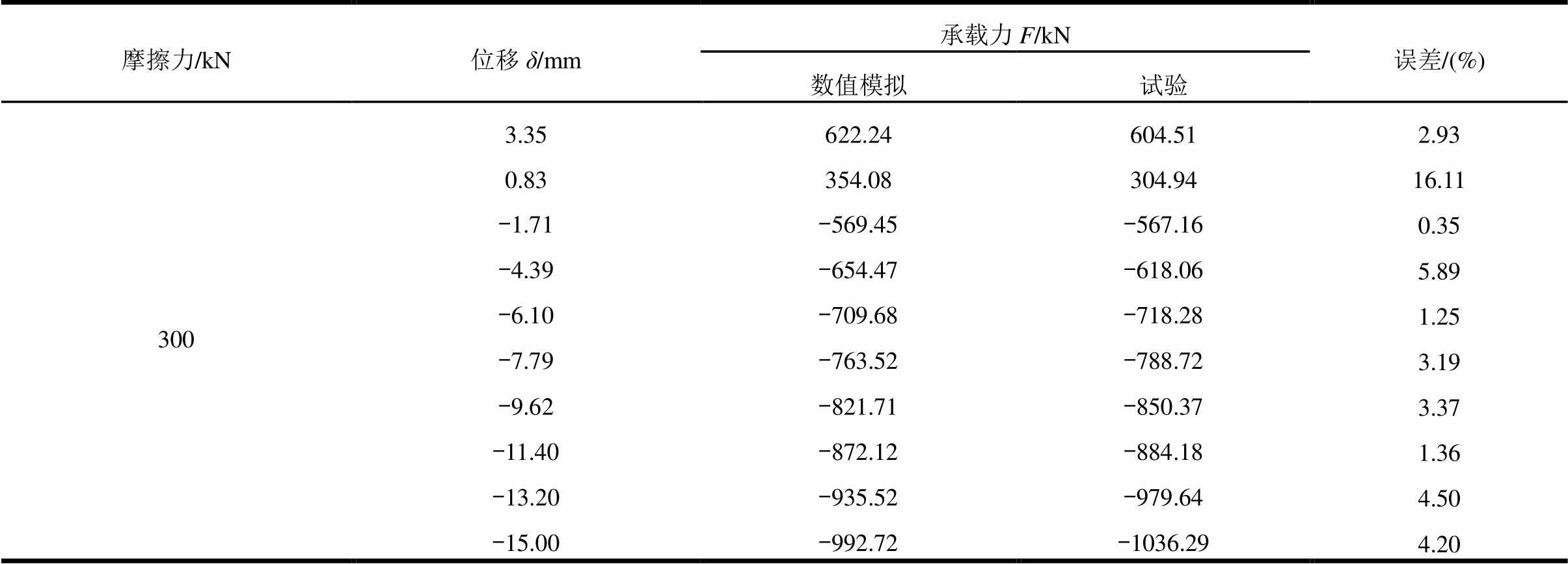
摩擦力/kN位移δ/mm承载力F/kN误差/(%) 数值模拟试验 3003.35622.24604.512.93 0.83354.08304.9416.11 -1.71-569.45-567.160.35 -4.39-654.47-618.065.89 -6.10-709.68-718.281.25 -7.79-763.52-788.723.19 -9.62-821.71-850.373.37 -11.40-872.12-884.181.36 -13.20-935.52-979.644.50 -15.00-992.72-1036.294.20
图5为不同加载位移情况下,PS-SCED支撑耗能能力数值模拟和试验结果对比。可以看出,摩擦力为200 kN时,支撑在较大加载位移处两者耗能误差在5%~25%之间,在较小加载位移处耗能误差在60%~75%之间,支撑数值模拟总耗能为108.97 kJ,试验总耗能为112.45 kJ,总耗能误差为3.1%;摩擦力为300 kN时,支撑在较大加载位移处耗能能力数值模拟与试验结果误差在1%~13%之间,在较小加载位移处两者耗能误差在25%~75%之间,支撑数值模拟总耗能为157.78 kJ,试验总耗能为146.01 kJ,总耗能误差为8.1%,说明支撑简化分析模型能够较好地反映支撑耗能情况。
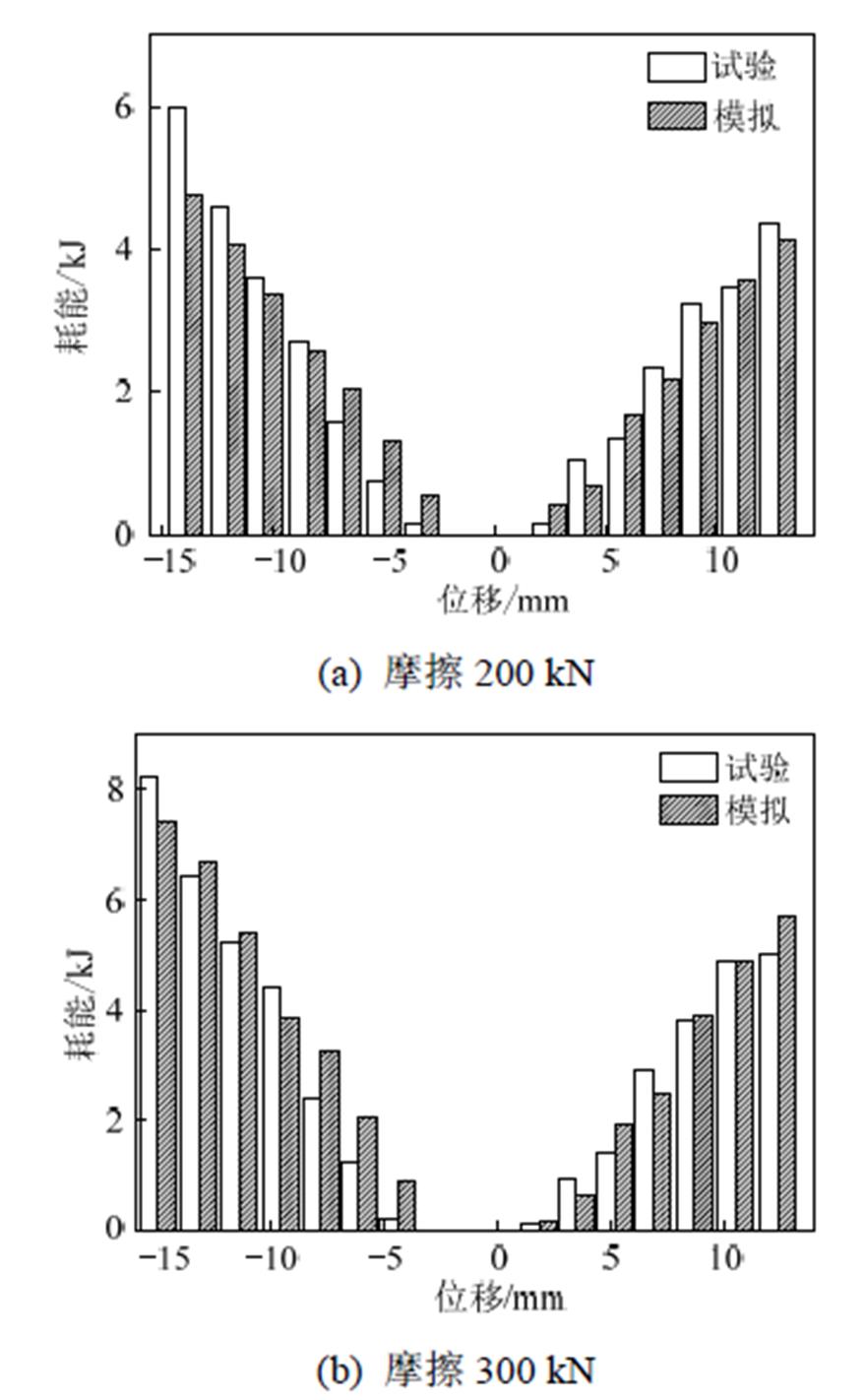
图5 PS-SCED支撑耗能能力数值模拟与试验结果对比
Fig.5 Comparison of energy dissipation between simulation and tests of PS-SCED brace
表2列出了两种工况下PS-SCED支撑刚度数值模拟与试验结果对比情况。可以看出,支撑刚度具有较好的拉压对称性,在受压时试验碟簧刚度大于数值模拟碟簧刚度,支撑第一刚度数值模拟与试验结果误差在3%~7%之间;碟簧刚度误差在3%~9%之间,说明PS-SCED支撑数值模型能够较好反映支撑刚度变化情况,因此可采用简化模型对支撑结构做进一步分析。
表2 PS-SCED支撑刚度数值模拟与试验结果对比
Table 2 Comparison of stiffness between simulation and tests of PS-SCED brace
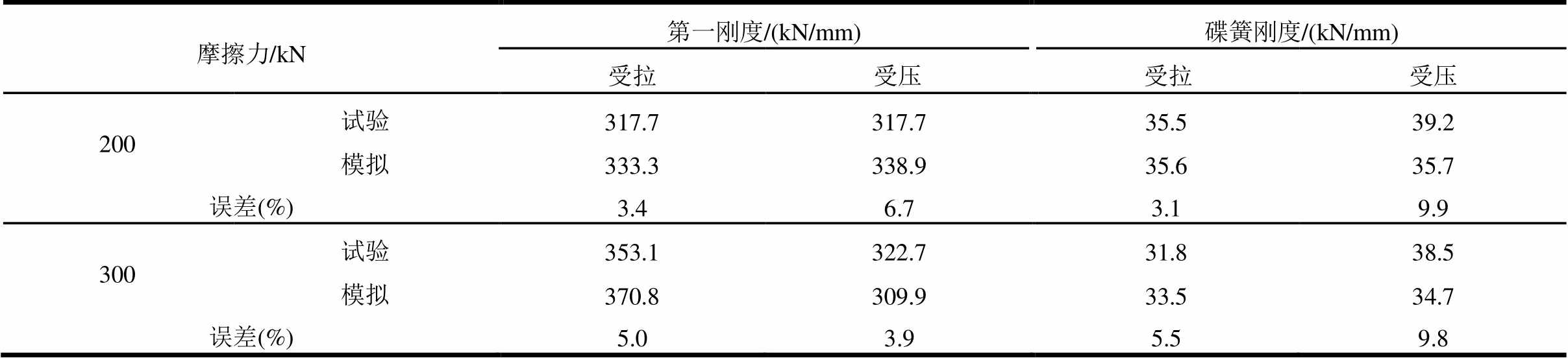
摩擦力/kN第一刚度/(kN/mm)碟簧刚度/(kN/mm) 受拉受压受拉受压 200试验317.7317.735.539.2 模拟333.3338.935.635.7 误差(%)3.46.73.19.9 300试验353.1322.731.838.5 模拟370.8309.933.534.7 误差(%)5.03.95.59.8
影响PS-SCED支撑力学性能的参数有支撑初始刚度、碟簧刚度和起滑力,选择合理的支撑参数可以实现主梁位移和墩塔内力的平衡统一。为了研究PS-SCED支撑对斜拉桥抗震性能的影响,首先需要确定支撑的三个参数,本文在Camara等[10]提出的斜拉桥钢阻尼器设计方法基础上考虑PS-SCED支撑力学性能特点对其进行了改进,图6为斜拉桥中PS-SCED支撑参数的设计流程。
分别在桥墩和桥塔处横向布置PS-SCED支撑,假设主梁在横向能够共同运动,则可以将斜拉桥结构等效为一个单自由度系统,主梁通过支撑与桥墩和桥塔相连,等效模型如图7所示。
PS-SCED支撑参数设计步骤为:
第一步,在桥塔下横梁处施加横向水平力,得到桥塔横向荷载位移曲线,找到主梁传递给桥塔的最大容许力,定为桥塔处支撑的最大承载力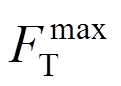 ,支撑起滑力与最大承载力之比为l,则桥塔处起滑力为:
,支撑起滑力与最大承载力之比为l,则桥塔处起滑力为:
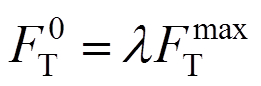 (1)
(1)为使桥墩和桥塔处支撑能共同起滑耗能,对斜拉桥结构进行反应谱分析,得到桥墩和桥塔支座处反力之比kR,桥墩处支撑起滑力为:
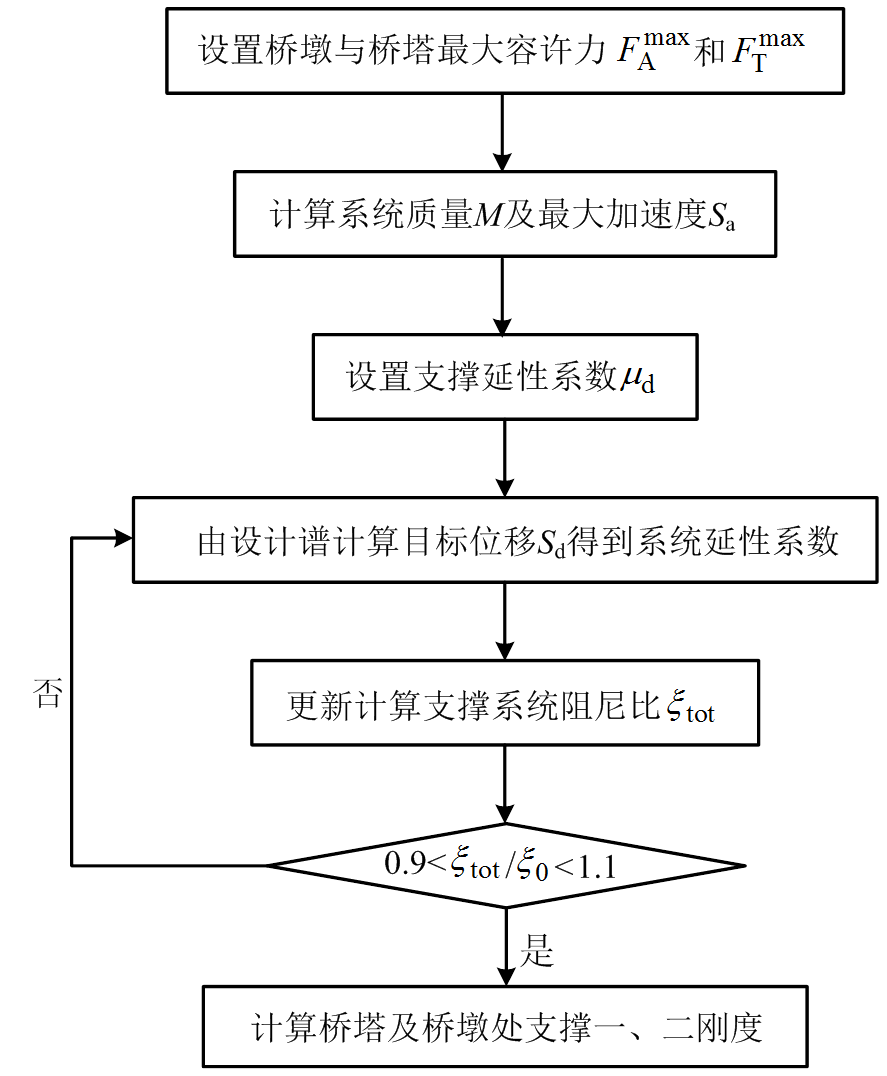
图6 PS-SCED支撑参数设计流程图
Fig.6 Parameter design flowchart of PS-SCED brace

图7 PS-SCED支撑参数设计中的等效单自由度模型
Fig.7 Equivalent single degree of freedom model in PS-SCED brace parameter design
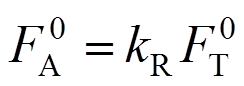 (2)
(2)第二步,计算对应于桥墩部位的主梁质量MA和对应于桥塔部分的质量MT,假设两者之比为kR,则有MA=kRMT,总质量MD=MA+MT。假设等效单自由度系统最大加速度为:
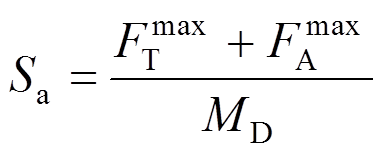 (3)
(3)
第三步,设置支撑延性系数md,即最大位移与起滑位移之比,其取值受支撑构造及主梁横向最大位移的限制。
第四步,通过设计反应谱和Sa得到等效单自由度系统振动周期T,假定等效单自由度系统的初始阻尼比为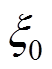 ,根据阻尼比定义设计谱,可以计算出等效单自由度系统的目标位移:
,根据阻尼比定义设计谱,可以计算出等效单自由度系统的目标位移:
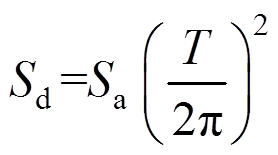 (4)
(4)则系统的延性系数为:
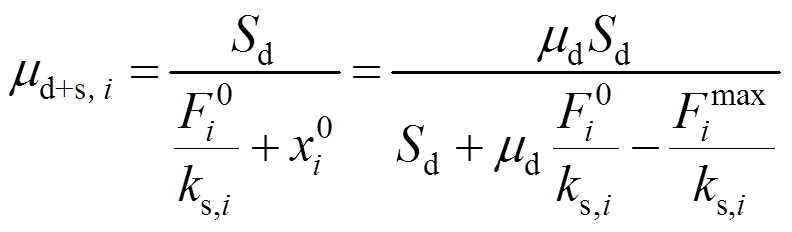 (5)
(5)
式中: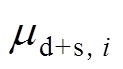 是i处支撑对应的斜拉桥下部结构延性系数,i=A代表桥塔,i=T代表桥墩;
是i处支撑对应的斜拉桥下部结构延性系数,i=A代表桥塔,i=T代表桥墩;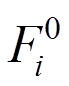 为i处支撑的起滑力;
为i处支撑的起滑力;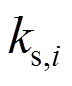 为i处支撑处对应的斜拉桥下部结构横向刚度;
为i处支撑处对应的斜拉桥下部结构横向刚度;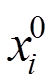 为i处支撑的起滑位移。
为i处支撑的起滑位移。
第五步,对等效单自由度系统的阻尼比进行更新,对于具有旗形滞回特性系统的模型,其更新后的阻尼比可由下式计算[11]:
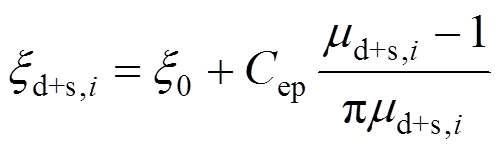 (6)
(6)式中: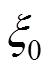 为结构初始阻尼比,斜拉桥阻尼比组成复杂,各阶振型的阻尼比分布不均匀[12],叠合梁斜拉桥各阶振型的实测阻尼比集中在0.01附近[13],故本文中取0.01,当振动周期T>1 s,
为结构初始阻尼比,斜拉桥阻尼比组成复杂,各阶振型的阻尼比分布不均匀[12],叠合梁斜拉桥各阶振型的实测阻尼比集中在0.01附近[13],故本文中取0.01,当振动周期T>1 s,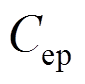 =0.3,当T<1 s,
=0.3,当T<1 s,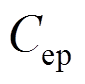 =0.3+0.0035(1-T)。系统总阻尼比可由下式计算:
=0.3+0.0035(1-T)。系统总阻尼比可由下式计算:
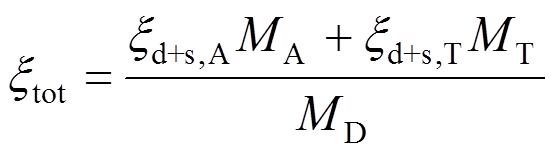 (7)
(7)
将计算得到的系统阻尼比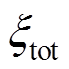 与初始假设阻尼比作比较,两者相差超过10%时需要将计算得到的阻尼比代回到第四步重新计算。
与初始假设阻尼比作比较,两者相差超过10%时需要将计算得到的阻尼比代回到第四步重新计算。
第六步,分别计算桥墩和桥塔处支撑的初始刚度和碟簧刚度。此时支撑初始刚度为:
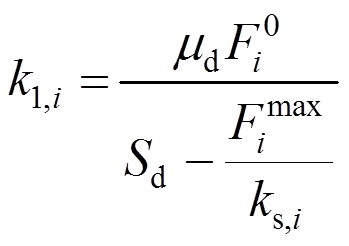 (8)
(8)碟簧刚度为:
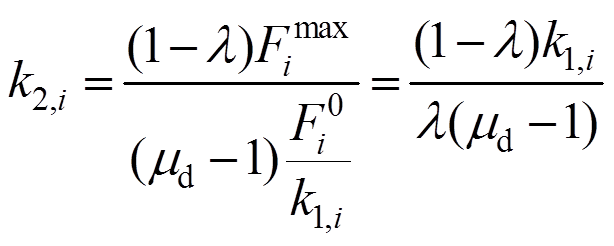 (9)
(9)
选择美国伊利诺伊州Quincy Bayview斜拉桥作为研究对象[14],该桥为双塔双索面钢板梁斜拉桥,主跨跨径为133 m+276 m+133 m,桥面宽14 m,H型钢筋混凝土桥塔高70.7 m,桥塔采用变截面形式,截面为空心矩形截面,全桥共4×14根拉索。采用ABAQUS建立斜拉桥有限元模型,如图7所示。主梁和桥塔采用ABAQUS中梁单元模拟,考虑剪切和弯曲变形,梁单元中混凝土拉应力始终为零,受压骨架曲线上升段采用Hognested曲线,下降段为直线,钢筋采用理想弹塑性模型,在达到屈服强度后应力不再增加;拉索采用杆单元模拟,只受拉不受压,无剪切弯曲变形,考虑斜拉桥材料非线性响应,不考虑温度效应。主梁在桥塔和桥墩处纵向无约束,竖向约束,横向分别考虑以下两种情况:1) 桥塔桥墩与主梁刚性连接,为固结体系; 2) 桥塔桥墩与主梁间采用PS-SCED支撑连接,为支撑体系。
斜拉桥结构按8度设防,二类场地条件,根据公路桥梁抗震设计细则中的设计谱[15],从美国太平洋地震研究中心强震数据库中选取了3条地震波,地震波时长30 s。采用SeismoMatch对地震波进行了处理,3条地震波加速度谱曲线与规范设计谱曲线如图8所示。
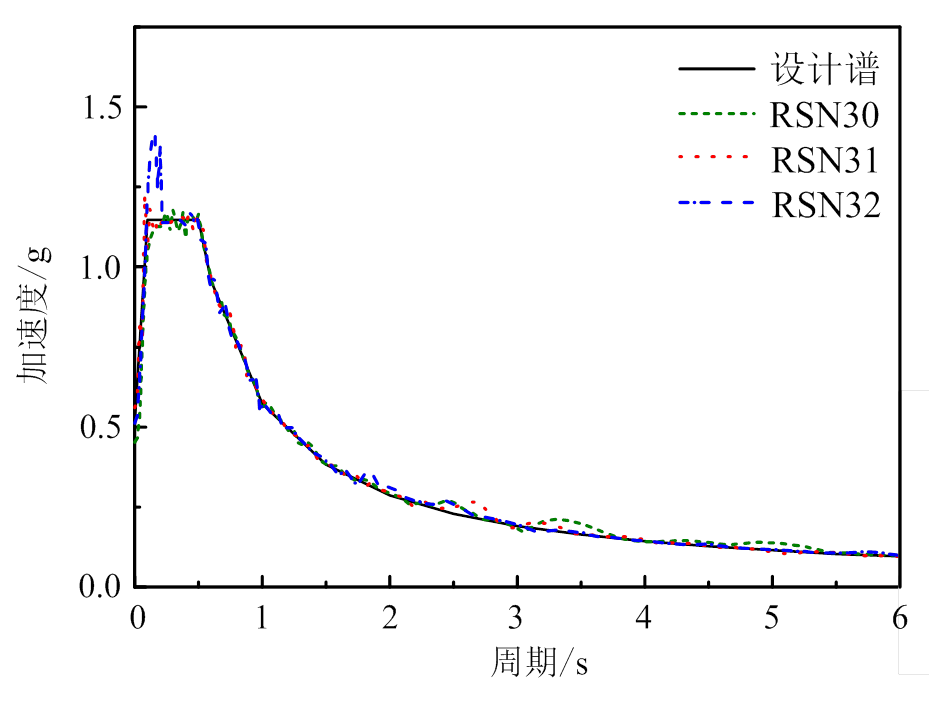
图8 地震波反应谱与设计谱
Fig.8 Earthquake spectrums and design spectrum
根据前面介绍方法对PS-SCED支撑参数进行设计,首先在桥塔下横梁处施加横向水平力,得到桥塔荷载位移曲线,如图9所示。从图中看出,桥塔刚度随着推力增大逐渐下降,当推力大于E点时,桥塔塔底钢筋开始发生屈服,为避免桥塔受力过大发生损伤破坏,选择E点的力作为主梁传递给桥塔的最大力,桥塔处支撑最大承载力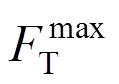 =6000 kN,支撑起滑力与极限承载力之比l取2/3,则桥塔处支撑起滑力
=6000 kN,支撑起滑力与极限承载力之比l取2/3,则桥塔处支撑起滑力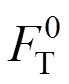 =4000 kN。再对斜拉桥结构进行反应谱分析得到桥墩和桥塔处支座的反力比kR=0.37,由此计算出桥墩处支撑起滑力。
=4000 kN。再对斜拉桥结构进行反应谱分析得到桥墩和桥塔处支座的反力比kR=0.37,由此计算出桥墩处支撑起滑力。
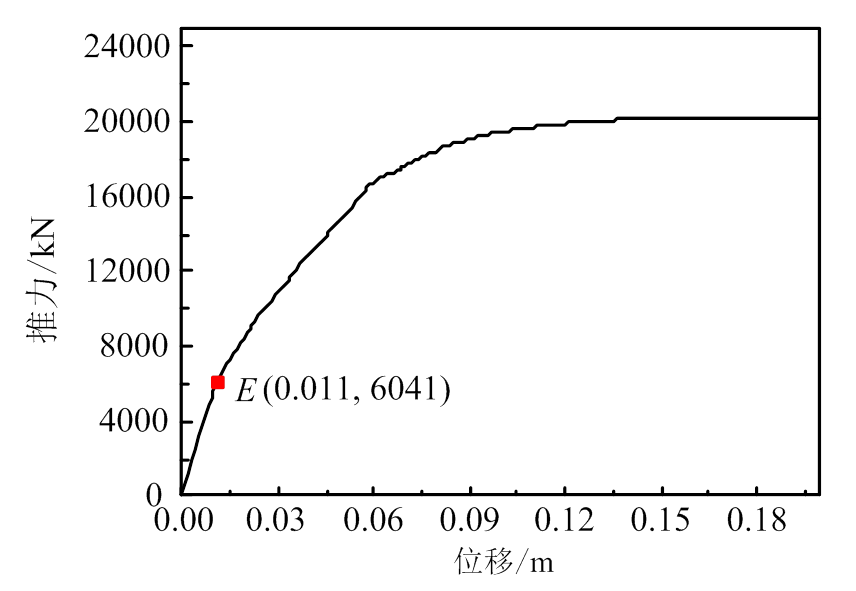
图9 桥塔横向荷载-位移曲线
Fig.9 Load-displacement curve of the tower in transverse direction
在步骤二中,MA取边跨质量一半,计算可得MA=805398 kg,则MT=2154622 kg,MD=2960020 kg,单自由度系统最大设计加速度Sa=2.46 m/s2。
在步骤三中,支撑延性系数取值不同,支撑设计参数不同,其取值要在合理范围内,满足支撑构造设计要求,支撑起滑位移一般小于10 mm,其设计目标位移Sd=172 mm,故在此取md=20对支撑参数进行设计。在确定目标位移Sd和支撑延性系数md后,则可得到支撑初始刚度和碟簧刚度。结合有限元模型,分别在每个桥塔和桥墩处布置两个PS-SCED支撑,全桥共布置8个,支撑参数如表3所示。
表3 PS-SCED支撑设计参数
Table 3 PS-SCED brace design parameters

支撑起滑力/kN初始刚度/(kN/mm)碟簧刚度/(kN/mm) 桥塔处2000248.16.5 桥墩处747.686.92.3
3.3.1 关键位置地震响应
表4中列出了固结体系和支撑体系在桥墩和桥塔处主梁与支座间的相对位移及主梁的残余位移。从表中可知,支撑体系相对于固结体系在桥墩处相对位移增加较大,在桥塔处相对位移增加较小;支撑体系和固结体系在桥墩处无残余位移,固结体系在桥塔处有残余位移,主要是由于桥塔下部发生了塑性变形;支撑体系在桥塔处相比于固结体系残余位移降低了63%以上,对主梁残余位移有明显的控制效果。
表4 两种体系的墩塔处主梁横向位移比较
Table 4 Comparison of transverse displacement of the beam on the pier and tower of the two systems
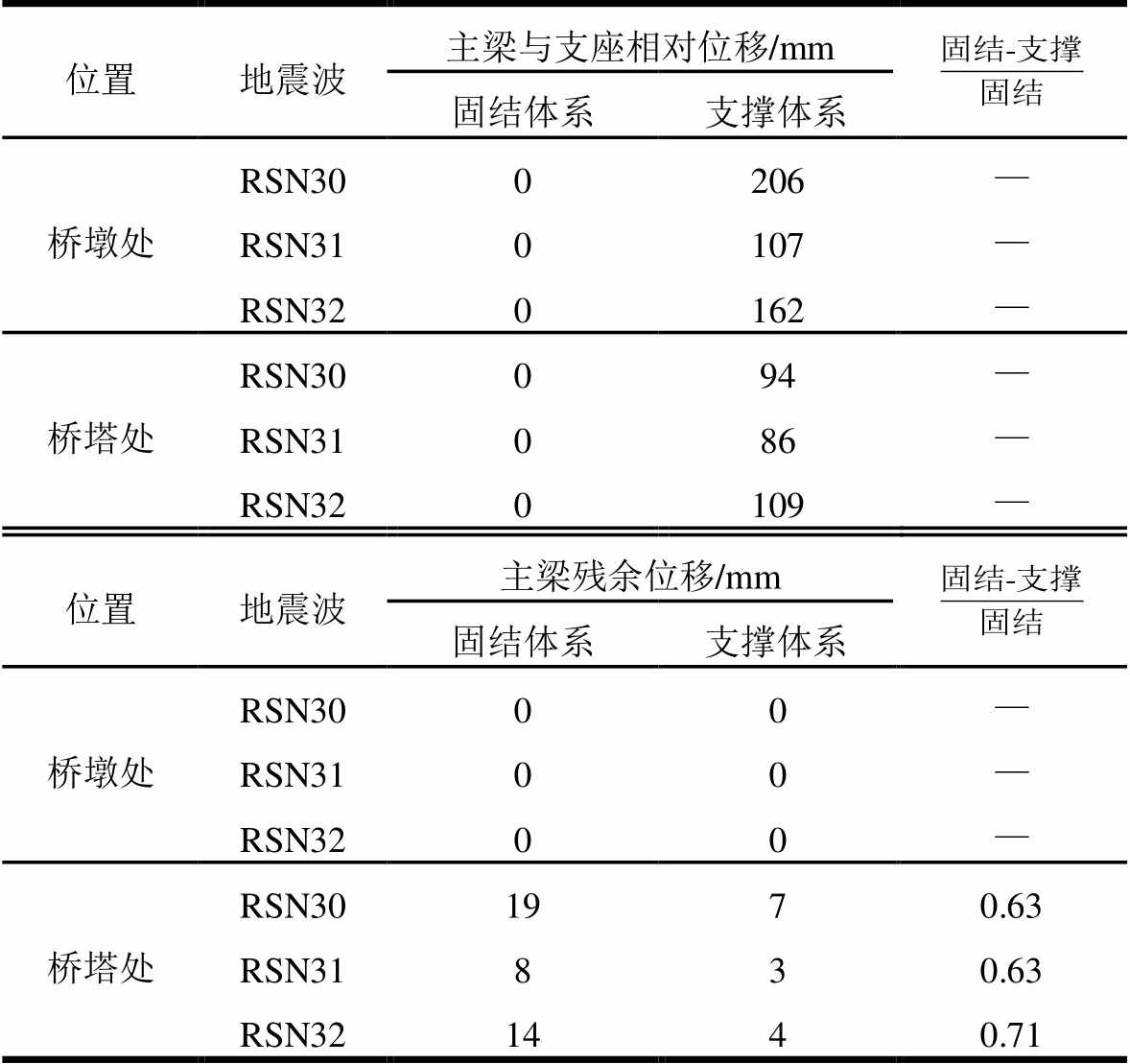
位置地震波主梁与支座相对位移/mm 固结体系支撑体系 桥墩处RSN300206— RSN310107— RSN320162— 桥塔处RSN30094— RSN31086— RSN320109— 位置地震波主梁残余位移/mm 固结体系支撑体系 桥墩处RSN3000— RSN3100— RSN3200— 桥塔处RSN301970.63 RSN31830.63 RSN321440.71
表5列出了两种体系桥墩和桥塔基底内力。从表中可以看出,支撑体系相对于固结体系剪力弯矩都有所减小,桥墩处基底剪力最大减小了46%,最小减小6%,桥塔处剪力减小约15%;支撑体系在桥墩处弯矩控制效果优于桥塔处,在桥墩处弯矩最大减小了46%,桥塔处弯矩最大减小11%。以上分析得出,附加PS-SCED支撑能有效控制基底内力,实现斜拉桥下部结构内力与主梁位移平衡统一。
表5 两种体系的基底内力比较
Table 5 Comparison of the base force of the two systems
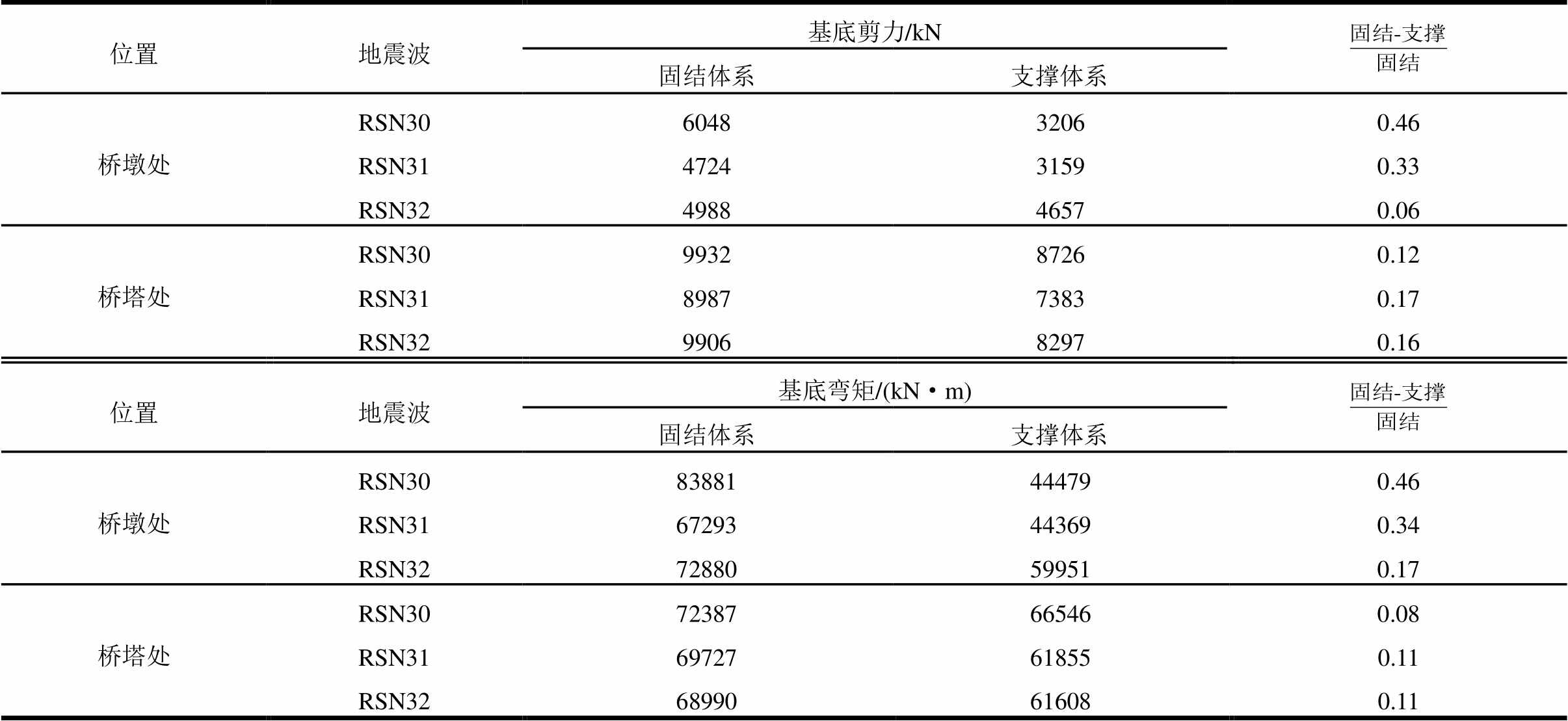
位置地震波基底剪力/kN 固结体系支撑体系 桥墩处RSN30604832060.46 RSN31472431590.33 RSN32498846570.06 桥塔处RSN30993287260.12 RSN31898773830.17 RSN32990682970.16 位置地震波基底弯矩/(kN·m) 固结体系支撑体系 桥墩处RSN3083881444790.46 RSN3167293443690.34 RSN3272880599510.17 桥塔处RSN3072387665460.08 RSN3169727618550.11 RSN3268990616080.11
3.3.2 桥塔塔身响应
图10为不同地震波输入下两种体系桥塔峰值位移随塔高的变化情况,从图中可以看出,支撑体系桥塔横向位移相比于固结体系明显降低。在塔横梁处,支撑体系桥塔横向位移小于固结体系,这是因为地震作用下固结体系横向刚度大,主梁传递给桥塔的惯性力大,而支撑体系中主梁通过支撑传递给桥塔的惯性力较小;随着塔高的增加,支撑体系横向位移减小越大,在塔顶处支撑体系相对于固结体系位移最大减小了34%,说明附加PS-SCED支撑能够有效控制桥塔横向位移。
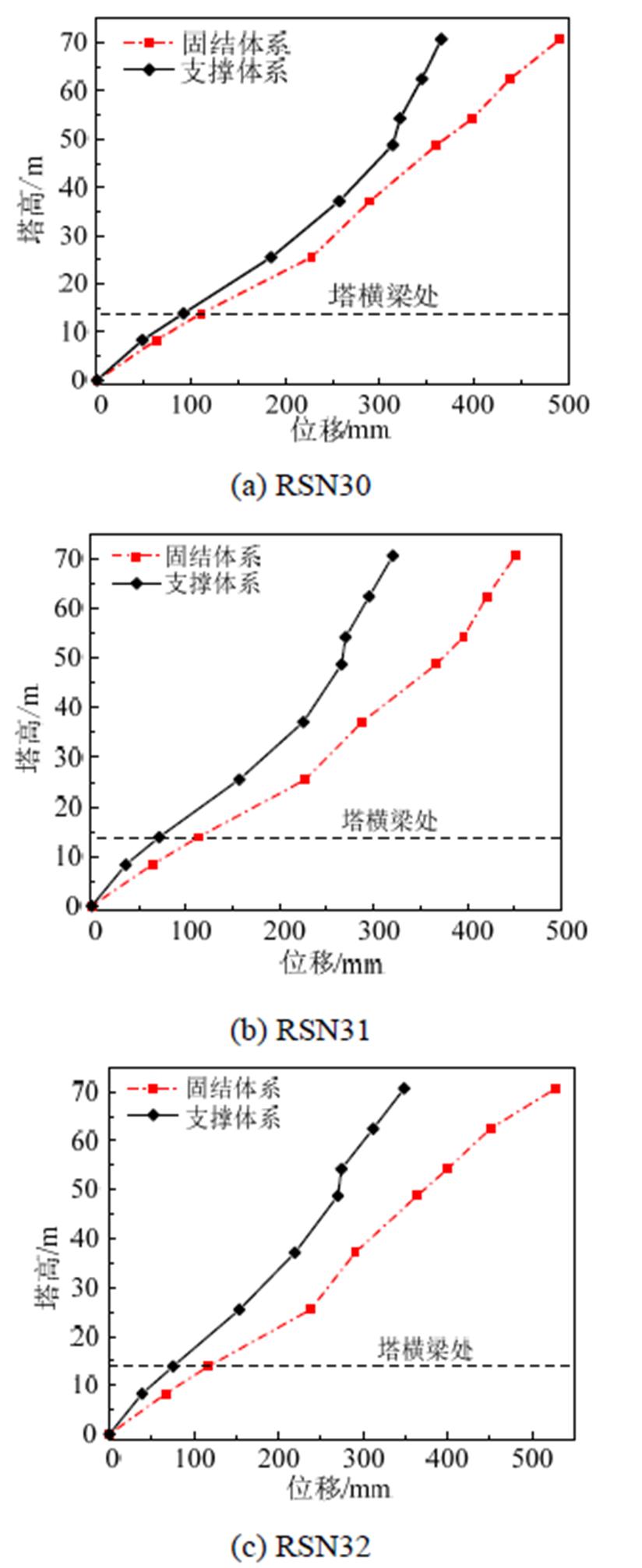
图10 不同地震波下两种体系塔身横向位移曲线
Fig.10 Tower transverse displacement curve of two systems under different earthquakes
图11为不同地震波作用下两种体系桥塔应变随塔高变化情况,结果包含自重的影响。其中负值代表桥塔截面混凝土压缩变形,正值代表截面钢筋拉伸变形。从图中可以看出,支撑体系塔身钢筋拉应变和混凝土压应变小于固结体系且钢筋应变减小比较明显。固结体系桥塔底部钢筋应变远超过钢筋屈服应变εsy=0.2%,支撑体系将塔底钢筋应变降低了31%以上,减小了塔底塑性损伤程度;支撑体系塔底混凝土压缩应变相比于固结体系减小8%以上;在桥塔横梁附近,支撑体系钢筋拉应变和混凝土压应变较固结体系分别减小50%和20%左右,附加PS-SCED支撑对桥塔变形有明显的改善。
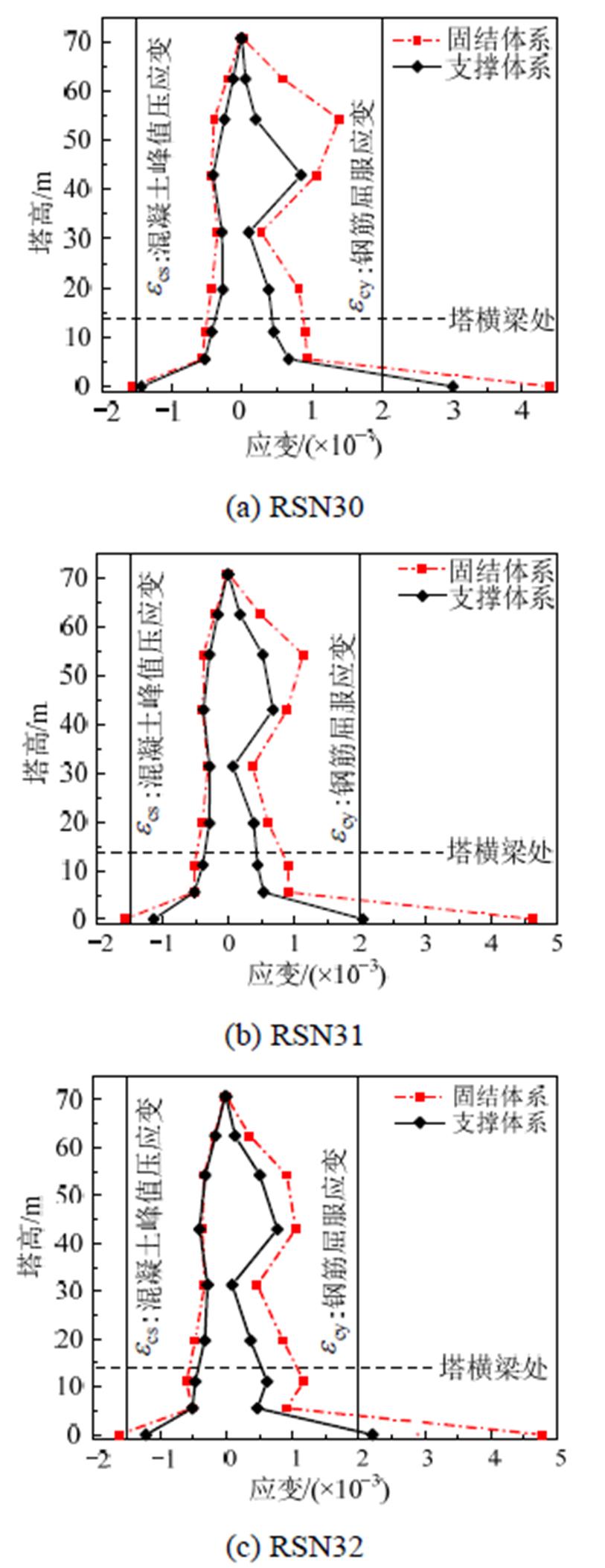
图11 不同地震波下两种体系塔身应变曲线
Fig.11 Tower strain curve of the two systems under different earthquakes
图12为不同地震波输入下两种体系桥塔剪力随塔高变化曲线,从图中可以看出,两种体系的桥塔上部剪力远小于下部剪力;支撑体系在桥塔上部的剪力相比于固结体系最大减小了67%,最小减小了8%,在桥塔下部剪力减小了约15%,可见附加PS-SCED支撑对桥塔塔身剪力有很好的改善效果。
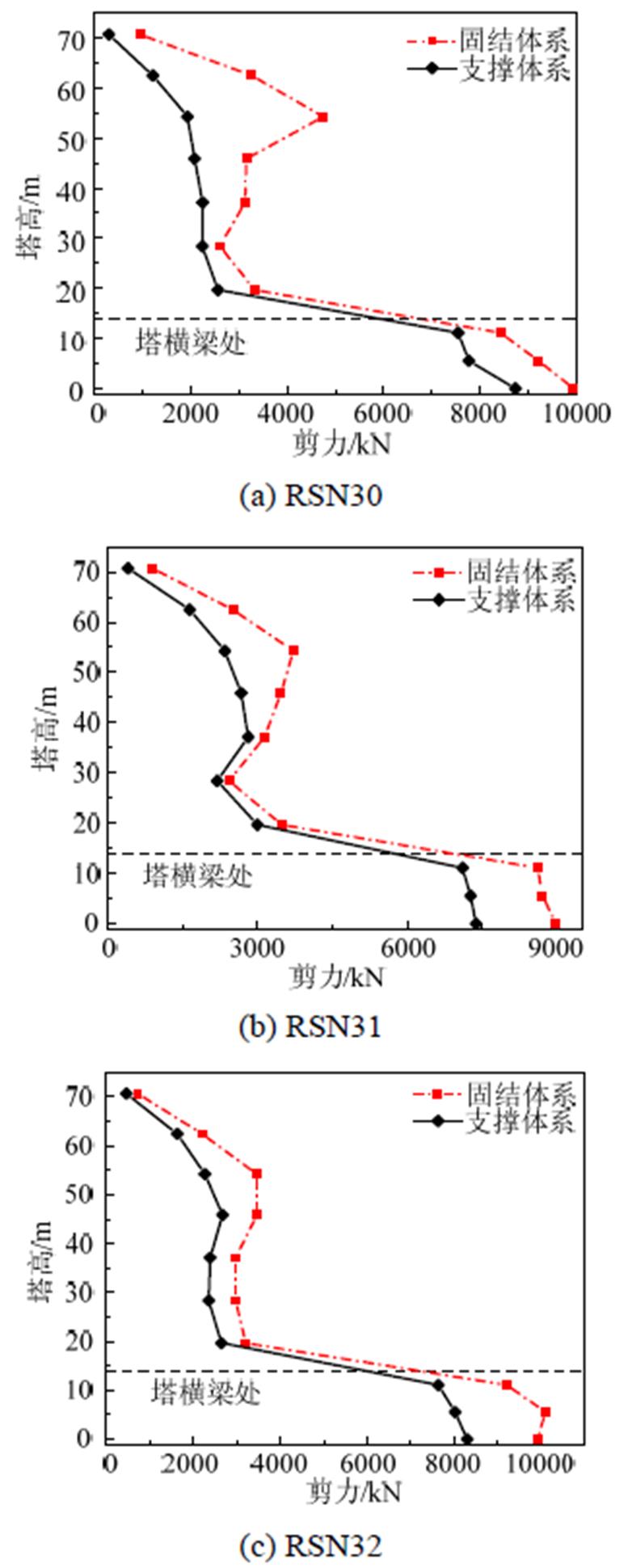
图12 不同地震波下两种体系塔身剪力曲线
Fig.12 Tower shear force curve of the two systems under different earthquakes
图13为不同地震波输入下两种体系桥塔弯矩随塔高的变化曲线,从图中可以看出,在桥塔上部,支撑体系相比于固结体系弯矩最大减小了38%,最小减小了8%;支撑体系在桥塔下部弯矩小于固结体系,其值最大减小了61%,最小减小7%,可见附加PS-SCED支撑同样能改善桥塔塔身弯矩。
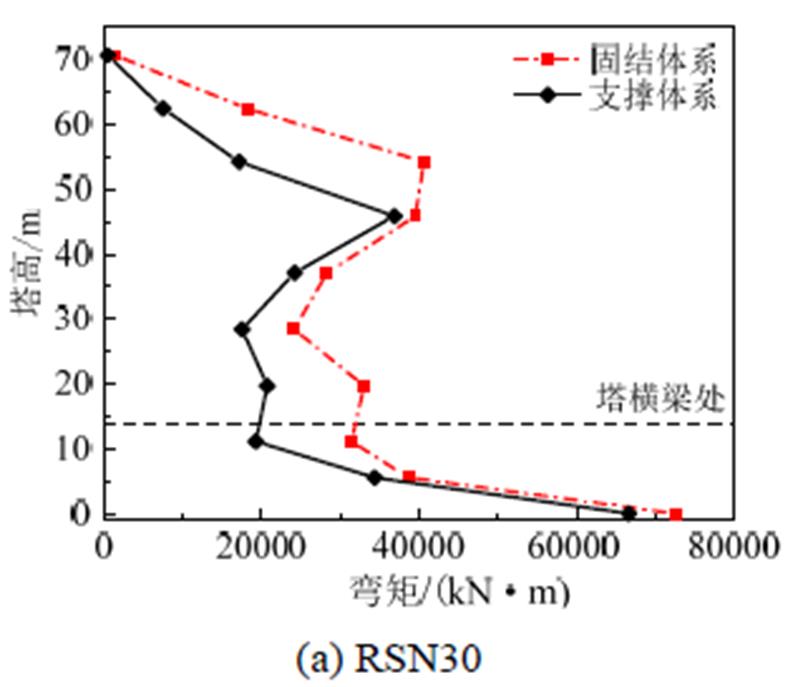
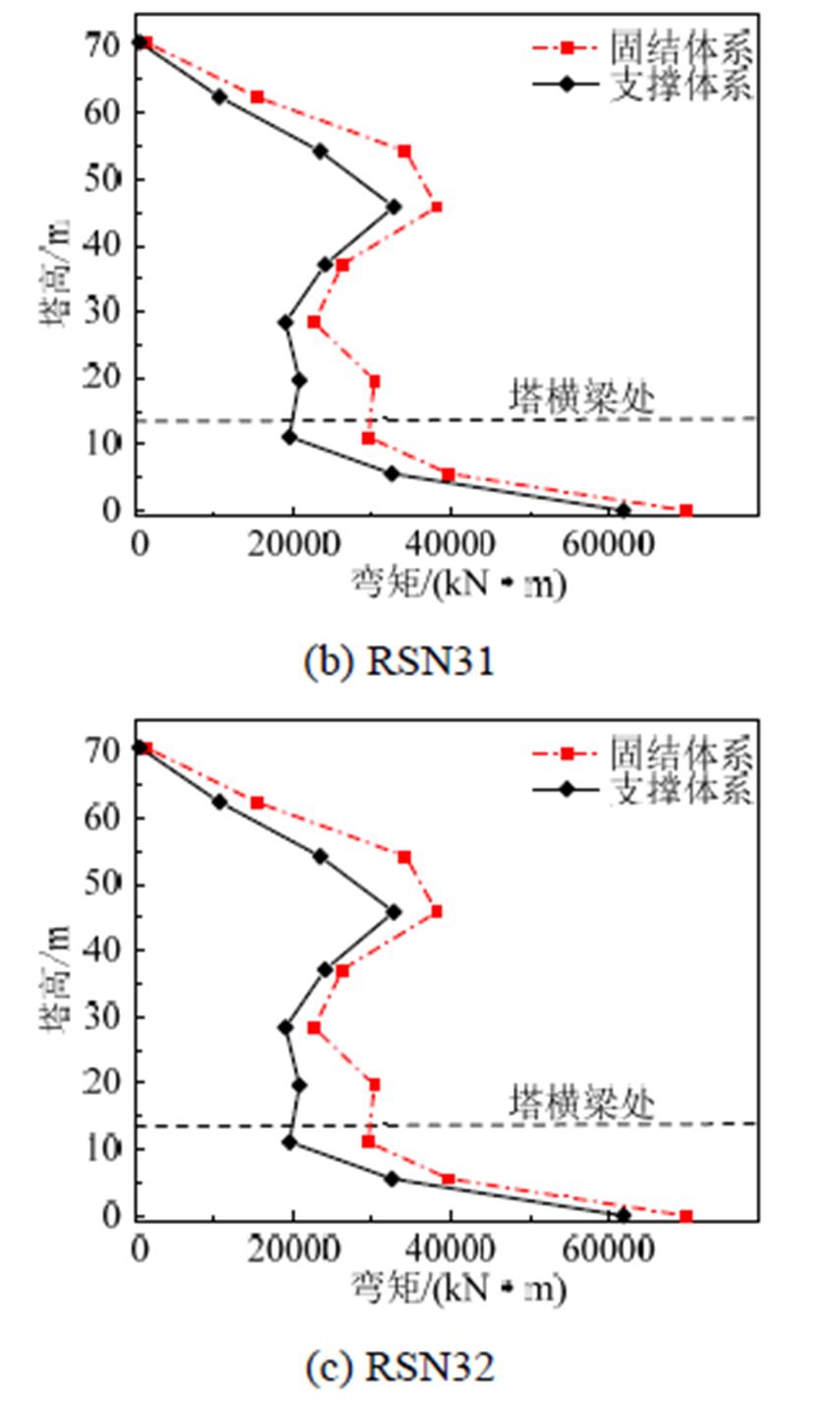
图13 不同地震波下两种体系塔身弯矩曲线
Fig.13 Tower moment curve of the two systems under different earthquake
3.3.3 主梁位移响应
图14为不同地震波输入下两种体系斜拉桥主梁横向位移情况。从图中可以看出,支撑体系主梁横向位移大于固结体系;固结体系在桥墩处横向位移最小,在跨中横向位移最大;支撑体系主梁横向位移不一致,主梁边跨位移较小,主跨位移较大,桥墩和桥塔处主梁横向位移分别相差37%、22%和3%,与等效单自由度模型的一致运动有差异,这主要是受主梁横向刚度的影响。从模拟结果来看,与固结体系相比,支撑体系在桥墩处位移增加较大,在桥塔处位移增加较小,增加了40%左右,但由于PS-SCED支撑的作用,支撑体系在桥墩和桥塔处的主梁位移相对整个主梁位移较小,PS-SCED支撑对主梁位移有一定的控制效果。
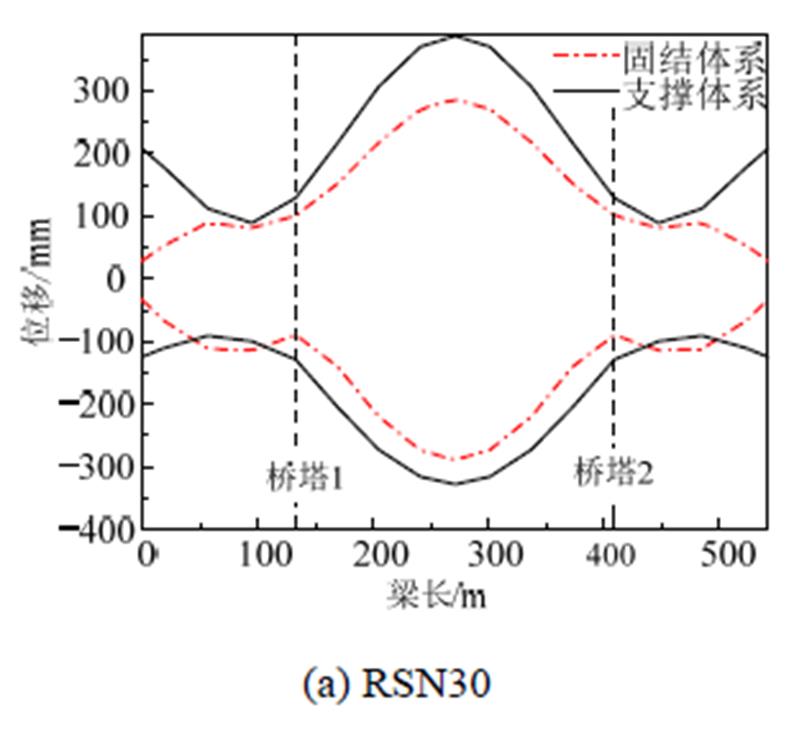
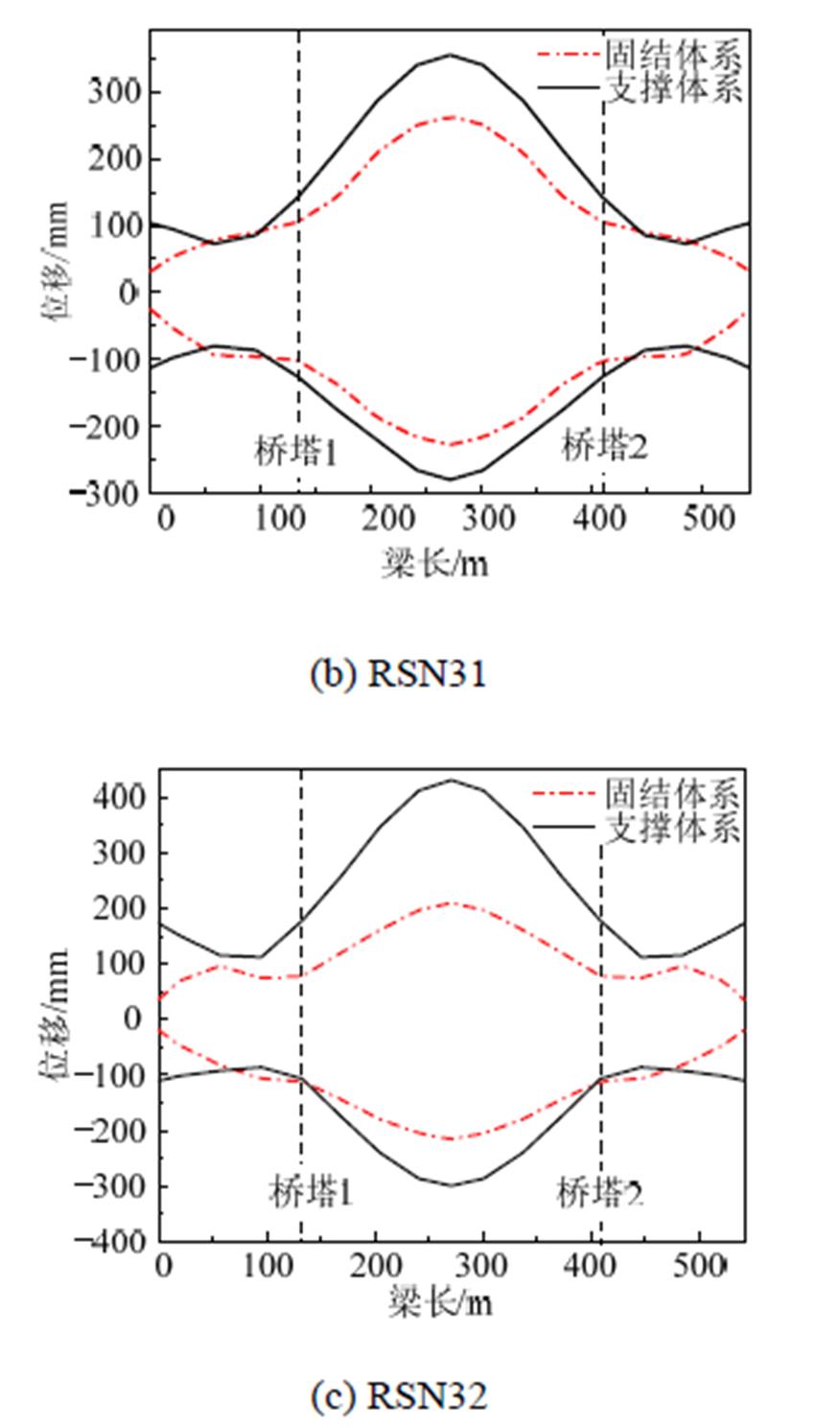
图14 不同地震波下两种体系主梁横向位移
Fig.14 Beam transverse displacement of the two systems under different earthquakes
3.3.4 耗能分析
图15为不同地震波输入下支撑体系桥塔和桥墩处PS-SCED支撑滞回曲线。可以看出,在地震作用中边墩处支撑最大位移大于桥塔处支撑最大位移,最大轴力远小于桥塔处支撑最大轴力,边墩处支撑耗能约为桥塔处支撑耗能的60%。
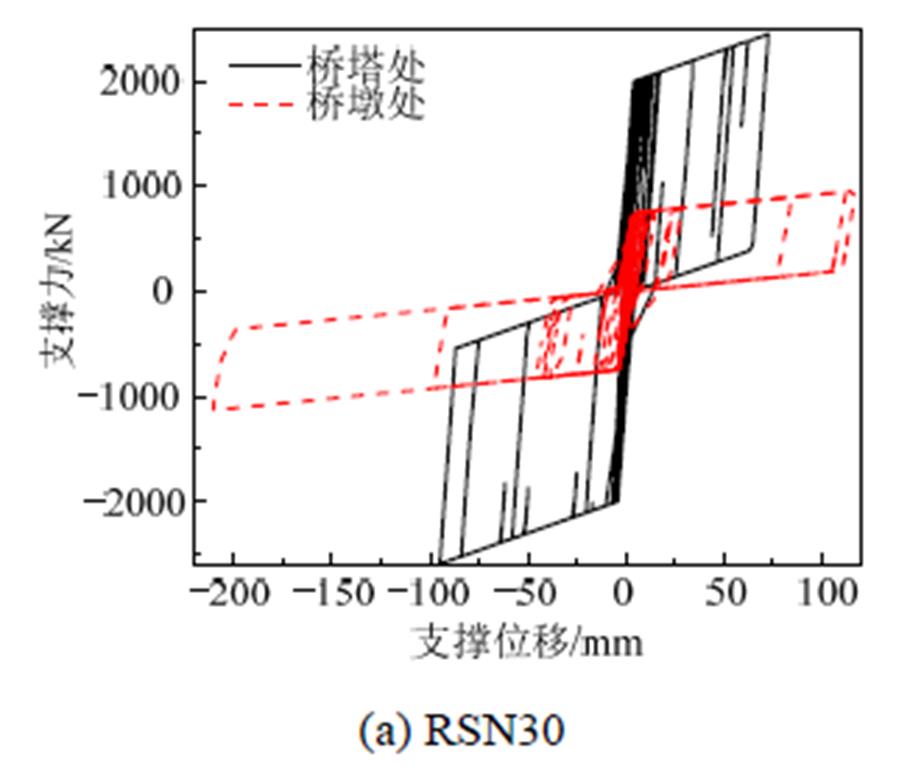
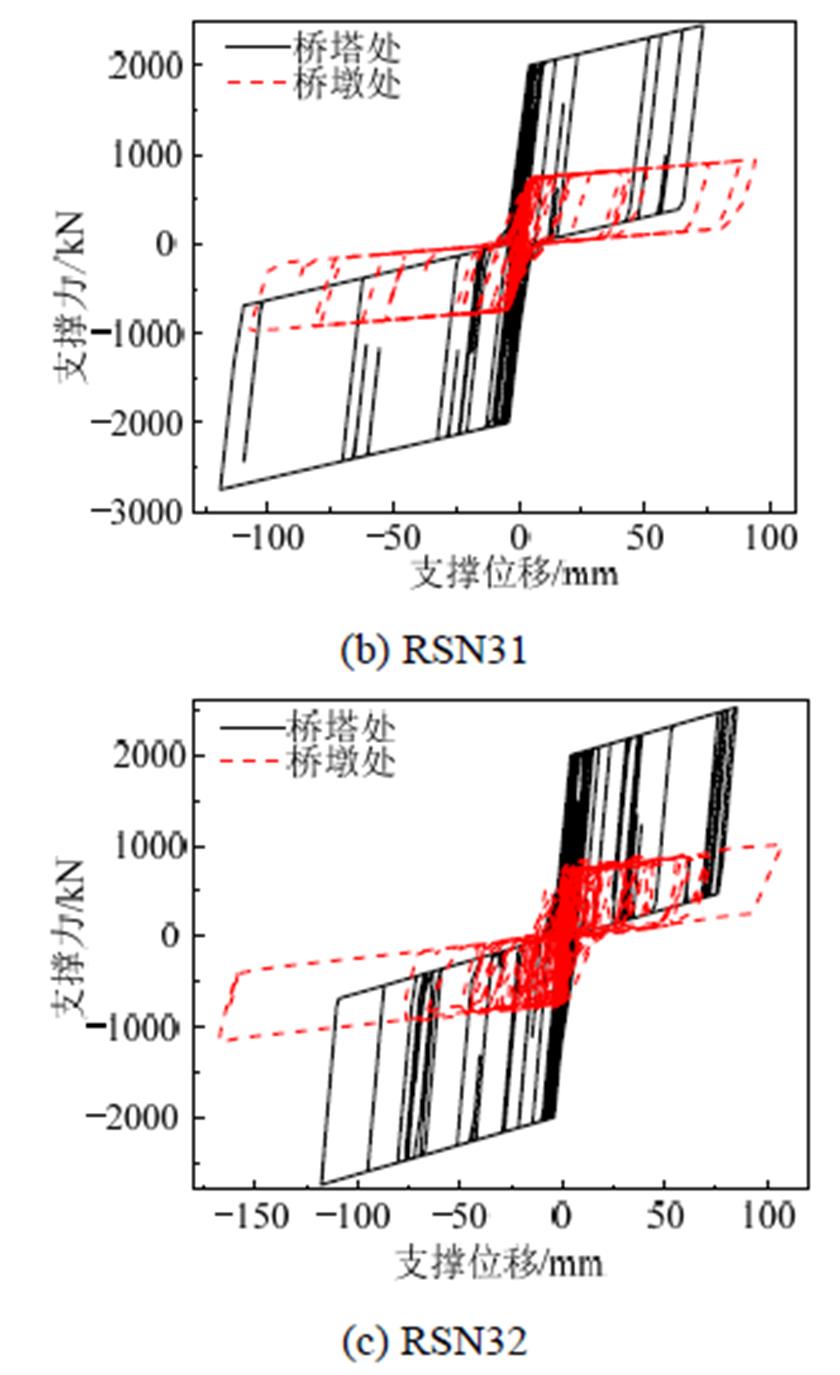
图15 不同地震波下墩塔处支撑滞回曲线
Fig.15 Hysteretic curve of the brace on the pier and tower under different earthquakes
为进一步比较PS-SCED支撑在地震作用下耗散能量大小,图16给出了两种体系能量时程曲线。从图中可以看出,由于地震波不同,地震输入能也不相同;支撑体系中,阻尼耗能约占地震输入能35%,结构滞回耗能约占25%,支撑耗能约占40%,支撑消耗了相当大的地震能量,且支撑体系的结构滞回耗能相对于固结体系减小了约65%,有效降低了结构损伤程度,对斜拉桥起到很好的保护 作用。
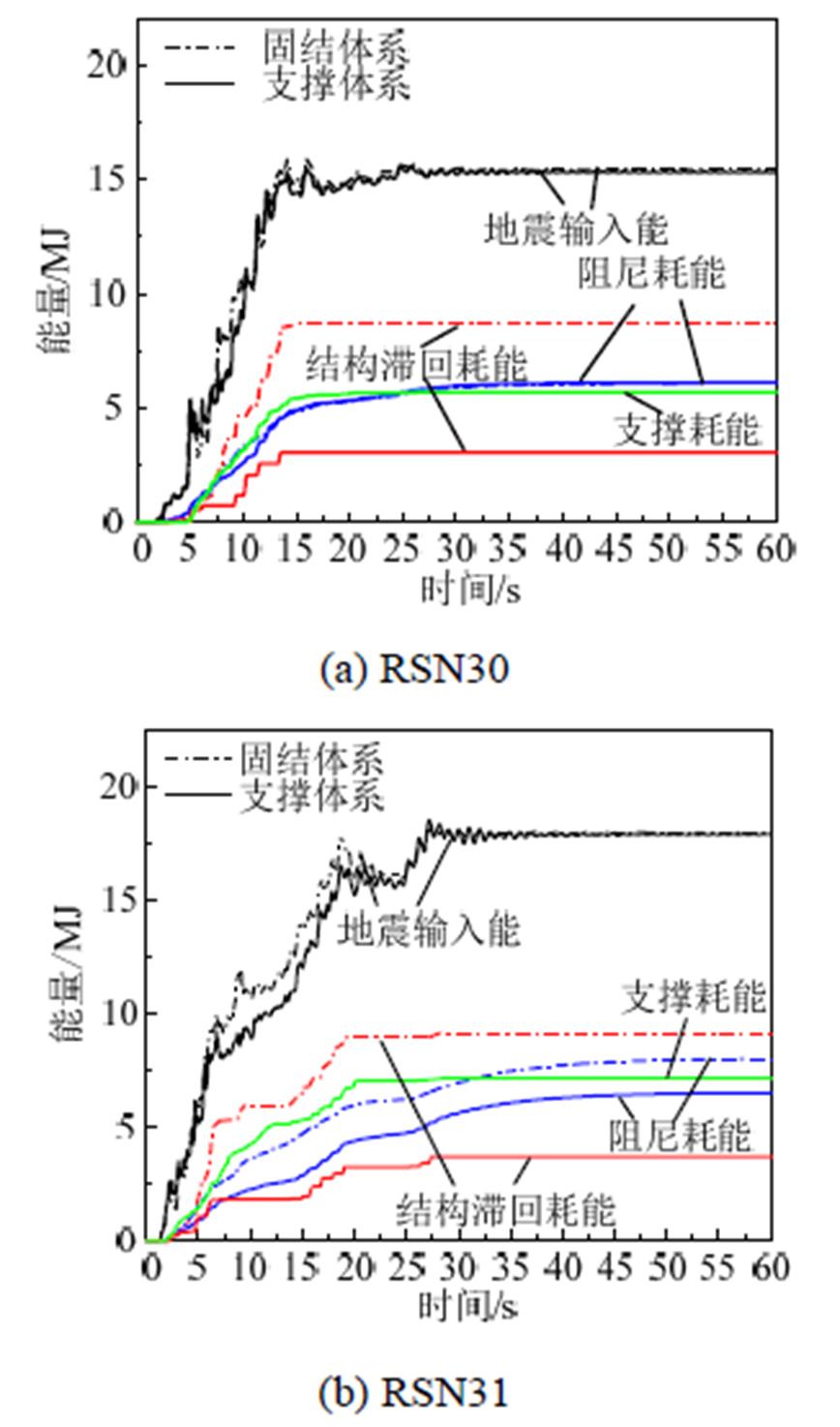
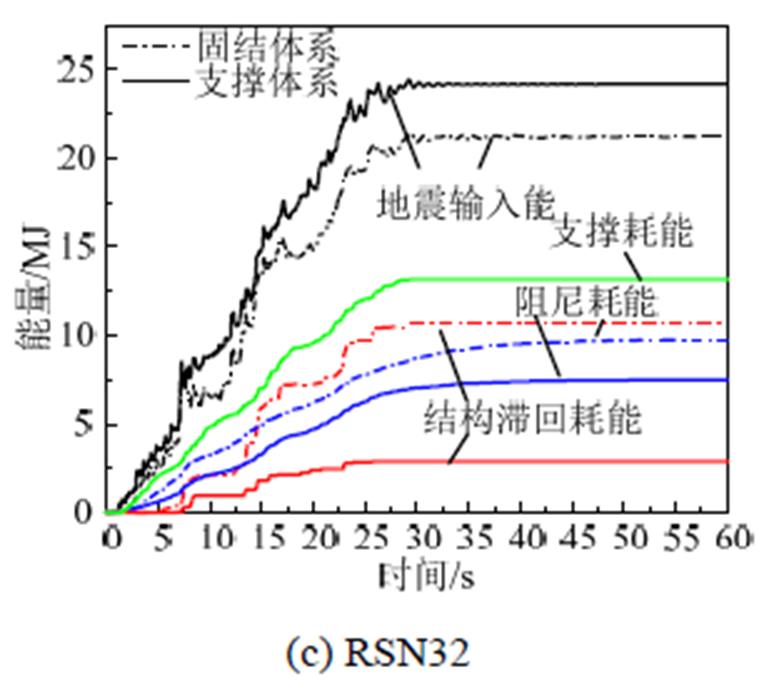
图16 不同地震波下两种体系能量时程曲线
Fig.16 Energy time history curve of the two systems under different earthquakes
本文提出一种设置PS-SCED支撑的斜拉桥横向减震体系及支撑参数设计方法,结合一斜拉桥实例,对支撑参数设计方法的合理性进行验证。通过对比两种体系斜拉桥的地震响应,得到以下结论:
(1) PS-SCED支撑简化分析模型能较好反映实际支撑受力及耗能情况,可采用该简化模型对支撑结构进行分析;
(2) PS-SCED支撑有较好的复位效果,在桥塔处主梁残余位移较固结体系减小了63%以上,且支撑体系相对于固结体系塔底墩底剪力弯矩都有所减小,在桥墩处弯矩控制效果优于桥塔处,附加PS-SCED支撑能有效实现斜拉桥下部结构内力与主梁位移平衡统一;
(3) PS-SCED支撑能够有效减小地震作用下斜拉桥桥塔塔身横向位移,对塔身钢筋混凝土应变有较好的控制效果,减小了塔底塑性损伤程度,改善了塔身弯矩剪力,对桥塔起到较好的保护作用;
(4) 斜拉桥横桥向采用PS-SCED支撑的减震体系通过支撑耗散了约40%的地震能量,且支撑体系的结构滞回耗能相对于固结体系减小了约65%,可以有效降低斜拉桥损伤程度。
参考文献:
[1] 聂利英, 郭其远, 李建中. 设置纵向大型液体粘滞阻尼器的大跨斜拉桥主梁纵向运动阻尼水平研究[J]. 工程力学, 2015, 32(9): 141-148. Nie Liying, Guo Qiyuan, Li Jianzhong. Longitudinal damping level of girder motion of long-span cable stayed bridge with large longitudinal fluid viscous dampers [J]. Engineering Mechanics, 2015, 32(9): 141-148. (in Chinese)
[2] Sharabash A M, Andrawes B O. Application of shape memory alloy dampers in the seismic control of cable-stayed bridges [J]. Engineering Structures, 2009, 31(2): 607-616.
[3] 徐艳, 王瑞龙, 李建中, 等. 弹塑性钢阻尼器对中等跨径斜拉桥横桥向减震效果的振动台试验研究[J]. 工程力学, 2016, 33(8): 101-109. Xu Yan, Wang Ruilong, Li Jianzhong, et al. Shaking table test of transverse seismic response reduction of medium-span cable-stayed bridges using yielding steel dampers [J]. Engineering Mechanics, 2016, 33(8): 101-109. (in Chinese)
[4] Astiz M A, Camara A. Analysis and control of cable-stayed bridges subject to seismic action [J]. Structural Engineering International, 2014, 24(1): 27-36.
[5] Xu L H, Fan X W, Li Z X. Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace [J]. Engineering Structures, 2016, 127(15): 49-61.
[6] Xu L H, Fan X W, Li Z X. Cyclic behavior and failure mechanism of self-centering energy dissipation braces with pre-pressed combination disc springs [J]. Earthquake Engineering and Structural Dynamics, 2017, 46(7): 1065-1080.
[7] Xu L H, Fan X W, Lu D C, et al. Hysteretic behavior studies of self-centering energy dissipation bracing system [J]. Steel and Composite Structures, 2016, 20(6): 1205-1219.
[8] 徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016, 33(10): 116-122. Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al. Study on restoring force model and hysterstic behaviors of pre-pressed spring self-centering energy dissipation brace [J]. Engineering Mechanics, 2016, 33(10): 116-122. (in Chinese)
[9] 徐龙河, 代长顺, 樊晓伟, 等. 预压弹簧自恢复耗能支撑子结构抗震性能研究[J]. 建筑结构学报, 2017, 38(6): 155-162. Xu Longhe, Dai Changshun, Fan Xiaowei, et al. Seismic performance research on substructures with pre-pressed spring self-centering energy dissipation brace [J]. Journal of Building Structures, 2017, 38(6): 155-162. (in Chinese)
[10] Camara A, Cristantielli R, Astiz M A. Design of hysteretic dampers with optimal ductility for the transverse seismic control of cable-stayed bridges [J]. Earthquake Engineering and Structural Dynamics, 2017, 46(4): 1811-1833.
[11] Dwairi H M, Kowalsky M J, Nau J M. Equivalent damping in support of direct displacement-based design [J]. Journal of Earthquake Engineering, 2007, 11(4): 512-530.
[12] 张宝胜, 布占宇, 徐爱敏. 斜拉桥地震响应分析中比例阻尼参考振型的选取[J]. 中国公路学报, 2008, 21(6): 76-82. Zhang Baosheng, Bu Zhanyu, Xu Aimin. Reference vibration shape selection of proportional damping in seismic response analysis of cable-stayed bridge [J]. China Journal of Highway and Transport, 2008, 21(6): 76-82. (in Chinese)
[13] 薛瑞杰. 大跨径斜拉桥地震作用相关设计标准规范比较[D]. 上海: 同济大学, 2009. Xue Ruijie. Comparison of design standard Specifications for seismic behavior of long span cable-stayed bridges [D]. Shanghai: Tongji University, 2009. (in Chinese)
[14] Wilson J C, Gravelle W. Modelling of a cable-stayed bridge for dynamic analysis [J]. Earthquake Engineering and Structural Dynamics, 1991, 20(8): 707-721.
[15] JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. 北京: 人民交通出版社, 2008. JTG/T B02-01-2008, Guidelines for seismic design of highway bridges [S]. Beijing: China Communications Press, 2008. (in Chinese)
SEISMIC PERFORMANCE STUDY ALONG THE TRANSVERSE DIRECTION OF CABLE-STAYED BRIDGES WITH SELF-CENTERING ENERGY DISSIPATION BRACES
Abstract:To mitigate the seismic-induced responses of cable-stayed bridges in the transverse direction, a transverse seismic mitigation system of cable-stayed bridges with pre-pressed spring self-centering energy dissipation braces was proposed in this study. A parameter design method for the braces was developed. Taking a cable-stayed bridge as the study example, the brace parameters were designed and the time history analysis of the tower-beam fixed system and the seismic mitigation system with braces were carried out. The seismic performance of the braced systems was analyzed in terms of the seismic responses at key locations, the energy dissipation capabilities, etc. The results show that the seismic mitigation system of the cable-stayed bridge with pre-pressed spring self-centering energy dissipation braces in the transverse direction utilizes the good hysteretic energy dissipation characteristics of the braces to reduce the displacement and strain of the bridge tower, improve the force distribution of the bridge tower and reduce the residual displacement of the beam. Cable-stayed bridges with pre-pressed spring self-centering energy dissipation braces has good mitigation and control effects on the seismic responses, which is a prominent and promising seismic resistance system.
Key words: cable-stayed bridge; pre-pressed spring self-centering energy dissipation brace; seismic mitigation design; transverse direction; seismic performance
文章编号:1000-4750(2019)04-0177-11
中图分类号:TU352.1+1;U448.27
文献标志码:A
doi:10.6052/j.issn.1000-4750.2018.03.0107
收稿日期:2018-03-05;
修改日期:2018-06-27
基金项目:国家自然科学基金项目(51578058);北京市自然科学基金项目(8172038)